2.1. Pre-Pulse and Preformed Plasma

The plasma profile inside the cone was measured by X-ray pinhole images in 2009 experiments (Mima et al., Reference Mima, Sunahara, Shiraga, Nishimura, Azechi, Nakamura, Johzaki, Nagatomo, Garcia and Veralde2010). The time-integrated X-ray image shows a wide bright area at ~100 µm away from the cone tip. It means that the heating laser is absorbed far away from the cone tip even though it is focused at the center of the cone tip, and indicates that the inside of the cone is filled with preformed plasmas, which are generated by the pre-pulse. To estimate the pre-pulse level, we compared STAR-2D simulation results with experimental data for planar targets (Sunahara et al., Reference Sunahara, Johzaki, Nagatomo and Mima2011). When the laser intensity in the simulation is 10¹³ W/cm², the density scale length of the preformed plasma is measured as 100 µm and the blow off speed of ablated plasmas as 1 × 10⁷ cm/s at 1 ns. These values are in good agreement with experimental observations, and we can conclude that the cone is illuminated by the pre-pulse of the heating laser with 10¹³ W/cm² intensity and 1 ns duration before it is irradiated by the main pulse. The corresponding pre-pulse energy is estimated to be 130 mJ. For the next step, we also simulated the pre-plasma formation inside the cone with STAR-2D (Sunahara et al., Reference Sunahara, Johzaki, Nagatomo and Mima2011). The temporal profile of the laser is flattop with 1 ns duration, and the wavelength and the spot diameter are set to 1.06 µm and 40 µm (Gaussian FWHM), respectively. The tip diameter of the cone is 30 µm. Preformed plasma profiles are shown in Figure 1 for different intensities (1 × 10¹¹, 1 × 10¹², and 1 × 10¹³ W/cm²) and different open angles (30°, 45°, and 60°) after 1 ns irradiation. For the pre-pulse intensity estimated above (10¹³ W/cm²) and the open angle in 2009 experiments (30° or 45°), the preformed plasma expands to the inner space of the cone up to 300 µm away from the cone tip. As the cone with the larger open angle has the larger volume to be filled, the density scale length of the preformed plasma is reduced when the open angle of the cone increases. While the critical density (n _cr = 10²¹ cm⁻³ for 1.06 µm laser) point is still close to the cone tip, underdense plasmas with long-scale length exist inside the cone and the main pulse of the heating laser must interact with these plasmas.

Fig. 1. (Color online) Preformed plasma profiles for different intensities of the pre-pulse (1 × 10¹¹, 1 × 10¹² or 1 × 10¹³ W/cm²) and different open angles of the cone (30°, 45°, or 60°) after 1 ns irradiation.

To evaluate preformed plasma effects inside the cone, we carried out ASCENT-2D simulations (Johzaki, et al., Reference Johzaki, Nagatomo, Sunahara, Cai, Sakagami, Nakao and Mima2011). The Au cone plasma (Z = 40, 100n _cr, 30° open angle, 12 µm tip inner width, 5 µm tip thickness and 8 µm side wall thickness) is surrounded by the imploded CD plasma (Z = 3.5 and 50n _cr). As the case without preformed plasmas, surface plasmas with the short scale length (1 µm) from 100n _cr to 0.1n _cr are introduced in front of the cone tip. According to preformed plasma parameters in Figure 1 simulated by STAR-2D, the scale length of plasmas ablated by the pre-pulse is very short in overdense region and relatively longer in underdense region. Thus, preformed plasmas with the scale length 10 µm are attached from 5n _cr point in addition to surface plasmas for the case with preformed plasmas. The cone is irradiated by the p-polarized main pulse of the heating laser with 1.06 µm wavelengths, 3 × 10¹⁹ W/cm² intensity and 16.5 µm spot diameter (Gaussian FWHM). The laser rises to its peak within 33 fs. Fast electron energy densities at 1 ps are shown in Figure 2 for both (a) without and (b) with preformed plasmas. For the case without preformed plasmas, the central part of the main pulse directly hits the tip of the cone, and the surrounding parts are reflected at the sidewall of the cone and headed to the tip. Thus, most of fast electrons are generated at the tip. On the other hand, fast electrons are mainly generated in the underdense preformed plasma region and their energy is much higher than that without the preformed plasma case.

Fig. 2. (Color online) Fast electron energy densities at 1 ps for (a) without and (b) with preformed plasmas. Energy density is normalized by m _e·c ²·n _cr, where m_e and c are electron rest mass and speed of light, respectively.

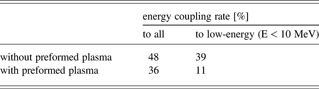
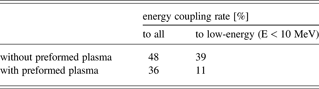
Energy coupling rates from the heating laser to all fast electrons or to low-energy (<10 MeV) fast electrons observed at the cone tip (15 µm width) are summarized in Table 1. The energy coupling rate is reduced in the case with preformed plasmas. This reduction, however, is much significant, namely about 1/4 for the case to low-energy fast electrons, which are more suitable for heating the core. In addition, fewer fast electrons can reach the core than those without preformed plasmas as the preformed plasma makes the distance from the generation point of fast electrons to the core longer. Therefore, coupling efficiency from the heating laser to the core is drastically degraded by the preformed plasma and it is indispensable to reduce the pre-pulse level as small as possible for efficient core heating. According to STAR-2D simulations, preformed plasmas are much localized around the cone tip when the pre-pulse intensity is 1 × 10¹¹ W/cm² (see Fig. 1), and we can expect very little effect of the preformed plasma. This means that we must reduce the pre-pulse level to about 1/100 compared with the current status.

Table 1. Energy coupling rates from laser to fast electrons

From an additional point of view, the Au cone tip causes the degradation of the energy coupling due to collisional and resistive drags during the transport of fast electrons in the cone tip. Therefore CH is proposed as an alternative material of the cone tip to reduce collisional defects and it is found that in comparison with the Au cone tip, a twice higher rise in temperature of the compressed CD core has been achieved with the CH cone tip (Johzaki et al., Reference Johzaki, Sentoku, Nagatomo, Sakagami, Nakao and Mima2009). The CH cone tip has another good feature that the preformed plasma would be smaller than that with the Au cone tip due to low-Z materiality. Thus, using the CH cone instead of the Au cone could also improve this severe problem to a certain extent, but it's beyond this paper.

2.2. Thin Film Absorber

An amplified optical parametric fluorescence quencher (Kondo et al., Reference Kondo, Maeda, Hama, Morita, Zoubir, Kodama, Tanaka, Kitagawa and Izawa2006) or a saturable absorber can be used to suppress the pre-pulse level. It is, however, still a technical challenge to maintain the pre-pulse intensity below 1 × 10¹¹ W/cm². The other method to mitigate the pre-pulse problem, the entrance of the cone is suggested to be covered with an extremely thin film. The pre-pulse could be interrupted and absorbed by this film, and the cone wall cannot be irradiated by the pre-pulse and long-scale preformed plasmas are not produced (Kinoshita et al., Reference Kinoshita, Zhidkov, Hosokai, Ohkubo and Uesaka2004; Mima et al., Reference Mima, Sunahara, Shiraga, Nishimura, Azechi, Nakamura, Johzaki, Nagatomo, Garcia and Veralde2010). Before the cone is irradiated by the main pulse, this film should be ionized by the pre-pulse and must diffuse to quite low density not to disturb the main pulse propagation. As the pulse duration of the pre-pulse is the order of nano second, plasmas are expected to expand much below the critical density.

To evaluate remnant plasmas of the thin film, we performed STAR-2D simulations (Sunahara et al., Reference Sunahara, Johzaki, Nagatomo and Mima2011). As the thin film is placed at the entrance of the cone 1 mm away from the cone tip, the irradiation intensity and the spot size are lower and larger than those at the focus point. So we assume the pre-pulse of 3 × 10¹¹ W/cm² intensity, 100 µm spot diameter (Gaussian FWHM) and flattop temporal profile. The thin film, which is made from CH and 0.1 µm thickness is irradiated by this pre-pulse. Contour plots of the electron density are shown in Figure 3 at (a) 1.2 ns and (b) 1.8 ns. The electron density and the thickness of plasmas within the spot diameter along the laser axis become below 1/10 of the critical density and about 500 µm at 1.2 ns, or 1/30 and 800 µm at 1.8 ns, respectively. Anyway, the main pulse must propagate through these very long rarefied plasmas.

Fig. 3. (Color online) Electron density contour plots for remnant plasmas of the thin film at (a) 1.2 ns and (b) 1.8 ns.

3.1. Fast Electron Characteristics

To investigate effects of the long rarefied plasma around the entrance of the cone on fast electron characteristics, laser-plasma interactions are computed by FISCOF-1D using a time step of 5 × 10⁻³ fs, a resolution of 250 cells per laser wavelength, up to 200 particles per cell for electrons or ions. The heating laser is set to I _L = 10²⁰ W/cm², λ_L = 1.06 µm, τ_FWHM = 1 ps Gaussian, and the Au (A = 197, Z = 30) cone tip is introduced as a 10 µm, 500n _cr flat profile plasma, which is followed by 20 µm long CD (500n _cr, A = 7, Z = 3.5) plasma. We put the CH foam plasma (10n _cr, A = 6.5, Z = 3.5) with 50 µm thickness in front of the Au cone tip plasma to efficiently generate fast electrons (Sakagami et al., Reference Sakagami, Johzaki, Nagatomo and Mima2009). We also put the H uniform plasma (A = 1, Z = 1, L _rare = 150 or 300 µm thickness) with different densities (n _rare = 0.01n _cr ~ n _cr) in front of the CH foam plasma as the long rarefied plasma. The proton-electron mass ratio is set to1836, and initial temperatures of electrons and ions in all plasmas are set to 10 and 0.3 keV, respectively. A fast electron beam is observed in CD plasma, 10 µm behind the Au-CD boundary. To ignore a circulation of fast electrons that are reflected by the sheath field at the right edge of the CD plasma, we introduce an artificial cooling region (7 µm long) at the rear of CD plasma, in which fast electrons are gradually cooled down to the initial temperature.

Time evolutions of fast electron beam intensity are shown in Figure 4 without rarefied plasmas and with rarefied plasmas of different densities (0.01, 0.05, 0.1, 0.5, and 1n _cr) for (a) L _rare = 150 and (b) 300 µm. As the intensity of the heating laser is 10²⁰ W/cm², the fast electron beam intensity of 10¹⁹ W/cm² means that the instantaneous energy coupling rate from the laser to fast electrons is 10%. Fast electron beam intensities are similar to those in the case without rarefied plasmas for n _rare < 0.1n _cr with L _rare = 150 µm and n _rare = 0.01n _cr with L _rare = 300 µm. On the other hand, fast electron beam intensities become larger than that without rarefied plasmas due to the large energy coupling rate from the laser to electrons for n _rare > 0.5n _cr with L _rare = 150 µm and n _rare > 0.05n _cr with L _rare = 300 µm. When the laser propagates through the plasma, a group velocity of light becomes slower as the density increases. So the leading edge of the fast electron beam delays more with the larger density of the rarefied plasma in the case of n _rare > 0.5n _cr with L _rare = 150 µm. The rarefied plasma with L _rare = 300 µm enhances this delay much more. Total fast electron fluences, which are calculated by time-integrating fast electron beam intensities, are shown in Figure 5 as a function of ρL n _cr·μm for both L _rare = 150 and 300 µm, where ρ and L are the rarefied plasma density and thickness, respectively. In the case without rarefied plasmas (ρL = 0), fast electrons are mainly generated by interactions between the heating laser and the CH foam plasma, and the total fast electron fluence of about 2.4 × 10⁷ J/cm² is obtained. If the rarefied plasma exists, the laser is absorbed within underdense plasmas and generates very energetic fast electrons. Thus, energy increment of fast electrons is roughly proportional to ρL due to absorption increment up to ρL = 150 n _cr·μm. When ρL is 300 n _cr·μm, the energy increment tends to saturate because the laser intensity decreases before reaching the CH foam plasma due to large absorption. So less fast electrons are generated by interactions between the heating laser and the CH foam plasma.

Fig. 4. (Color online) Time evolutions of fast electron beam intensity without rarefied plasmas (purple) and with rarefied plasmas of different densities, 0.01(green), 0.05(red), 0.1(blue), 0.5(yellow), and 1(gray) n _cr for (a) L _rare=150 and (b) 300 µm.

Fig. 5. (Color online) Total fast electron fluences as a function of ρL n _cr·μm for both L _rare = 150(blue) and 300(red) μm.

Time averaged fast electron energy distributions are shown in Figure 6 without rarefied plasmas and with rarefied plasmas of different densities (0.01, 0.05, 0.1, 0.5, and 1n _cr) for (a) L _rare = 150 and (b) 300 µm with wide energy range, and (c) L _rare = 150, and (d) 300 µm with narrow energy range. When the density of the rarefied plasma is less than 0.1n _cr for L _rare = 150 µm or 0.05n _cr for 300 µm, fast electron energy distributions are almost same as those in the case without rarefied plasmas. If the density is greater than 0.5n _cr for L _rare = 150 µm or 0.1n _cr for 300 µm, more laser energy is absorbed by the underdense rarefied plasma, and fast electrons with energies above 3 MeV are generated much more. They mainly contribute enhancement of the fast electron beam intensity (see Fig. 4), however, and these energetic fast electrons are not suitable for core heating at all. Fast electrons with energies less than 2 MeV are strongly reduced in the case of n _rare = n _cr and L _rare = 300 µm, because the heating laser is exhausted by the long rarefied plasma prior to reach the CH foam plasma and it can not generate many fast electrons with moderated energy from the CH foam plasma.

Fig. 6. (Color online) Time averaged fast electron energy distributions without rarefied plasmas and with rarefied plasmas of different densities (0.01, 0.05, 0.1, 0.5, and 1n _cr) for (a) L _rare = 150 and (b) 300 µm with wide energy range, and (c) L _rare = 150 and (d) 300 µm with narrow energy range. Line colors of purple, green, red, blue, yellow and gray indicate 0 (without rarefied plasma), 0.01, 0.05, 0.1, 0.5, and 1n _cr, respectively.

3.2. Integrated Simulations for Core Heating

As core heating is greatly affected by not only the beam intensity but also the energy distribution of fast electrons, we have performed FI³ integrated simulations to estimate core temperatures, assuming the same core parameters as in Johzaki et al. (Reference Johzaki, Sakagami, Nagatomo and Mima2007). Observed fast electron profiles by FISCOF-1D in the previous section are used as the time-dependent momentum distributions of fast electrons for FIBMET-1D. Time evolutions of averaged core electron temperature computed by FIBMET-1D, which are averaged over the dense region (ρ > 10 g/cm³), are shown in Figure 7 without rarefied plasmas and with rarefied plasmas of different densities (0.01, 0.05, 0.1, 0.5, and 1n _cr) for (a) L _rare = 150 and (b) 300 µm. Maximum averaged core electron temperature is measured from Figure 7, and the increment from the initial temperature is calculated. Degradations of electron temperature increment against the case without rarefied plasmas are shown in Figure 8 as a function of ρL n _cr·μm for both L _rare = 150 and 300 µm. In the case of 150 µm thickness rarefied plasma, fast electrons that are suitable for core heating (< 2 MeV) are not affected so much by the rarefied plasma (see Fig. 6c), and time evolutions are similar to the case without rarefied plasmas. Thus, the maximum core electron temperature is only reduced by 15% even for the n _rare = n _cr case. The electron temperature increment of the n _rare = n _cr and 300 µm thickness case is, however, strongly reduced and the degradation reaches 50% because of much less appropriate fast electrons for core heating. (see Fig. 6d) If the degradation of less than 10% is acceptable for the fast ignition, ρL of the rarefied plasma must be smaller than 50 n _cr·μm. On the other hand, too small ρL plasma cannot absorb the pre-pulse and it hits the cone wall to generate long-scale preformed plasmas. Therefore, we must optimize the film thickness against the pre-pulse intensity and more researches are needed.

Fig. 7. (Color online) Time evolutions of averaged core electron temperature over the dense region (ρ > 10 g/cm³) without rarefied plasmas (purple) and with rarefied plasmas of different densities, 0.01(green), 0.05(red), 0.1(blue), 0.5(yellow), and 1(gray) n _cr for (a) L _rare = 150 and (b) 300 µm.

Fig. 8. (Color online) Degradations of electron temperature increment against the case without rarefied plasmas as a function of ρL n _cr·μm for both L _rare = 150(blue) and 300(red) μm.