INTRODUCTION
The recent rapid advances in ultra-intense short pulse lasers and their numerous applications stimulated the research activities in this field such as generation of high energy electron and ion beams and their acceleration (Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Mangles et al., Reference Mangles, Walton, Najmudin, Dangor, Krushelnick, Malka, Manclossi, Lopes, Carias, Mendes and Dorchies2006; Chyla, Reference Chyla2006; Bessonov et al., Reference Bessonov, Gorbunkov, Ishkhanov, Kostryukov, Maslova, Shvedunov, Tunkin and Vinogradov2008; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Habibi and Yazdani2010sc, Reference Sadighi-Bonabi and Moshkelgosha2011) mono-energetic electron beam (Glinec et al., Reference Glinec, Faure, Pukhov, Kiselev, Gordienko, Mercier and Malka2005; Zobdeh et al., Reference Zobdeh, Sadighi-Bonabi and Afarideh2008; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Navid and Zobdeh2009a; Reference Sadighi-Bonabi, Rahmatallahpor, Navid, Lotfi, Zobdeh, Reiazi, Nik and Mohamadian2009b; Reference Sadighi-Bonabia and Rahmatollahpur2010a; Reference Sadighi-Bonabi and Rahmatollahpur2010b), mono-energetic ion beam generation (Badziak, Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005), X-ray emission (Nikzad et al., Reference Nikzad, Sadighi-Bonabi, Riazi, Mohammadi and Heydarian2012), high harmonic generation, and X-ray lasers (L'Huillier et al., Reference L’huillier and Balcou1993). Among all possible applications of laser, produced X-rays are useful for inertial confinement fusion (ICF) (Keith Matzen et al., Reference Keith Matzen, Sweeney, Adams, Asay, Bailey, Bennett, Bliss, Bloomquist, Brunner, Campbell, Chandler, Coverdale, Cuneo, Davis, Deeney, Desjarlais, Donovan, Garasi, Haill, Hall, Hanson, Hurst, Jones, Knudson, Leeper, Lemke, Mazarakis, Mcdaniel, Mehlhorn, Nash, Olson, Porter, Rambo, Rosenthal, Rochau, Ruggles, Ruiz, Sanford, Seamen, Sinars, Slutz, Smith, Struve, Stygar, Vesey, Weinbrecht, Wenger and Yu2005; Yazdani et al., Reference Yazdani, Cang, Sadighi-Bonabi, Hora and Osman2009; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Hora, Riazi, Yazdani and Sadighi2010d), which is the most challenging problem. In these systems, X-rays are employed not only to diagnose the physical properties of the plasma, but also to reach the ignition conditions. Recently, interaction of intense lasers with over-dense plasma and the reflection of laser pulse from the over-dense plasma electrons is introduced as one of most powerful and efficient method of high harmonic x-ray generation (Thaury et al., Reference Thaury, Quéré, Geindre, Levy, Ceccotti, Monot, Bougeard, Réau, D'oliveira, Audebert, Marjoribanks and Martin2007).
In the process of obtaining intense extreme ultra-violet and soft X-ray emission by means of high order harmonics generation, in 1981, the first experimental work is reported by means of mid-infrared nanosecond CO2 laser pulses in the interaction with confined plasma (Carman et al., Reference Carman, Rhodes and Benjamin1981). More than 10 years later the dream of reaching the higher and more efficient harmonics become transparent by means of implying the femtosecond multi-terawatt power laser pulses (Wille et al., Reference Wille, Rodriguez, Kasparian, Mondelain, Yu, Mysyrowicz, Sauerbrey, Wolf and Wöste2002). The comprehensive theoretical investigation of generating high harmonics by ultra-fast intense laser pulse interacting with over-dense plasma was proposed by Bulanov et al. (Reference Bulanov, Naumova and Pegoraro1994). Later, the concept of these nonlinear phenomena has been developed by means of the ROM model in the interaction of intense laser pulses with a step boundary of plane over-dense plasma (Lichters et al., Reference Lichters, Meyer-Ter-Vehn and Pukhov1996). The cornerstone of this model was the Doppler shift of the incident pulse due to the relativistic oscillating surface of the plasma. Since then, other experimental and theoretical studies have been reported on the relativistic oscillating mirror (ROM) model (Roso et al., Reference Roso, Plaja, Rzazewski and Von Der Linde2000; Gordienko et al., Reference Gordienko, Pukhov, Shorokhov and Baeva2004; Tsakiris et al., Reference Tsakiris, Eidmann, Meyer-Ter-Vehn and Krausz2006).
In 2006, a fresh look at the high order harmonic generation with intense laser-plasma interaction is presented by Baeva et al. (Reference Baeva, Gordienko and Pukhov2006), which is named after them as BGP theory. In this model, the high harmonic generation is based on sharp spikes in the relativistic γ-factor of the plasma surface electrons. This is due to eliminating of the tangential momentum component of the plasma surface electrons and subsequently the normal component of the electrons velocity approaches the speed of light in vacuum (c) (Pukhov et al., Reference Pukhov, Baeva and An Der Brügge2009a). This model leads to the universal spectrum of in-phase harmonics. Using a proper frequency filtering a coherent attosecond (1 as =10−18 s) (Corkum et al., Reference Corkum and Krausz2007) and even sub-attosecond X-ray pulse trains (Pukhov et al., Reference Pukhov, Baeva, An Der Brügge and Münster2009b) can be extracted from the reflected radiation.
In 2010, a new model for relativistic harmonics generation for the interaction of extremely intense laser pulse with overdense plasma surface has been introduced by an der Brügge and Pukhov (Reference An Der Brügge and Pukhov2010). By using the PIC simulation they could introduce a certain relation between parameters of incoming laser and plasma slab, which yields different results from the preceding recognized theories. The exciting distinction of this model is that electron density distribution at the moment of the radiation generation experiences a very narrow δ-like peak that manifests the formation of electron nano-bunches in front of the plasma surface. In this model, they have investigated the high relativistic nonlinearity of the surface electrons and the sensitivity of nano-bunch generation to the parametric changes of laser and the produced plasma during the interaction with target. In nano-bunching regime, this mobile extremely compressed electron bunches can emit intense coherent synchrotron emission (CSE) as the attosecond X-ray pulses. The most important characteristic of this novel regime is the high efficiency of the generated attosecond pulse in comparison with the predictions of earlier BGP model. Although very interesting results are obtained by considering some aspects of the incident laser pulse in this fruitful model, however, many other aspects of this effect was not presented. Considering the effects of polarization on electron distribution clarify the significant effects of laser polarization on nano-bunch generation and has not presented yet. Substantial difference between the nano-bunches which are generated in different polarization is observed in this study and the reasons of these differences are clarified based on the effect of ponderomotive force and electron velocities in relativistic regime.
In the present work, the BGP theory and the nano-bunching regime are discussed and compared with each other. Then the role of different polarized incident laser pulses in nano-bunching regime for the formation of the ultrathin and dense electron bunches analytically and numerically presented.
THE MODELS
As an introduction to the models of high harmonic generation by intense laser and overdense plasma, one can start from the classical one-dimensional (1D) wave equation of tangential vector potential A and current density in vacuum j(t,x) for obtaining the boundary conditions of the model in Coulomb gauge (∇.A = 0) (Jackson, Reference Jackson1999):
$$\displaystyle{{\partial ^2 {\bf A}\lpar t\comma \; x\rpar } \over {\partial ^2 x}} - \displaystyle{1 \over {c^2 }}\displaystyle{{\partial ^2 {\bf A}\lpar t\comma \; x\rpar } \over {\partial ^2 t}} = - \displaystyle{{4{\rm \pi} } \over c}{\bf j}\lpar t\comma \; x\rpar.$$
By using the Green function solution, consideration of the boundary condition 
$\vert {\bf A}\lpar t\comma \; -\! \infty \rpar \vert \to 0$ and with the uses of retarded time for the electric field in the totally reflecting regime, one can drive 
${\bf E} = \displaystyle{{ - 1} \over c}\displaystyle{{\partial {\bf A}} \over {\partial t}} = {\bf E}_i \lpar t - x/c\rpar + {\bf E}_r \lpar t + x/c\rpar $ and achieve the reflected electric field:
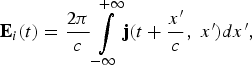$${\bf E}_i \lpar t\rpar = \displaystyle{{2{\rm \pi} } \over c}\int\limits_{ - \infty }^{ + \infty } {\bf j} \lpar t + \displaystyle{{x^{\prime}} \over c}\comma \; x^{\prime}\rpar dx^{\prime}\comma \;$$
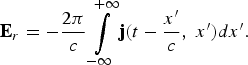$${\bf E}_r = - \displaystyle{{2{\rm \pi} } \over c}\int\limits_{ - \infty }^{ + \infty } {{\bf j}\lpar t - \displaystyle{{x^{\prime}} \over c}\comma \; x^{\prime}\rpar } dx^{\prime}.$$Based on these equations and by using the incident laser electric field Ei(t) the current density of plasma surface j(t + x/c,x) can be calculated and consequently, the reflected field Er(t) is obtained. In the BGP model, the normal incident of intense laser pulse in the range of 1018–1020 Wcm−2 onto the over-dense step-like boundary plasma is reflected at the points attached to the oscillating plasma surface so called the apparent reflection point (ARP) (Baeva et al., Reference Baeva, Gordienko and Pukhov2006). Regarding the property of the apparent point, due to destructive interference of the tangential components of the electric field, the boundary condition for this point at the moment of γ-spikes creation can be reached (Baeva et al., Reference Baeva, Gordienko and Pukhov2006):
$$E_i^t \lpar x_{{\rm ARP}} + ct\rpar + E_r^t \lpar x_{{\rm ARP}} - ct\rpar = 0.$$The ARP boundary condition Eq. (4) indicates that the magnitude of the reflected electric field is the same as the incident one. The boundary equation is approximately satisfied by this model.
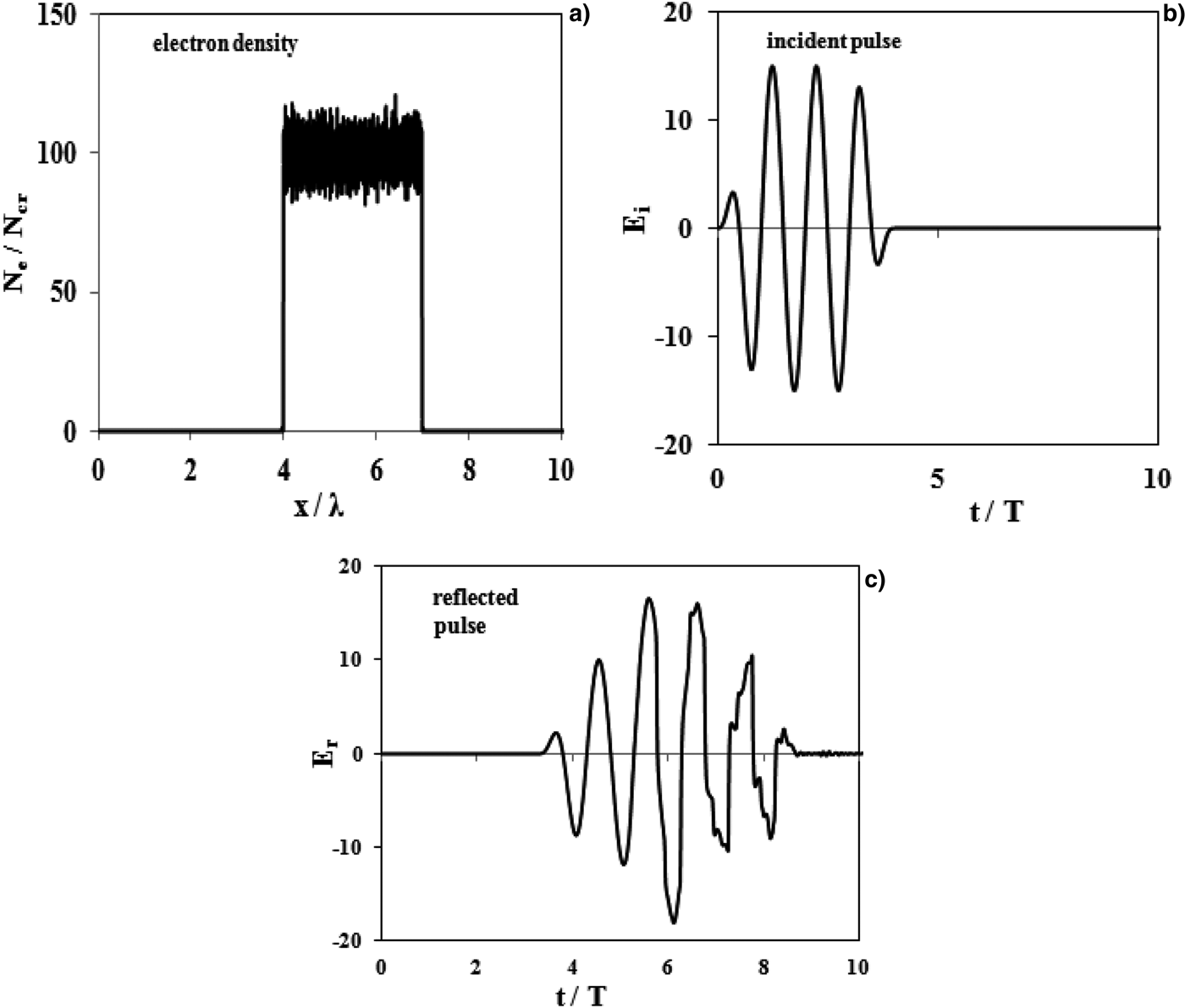
In Figure 1 the validity of this theory is checked by numerical 1D PIC simulation for four-cycle intense Ti: Sapphire laser at λ = 0.8 µm emitting onto the over-dense step-like plasma layer. The incident pulse supposed to be P-polarized with the intensity of 1019 Wcm−2 which corresponds to the normalized intensity parameter of 
$a = \sqrt {I_L {\rm \lambda} ^2 _L /\lpar 1.37 \times 10^{18} {\rm W}{\rm .{\rm \mu} m}^{\rm 2} {\rm .cm}^{{\rm - 2}} {\rm \rpar }} = 15$ and the initial electron density of plasma is regarded as N e= 95N cr. N cr = m e ωL2/4πe 2 is the critical density of the plasma with m e, e and ωL are the electron mass and charge and incident laser angular frequency, respectively. Figure 1a indicates that the incident laser light pressure generates electron density fluctuations on the plasma slab around the initial electron density N e= 95N cr. As one can see, there is not any considerable peak of electron density distribution on the plasma surface at x = 4λ through 7λ. Figures 1b and 1c show the electric fields of the incident and reflected pulse, respectively. The obtained results show the conformity with Eq. (4), which indicates that the magnitude of the reflected electric field is so close to the incident electric field. The perturbations at the tail of the reflected pulse are the source of the high harmonics generation which can be extracted by Fourier transform.
Fig. 1. Simulation results for interaction of intense laser with step-like overdense hydrogen plasma in BGP regime. (a) Electron density distribution at t = 6.56T where T is the incident pulse cycle. The electric field of incident pulse and the reflected pulse is shown in (b) and (c), respectively. The laser and plasma parameters regarded as a = 15, N e95N cr, P-polarized and normal incidence pulse.
BGP theory is valid for normal incident pulses of moderate intensity interacting with step-like plasma profile but the interaction with extremely intense oblique and ramped plasma cannot be studied by this approach. The model of totally reflecting oscillating mirror is a suitable regime and it does not have the limitations of BGP model for ultra-intense incident laser pulses or for plasma with variable densities. In this regime, the coherent synchrotron emission at the reflected pulse and the universal harmonics generation frequencies can be obtained (an der Brügge et al., Reference An Der Brügge2010). This radiation are generated by a thin bunch of electrons that perfectly localized on the surface as an infinitely narrow layer and accelerate simultaneously in front of the plasma. Accordingly, the electron current density is supposed as:
$$\,j\lpar x^{\prime}\comma \; t\rpar = \tilde j\lpar t\rpar \; f\lpar x^{\prime} - x_{el} \lpar t\rpar \rpar$$
where 
$\tilde j\lpar t\rpar $ is time dependent current density, x el(t) is the electron position on the surface, and f (x) is the function of localized electron position. As the f (x) reaches the Dirac delta function, more coherency of the reflected pulses will be obtained and generation of single attosecond pulses with maximum efficiency becomes possible (Pukhov et al., Reference Pukhov, An Der Brügge and Kostyukov2010).
The attosecond pulse generation from electron nano-bunches is verified experimentally (Dromey et al., Reference Dromey, Rykovanov, Yeung, Hörlein, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Ruhl, Fernandez, Lewis, Zepf and Hegelich2012). As represented earlier by regarding the current density of Eq. (5) into Eqs. (2) and Eq. (3) the reflected field can be obtained as (an der Brügge, Reference An Der Brügge2010):
$$E_r \lpar t + \displaystyle{{x_{{\rm TROM}} \lpar t\rpar } \over c}\rpar + \displaystyle{{1 - \dot x_{{\rm TROM}} /c} \over {1 + \dot x_{{\rm TROM}} /c}}E_r \lpar t - \displaystyle{{x_{{\rm TROM}} \lpar t\rpar } \over c}\rpar = 0.$$
Evidently, the boundary condition of the nano-bunching regime is different from the BGP model (Eq. (4)) and the reflected field is amplified relative to the incident field by a positive coefficient as the bunch propagate towards the observer (
$\dot x_{{\rm TROM}} \lt 0$). Therefore, the efficient intense single attosecond pulses in the reflected beam can be produced.
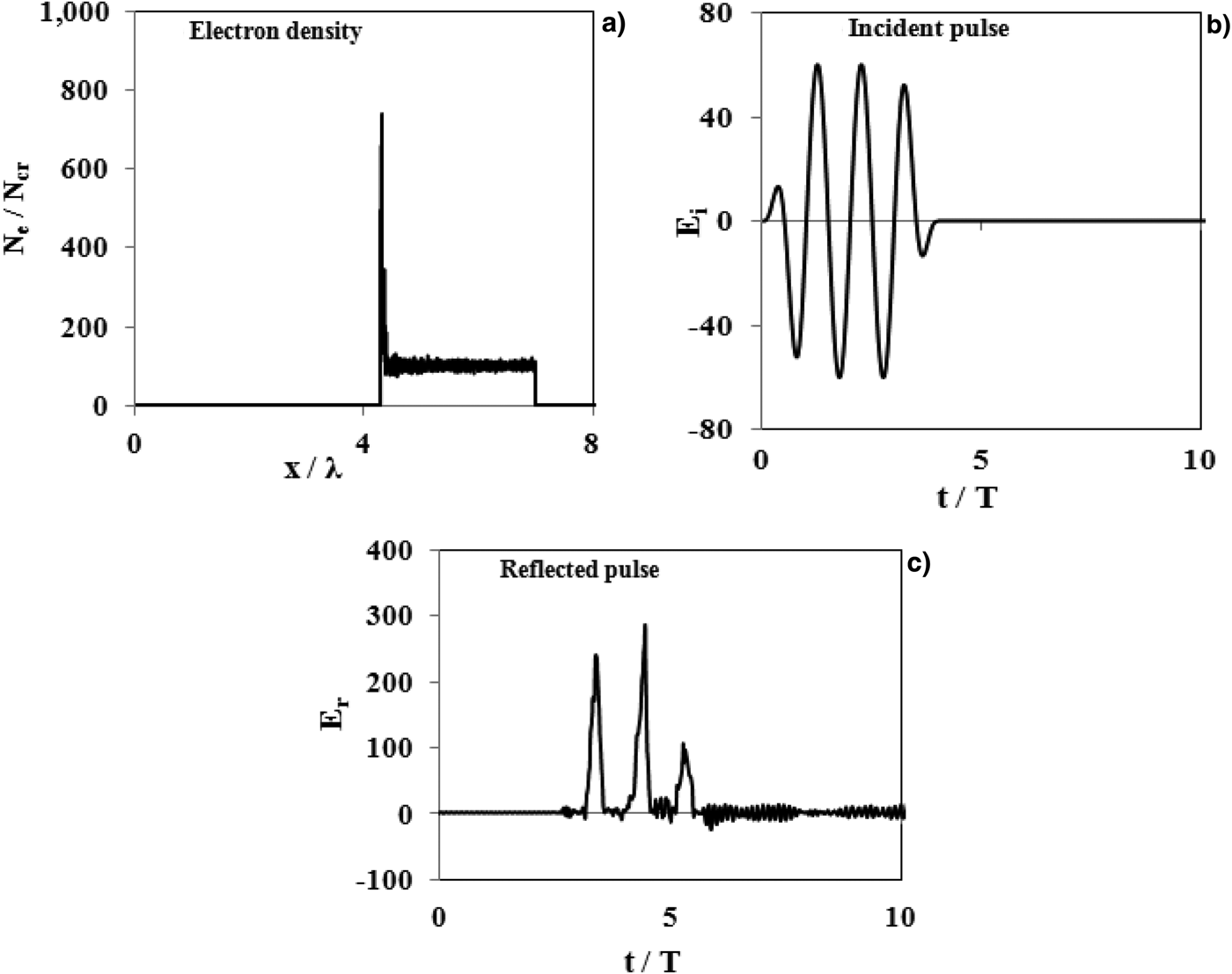
Figure 2 shows the result of PIC simulation for the electron density distribution and the reflected pulse of laser in the condition that leads to nano-bunching regime. The laser and plasma parameters in order to reach the recent regime are regarded as a = 55, N e = 100N cr and the linear pre-plasma of n e = 100n crx / L with L= 0.33λ from x = 4λ to x = 4.33λ. As one can see in spite of the homogenous distribution of electron density in BGP conditions, evident Delta shape peaks in the electron density distribution is performed and the formation of compressed electron nano-bunches is produced at the plasma surface. This localized distribution of electron density is the source of reflected electric field in Figure 2c and eventually coherent synchronizes emission and generation of isolated attosecond pulses without frequency filtering.
Fig. 2. The results for interaction of intense laser with pre-plasma ramp n e = 100n crx/L with L = 0.33λ) in nano-bunching regime. (a) Electron density distribution at t = 5.43T, (b) the electric field of incident pulse, and (c) the reflected pulse. The laser and plasma parameters regarded as a = 55, N e= 100N cr, P-polarized and oblique incidence at angle θ = 60o.
In the following section, the effect of incident pulse polarization on the electron density distribution, nano-bunches properties and the velocity of the plasma surface electrons is discussed for ROM model and nano-bunching regime.
RESULTS AND DISCUSSION
Generation of such extreme nano-bunching is highly sensitive to changes in various plasma and laser pulse parameters including the plasma density profile, laser intensity, duration, angle of incidence, and even the carrier envelope phase of the laser and it is does not easily occur in any initial laser and plasma conditions and an optimum condition is required (an der Brügge & Pukhov, Reference An Der Brügge and Pukhov2010). In this work, it is found that another important parameter which affects the process is the polarization of the incident laser pulse. In the following, the role of polarization as one of the important parameter of the incident pulse on electron density distribution is presented.
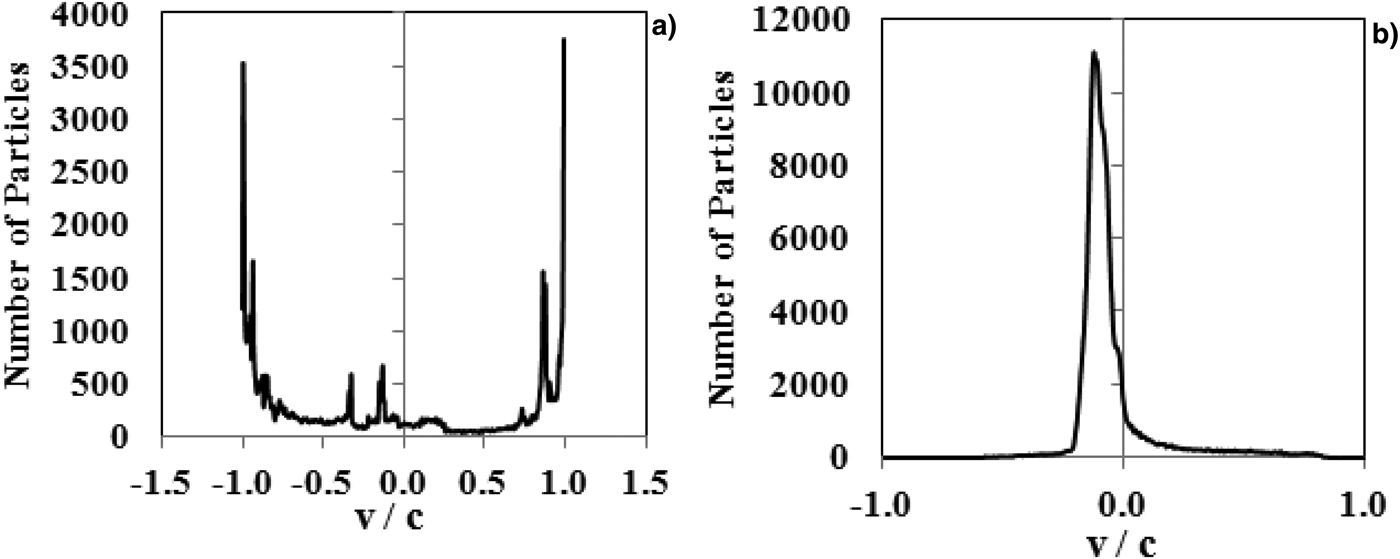
Extremely intense laser pulse is driven the plasma surface results to high speed electrons close to the speed of light in BGP model. However, in the nano-bunching regime the dense nanobunches cannot reach the relativistic velocity at the moment of radiation generation. Therefore, as depicted in Figure 3 a main difference between these two models is the velocity of the plasma surface electrons.
In Figure 3a, the velocity distribution of the electrons is depicted for a P-polarized incident pulse at the moment of high harmonics generation in ROM regime. In this case, the electrons oscillate back and forth in front of the plasma surface and reach near the light speed. Moreover, in Figure 3b, the velocity distribution of the electrons at the moment of nano-bunch generation is showed. In this case, as mentioned before, the formation of heavy nano-bunch is the reason of velocity distribution in the range of much lower than the light speed.
Fig. 3. Velocity distribution of the electrons in two regimes: (a) Velocity distribution of the electron at P-polarized laser in ROM model for the laser and plasma parameters of Figure 1. (b) Velocity distribution of the electron with circular polarization in Nano-bunching regime at the moment of bunch generation is shown for the laser and plasma parameters as in Figure 2. As mentioned in the text, the produced dense group of electron cannot reach to the relativistic velocities.
The effect of different polarization stage of the incident laser pulse in interaction with plasma was discussed (Eliezer, Reference Eliezer2006). The nonlinear ponderomotive force at the front part of the incident laser pulse is accountable for nonlinear phenomena of nano-bunch generation. Therefore, we have to investigate the distinction of this force in different polarized laser pulses. Starting with the related formula in the 1D, the vector potential A with circular polarization, becomes:
$${\bf A} = A_{\; 0} \left[{{\bf e}_{\bf y} \cos \lpar {\rm \omega} t - kx\rpar + {\bf e}_{\bf z} \sin \lpar {\rm \omega} t - kx\rpar } \right]\exp \lpar \!- t^2 /T^2 \rpar.$$The parameters of this pulse propagating in x-direction are e y, e z, and k = nω/c are unit vector in y and z directions and the wave vector of the pulse with refractive index n = 1, respectively. Therefore, in high intensity regime the fast time-averaged ponderomotive force of a circularly polarized laser pulse which exerted on the electrons is given by (Sazegari et al., Reference Sazegari, Mirzaie and Shokri2006):
$$F_p = - \displaystyle{{m_e c^2 } \over {2{\rm \gamma} }}\displaystyle{{\partial a^2 } \over {\partial x}}.$$a = eA/m ec is the normalized laser vector potential amplitude. Since for a linearly polarized laser pulse a 2/2 should be substituted with a 2 in the ponderomotive force equation; therefore, the magnitude of ponderomotive force in the circular polarization is larger than in linear case and this leads to denser nano-bunch generation. It is worth noting that, the same phenomenon occurs in the electron acceleration process by a circularly polarized laser pulse in the plasma that ponderomotive force plays fundamental role (Singh, Reference Singh2004). This is due to the lower threshold of laser intensity needed for a circularly polarized laser pulse (Sazegari et al., Reference Sazegari, Mirzaie and Shokri2006). These results are confirmed with the PIC simulation presented in this work.
In Figure 4 the electron distribution of the plasma in ROM regime is denoted. As shown in the Figure 4a for S-polarization the oscillation in the plasma is higher and almost comparable to the one from P-polarized as denoted in Figure 4b. Evidently, the linearly polarized laser drives oscillation on the plasma surface, but there are no oscillations on the plasma-vacuum interface in circular polarized incident laser pulse. In this particular case, the Lorentz force of the incident laser pulse is constant and consequently no attosecond pulses can be generated (Rykovanov et al., Reference Rykovanov, Geissler, Meyer-Ter-Vehn and Tsakiris2008). The electron density (N e /N cr) versus position and time in different polarizations of the incident pulse are depicted in Figures 4d, 4e, and 4f. At t = 6.7T of Figure 4d for S-polarization, one can see the oscillation of the surface have its maximum amplitude with electron density about N e = 220N cr, when the surface electrons approach to the observer.
Fig. 4. (Color online) The Electron density distribution for linear S-polarized incident laser pulse at t = 6.7T (a), P-polarized laser pulse at t = 6.3T, (b) and Circular polarized laser pulse at t = 6.0T (c) at the moment of harmonic generation in ROM theory is shown. The electron density (N e /N cr) versus position and time are depicted in (d), (e), and (f) for S, P, and circular polarization, respectively. In the case of circularly polarized laser pulse, there is no oscillation on the plasma surface. Simulation parameters are: normal incident laser pulse with field amplitude of a = 15 and step like plasma with N e = 95N cr.
Figure 5 denotes the result of PIC simulation for nano-bunching regime. Figures 5a, 5b, and 5c illustrate the electrons distribution due to the different incident laser polarizations including S-polarization, P-polarization, and the circular polarization, respectively. In addition, the electron density distribution versus position and time for these parameters are shown in Figures 5d, 5e, and 5f for S, P, and circular polarization, respectively. Figure 5 indicates that circular polarization of the incident pulse has much better effect on the generation of denser electron bunch in front of the plasma. As one can notice the electron density in circular polarization case is far more than that in linear polarization and it performs N e/N cr of 1500, which is almost two and seven times more than the similar amounts for P-polarized and S-polarized, respectively.
Fig. 5. (Color online) The Electron density distribution for linear S-polarized incident laser pulse at t = 4.4T (a), p-polarized laser pulse at t = 4.8T (b), and Circular polarized laser pulse at t = 5.2T (c) at the moment of harmonic generation in the nano-bunching regime is shown. The electron density (N e/N cr) versus position and time are depicted in (d), (e), and (f) for S, P, and circular polarization, respectively. The electron density of nanobunch in circular polarization case is far more than that in linear polarization. The laser and plasma parameters are the same as in Figure 2.
CONCLUSION
In this study, the effect of incident laser polarization for the initial laser and plasma parameters of BGP and nano-bunching models are discussed. The effect of ponderomotive force on nano-bunch generation, the effect of circularly polarized incident pulses on reaching the extreme localized and high current electron bunches in nano-bunching regime is discussed. The electrons velocity in BGP and nano-bunching conditions is also discussed for linear and circular incident polarization. It is found that due to higher ponderomotive force of circular polarization much more dense nano-bunches are generated. The analytical results predict more localization and high density nano-bunches in nano-bunching regime. This is verified with the results from presented PIC simulation.
ACKNOWLEDGEMENTS
The authors want to thank the research deputy of Sharif University of Technology and also the Oil and Gas Company of the Ministry of Oil (IRI) for their partial support of this work under contract number PT 1211. We would like to thank nice discussions and valuable comments of Dr. P. Zobdeh.
