Introduction
The possibility of electron attraction in the presence of a plane electromagnetic wave was firstly shown by Oleinik (Reference Oleinik1967). However, the theoretical proof of the attraction possibility was given by Kazantsev and Sokolov (Reference Kazantsev and Sokolov1984) for the interaction of classical relativistic electrons in the field of a plane wave. Zavtrak (Reference Zavtrak1989) has investigated the force of radiation pressure in relation to the Coulomb force. He showed the principle possibility of the formation of bound states between same-charged particles. It is very important to point out that the attraction of classical electrons in the field of a plane monochromatic electromagnetic wave is possible only for particles with relativistic energies. In the works of Starodub and Roshchupkin (Reference Starodub and Roshchupkin2012, Reference Starodub and Roshchupkin2015), Starodub et al. (Reference Starodub, Roshchupkin and Dubov2016), the possibility of attraction of non-relativistic electrons (identically charged ions) in the pulsed laser field was shown. Thus, in the review of Starodub and Roshchupkin (Reference Starodub and Roshchupkin2012), the following processes were discussed: interaction of electrons (light ions) in the pulsed field of a single laser wave; interaction of non-relativistic electrons in the pulsed field of two counter-propagating laser waves moving perpendicularly to the initial direction of electrons motion; the interaction of non-relativistic light ions moving almost parallel to each other in the propagation direction of the pulsed field of two counter-propagating laser waves moving in parallel direction to ions; interaction of two non-relativistic heavy nuclei (uranium 235), moving toward each other perpendicularly to the propagation direction of two counter-propagating laser waves. Influence of the pulsed field of two co-propagating laser waves on the effective force of interaction of two electrons and two identically charged heavy nuclei was studied in Starodub and Roshchupkin (Reference Starodub and Roshchupkin2015). It was shown that the phase shift allows to increase duration of electron's confinement at a certain averaged effective distance by 1.5 time in comparison with the case of one and two counter-propagating pulsed laser waves. Interaction of two classical non-relativistic electrons in the strong-pulsed laser field of two light mutually perpendicular waves, when the maxima laser pulses coincide, was studied in Starodub et al. (Reference Starodub, Roshchupkin and Dubov2016). It is shown that the effective force of electron interaction becoming the attraction force or anomalous repulsion force after approach of electrons to the minimum distance.
In the present paper, in contrast to the mentioned above, interaction of two classical non-relativistic electrons in the strong-pulsed laser field of two light mutually perpendicular waves with the phase shifts of pulse peaks of the first and second waves is studied. It is shown that phase shifts of pulse peaks allow essentially change effective interaction of electrons than without phase shifts when the maxima laser pulses coincide. The obtained results can be used for experiments in the framework of modern research projects, where the sources of pulsed laser radiation are used (SLAC, FAIR) (see Bula et al., Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996; Burke et al., Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997; Di Piazza et al., Reference Di Piazza, Müller, Hatsagortsyan and Keitel2012).
Equations of electron interaction in the pulsed field of two laser waves
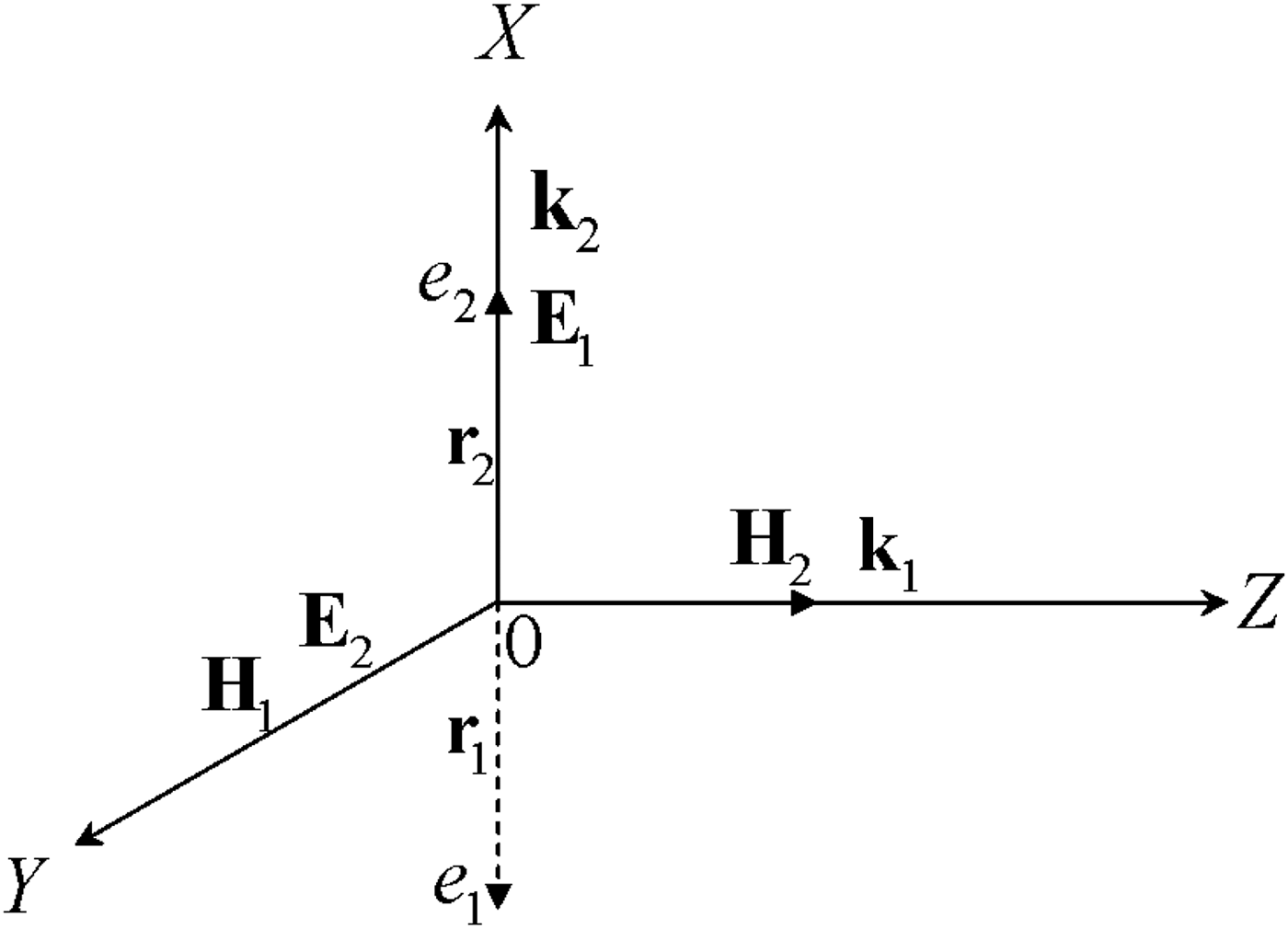
Consider the interaction of two non-relativistic electrons moving toward each other along the x axis in the field of two linearly polarized pulsed electromagnetic waves. Waves propagate perpendicularly to each other. The first wave propagates along the z axis, the second wave propagates along the x axis (see Fig. 1).
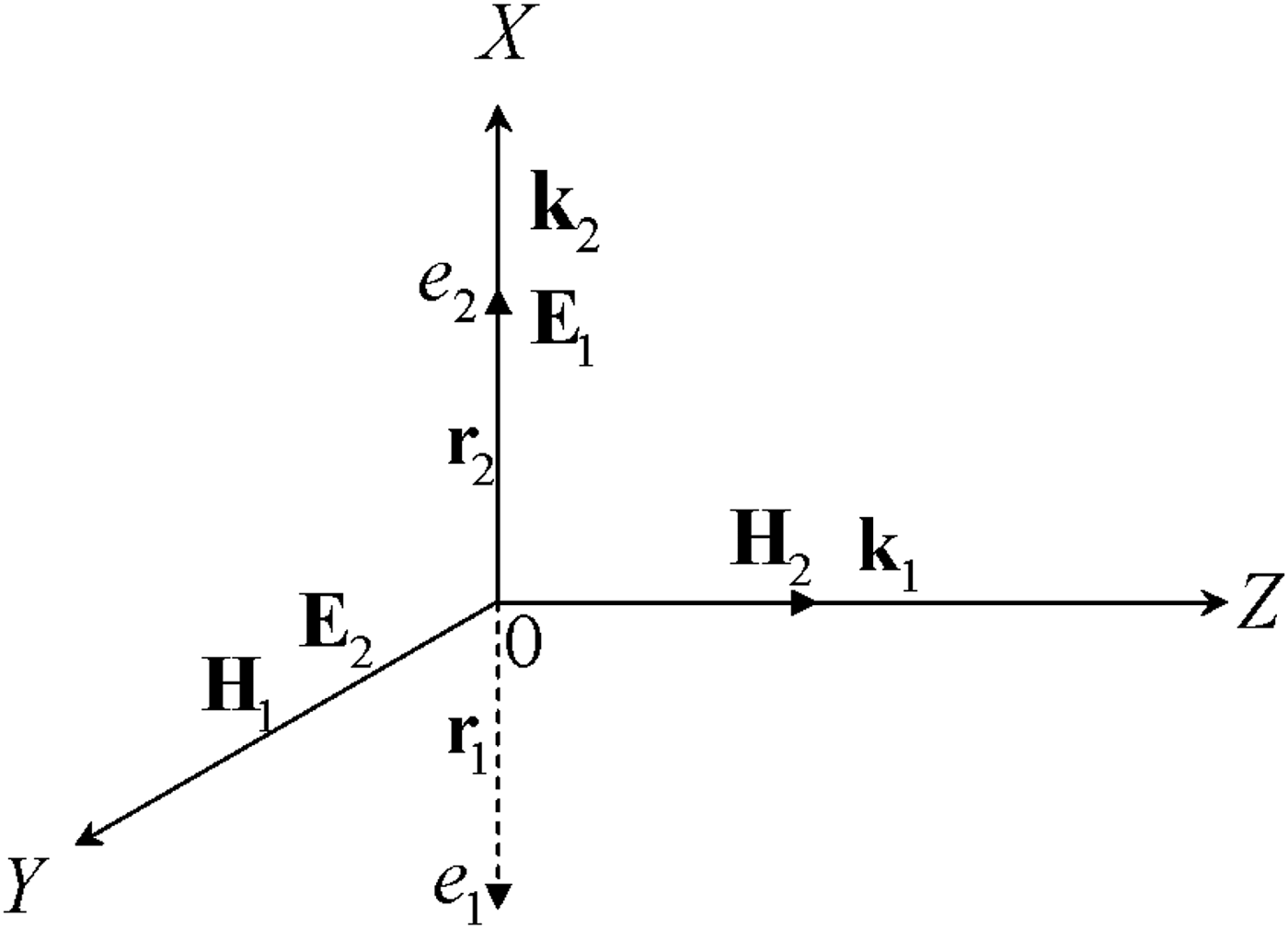
Fig. 1. Interaction kinematics of two classical electrons in the field of two light mutually perpendicular waves.
The strengths of the electric and magnetic fields are given in the following form:
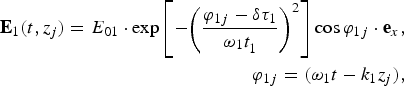 $$\eqalign{ {\bf E}_1(t,z_j) = E_{01} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{1j} - {\rm \delta} {\rm \tau} _1} \over {{\rm \omega} _1t_1^{}}}} \right)}^2} \right]\cos {\rm \varphi} _{1j} \cdot {\bf e}_x, & \cr \quad {\rm \varphi} _{1j} = ({\rm \omega} _1t - k_1z_j),&} $$
$$\eqalign{ {\bf E}_1(t,z_j) = E_{01} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{1j} - {\rm \delta} {\rm \tau} _1} \over {{\rm \omega} _1t_1^{}}}} \right)}^2} \right]\cos {\rm \varphi} _{1j} \cdot {\bf e}_x, & \cr \quad {\rm \varphi} _{1j} = ({\rm \omega} _1t - k_1z_j),&} $$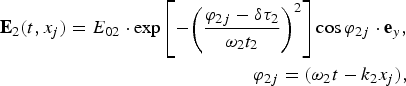 $$\eqalign{ {\bf E}_2(t,x_j) = E_{02} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{2j} - {\rm \delta} {\rm \tau} _2} \over {{\rm \omega} _2t_2}}} \right)}^2} \right]\cos {\rm \varphi} _{2j} \cdot {\bf e}_y, & \cr \quad {\rm \varphi} _{2j} = ({\rm \omega} _2t - k_2x_j), & } $$
$$\eqalign{ {\bf E}_2(t,x_j) = E_{02} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{2j} - {\rm \delta} {\rm \tau} _2} \over {{\rm \omega} _2t_2}}} \right)}^2} \right]\cos {\rm \varphi} _{2j} \cdot {\bf e}_y, & \cr \quad {\rm \varphi} _{2j} = ({\rm \omega} _2t - k_2x_j), & } $$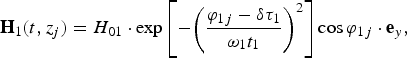 $${\bf H}_1(t,z_j) = H_{01} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{1j} - {\rm \delta} {\rm \tau} _1} \over {{\rm \omega} _1t_1}}} \right)}^2} \right]\cos {\rm \varphi} _{1j} \cdot {\bf e}_y,$$
$${\bf H}_1(t,z_j) = H_{01} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{1j} - {\rm \delta} {\rm \tau} _1} \over {{\rm \omega} _1t_1}}} \right)}^2} \right]\cos {\rm \varphi} _{1j} \cdot {\bf e}_y,$$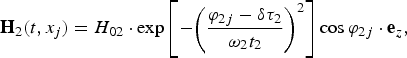 $${\bf H}_2(t,x_j) = H_{02} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{2j} - {\rm \delta} {\rm \tau} _2} \over {{\rm \omega} _2t_2}}} \right)}^2} \right]\cos {\rm \varphi} _{2j} \cdot {\bf e}_z,$$
$${\bf H}_2(t,x_j) = H_{02} \cdot \exp \left[ { - {\left( {\displaystyle{{{\rm \varphi} _{2j} - {\rm \delta} {\rm \tau} _2} \over {{\rm \omega} _2t_2}}} \right)}^2} \right]\cos {\rm \varphi} _{2j} \cdot {\bf e}_z,$$where φij are phases of the corresponding wave (i = 1, 2) and corresponding electron (j = 1, 2); E 0i and H 0i are the strength of the electric and magnetic fields in the pulse peak, respectively; δτi are phase shifts of pulse peaks of the first and second waves; t i and ωi are the pulse duration and frequency of the first and the second waves; ![]() ${\bf e}_x$,
${\bf e}_x$, ![]() ${\bf e}_y$,
${\bf e}_y$, ![]() ${\bf e}_z$ are unit vectors directed along the x, y, and z axes.
${\bf e}_z$ are unit vectors directed along the x, y, and z axes.
It is a well-known fact that in the frame of the dipole approximation (k = 0) and without taking into account the terms of the order v/c ≪ 1, the particle interaction with the plane-wave field does not affect the particle relative motion in the center-of-mass system. Thereby, we consider particle motion in the laser field beyond the dipole approximation and an accuracy of quantities of the order v/c ≪ 1 (v is the relative velocity). Newton equations for motion of two identically charged particles with the mass m and charge e (e = e 1 = e 2) in the pulsed field of two mutually perpendicular laser waves 1–6 are determined by the following expressions:
where ![]() ${\bf r}_1$ and
${\bf r}_1$ and ![]() ${\bf r}_2$ are electron radius-vectors.
${\bf r}_2$ are electron radius-vectors.
Hereafter, the wave frequencies are the same:
Subsequent consideration should be carried out in the center-of-mass system:
The following equations are for the particle relative motion in the center-of-mass system:
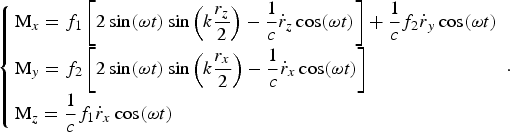 $$\left\{ {\matrix{ {{\rm M}_x = f_1\left[ {2\sin ({\rm \omega} t)\sin \left( {k\displaystyle{{r_z} \over 2}} \right) - \displaystyle{1 \over c}{\dot r}_z\cos ({\rm \omega} t)} \right] + \displaystyle{1 \over c}f_2{\dot r}_y\cos ({\rm \omega} t)} \hfill \cr {{\rm M}_y = f_2\left[ {2\sin ({\rm \omega} t)\sin \left( {k\displaystyle{{r_x} \over 2}} \right) - \displaystyle{1 \over c}{\dot r}_x\cos ({\rm \omega} t)} \right]\quad {\rm}} \hfill \cr {{\rm M}_z = \displaystyle{1 \over c}f_1{\dot r}_x\cos ({\rm \omega} t){\rm}} \hfill \cr}} \right..$$
$$\left\{ {\matrix{ {{\rm M}_x = f_1\left[ {2\sin ({\rm \omega} t)\sin \left( {k\displaystyle{{r_z} \over 2}} \right) - \displaystyle{1 \over c}{\dot r}_z\cos ({\rm \omega} t)} \right] + \displaystyle{1 \over c}f_2{\dot r}_y\cos ({\rm \omega} t)} \hfill \cr {{\rm M}_y = f_2\left[ {2\sin ({\rm \omega} t)\sin \left( {k\displaystyle{{r_x} \over 2}} \right) - \displaystyle{1 \over c}{\dot r}_x\cos ({\rm \omega} t)} \right]\quad {\rm}} \hfill \cr {{\rm M}_z = \displaystyle{1 \over c}f_1{\dot r}_x\cos ({\rm \omega} t){\rm}} \hfill \cr}} \right..$$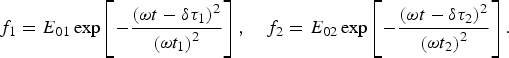 $$f_1 = E_{01}\exp \left[ { - \displaystyle{{{\left( {{\rm \omega} t - {\rm \delta} {\rm \tau} _1} \right)}^2} \over {{\left( {{\rm \omega} t_1} \right)}^2}}} \right],\quad f_2 = E_{02}\exp \left[ { - \displaystyle{{{\left( {{\rm \omega} t - {\rm \delta} {\rm \tau} _2} \right)}^2} \over {{\left( {{\rm \omega} t_2} \right)}^2}}} \right].$$
$$f_1 = E_{01}\exp \left[ { - \displaystyle{{{\left( {{\rm \omega} t - {\rm \delta} {\rm \tau} _1} \right)}^2} \over {{\left( {{\rm \omega} t_1} \right)}^2}}} \right],\quad f_2 = E_{02}\exp \left[ { - \displaystyle{{{\left( {{\rm \omega} t - {\rm \delta} {\rm \tau} _2} \right)}^2} \over {{\left( {{\rm \omega} t_2} \right)}^2}}} \right].$$Note that the equations for relative motion (10), (11) are written beyond the dipole approximation (k ≠ 0) and an accuracy of term of order v/c ≪ 1. Note, small influence of external strong-pulsed laser field on radius-vector of the center-of-mass motion was shown in Starodub et al. (Reference Starodub, Roshchupkin and Dubov2016). Thereby, it is necessary to study only the relative motion.
Equations (10), (11) can be written in the dimensionless form:
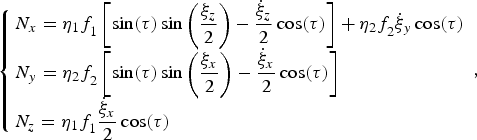 $$\left\{ {\matrix{ {N_x = {\rm \eta} _1f_1^{} \left[ {\sin ({\rm \tau} )\sin \left( {\displaystyle{{{\rm \xi} _z} \over 2}} \right) - \displaystyle{{{\dot {\rm \xi}} _z} \over 2}\cos ({\rm \tau} )} \right] + {\rm \eta} _2f_2^{} {\dot {\rm \xi}} _y\cos ({\rm \tau} )} \hfill \cr {N_y = {\rm \eta} _2f_2^{} \left[ {\sin ({\rm \tau} )\sin \left( {\displaystyle{{{\rm \xi} _x} \over 2}} \right) - \displaystyle{{{\dot {\rm \xi}} _x} \over 2}\cos ({\rm \tau} )} \right]{\rm}} \hfill \cr {N_z = {\rm \eta} _1f_1^{} \displaystyle{{{\dot {\rm \xi}} _x} \over 2}\cos ({\rm \tau} ){\rm}} \hfill \cr}} \right.,$$
$$\left\{ {\matrix{ {N_x = {\rm \eta} _1f_1^{} \left[ {\sin ({\rm \tau} )\sin \left( {\displaystyle{{{\rm \xi} _z} \over 2}} \right) - \displaystyle{{{\dot {\rm \xi}} _z} \over 2}\cos ({\rm \tau} )} \right] + {\rm \eta} _2f_2^{} {\dot {\rm \xi}} _y\cos ({\rm \tau} )} \hfill \cr {N_y = {\rm \eta} _2f_2^{} \left[ {\sin ({\rm \tau} )\sin \left( {\displaystyle{{{\rm \xi} _x} \over 2}} \right) - \displaystyle{{{\dot {\rm \xi}} _x} \over 2}\cos ({\rm \tau} )} \right]{\rm}} \hfill \cr {N_z = {\rm \eta} _1f_1^{} \displaystyle{{{\dot {\rm \xi}} _x} \over 2}\cos ({\rm \tau} ){\rm}} \hfill \cr}} \right.,$$where,
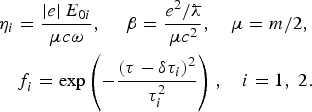 $$\eqalign{& {\rm \eta} _i = \displaystyle{{\left \vert e \right \vert E_{0i}} \over {{\rm \mu} c{\rm \omega}}}, \;\quad {\rm \beta} = \displaystyle{{{e^2} / {\lambdabar}} \over {{\rm \mu} c^2}},\quad {\rm \mu} = {m / 2}, \cr & \quad f_i^{} = \exp \left( { - \displaystyle{{{\left( {{\rm \tau} - {\rm \delta} {\rm \tau} _i} \right)}^2} \over {{\rm \tau} _i^2}}} \right),\quad i = 1,\;2.} $$
$$\eqalign{& {\rm \eta} _i = \displaystyle{{\left \vert e \right \vert E_{0i}} \over {{\rm \mu} c{\rm \omega}}}, \;\quad {\rm \beta} = \displaystyle{{{e^2} / {\lambdabar}} \over {{\rm \mu} c^2}},\quad {\rm \mu} = {m / 2}, \cr & \quad f_i^{} = \exp \left( { - \displaystyle{{{\left( {{\rm \tau} - {\rm \delta} {\rm \tau} _i} \right)}^2} \over {{\rm \tau} _i^2}}} \right),\quad i = 1,\;2.} $$Here, ![]() ${\bf { \xi}} $ is the radius-vector of the relative distance between electrons in unit of the wavelength, the parameters η1,2 are numerically equal to the ratio of the oscillation velocity of an electron in the peak of a pulse of the first or second wave to the velocity of light c (hereinafter, should consider parameters η1,2 as oscillation velocities); the parameter β is numerically equal to the ratio of the energy of Coulomb interaction of electrons with the reduced mass μ at the wavelength to the particle rest energy.
${\bf { \xi}} $ is the radius-vector of the relative distance between electrons in unit of the wavelength, the parameters η1,2 are numerically equal to the ratio of the oscillation velocity of an electron in the peak of a pulse of the first or second wave to the velocity of light c (hereinafter, should consider parameters η1,2 as oscillation velocities); the parameter β is numerically equal to the ratio of the energy of Coulomb interaction of electrons with the reduced mass μ at the wavelength to the particle rest energy.
The pulse duration exceeds considerably the period of wave rapid oscillation (~ω−1) for a majority of modern pulsed lasers:
Consequently, the relative distance between electrons should be averaged over the period of wave rapid oscillation:
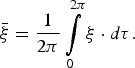 $$\bar {\rm \xi} = \displaystyle{1 \over {2{\rm \pi}}} \int\limits_0^{2{\rm \pi}} {{\rm \xi} \cdot d{\rm \tau}}. $$
$$\bar {\rm \xi} = \displaystyle{1 \over {2{\rm \pi}}} \int\limits_0^{2{\rm \pi}} {{\rm \xi} \cdot d{\rm \tau}}. $$It is worth to note that expressions (13), (14) consider interaction with the Coulomb field and the pulsed-wave field strictly, and do not have the analytical solution. For subsequent analysis, all equations will be studied numerically.
Electrons initial relative coordinates and velocities are the following:
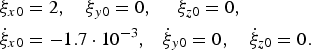 $$\eqalign{& {\rm \xi} _{x0} = 2,\quad {\rm \xi} _{y0} = 0,\quad \;{\rm \xi} _{z0} = 0, \cr & {\dot {\rm \xi}} _{x0} = - 1.7 \cdot 10^{ - 3}{\rm,} \quad {\dot {\rm \xi}} _{y0} = 0,\quad {\dot {\rm \xi}} _{z0} = 0.} $$
$$\eqalign{& {\rm \xi} _{x0} = 2,\quad {\rm \xi} _{y0} = 0,\quad \;{\rm \xi} _{z0} = 0, \cr & {\dot {\rm \xi}} _{x0} = - 1.7 \cdot 10^{ - 3}{\rm,} \quad {\dot {\rm \xi}} _{y0} = 0,\quad {\dot {\rm \xi}} _{z0} = 0.} $$The interaction time is ![]() ${\rm \tau} = 1200\;({\rm \tau} \in \left[ { - 600 \div 600} \right])$, (t = 600 fs) and it was increased, if necessary for more clear results. Frequencies of waves are ω1 = ω2 = 2 Ps−1 (
${\rm \tau} = 1200\;({\rm \tau} \in \left[ { - 600 \div 600} \right])$, (t = 600 fs) and it was increased, if necessary for more clear results. Frequencies of waves are ω1 = ω2 = 2 Ps−1 (![]() ${\lambdabar} = 0.15{\rm \mu} {\rm m}$), pulse durations are τ1 = τ2 = 600 (t 1 = t 2 = 300 fs). Field intensities (oscillations velocities η1, η2) are varied. Phase shifts are vary within
${\lambdabar} = 0.15{\rm \mu} {\rm m}$), pulse durations are τ1 = τ2 = 600 (t 1 = t 2 = 300 fs). Field intensities (oscillations velocities η1, η2) are varied. Phase shifts are vary within ![]() ${\rm \delta} {\rm \tau} _{1,2} \in \left[ { - 600 \div 600} \right]$ and step is h = 50. Initial conditions are the same as in (9). That allows to estimate the influence of phase shifts on relative motion of electrons and compare results. Note, in the work (9) the parameter of the phase shift of a pulse of a wave (δτ1,2 = 0) was absent, and pulse peaks of both waves were in moment τ = 0. Initial coordinates and velocities of electrons are chosen, so that at the point τ = 0 electrons were in maximum approach (the Coulomb force was maximum). In this work, the pulse peaks of waves can be maximum at any moment of time (unlike the previous publication (9)) and it leads to significant change in the behavior of electron interaction. Numerical solving of equations for relative motion (13) results to several cases.
${\rm \delta} {\rm \tau} _{1,2} \in \left[ { - 600 \div 600} \right]$ and step is h = 50. Initial conditions are the same as in (9). That allows to estimate the influence of phase shifts on relative motion of electrons and compare results. Note, in the work (9) the parameter of the phase shift of a pulse of a wave (δτ1,2 = 0) was absent, and pulse peaks of both waves were in moment τ = 0. Initial coordinates and velocities of electrons are chosen, so that at the point τ = 0 electrons were in maximum approach (the Coulomb force was maximum). In this work, the pulse peaks of waves can be maximum at any moment of time (unlike the previous publication (9)) and it leads to significant change in the behavior of electron interaction. Numerical solving of equations for relative motion (13) results to several cases.
Anomalous repulsion of electrons
The case when the oscillation velocity of the first wave is greater than the initial velocity of electrons (![]() ${\rm \eta} _1 \gt \dot {\rm \xi} _0$), and oscillation velocity of the second wave considerably exceeds the initial velocity (
${\rm \eta} _1 \gt \dot {\rm \xi} _0$), and oscillation velocity of the second wave considerably exceeds the initial velocity (![]() ${\rm \eta} _2 \gg \dot {\rm \xi} _0$).
${\rm \eta} _2 \gg \dot {\rm \xi} _0$).
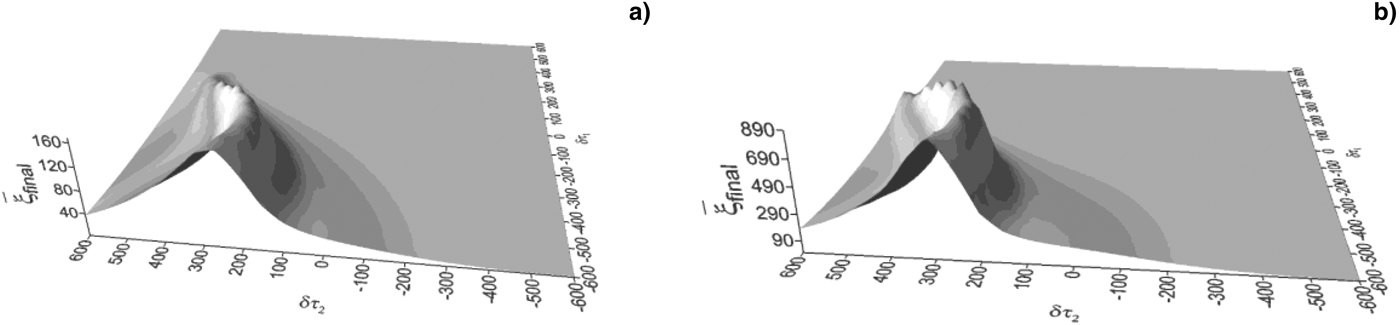
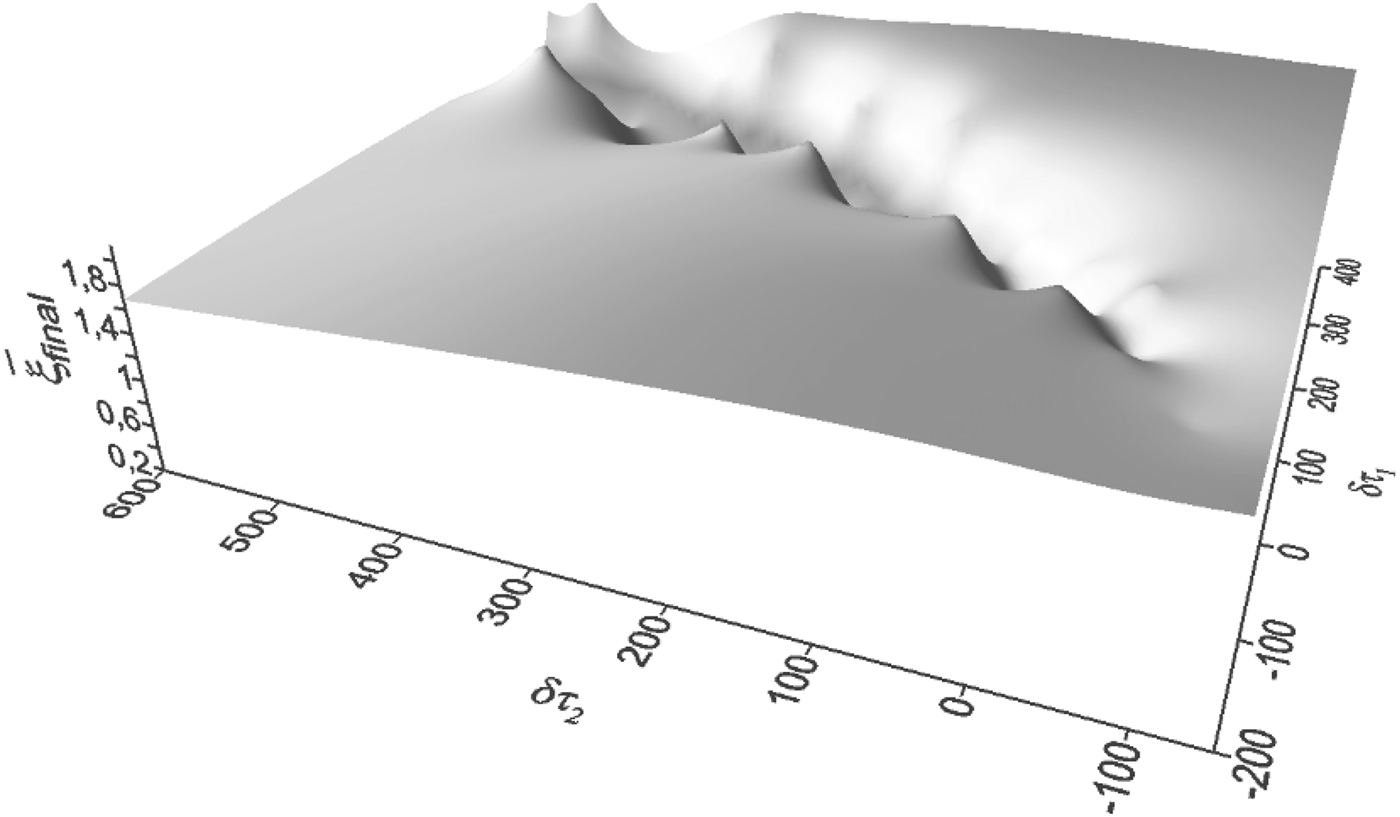
Calculations over all values of phase shifts allowed to find out areas of anomalous repulsion of electrons. In these areas, electrons can scatter at very long distances exceeding the distance of electron scattering without an external field in hundreds of times (see Fig. 2a, 2b). Let us designate the final distance at which electrons scatter in the time moment as τCfinal = 600: without an external field as ![]() $\bar {\rm \xi} _{{\rm Cfinal}} = 2$; in the external field, when δτ1 = 0, δτ2 = 0 as
$\bar {\rm \xi} _{{\rm Cfinal}} = 2$; in the external field, when δτ1 = 0, δτ2 = 0 as ![]() $\bar {\rm \xi} ^{(0)}_{{\rm final}} $; in an external field, when δτ1 ≠ 0, δτ2 ≠ 0 as
$\bar {\rm \xi} ^{(0)}_{{\rm final}} $; in an external field, when δτ1 ≠ 0, δτ2 ≠ 0 as ![]() $\bar {\rm \xi} _{{\rm final}}$.
$\bar {\rm \xi} _{{\rm final}}$.
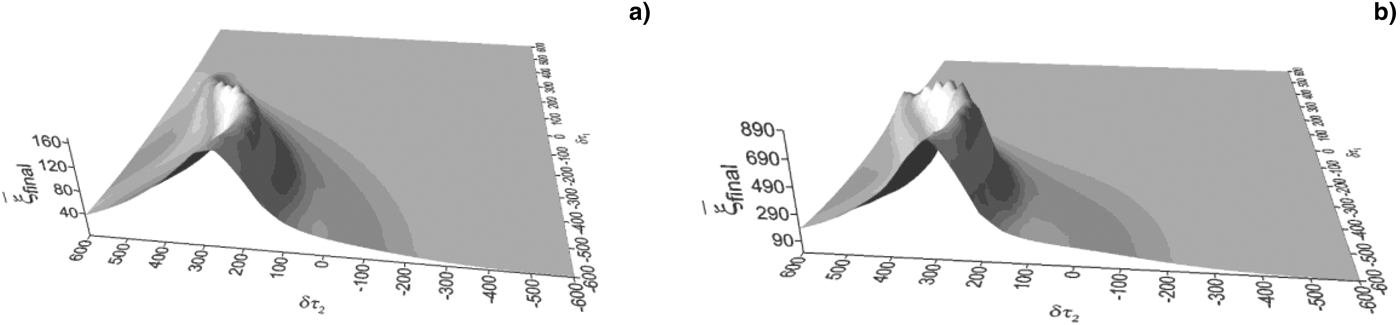
Fig. 2. The final averaged relative distance ![]() $\bar {\rm \xi} _{{\rm final}}$ (in the time moment τCfinal = 600,
$\bar {\rm \xi} _{{\rm final}}$ (in the time moment τCfinal = 600, ![]() $\bar {\rm \xi} _{{\rm Cfinal}} = 2$) against different phase shifts of pulse peaks δτ1, δτ2. Oscillation velocities: η1 = 3 × 10−3, (a) η2 = 6 × 10−2, (b) η2 = 10−1 (field intensities: I 1 = 3.4 × 1012 W/cm2, (a) I 2 = 1.3 × 1015 W/cm2, (b) I 2 = 3.8 × 1015 W/cm2).
$\bar {\rm \xi} _{{\rm Cfinal}} = 2$) against different phase shifts of pulse peaks δτ1, δτ2. Oscillation velocities: η1 = 3 × 10−3, (a) η2 = 6 × 10−2, (b) η2 = 10−1 (field intensities: I 1 = 3.4 × 1012 W/cm2, (a) I 2 = 1.3 × 1015 W/cm2, (b) I 2 = 3.8 × 1015 W/cm2).
Figure 2a, 2b show dependence of the final distance ![]() $\bar {\rm \xi} _{{\rm final}}$ at which the electrons scatter at the time moment τCfinal = 600 for different values of phase shifts δτ1, δτ2 and for two values of the oscillation velocity of the second wave. One can see that the final distance
$\bar {\rm \xi} _{{\rm final}}$ at which the electrons scatter at the time moment τCfinal = 600 for different values of phase shifts δτ1, δτ2 and for two values of the oscillation velocity of the second wave. One can see that the final distance ![]() $\bar {\rm \xi} _{{\rm final}}$ considerably depends from the oscillation velocity of the second wave and has maximum values for next ranges of the phase shifts:
$\bar {\rm \xi} _{{\rm final}}$ considerably depends from the oscillation velocity of the second wave and has maximum values for next ranges of the phase shifts: ![]() ${\rm \delta} {\rm \tau} _1 \in \left[ { - 600 \div - 50} \right]$,
${\rm \delta} {\rm \tau} _1 \in \left[ { - 600 \div - 50} \right]$, ![]() ${\rm \delta} {\rm \tau} _2 \in \left[ {100 \div 500} \right]$. Thus, for the oscillation velocity η2 = 6 × 10−2, the final distance can reach the value
${\rm \delta} {\rm \tau} _2 \in \left[ {100 \div 500} \right]$. Thus, for the oscillation velocity η2 = 6 × 10−2, the final distance can reach the value ![]() $\bar {\rm \xi} _{{\rm final}} \approx 160$ (see Fig. 2a), and for the oscillation velocity η2 = 10−1, the final distance can reach the value
$\bar {\rm \xi} _{{\rm final}} \approx 160$ (see Fig. 2a), and for the oscillation velocity η2 = 10−1, the final distance can reach the value ![]() $\bar {\rm \xi} _{{\rm final}} \approx 900$ (see Fig. 2b). Figures 3 and 4 show dependence of averaged relative distance
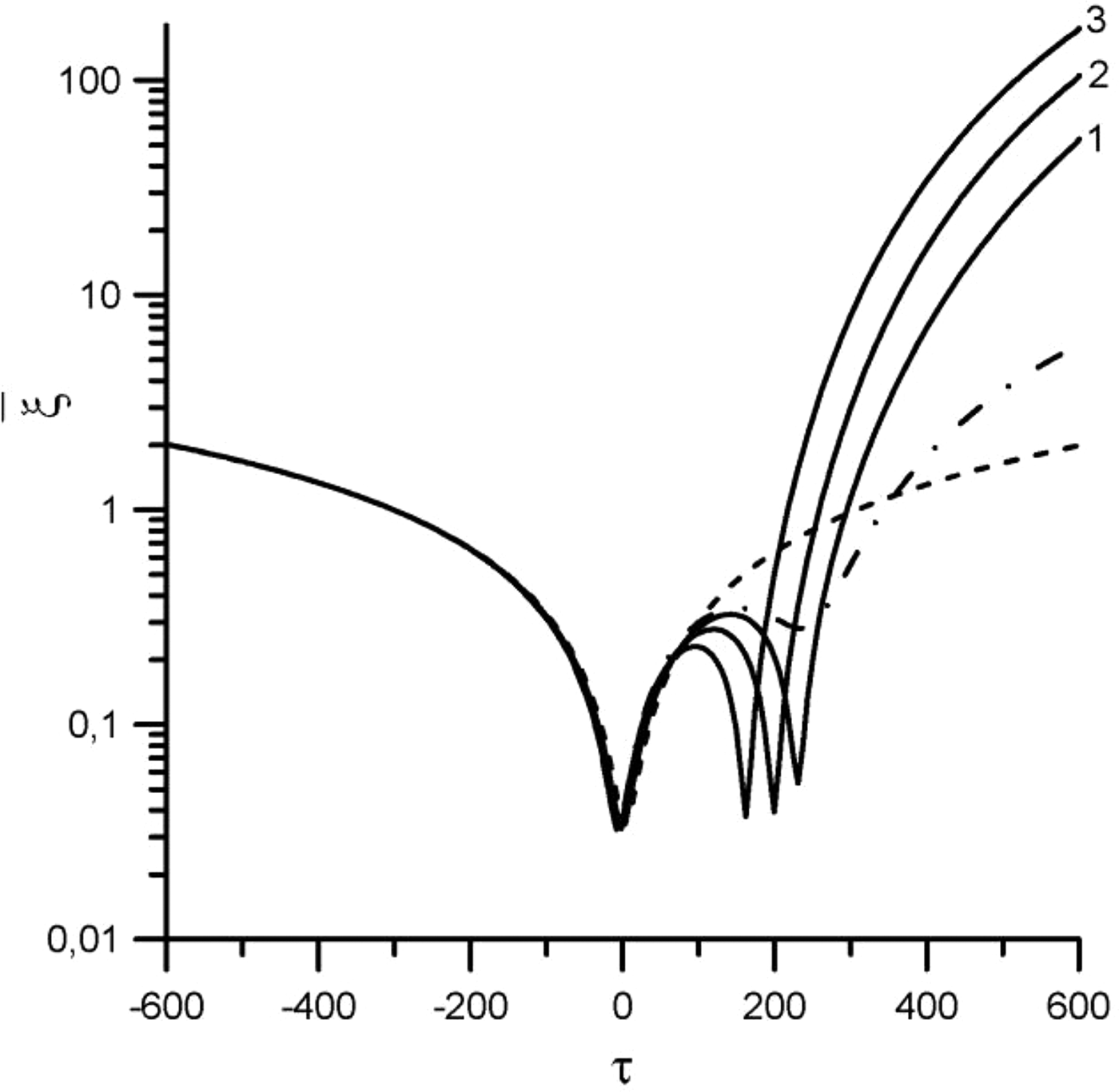
$\bar {\rm \xi} _{{\rm final}} \approx 900$ (see Fig. 2b). Figures 3 and 4 show dependence of averaged relative distance ![]() $\bar {\rm \xi} $ (in logarithmic units) against the interaction time τ for mainly interesting values of the phase shifts. It is seen that taking into account of the phase shifts of pulse peaks can considerably increase the repulsion force. Thus, for η1 = 3 × 10−3, η2 = 6 × 10−2 and δτ1 = −550, δτ2 = 250 ratio
$\bar {\rm \xi} $ (in logarithmic units) against the interaction time τ for mainly interesting values of the phase shifts. It is seen that taking into account of the phase shifts of pulse peaks can considerably increase the repulsion force. Thus, for η1 = 3 × 10−3, η2 = 6 × 10−2 and δτ1 = −550, δτ2 = 250 ratio ![]() $\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} _{{\rm Cfinal}} \approx 80$ and ratio
$\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} _{{\rm Cfinal}} \approx 80$ and ratio ![]() $\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} ^{(0)}_{{\rm final}} \approx 32$ (see curve 3 in Fig. 3), and for oscillation velocities η1 = 3 × 10−3, η2 = 10−1 and δτ1 = −450, δτ2 = 250 the ratio
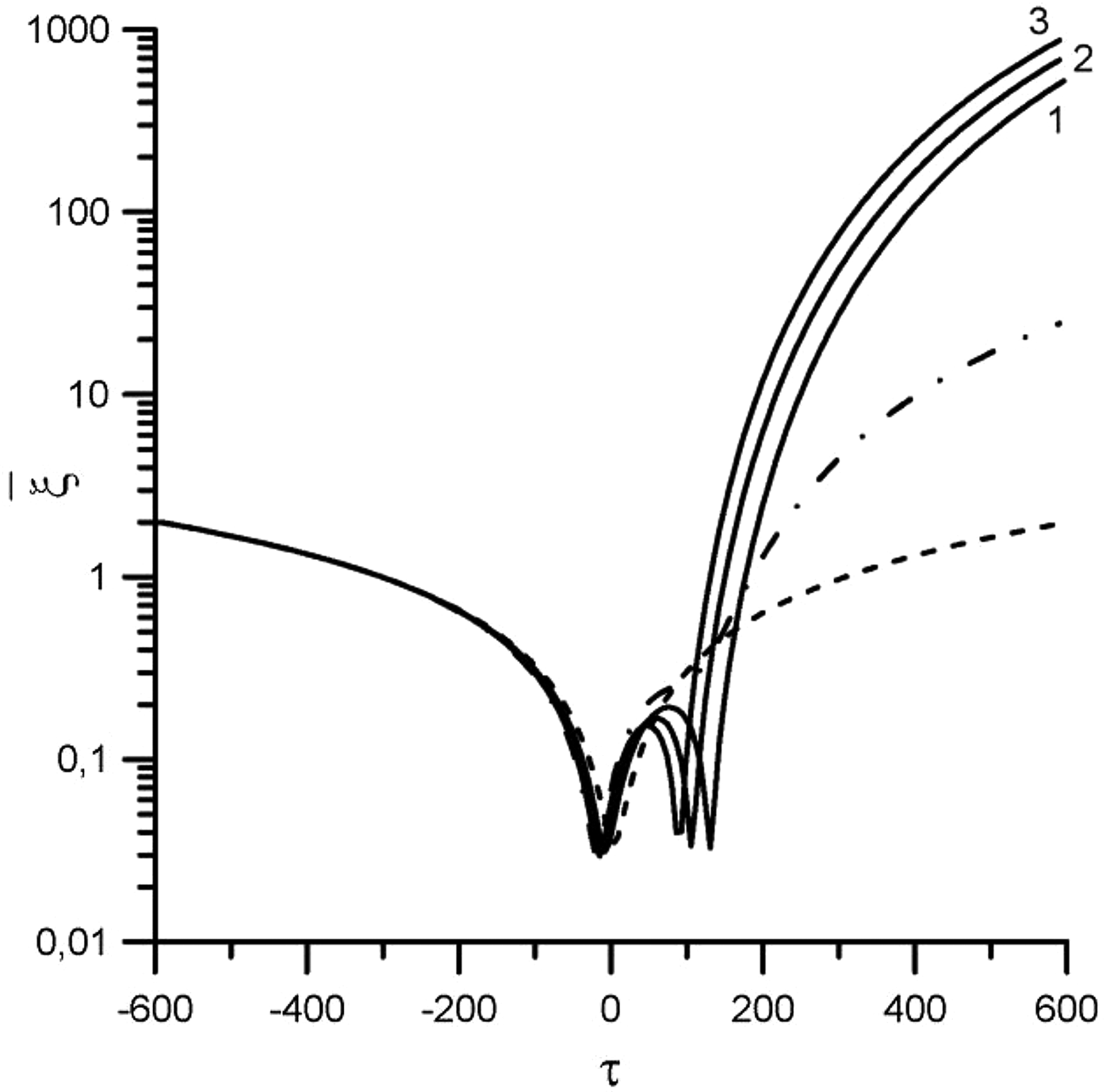
$\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} ^{(0)}_{{\rm final}} \approx 32$ (see curve 3 in Fig. 3), and for oscillation velocities η1 = 3 × 10−3, η2 = 10−1 and δτ1 = −450, δτ2 = 250 the ratio ![]() $\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} _{{\rm Cfinal}} \approx 450$ and the ratio
$\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} _{{\rm Cfinal}} \approx 450$ and the ratio ![]() $\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} ^{(0)}_{{\rm final}} \approx 180$ (see curve 3 in Fig. 4).
$\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} ^{(0)}_{{\rm final}} \approx 180$ (see curve 3 in Fig. 4).
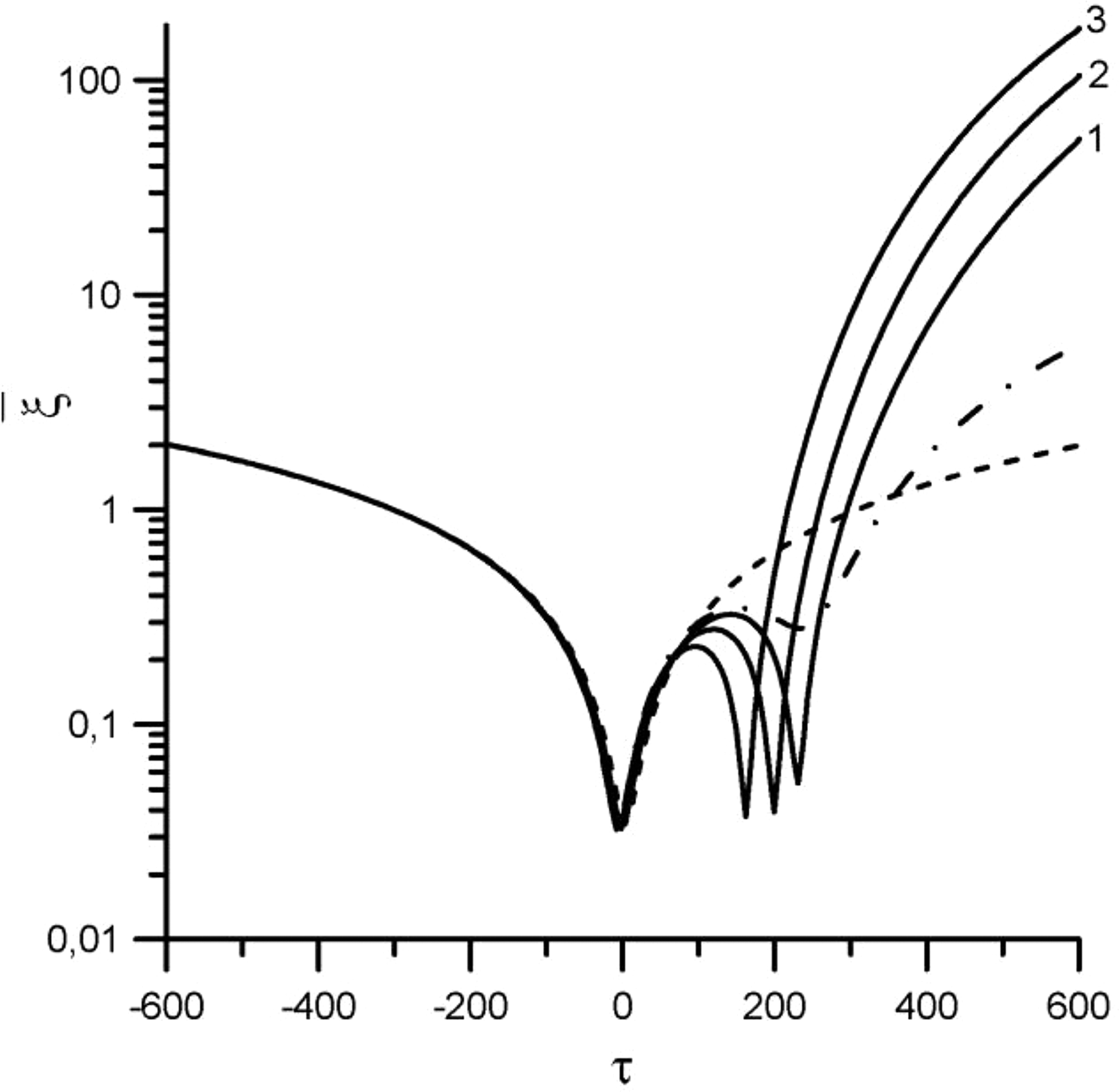
Fig. 3. The averaged relative distance ![]() $\bar {\rm \xi} $ (in logarithmic units) against the interaction time τ. The dashed line corresponds to the case of the absence of the external field. The dashed-dot line and solid lines correspond to oscillation velocities: η1 = 3 × 10−3, η2 = 6 × 10−2 (field intensities: I 1 = 3.4 × 1012 W/cm2, I 2 = 1.3 × 1015 W/cm2), phase shifts of pulse peaks: 1 – δτ1 = −450, δτ2 = 450; 2 – δτ1 = −350, δτ2 = 300; 3 – δτ1 = −550, δτ2 = 250; the dashed line with a dot – δτ1 = 0, δτ2 = 0.
$\bar {\rm \xi} $ (in logarithmic units) against the interaction time τ. The dashed line corresponds to the case of the absence of the external field. The dashed-dot line and solid lines correspond to oscillation velocities: η1 = 3 × 10−3, η2 = 6 × 10−2 (field intensities: I 1 = 3.4 × 1012 W/cm2, I 2 = 1.3 × 1015 W/cm2), phase shifts of pulse peaks: 1 – δτ1 = −450, δτ2 = 450; 2 – δτ1 = −350, δτ2 = 300; 3 – δτ1 = −550, δτ2 = 250; the dashed line with a dot – δτ1 = 0, δτ2 = 0.
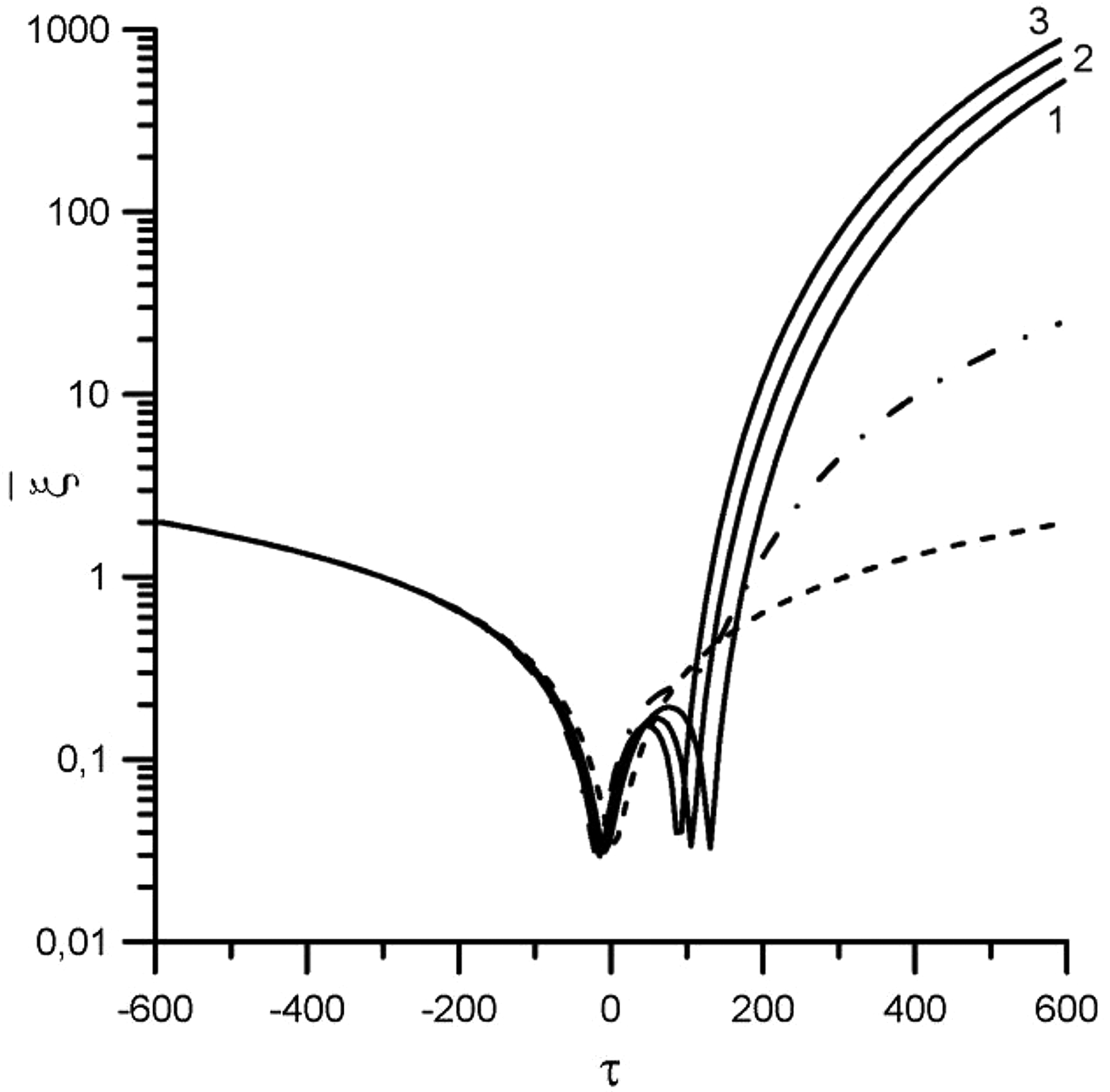
Fig. 4. The averaged relative distance ![]() $\bar {\rm \xi} $ (in logarithmic units) against the interaction time τ. The dashed line corresponds to case without external field. The dashed-dot line and solid lines correspond to oscillation velocities: η1 = 3 × 10−3, η2 = 10−1 (the field intensities: I 1 = 3.4 × 1012 W/cm2, I 2 = 3.8 × 1015 W/cm2), the phase shifts of pulse peaks: 1 – δτ1 = −300, δτ2 = 350; 2 – δτ1 = −400, δτ2 = 300; 3 – δτ1 = −450, δτ2 = 250; the dashed-dot line – δτ1 = 0, δτ2 = 0.
$\bar {\rm \xi} $ (in logarithmic units) against the interaction time τ. The dashed line corresponds to case without external field. The dashed-dot line and solid lines correspond to oscillation velocities: η1 = 3 × 10−3, η2 = 10−1 (the field intensities: I 1 = 3.4 × 1012 W/cm2, I 2 = 3.8 × 1015 W/cm2), the phase shifts of pulse peaks: 1 – δτ1 = −300, δτ2 = 350; 2 – δτ1 = −400, δτ2 = 300; 3 – δτ1 = −450, δτ2 = 250; the dashed-dot line – δτ1 = 0, δτ2 = 0.
The effective slowing-down of electrons
The case, when the oscillation velocity η1 has to be close to the initial relative velocity ![]() ${\rm \eta} _1 \approx \dot {\rm \xi} _0$ and the oscillation velocity η2 is greater an order of magnitude, increasing the interaction time allows us to see oscillations of the effective attraction of electrons. Electrons, after approaching and scattering, get the strong pulse of the attraction and then they re-approach. Let us designate the time at which the averaged relative distance between electrons is equal to
${\rm \eta} _1 \approx \dot {\rm \xi} _0$ and the oscillation velocity η2 is greater an order of magnitude, increasing the interaction time allows us to see oscillations of the effective attraction of electrons. Electrons, after approaching and scattering, get the strong pulse of the attraction and then they re-approach. Let us designate the time at which the averaged relative distance between electrons is equal to ![]() $\bar {\rm \xi} _{{\rm Cfinal}} = 2$: in the external field, when δτ1 = 0, δτ2 = 0 –
$\bar {\rm \xi} _{{\rm Cfinal}} = 2$: in the external field, when δτ1 = 0, δτ2 = 0 – ![]() ${\rm \tau} _{{\rm final}}^{(0)} $; in the external field, when δτ1 ≠ 0, δτ2 ≠ 0 – τfinal. Fig. 5 shows dependence of the final distance
${\rm \tau} _{{\rm final}}^{(0)} $; in the external field, when δτ1 ≠ 0, δτ2 ≠ 0 – τfinal. Fig. 5 shows dependence of the final distance ![]() $\bar {\rm \xi} _{{\rm final}}$ at which electrons scatter at the time τ = 2000 for different values of phase shifts δτ1, δτ2 and next values of oscillation velocities η1 = 1.7 × 10−3, η2 = 3 × 10−2. It is seen that the final distance
$\bar {\rm \xi} _{{\rm final}}$ at which electrons scatter at the time τ = 2000 for different values of phase shifts δτ1, δτ2 and next values of oscillation velocities η1 = 1.7 × 10−3, η2 = 3 × 10−2. It is seen that the final distance ![]() $\bar {\rm \xi} _{{\rm final}}$ is smaller
$\bar {\rm \xi} _{{\rm final}}$ is smaller ![]() $\bar {\rm \xi} _{{\rm Cfinal}} = 2$ and it has the minimum value down to
$\bar {\rm \xi} _{{\rm Cfinal}} = 2$ and it has the minimum value down to ![]() $\bar {\rm \xi} _{{\rm final}} = 10^{ - 1}$ for the next ranges of phase shifts
$\bar {\rm \xi} _{{\rm final}} = 10^{ - 1}$ for the next ranges of phase shifts ![]() ${\rm \delta} {\rm \tau} _1 \in \left[ {200 \div 400} \right]$,
${\rm \delta} {\rm \tau} _1 \in \left[ {200 \div 400} \right]$, ![]() ${\rm \delta} {\rm \tau} _2 \in \left[ {100 \div 600} \right]$.
${\rm \delta} {\rm \tau} _2 \in \left[ {100 \div 600} \right]$.
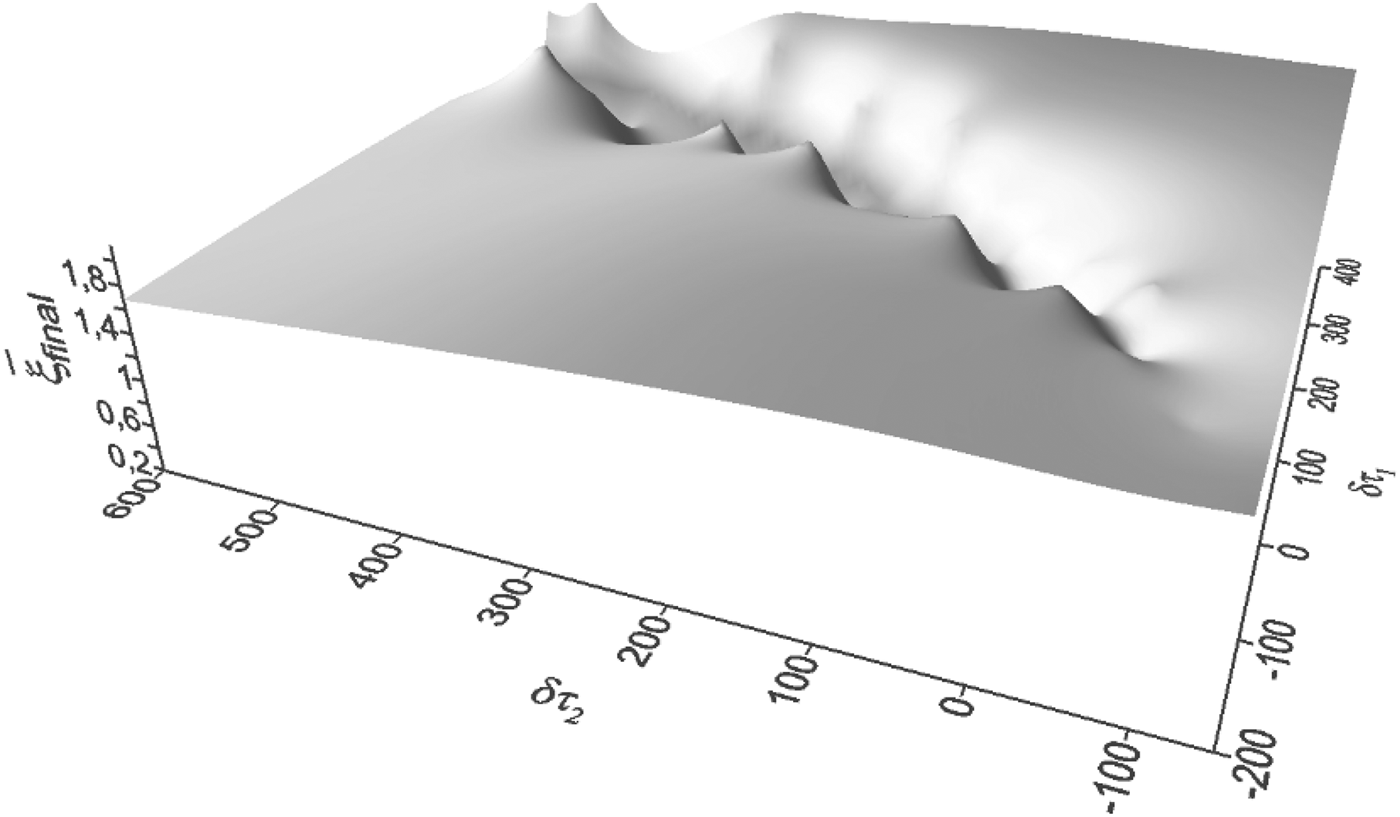
Fig. 5. The final averaged relative distance ![]() $\bar {\rm \xi} _{{\rm final}}$ (in the time moment τ = 2000,
$\bar {\rm \xi} _{{\rm final}}$ (in the time moment τ = 2000, ![]() $\bar {\rm \xi} _{{\rm Cfinal}} = 2$) against different phase shifts of the pulse peaks δτ1, δτ2. Oscillation velocities:
$\bar {\rm \xi} _{{\rm Cfinal}} = 2$) against different phase shifts of the pulse peaks δτ1, δτ2. Oscillation velocities: ![]() ${\rm \eta} _1 = \dot {\rm \xi} _0 = 1.7 \times 10^{ - 3}$, η2 = 3 × 10−2 (field intensities: I 1 = 1.1 × 1012 W/cm2, I 2 = 3.4 × 1014 W/cm2).
${\rm \eta} _1 = \dot {\rm \xi} _0 = 1.7 \times 10^{ - 3}$, η2 = 3 × 10−2 (field intensities: I 1 = 1.1 × 1012 W/cm2, I 2 = 3.4 × 1014 W/cm2).
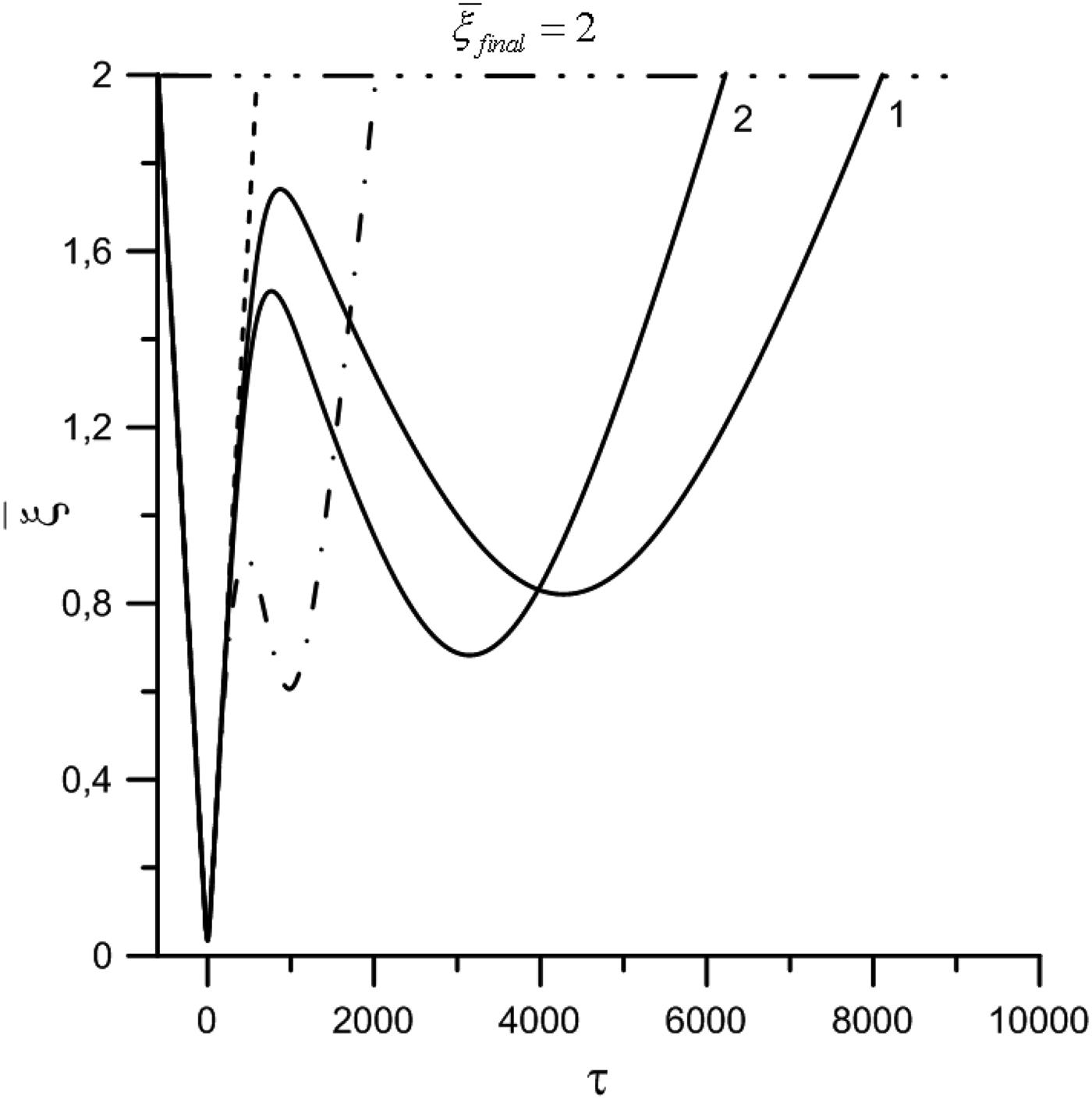
Figure 6 shows dependence of averaged relative distance ![]() $\bar {\rm \xi} $ on the interaction time τ for mainly interesting values of the phase shifts. One can see that taking into account of the phase shifts can considerably increase the attraction force. Thus, the time of electron scattering to the initial value of the distance (
$\bar {\rm \xi} $ on the interaction time τ for mainly interesting values of the phase shifts. One can see that taking into account of the phase shifts can considerably increase the attraction force. Thus, the time of electron scattering to the initial value of the distance (![]() $\bar {\rm \xi} _{{\rm Cfinal}} = 2$) is increased in comparison with the case without an external field to τfinal/τCfinal ≈ 13.5 (see Fig. 6 curve 1 and the dashed line); in the external field when δτ1 = 0, δτ2 = 0 the time is increased to
$\bar {\rm \xi} _{{\rm Cfinal}} = 2$) is increased in comparison with the case without an external field to τfinal/τCfinal ≈ 13.5 (see Fig. 6 curve 1 and the dashed line); in the external field when δτ1 = 0, δτ2 = 0 the time is increased to ![]() ${\rm \tau} _{{\rm final}}/{\rm \tau} _{{\rm final}}^{(0)} \approx 4$ (see Fig. 6 curve 1 and the dashed-dot line) for oscillation velocities η1 = 1.7 × 10−3, η2 = 3 × 10−2 and phase shifts δτ1 = 350, δτ2 = 400. The effect is a bit weaker for phase shifts δτ1 = 300, δτ2 = 300 (see Fig. 6 curve 2).
${\rm \tau} _{{\rm final}}/{\rm \tau} _{{\rm final}}^{(0)} \approx 4$ (see Fig. 6 curve 1 and the dashed-dot line) for oscillation velocities η1 = 1.7 × 10−3, η2 = 3 × 10−2 and phase shifts δτ1 = 350, δτ2 = 400. The effect is a bit weaker for phase shifts δτ1 = 300, δτ2 = 300 (see Fig. 6 curve 2).

Fig. 6. The averaged relative distance ![]() $\bar {\rm \xi} $ against the interaction time τ. The dashed line corresponds to case without external field. The dashed-dot line and solid lines correspond to the oscillation velocity:
$\bar {\rm \xi} $ against the interaction time τ. The dashed line corresponds to case without external field. The dashed-dot line and solid lines correspond to the oscillation velocity: ![]() ${\rm \eta} _1 = \dot {\rm \xi} _0 = 1.7 \times 10^{ - 3}$, η2 = 3 × 10−2 (the field intensity: I 1 = 1.1 × 1012 W/cm2, I 2 = 3.4 × 1014 W/cm2), phase shifts of pulse peaks: 1 – δτ1 = 350, δτ2 = 400, 2 – δτ1 = 300, δτ2 = 300; the dashed-dot line – δτ1 = 0, δτ2 = 0.
${\rm \eta} _1 = \dot {\rm \xi} _0 = 1.7 \times 10^{ - 3}$, η2 = 3 × 10−2 (the field intensity: I 1 = 1.1 × 1012 W/cm2, I 2 = 3.4 × 1014 W/cm2), phase shifts of pulse peaks: 1 – δτ1 = 350, δτ2 = 400, 2 – δτ1 = 300, δτ2 = 300; the dashed-dot line – δτ1 = 0, δτ2 = 0.
Conclusion
Performed study shows that taking into account of phase shifts of pulse peaks can essentially change the behavior of the effective interaction of electrons. Finally, the following results are achieved:
1. The anomalous repulsion of electrons is observed when the oscillation velocity of the first wave is greater than the initial velocity of electrons (
 ${\rm \eta} _1 \gt \dot {\rm \xi} _0$), and the oscillation velocity of the second wave is considerably greater (
${\rm \eta} _1 \gt \dot {\rm \xi} _0$), and the oscillation velocity of the second wave is considerably greater ( ${\rm \eta} _2 \gg \dot {\rm \xi} _0$). Thus, the maximum effect of anomalous repulsion of electrons corresponds to the following ranges of phase shifts of pulse peaks:
${\rm \eta} _2 \gg \dot {\rm \xi} _0$). Thus, the maximum effect of anomalous repulsion of electrons corresponds to the following ranges of phase shifts of pulse peaks:  ${\rm \delta} {\rm \tau} _1 \in \left[ { - 300 \div -550} \right]$,
${\rm \delta} {\rm \tau} _1 \in \left[ { - 300 \div -550} \right]$,  ${\rm \delta} {\rm \tau} _2 \in \left[ {250 \div 450} \right]$. So, for intensities of the waves I 1 = 3.4 × 1012 W/cm2, I 2 = 3.8 × 1015 W/cm2 and phase shifts δτ1 = −450, δτ2 = 250 the ratio,
${\rm \delta} {\rm \tau} _2 \in \left[ {250 \div 450} \right]$. So, for intensities of the waves I 1 = 3.4 × 1012 W/cm2, I 2 = 3.8 × 1015 W/cm2 and phase shifts δτ1 = −450, δτ2 = 250 the ratio,  $\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} _{{\rm Cfinal}} \approx 450$ and the ratio
$\bar {\rm \xi} _{{\rm final}}/\bar {\rm \xi} _{{\rm Cfinal}} \approx 450$ and the ratio  $\bar {\rm \xi} _{{\rm final}}\bar {\rm \xi} ^{(0)}_{{\rm final}} \approx 180$.
$\bar {\rm \xi} _{{\rm final}}\bar {\rm \xi} ^{(0)}_{{\rm final}} \approx 180$.2. The effective attraction of electrons takes place, when the oscillation velocity η1 has to be close to the initial relative velocity (
 ${\rm \eta} _1 \approx \dot {\rm \xi} _0$), and the oscillation velocity of the second wave is greater in an order of the magnitude. Thus, the maximum effect of slowing-down of electrons corresponds to the following ranges of phase shifts of pulse peaks:
${\rm \eta} _1 \approx \dot {\rm \xi} _0$), and the oscillation velocity of the second wave is greater in an order of the magnitude. Thus, the maximum effect of slowing-down of electrons corresponds to the following ranges of phase shifts of pulse peaks:  ${\rm \delta} {\rm \tau} _1 \in \left[ {350 \div 400} \right]$,
${\rm \delta} {\rm \tau} _1 \in \left[ {350 \div 400} \right]$,  ${\rm \delta} {\rm \tau} _2 \in \left[ {400 \div 550} \right]$. So, for intensities of waves I 1 = 1.1 × 1012 W/cm2, I 2 = 3.4 × 1014 W/cm2 and phase shifts δτ1 = 400, δτ2 = 550 the values of slowing-down of electrons may be equal τfinal/τCfinal ≈ 16.5 and
${\rm \delta} {\rm \tau} _2 \in \left[ {400 \div 550} \right]$. So, for intensities of waves I 1 = 1.1 × 1012 W/cm2, I 2 = 3.4 × 1014 W/cm2 and phase shifts δτ1 = 400, δτ2 = 550 the values of slowing-down of electrons may be equal τfinal/τCfinal ≈ 16.5 and  ${\rm \tau} _{\rm final}/{\rm \tau} _{\rm final}^{(0)} \approx 5$.
${\rm \tau} _{\rm final}/{\rm \tau} _{\rm final}^{(0)} \approx 5$.