1. INTRODUCTION
Electron atom and electron ion collision strengths are of crucial importance in the analysis of many laboratory and astrophysical plasmas including those arising in laser-plasma interactions, controlled thermonuclear fusion devices such as tokamaks, planetary atmospheres, stellar atmospheres, gaseous nebulae, and active galactic nuclei and supernovae. The interpretation of measured line intensities requires the knowledge of atomic physics describing the specific radiation from the plasma. Electron impact data is therefore required to model the populating processes of the radiating levels. Theoretical calculations are the primary source of information on electron collisions with many atomic and molecular systems.
Li-like ions are of particular importance, especially those with high nuclear charge Z which are present due to evaporation of some of the wall material of the plasma container in controlled thermonuclear plasmas. These ions are also of importance in determining temperatures in the solar corona. Amplification of XUV radiation in plasmas produced by powerful lasers on Al target has also been reported (Klisnick et al., 1990). X-ray signals from the H- and He-like ionization stages of Al ions were observed at the ambiorix Z-pinch facility on the use of an Al vapor jet onto a very thin coaxial wire (Rosch et al., 2000). Additional, theoretical analysis of the spectral intensities distribution in well-resolved Ly (alpha) satellites from the X-ray diagnostics of Z-pinch hot points formed during fast electrical discharges through exploding Al wires, have been carried out by Politov et al. (2000). Recently, spatial distribution of gain coefficients of Li-like Al ion transition line has been measured by micro-dot array irradiation method (Yamaguchi et al., 2002). The li-like scheme appears to be a good candidate for lasing in the water window, owing to its relatively low requirement in driving-laser energy.
Laser ablated Al plasma and the corresponding optical emission is used to simulate energetic protons accelerated from the rear side of the target. Characteristic X-ray generated by high-intensity laser interaction with solids is used for determining the resulting hot electron populations (Pretzler et al., 2001). Recent experimental works studying high intensity laser-plasma interactions at intensities greater than 1019 W/cm2 has shown that such plasmas can potentially be an efficient source of very energetic electrons, gamma rays, and ions.
The field of electron-ion collision studies has reached a level of maturity where both, recombination and ionization-total cross sections, are investigated with excellent precision. Electronic excitation and recombination cross sections are needed for a variety of applications and their calculation places more emphasis on the accurate representation of target electron wave functions than the study of other processes. Calculations of the collision strengths are computationally demanding because of the dense Rydberg resonance structure below the highest target threshold. The low-temperature effective collision strength will be sensitive to the resonance structure.
The work by Bhada and Henry (1982) refers to effect of resonances on 2s–2p and 3l–3l′ excitation in O5+, C3+, Ne7+, and Ar15+. It has been shown that the resonance contribution to excitation cross sections or collision strengths can be very important for allowed transitions as well as for forbidden ones. Intermediate coupling collision strengths for inner-shell excitation of highly charged Li-like Ar, Fe, and Mo ions have been reported by Sampson et al. (1979). The approach used is a Coulomb–Born-exchange method that can be regarded as a perturbation theory approach in which the zero-order functions are composed of hydrogenic orbitals. Including intermediate coupling, configuration mixing, and parentage mixing effects, their results are expressed in a simple form.
A very limited number of collision strength calculations have been published for Al10+. Zhang et al. (1990) gave extensive tables of collision strengths Ω for transitions in Li-like ions with atomic numbers Z = 8, 14, 22, 30, 42, 56, 74, 92. Their work was based on relativistic distorted wave approximation method. Making use of an eight parameter analytic fit in Z, these authors completed their tabulation for the remaining ions in the sequence between O5+ and U89+. These results were further considered by Burgess et al. (1998) to get out compact effective collision strengths for 2s − ns, nd (n ≤ 5) including forbidden transitions. These authors fit the extensive tables by Zhang et al. (1990) for non-optically allowed transitions to get values for Li-like ions of charge 1 to 23 in a compact form. The atomic data themselves are not available in this work.
In this paper, we report collision strengths for allowed and forbidden transitions in excitation by electron impact in Al10+. For LS coupling calculation, we used the code FARM of Burke and Noble (1995). SUPERSTRUCTURE code by Eissner et al. (1974) has been used to output values in intermediate coupling scheme. The effective collision strengths are calculated as a function of temperature, up to a temperature that does not exceed half of the maximum energy in the R-matrix run. In general, the highest energy for which accurate collision strengths can be calculated is about half the maximum eigen-energy of the continuum basis orbitals.
2. CALCULATION
An initial calculation using LS coupling with FARM—a flexible asymptotic R-matrix package—has been performed for solving the scattering in the external region of configuration space where exchange effects may be neglected. The package uses a combination of R-matrix propagation techniques to ensure optimum stability and efficiency in integrating the coupled Schrödinger equations. The radial distance over which the equations must be integrated is minimized by matching to an asymptotic wave-function determined by an accelerated Gailitis (1976) expansion. Results are referred to allowed transitions involving five target states in LS coupling.
R-matrix theory has been developed into a highly efficient computational technique for studying collisions between electrons or positrons, and both atomic (Burke & Robb, 1975) and molecular targets. The compilation volume by Burke and Berrington (1993) provides both a general review of the R-matrix method as applied to atomic and molecular collision processes, and a very extensive bibliography. Following the R-matrix approach, the collision is considered separately according to whether the projectile is inside or external to the charge cloud of the target. The solutions obtained in each of these regions are related by the R-matrix which corresponds to the inverse of the logarithmic derivative of the wave-function on the boundary of the two regions. FARM includes interface code allowing the required input information to be obtained directly from the H-files used in the atomic R-matrix scattering programs. Six orthogonal one-electron orbitals 1s, 2s, 2p, 3s, 3p, 3d were used in the present work.
An initial structure calculation was carried out for Al10+ to determine the lowest five states in LS coupling with the configurations 1s22l and 1s23l. The configuration interaction structure code CIV3 (Hibbert, 1975) was used. The radial orbitals 1s, 2s, 2p, 3s, 3p, 3d were taken from Tully et al. (1990). A comparison of the calculated energy of the states relative to the ground agreed well with the observed values (Stancalie, 2000) to better than 2.5%.We converted our results in jj coupling scheme to obtain fine structure atomic data as line strengths for electric dipole, -quadrupole, and octupole transitions. Contribution to the generalized oscillator strength of the forbidden transition in excitation by electron impact from the ground state 1s22s1/2 and from the first excited states 1s22p1/2, 1s22p3/2, to all states nlj, with n ≤ 5, has been considered in our earlier work (Stancalie et al., 1999).
In order to calculate the scattering observables, it is necessary to match the R-matrix obtained by outward propagation from the internal region boundary to the asymptotic radial solutions. The radial scattering equations must be integrated outward from the boundary of the R-matrix internal region, to a point where they can be matched to the asymptotic form of the solution with the appropriate boundary conditions.
FARM uses a simplified version of the Padé algorithm (Noble & Nesbet, 1984) to obtain the expansion coefficients in terms of Z/k rather than of (Z/k)2. The method allows the expansion is determined directly from a single set of recursion relations rather than indirectly by expanding and dividing out the Coulomb factors. Finally, collision strengths, phase shift, and cross sections may be obtained directly from the scattering K-matrix. The total collision strength, Ω(p,q) for excitation from target state p to target state q in LS coupling is given by:

where the first sum is over all partial waves, and the second over channels pi, qj involving the states p,q, respectively. In jj coupling, the statistical weights need to be changed in the above equations. The transmission matrix T is given by:
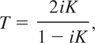
which is related to the scattering matrix S by: T = S − 1.
Scaled units are used by the code. For positively charged ions energies are scaled by a factor 1/Z2, where Z is the charge on the ion (Z = 10 for Li-like Al). Results refer to five scattering energies of which the highest is 2.5 scaled Rydbergs (25 Rydbergs) relative to the ground state of Al XI. The K-matrices, T-matrices, eigen-phases, and total collision strengths are output from the code. The final R-matrix radius was 44 scaled Bohr (4.4 Bohr). Exchange was neglected for total L > 20. Using an initial radius of 2 scaled Bohr (0.2 Bohr) at which the R-matrix is calculated, the number of multi-poles retained in potential was four. Five target states, in energy order 1s22s2S, 1s22p2P0, 1s23s2S, 1s23p2P0, and 1s23d2D have been included in the R-matrix expansion of the total wave function. They are indexed from 1 to 5 in Table 1, where are presented the calculated state energy relative to the ground in scaled rydberg units.
Target states in excitation by electron impact. Energies are scaled by a factor 1/Z2, where Z = 10 for Li-like Al ion. The indexing is in the order of the listing of the five states above with the ground state, 1s22s2S, indexed as 1.

We carried out calculation in a five-state close coupling approximation in the energy region below the third threshold. Selected results for total collision strength based on partial waves with L = 0 and 1 are presented in Table 2. The transitions are described by index of the lower and upper state where the indexing is in the order of the listing of the five states above with the ground state, 1s22s2S, indexed as 1. In scattering calculations involving long-range potentials, there may be significant contributions to cross sections from high partial waves (large orbital angular momentum values). This is especially true for the calculation of differential cross sections. In these cases, it is inefficient and unnecessary to carry out full variational calculations in the inner R-matrix region. For example, for partial waves greater than some empirically determined value (typically around L = 12), it is a good approximations to neglect electron exchange effects in the inner region calculations. For somewhat higher partial waves, the scattering wave function is suppressed throughout a significant part of the internal region, and only the periphery of the charge distribution of the target is seen by the scattering electron. For these contributions it is clear that this approximation includes coupling effects between the scattering channels and is therefore accurate for partial waves below those for which the Born approximation is valid.
Total collision strengths for partial waves with total angular momentum L = 0, 1. Values a−b read a × 10−b. Energy is given in scaled rydbergs units (scaled by a factor 1/Z2). The transitions are described by index of the lower and upper state where the indexing is in the order of the listing of the five states above with the ground state, 1s22s2S, indexed as 1.

The intermediate-coupling calculations were performed using the SUPERSTRUCTURE program. The SUPERSTRUCTURE code is based on a scaled Thomas-Fermi-Dirac-Amadi potential. The scaling parameter is different for each angular momentum l. These parameters are iterated to give a minimum energy of a term or a group of terms. It should be noted that this method does not take into account correlation effects properly, which explains the disagreement of these atomic data with the previously reported, for some states. SUPERSTRUCTURE computes atomic energies and radiative data in LS coupling and in intermediate coupling using the Breit-Pauli Hamiltonian as in CIV3. It applies Slater techniques of Condon and Shortley (1951) to expand the angular terms in the usual multi-configuration approach. Unless the user supplies radial orbitals Pnl(r) in tabulated form, the program internally calculates radial functions in a scaled statistical model potential, the scaled parameter are determined variationally. Among subsequent intermediate coupling extensions, the first feature incorporated originates in the work of Blume and Watson (1962), who showed that mutual spin-orbit effects of a closed electronic shell on a valence electron, behave like an effective screening on the spin-orbit coupling parameter. The code incorporates corrections to radiative operators that contribute to the transition amplitude with terms of equal order in α2 as the Breit-Pauli components in the wave function. In Table 3 we report comparative results for electric quadru-pole and octupole line strengths, as obtained from the calculation with SST and previous calculation based on the CIV3.
Calculated transition line strengths, S, in atomic units (a.u.) for electric-quadrupole(E2), and -octupole(E3) transitions in Al10+

High energy Born collision strengths for forbidden transitions are calculated and compared in Table 4, with those reported by using compact formula by Burgess et al. (1998). The effective collision strength as a function of temperature, have been obtained up to a temperature that does not exceed half of the maximum energy in the R-matrix run. In Table 5 are reported results on effective collision strengths for transition type 2s1/2 − nlj, Ω(nlj). Table 6 reports LS coupling results.
High energy Born collision strengths Ω(nlj − n′l′j′), for Eλ(λ = 0,2,3,4) transitions in Al10+

Effective collision strengths for transitions 2s1/2 − nlj, Ω(nlj), a non-exchange R-matrix calculation. Collision energy is given in scaled rydbergs units (scaled by a factor 1/Z2)

Effective collision strengths, Ω(n1 l1 → n2 l2), full-exchange LS coupling R-matrix calculation. Collision energy is scaled by a factor 1/Z2

3. CONCLUSIONS
This paper concerns some developments on electron-scattering Al10+ analysis in the context of R-matrix calculation. The work is motivated by the need for accurate and systematic procedures for calculating auto-ionizing levels, particularly for laboratory and astrophysical opacity calculations. Recently, position and widths for Rydberg states of configuration 1s22sns(1S) and 1s22pns (1P), 9 ≤ n ≤ 12, have been reported (Stancalie, 2005a, 2005b) on the use of the QDT/R-matrix floquet and its extension to laser induced degenerate state phenomenon. Earlier work by Quigley and Berrington (1996) proposed a study of resonances exploiting the analytic properties of R-matrix theory (the QB method). In order to compare the above mentioned methods, we have inferred the R-matrix calculation with FARM to get out eigen-phases, then to apply the QB method. Partial results referring to collision strengths have been presented in this work. A huge number of collision strengths have been reported for Li-like system, but only a few refer to Al10+ and they are output from interpolation over the lithium sequence. In this work, we used SUPERSTRUCTURE code and the intermediate coupling parameters to calculate collision strengths for forbidden transitions. Results do not take into account the effect of resonances. This paper gives effective collision strengths for collision energy of interest in analyzing resonances. Comparisons are provided with available data for high collision strengths in Table 4. The presented results agreed well with more accurate calculations for 2s1/2 − 3d3/2, but less for the other. The accuracy should be improved and such work is in progress.
ACKNOWLEDGMENTS
This work was conducted under COST Action P14 laser-matter interactions with ultrashort pulses, high-frequency pulses and ultra intense pulses. From astrophysics to petawatt physics. V.S. acknowledges the Department of Applied Mathematics and Theoretical Physics, The Queen's University of Belfast, where part of this work was performed under European ERB-CHRX CT920013, additional 940025. The author takes this opportunity to thank Professor P. G. Burke and Mrs. V. M. Burke for their help, guidance, and friendship over many years.








