2. ANALYTICAL FORMULATION

2.1. Nonlinear Dielectric Constant of the Plasma

Consider the propagation of a Gaussian laser beam of frequency ω₀ and wave number k ₀ in collisionless homogeneous plasma along the z direction. The initial intensity distribution of the main beam can be represented by

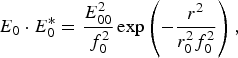(1)$$E_0 \cdot E_0^{\ast} = \displaystyle{{E_{00}^2 } \over {\,f_0^2 }}\exp \left({ - \displaystyle{{r^2 } \over {r_0^2 f_0^2 }}} \right)\comma \;$$

and the initial intensity distribution of the ripple superimposed on the main beam may be expressed as

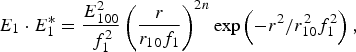(2)$$E_1 \cdot E_1^{\ast} = \displaystyle{{E_{100}^2 } \over {\,f_1^2 }}\left({\displaystyle{r \over {r_{10}f_1 }}} \right)^{2n} \exp \left({ - r^2/r_{10}^2 f_1^2 } \right)\comma \;$$

where r ₀ is the initial beam width, r is the radial coordinate of cylindrical coordinate system, and E ₀₀ is the axial amplitude of the main beam, E ₁₀₀ refers to the initial amplitude of the ripple, n is a positive number characterize the position of the ripple, r ₁₀ is the width of the ripple; as n increases, the maximum (r _max = r ₁₀f ₁n ^1/2) of the ripple shifts away from the axis, and f ₀ and f ₁ are the beam width parameters of the main beam and the rippled beam. The ripple is usually a small perturbation over the main beam and its parameters may be assumed to satisfy

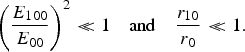$$\left({\displaystyle{{E_{100} } \over {E_{00} }}} \right)^2 \lt\!\!\! \lt 1 \quad {\rm and} \quad \displaystyle{{r_{10} } \over {r_0 }} \lt\!\!\! \lt 1.$$

The total electric vector E of a Gaussian beam with ripple can be expressed as

(3)$$E = E_0 + E_1.$$

The intensity distribution of the beam is given by

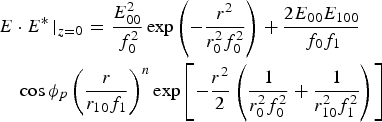(4)$$\eqalign {& E \cdot E^{\ast} \left\vert _{z = 0} \right. = \displaystyle{{E_{00}^2 } \over {\,f_0^2 }}\exp \left({ - \displaystyle{{r^2 } \over {r_0^2 f_0^2 }}} \right)+ \displaystyle{{2E_{00} E_{100} } \over {\,f_0 f_1 }} \cr & \quad \cos {\rm \phi} _p \left({\displaystyle{r \over {r_{10} f_1 }}} \right)^n \exp \left[{ - \displaystyle{{r^2 } \over 2}\left({\displaystyle{1 \over {r_0^2 f_0^2 }} + \displaystyle{1 \over {r_{10}^2 f_1^2 }}} \right)} \right]}$$

where ϕ_p is the angle between the electric vectors of the main beam and the ripple.

The effective dielectric constant of the plasma at frequency ω₀ can be expressed as

(5)$${\rm \varepsilon} = {\rm \varepsilon} _0 + {\rm \varphi} \lpar E \cdot E^{\ast} \rpar$$

Here ε₀ and ϕ(E.E*) are the linear and nonlinear parts of the dielectric constant and are given by

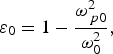$${\rm \varepsilon} _0 = 1 - \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }}\comma \;$$

and

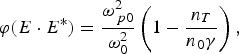$${\rm \varphi} \lpar E \cdot E^{\ast} \rpar = \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }}\left({1 - \displaystyle{n_T \over {n_0 {\rm \gamma} }}} \right)\comma \;$$

where ω_p0 is the relativistic plasma frequency given by ω_p0 = 4πn ₀e ²/m ₀γ (with e being the charge of an electron, m ₀ its rest mass, and n ₀ is the density of plasma electrons in the absence of laser beam) and γ is the relativistic factor. The relativistic-ponderomotive force on an electron in the presence of an intense laser beam may be represented as (Borishov et al., Reference Borisov, Borovisiky, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992; Brandi et al., Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993; Gupta et al., Reference Gupta, Sharma and Gupta2005)

(6)$$F_P = - m_0 c^2 \nabla \lpar {\rm \gamma} - 1\rpar .$$

The relativistic factor γ is given by

(7)$${\rm \gamma} = \left[{1 + \alpha E_0 \cdot E_0^{\ast} } \right]^{1/2}\comma \;$$

and

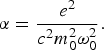$${\rm \alpha} = \displaystyle{{e^2 } \over {c^2 m_0^2 {\rm \omega} _0^2 }}.$$

Eq. (6) is valid, when there is no change in the plasma density. Using the electron continuity equation and the current density equation for second-order correction in the electron density equation (with the help of ponderomotive force), the total density n_T is given by (Brandi et al., Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993)

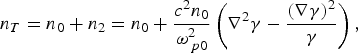(8)$${n_{T}} = n_0 + n_2 = n_0 + \displaystyle{{c^2 n_0 } \over {{\rm \omega} _{\,p0}^2 }}\left({\nabla ^2 {\rm \gamma} - \displaystyle{{\lpar \nabla {\rm \gamma} \rpar ^2 } \over {\rm \gamma} }} \right)\comma \;$$

where, n ₂ is the nonlinear variation of the density together with the relativistic correction i.e. second order correction in the electron density equation and

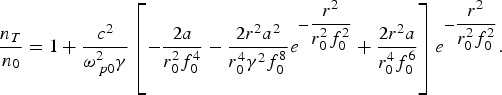$$\displaystyle{{n_T} \over {n_0}} = 1 + \displaystyle{{c^2 } \over {{\rm \omega} _{\,p0}^2 {\rm \gamma} }}\left[{ - \displaystyle{{2a} \over {r_0^2 f_0^4 }} - \displaystyle{{2r^2 a^2 } \over {r_0^4 {\rm \gamma} ^2 f_0^8 }}e^{ - \displaystyle{{r^2 } \over {r_0^2 f_0^2 }}} + \displaystyle{{2r^2 a} \over {r_0^4 f_0^6 }}} \right]e^{ - \displaystyle{{r^2 } \over {r_0^2 f_0^2 }}}.$$

To write the dielectric constant of the plasma (in the presence of the main laser beam) in the paraxial region where (E ₁·E ₁* ≤ E ₀·E ₀*), it is a good approximation to assume ε(r, z) to be function of E ₀ alone, i.e., ϕ(E·E*) ~ ϕ(E ₀·E ₀*). Thus in Eq. (5), ε(r, z) may be replaced by ε₀(r, z) where

(9)$${\rm \varepsilon} _0 \lpar r\comma \; z\rpar = {\rm \varepsilon} _0 + {\rm \phi} \lpar E_0\cdot E_0^{\ast}\rpar \comma \;$$

and expanding the dielectric constant in Eq. (5) around r = 0 by Taylor expansion, one can write

(10)$${\rm \varepsilon}_0 \lpar r\comma \; z\rpar = {\rm \varepsilon} _0 \lpar z\rpar + {\rm \gamma} _0 r^2\comma \;$$

where

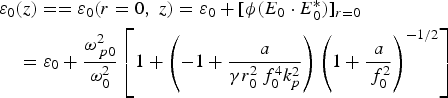$$\eqalign {& {\rm \varepsilon} _0 \lpar z\rpar = = {\rm \varepsilon} _0 \lpar r = 0\comma \; z\rpar = {\rm \varepsilon} _0 + [{\rm \phi} \lpar E_0 \cdot E_0^{\ast} \rpar] _{r = 0} \, \cr & \quad = {\rm \varepsilon} _0 + \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }} \left[{1 + \left({ - 1 + \displaystyle{a \over {{\rm \gamma} r_0^2 \,f_0^4 k_p^2 }}} \right)\left({1 + \displaystyle{a \over {\,f_0^2 }}} \right)^{ - 1/2} } \right]}$$

and

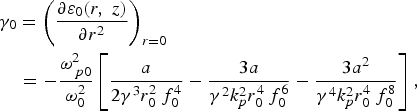$$\eqalign{& {\rm \gamma} _0 = \left({\displaystyle{{\partial {\rm \varepsilon} _0 \lpar r\comma \; z\rpar } \over {\partial r^2 }}} \right)_{r = 0} \cr & \quad = - \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }}\left[{\displaystyle{a \over {2{\rm \gamma} ^3 r_0^2 \,f_0^4 }} - \displaystyle{{3a} \over {{\rm \gamma} ^2 k_p^2 r_0^4 \,f_0^6 }} - \displaystyle{{3a^2 } \over {{\rm \gamma} ^4 k_p^2 r_0^4 \,f_0^8 }}} \right]\comma \; }$$

where a = αA ₀² (A ₀² = E ₀₀²) is square of dimensionless vector potential, f ₀ is the dimensionless beam width parameter of laser beam at z as given by Eq. (15), k _p² = ω_p0²/c ², and the rest of symbols have their usual meaning.

In order to obtain the dielectric constant of a rippled laser beam in plasma, we have taken the contribution of E·E*_, i.e., E·E* = (E ₀ + E ₁)·(E*₀ + E*₁), and the maximum intensity of ripple at (r _max² = r ₁₀²f ₁²n). One can write

(11)$${\rm \varepsilon} \lpar r\comma \; z\rpar = {\rm \varepsilon} _1 \lpar z\rpar + {\rm \gamma} _1 \lpar r^2 = r_{10}^2 f_1^2 n\rpar \comma \;$$

where

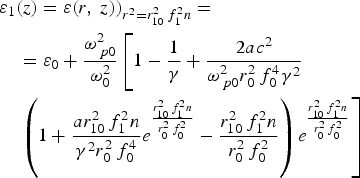$$\eqalign{& {\rm \varepsilon}_1 \lpar z\rpar = {\rm \varepsilon} \lpar r\comma \; z\rpar \rpar _{r^2 = r_{10}^2 \,f_1^2 n} = \cr & \quad = {\rm \varepsilon} _0 + \displaystyle{{\rm \omega}_{\,p0}^2 \over {\rm \omega}_0^2} \left[1 - \displaystyle{1 \over {\rm \gamma} } + \displaystyle{2ac^2 \over {\rm \omega}_{\,p0}^2 r_0^2 \,f_0^4 {\rm \gamma}^2} \right. \cr & \quad \left. \left(1 + \displaystyle{ar_{10}^2 \,f_1^2 n \over {\rm \gamma}^2 r_0^2 \,f_0^4}e^{{r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2}} - \displaystyle{r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2} \right)e^{{r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2}} \right]}$$

and

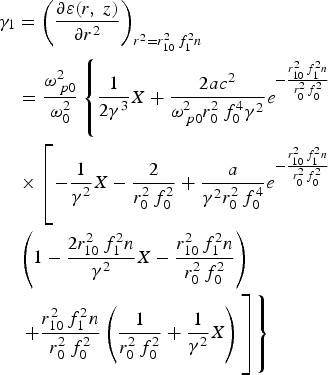$$\eqalign{& {\rm \gamma} _1 = \left({\displaystyle{{\partial {\rm \varepsilon} \lpar r\comma \; z\rpar } \over {\partial r^2 }}} \right)_{r^2 = r_{10}^2 \,f_1^2 n} \cr & \quad = \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }}\left\{{1 \over 2{\rm \gamma} ^3 } X + {2ac^2 \over {\rm \omega} _{\,p0}^2 r_0^2 \,f_0^4 {\rm \gamma} ^2 }e ^{ - {r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2 }} \right. \cr &\quad \times \left[- {1 \over {\rm \gamma} ^2} X - {2 \over r_0^2 \,f_0^2} + {a \over {\rm \gamma}^2 r_0^2 \,f_0^4} e^{- {r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2}} \right. \cr &\quad \left(1 - \displaystyle{2r_{10}^2 \,f_1^2 n \over {\rm \gamma}^2} X - \displaystyle{r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2} \right)\cr &\quad \left. \left. + \displaystyle{r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2} \left(\displaystyle{1 \over r_0^2 \,f_0^2} + \displaystyle{1 \over {\rm \gamma}^2} X \right)\vphantom{e ^{ - {r_{10}^2 \,f_1^2 n \over r_0^2 \,f_0^2 }}}\right]\right\}}$$

Here

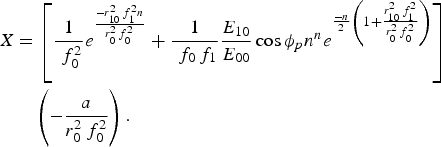$$\eqalign{X & = \left[{\displaystyle{1 \over {\,\,f_0^2 }}e^{{{ - r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} + \displaystyle{1 \over {\,\,f_0 \,f_1 }}\displaystyle{{E_{10} } \over {E_{00} }}\cos {\rm \phi} _p n^n e^{{{ - n} \over 2}\left({1 + {{r_{10}^2 \,f_1^2 } \over {r_0^2 \,f_0^2 }}} \right)} } \right]\cr & \quad \left({ - \displaystyle{a \over {r_0^2 \,f_0^2 }}} \right).}$$

2.2. Solution of Wave Equations and Growth of Laser Ripple in Plasma

The effective electric vector E satisfies the wave equation

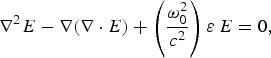(12)$$\nabla^2E - \nabla \lpar \nabla \cdot E\rpar + \left({\displaystyle{{{\rm \omega} _0^2 } \over {c^2 }}} \right){\rm \varepsilon} \, E = 0\comma \;$$

where ε is the effective dielectric constant of the plasma and c is the speed of light in free space. Under the Wentzel-Kramers-Brillouin approximation the second term of Eq. (12) can be neglected. Assuming the ripple to be a small perturbations one can write the wave equation for main beam (E ₀) and the ripple (E ₁), respectively,

(13)$$\nabla^2E_0 + \displaystyle{{{\rm \omega} _0^2 } \over {c^2}}{\rm \varepsilon} \lpar E_0 \cdot E_0^{\ast} \rpar E_0 = 0.$$

and

(14)$$\eqalign{\nabla^2E_1 + \displaystyle{{{\rm \omega} _0^2 } \over {c^2}}{\rm \varepsilon} \lpar E \cdot E^{\ast} \rpar E_1 + \displaystyle{{{\rm \omega} _0^2 } \over {c^2}}[ {\rm \phi} \lpar E \cdot E^{\ast} \rpar E_1 - {\rm \phi} \lpar E_0 \cdot E_0\rpar ] E_0 = 0.}$$

The solution of Eq. (13) can be written as (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976)

(15)$$E_0 = A_0\exp [ \!- ik_0\lpar z + S_0\rpar ] \comma \; \quad \quad S_0 = \lpar r^2/2\rpar {\rm \beta} _0\lpar Z\rpar + {\rm \phi} _0\lpar z\rpar \comma \;$$

$${\rm \beta} _0\lpar z\rpar = \displaystyle{1 \over {\,\,f_0}}\displaystyle{{d\,f_0} \over {dZ}}\comma \; \quad\quad k_0 = \displaystyle{{{\rm \omega} _0} \over c}{\rm \varepsilon} _0^{1/2} \comma \;$$

and the intensity of the main laser beam as

(16a)$$A_0^2 = \lpar E_{00}^2 /\,f_0^2 \rpar \exp \lpar - r^2/r_0^2 \,f_0^2 \rpar$$

The dimensionless beam width parameter f ₀ of the main beam can be obtained by using the initial boundary conditions $\,f_0 \left\vert {_{z = 0} } \right. = 1\,\, {\rm and}\,\, d\,f_0 /dz\left\vert {_{z = 0} \, = 0} \right.$ (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968)

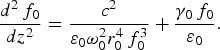(16b)$$\displaystyle{{d^2 \,f_0 } \over {dz^2 }} = \displaystyle{{c^2 } \over {{\rm \varepsilon} _0 {\rm \omega} _0^2 r_0^4 \,f_0^3 }} + \displaystyle{{{\rm \gamma} _0 \,f_0 } \over {{\rm \varepsilon} _0 }}.$$

To obtain the solution of Eq. (14) we express

(17)$$E_1 = A_1 \lpar r\comma \; z\rpar \exp \lpar \!- ik_0 z\rpar \comma \;$$

where A ₁(r, z) is a complex function of its argument. Substituting for E ₁ from Eq. (17) into Eq. (14) we get the following equation within the Wentzel-Kramers-Brillouin approximation:

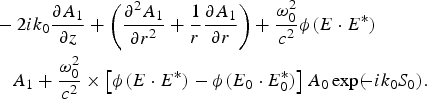(18)$$\eqalign{&- 2ik_0 \displaystyle{{\partial A_1} \over {\partial z}} + \left({\displaystyle{{\partial ^2A_1 } \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A_1 } \over {\partial r}}} \right)+ \displaystyle{{{\rm \omega} _0^2 } \over {c^2}}{\rm \phi} \lpar E \cdot E^{\ast} \rpar \cr & \quad A_1 + \displaystyle{{{\rm \omega} _0^2 } \over {c^2}} \times \left[{{\rm \phi} \lpar E \cdot E^{\ast} \rpar - {\rm \phi} \lpar E_0 \cdot E_0^{\ast} \rpar } \right]A_0\exp \lpar\!\! - ik_0S_0\rpar .}$$

Further, substituting for A ₁ in Eq. (18)

(19)$$A_1 = A_{10}\lpar r\comma \; z\rpar \exp [\!- ik_0S_1\lpar r\comma \; z\rpar] \comma \;$$

where A ₁₀ is a real function and S ₁ is the Eikonal. Using Eq. (19) into Eq. (18) and separating the real and imaginary parts we get

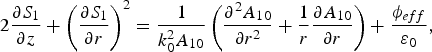(20a)$$2\displaystyle{{\partial S_1} \over {\partial z}} + \left({\displaystyle{{\partial S_1} \over {\partial r}}} \right)^2 = \displaystyle{1 \over {k_0^2 A_{10}}}\left({\displaystyle{{\partial ^2A_{10} } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_{10} } \over {\partial r}}} \right)+ \displaystyle{{{\rm \phi} _{eff} } \over {{\rm \varepsilon} _0 }}\comma \;$$

and

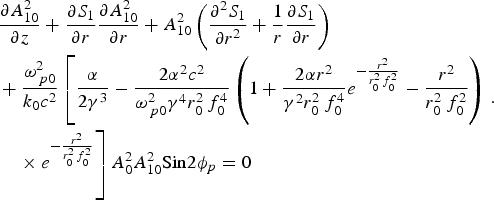(20b)$$\eqalign{& \displaystyle{{\partial A_{10}^2 } \over {\partial z}} + \displaystyle{{\partial {S_1}} \over {\partial r}}\displaystyle{{\partial A_{10}^2 } \over {\partial r}} + A_{10}^2 \left({\displaystyle{{{\partial ^2}{S_1}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {S_1}} \over {\partial r}}} \right)\cr & + \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{k_0}{c^2}}}\left[{\displaystyle{{\rm \alpha} \over {2{{\rm \gamma} ^3}}} - \displaystyle{{2{{\rm \alpha} ^2}{c^2}} \over {{\rm \omega} _{\,p0}^2 {{\rm \gamma} ^4}r_0^2 \,f_0^4 }}\left({1 + \displaystyle{{2{\rm \alpha} {r^2}} \over {{{\rm \gamma} ^2}r_0^2 \,f_0^4 }}{e^{ -{{{r^2}} \over {r_0^2 \,f_0^2 }}}} - \displaystyle{{{r^2}} \over {r_0^2 \,f_0^2 }}} \right)} \right. \cr & \quad \left. \times \ {{e^{ - {{{r^2}} \over {r_0^2 \,f_0^2 }}}}} \right]A_0^2 A_{10}^2 {\rm Sin}2{\phi _p} = 0}.$$

where

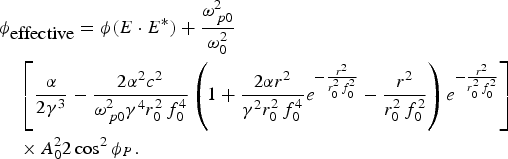$$\eqalign{& {\rm \phi} _{\hbox{effective}} = {\rm \phi} \lpar E \cdot E^{\ast} \rpar + \displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }} \cr & \quad \left[{\displaystyle{{\rm \alpha} \over {2{\rm \gamma} ^3 }} - \displaystyle{{2{\rm \alpha} ^2 c^2 } \over {{\rm \omega} _{\,p0}^2 {\rm \gamma} ^4 r_0^2 \,f_0^4 }}\left({1 + \displaystyle{{2{\rm \alpha} r^2 } \over {{\rm \gamma} ^2 r_0^2 \,f_0^4 }}e^{ -{{r^2 } \over {r_0^2 \,f_0^2 }}} - \displaystyle{{r^2 } \over {r_0^2 \,f_0^2 }}} \right)e^{ - {{r^2 } \over {r_0^2 \,f_0^2 }}} } \right]\cr & \quad \times A_0^2 2\cos ^2 {\rm \phi} _P.}$$

Eq. (20) can be expanded as

$$\Phi \lpar E \cdot E^{\ast} \rpar = \Phi \lpar E_0 \cdot E_0^{\ast} \rpar + \displaystyle{{d\Phi } \over {dE \cdot E^{\ast} }}\left\vert \matrix{\cr _{E \cdot E^{\ast} = E_0 \cdot E_0^{\ast} }} \right.\lpar E \cdot E^{\ast} - E_0 \cdot E_0^{\ast} \rpar .$$

The solution of Eqs. (20a) and (20b) can be written as (Sodha et al., Reference Sodha, Singh, Singh and Sharma1981)

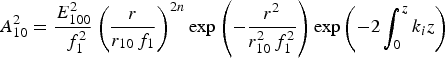(21a)$$A_{10}^2 = \displaystyle{{E_{100}^2 } \over {\,\,f_1^2 }}\left({\displaystyle{r \over {r_{10} \,f_1 }}} \right)^{2n} \exp \left({ - \displaystyle{{r^2 } \over {r_{10}^2 \,f_1^2 }}} \right)\exp \left({ - 2\int_0^z {k_i z} } \right)$$

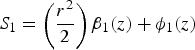$$S_1 = \left({\displaystyle{{r^2 } \over 2}} \right){\rm \beta} _1\lpar z\rpar + {\rm \phi} _1 \lpar z\rpar$$

$${\rm \beta} _1 \lpar z\rpar = \displaystyle{1 \over {\,\,f_1 }}\displaystyle{{d\,f_1 } \over {dz}}$$

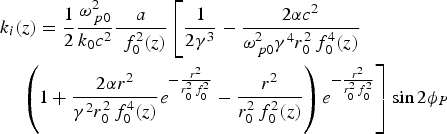(21b)$$\eqalign{& {k_{i }}\lpar z\rpar = \displaystyle{1 \over 2}\displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{k_0}{c^2}}}\displaystyle{a \over {\,\,f_0^2 \lpar z\rpar }}\left[{\displaystyle{1 \over {2{{\rm \gamma} ^3}}} - \displaystyle{{2{\rm \alpha} {c^2}} \over {{\rm \omega} _{\,p0}^2 {{\rm \gamma} ^4}r_0^2 \,f_0^4 \lpar z\rpar }}} \right. \cr & \quad \left. { \left({1 + \displaystyle{{2{\rm \alpha} {r^2}} \over {{{\rm \gamma} ^2}r_0^2 \,f_0^4 \lpar z\rpar }}{e^{ -{{{r^2}} \over {r_0^2 \,f_0^2 }}}} - \displaystyle{{{r^2}} \over {r_0^2 \,f_0^2 \lpar z\rpar }}} \right){e^{ - {{{r^2}} \over {r_0^2 \,f_0^2 }}}}} \right]\sin 2{{\rm \phi} _P}}$$

where k _i an f ₁ are the growth rate and the dimensionless beam width parameter of the ripple respectively, and ϕ₁(z) is a constant. Eq. (21a) describes the axial intensity of rippled laser beam, which depends upon the growth rate of laser ripple in plasma. It is obvious from Eq. (21) for A ₁₀² is the ripple grows/decays inside the plasma and the growth rate is k _i. The growth rate depends on the intensity of the main beams, the phase angle ϕ_p, parameter of the pump wave and plasma. For a plane wave front d f ₁/dz = 0 and f ₁ = 1 at z = 0. Substituting for A ₁₀ and S ₁ from Eq. (21) into Eq. (20a) and expanding around r = r ₁₀f ₁n ^1/2 by Taylor expansion as

$${\rm \phi} _{efff} = {\rm \phi} _{eff} \lpar r^2 = r_{10}^2 \,f_1 n\rpar + {\rm \phi} ^{\prime} r^2 \comma \;$$

where

$$\eqalign{& {{\rm \phi} ^{\prime}} = \displaystyle{{d{{\rm \phi} _{eff}}} \over {d{r^2}}}\left\vert {_{{r^2} = r_{10}^2 \,f_1^2 n} } \right. = \left({\displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }}} \right)\cr & \quad \left\{{\left({ - \displaystyle{a \over {2{{\rm \gamma} ^3}r_0^2 \,f_0^4 }}{e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} + \displaystyle{{2{\rm \alpha} {c^2}} \over {{\rm \omega} _{\,p0}^2 r_0^2 \,f_0^4 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \times [A] } \right)} \right. \cr & + 2a\displaystyle{{{E_{100}}} \over {{E_{00}}}} {n^{n/2}}\exp \lpar\! - {k_i}z\rpar {e^{ - {n \over 2}\left({1 + {{r_{10}^2 \,f_1^2 } \over {r_0^2 \,f_0^2 }}} \right)}}\cr & \quad \left. {\left({\displaystyle{{3a} \over {4{{\rm \gamma} ^5}r_0^2 \,f_0^4 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} - \displaystyle{1 \over {4{{\rm \gamma} ^3}r_0^2 \,f_0^2 }} - \displaystyle{{2{\rm \alpha} {c^2}} \over {{\rm \omega} _{\,p0}^2 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \times [B] \rpar } \right.} \right)\cos {{\rm \phi} _p}\cr & + \displaystyle{1 \over {r_0^2 \,f_0^2 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}}\left({\displaystyle{{3{a^2}} \over {4{{\rm \gamma} ^5}\,f_0^4 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} - \displaystyle{a \over {2{{\rm \gamma} ^3}\,f_0^2 }} - \displaystyle{{2{\rm \alpha} {c^2}} \over {{\rm \omega} _{\,p0}^2 \,f_0^2 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \times [C] } \right)\cr &\left. \quad \vphantom{\left({\displaystyle{{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} _0^2 }}} \right)} 2 \,{\cos ^2}{{\rm \phi} _p}\right\}}$$

and

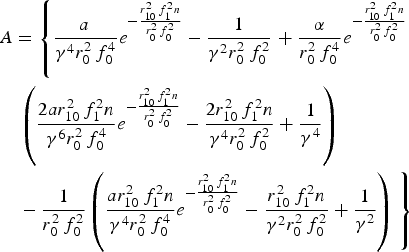$$\eqalign{& A = \left\{{\displaystyle{{a\, } \over {{\rm \gamma} ^4 r_0^2 \,f_0^4 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{1 \over {{\rm \gamma} ^2 r_0^2 \,f_0^2 }}} \right. + \displaystyle{{\rm \alpha} \over {r_0^2 \,f_0^4 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} \cr & \quad \left(\displaystyle{{2ar_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^6 r_0^2 \,f_0^4 }}e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{{2r_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^4 r_0^2 \,f_0^2 }} + \displaystyle{1 \over {{\rm \gamma} ^4 }}\right)\cr & \quad - \displaystyle{1 \over {r_0^2 \,f_0^2 }}\left(\displaystyle{{ar_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^4 r_0^2 \,f_0^4 }}e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - {{r_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^2 r_0^2 \,f_0^2 }} + \displaystyle{1 \over {{\rm \gamma} ^2 }}\right)\left. \vphantom{\displaystyle{{a\, } \over {{\rm \gamma} ^4 r_0^2 \,f_0^4 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \right\}}$$

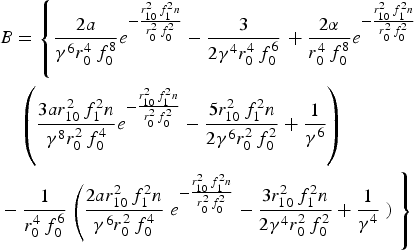$$\eqalign{& B = \left\{\displaystyle{{2a} \over {{\rm \gamma} ^6 r_0^4 \,f_0^8 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{3 \over {2{\rm \gamma} ^4 r_0^4 \,f_0^6 }} \right. + \displaystyle{{2{\rm \alpha} } \over {r_0^4 \,f_0^8 }}e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} \cr & \quad \left({\displaystyle{{3ar_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^8 r_0^2 \,f_0^4 }}} e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{{5r_{10}^2 \,f_1^2 n} \over {2{\rm \gamma} ^6 r_0^2 \,f_0^2 }} + \displaystyle{1 \over {{\rm \gamma} ^6 }} \right)\cr & - \displaystyle{1 \over {r_0^4 \,f_0^6 }}\left({\displaystyle{{2ar_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^6 r_0^2 \,f_0^4 }}} \right.e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{{3r_{10}^2 \,f_1^2 n} \over {2{\rm \gamma} ^4 r_0^2 \,f_0^2 }} + \displaystyle{1 \over {{\rm \gamma} ^4 }}\left. \right)\left.\vphantom{\displaystyle{{2a} \over {{\rm \gamma} ^6 r_0^4 \,f_0^8 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \right\}}$$

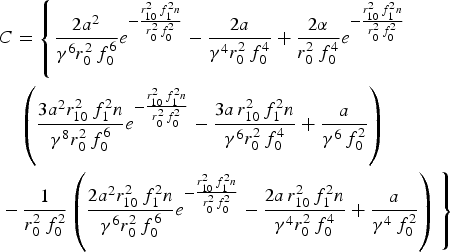$$\eqalign{& C = \left\{\displaystyle{{2a^2 } \over {{\rm \gamma} ^6 r_0^2 \,f_0^6 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{{2a} \over {{\rm \gamma} ^4 r_0^2 \,f_0^4 }} + \displaystyle{{2{\rm \alpha} } \over {r_0^2 \,f_0^4 }}e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} \right. \cr & \quad \left({\displaystyle{{3a^2 r_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^8 r_0^2 \,f_0^6 }}e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{{3a\, r_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^6 r_0^2 \,f_0^4 }} + \displaystyle{a \over {{\rm \gamma} ^6 \,f_0^2 }}} \right)\cr & - \displaystyle{1 \over {r_0^2 \,f_0^2 }}\left({\displaystyle{{2a^2 r_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^6 r_0^2 \,f_0^6 }}e^{ -{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} - \displaystyle{{2a\, r_{10}^2 \,f_1^2 n} \over {{\rm \gamma} ^4 r_0^2 \,f_0^4 }} + \displaystyle{a \over {{\rm \gamma} ^4 \,f_0^2 }}} \right)\left. \vphantom{\displaystyle{{2a^2 } \over {{\rm \gamma} ^6 r_0^2 \,f_0^6 }}e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}}\right\}}$$

We get the following equation for f ₁ after equating the coefficient of r ²

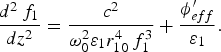(22)$$\displaystyle{{d^2 \,f_1 } \over {dz^2 }} = \displaystyle{{c^2 } \over {{\rm \omega} _0^2 {\rm \varepsilon} _1 r_{10}^4 \,f_1^3 }} + \displaystyle{{{\rm \phi} _{eff}^{\prime} } \over {{\rm \varepsilon} _1 }}.$$

Eq. (22) determines the focusing/defocusing of the ripple and has the same form as the equation of self-focusing for the main beam Eq. (16).

3. EFFECT OF THE GROWTH OF RIPPLE ON THE EXCITATION OF IAW

Nonlinear interaction of an IAW with the laser beam filaments leads to its excitation. To analyze the excitation process of IAW in the presence of relativistic and ponderomotive nonlinearity and rippled laser beam, we use the following fluid equations: (1) the continuity equation

(23)$$\displaystyle{{\partial N_i } \over {\partial t}} + \nabla \cdot \lpar N_i V_i \rpar = 0\comma \;$$

(2) momentum balance equation

(24)$$m_i \left[{\displaystyle{{\partial V_i } \over {\partial t}} + \lpar V_i \cdot \nabla \rpar V_i } \right]= - eE_i - \displaystyle{e \over c}\lpar V_i \times B\rpar - 2\Gamma _i m_i V_i - \displaystyle{{{\rm \gamma} _i } \over N}\nabla P_i\comma \;$$

and (3) Poisson's equation

(25)$$\nabla \cdot E_{ia} = - 4{\rm \pi} e\lpar n_e - n_i \rpar \comma \;$$

where N _i is the total ion density, V _i is the velocity of ion-fluid, B is the total magnetic field of the IAW wave, E _i is the total electric field in the plasma, γ_i is the ratio of specific heat of ion-gas, P _i (=N i k _BTi) is the electronic pressure, E _ia is the electric field associated with the generated ion acoustic, n _e and n _i corresponds to perturbations in the electron and ion densities, and are related to each other by following equation:

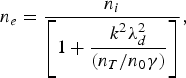(26)$${n_e} = \displaystyle{{{n_i}} \over {\left[{1 + \displaystyle{{k^2{\rm \lambda} _d^2 } \over {\lpar n_T/{n_0}{\rm \gamma} \rpar }}} \right]}}\comma \;$$

where k is the propagation constant for IAW and λ_d (=k _BT ₀/4πN _ie ²)^1/2 is the Debye length. The Landau damping coefficient Γ_i for IAW is given by Krall and Trivelpiece (Reference Krall and Trivelpiece1973)

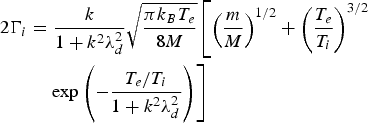(27)$$\eqalign{ 2{\Gamma _i} & = \displaystyle{k \over {1 + {k^2}{\rm \lambda} _d^2 }} \sqrt {\displaystyle{{{\rm \pi} {k_B}{T_e}} \over {8M}}} \left[ {\left(\displaystyle{m \over M} \right)}^{1/2} + {\left(\displaystyle{{T_e} \over {T_i}} \right)}^{3/2} \right. \cr & \quad \left. \exp \left({ - \displaystyle{{{T_e}/{T_i}} \over {1 + {k^2}{\rm \lambda} _d^2}}} \right) \right]}$$

where T _e and T _i are the electron and ion temperatures. Applying the perturbation approximation in Eqs. (23)–(25), we have

(28)$${N_i} = {N_i}_0 + n_i\comma \; \quad V_i = V_{i_0} + n_i\comma \; \quad E_{ia} = E + E_{i_0}$$

where

$${n_i} \ll \; {N_i}_0\comma \; \quad {v_{i\; }} \ll \; {V_i}_0 \comma \; \quad {\rm and} \quad {E_i}_0 \ll \; E$$

N _i0 is the background ion density modified by the dc component of the relativistic-ponderomotive force, V _i0 is the ion drift velocity in the pump field, E (= E ₀ + E ₁) is the total electric field of the laser beam having ripple and ν _i is the drift velocity of ion in the electrostatic field E _i0 of the IAW. With the help of Eqs. (23)–(28), one obtain the following equation for the excitation of the IAW

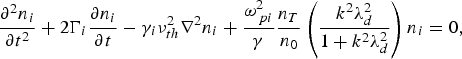(29)$$\displaystyle{{\partial ^2 n_i } \over {\partial t^2 }} + 2\Gamma _i \displaystyle{{\partial n_i } \over {\partial t}} - {\rm \gamma} _i {\rm \nu} _{th}^2 \nabla ^2 n_i + \displaystyle{{{\rm \omega} _{\,pi}^2 } \over {\rm \gamma} }\displaystyle{n_T \over {n_0 }}\left({\displaystyle{{k^2 {\rm \lambda} _d^2 } \over {1 + k^2 {\rm \lambda} _d^2 }}} \right)n_i = 0\comma \;$$

where ν_th = (K_BT_i/M_i)^1/2 is the ion thermal velocity. To solve Eq. (29) for n _i we used the approach developed by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and Sodha et al. (Reference Sodha, Ghatak and Tripathi1976) and writing

(30)$$n_i = n_{i0} \lpar r\comma \; z\rpar \exp \lpar i\lpar {\rm \omega} t - k_i [z + S\lpar r\comma \; z\rpar] \rpar \comma \;$$

where n _i0 is the slowly varying real function of r and z and S is the Eikonal for IAW.

Substituting for n _i from Eq. (30) in Eq. (29), and separating real and imaginary parts of the resulting equation, we obtain

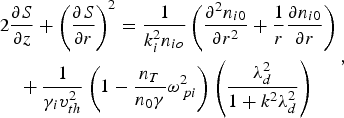(31)$$\eqalign{& 2\displaystyle{{\partial S} \over {\partial z}} + {\left({\displaystyle{{\partial S} \over {\partial r}}} \right)^2} = \displaystyle{1 \over {k_i^2 {n_{io}}}}\left({\displaystyle{{{\partial ^2}{n_{i0}}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {n_{i0}}} \over {\partial r}}} \right)\cr & \quad + \displaystyle{1 \over {{{\rm \gamma} _i}v_{th}^2 }}\left({1 - \displaystyle{n_T \over {{n_0}{\rm \gamma} }}{\rm \omega} _{\,pi}^2 } \right)\left({\displaystyle{{{\rm \lambda} _d^2 } \over {1 + k^2{\rm \lambda} _d^2 }}} \right)}\comma \;$$

and

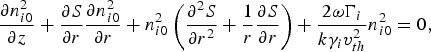(32)$$\displaystyle{{\partial n_{i0}^2 } \over {\partial z}} + \displaystyle{{\partial S} \over {\partial r}}\displaystyle{{\partial n_{i0}^2 } \over {\partial r}} + n_{i0}^2 \left({\displaystyle{{\partial ^2 S} \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right)+ \displaystyle{{2{\rm \omega} \Gamma _i } \over {k{\rm \gamma} _i v_{th}^2 }}n_{i0}^2 = 0\comma \;$$

To solve the coupled Eqs. (31) and (32) we assume the initial radial variation of the density perturbation in the IAW at z = 0 to be

$$n_{i0}^2 \left\vert {_{Z = 0} } \right. = \lpar n_{i00} \rpar ^2 \exp \lpar r^2 /a_0^2 \rpar \comma \;$$

where n _i00 is the axial amplitude of density perturbation of IAW and a ₀ is the initial beam width of the acoustic wave. The solution of Eqs. (31) and (32) can be written as (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968),

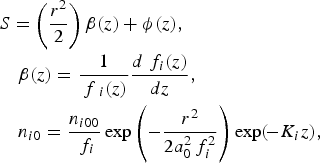(33)$$\eqalign{& S = \left({\displaystyle{{r{}^2} \over 2}} \right){\rm \beta} \lpar z\rpar + {\rm \phi} \lpar z\rpar \comma \cr & \quad {\rm \beta} \lpar z\rpar = \displaystyle{1 \over {\,f\,{}_i\lpar z\rpar }}\displaystyle{{d{\,\,f_i}\lpar z\rpar } \over {dz}}\comma \cr & \quad {n_{i0}} = \displaystyle{{{n_{i00}}} \over {{\,\,f_i}}}\exp \left({ - \displaystyle{{{r^2}} \over {2a_0^2 \,f_i^2 }}} \right)\exp \lpar \!- {K_i}z\rpar \comma}$$

where $K_i = \displaystyle{{\Gamma _i {\rm \omega} } \over {k{\rm \nu} _{th}^2 }}$ is the damping factor. Using Eq. (33) in Eq. (31) and equating the coefficients of r ² on both sides, we obtain the following dimensionless beam width parameter (f _i) equation of the acoustic wave under the boundary conditions: df _i/dz = 0, f _i= 1 at z = 0

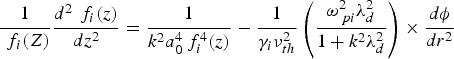(34)$$\displaystyle{1 \over {{\,\,f_i}\lpar Z\rpar }}\displaystyle{{d{}^2{\,\,f_i}\lpar z\rpar } \over {d{z^2}}} = \displaystyle{1 \over {{k^2}a_0^4 \,f_i^4 \lpar z\rpar }} - \displaystyle{1 \over {{{\rm \gamma} _i}{\rm \nu} _{th}^2 }}\left({\displaystyle{{{\rm \omega} _{\,pi}^2 {\rm \lambda} _d^2 } \over {1 + {k^2}{\rm \lambda} _d^2 }}} \right)\times \displaystyle{{d{\rm \phi} } \over {dr{}^2}}$$

where

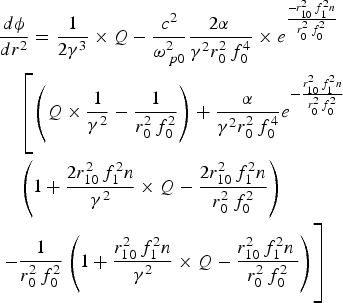$$\eqalign{& \displaystyle{{d{\rm \phi} } \over {d{r^2}}} = \displaystyle{1 \over {2{{\rm \gamma} ^3}}} \times Q - \displaystyle{{{c^2}} \over {{\rm \omega} _{\,p0}^2 }}\displaystyle{{2{\rm \alpha} \, } \over {{{\rm \gamma} ^2}r_0^2 \,f_0^4 }} \times {e^{{{ - r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \cr & \quad \left[{\left({Q \times \displaystyle{1 \over {{{\rm \gamma} ^2}}} - \displaystyle{1 \over {r_0^2 \,f_0^2 }}} \right)+ \displaystyle{{\rm \alpha} \over {{{\rm \gamma} ^2}r_0^2 \,f_0^4 }}{e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}}} \right. \cr & \quad \left({1 + \displaystyle{{2r_{10}^2 \,f_1^2 n} \over {{{\rm \gamma} ^2}}} \times Q - \displaystyle{{2r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}} \right)\cr & \left. { - \displaystyle{1 \over {r_0^2 \,f_0^2 }}\left({1 + \displaystyle{{r_{10}^2 \,f_1^2 n} \over {{{\rm \gamma} ^2}}} \times Q - \displaystyle{{r_{10}^2 \,f_1^2 n\, } \over {r_0^2 \,f_0^2 }}} \right)}\vphantom{e^{{{ - r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} \right]}$$

here

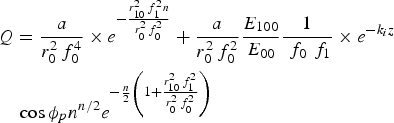$$\eqalign{& Q = \displaystyle{a \over {r_0^2 \,f_0^4 }} \times {e^{ - {{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} + \displaystyle{a \over {r_0^2 \,f_0^2 }}\displaystyle{{{E_{100}}} \over {{E_{00}}}}\displaystyle{1 \over {{\,\,f_0}{\,\,f_1}}} \times {e^{ - {k_i}z}} \cr & \quad \cos {{\rm \phi} _p}{n^{n/2}}{e^{ - {n \over 2}\left({1 +{{r_{10}^2 \,f_1^2 } \over {r_0^2 \,f_0^2 }}} \right)}}}$$

and the modified value of γ (due to the contribution of E·E*)

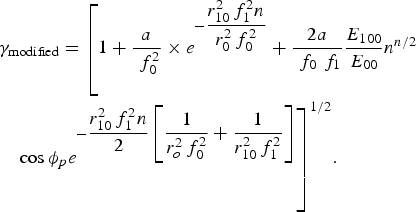$$\eqalign{& {{\rm \gamma} _{{\rm modified}}} = \left[{{\rm 1} + \displaystyle{a \over {\,\,f_0^2 }} \times {e^{ - \displaystyle{{r_{10}^2 \,f_1^2 n} \over {r_0^2 \,f_0^2 }}}} + \displaystyle{{2a} \over {{\,\,f_0}{\,\,f_1}}}\displaystyle{{{E_{100}}} \over {{E_{00}}}}{n^{n/2}}} \right. \cr & \quad {\left. {\cos {{\rm \phi} _p}{e^{ - \displaystyle{{r_{10}^2 \,f_1^2 n} \over 2}\left[{\displaystyle{1 \over {r_o^2 \,f_0^2 }} + \displaystyle{1 \over {r_{10}^2 \,f_1^2 }}} \right]}}} \right]^{1/2}}.}$$

Eq. (34) describe the beam width parameter (f _i) of the excited IAW in collisionless plasma with df _i/dz = 0 and f _i = 1 at z = 0. To see the effect of the ripple on the excitation of IAW, we have solved Eq. (33) with the help of Eq. (34) numerically to obtain the amplitude of the density perturbation associated with the IAW at finite z.

4. NUMERICAL RESULTS AND DISCUSSION

In order to understand the dynamics of the propagation of rippled laser beam in plasma in the presence of both relativistic and ponderomotive nonlinearities at high laser power flux and its effect on the excitation of IAW, we have performed a numerical computation of Eqs. (16a), (16b), (21a), (21b), (22), (33), and (34) at high laser power flux. We have also solved the coupled equations and obtained the numerical results with typical plasma and laser beam parameters. The following set of the parameters has been used in numerical calculation: ω₀ = 1.77 × 10¹⁵ rad/s, r ₀ = 20 µm, r ₁₀ = 0.75r ₀, ω_p0 = 0.3ω₀, 2ϕ_p = π/2, n = 1.5, ν _th = 0.5c, E ₁₀₀ = 0.01E ₀₀, a ₀ = 0.5r ₀. Normalized intensity of laser beam (a = 0.5, 1.0, 1.5, 2.0) are equivalent to 3.5 × 10¹⁷, 1.4 × 10¹⁸, 3.1 × 10¹⁸, and 5.5 × 10¹⁸ W/cm², respectively. For initial wave front of the beams, the initial conditions for both f ₀ and f ₁ are:

$$\displaystyle{{d{f_0}} \over {dz}} = \displaystyle{{d{f_1}} \over {dz}} = 0\comma \; \, \, {\rm and}\, {\,\,f_0} = {\,\,f_1} = 0\, \, \, {\rm at}\, \, \, z = 0.$$

Eqs. (16b) and (22) determine the focusing/defocusing of the main laser beam and the rippled beam, along with the distance of propagation in the plasma. In both equations, the first term on right-hand side represents the diffraction phenomenon and the second term describes the nonlinear refraction of the beam, which arises due to the relativistic and ponderomotive nonlinearities. The relative magnitudes of these two terms determine the focusing and defocusing behavior of the beams. Eq. (16a) gives the intensity profile of the main laser beam in the plasma in the presence of relativistic and ponderomotive nonlinearities. The intensity profile of main laser beam depends on the beam width parameter (f ₀) in the paraxial regime. Figure 1 shows intensity profile of the laser beam in plasma with the normalized distance of propagation for different values of intensities. It is obvious that as the laser beam propagates through the plasma it gets filamented due to the laser plasma coupling. The generated filaments of the laser beam are shown in Figures 1a–1d for a fixed value of ω_p0 = 0.3ω₀ and varying laser beam intensity, a = 0.5, 1.0, 1.5, 2.0, respectively. It clearly shows, as the intensity increases, the normalized intensity of the laser beam also increases.

Fig. 1. Variation in laser beam intensity with normalized distance (Z = zc/ω₀r ₀²) and radial distance (R = r/r ₀), when relativistic and ponderomotive nonlinearities are operative, keeping ω_p0 = 0.030ω₀ constant, at different laser beam intensities, (a) αE ₀₀² = 0.5, (b) αE ₀₀² = 1.0, (c) αE ₀₀² = 1.5, (d) αE ₀₀² = 2.0, respectively.

The growth rate of the ripple (k _i) is given by Eq. (21b) which depends on the effective intensity and frequency of the main laser beam in the plasma, electron density in the plasma and the phase angle ϕ_p. Due to the coupling between the main beam and the ripple, ripple grow/decay in the plasma. From numerical analysis, it has been observed that the ripple will grow only when sin 2ϕ_p is negative. In Figures 2a and 2b, we have plotted the growth rate of ripple in the plasma with the distance of propagation for different values of laser intensities and plasma frequencies. It is clearly shown in the figures that the growth rate of ripple increases with increase in laser intensity and plasma frequency in the presence of both relativistic and ponderomotive nonlinearities. It is also important to mention here that both ϕ_p and n significantly affected the intensity profile of the of the ripple, growth rate of the ripple, intensity profile of IAW, beam width parameters of the rippled beam (f ₁) and IAW (f _i), respectively. The effect of ϕ_p and the parameters n on the above has been reported earlier (Sodha et al., Reference Sodha, Singh, Singh and Sharma1981; Saini et al., Reference Saini and Gill2000; Purohit et al., Reference Purohit, Pandey, Mahmoud and Sharma2004; Reference Purohit, Chauhan, Sharma and Pandey2005) and hence not repeated in present study.

Fig. 2. (a) Variation of the growth rate of laser ripple with normalized distance of propagation (Z = zc/ω₀r ₀²) for n = 1.5, 2ϕ_p = π/2, ω_p0 = 0.030ω₀ and for different laser beam intensities (b) Variation of the growth rate of laser ripple with normalized distance of propagation (Z = zc/ω₀r ₀²) for n = 1.5, 2ϕ_p = π/2, αE ₀₀² = 1, and for different plasma frequencies (green, red and blue lines corresponds to ω_p0 = 0.015, 0.025, and 0.035, respectively.

The intensity profile of the rippled laser beam is expressed by Eq. (21) when relativistic and ponderomotive nonlinearities are operative. It depends on the beam width of the rippled laser beam (f ₁) and the growth rate (k _i) of ripple in plasma. Figures 3a–3d shows the filamentary structures of the rippled beam at different laser intensities. It shows that a small ripple on the axis of the main beam grows very rapidly with distance of propagation as compared with the intensity profile of the main beam. It is also observed that in the presence of both nonlinearities, the ripple intensity starts decreasing with the increase in the laser intensity at constant ω_p0. This is due to the complex dependency of beam width parameter (f ₁) and the growth rate (k _i) on laser intensity.

Fig. 3. Variation in axial intensity of laser ripple with normalized distance (Z = zc/ω₀r ₀²) and radial distance (R = r/r ₁₀), when relativistic and ponderomotive nonlinearities are operative, keeping ω_p0 = 0.030ω₀ constant, at different laser beam intensities, (a) αE ₀₀² = 0.5, (b) αE ₀₀² = 1.0, (c) αE ₀₀² = 1.5, (d) αE ₀₀² = 2.0, respectively.

The IAW excited due to nonlinear coupling between rippled laser beam and plasma in the presence of relativistic and ponderomotive nonlinearities. This coupling arises on account of the relativistic change in the electron mass and the modification of the background electron density due to ponderomotive nonlinearity, consequently the laser beam gets filamented. In these filaments, the laser beam intensity is very intense and the plasma density is also changed due to ponderomotive force. Thus, the amplitude of IAW, which depends upon the background electron density, gets strongly coupled to the laser beam. The magnitude of relativistic ponderomotive force is modified in the presence of the ripple because it depends on the intensity of the main beam and of the ripple. The presence of the ripple also leads to a change in modified ion density; consequently, the excitation of IAW is modified. Eq. (28) represents an expression for the excitation of IAW, used in laser heating experiments, where the last term represents the nonlinear coupling of IAW to the modified background density.

In order to study the effect of rippled laser beam in the presence of both relativistic and ponderomotive nonlinearities on the excitation of IAW, we have solved numerically Eq. (33) with the help of Eq. (34) to obtain the amplitude of the density perturbation associated with excited IAW at finite z. The intensity profile of the IAW depends on the beam width parameter (f _i) in the paraxial regime. The results are displayed in Figures 4a–4d and Figures 5a–5c at different laser intensities and plasma frequencies respectively, which show that the IAW excited due to nonlinear coupling with intense rippled laser beam in the presence of relativistic and ponderomotive nonlinearities. It is obvious from the figures that in paraxial regime the intensity of the IAW decreases with increase in laser intensity and plasma frequency. This is due to the fact that the Landau damping term in Eq. (33) and growth rate are sensitive to the intensity of the IAW, which reduces the growth and intensity of the IAW.

Fig. 4. Variation in IAW intensity with normalized distance (Z = zc/ω₀r ₀²) and radial distance (R = r/r ₀), when relativistic and ponderomotive nonlinearities are operative, keeping ω_p0 = 0.030ω₀ constant, n = 1.5, 2ϕ_p = π/2, at different laser beam intensities, (a) αE ₀₀² = 0.5, (b) αE ₀₀² = 1.0, (c) αE ₀₀² = 1.5, (d) αE ₀₀² = 2.0, respectively.

Fig. 5. Variation in IAW intensity with normalized distance (Z = zc/ω₀r ₀²) and radial distance (R = r/r ₀), when relativistic and ponderomotive nonlinearities are operative, keeping αE ₀₀² = 1 constant, n = 1.5, 2ϕ_p = π/2, at different plasma frequencies, (a) ω_p0 = 0.015ω₀, (b) ω_p0 = 0.025ω₀, (c) ω _p0 = 0.035ω₀, respectively.