Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T13:40:57.101Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of laser pulse time profile on its absorption by argon clusters

Published online by Cambridge University Press:  13 July 2011

Gaurav Mishra ,
Amol R. Holkundkar  and
N.K. Gupta
Gaurav Mishra*
Affiliation:
Theoretical Physics Division, Bhabha Atomic Research Centre, Mumbai, India
Amol R. Holkundkar
Affiliation:
Department of Physics, Umeå University, Umeå, Sweden
N.K. Gupta
Affiliation:
Theoretical Physics Division, Bhabha Atomic Research Centre, Mumbai, India
*
Address correspondence and reprint requests to: Gaurav Mishra, Theoretical Physics Division, Bhabha Atomic Research Centre, Mumbai-400 085, India. E-mail: gauravm@barc.gov.in
Rights & Permissions [Opens in a new window]

Abstract

The interaction of medium sized Argon clusters (30 Å) with high-intensity femtosecond laser pulses (806 nm, 8 × 1016 W/cm2) of durations ranging from 10 fs to 120 fs have been studied using a three-dimensional relativistic time dependent molecular dynamic approach. The dynamics of cluster expansion is explained in terms of temporal evolution of electron population in the cluster and snapshots of particle positions at various times. The effects of inter-cluster distance on ionization dynamics are presented. It is observed that the collisional ionization increases with decreasing inter-cluster distance. The effect of pulse duration on laser energy absorption is also studied. For a laser pulse of gaussian time profile, there exists an optimum pulse duration for maximum absorption. No such optimum exists for a nearly flat top (super-gaussian) laser pulse. Results indicate the existence of resonance absorption inside the cluster. It is also observed that the high energy component of ion emission from cluster is anisotropic, showing a preferential direction of emission along laser polarization while the low energy ions emerge almost isotropically.

Keywords

Anisotropic emissionClusterCluster dynamicsFemtosecond laserResonance absorption
Type
Research Article
Information
Laser and Particle Beams , Volume 29 , Issue 3 , September 2011 , pp. 305 - 313
Copyright
Copyright © Cambridge University Press 2011

1. INTRODUCTION

The development of high intensity (>1014 W/cm2) and short pulse (<1 ps) lasers has revived the field of laser matter interaction research and led to the observation of exciting new results in this subject (Perry & Mourou, Reference Perry and Mourou1994). More recently, interest has been focussed on using rare gas clusters as targets for high intensity laser pulse because they contain the advantages of both gas and solid phases (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996). These clusters are produced by the isentropic expansion of a high pressure gas through a nozzle (Hagena & Obert, Reference Hagena and Obert1972). The decrease of temperature, inherent in the expansion process, combined with high pressure, results in the formation of near-solid state density droplets, so-called clusters, embedded in a low density surrounding gas. The laser heating of clusters is dominated by collisional absorption due to their internal solid like densities, a process more typical to solid state targets. This enhances the energy absorbed compared with unclustered sub-critical density gases. Clusters can be used to generate a compact source of coherent and incoherent X-rays (Adoui et al., Reference Adoui, Gobert, Indelicato, Lamour, Meynadier, Normand, Perdrix, Prigent, Rozet and Vernhet2003; Borisov et al., Reference Borisov, Song, Frigeni, Koshman, Dai, Boyer and Rhodes2003), and fast ions capable of driving a fusion reaction in a deuterated plasma (Ditmire et al., 1977b). Some of the other potential applications include extreme ultraviolet (EUV) lithography (Kubiak et al., Reference Kubiak, Bernardez, Krenz, O Connell, Gutowski and Todd1996), EUV and X-ray microscopy (Kirz et al., Reference Kirz, Jacobsen and Howells1995), and X-ray tomography (Levine et al., Reference Levine, Kalukin, Frigo, McNulty and Kuhn1999).

Theoretical modelling of the intense laser pulse interaction with rare-gas clusters is a challenging subject involving the nonlinear, nonperturbative response of many ions and electrons. Recent review (Fennel et al., Reference Fennel, Meiwes-Broer, Tiggesbäumker, Reinhard, Dinh and Suraud2010) provide the overall status of the subject. The laser-cluster interaction involves three sub-processes: ionization of atoms, absorption of laser energy, and expansion of cluster. In order to investigate these processes and explain the observed experimental results, several models have been put forward. Among them the most popular is the so-called “nanoplasma model” (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996), which treats the cluster as a spherical plasma ball with an assumption that the radial plasma density is uniform. This model describes the dynamics of ionization, electron-heating, and cluster expansion. An improvement of this picture (Liu et al., Reference Liu, Li, Zhu, Xu and Liu2001) includes the replacement of quasi-static plasma dielectric constant derived from the Drude model by an effective plasma dielectric constant, obtained by solving the Maxwell's equations. The spatial non-uniformities during the time of cluster expansion were incorporated in a modified model (Holkundkar & Gupta, Reference Holkundkar and Gupta2008). Recent investigations showed the inadequacy of the above mentioned fluid models to describe the complete description of laser cluster dynamics (Parra et al., Reference Parra, Alexeev, Fan, Kim, McNaught and Milchberg2003) and this led to development of other alternative approaches like Particle-in-cell (PIC) (Jungreuthmayer et al., Reference Jungreuthmayer, Geissler, Zanghellini and Brabec2004) and molecular dynamic (MD) (Last & Jortner, Reference Last and Jortner1999) models. In both PIC and MD, particles are advanced by solving equations of motion, which for charged particles, require the computation of the electromagnetic force acting on each particle. In the MD approach, the force on a particle is computed as a sum over all individual two-body interactions whereas in the PIC method, the field is computed on a grid of cells, and the force on the particle is interpolated from the the fields on the grid. The grid-less methodology felicitates the extension of MD approach toward more than one dimension that otherwise becomes difficult in case of PIC simulation. The limited number of particles in a cluster (103–105), combined with the numerous advantages of grid-less calculations gives preference to MD simulations for laser cluster interaction.

The energy absorption by cluster is of great interest. It has been demonstrated experimentally (Ditmire et al., Reference Ditmire, Smith, Tisch and Hutchinson1997a) that the clusters absorbs almost all the laser energy incident on them. The mechanism of laser energy absorption by atomic clusters is still debatable. Initial studies suggested the linear (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996) or nonlinear (Kundu & Bauer, Reference Kundu and Bauer2006a) resonance absorption to be responsible for this high energy absorption. The linear resonance theory, proposed by Ditmire et al. (1996) considers the cluster plasma as a dielectric sphere in spatially uniform yet time dependent electric field. The electron density was assumed to be radially constant throughout the cluster expansion. The dielectric constant of this nanoplasma is calculated using Drude model of free electron gas (Ashcroft & Mermin, Reference Ashcroft and Mermin1976). As cluster expands, a resonance occurs when electron density approaches three times the critical density. At this density the dielectric constant approaches infinity leading to an enhancement of the electric field inside the cluster which leads to the enhanced energy absorption. This short interval of enhanced absorption was smeared out in the time with lesser peak value when non-uniformity of electron density is included in the cluster expansion (Milchberg et al., Reference Milchberg, McNaught and Parra2001) resulting in the long-time resonance at the critical density plasma layer. The nonlinear resonance theory treats both the ions and electrons separately as charged spheres, oscillating around their common center of mass under the action of laser light. Energy is absorbed resonantly when the normalized effective oscillation frequency becomes unity (Kundu & Bauer, Reference Kundu and Bauer2006b). Apart from resonance absorption, various other energy absorption mechanism like vacuum heating (Brunel, Reference Brunel1987), collision-less resonance absorption (Kostyukov & Rax, Reference Kostyukov and Rax2003) and scattering at the cluster potential (Smirnov & Krainov, Reference Smirnov and Krainov2003) have been also suggested. Although various energy mechanisms have been proposed, resonance absorption is still believed to be the main method for energy absorption. There are, however, simulation results that contradict this perception. For example, Davis et al. (Reference Davis, Petrov and Velikovich2007) found no such resonance in their MD simulations and discarded the idea of both the Drude model and rigid sphere model. The energy absorbed by the cluster is calculated by evaluating the electrostatic energy of the spherical capacitor that in turn depends on the outer ionization and volume distribution of charges. The higher energy absorption of the cluster was explained on the basis of capacitor model that treated the expanding cluster as two concentric spheres: an ion core surrounded by a large radius electron cloud. Similarly, findings of Deiss et al. (Reference Deiss, Rohringer, Burgdörfer, Lamour, Prigent, Rozet and Vernhet2006) reflects the absence of plasma resonance and high energy X-ray emission is attributed to highly energetic quasi free electrons arising due to their elastic large-angle back scattering at ionic cores in the presence of laser field. The above discussion reflects that the reason responsible to the high energy absorption inside the cluster is still not clearly understood. We have tried to investigate the presence of resonance absorption in Argon cluster irradiated by the laser of various pulse durations, as the process of resonance is strongly correlated with the duration of the incident laser pulse.

In addition to this, we also present in this paper our results on anisotropy of ion emission from laser irradiated clusters. Recently, it was shown (Kumarappan et al., Reference Kumarappan, Krishnamurthy and Mathur2001) that ion emission from Ar clusters has two components: a low-energy isotropic component and an other high-energy part emitting preferentially along the laser polarization direction. The observed anisotropy was explained on the basis of “charge-flipping” model (Kumarappan et al., Reference Kumarappan, Krishnamurthy and Mathur2002). We have investigated the dynamics of ejected ions from Argon clusters by using the MD approach and indeed confirmed the above observation.

The paper is organized as follows: In section 2, we describe our MD model very briefly as details are published elsewhere (Holkundkar et al., Reference Holkundkar, Mishra and Gupta2011). Section 3 presents the main results of the study and the paper is concluded in Section 4.

2. MOLECULAR DYNAMIC MODEL

The space and time evolution of cluster is modeled with a fully relativistic time-dependent three-dimensional MD approach. We may mention here that for results presented in this paper, relativistic effects are not important as laser intensities are not very high. However, keeping in mind experiments and simulations at high intensities (1018 W/cm2), we have incorporated the relativistic effects in our general purpose MD code for its application toward these studies. The magnetic field starts affecting the shape and trajectory of electron cloud only at these ultra high intensities (1020 W/cm2) (Petrov et al., Reference Petrov, Davis, Velikovich, Kepple, Dasgupta, Clark, Borisov, Boyer and Rhodes2005) where the collective oscillation of electrons comes into play. Therefore, the effects of magnetic fields are ignored in our studies. The number of atoms in a cluster is obtained from the Wigner-Seitz radius (R W) as, N Atoms = (R 0/R W)3 where R 0 is the initial radius of the cluster. The value of R W depends on the species of the gas cluster under study. For example, R W is 1.70, 2.02, 2.40, and 2.73 Å for Deuterium, Neon, Argon, and Xenon clusters, respectively (Petrov & Davis, Reference Petrov and Davis2008). The center of the cluster is assumed to be at the origin of the coordinate system (x = y = z = 0) and three-dimensional computational box surrounding the cluster has equal sides extending from −R IC/2 to R IC/2. R IC denotes the inter-cluster distance. To reduce the computation time, we use the procedure of lumping of particles to form pseudo-particles or macro-particles (Last & Jortner, Reference Last and Jortner2000), which is described by choosing a predefined number of macro particles, N Macro, instead of individual particles (electrons or ions). As the dimensions of the simulation domain are small as compared to the laser wavelength, only the time variation in laser pulse intensity and electric field is taken in to account. The amplitude of the laser pulse intensity and electric field will remain constant in simulation domain at a given time instant. The ionization of the cluster atoms are carried out by optical field and collisional ionization using Monte-Carlo method. The optical field ionization rate are calculated as a function of laser strength by using Ammosov, Dellone, and Krainov tunnel ionization formula (Ammosov et al., Reference Ammosov, Delone and Krainov1986),

(1)
\eqalign {\nu_{ofi} &= \left( {3En^{\ast 3} \over \pi {\bar Z}^3}\right) ^{1/2} {\lpar 2\ell + 1\rpar \lpar \ell + \vert m \vert\rpar ! \over 2^{\vert m \vert} \lpar \vert m \vert\rpar !\lpar \ell - \vert m \vert\rpar !} \cr &\quad\times \left( {2e \over n^{\ast}}\right) ^{2n^{\ast}} {1 \over 2 \pi n^{\ast}} \left( {2 {\bar Z}^3 \over En^{\ast 3}}\right) ^{2n^{\ast} - \vert m \vert - 1} \cr &\quad \times \left( {{\bar Z}^2 \over 2n^{\ast 2}}\right) exp \left( -{2 {\bar Z}^3 \over 3n^{\ast 3} E}\right) {1 \over 2.4 \times 10^{ - 17}} \quad s^{ - 1}\comma}

where $E = \sqrt {2 \times 10^4 I/\lpar c \, {\rm \varepsilon}_o \rpar } /5.14 \times 10^{11}$ is the electric field in atomic units, I(W/cm2) is the intensity of laser light and c is the speed of light in SI units, ɛo is the permittivity of free space, $\bar Z$ is the degree of ionization, $n^{\ast} = \bar Z/ \sqrt {2I_p}$ is the effective quantum number, I p is the ionization potential in atomic units, e is the charge of electron, ℓ and m are the orbital and magnetic quantum numbers of outer electron respectively. Ionization rate is calculated for each value of m and averaged over it.

Once the sufficient number of electrons are accumulated in the system, they further produce ionization via collision with ions (collisional ionization). To calculate the collisional ionization rate νci, we have used a fitted formula for the atomic species of the cluster with Z < 28 (Voronov, Reference Voronov1997). For atomic species with Z > 28, we use Lotz' formulation (Lotz, Reference Lotz1968) to calculate the ionization rate as

(2)
\nu_{ci} = 6.7 \times 10^{- 7} {n_e a \, q \over I_p \sqrt {kT_e }} \vint_{I_p /kT_e }^{\infty} {e^{ - x} \over x} dx \quad \quad s^{ - 1}\comma

where, n e (cm− 3) is electron density, a = 4.5 is constant, q is number of electrons in outer orbital of particular ion, I p (eV) is the ionization potential for a particular ion, kT e (eV) is the electron energy. Recombination of electrons with ions is not considered in the present model as it is expected to be small for short pulse duration considered in these studies. In particular, the recombination is important when plasma cools from its hot state and this occurs at relatively longer time scale (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996). Furthermore, we have not accounted for the bound states explicitly. These bound states play an important role in the studies of X-ray emission from clusters. They can also influence the degree of ionization through two-step process viz. excitation followed by ionization (Prigent et al., Reference Prigent, Deiss, Lamour, Rozet, Vernhet and Burgdörfer2008). However, we have ignored this two-step process following the earlier MD simulations (Ishikawa & Blenski, Reference Ishikawa and Blenski2000; Last & Jortner, Reference Last and Jortner2000; Rose-Petruck et al., Reference Rose-Petruck, Schafer, Wilson and Barty1997).

The charged macro particles move under the combined action of laser electromagnetic field and coulomb field generated in the cluster due to the separation of charges. The force acting on i th particle at time t is given as,

(3)
{\bf F}_{\bf i} = q_i \lsqb {\bf E}\lpar {\bf t}\rpar + {\bf v}_{\bf i} \times {\bf B} \lpar {\bf t}\rpar \rsqb + \sum_{k \atop i \ne k} {1 \over 4 {\rm \pi} {\rm \epsilon}_0} {q_i q_k {\bf r}_{\bf ik} \over r_{ik}^3}\comma

where, vi and q i are the velocity and charge of the i th particle, E(t) and B(t) being the laser electric and magnetic fields, respectively, and r ik is the distance between two particles defined as $r_{ik} = \sqrt {\vert r_i - r_k \vert ^2 + r_s^2}$, with r s being the size of the macro-particles. The smoothing term r s is introduced in the definition of r ik to avoid a steep increase in forces at very small distances, which can otherwise lead to violation of energy conservation (Last & Jortner, Reference Last and Jortner1999). After the calculation of the force, each particle is then advanced to its new position according to its relativistic equations of motion ($d{\bf p}_{\bf i} /dt = {\bf F}_{\bf i}\comma \; {\bf v}_{\bf i} = {\bf p}_{\bf i} /\lpar m_i \sqrt {1+\vert {\bf p}_{\bf i} \vert ^2 /\lpar m_i c\rpar ^2 } \rpar $, d ri/dt = vi; where pi, vi, ri, and m i are relativistic momentum, velocity, coordinate and mass of the i th particle.)

The phase-spaces of all particles are stored after certain time steps which are later post-processed to calculate the electron and the ion distribution functions EEDF and IEDF, respectively.

3. RESULTS AND DISCUSSIONS

The interaction of 806 nm laser pulse of intensity 8 × 1016 W/cm2 with 30 Å argon cluster is studied in the femtosecond regime by varying the full width at half maximum pulse duration from 10–120 fs. Simulation box is considered to be 900 Å wide. The energy spectrum is calculated at 225 Å from the center of the simulation box for all the laser pulse durations. Laser pulse is linearly polarized along x-direction.

The dynamics of cluster ionization and the subsequent coulomb explosion during the pulse irradiation is presented in Figures 1 and 2 for a representative laser pulse duration of 70 fs. The temporal evolutions of inner, outer, and total number of electrons are shown in Figure 1. Inner electrons are those that are quasi free to move freely within the cluster, but can not escape it whereas outer electrons leave the cluster boundary. The inner electrons cause ionization via collisions with atoms inside the cluster. On the other hand, outer electrons lead to further collisional ionization if they enter the neighboring cluster. The time dependent variation in electron population is a result of constant interplay among the various processes viz ionization, removal of electrons from the cluster boundary and expansion of cluster. At time t = 0, all particles are neutral and remain inside the cluster. As laser is switched on, various ionization processes lead to the rapid build-up of inner electrons along with slow increase in the number of outer electrons. As the time progresses, the number of outer electrons increases due to escape of electrons from cluster up to about 40 fs. Beyond this time, the decrement in the population of outer electrons and the increment in the population of inner electrons are caused by electron recapture due to cluster expansion. In Figures 2a and 2b, we show the snapshots of the electron and ion positions at two representative times before and after the coulomb explosion, respectively, of the cluster. At earlier times (Fig. 2a) ions remain almost immobile due to their heavy mass while electrons move out from the cluster. When sufficiently large number of electrons escape the cluster leaving behind a positively charged sphere, which explodes due to repulsion among ions. The time of occurrence of coulomb explosion depends upon the laser and cluster parameters. The position of ions and electrons after the coulomb explosion is shown in Figure 2b. Figure 3 shows the temporal history of the average degree of ionization for different laser pulse durations. When the laser intensity approaches sufficient value to ionize the neutral argon atoms through tunnel ionization, average charge per ion increases as shown in the Figure 3. The initial electrons produced by tunnel ionization gives rise to further ionization due to collisional ionization. The larger the pulse duration, later the ionization starts as the laser pulse reaches the ionization threshold intensity later for longer pulses. However, the average degree of ionization saturates to 8 for all the cases. Number fraction for various charge states obtained are shown in Figure 4 for 85 Å cluster. Two sets of data in this plot corresponds to inter cluster distances (R IC) of 3.5R 0 and 30R 0. Inter cluster distance depends upon cluster density, larger the cluster density, lesser is R IC and vice versa. In our simulations, the neighboring clusters are accounted for using a periodic boundary condition at simulation box boundary with box dimension equal to R IC. We also note that fractional ionization for R IC = 3.5R 0 shown in Figure 4 agrees well with the experimental and theoretical results of Prigent et al. (Reference Prigent, Deiss, Lamour, Rozet, Vernhet and Burgdörfer2008). We also observe that additional ionization states of charge 13 and 14 start appearing for R IC = 3.5R0. These additional charge states originate due to collisional ionization caused by electrons with the neighboring clusters. Clearly, this collisional ionization with neighboring clusters increases as R IC reduces. This fact is further elaborated from results presented in Figure 5. In this plot, upper set of curves show the variation of Z avg for various values of R IC varying from 3.5R 0 to 30R 0, whereas the lower curve shows the variation in Z avg in the absence of collisional ionization. We note that Z avg is independent on R IC when we ignore the collisional ionization (lower most curve). We further observe from the upper set of curves that saturating value of Z avg increases as the value of R IC reduces. We may also note that Z avg remains nearly independent to values of R IC until about 50 fs, which shows that it takes about 50 fs for electrons to escape from the parent cluster and start making collisions with neighboring clusters.

Fig. 1. (Color online) Temporal variation of electron population for Ar cluster of radius R 0 = 30 Å irradiated by a representative gaussian laser pulse of duration τ = 70 fs, wavelength λ = 806 nm and peak intensity I p = 8 × 1016 W/cm2.

Fig. 2. (Color online) Snapshots of particle positions at 80 fs (a) and 200 fs (b) for the same laser and cluster parameters as in Figure 1.

Fig. 3. (Color online) Time history of average degree of ionization for Ar clusters for various laser pulse durations. The other laser parameters are same as in Fig. 1.

Fig. 4. (Color online) Comparison between charge state distribution for different inter-cluster distances (R IC) for I p = 4.0 × 1016 W/cm2, τ = 55.0 fs, λ =800 nm, and R 0 =85 Å. Red bars for R IC = 3.5R 0, green bars for R IC = 3.5R 0.

Fig. 5. (Color online) Effect of collisional ionization and R IC on average degree of ionization Z avg for Ar clusters with the same simulation parameters as used in Fig. 4.

In Figure 6, we present our results showing the effect of laser pulse duration on the energy absorption by cluster. Figures 6a and 6b, respectively, show the variation of total energy absorbed by laser and mean energy of ejected ions from the cluster with the laser pulse duration. From Figure 6a, we observe that there exists an optimum pulse duration of about 25 fs at which energy absorption is maximum. Figure 6b shows that mean ion energy saturates to a value of 25 KeV for the optimum pulse duration of about 25 fs. This saturation value is lower for other pulse duration. This optimum absorption can be explained in terms of resonance absorption. Figure 7 shows the temporal variation of laser intensity along with electron density (in units of n c) inside the cluster for various pulse durations. As per the linear resonance theory, the resonance occurs when electron density (total number of inner electrons divided by the cluster volume) of expanding clusters equals the three times the critical density (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996). The dashed horizontal lines in these figures show the n e = 3n c condition. The time at which this dashed line intersects the electron density curve represent the resonance condition (n e = 3n c). One can note that there are two such points of intersection. The first crossover is because of electron population that is building up from zero to maximum value due to ionization. The cluster expansion leads to the second point of intersection (T = T R) where the resonance absorption really occurs. For smallest laser pulse duration (10 fs), T R appears after laser has passed its peak value (time of peak laser intensity is termed as T P) as shown in Figure 7a. Similarly, for larger pulse durations (50 fs, 70 fs, and 120 fs: Figs 7c, 7d, and 7e), T P happens to be much larger than T R. For the case of 25 fs, T = T R and T P are close by (Fig. 7b). We may further note that there should be no such optimum pulse duration for a temporally constant (ideally a rectangular pulse) laser pulse profile. To confirm it, we repeated the above simulations for a pulse profile of second order super-gaussian (nearly flat top). Results are presented in Figure 8. We do observe the energy absorbed to be almost constant (between 116 MeV to 124 MeV). This slight variation may be attributed to the fact that pulse shape is different ideal (rectangular). Thus, we conclude that the presence of an optimum pulse duration is a clear indication of existence of linear resonance occurring during the cluster expansion. Zweiback et al. (Reference Zweiback, Ditmire and Perry1999) have studied experimentally the effect of pulse duration on laser energy absorption at fixed laser energy. In their study, they measured the absorption for large Xenon and Argon clusters with a laser of wavelength of 810 nm, capable of producing 50 mJ in 50 fs. They also found an optimum pulse duration for maximum absorption for relatively large cluster size (85 Å to 205 Å for Xenon and 110 Å to 165 Å for Argon). The cluster sizes employed in our simulations were rather smaller (30 Å). So we note that resonance is observed for a wide-range of cluster sizes. One also expects an optimum cluster size for fixed laser pulse duration on the same argument given earlier. Indeed, an optimum cluster size was observed experimentally for a constant laser pulse duration (Springate et al., Reference Springate, Hay, Tisch, Mason, Ditmire, Hutchinson and Marangos2000).

Fig. 6. (Color online) Laser energy absorbed (a), and mean ion energy variation with laser pulse durations (b).

Fig. 7. (Color online) Time Variation of normalised electron density (ne/nc) along with the laser intensity profile for laser pulse durations of 10 fs (a), 25 fs (b), 50 fs (c), 70 fs (d) and, 120 fs (e). The other laser parameters are same as in Fig. 1.

Fig. 8. Effect of pulse duration on total laser energy absorbed for super-gaussian laser pulse.

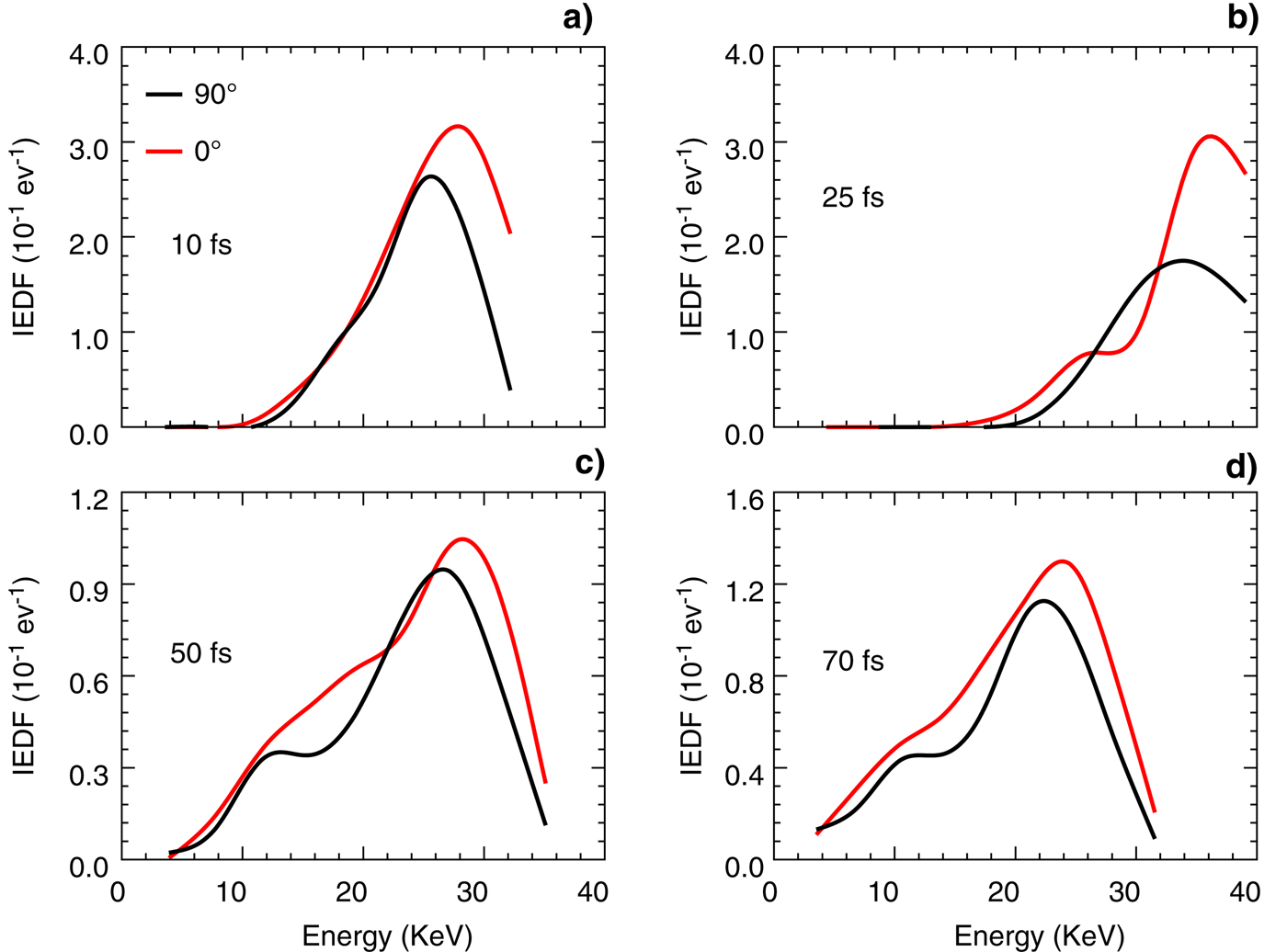
Next we present out results on anisotropy of ion emission. The heating of the cluster and its subsequent evolution is described by two models viz. Coulomb explosion or hydrodynamic expansion depending upon the population of electrons inside the cluster. In Coulomb explosion, all electrons are removed quickly from the cluster under the action of incident laser pulse causing the cluster to explode isotropically due to the Coulomb repulsion among ions (Last & Jortner, Reference Last and Jortner2007). On the other hand, if a significant number of electrons remain inside the cluster (hydrodynamic regime) upon irradiation by the laser, a nanoplasma is formed and ion emission is again isotropic due to the electron gas pressure inside the cluster plasma. When the laser irradiated clusters consists of intermediate population of electrons, ion emission happens to be anisotropic due to the combined action of laser and radial field inside the cluster (Kumarappan et al., Reference Kumarappan, Krishnamurthy and Mathur2002). This anisotropy depends upon the direction of laser polarization: more ions are emitted along the laser polarization direction rather than the perpendicular direction. Various experiments have reported this anisotropy in ion energy emission (Krishnamurthy et al., Reference Krishnamurthy, Mathur and Kumarappan2004; Kumarappan et al., Reference Kumarappan, Krishnamurthy and Mathur2001). We have also observed the similar kind of anisotropic ion emission in our MD simulation. In Figure 9, we present ion energy distribution for the four pulse durations considered in our studies. For the pulse duration of 10 fs (Fig. 9a), the ions are emitted isotropically till ion energy of about 25 keV. For ion energies ≥ 25 keV, more ions are emitted along the laser polarization direction (0° direction) rather than the perpendicular direction (90° direction). The trend remains the same for pulse duration for 25 fs (Figure 9b), but this anisotropic emission become less pronounced as we further go for higher pulse durations (50 and 70 fs) as shown in Figure 9c and 9d.

Fig. 9. (Color online) Time integrated ion energy spectrum along 0° and 90° of laser polarization direction for various laser pulse duration.

4. CONCLUSIONS

The dynamics of Argon cluster of initial radius 30 Å irradiated by high intensity laser pulse (806 nm, 8 × 1016 W/cm2) was investigated by varying the full width at half maximum pulse duration of the gaussian laser starting from 10 fs to 120 fs. The evolution of the cluster is modelled with a relativistic time dependent three-dimensional molecular dynamic model. Key parameters governing the cluster dynamics like temporal evolution of electrons inside and outside the cluster, particle positions, total absorbed energy, mean energy of ions, ion energy distribution function etc. were studied. Effect of inter-cluster distance was also studied. A decrease in inter-cluster distance (which can be thought as increased cluster density in experimental scenario) leads to enhanced collisional ionization. There exists an optimum pulse duration at which the cluster absorbs maximum energy for the laser pulse with gaussian time profile. No optimum pulse duration exists when the gaussian time profile is replaced by the supergaussian on the order of two (nearly flat top). These results are explained on the basis of resonance absorption. Furthermore, anisotropic emission of high energy ions is observed for all pulse durations under investigation. The low energy ions show a low directional preference with respect to laser polarization while high energy ions emit preferably along the laser polarization direction.

ACKNOWLEDGMENTS

Authors are thankful to G. M. Petrov for various discussions and suggestions regarding the development of the code. Authors are also thankful to Prof. Deepak Mathur of TIFR for suggesting the problem and Ms. Vibhuti Duggal of Computer Division for the help in making our code parallel using OpenMP framework and other technical support.

References

REFERENCES

Adoui, L., Gobert, O., Indelicato, P., Lamour, E., Meynadier, P., Normand, D., Perdrix, M., Prigent, C., Rozet, J. & Vernhet, D. (2003). Xe(l) X-ray emission from laser-cluster interaction. Nucl. Instrum. Methods Phys. Res. B 205, 341–345.CrossRefGoogle Scholar
Ammosov, M.V., Delone, N.B. & Krainov, V.P. (1986). Tunnel ionization of complex atoms ans atomic ions by an alternating electromagnetic field. Sov. Phys. JETP 64, 1191–1194.Google Scholar
Ashcroft, N. & Mermin, N. (1976). Solid State Physics. Orlando: Saunders College Publishing.Google Scholar
Borisov, A.B., Song, X., Frigeni, F., Koshman, Y., Dai, Y., Boyer, K. & Rhodes, C.K. (2003). Ultrabright multikilovolt coherent tunable X-ray source at λ ~2.71-2.93 Å. J. Phys. B 36, 3433–3455.CrossRefGoogle Scholar
Brunel, F. (1987). Not-so-resonant, resonant absorption. Phys. Rev. Lett. 59, 52–55.CrossRefGoogle ScholarPubMed
Davis, J., Petrov, G.M. & Velikovich, A. (2007). Nonlinear energy absorption of rare gas clusters in intense laser field. Phys. Plasmas 14, 0607011–4.CrossRefGoogle Scholar
Deiss, C., Rohringer, N., Burgdörfer, J., Lamour, E., Prigent, C., Rozet, J.P. & Vernhet, D. (2006). Laser-cluster interaction: X-ray production by short laser pulses. Phys. Rev. Lett. 96, 0132031–4.CrossRefGoogle ScholarPubMed
Ditmire, T., Donnelly, T., Rubenchik, A.M., Falcone, R.W. & Perry, M.D. (1996). Interaction of intense laser pulses with atomic clusters. Phy. Rev. A 53, 3379–3402.CrossRefGoogle ScholarPubMed
Ditmire, T., Smith, R.A., Tisch, J.W.G. & Hutchinson, M.H.R. (1997a). High intensity laser absorption by gases of atomic clusters. Phys. Rev. Lett. 78, 3121–3124.CrossRefGoogle Scholar
Ditmire, T., Tisch, J.W.G., Springate, E., Mason, M.B., Hay, N., Smith, R.A., Marangos, J. & Hutchinson, M.H.R. (1997b). High-energy ions produced in explosions of superheated atomic cluster. Nature 386, 54–56.CrossRefGoogle Scholar
Fennel, T., Meiwes-Broer, K.H., Tiggesbäumker, J., Reinhard, P.G., Dinh, P.M. & Suraud, E. (2010). Laser-driven nonlinear cluster dynamics. Rev. Mod. Phys. 82, 1793–1842.CrossRefGoogle Scholar
Hagena, O.F. & Obert, W. (1972). Cluster formation in expanding supersonic jets: Effect of pressure, temperature, nozzle size, and test gas. J. Chem. Phys. 56, 1793–1802.CrossRefGoogle Scholar
Holkundkar, A.R. & Gupta, N.K. (2008). Role of radial nonuniformities in the interaction of an intense laser with atomic clusters. Phys. Plasmas 15, 0131051–9.CrossRefGoogle Scholar
Holkundkar, A.R., Mishra, G. & Gupta, N.K. (2011). Molecular dynamic simulation for laser-cluster interaction. Phys. Plasmas (in press).Google ScholarPubMed
Ishikawa, K. & Blenski, T. (2000). Explosion dynamics of rare-gas clusters in an intense laser field. Phys. Rev. A 62, 0632041–11.CrossRefGoogle Scholar
Jungreuthmayer, C., Geissler, M., Zanghellini, J. & Brabec, T. (2004). Microscopic analysis of large-cluster explosion in intense laser fields. Phys. Rev. Lett. 92, 1334011–4.CrossRefGoogle ScholarPubMed
Kirz, J., Jacobsen, C. & Howells, M. (1995). Soft X-ray microscopes and their biological applications. Q. Rev. Biophys. 28, 33–130.CrossRefGoogle ScholarPubMed
Kostyukov, I. & Rax, J.M. (2003). Collisional versus collisionless resonant and autoresonant heating in laser-cluster interaction. Phys. Rev. E 67, 0664051–6.CrossRefGoogle ScholarPubMed
Krishnamurthy, M., Mathur, D. & Kumarappan, V. (2004). Anisotropic “charge-flipping” acceleration of highly charged ions from clusters in strong optical fields. Phys. Rev. A 69, 0332021–5.CrossRefGoogle Scholar
Kubiak, G.D., Bernardez, L.J., Krenz, K.D., O Connell, D.J., Gutowski, R. & Todd, M.M. (1996). Debris-free euvl sources based on gas jets. OSA Trends Opt. Photonics Ser. 4, 66–71.Google Scholar
Kumarappan, V., Krishnamurthy, M. & Mathur, D. (2001). Asymmetric high-energy ion emission from argon clusters in intense laser fields. Phys. Rev. Lett. 87, 0850051–4.CrossRefGoogle ScholarPubMed
Kumarappan, V., Krishnamurthy, M. & Mathur, D. (2002). Two-dimensional effects in the hydrodynamic expansion of xenon clusters under intense laser irradiation. Phys. Rev. A 66, 0332031–4.CrossRefGoogle Scholar
Kundu, M. & Bauer, D. (2006 a). Collisionless energy absorption in the short-pulse intense laser-cluster interaction. Phys. Rev. A 74, 0632021–11.CrossRefGoogle Scholar
Kundu, M. & Bauer, D. (2006 b). Nonlinear resonance absorption in the laser-cluster interaction. Phys. Rev. Lett. 96, 1234011–4.CrossRefGoogle ScholarPubMed
Last, I. & Jortner, J. (1999). Quasiresonance ionization of large multicharged clusters in a strong laser field. Phys. Rev. A 60, 2215–2221.CrossRefGoogle Scholar
Last, I. & Jortner, J. (2000). Dynamics of the coulomb explosion of large clusters in a strong laser field. Phys. Rev. A 62, 0132011–9.CrossRefGoogle Scholar
Last, I. & Jortner, J. (2004). Electron and nuclear dynamics of molecular clusters in ultraintense laser fields. iii. coulomb explosion of deuterium clusters. J. Chem. Phys. 121, 3030–3043.CrossRefGoogle ScholarPubMed
Levine, Z.H., Kalukin, A.R., Frigo, S.P., McNulty, I. & Kuhn, M. (1999). Tomographic reconstruction of an integrated circuit interconnect. Appl. Phys. Lett. 74, 150–152.CrossRefGoogle Scholar
Liu, J., Li, R., Zhu, P., Xu, Z. & Liu, J. (2001). Modified hydrodynamic model and its application in the investigation of laser-cluster interactions. Phys. Rev. A 64, 0334261–7.CrossRefGoogle Scholar
Lotz, W. (1968). Electron-impact ionization cross-sections and ionization rate coefficients for atoms and ions from hydrogen to calcium. Z. Phys 216, 241–247.CrossRefGoogle Scholar
Milchberg, H.M., McNaught, S.J. & Parra, E. (2001). Plasma hydrodynamics of the intense laser-cluster interaction. Phys. Rev. E 64, 0564021–7.CrossRefGoogle ScholarPubMed
Parra, E., Alexeev, I., Fan, J., Kim, K.Y., McNaught, S.J. & Milchberg, H.M. (2003). Hydrodynamic time scales for intense laser-heated clusters. J. Opt. Soc. Am. B 20, 118–124.CrossRefGoogle Scholar
Perry, M.D. & Mourou, G. (1994). Terawatt to Petawatt Subpicosecond Lasers. Science 264, 917–924.CrossRefGoogle ScholarPubMed
Petrov, G.M. & Davis, J. (2008). Interaction of intense ultrashort pulse lasers with clusters. Physics of Plasmas 15, 0567051–8.Google Scholar
Petrov, G.M., Davis, J., Velikovich, A.L., Kepple, P.C., Dasgupta, A., Clark, R.W., Borisov, A.B., Boyer, K. & Rhodes, C.K. (2005). Modeling of clusters in a strong 248-nm laser field by a three-dimensional relativistic molecular dynamic model. Phys. Rev. E 71, 0364111–10.CrossRefGoogle Scholar
Prigent, C., Deiss, C., Lamour, E., Rozet, J.P., Vernhet, D. & Burgdörfer, J. (2008). Effect of pulse duration on the x-ray emission from ar clusters in intense laser fields. Phys. Rev. A 78, 0532011–12.CrossRefGoogle Scholar
Rose-Petruck, C., Schafer, K.J., Wilson, K.R. & Barty, C.P.J. (1997). Ultrafast electron dynamics and inner-shell ionization in laser driven clusters. Phys. Rev. A 55, 1182–1190.CrossRefGoogle Scholar
Smirnov, M.B. & Krainov, V.P. (2003). Hot electron generation in laser cluster plasma. Phys. Plasmas 10, 443–447.CrossRefGoogle Scholar
Springate, E., Hay, N., Tisch, J.W.G., Mason, M.B., Ditmire, T., Hutchinson, M.H.R. & Marangos, J.P. (2000). Explosion of atomic clusters irradiated by high-intensity laser pulses: Scaling of ion energies with cluster and laser parameters. Phys. Rev. A 61, 0632011–7.Google Scholar
Voronov, G.S. (1997). A practical fit formula for ionization rate coefficients of atoms and ions by electron impact : Z = 1-28. At. Data Nucl. Data Tables 65, 1–35.CrossRefGoogle Scholar
Zweiback, J., Ditmire, T. & Perry, M.D. (1999). Femtosecond time-resolved studies of the dynamics of noble-gas cluster explosions. Phys. Rev. A 59, R3166–R3169.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) Temporal variation of electron population for Ar cluster of radius R0 = 30 Å irradiated by a representative gaussian laser pulse of duration τ = 70 fs, wavelength λ = 806 nm and peak intensity Ip = 8 × 1016 W/cm2.

Figure 1

Fig. 2. (Color online) Snapshots of particle positions at 80 fs (a) and 200 fs (b) for the same laser and cluster parameters as in Figure 1.

Figure 2

Fig. 3. (Color online) Time history of average degree of ionization for Ar clusters for various laser pulse durations. The other laser parameters are same as in Fig. 1.

Figure 3

Fig. 4. (Color online) Comparison between charge state distribution for different inter-cluster distances (RIC) for Ip = 4.0 × 1016 W/cm2, τ = 55.0 fs, λ =800 nm, and R0 =85 Å. Red bars for RIC = 3.5R0, green bars for RIC = 3.5R0.

Figure 4

Fig. 5. (Color online) Effect of collisional ionization and RIC on average degree of ionization Zavg for Ar clusters with the same simulation parameters as used in Fig. 4.

Figure 5

Fig. 6. (Color online) Laser energy absorbed (a), and mean ion energy variation with laser pulse durations (b).

Figure 6

Fig. 7. (Color online) Time Variation of normalised electron density (ne/nc) along with the laser intensity profile for laser pulse durations of 10 fs (a), 25 fs (b), 50 fs (c), 70 fs (d) and, 120 fs (e). The other laser parameters are same as in Fig. 1.

Figure 7

Fig. 8. Effect of pulse duration on total laser energy absorbed for super-gaussian laser pulse.

Figure 8

Fig. 9. (Color online) Time integrated ion energy spectrum along 0° and 90° of laser polarization direction for various laser pulse duration.