1. INTRODUCTION
Raman scattering is a parametric instability in which an incident light wave decays resonantly into an electron plasma wave and a scattered sideband wave at a shifted frequency. The sideband wave interacts with the pump wave field producing a ponderomotive bunching force which amplifies the original density perturbation created by electron plasma wave leading to the instability and transferring energy into the plasma. This instability is an excellent example of an important nonlinear optical process and decreases the efficiency in inertial confinement fusion (ICF) hohlraums or particle acceleration experiments (Barr et al., Reference Barr, Boyd, Gordon and Berwick1984b; Kruer, Reference Kruer2000). Raman scattering takes place in the subcritical (underdense) region of the plasma. Occurrence of this instability can potentially prevent laser energy from ever arriving at the critical surface where the enhanced absorption mechanism can operate (Forslund et al., Reference Forslund, Kindel and Lindman1975). In an early basic work on scattering instabilities, Drake et al., derived the general dispersion relation in the interaction of high amplitude electromagnetic wave with homogeneous unmagnetized plasma for nonrelativistic case and obtained the linear growth rates for Raman instability as well as the other parametric instabilities. They showed that, in general, stimulated scattering of the incident pump electromagnetic wave is strongest in the backscatter direction (Drake et al., Reference Drake, Kaw, Lee, Schmid, Liu and Marshall1974). Raman backward scattering (RBS) is significant for a number of reasons. As the RBS mode grows to large amplitude, it can trap background plasma electrons, thus heating the plasma and creating a fast tail on the electron distribution. It has been reported that spontaneous dc-magnetic field of the order of a few Mega-gauss which are easily achieved in laser–plasma interactions and laser-produced plasmas can affect the propagation of both the laser and plasma wave as well as transport coefficients in plasma (Sharma & Dragila, Reference Sharma and Dragila1988; Nicolai et al., Reference Nicolai, Vandenboomgaerde, Canaud and Chaigneau1994; McKenna et al., Reference Mckenna, Neely, Bingham and Jaroszynski2013). The constant dc-magnetic field could be externally applied or self-generated in the plasma (Bawaaneh, Reference Bawaaneh2006). In the context of ICF, experiments and theory have shown that the self-generated-dc magnetic field is perpendicular to the polarization and propagation vector of the incident laser radiation (Stamper et al., Reference Stamper, Mclean and Ripin1978; Grebogi & Liu, Reference Grebogi and Liu1980; Nabil, Reference Nabil1995). It has been shown experimentally that the self-generated magnetic field rises from 600 KG at the critical density to 2–3 MG around quarter critical density. Then, it drops steeply with decreasing density until it reaches zero at about 0.1 critical density (Nabil, Reference Nabil1995). When an electromagnetic wave travels perpendicularly to the external magnetic field in magnetized plasma, it becomes partly longitudinal and gains a longitudinal electric field which makes it an extraordinary wave which is elliptically polarized (Krall & Trivelpiece, Reference Krall and Trivelpiece1973; Cho et al., Reference Cho, Kim and Hur2014). In this case, we say that the electromagnetic wave propagates in its X-mode in plasma. As such a wave propagates through a region in which plasma frequency and electron cyclotron frequency are changing; it may encounter cut-offs and resonances which correspond to plasmas, respectively. A wave generally reflected at a cut-off and absorbed at a resonance. Since we consider the interaction of a high frequency laser pulse with underdense plasma, the cut-off points therefore do not appear in our investigation. It has been found from the X-mode dispersion relation that the frequency of the backward scattered wave is downshifted by an amount of upper hybrid frequency (Cho et al., Reference Cho, Kim and Hur2014). So, Raman scattering process in the transversely magnetized plasma with a constant dc-magnetic field includes the decay of an electromagnetic pump wave into an upper hybrid wave and two scattered daughter waves (Paknezhad & Dorranian, Reference Paknezhad and Dorranian2011; Paknezhad, Reference Paknezhad2013a). In this process, the laser and the sidebands exert a nonlinear ponderomotive force on electrons driving the upper hybrid wave. In the previous works, some researchers have tried to investigate the Raman scattering instability of X-mode laser in magnetized plasma. Nabil studied the effect of static self-generated magnetic field on the growth rate of Raman backscattering in homogeneous collisionless plasma and obtained a general expression for the growth rate of Raman backscattering instability in homogeneous plasma by ignoring the relativistic effect and effects due to other nonlinearities. He found that the growth rate of this instability decreases and its threshold power increases if self-generated magnetic fields are taken into consideration (Nabil, Reference Nabil1995). Grebogi and Liu (Reference Grebogi and Liu1980) made a theoretical study and examined the effects of self-generated dc-magnetic field on the Brillouin and Raman scattering of an extraordinary electromagnetic pump in plasma without taking the relativistic and ponderomotive nonlinearities into account and found the expressions for the Raman and Brillouin growth rates in the fluid theory limit. They reported that for laser fusion parameters in the magnetized plasma, the Raman scattering by the upper hybrid wave has substantial growth rate. Barr et al. (Reference Barr, Boyd, Gardner and Rankin1984a), studied the Raman backscatter of intense laser light from an inhomogeneous plasma in the presence of a self-generated magnetic field. They observed a significant blue shift in the frequency of the Raman backscattered wave. They also remarked reduced levels of Raman backscatter. They attributed these reduced levels to the linear mode conversion of the daughter wave of Raman instability. Sharma et al. (Reference Sharma, Monika, Sharma, Chauhan and Ji2010), analyzed the RFS instability in the presence of a background dc-magnetic field and found an explicit expression for the growth rate of instability. They demonstrated that the presence of the dc-magnetic field causes an increase of the growth rate for the perpendicular propagation of the pump laser beam as an elliptically polarized extraordinary wave. Hassoon et al. (Reference Hassoon, Salih and Tripathi2009), studied the effect of a transverse magnetic field on the stimulated Raman forward scattering (RFS) in a laser-produced plasma and showed that the growth rate of stimulated RFS instability first increases on increasing magnetic field, maximizes at some optimum value of magnetic field, and then decreases. In our previous theoretical study (Paknezhad & Dorranian, Reference Paknezhad and Dorranian2011), we considered the interaction of a linearly polarized laser with a transversely magnetized underdense cold plasma and we investigated the RBS instability and obtained an explicit expression for the temporal growth rate of the instability by ignoring the effect of extraordinary property of laser in underdense plasma. We showed that in transversely magnetized cold plasma, the growth rate of RBS instability increases by increasing the external magnetic field. Gill and Saini (Reference Gill and Saini2007), studied the growing interaction of the rippled laser beam with upper hybrid mode leading to enhanced Raman scattering for collisional plasma. They demonstrated that the electron–ion collisions maintain almost less oscillatory intensity of ripple. However, collisions between electrons and di-atomic molecules do not play significant role in the intensity dynamics of the ripple. They also concluded that increasing the strength of the magnetic field leads to substantial increase in the scattered power. In another similar study, Liu et al. (Reference Liu, Zhu, Cao, Zheng, He and Wang2009) developed 1D Vlasov–Maxwell numerical simulation to examine RBS instability in unmagnetized collisional plasma. Their results showed that RBS will be enhanced by electron–ion collisions. The present work reports the effect of self-generated magnetic field on the growth rate of Raman backscattering of X-mode laser in the presence of electron–ion collisions. Here, we consider homogeneous plasma in which the uniform self-generated magnetic field is perpendicular to both, the direction of propagation and electric vector of the radiation field. Nonlinear wave equation is set up and nonlinear ponderomotive force is obtained and coupled equations are solved to find the growth rate. Thermal effects of the plasma electrons and effect of the electron–ion collisions are examined in this research. Since we consider the weakly relativistic regime, we neglect the self-focusing and filamentation effects. These effects may enhance the growth rate (Saini & Gill, Reference Saini and Gill2004). Our resulting analysis is only valid for short time compared with the characteristic evolution time of the pump laser (laser duration). This paper is organized as follows. In Section 2, a theoretical analysis is introduced and an expression for the nonlinear ponderomotive force is acquired. In Section 3, we obtain a mathematical expression for the dispersion relation of the Raman-scattered wave and find a new expression for the maximum nonlinear growth rate. The discussion is presented in Section 4.
2. NONLINEAR PONDEROMOTIVE FORCE
When a laser beam propagates through a plasma imbedded in a background dc-magnetic field, a longitudinal electrostatic field is generated due to the ponderomotive force acting on plasma electrons, and this makes the laser beam to become extraordinary which is called X-mode laser. Consider the propagation of an X-mode intense laser pump wave with electric field ![]() ${\bf E} = 1/2{E_0}(\hat x + i{{\rm \beta} _0}\hat z){e^{i{{\rm \theta} _0}}}$ at (ω0, k 0) in a plasma of initial electron density n 0 immersed in a static transverse magnetic field
${\bf E} = 1/2{E_0}(\hat x + i{{\rm \beta} _0}\hat z){e^{i{{\rm \theta} _0}}}$ at (ω0, k 0) in a plasma of initial electron density n 0 immersed in a static transverse magnetic field ![]() ${\bf B} = {B_0}\hat y$, with θ0 = (k 0z − ω0t) and
${\bf B} = {B_0}\hat y$, with θ0 = (k 0z − ω0t) and
 $${{\rm \beta} _0} = \displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _0}}}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2 - {\rm \omega} _{{\rm UH}}^2}} $$
$${{\rm \beta} _0} = \displaystyle{{{{\rm \omega} _{\rm c}}} \over {{{\rm \omega} _0}}}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2 - {\rm \omega} _{{\rm UH}}^2}} $$where, ωp, ωc, and ωUH are the plasma frequency, electron cyclotron frequency, and upper-hybrid frequency, respectively (Liu et al., Reference Liu, Zhu, Cao, Zheng, He and Wang2009).
The response of plasma electrons to the laser radiation field is described by the Lorentz force
Here, γ0 is the relativistic factor. Using the Lorentz equation, the orders of electron velocity components in the interaction of X-mode laser with magnetized plasma are read as (Paknezhad, Reference Paknezhad2013a)
 $$v_x^{(1)} = - ic{a_0}\left( {\displaystyle{{{\rm \omega} _0^2 + {{\rm \beta} _0}{{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}}} \right){e^{i{{\rm \theta} _0}}}$$
$$v_x^{(1)} = - ic{a_0}\left( {\displaystyle{{{\rm \omega} _0^2 + {{\rm \beta} _0}{{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}}} \right){e^{i{{\rm \theta} _0}}}$$ $$v_z^{(1)} = - c{a_0}\left( {\displaystyle{{{{\rm \beta} _0}{\rm \omega} _0^2 + {{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}}} \right){e^{i{{\rm \theta} _0}}}$$
$$v_z^{(1)} = - c{a_0}\left( {\displaystyle{{{{\rm \beta} _0}{\rm \omega} _0^2 + {{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}}} \right){e^{i{{\rm \theta} _0}}}$$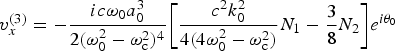 $$v_x^{(3)} = - \displaystyle{{ic{{\rm \omega} _0}a_0^3} \over {2({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}}}\bigg[\displaystyle{{{c^2}k_0^2} \over {4(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}{N_1} - \displaystyle{3 \over 8}{N_2}\bigg]{e^{i{{\rm \theta} _0}}}$$
$$v_x^{(3)} = - \displaystyle{{ic{{\rm \omega} _0}a_0^3} \over {2({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}}}\bigg[\displaystyle{{{c^2}k_0^2} \over {4(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}{N_1} - \displaystyle{3 \over 8}{N_2}\bigg]{e^{i{{\rm \theta} _0}}}$$ $$v_z^{(3)} = - \displaystyle{{c{{\rm \omega} _0}a_0^3} \over {2({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}}}\bigg[\displaystyle{{{c^2}k_0^2} \over {4(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}{N_3} - \displaystyle{3 \over 8}{N_4}\bigg]{e^{i{{\rm \theta} _0}}}$$
$$v_z^{(3)} = - \displaystyle{{c{{\rm \omega} _0}a_0^3} \over {2({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}}}\bigg[\displaystyle{{{c^2}k_0^2} \over {4(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}{N_3} - \displaystyle{3 \over 8}{N_4}\bigg]{e^{i{{\rm \theta} _0}}}$$ It may be noted that the second-order velocities ![]() $v_x^{(2)} $,
$v_x^{(2)} $, ![]() $v_z^{(2)} $ are not in resonance, that is, are not proportional to e iθ0 and do not satisfy the phase-matching condition and do not appear in our calculations. So, just the third-order velocities need to be considered to find the nonlinear current density. Plasma electrons initially oscillate at the pump wave frequency. The response of plasma electron to the laser radiation field is described by the longitudinal and transverse components of the current density,
$v_z^{(2)} $ are not in resonance, that is, are not proportional to e iθ0 and do not satisfy the phase-matching condition and do not appear in our calculations. So, just the third-order velocities need to be considered to find the nonlinear current density. Plasma electrons initially oscillate at the pump wave frequency. The response of plasma electron to the laser radiation field is described by the longitudinal and transverse components of the current density,
where,
 $$\eqalign{ {{\rm \zeta} _0} & = \left( {\displaystyle{{{\rm \omega} _0^2 + {{\rm \beta} _0}{{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}}} \right) + a_0^2 [\displaystyle{{{c^2}k_0^2 {{\rm \omega} _0}} \over {4({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}} \cr & \quad {N_1} - \displaystyle{3 \over 8}\displaystyle{{{{\rm \omega} _0}} \over {{{({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}^4}}}{N_2}]}$$
$$\eqalign{ {{\rm \zeta} _0} & = \left( {\displaystyle{{{\rm \omega} _0^2 + {{\rm \beta} _0}{{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}}} \right) + a_0^2 [\displaystyle{{{c^2}k_0^2 {{\rm \omega} _0}} \over {4({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}} \cr & \quad {N_1} - \displaystyle{3 \over 8}\displaystyle{{{{\rm \omega} _0}} \over {{{({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}^4}}}{N_2}]}$$and
 $$\eqalign{ {\rm \eta _0} & = \displaystyle{{{{\rm \beta} _0}{\rm \omega} _0^2 + {{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}} \cr & \quad + a_0^2 \left[ {\displaystyle{{{c^2}k_0^2 ({N_1}{{\rm \omega} _{\rm c}} + {N_3}({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ))} \over {4({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{3{N_2}{{\rm \omega} _{\rm c}} + {N_4}({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )} \over {8({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}}}} \right]}$$
$$\eqalign{ {\rm \eta _0} & = \displaystyle{{{{\rm \beta} _0}{\rm \omega} _0^2 + {{\rm \omega} _0}{{\rm \omega} _{\rm c}}} \over {{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2}} \cr & \quad + a_0^2 \left[ {\displaystyle{{{c^2}k_0^2 ({N_1}{{\rm \omega} _{\rm c}} + {N_3}({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ))} \over {4({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}(4{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{3{N_2}{{\rm \omega} _{\rm c}} + {N_4}({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )} \over {8({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 {)^4}}}} \right]}$$with
 $$\eqalign{{N_1} & = 2{\rm \beta }_0^2 {\rm \omega }_0^7 + {{\rm \beta }_0}(6{\rm \beta }_0^2 - 25){\rm \omega }_0^4 {\rm \omega }_{\rm c}^3 \cr & \quad + (26{\rm \beta }_0^2 - 5){\rm \omega }_0^3 {\rm \omega }_{\rm c}^4 - (30{\rm \beta }_0^2 + 5){\rm \omega }_0^5 {\rm \omega }_{\rm c}^2 \cr & \quad + 27{{\rm \beta }_0}{\rm \omega }_0^2 {\rm \omega }_{\rm c}^5 - {{\rm \beta }_0}(6{\rm \beta }_0^2 - 5){\rm \omega }_0^6 {{\rm \omega }_{\rm c}} + 10{{\rm \omega }_0}{\rm \omega }_{\rm c}^6 + {{\rm \beta }_0}{\rm \omega }_{\rm c}^7 \cr {N_2} & = (3{\rm \beta }_0^2 + 1)({\rm \omega }_0^7 + 6{\rm \omega }_0^5 {\rm \omega }_{\rm c}^2 + {\rm \omega }_0^3 {\rm \omega }_{\rm c}^4 ) \cr & \quad + 4{{\rm \beta }_0}({\rm \beta }_0^2 + 3)({\rm \omega }_0^6 {{\rm \omega }_{\rm c}} + {\rm \omega }_0^4 {\rm \omega }_{\rm c}^3 ) \cr {N_3} & = {{\rm \beta }_0}(3{\rm \beta }_0^2 - 25){\rm \omega }_0^4 {\rm \omega }_{\rm c}^2 + (14{\rm \beta }_0^2 - 9){\rm \omega }_0^3 {\rm \omega }_{\rm c}^3 \cr & \quad - (26{\rm \beta }_0^2 + 1){\rm \omega }_0^5 {{\rm \omega }_{\rm c}} - {{\rm \beta }_0}(6{\rm \beta }_0^2 + 3){\rm \omega }_0^6 + 15{\rm \beta }_0^2 {\rm \omega }_{\rm c}^4 + 7{{\rm \omega }_0}{\rm \omega }_{\rm c}^5 \cr {N_4} & = {{\rm \beta }_0}({\rm \beta }_0^2 + 3){\rm \omega }_0^6 + (3{\rm \beta }_0^2 + 1)({\rm \omega }_0^3 {\rm \omega }_{\rm c}^3 + 3{\rm \omega }_0^5 {{\rm \omega }_{\rm c}}) \cr & \quad + {{\rm \beta }_0}(3{\rm \beta }_0^2 + 6{{\rm \beta }_0} + 3){\rm \omega }_0^4 {\rm \omega }_{\rm c}^2 } $$
$$\eqalign{{N_1} & = 2{\rm \beta }_0^2 {\rm \omega }_0^7 + {{\rm \beta }_0}(6{\rm \beta }_0^2 - 25){\rm \omega }_0^4 {\rm \omega }_{\rm c}^3 \cr & \quad + (26{\rm \beta }_0^2 - 5){\rm \omega }_0^3 {\rm \omega }_{\rm c}^4 - (30{\rm \beta }_0^2 + 5){\rm \omega }_0^5 {\rm \omega }_{\rm c}^2 \cr & \quad + 27{{\rm \beta }_0}{\rm \omega }_0^2 {\rm \omega }_{\rm c}^5 - {{\rm \beta }_0}(6{\rm \beta }_0^2 - 5){\rm \omega }_0^6 {{\rm \omega }_{\rm c}} + 10{{\rm \omega }_0}{\rm \omega }_{\rm c}^6 + {{\rm \beta }_0}{\rm \omega }_{\rm c}^7 \cr {N_2} & = (3{\rm \beta }_0^2 + 1)({\rm \omega }_0^7 + 6{\rm \omega }_0^5 {\rm \omega }_{\rm c}^2 + {\rm \omega }_0^3 {\rm \omega }_{\rm c}^4 ) \cr & \quad + 4{{\rm \beta }_0}({\rm \beta }_0^2 + 3)({\rm \omega }_0^6 {{\rm \omega }_{\rm c}} + {\rm \omega }_0^4 {\rm \omega }_{\rm c}^3 ) \cr {N_3} & = {{\rm \beta }_0}(3{\rm \beta }_0^2 - 25){\rm \omega }_0^4 {\rm \omega }_{\rm c}^2 + (14{\rm \beta }_0^2 - 9){\rm \omega }_0^3 {\rm \omega }_{\rm c}^3 \cr & \quad - (26{\rm \beta }_0^2 + 1){\rm \omega }_0^5 {{\rm \omega }_{\rm c}} - {{\rm \beta }_0}(6{\rm \beta }_0^2 + 3){\rm \omega }_0^6 + 15{\rm \beta }_0^2 {\rm \omega }_{\rm c}^4 + 7{{\rm \omega }_0}{\rm \omega }_{\rm c}^5 \cr {N_4} & = {{\rm \beta }_0}({\rm \beta }_0^2 + 3){\rm \omega }_0^6 + (3{\rm \beta }_0^2 + 1)({\rm \omega }_0^3 {\rm \omega }_{\rm c}^3 + 3{\rm \omega }_0^5 {{\rm \omega }_{\rm c}}) \cr & \quad + {{\rm \beta }_0}(3{\rm \beta }_0^2 + 6{{\rm \beta }_0} + 3){\rm \omega }_0^4 {\rm \omega }_{\rm c}^2 } $$ The nonlinear terms in the definition of above parameters comes from the relativistic effects and effects due to the presence of the uniform magnetic field. In the weakly relativistic regime![]() $(a_0^2 \ll 1)$, the second term in the definitions of ζ0 and η0 can be neglected. In the absence of the self-generated magnetic field, the nonlinear coefficients are reduced to
$(a_0^2 \ll 1)$, the second term in the definitions of ζ0 and η0 can be neglected. In the absence of the self-generated magnetic field, the nonlinear coefficients are reduced to ![]() ${{\rm \zeta} _0} = 1 - (3/8)a_0^2 $ and η0 = 0. In this case, the incident radiation field will not appear in its extraordinary mode. Nonlinear dispersion relation for the X-mode pump laser beam propagating in the transversely magnetized plasma is of the form (Paknezhad, Reference Paknezhad2013a),
${{\rm \zeta} _0} = 1 - (3/8)a_0^2 $ and η0 = 0. In this case, the incident radiation field will not appear in its extraordinary mode. Nonlinear dispersion relation for the X-mode pump laser beam propagating in the transversely magnetized plasma is of the form (Paknezhad, Reference Paknezhad2013a),
 $$\displaystyle{{c{k_0}} \over {{{\rm \omega} _0}}} = {\left[ {1 - {{\rm \zeta} _0}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2}}} \right]^{1/2}}$$
$$\displaystyle{{c{k_0}} \over {{{\rm \omega} _0}}} = {\left[ {1 - {{\rm \zeta} _0}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2}}} \right]^{1/2}}$$In the weakly relativistic regime, this dispersion relation is simplified to
 $$\displaystyle{{c{k_0}} \over {{{\rm \omega} _0}}} = {\left[ {1 - \left( {\displaystyle{{1 + {{\rm \beta} _0}({{\rm \omega} _{\rm c}}/{{\rm \omega} _0})} \over {1 - {\rm \omega} _{\rm c}^2 /{\rm \omega} _0^2}}} \right)\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2}}} \right]^{1/2}}$$
$$\displaystyle{{c{k_0}} \over {{{\rm \omega} _0}}} = {\left[ {1 - \left( {\displaystyle{{1 + {{\rm \beta} _0}({{\rm \omega} _{\rm c}}/{{\rm \omega} _0})} \over {1 - {\rm \omega} _{\rm c}^2 /{\rm \omega} _0^2}}} \right)\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2}}} \right]^{1/2}}$$Now, let us consider the response of plasma electrons to the nonlinear ponderomotive force Fp and a self-consistent potential ϕ which is governed by the equation of motion and continuity
where, ![]() ${{\rm \omega} _{\bf c}}( = e{{\bf B}_{\bf 0}}/mc)$ the vector of electron cyclotron frequency and
${{\rm \omega} _{\bf c}}( = e{{\bf B}_{\bf 0}}/mc)$ the vector of electron cyclotron frequency and ![]() ${v_{\rm T}}( = \sqrt {{T_{\rm e}}/m} $) is the electron thermal velocity in plasma. Using the perturbed equations of motion of an electron in the external magnetic field (
${v_{\rm T}}( = \sqrt {{T_{\rm e}}/m} $) is the electron thermal velocity in plasma. Using the perturbed equations of motion of an electron in the external magnetic field (![]() $\partial {\tilde v_x}/\partial t = {{\rm \omega} _{\rm c}}{\tilde v_z}$,
$\partial {\tilde v_x}/\partial t = {{\rm \omega} _{\rm c}}{\tilde v_z}$, ![]() $\partial {\tilde v_z}/\partial t = - {{\rm \omega} _{\rm c}}{\tilde v_x}$), the longitudinal component of Eq. (3) takes the form
$\partial {\tilde v_z}/\partial t = - {{\rm \omega} _{\rm c}}{\tilde v_x}$), the longitudinal component of Eq. (3) takes the form
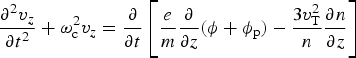 $$\displaystyle{{{\partial ^2}{v_z}} \over {\partial {t^2}}} + {\rm \omega} _{\rm c}^2 {v_z} = \displaystyle{\partial \over {\partial t}}\left[ {\displaystyle{e \over m}\displaystyle{\partial \over {\partial z}}({\rm \phi} + {{\rm \phi} _{\rm p}}) - \displaystyle{{3v_{\rm T}^2} \over n}\displaystyle{{\partial n} \over {\partial z}}} \right]$$
$$\displaystyle{{{\partial ^2}{v_z}} \over {\partial {t^2}}} + {\rm \omega} _{\rm c}^2 {v_z} = \displaystyle{\partial \over {\partial t}}\left[ {\displaystyle{e \over m}\displaystyle{\partial \over {\partial z}}({\rm \phi} + {{\rm \phi} _{\rm p}}) - \displaystyle{{3v_{\rm T}^2} \over n}\displaystyle{{\partial n} \over {\partial z}}} \right]$$ Assuming that the phase matching condition is satisfied, multiplying Eq. (5) by ![]() $n = {n_0} + \tilde n$, and then taking its divergence, yields,
$n = {n_0} + \tilde n$, and then taking its divergence, yields,
 $$\left( {\displaystyle{{{\partial ^2}} \over {\partial {t^2}}} + {\rm \omega} _{\rm c}^2} \right)\displaystyle{\partial \over {\partial z}}({n_0}{v_z}) = \displaystyle{\partial \over {\partial t}}\left[ {\displaystyle{{{n_0}e} \over m}\displaystyle{{{\partial ^2}} \over {\partial {z^2}}}({\rm \phi} + {{\rm \phi} _{\rm p}}) - 3v_{\rm T}^2 \displaystyle{{{\partial ^2}\tilde n} \over {\partial {z^2}}}} \right]$$
$$\left( {\displaystyle{{{\partial ^2}} \over {\partial {t^2}}} + {\rm \omega} _{\rm c}^2} \right)\displaystyle{\partial \over {\partial z}}({n_0}{v_z}) = \displaystyle{\partial \over {\partial t}}\left[ {\displaystyle{{{n_0}e} \over m}\displaystyle{{{\partial ^2}} \over {\partial {z^2}}}({\rm \phi} + {{\rm \phi} _{\rm p}}) - 3v_{\rm T}^2 \displaystyle{{{\partial ^2}\tilde n} \over {\partial {z^2}}}} \right]$$Using the continuity equation in Eq. (6), gives
 $$\left( {\displaystyle{{{\partial ^2}} \over {\partial {t^2}}} + {\rm \omega} _{\rm c}^2} \right)\tilde n = - \displaystyle{{{n_0}e} \over m}\displaystyle{{{\partial ^2}} \over {\partial {z^2}}}({\rm \phi} + {{\rm \phi} _{\rm p}}) + 3v_{\rm T}^2 \displaystyle{{{\partial ^2}\tilde n} \over {\partial {z^2}}}$$
$$\left( {\displaystyle{{{\partial ^2}} \over {\partial {t^2}}} + {\rm \omega} _{\rm c}^2} \right)\tilde n = - \displaystyle{{{n_0}e} \over m}\displaystyle{{{\partial ^2}} \over {\partial {z^2}}}({\rm \phi} + {{\rm \phi} _{\rm p}}) + 3v_{\rm T}^2 \displaystyle{{{\partial ^2}\tilde n} \over {\partial {z^2}}}$$Now, replacing ∂/∂t with −iω and replacing ∂/∂z with ik in Eq. (7), one obtains
Using the definition of plasma frequency ![]() ${{\rm \omega} _{\rm p}} = \sqrt {4{\rm \pi} {n_0}{e^2}/m} $ in Eq. (8), we obtain the perturbed density
${{\rm \omega} _{\rm p}} = \sqrt {4{\rm \pi} {n_0}{e^2}/m} $ in Eq. (8), we obtain the perturbed density ![]() $\tilde n$, arising from the scattering of the large-amplitude incident wave into the sideband daughter wave
$\tilde n$, arising from the scattering of the large-amplitude incident wave into the sideband daughter wave
 $$\tilde n = - \displaystyle{{{k^2}({\rm \phi} + {{\rm \phi} _{\rm p}})} \over {4{\rm \pi} e}}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 - 3{k^2}v_{\rm T}^2}} $$
$$\tilde n = - \displaystyle{{{k^2}({\rm \phi} + {{\rm \phi} _{\rm p}})} \over {4{\rm \pi} e}}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 - 3{k^2}v_{\rm T}^2}} $$ Now, substituting Eq. (9) in the Poisson's equation, ![]() ${\nabla ^2}{\rm \phi} = 4{\rm \pi} \tilde ne$, and solving, we reach to
${\nabla ^2}{\rm \phi} = 4{\rm \pi} \tilde ne$, and solving, we reach to
 $${\rm \phi} = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 - 3{k^2}v_{\rm T}^2}} {{\rm \phi} _{\rm p}}$$
$${\rm \phi} = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 - 3{k^2}v_{\rm T}^2}} {{\rm \phi} _{\rm p}}$$Let the ponderomotive force due to the beating of the pump and sideband waves be such that
Here, ![]() ${{\bf v}_{\bf 0}} = {v_{0x}}\hat x + {v_{0z}}\hat z$ and
${{\bf v}_{\bf 0}} = {v_{0x}}\hat x + {v_{0z}}\hat z$ and ![]() ${{\bf v}_{\bf 1}} = {v_{1x}}\hat x + {v_{1z}}\hat z$, are the oscillatory velocities of electrons due to the pump and scattered sideband waves, respectively, with v 0x = −(i/2)ca 0ζ0e iθ0, v 1x = −(i/2)ca 1ζ1e iθ1, v 0z = (1/2)ca 0η0e iθ0, and v 1z = (1/2)ca 1η1e iθ1, where θ1 = k 1z − ω1t. Note that, ζ1 and η1 are defined by replacing ω0, k 0 and a 0 with ω1, k 1, and a 1 in the definition of ζ0 and η0. Also, a 0 = eE 0/mcω0 and a 1 = eE 1/mcω1 are the normalized vector potential of the pump and the slowly-varying sideband wave, respectively, such that a 0 ≫ a 1. Hence, we obtain the ponderomotive potential from Eq. (11) as
${{\bf v}_{\bf 1}} = {v_{1x}}\hat x + {v_{1z}}\hat z$, are the oscillatory velocities of electrons due to the pump and scattered sideband waves, respectively, with v 0x = −(i/2)ca 0ζ0e iθ0, v 1x = −(i/2)ca 1ζ1e iθ1, v 0z = (1/2)ca 0η0e iθ0, and v 1z = (1/2)ca 1η1e iθ1, where θ1 = k 1z − ω1t. Note that, ζ1 and η1 are defined by replacing ω0, k 0 and a 0 with ω1, k 1, and a 1 in the definition of ζ0 and η0. Also, a 0 = eE 0/mcω0 and a 1 = eE 1/mcω1 are the normalized vector potential of the pump and the slowly-varying sideband wave, respectively, such that a 0 ≫ a 1. Hence, we obtain the ponderomotive potential from Eq. (11) as
Now, substituting Eq. (12) in Eq. (10), we come into the self-consistent electrostatic potential
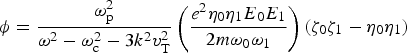 $${\rm \phi} = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 - 3{k^2}v_{\rm T}^2}} \left( {\displaystyle{{{e^2}{{\rm \eta} _0}{{\rm \eta} _1}{E_0}{E_1}} \over {2m{{\rm \omega} _0}{{\rm \omega} _1}}}} \right)({{\rm \zeta} _0}{{\rm \zeta} _1} - {{\rm \eta} _0}{{\rm \eta} _1})$$
$${\rm \phi} = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2} - {\rm \omega} _{\rm c}^2 - 3{k^2}v_{\rm T}^2}} \left( {\displaystyle{{{e^2}{{\rm \eta} _0}{{\rm \eta} _1}{E_0}{E_1}} \over {2m{{\rm \omega} _0}{{\rm \omega} _1}}}} \right)({{\rm \zeta} _0}{{\rm \zeta} _1} - {{\rm \eta} _0}{{\rm \eta} _1})$$3. GROWTH RATE
The nonlinear growth rate of Raman instability can be obtained by the use of the nonlinear wave equation. In order to find the nonlinear wave equation, we need to set up the nonlinear current density at (ω1, k 1), so we call the definition of the current density, ![]() ${J_{1x}} = - {n_0}e{v_{1x}} - \tilde ne{v_{0x}}$. Using the Poisson's equation and the definitions of v 1x and v 0x, we get
${J_{1x}} = - {n_0}e{v_{1x}} - \tilde ne{v_{0x}}$. Using the Poisson's equation and the definitions of v 1x and v 0x, we get
where, ![]() ${{\bf E}_1} = 1/2{E_1}(\hat x + i{\beta _1}\hat z){e^{i{{\rm \theta} _1}}}$ and
${{\bf E}_1} = 1/2{E_1}(\hat x + i{\beta _1}\hat z){e^{i{{\rm \theta} _1}}}$ and ![]() ${{\rm \beta} _1} = {{\rm \omega} _{\rm c}}/{{\rm \omega} _1}({\rm \omega} _{\rm p}^2 /{\rm \omega} _1^2 - {\rm \omega} _{{\rm UH}}^2 )$ are the amplitude of the scattered wave and its extraordinary coefficient, respectively. As a matter of fact, the ponderomotive potential due to the nonlinear interaction between the laser and density ripple generates a nonlinear current at a different frequency (Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Ji2010). The response of electrons to the sideband wave is governed by the nonlinear wave equation
${{\rm \beta} _1} = {{\rm \omega} _{\rm c}}/{{\rm \omega} _1}({\rm \omega} _{\rm p}^2 /{\rm \omega} _1^2 - {\rm \omega} _{{\rm UH}}^2 )$ are the amplitude of the scattered wave and its extraordinary coefficient, respectively. As a matter of fact, the ponderomotive potential due to the nonlinear interaction between the laser and density ripple generates a nonlinear current at a different frequency (Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Ji2010). The response of electrons to the sideband wave is governed by the nonlinear wave equation
 $$\left( {\displaystyle{{{\partial ^2}} \over {\partial {z^2}}} - \displaystyle{1 \over {{c^2}}}\displaystyle{{{\partial ^2}} \over {\partial {t^2}}}} \right){E_{1x}} = \displaystyle{{4{\rm \pi}} \over {{c^2}}}\displaystyle{{\partial {J_{1x}}} \over {\partial t}}$$
$$\left( {\displaystyle{{{\partial ^2}} \over {\partial {z^2}}} - \displaystyle{1 \over {{c^2}}}\displaystyle{{{\partial ^2}} \over {\partial {t^2}}}} \right){E_{1x}} = \displaystyle{{4{\rm \pi}} \over {{c^2}}}\displaystyle{{\partial {J_{1x}}} \over {\partial t}}$$Combining Eqs (13)–(15) gives the dispersion relation of the scattered sideband wave
where, ![]() ${D_1} = {\rm \omega} _1^2 - {c^2}k_1^2 - {{\rm \zeta} _1}{\rm \omega} _{\rm p}^2 $ is the dispersion coefficient of the downshifted scattered sideband wave. The total maximum growth rate of Raman scattering instability of X-mode laser γTmax, which occurs in backward scattering is obtained easily by replacing ω = Ω + iγTmax with ω in Eq. (16) and choosing the real part, where
${D_1} = {\rm \omega} _1^2 - {c^2}k_1^2 - {{\rm \zeta} _1}{\rm \omega} _{\rm p}^2 $ is the dispersion coefficient of the downshifted scattered sideband wave. The total maximum growth rate of Raman scattering instability of X-mode laser γTmax, which occurs in backward scattering is obtained easily by replacing ω = Ω + iγTmax with ω in Eq. (16) and choosing the real part, where ![]() $\Omega = ({\rm \omega} _{{\rm UH}}^2 + 3{k^2}v_{\rm T}^2 {)^{1/2}}$ is the frequency of the excited upper-hybrid wave in warm plasma. Thus, the total growth rate γmax turns out to be
$\Omega = ({\rm \omega} _{{\rm UH}}^2 + 3{k^2}v_{\rm T}^2 {)^{1/2}}$ is the frequency of the excited upper-hybrid wave in warm plasma. Thus, the total growth rate γmax turns out to be
 $${{\rm \gamma} _{{\rm Tmax}}} = \displaystyle{{ck{a_0}{{\rm \omega} _{\rm p}}} \over 4}\sqrt {\displaystyle{{{{\rm \zeta} _0}({{\rm \zeta} _0}{{\rm \zeta} _1} - {{\rm \eta} _0}{{\rm \eta} _1})} \over {\Omega ({{\rm \omega} _0} - \Omega )}}} $$
$${{\rm \gamma} _{{\rm Tmax}}} = \displaystyle{{ck{a_0}{{\rm \omega} _{\rm p}}} \over 4}\sqrt {\displaystyle{{{{\rm \zeta} _0}({{\rm \zeta} _0}{{\rm \zeta} _1} - {{\rm \eta} _0}{{\rm \eta} _1})} \over {\Omega ({{\rm \omega} _0} - \Omega )}}} $$For the weakly relativistic regime, the maximum growth rate of RBS of extraordinary mode laser in magnetized plasma tends to be
 $${{\rm \gamma} _{{\rm max}}} = \displaystyle{{ck{a_0}{{\rm \omega} _{\rm p}}} \over 4}\sqrt {\displaystyle{\matrix{({\rm \omega} _0^2 + {{\rm \beta} _0}{{\rm \omega} _0}{{\rm \omega} _{\rm c}}/{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ) \cr \quad\times ({\rm \omega} _1^2 + {{\rm \beta} _1}{{\rm \omega} _1}{{\rm \omega} _{\rm c}}/{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 ) \cr \quad - ({{\rm \beta} _0}{\rm \omega} _0^2 + {{\rm \omega} _0}{{\rm \omega} _{\rm c}}/{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ) \cr \quad\times ({{\rm \beta} _1}{\rm \omega} _1^2 + {{\rm \omega} _1}{{\rm \omega} _{\rm c}}/{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )} \over {\Omega ({{\rm \omega} _0} - \Omega )}}} $$
$${{\rm \gamma} _{{\rm max}}} = \displaystyle{{ck{a_0}{{\rm \omega} _{\rm p}}} \over 4}\sqrt {\displaystyle{\matrix{({\rm \omega} _0^2 + {{\rm \beta} _0}{{\rm \omega} _0}{{\rm \omega} _{\rm c}}/{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ) \cr \quad\times ({\rm \omega} _1^2 + {{\rm \beta} _1}{{\rm \omega} _1}{{\rm \omega} _{\rm c}}/{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 ) \cr \quad - ({{\rm \beta} _0}{\rm \omega} _0^2 + {{\rm \omega} _0}{{\rm \omega} _{\rm c}}/{\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ) \cr \quad\times ({{\rm \beta} _1}{\rm \omega} _1^2 + {{\rm \omega} _1}{{\rm \omega} _{\rm c}}/{\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )} \over {\Omega ({{\rm \omega} _0} - \Omega )}}} $$where, ω1 = ω0 − Ω is the frequency of the scattered sideband wave. It may be noted that, in the absence of external magnetic field, by neglecting the nonlinear terms in Eq. (18), this growth rate reduces to the conventional growth rate of RBS instability in unmagnetized plasma (Kruer, Reference Kruer1988)
where, ![]() ${{\rm \omega} _{{\rm ek}}} = ({\rm \omega} _{\rm p}^2 + 3{k^2}v_{\rm T}^2 {)^{1/2}}$ is the frequency of the excited plasma wave in unmagnetized plasma. The wave number of the excited upper-hybrid wave can be calculated from the resonance condition (ω = Ω, ω1 = ω0 − Ω, D 1 = 0) of the sideband wave that is,
${{\rm \omega} _{{\rm ek}}} = ({\rm \omega} _{\rm p}^2 + 3{k^2}v_{\rm T}^2 {)^{1/2}}$ is the frequency of the excited plasma wave in unmagnetized plasma. The wave number of the excited upper-hybrid wave can be calculated from the resonance condition (ω = Ω, ω1 = ω0 − Ω, D 1 = 0) of the sideband wave that is, ![]() ${({{\rm \omega} _0} - {\rm \Omega} )^2} - {c^2}{(k - {k_0})^2} - {{\rm \zeta} _1}{\rm \omega} _{\rm p}^2 = 0$. Therefore, the wave number k takes the form
${({{\rm \omega} _0} - {\rm \Omega} )^2} - {c^2}{(k - {k_0})^2} - {{\rm \zeta} _1}{\rm \omega} _{\rm p}^2 = 0$. Therefore, the wave number k takes the form
 $$k = {k_0}(1 + \sqrt {{{\left( {1 - \displaystyle{{{{\rm \omega} _{{\rm UH}}}} \over {c{k_0}}}} \right)}^2} - {{\rm \zeta} _1}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{c^2}k_0^2}}} )$$
$$k = {k_0}(1 + \sqrt {{{\left( {1 - \displaystyle{{{{\rm \omega} _{{\rm UH}}}} \over {c{k_0}}}} \right)}^2} - {{\rm \zeta} _1}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{c^2}k_0^2}}} )$$To consider the effects of collisional damping and Landau damping on the growth rate, we employ the conventional instability analysis. Thus, the total growth rate of Raman backscattering instability of the X-mode laser in plasma Γ comes in the form
where, ![]() ${\Gamma _1} = {\nu _{{\rm ei}}}{\rm \omega} _{\rm p}^2 /2({{\rm \omega} _0} - {\rm \Omega} {)^2}$ is the damping rate of amplitude for the scattered sideband wave and
${\Gamma _1} = {\nu _{{\rm ei}}}{\rm \omega} _{\rm p}^2 /2({{\rm \omega} _0} - {\rm \Omega} {)^2}$ is the damping rate of amplitude for the scattered sideband wave and ![]() ${\Gamma _2} = {\nu _{{\rm ei}}}{\rm \omega} _{\rm p}^2 /2{\Omega ^2} +$
${\Gamma _2} = {\nu _{{\rm ei}}}{\rm \omega} _{\rm p}^2 /2{\Omega ^2} +$![]() ${\sqrt {{\rm \pi} /8} ({\rm \omega} _{\rm p}^2 {{\rm \Omega} ^2}v_{\rm T}^3 ){\rm exp}( - {\rm \Omega} /2{k^2}v_{\rm T}^2 )}$ is the amplitude damping rate of the excited upper-hybrid wave in which the first and second terms are associated with the collisional damping and Landau damping, respectively (Jiang et al., Reference Jiang, Zhanjun and Chunyang2011). Here,
${\sqrt {{\rm \pi} /8} ({\rm \omega} _{\rm p}^2 {{\rm \Omega} ^2}v_{\rm T}^3 ){\rm exp}( - {\rm \Omega} /2{k^2}v_{\rm T}^2 )}$ is the amplitude damping rate of the excited upper-hybrid wave in which the first and second terms are associated with the collisional damping and Landau damping, respectively (Jiang et al., Reference Jiang, Zhanjun and Chunyang2011). Here, ![]() ${\nu _{{\rm ei}}} \approx 3 \times {10^{ - 6}}{n_0}Zln\Lambda /T_{\rm e}^{3/2} $ is the electron–ion collision frequency in which Λ is the coulomb logarithm, T e is the electron temperature in eV and Z the ion charge state (Paknezhad, Reference Paknezhad2013b). In our assumption, we have followed typical laser fusion parameters in the interaction of a pump laser with intensity I = 1015 W/cm2 with an underdense magnetized plasma with v T/c = 0.03, Z = 10 and LnΛ = 81. Therefore, the normalized electron–ion frequency becomes νei/ω0 = 1.45 × 10−7(ωp/ω0)2(v T/c)3.
${\nu _{{\rm ei}}} \approx 3 \times {10^{ - 6}}{n_0}Zln\Lambda /T_{\rm e}^{3/2} $ is the electron–ion collision frequency in which Λ is the coulomb logarithm, T e is the electron temperature in eV and Z the ion charge state (Paknezhad, Reference Paknezhad2013b). In our assumption, we have followed typical laser fusion parameters in the interaction of a pump laser with intensity I = 1015 W/cm2 with an underdense magnetized plasma with v T/c = 0.03, Z = 10 and LnΛ = 81. Therefore, the normalized electron–ion frequency becomes νei/ω0 = 1.45 × 10−7(ωp/ω0)2(v T/c)3.
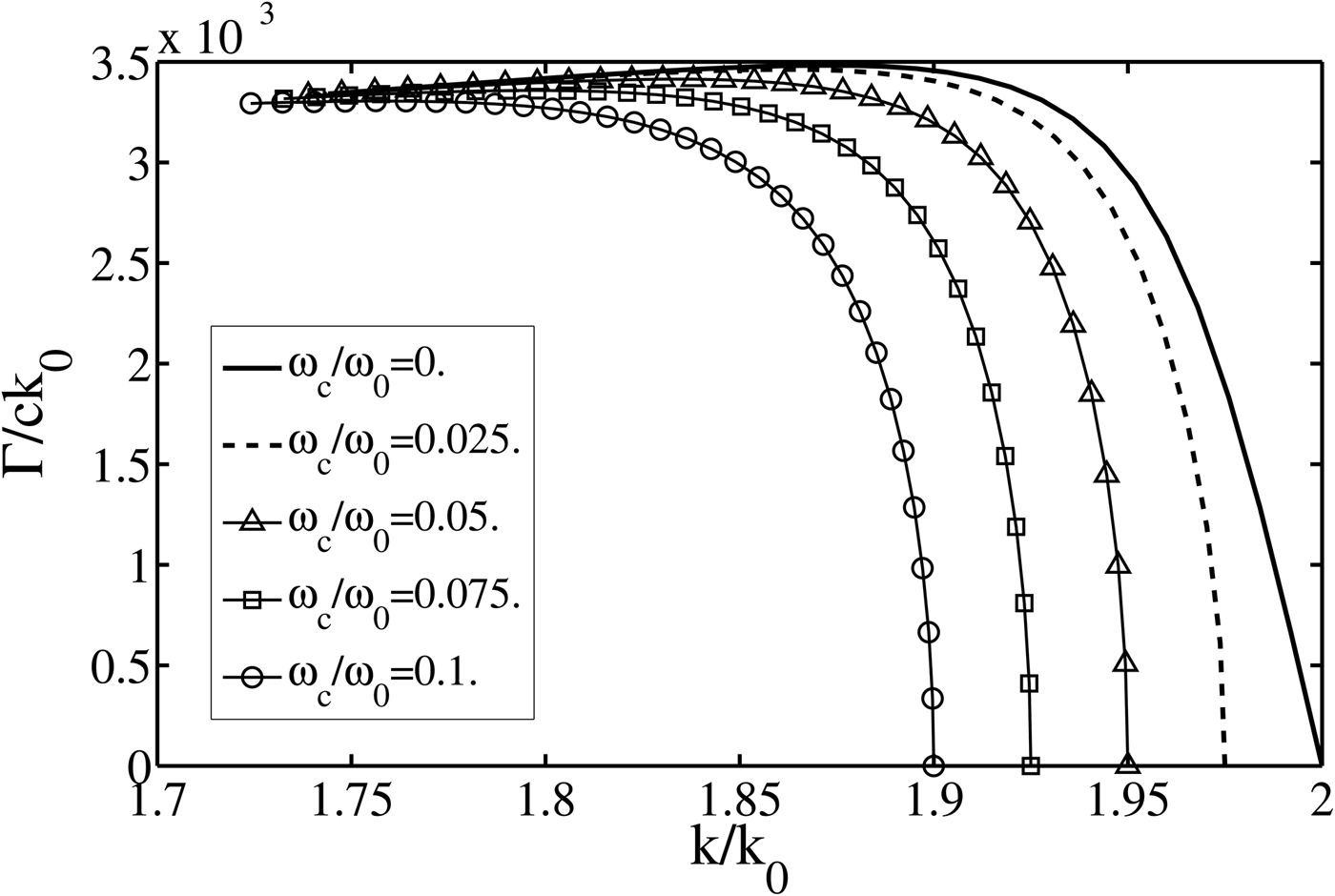
In Figure 1, variation of the normalized growth rate Γ/ck 0 of RBS instability has been plotted against the normalized wave number of the upper-hybrid wave k/k 0 for a 0 = 0.01, 0 <ωp/ω0 <0.25. Here, we assumed the weakly relativistic regime in which, for the onset of Raman scattering at least, filamentation and self-focusing may really not play a role and we consider the situation where the scattered sideband wave varies slowly with time during the instability and it does not affect the variation of the growth rate significantly. So, the amplitude of the scattered sideband wave varies slowly and we assigned a nearly constant value for a 1 (a 1 = 0.001) for the sake of simplicity. For the given values of ωc/ω0, it is observed from this figure that the growth rate has a sharp decrease at the cut-off points in k/k 0 and it goes to zero at these points. It is observed that the value of the normalized wave number of the excited upper-hybrid wave in magnetized plasma, arising due to the Raman backscattering of X-mode laser in plasma, is less than that in unmagnetized plasma. One can also see from this figure that the cut-off points in k/k 0 become smaller by increasing the magnetic field.

Fig. 1. Variation of the normalized growth rate of Raman backscattering instability of X-mode laser versus the normalized wave number of the upper-hybrid wave for v T/c = 0.03.
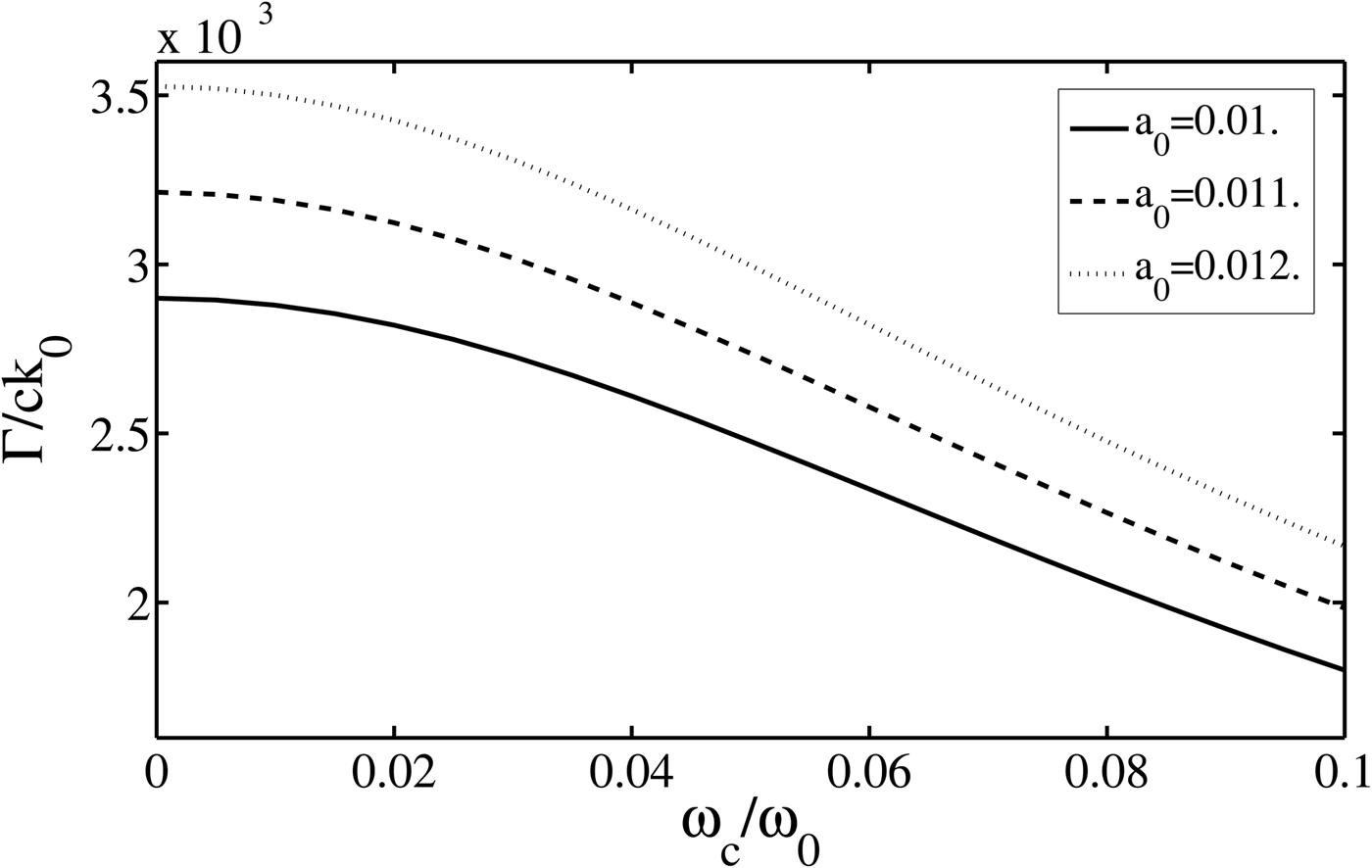
Figure 2, represents the variation of the normalized growth rate Γ/ck 0 versus the normalized cyclotron frequency ωc/ω0 for ωp/ω0 = 0.05 and other same parameters as for Figure 1. The growth rate decreases by increasing the external magnetic field. The reason is that the upper hybrid frequency increases by increasing the external magnetic field and this effect reduces the frequency of the scattered sideband wave, therefore the matching condition for the Raman backscattering instability cannot be significantly satisfied, and hence, the growth rate decreases by increasing the external magnetic field. The growth rate is also sensitive to the normalized vector potential of the pump wave and it increases by increasing the pump amplitude.

Fig. 2. Variation of the normalized growth rate of Raman backscattering instability of X-mode laser versus the normalized electron cyclotron frequency for v T/c = 0.03.
4. CONCLUSION
In this paper, the problem of RBS of X-mode laser beam propagating in transversely magnetized plasma considered in the presence of electron–ion collisions. The dispersion relation of the scattered sideband wave as well as the dispersion relation of the excited upper-hybrid wave was derived and an expression for the wave number of the excited upper-hybrid wave was obtained. Using the nonlinear wave equation and the nonlinear ponderomotive force, and considering the coupling between the sideband wave and the upper-hybrid wave, we obtained an expression for the maximum growth rate of Raman instability. As a result, we demonstrated that the growth rate decreases by increasing the external magnetic field since the coupling between the scattered wave and upper-hybrid wave is weak and phase matching condition is not well satisfied for higher external magnetic field. Also, the cut-off points in the normalized wave number of the upper-hybrid wave become smaller by increasing the magnetic field. The results of our investigation should be useful in laser–plasma interaction in ICF hohlraums.
ACKNOWLEDGMENT
This work is a part of a scientific research plan and was supported in part by the Shabestar Branch-Islamic Azad University under contract number 51953890818005.