Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T13:37:52.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of Gaussian spikes on Gaussian laser beam in relativistic plasma

Published online by Cambridge University Press:  14 September 2009

A. Singh ,
M. Aggarwal  and
T.S. Gill
A. Singh*
Affiliation:
Department of Physics, National Institute of TechnologyJalandhar, Punjab, India
M. Aggarwal
Affiliation:
Department of Physics, National Institute of TechnologyJalandhar, Punjab, India
T.S. Gill
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
*
Address correspondence and reprint requests to: Arvinder Singh, Department of Physics, National Institute of TechnologyJalandhar, Punjab, India. E-mail: arvinder6@lycos.com
Rights & Permissions [Opens in a new window]

Abstract

In the present paper, we have investigated the growth of a Gaussian perturbation superimposed on a Gaussian laser beam. The nonlinearity we have considered is of relativistic type. We have setup the nonlinear differential equations for beam width parameter of the main beam, growth and width of the laser spike by using the WKB and paraxial ray approximation. These are coupled ordinary differential equations and therefore these are simultaneously solved numerically using the Runge Kutta method. It has been observed from the analysis that self-focusing/defocusing of the main beam and the spike determine the growth dynamic of the spike.

Keywords

GaussianGrowthRelativisticRippleSelf-focusing
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 4 , December 2009 , pp. 587 - 593
Copyright
Copyright © Cambridge University Press 2009

1. INTRODUCTION

The most important problem in the laser driven fusion is the efficient coupling of the laser beam with the plasma, so that the plasma can be heated to high temperature. In the experimental situation, where an intense laser beam, traveling through nonlinear self-focusing media, results in multiple filament formation, there is a one-to-one correspondence between filaments and intensity spikes riding with incident laser beam (Abbi & Mahr, Reference Abbi and Mahr1971). The plasma is one of such nonlinear media. Model used to study the growth dynamics of intensity spikes was proposed as ripple model by Sodha et al. (Reference Sodha, Ghatak and Tripathi1976) and later on developed to study laser plasma related physics by a number of researchers (Singh & Singh, Reference Singh and Singh1991a, Reference Singh and Singh1991b; Gill & Saini, Reference Gill and Saini2007; Purohit et al., Reference Purohit, Chauhan and Sharma2008). Filamentation of the electromagnetic beam in the plasma has been investigated theoretically as well as experimentally in considerable details (Drake et al., Reference Drake, Kaw, Lee, Schimd, Liu and Rosenbluth1974; Bingham & Lashmore-Davies, Reference Bingham and Lashmore-Davies1976, Reference Bingham and Lashmore-Davies1979, Reference Bingham, Short, Williams, Villeneuve and Richardson1984; Herbst et al., Reference Herbst, Clayton, Peebles and Chen1980, Reference Herbst, Stamper, Whitlock, Lehmberg and Ripin1981; Joshi et al., Reference Joshi, Clayton and Chen1982; ZhiZan et al., Reference ZhiZhan, Yuguang, Guangyu, Yanzhen, Jiajin and Lee1983; Willi et al., Reference Willi, Rumsby, Zunqi, Hora and Miley1984; Young et al., Reference Young, Baldis, Drake, Campbell and Estabrook1988; Rankin et al., Reference Rankin, Capjack and James1989). The origin of filamentation instabilities may be due to small scale density perturbation or small scale intensity spike associated with the main beam. The physics of the perturbation, growing at the cost of the main beam is relevant to the inertially confined fusion plasmas. Direct or indirect evidence concentrate on the intensity of the filaments just after its threshold is crossed, and do not go into intermediate details of its growth dynamics. The whole beam self-focusing of laser beam may arise on account of a variety of nonlinearities e.g., from ponderomotive force, collisional non-uniform heating, relativistic effects, etc. Several nonlinear processes occur due to self-focusing effects as observed in a number of recent experiments (Torrisi et al., Reference Torrisi, Margarone, Laska, Krasa, Velyhan, Pfeifer, Ullschmied and Ryc2008; Faenov et al., Reference Faenov, Magunov, Pikuz, Skobelev, Gasilov, Stagira, Calegari, Nisoli, De Silvestri, Poletto, Villoresi and Andreev2007). Further dynamics of ponderomotive channeling in underdense plasma has recently been reported in the experimental observation of large amplitude electric and magnetic fields (Borghesi et al., Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007). In theoretical work on the laser-plasma interaction, it is yet to be understood how the development of the intensity in filaments control its growth dynamics. When a high power laser beam is involved, then it can cause an electron oscillatory velocity comparable to the velocity of light, which modifies the effective dielectric constant of the plasma, and hence affects the self-focusing of the beam. The self-focusing is due to the relativistic mass increase of plasma electrons. Relativistic laser-plasma interaction has been studied in detail by many authors, both theoretically (Kruer, Reference Kruer2000; Osman et al., Reference Osman, Castillo and Hora1999) and experimentally (Tanaka et al., Reference Tanaka, Kodama, Fujita, Heya, Izumi, Kato, Kitagawa, Mima, Miyanaga, Norimatsu, Pukhov, Sunahara, Takahashi, Allen, Habara, Iwatani, Matusita, Miyakosi, Mori, Setoguchi, Sonomoto, Tanpo, Tohyama, Azuma, Kawasaki, Komeno, Maekawa, Matsuo, Shozaki, Suzuki, Yoshida and Yamanaka2000; Fuchs et al., Reference Fuchs, Adams, Amiranoff, Baton, Blanchot, Gallant, Gremillet, Heron, Kieffer, Laval, Malka, Miquel, Mora, Pepin and Rousseaux1999; Monot et al., Reference Monot, Auguste, Gibbon, Jakober and Mainfray1995), and reviewed thoroughly (Umstadter, Reference Umstadter2003; Gibbon & Forster, Reference Gibbon and Forster1996). Nonlinear processes, playing key role in the generation of new ion sources has been recently reported (Laska et al., Reference Laska, Badziak, Boody, Gammino, Jungwirth, Krasa, Krousky, Parys, Pfeifer, Rohlena, Ryc, Skala, Torrisi, Ullschmied and Wolowski2007; Torrisi et al., Reference Torrisi, Margarone, Laska, Krasa, Velyhan, Pfeifer, Ullschmied and Ryc2008; Strangio et al., Reference Strangio, Caruso, Neely, Andreoli, Anzalone, Clarke, Cristofari, Del Prete, Di Giorgio, Murphy, Ricci, Stevens and Tolley2007). Further, the importance and relevance of laser produced plasma have opened new vistas in rich field of experiments to study novel physics issues in nuclear and particle physics, atomic physics (Stoehlker et al., Reference Stoehlker, Backe, Beyer, Bosch, Braeuning-Demian, Hagman, Ionescu, Jungmann, Kluge, Kozhuharov, Kuehl, Lisen, Mann, Mokler and Quint2003), plasma physics (Hoffman et al., Reference Hoffmann, Blazevic, Ni, Rosmej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005; Schaumann et al., Reference Schaumann, Schollmeier, Rodriguez-Prieto, Blazevic, Brambrink, Geissel, Korostiy, Pirzadeh, Roth, Rosmej, Faenov, Pikuz, Tsigutkin, Maron, Tahir and Hoffmann2005), and applied sciences (Kuehl et al., Reference Kuehl, Ursescu, Bagnoud, Javorkova, Rosmej, Cassou, Kazamias, Klisnick, Ros, Nickles, Zielbauer, Dunn, Neumayer and Pert2007; Kasperczuk et al., Reference Kasperczuk, Pisarczyk, Kalal, Martinkova, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2008).

A laser beam propagating in underdense plasma with a frequency ωp smaller than the laser frequency ω undergoes relativistic self-focusing as soon as its total power P exceeds the critical value $P_{\rm cr} \sim 17 \left(\textstyle{{\omega / \omega_{\,\rm p}}}\right)^{2}\, \hbox{GW}$, this has been established both theoretically (Max et al., Reference Max, Arons and Langdon1974; Hora, Reference Hora1975; Schmidt & Horton, Reference Schmidt and Horton1985; Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992a), and experimentally (Borisov et al., Reference Borisov, Borovskiy, Korobkin, Prokhorov, Shiryaev, Shi, Luk, McPherson, Solem, Boyer and Rhodes1992b; Monot et al., Reference Monot, Auguste, Gibbon, Jakober and Mainfray1995).

The study of the interaction of intense laser pulses with plasmas is relevant for a number of applications such as plasma based accelerators (Modena et al., Reference Modena, Najmudin, Dangor, Clayton, Marsh, Joshi, Malka, Darrow, Danson, Neely and Walsh1995; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1996; Umstadter et al., Reference Umstadter, Chen, Maksimchuk, Mourou and Wagner1996) and the fast ignitor schemes (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) for inertial confinement fusion. Pukhov and Meyer-ter-Vehn (Reference Pukhov and Meyer-ter-Vehn1996) reported three-dimensional particle in cell (3D PIC) simulations for laser pulse propagation in near critical underdense plasmas far above the threshold for relativistic filamentation. The key feature predicted by these simulations is the formation of the narrow, single propagation channel, containing the significant part of the laser energy. The simulation reveals the importance of relativistic electrons traveling with the light pulse and generating multi-mega Gauss magnetic fields that strongly influence the light propagation.

In the present work, we have investigated the growth of the Gaussian ripple superimposed on Gaussian laser beam by taking into account the relativistic nonlinearity. In Section 2, we have setup and solved the wave equation for the main beam. In section 3, we have solved the nonlinearly coupled ordinary differential equations for the growth parameter, and the beam width of the spike. Finally a detailed discussion of the results is presented in Section 4.

2. PROPAGATION OF GAUSSIAN LASER BEAM

Consider the propagation of an electromagnetic wave of angular frequency ωo in a homogeneous plasma along the z-axis. The initial intensity distribution of the main beam is assumed to be Gaussian and is given by

(1)
E_{\rm o} \cdot E_{\rm o}^{\star} \vert_{{\rm z} = 0} = E_{\rm oo}^2 \exp \big[ -r^2 /r_{\rm o}^2\big] \comma \;

where r 2 = x 2 + y 2 and r o is the initial width of the main beam.

The electric vector E o of the main beam satisfies the wave equation

(2)
\nabla^2 E_{\rm o} - \nabla \lpar \nabla \cdot E_{\rm o}\rpar + {\omega_{\rm o}^2 \epsilon E_{\rm o} \over c^2} = 0\comma \;
(3)
\epsilon = \epsilon_{\rm o} + \Phi \lpar E_{\rm o} \cdot E_{\rm o}^{\star}\rpar

where ϵo and Φ (E o · E o★) are the linear and nonlinear parts of the dielectric constant, respectively and

(4)
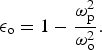
\epsilon_{\rm o} = 1 - {\omega_{\rm p}^2 \over \omega_{\rm o}^2}.

Here, ωp is the plasma frequency, given by ωp2 = 4πn ee 2/m o where e o and m o are the charge and rest mass of the electron, respectively, and n e is the density of the plasma electrons. The relativistic general expression for the plasma frequency is given by

(5)
\omega_{\rm pe}^2 = {\omega_{\rm p}^2 \over \gamma}\comma \;

where γ is the relativistic factor given by

(6)
\gamma = \lsqb 1 + \alpha E_{\rm o} .E_{\rm o}^{\star}\rsqb ^{1 / 2},

where $\alpha = {e^2 / m_{\rm o}^{2} c^2 \omega_{\rm o}^2}$. We can express the nonlinear part of the dielectric constant by the following equation

(7)
\Phi \lpar E_{\rm o} \cdot E_{\rm o}^{\star}\rpar = {\omega_{\rm p}^2 \over \omega_{\rm o}^2} \left[1 - \lpar 1 + \alpha E_{\rm o} \cdot E_{\rm o}^{\star}\rpar ^{ - 1/2} \right]

In Wentzel-Kramers-Brillouin (WKB) approximation, the second term of Eq. (2) can be neglected and the electric vectors of the main beam (E o) satisfy the following equation

(8)
\nabla^2 E_{\rm o} + {\omega_{\rm o}^2 \epsilon \lpar E_{\rm o} E_{\rm o}^{\star}\rpar E_{\rm o} \over c^2} = 0.

It should be mentioned that the neglection of the term ∇ (∇·E o) in Eq. (2) is justified when $\textstyle{{(c^2 / \omega_{\rm o}^2)}} \left\vert {(1 / \epsilon)} \nabla^2 ln\epsilon \right\vert \lt \lt 1$. Now, E o = A(r, z) exp [−ιk oz] is introduced, where A(r,z) is a complex function of its argument. The behavior of the complex amplitude A(r, z) is described by the parabolic equation obtained from the wave Eq. (8) in the WKB approximation assuming that the variations in the z -direction are slower than those in the radial direction

(9)
- 2\iota k_{\rm o} {\partial A \over \partial z} + \nabla_{\bot}^2 A + {\omega_{\rm o}^2 \Phi \lpar E_{\rm o} \cdot E_{\rm o}^{\star}\rpar A \over c^2} = 0.

In the absence of any spike, one can write

(10)
A = A_{\rm o} \lpar r\comma \; z\rpar \exp \lsqb - \iota k_{\rm o} S_{\rm o}\rsqb \comma \;

where A o (r, z) and S o are real functions of r and z (S o being the ekional). Substituting Eq. (10) for A in Eq. (9) and separating the real and imaginary parts, one can obtain

(11)
\eqalign{&2\left({\partial S_{\rm o} \over \partial z} \right)+ \left({\partial S_{\rm o} \over \partial r} \right)^2 = {1 \over k_{\rm o}^2 A_{\rm o}} \nabla_{\bot}^2 A_{\rm o} \cr &\quad + {\omega_{\rm p}^2 \over \omega_{\rm o}^2 \epsilon_{\rm o}} \left[1 - \lpar 1 + \alpha E_{\rm o} \cdot E_{\rm o}^{\star}\rpar ^{ - 1/2} \right]\comma \; }

and

(12)
{\partial A_{\rm o}^2 \over \partial z} + \left({\partial S_{\rm o} \over \partial r} \right){\partial A_{\rm o}^2 \over \partial r} + A_{\rm o}^2 \nabla_{\bot}^2 S_{\rm o} = 0,

Following Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and Sodha et al. (Reference Sodha, Ghatak and Tripathi1976), the solution for E o can be written as

(13)
\eqalign{E_{\rm o} &= A_{\rm o} \exp \lsqb - \iota k_{\rm o} \lpar S_{\rm o} + z\rpar \rsqb \comma \; \cr A_{\rm o}^2 &= {E_{\rm oo}^2 \over f_{\rm o}^2} \exp \left[- {r^2 \over r_{\rm o}^2\, f_{\rm o}^2} \right]\comma \; \cr S_{\rm o} &= {r^2 \over 2} \beta \lpar z\rpar + \Phi_{\rm o} \lpar z\rpar \comma \; }

where $\beta_{\rm o} \lpar z\rpar ={(1 / f_{\rm o})} ({df_{\rm o} / dz})$ and $k_{\rm o} = {\omega_{\rm o} \epsilon_{\rm o}^{1/2} / c}$. The parameter βo−1 may be interpreted as the radius of the curvature of the main beam. f o is the dimensionless beam width parameter described by the differential equation

(14)
{d^2 f_{\rm o} \over dz^2 } = {c^2 \over \omega_{\rm o}^2 \epsilon_{\rm o} r_{\rm o}^4\, f_{\rm o}^3} - {\alpha E_{\rm o}^2 \over 2\epsilon_{\rm o} r_{\rm o}^2\, f_{\rm o}^3} \left({\omega_{\rm p}^2 \over \omega_{\rm o}^2} \right)\left(1 + {\alpha E_{\rm o}^2 \over f_{\rm o}^2} \right)^{ - {(3 / 2)}}.

Eq. (14) can be solved numerically with appropriate boundary conditions. One can take f o = 1 and $\textstyle{{df_{\rm o} / dz}} = 0$, corresponding to an initial plane wave front.

3. TREATMENT FOR THE GAUSSIAN PERTURBATION

Now, we obtain a solution of the quasioptic Eq. (9) for the situation when a single profile of Gaussian spike propagates co-axially with the main laser beam. To obtain a perturbation treatment for the laser spike, we write the optical electric field amplitude in the form

(15)
A = \lpar A_{\rm o} + E_1 + \iota E_2\rpar \exp \lpar -\iota k_{\rm o} S_{\rm o}\rpar,

where E = E 1 + ιE 2 is the complex electric field of the perturbation with E 1, E 2 ≪ A o, A o being the unperturbed amplitude of the main laser beam. Substituting Eq. (15) in Eq. (9), one can obtain the following two coupled equations for E 1 and E 2

(16)
\eqalign{&{E_1 \over A_{\rm o}} \nabla_{\bot}^2 A_{\rm o} - 2k_{\rm o} {\partial E_2 \over \partial z} = \nabla_{\bot}^2 E_1 + k_{\rm o} E_2 \nabla_{\bot}^2 S_{\rm o} + 2k_{\rm o} {\partial E_2 \over \partial r} {\partial S_{\rm o} \over \partial r} \cr &\quad + 2\alpha A_{\rm o}^2 {\omega_{\,\rm po}^2 \over \omega_{\rm o}^2} \left(1 + {\alpha E_{\rm o}^2 \over f_{\rm o}^2}\right)^{-\textstyle{{(3 / 2)}}}\comma \; \cr}

and

(17)
{E_2 \over A_{\rm o}} \nabla_{\bot}^2 A_{\rm o} + 2k_{\rm o} {\partial E_1 \over \partial z} = \nabla_{\bot}^2 E_2 - k_{\rm o} E_1 \nabla_{\bot}^2 S_{\rm o} - 2k_{\rm o} {\partial E_1 \over \partial r} {\partial S_{\rm o} \over \partial r}.

Now we take the form of A o and S o as given by Eq. (13), and E 1 and E 2 as

(18)
E_{1\comma 2} = E_{10\comma 20} \exp \lsqb \alpha \lpar z\rpar \rsqb \exp \left[-{r^2 \over 2b^2 \lpar z\rpar }\right].

This equation defines the growth parameter α(z), and b(z) is the size of the Gaussian perturbation inside the plasma. The substitution of the Eqs. (13) and (18) in Eqs. (16) and (17) gives the following relations for α(z) and b(z):

(19)
\eqalign{&{\partial \alpha \over \partial z} = {1 \over k_{\rm o}} \left[\left({1 \over b^2} - {1 \over r_{\rm o}^2 f_{\rm o}^2}\right){\omega_{\rm p}^2 \over \omega_{\rm o}^2} {\alpha E_{\rm o}^2 \over f_{\rm o}^2} \left(1 + {\alpha E_{\rm o}^2 \over f_{\rm o}^2}\right)^{-\textstyle{{(3 / 2)}}}\right. \cr &\quad \left.- \left({1 \over b^2} - {1 \over r_{\rm o}^2\, f_{\rm o}^2}\right)\right]^{\textstyle{{1 / 2}}} - \beta \lpar z\rpar \comma \; \cr}

and

(20)
\eqalign{&{\partial b\over \partial z} = {b^3 \over 2k_{\rm o}} \Bigg[\Bigg[\left({1 \over b^4} - {1 \over r_{\rm o}^4\, f_{\rm o}^4}\right)\Bigg\{-3 {\lpar \alpha E_{\rm o}^2\rpar ^2 \over r_{\rm o}^2\, f_{\rm o}^6} {\omega_{\rm p}^2 \over \omega_{\rm o}^2} \left(1 + {\alpha E_{\rm o}^2 \over f_{\rm o}^2}\right)^{-\textstyle{{(5/2)}}} \cr &\quad - \left({1 \over b^4} - {1 \over r_{\rm o}^4\, f_{\rm o}^4}\right)\Bigg\}\Bigg]^{\textstyle{{(1/2)}}} + {2k_{\rm o} \beta \over b^2}\Bigg]. \cr}

One can solve the differential equations for the initial conditions b(z = 0) = b o and α(z = 0) = 0.

4. DISCUSSION

Eqs. (14), (19), and (20) are coupled equations. We have solved these equations numerically for the following set of parameters.

\left({{r_{\rm o} \omega_{\rm p} \over c}}\right)^2 = 18.0\comma \; {{\omega_{\rm p} \over \omega_{\rm o}}} = 0.03\comma \;

ωo = 1.778 × 1014 rad s−1, b o = 4.0 × 10−4 cm and for different values of αE o2. The results are depicted in the form of graphs in Figures 1 to 6.

Fig. 1. Beam width parameter f 0 plotted against the distance of propagation Z in relativistic Plasma for intensities αE 002 = 1.0, 2.0, 3.0 and for the following set of parameters.

\eqalign{&\left({\omega_{\rm p} r_0 \over c}\right)^2= 18.0\comma \; {\omega_{\rm p} \over \omega_0} = 0.03\comma \; \omega_0 = 1.778\times 10^{14} rads^{-1} \cr &b_0 = 4 \times 10^{-4}\, {\it cm.} \cr}

Fig. 2. Spike width b(z) plotted against the distance of propagation Z in relativistic Plasma for intensities αE 002 = 1.0, 2.0, 3.0 and for the parameters mentioned in Figure 1.

Fig. 3. Growth α(z) of the spike plotted against the distance of propagation Z in relativistic Plasma for intensities αE 002 = 1.0, 2.0, 3.0 and for the parameters mentioned in Figure 1.

Fig. 4. Beam width parameter f 0 plotted against the distance of propagation Z in relativistic Plasma for ${\omega_{\rm p} / \omega_0} = 0.02\comma \; 0.03\comma \; 0.04$, αE 002 = 3.0 and for the parameters mentioned in Figure 1.

Fig. 5. Spike width b(z) plotted against the distance of propagation Z in relativistic Plasma for ${\omega_p / \omega_0} = 0.02\comma \; 0.03\comma \; 0.04$, αE 002 = 3.0 and for the parameters mentioned in Figure 1.

Fig. 6. Growth α(z) of the Spike plotted against the distance of propagation Z in relativistic Plasma for ${\omega_{\rm p} / \omega_{\rm o}} = 0.02\comma \; 0.03\comma \; 0.04$, αE oo2 = 3.0 and for the parameters mentioned in Figure 1.

Eq. (14) is a nonlinear ordinary differential equation governing the behavior of dimensionless beam width parameter f as a function of distance of propagation. The first term on the right-hand-side of this equation represents the diffraction of the main laser beam and arises due to the second term ∇⊥2A of Eq. (9). When high intense power laser beam is used, the second term in Eq. (14) arises due to the relativistic nonlinear effect resulting from the relativistic mass correction and depends on intensity factor αE o2 , relative plasma density $\textstyle{{\omega_{\rm p}^2 / \omega_0^2}}$ etc. The diffraction term leads to diffractional divergence of the main beam, while nonlinear term is responsible for self-focusing of beam due to the relativistic effect. The fate of the laser beam viz self-focusing/defocusing is ultimately determined by the relative magnitude of these terms. If the first term on right-hand-side of (14) dominates over the second term, the beam diverges, while opposite is true when the second term exceeds the first one. Eqs (19) and (20) are nonlinear ordinary differential equations and are coupled to each other as well as to the main laser beam. Eqs. (19) and (20) govern the evolution of growth rate and beam width of the spike respectively.

Figures 1, 2, 3 present the variation of the beam width parameter f o of the main beam, the beam width b(z) and the growth α(z) of the spike, respectively, with the distance of propagation for three values of intensity αE o2 = 1.0, 2.0, 3.0.

It is observed from Figure 1 that diffraction of the main beam starts earlier if the value of the intensity parameter is increased. This is due to the dominance of the diffractive term over the nonlinear self-focusing term with the increase in intensity. It is clear from the Eq. (14) that, if we increase the intensity, the term $\left(1 + ({{\alpha E_o^2 / f_o^2)}}\right)^{{{-3 / 2}}}$ will further weaken the nonlinear term in comparison with the diffractive term, and hence, the diffraction starts earlier at higher intensity. It is further observed from the graph that the distance of propagation of the beam, before it gets self-focussed, decreases with increase in the intensity of the main beam. This is due to the fact that at relativistic intensity, the quasi-stationary magnetic field is generated. So, if we increase the intensity of the main beam, a stronger magnetic field is generated, the pinching effect of which adds to the self-focusing (Pukhov & Meyer-ter-Vehn, Reference Pukhov and Meyer-ter-Vehn1996).

It is observed from Figure 2 that there exists a defocusing of the spike width for the initial distance of propagation. This is due to the dominance of the diffraction divergence over the refractive term for the initial distance of propagation, however, with the further increase in distance of propagation, there occurs a relative shift of focii with intensity, viz. the focusing length decreases proportionally to the increase in intensity. This is vividly shown in Figure 2. It is further observed that after the initial distance of propagation, the spike width shows a similar behavior as the main beam. So it is concluded that there is strong coupling between the main beam and the spike of the beam after the initial distance of propagation.

It is found from Figure 3 that the growth α(z) reaches its maximum value and then decreases slowly. The maxima corresponding to αE o2 = 1.0, 2.0, 3.0, obviously correspond to the minima of the main beam and the spike, and thereafter the growth gets stabilized. Thus, the stabilization of the growth is clearly linked with the defocusing of the main beam and the spike width b(z).

Figures 4, 5, and 6 depict the variation of beam width parameter f o of the main beam, beam width b(z) and growth α(z) of the spike, respectively, with distance of propagation for three values of plasma density, ωp/ωo = 0.02, 0.03, and 0.04, respectively at αE oo2 = 3.0.

It is observed from Figure 4 that focusing of the beam takes place earlier if we increase the plasma density. This is due to the fact that, at relativistic intensities, if we increase the plasma density a beam with more relativistic electrons travels with the laser pulse, which generates a higher current, and ultimately a very high quasi-stationary magnetic field is generated. Therefore, the pinching effect of the magnetic field becomes stronger, which further adds to self-focusing. This prediction is in agreement with the simulation (3D PIC) results reported by Pukhov and Meyer-ter-Vehn (Reference Pukhov and Meyer-ter-Vehn1996). The results observed from graph 5 and 6 for width b(z) and growth α(z) of the spike are similar to that obtained from Figure 2 and Figure 3.

5. CONCLUSIONS

In this research work, we have studied the growth of the Gaussian ripple superimposed on Gaussian laser beam by taking into account the relativistic nonlinearity. The results obtained have several ramifications as follows: (1) Our results confirm the role of relativistic electrons traveling with the light pulse, reported by Pukhov and Meyer-ter-Vehn (Reference Pukhov and Meyer-ter-Vehn1996) in their (3D PIC) simulation study. (2) Strong coupling between the main beam and the spike of the beam is observed. (3) Defocusing of the main beam and the spike leads to stabilization of the growth rate of the spike. The results of the present analysis are useful in understanding physics issues of the high power laser driven fusion, as well as the coupling physics involved in laser-plasma interactions.

ACKNOWLEDGMENTS

The authors are thankful to the Ministry of Human Resources and Development of India for providing financial assistance for carrying out this work.

References

REFERENCES

Abbi, S.C. & Mahr, H. (1971). Correlation of filaments in nitrobenzene with laser spikes. Phys. Rev. Lett. 26, 604–606.CrossRefGoogle Scholar
Akhmanov, S.A., Sukhorukov, A.P. & Khokhlov, R.V. (1968). Self-focusing and diffraction of light in a nonlinear medium. Sov. Phys. Uspekhi. 10, 609–636.CrossRefGoogle Scholar
Bingham, R. & Lashmore-Davies, C.N. (1976). Self-modulation and filamentation of electromagnetic waves in a plasma. Nuc. Fusion. 16, 67–72.CrossRefGoogle Scholar
Bingham, R. & Lashmore-Davies, C.N. (1979). On the nonlinear development of the filamentation of an electromagnetic wave in a plasma. Plasma Phys. 21, 433–453.CrossRefGoogle Scholar
Bingham, R., Short, R., Williams, E., Villeneuve, D. & Richardson, M.C. (1984). The filamentation instability at short wavelengths. Plasma Phys. Contr. Fusion 26, 1077–1082.CrossRefGoogle Scholar
Borisov, A.B., Borovskiy, A.V., Shiryaev, O.B., Korobkin, V.V., Prokhorov, A.M., Solem, J.C., Luk, T.S., Boyer, K. & Rhodes, C.K. (1992a). Relativistic and charge-displacement self-channeling of intense ultrashort laser pulses in plasmas. Phys. Rev. A 45, 5830–5845.CrossRefGoogle ScholarPubMed
Borisov, A.B., Borovskiy, A.V., Korobkin, V.V., Prokhorov, A.M., Shiryaev, O.B., Shi, X.M., Luk, T.S., McPherson, A., Solem, J.C., Boyer, K. & Rhodes, C.K. (1992b). Observation of relativistic and charge-displacement self-channeling of Intense sub picosecond Ultraviolet(248 nm) radiation in Plasmas. Phys. Rev. Lett. 68, 2309–2312.CrossRefGoogle Scholar
Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C.A., Fuchs, J., Galimberti, M., Gizzi, L.A., Grismayer, T., Lyseikina, T., Jung, R., Macchi, A., Mora, P., Osterholtz, J., Schiavi, A. & Willi, O. (2007). Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25, 161–167.CrossRefGoogle Scholar
Drake, J.F., Kaw, P.K., Lee, Y.C., Schimd, G., Liu, C.S. & Rosenbluth, M.N. (1974). Parametric instabilities of electromagnetic waves in plasmas. Phys. Fluids. 17, 778.CrossRefGoogle Scholar
Esarey, E., Sprangle, P., Krall, J. & Ting, A. (1996). Overview of plasma-based accelerator concepts. IEEE Trans Plasma Sci. 24, 252–288.CrossRefGoogle Scholar
Faenov, A.Ya., Magunov, A.I., Pikuz, T.A., Skobelev, I.Yu., Gasilov, S.V., Stagira, S., Calegari, F., Nisoli, M., De Silvestri, S., Poletto, L., Villoresi, P. & Andreev, A.A. (2007). X-ray spectroscopy observation of fast ions generation in plasma produced by short low-contrast laser pulse irradiation of solid targets. Laser Part. Beams 25, 267–275.CrossRefGoogle Scholar
Fuchs, J., Adams, J.C., Amiranoff, F., Baton, S.D., Blanchot, N., Gallant, P., Gremillet, L., Heron, A., Kieffer, J.C., Laval, G., Malka, G., Miquel, J.L., Mora, P., Pepin, H. & Rousseaux, C. (1999). Experimental study of laser penetration in overdense plasma at relativistic intensities. I: Hole boring through performed plasmas layers. Phys. Plasmas 6, 2563–2568.CrossRefGoogle Scholar
Gibbon, P. & Forster, E. (1996). Short-pulse laser-plasma interaction. Plasma Phys. Contr. Fusion, 38, 769–793.CrossRefGoogle Scholar
Gill, T.S. & Saini, N.S. (2007). Nonlinear interaction of a rippled laser beam with an electrostatic upper hybrid wave in collisional plasma. Laser Part. Beams 25, 283–293.CrossRefGoogle Scholar
Herbst, M.J., Clayton, C.E., Peebles, W.A. & Chen, F.F. (1980). Studies of sidescatter and backscatter from pre-ionized plasmas. Phys. Fluids. 23, 1319.CrossRefGoogle Scholar
Herbst, M.J., Stamper, J.A., Whitlock, R.R., Lehmberg, R.H. & Ripin, B.H. (1981). Evidence from X-Ray, 3/2 ω0, and 2ω0 emission for laser filamentation in a plasma. Phys. Rev. Lett. 46, 328–331.CrossRefGoogle Scholar
Hoffmann, D.H.H., Blazevic, A., Ni, P., Rosmej, O., Roth, M., Tahir, N., Tauschwitz, A., Udrea, S., Varentsov, D., Weyrich, K. & Maron, Y. (2005). Present and future perspective for high energy density physics with intense heavy ions and laser beams. Laser Part. Beams 23, 395–395.CrossRefGoogle Scholar
Hora, H. (1975). Theory of relativistic self-focusing of laser radiation in plasmas. J. Opt. Soc. Am. 65, 882–886.CrossRefGoogle Scholar
Joshi, C., Clayton, C.E. & Chen, F.F. (1982). Resonant self-focusing of laser light in a plasma. Phys.Rev. Lett. 46, 874–877.CrossRefGoogle Scholar
Kasperczuk, A., Pisarczyk, T., Kalal, M., Martinkova, M., Ullschmied, J., Krousky, E., Masek, K., Pfeifer, M., Rohlena, K., Skala, J. & Pisarczyk, P. (2008). PALS laser energy transfer into solid targets and its dependence on the lens focal point position with respect to the target surface. Laser Part. Beams 26, 189–196.CrossRefGoogle Scholar
Kruer, W.L. (2000). Interaction of plasmas with intense lasers. Phys. Plasmas 7, 2270–2278.CrossRefGoogle Scholar
Kuehl, Th., Ursescu, D., Bagnoud, v., Javorkova, D., Rosmej, O., Cassou, K., Kazamias, S., Klisnick, A., Ros, D., Nickles, P., Zielbauer, B., Dunn, J., Neumayer, P., Pert, G. & The Phelix Team. (2007). Optimization of the non thermal incidence, transient pumped plasma X-ray laser for laser spectroscopy and plasma diagnostics at the facility for antiproton and ion research (FAIR). Laser Part. Beams 25, 93–97.CrossRefGoogle Scholar
Laska, L., Badziak, J., Boody, F.P., Gammino, S., Jungwirth, K., Krasa, J., Krousky, E., Parys, P., Pfeifer, M., Rohlena, K., Ryc, L., Skala, J., Torrisi, L., Ullschmied, J. & Wolowski, J. (2007). Factor influencing parameters of laser ion sources. Laser Part. Beams 25, 199–205.CrossRefGoogle Scholar
Max, C.E., Arons, J. & Langdon, A.B. (1974). Self-modulation and self focusing of electromagnetic waves in plasmas. Phys. Rev. Lett. 33, 209–212.CrossRefGoogle Scholar
Modena, A., Najmudin, Z., Dangor, A.E., Clayton, C.E., Marsh, K.A., Joshi, C., Malka, V., Darrow, C.B., Danson, C., Neely, D. & Walsh, F.N. (1995). Electron acceleration from the breaking of relativistic plasma waves. Nat. (London) 377, 606–608.CrossRefGoogle Scholar
Monot, P., Auguste, T., Gibbon, P., Jakober, F. & Mainfray, G. (1995). Experimental demonstration of relativistic self channeling of a Multiterawatt laser pulse in an underdense plasma. Phys. Rev. Lett. 74, 2953–2956.CrossRefGoogle Scholar
Osman, F., Castillo, R. & Hora, H. (1999). Relativistic and ponderomotive self focusing at laser-plasma interaction. J. Plasma Phys. 61, 263–273.CrossRefGoogle Scholar
Pukhov, A. & Meyer-ter-Vehn, J. (1996). Relativistic magnetic self-channeling of light in near-critical plasma: Three-dimensional particle-in-cell simulation. Phys. Rev. Lett. 76, 3975–3978.CrossRefGoogle ScholarPubMed
Purohit, G., Chauhan, P.K. & Sharma, R.P. (2008). Excitation of an upper hybrid wave by a high power laser beam in plasma. Laser Part. Beams 26, 61–67.CrossRefGoogle Scholar
Rankin, R., Capjack, C.E. & James, C.R. (1989). Diffraction and the evolution of small scale filaments in a laser-produced plasma. Phys. Rev. Lett. 63, 1597–1600.CrossRefGoogle Scholar
Schaumann, G., Schollmeier, M.S., Rodriguez-Prieto, G., Blazevic, A., Brambrink, E., Geissel, M., Korostiy, S., Pirzadeh, P., Roth, M., Rosmej, F.B., Faenov, A.Y., Pikuz, T.A., Tsigutkin, K., Maron, Y., Tahir, N.A. & Hoffmann, D.H.H. (2005). High energy heavy ion jets emerging from laser plasma generated by long pulse laser beams from the NHELIX laser system at GSI. Laser Part. Beams, 23, 503–512.CrossRefGoogle Scholar
Schmidt, G. & Horton, W. (1985). Self focusing of laser beam in the beat-wave accelerator. Comments Plasma Phys. Contr. Fusion 9, 85.Google Scholar
Singh, A. & Singh, T. (1991 a). Nonlinear interaction of rippled laser beam with unmagnetized plasma. Plasma Phys. Contr. Fusion 33, 123–133.CrossRefGoogle Scholar
Singh, A. & Singh, T. (1991 b). Growth of a laser ripple on a gaussian beam in a collisionless Magnetoplasma and its effect on the Excitation of Ion Acoustic wave. Contrib. Plasma Phys. 31, 499–512.CrossRefGoogle Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1976). Progress in Optics. Amsterdam: North Holland.Google Scholar
Stoehlker, T., Backe, H., Beyer, H., Bosch, F., Braeuning-Demian, A., Hagman, S., Ionescu, D., Jungmann, K., Kluge, H.-J., Kozhuharov, C., Kuehl, Th., Lisen, D., Mann, R., Mokler, P. & Quint, W. (2003). Status and perspectives of atomic physics research at GSI: The new GSI accelerator project. Nucl. Instr. Meth. B 205, 156.CrossRefGoogle Scholar
Strangio, C., Caruso, A., Neely, D., Andreoli, P.L., Anzalone, R., Clarke, R., Cristofari, G., Del Prete, E., Di Giorgio, G., Murphy, C., Ricci, C., Stevens, R. & Tolley, M. (2007). Production of multi-Mev per nucleon ions in the controlled amount of matter mode (CAM) by using casually isolated targets. Laser Part. Beams 25, 85–91.CrossRefGoogle Scholar
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E.M., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultrapower high lasers. Phys. Plasmas. 1, 1626–1634.CrossRefGoogle Scholar
Tanaka, K.A., Kodama, R., Fujita, H., Heya, M., Izumi, N., Kato, Y., Kitagawa, Y., Mima, K., Miyanaga, N., Norimatsu, T., Pukhov, A., Sunahara, A., Takahashi, K., Allen, M., Habara, H., Iwatani, T., Matusita, T., Miyakosi, T., Mori, M., Setoguchi, H., Sonomoto, T., Tanpo, M., Tohyama, S., Azuma, H., Kawasaki, T., Komeno, T., Maekawa, O., Matsuo, S., Shozaki, T., Suzuki, K.A., Yoshida, H. & Yamanaka, T. (2000). Studies of ultra-intense laser plasma interaction for fast ignition. Phys. Plasmas 7, 2014–2022.CrossRefGoogle Scholar
Torrisi, L., Margarone, D., Laska, L., Krasa, J., Velyhan, A., Pfeifer, M., Ullschmied, J. & Ryc, L. (2008). Self focusing effects in Au-target induced by high power pulsed laser at PALS. Laser Part. Beams 26, 379–387.CrossRefGoogle Scholar
Umstadter, D., Chen, S.-Y., Maksimchuk, A., Mourou, G. & Wagner, R. (1996). Non linear optics in Relativistic plasmas and laser wake field accelerations of electrons. Scien. 273, 472–475.CrossRefGoogle Scholar
Umstadter, D. (2003). Relativistic laser-plasma interactions. J. Phys. D. 36, R151–R165.CrossRefGoogle Scholar
Willi, O., Rumsby, P.T. & Zunqi, L. (1984). Filamentation instability in laser produced plasmas. In proceedings of Laser interaction and related plasma phenomena, (Edited by Hora, and Miley, ) Vol.6, New York: Plenum Press.Google Scholar
Young, P.E., Baldis, H.A., Drake, R.P., Campbell, E.M. & Estabrook, K.G. (1988). Direct evidence of ponderomotive filamentation in a laser-produced plasma. Phys.Rev.Lett. 61, 2336–2339.CrossRefGoogle Scholar
ZhiZhan, X., Yuguang, X., Guangyu, Y., Yanzhen, Z., Jiajin, Y. & Lee, P.H.Y. (1983). Second-harmonic emission from laser-plasma interactions. J. App. Phys. 54, 4902.CrossRefGoogle Scholar
Figure 0

Fig. 1. Beam width parameter f0 plotted against the distance of propagation Z in relativistic Plasma for intensities αE002 = 1.0, 2.0, 3.0 and for the following set of parameters.\eqalign{&\left({\omega_{\rm p} r_0 \over c}\right)^2= 18.0\comma \; {\omega_{\rm p} \over \omega_0} = 0.03\comma \; \omega_0 = 1.778\times 10^{14} rads^{-1} \cr &b_0 = 4 \times 10^{-4}\, {\it cm.} \cr}

Figure 1

Fig. 2. Spike width b(z) plotted against the distance of propagation Z in relativistic Plasma for intensities αE002 = 1.0, 2.0, 3.0 and for the parameters mentioned in Figure 1.

Figure 2

Fig. 3. Growth α(z) of the spike plotted against the distance of propagation Z in relativistic Plasma for intensities αE002 = 1.0, 2.0, 3.0 and for the parameters mentioned in Figure 1.

Figure 3

Fig. 4. Beam width parameter f0 plotted against the distance of propagation Z in relativistic Plasma for ${\omega_{\rm p} / \omega_0} = 0.02\comma \; 0.03\comma \; 0.04$, αE002 = 3.0 and for the parameters mentioned in Figure 1.

Figure 4

Fig. 5. Spike width b(z) plotted against the distance of propagation Z in relativistic Plasma for ${\omega_p / \omega_0} = 0.02\comma \; 0.03\comma \; 0.04$, αE002 = 3.0 and for the parameters mentioned in Figure 1.

Figure 5

Fig. 6. Growth α(z) of the Spike plotted against the distance of propagation Z in relativistic Plasma for ${\omega_{\rm p} / \omega_{\rm o}} = 0.02\comma \; 0.03\comma \; 0.04$, αEoo2 = 3.0 and for the parameters mentioned in Figure 1.