Direct-indirect mixture implosion in heavy ion fusion

TETSUO SOMEYA; KENTAROU MIYAZAWA; TAKASHI KIKUCHI; SHIGEO KAWATA

doi:10.1017/S0263034606060526

Direct-indirect mixture implosion in heavy ion fusion

Published online by Cambridge University Press: 21 September 2006

TAKASHI KIKUCHI and

TETSUO SOMEYA: Affiliation:
Department of Energy and Environmental Science, Graduate School of Engineering, Utsunomiya University, Utsunomiya, Japan
KENTAROU MIYAZAWA: Affiliation:
Department of Energy and Environmental Science, Graduate School of Engineering, Utsunomiya University, Utsunomiya, Japan
TAKASHI KIKUCHI: Affiliation:
Department of Energy and Environmental Science, Graduate School of Engineering, Utsunomiya University, Utsunomiya, Japan
SHIGEO KAWATA: Affiliation:
Department of Energy and Environmental Science, Graduate School of Engineering, Utsunomiya University, Utsunomiya, Japan

Article contents

Abstract
1. INTRODUCTION
2. SIMULATION MODEL
3. SIMULATION RESULTS
5. CONCLUSIONS
ACKNOWLEDGMENTS
References

Rights & Permissions

Abstract

In order to realize an effective implosion, the beam illumination non-uniformity and implosion non-uniformity must be suppressed to less than a few percent. In this paper, a direct-indirect mixture implosion mode is proposed and discussed in heavy ion beam (HIB) inertial confinement fusion (HIF) in order to release sufficient fusion energy in a robust manner. On the other hand, the HIB illumination non-uniformity depends strongly on a target displacement (dz) in a reactor. In a direct-driven implosion mode dz of ∼20 μm was tolerance and in an indirect-implosion mode dz of ∼100 μm was allowable. In the direct-indirect mixture mode target, a low-density foam layer is inserted, and radiation is confined in the foam layer. In the foam layer the radiation transport is expected in the lateral direction for the HIB illumination non-uniformity smoothing. Two-dimensional implosion simulations are performed and show that the HIB illumination non-uniformity is well smoothed. The simulation results present that a large pellet displacement of ∼300 μm is tolerable in order to obtain sufficient fusion energy in HIF.

Keywords

Heavy ion beam Implosion non-uniformity Inertial confinement fusion Pellet gain Radiation transport

Type: Research Article
Information: Laser and Particle Beams , Volume 24 , Issue 3 , September 2006 , pp. 359 - 369

DOI: https://doi.org/10.1017/S0263034606060526 [Opens in a new window]
Copyright: © 2006 Cambridge University Press

1. INTRODUCTION

In heavy ion beam (HIB) inertial confinement fusion (ICF), critical issues include an accelerator design, a reactor design, an efficient HIB transport, a HIB-target interaction and more (Lindl et al., 1992; Hogan et al., 1992; Tabak & Miller, 1998; Callahan, 1995; Welch et al., 2002; Qin et al., 2001; Barnard et al., 2003; Davidson et al., 2002; Kawata et al., 2002; Someya et al., 2004). Generally, ICF has two implosion schemes, that is, indirect-driven (Tabak & Miller, 1998; Callahan, 1995; Callahan et al., 2002), and direct-driven (Basko, 1993; Kikuchi et al., 2005) implosion schemes. Each implosion scheme has merits and demerits: the indirect-driven scheme may be robust against the beam non-uniformity in spite of low beam number, although its structure may be complicated and may be relatively expensive. The direct-driven pellet structure may be simple, although the scheme may be sensitive to the HIB illumination non-uniformity. In this paper, a direct-indirect mixture implosion mode is proposed and discussed in HIB ICF (HIF) in order to release sufficient fusion energy in a robust manner. After impinging of the HIB particles onto the fuel target, the pusher layer is ablated by thermal expansion due to the HIB deposition energy. Then the pusher layer pushes the DT fuel to the central direction. The DT fuel is compressed and must achieve a high-density high-temperature state after the void close. During the DT compression (target implosion), the ablation front must be uniform to realize an effective implosion, and a fuel burning (Emery et al., 1982, 1991). However, the limited-HIB-number illumination may induce the non-uniform ablation front and non-uniform target implosion in realistic cases. Moreover, the pellet displacement from the chamber center influences the non-uniform implosion and the gain reduction. In order to calculate a fuel target implosion more realistically, we couple a hydrodynamics code with a HIB illumination code (Ogoyski et al., 2004), and analyze the target implosion.

The target energy gain required for energy production by ICF can be evaluated by considering a reactor energy balance as shown in Figure 1. A driver pulse delivers an energy E_d to the target, which releases an amount of fusion energy E_fus. The energy gain is G = E_fus /E_d. The fusion energy is first converted into thermal energy of a blanket in a reactor chamber and then converted into electricity by a standard thermal cycle with an efficiency η_th. A fraction f of the electric power is recirculated to a driver system, which converts it into beam energy with an efficiency η_d. The energy balance for this cycle can be written fη_dη_th G = 1. Taking η_th = 40% and requiring that the recirculated fraction of electrical energy be smaller than 1/4, we find the condition Gη_d > 10. For a driver efficiency in the range of η_d = 10–33%, the condition leads to a target gain of G = 30–100 required for power production. Especially, the required pellet gain is about 30 for the HIF because the HIB driver efficiency is about η_d = 30%.

Energy balance of ICF.

2. SIMULATION MODEL

In HIF, the pulsed HIBs are illuminated on a fuel target. During the HIB illumination, the fuel target temperature becomes higher and higher. Therefore, the behavior of the target can be treated as a plasma hydrodynamics. In our developed hydrodynamics code, we solve basic hydrodynamic equations as follows:

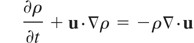
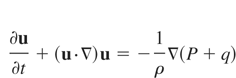
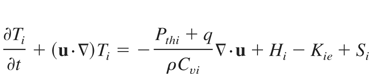
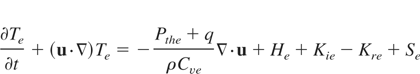
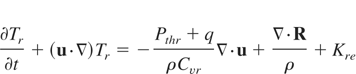
Here, ρ, u, T_i, T_e, and T_r are a target mass density, a velocity, an ion temperature, an electron temperature, and a radiation temperature, respectively. The P_thi, P_the, and P_thr are an ion, an electron, and a radiation pressures, respectively. The q is an artificial viscosity. The C_vi, C_ve, and C_vr show ion, electron, and radiation specific heats for constant volume, respectively. The K_ie and K_re are an energy exchange terms between an ion-electron and a radiation-electron, respectively. The H_i and H_e are an ion and electron heat conduction terms. The S_i and S_e represent source terms of an ion and electron from a stopping power. The F shows a limited radiation flux (Turner & Stone, 2001). To calculate advection terms in Eqs. (1)–(5), we use the R-CIP method. To capture a target material, we employ a color function (Xiao, 2001). We use an equation of state which is fitted the SESAMI library data (Bell, 1981).

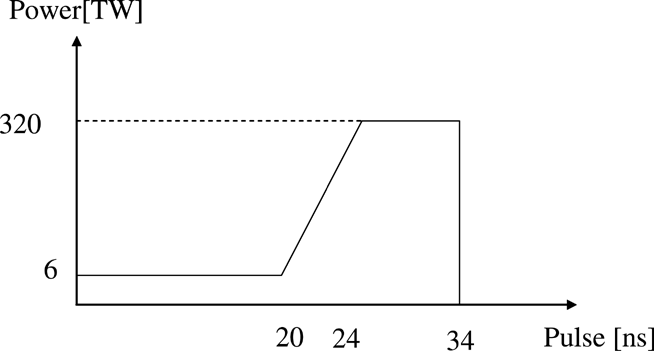
In order to study relationship between the HIB energy deposition on an energy absorber of a fuel pellet and the non-uniformity smoothing effect by the radiation transport effect on a pellet implosion, we calculate the target plasma hydrodynamics and fuel ignition by using the hydrodynamics code coupling with the HIB illumination code. Figure 2a shows the fuel target without a foam layer. The Pb, Al, and DT layer thicknesses and mass densities are 0.03 mm, 0.40 mm, 0.10 mm, 11.3 g/cm³, 2.69 g/cm³, and 0.19 g/cm³, respectively. Figures 2b and 2c show the target in the cases with a 0.5 mm and 1.0 mm thickness foam layers. As widely known, the radiation energy can be confined at a low density region. The radiation energy confined may smooth the HIB illumination non-uniformity. Therefore, we employ a foam layer to increase the confined radiation energy at the low density region (we call a “direct-indirect mixture mode” in this paper). The mass density of the foam layer is 0.01 times Al solid density in this study. The HIB pulse consists of a low power part (foot pulse) and a high power one (main pulse) as shown in Figure 3. In this case, the total HIB energy is 4.0 MJ. We employ a 32-HIBs illumination system as shown in Table 1. We evaluate the beam illumination non-uniformity at the target. In HIB ICF, the Bragg peak deposition area plays the most important role for a target implosion. Therefore, we define the total relative root-mean-square (RMS) as follows:

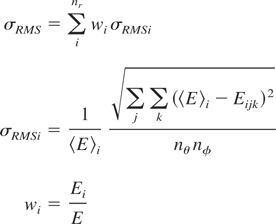
Here, σ_RMS is the RMS non-uniformity of beam irradiation. σ_RMSi is the RMS non-uniformity on the i-th (r = constant) surface of deposition. w_i is the weight function in order to include the Bragg peak effect or the deposition profile. n_r, n_θ, and n_φ are mesh numbers in each direction of the spherical coordinate. 〈E〉_i is the mean deposition energy on the i-th surface, E_i is the total deposition energy on the i-th surface, and E is the total deposition energy. In this paper, two-dimensional (in spherical coordinate) simulations are performed, and the two-dimensional HIB illumination time-dependent pattern at φ = 90 deg is employed from the HIB illumination code (Ogoyski et al., 2004).

Target structure of (a) without the foam layer, (b) the 0.5 mm foam, and (c) the 1.0 mm foam case.

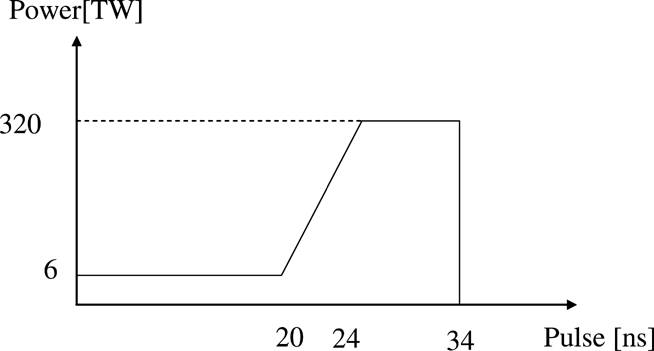
The HIB pulse consists of the low power part (foot pulse) and the high power one (main pulse).

The HIB illumination angle on the target in the 32-HIBs system

3. SIMULATION RESULTS

3.1. Without foam

Figure 4 presents a mean density and a radiation temperature averaged over the θ direction at: (a) 0.37 ns, (b) 34.9 ns, and (c) 36.2 ns for the target shown in Figure 2a, respectively. This case shows a direct-driven implosion mode. The averaged HIB illumination non-uniformity is 2.3% due to 32-HIBs irradiation on the target in this case. The Pb beam ions impinge the pellet surface as shown in Figure 4. The HIB deposition energy distribution induces an ablation region at the outside of the DT fuel, and then about one-third of Al pusher mass pushes the DT fuel. Figure 5 shows the target materials at: (a) the initial, (b) 24 ns, (c) 33 ns, and (d) 35 ns in the case without the foam. The limited number of HIBs induces the large non-uniform compression. Especially, we can see that the fuel DT is compressed non-uniformly near the void closure time.

The mean density and the radiation temperature averaged over the θ direction at (a) 0.37 ns, (b) 34.9 ns, and (c) 36.2 ns in the case without the foam.

The target materials at (a) the initial, (b) 24 ns, (c) 33 ns, and (d) 35 ns in the case without the foam.

3.2. With foam

In the direct-indirect mixture mode target, a low-density foam layer is inserted as shown in Figure 2b, and radiation is confined in the foam layer. In the foam layer, the radiation transport is expected in the lateral direction for the HIB illumination non-uniformity smoothing. Figure 2b presents the fuel target, and consists of five layers of solid Pb, a solid Al, a foam Al, a solid Al, and DT. The foam Al density is 0.01 times the Al solid density. In this section, we also employ the 32-HIBs illumination system. Figure 6 shows the mean target density and the mean radiation temperature at: (a) 0.29 ns, (b) 40.4 ns, and (c) 44.6 ns in the case of the 0.5 mm foam, respectively. In Figure 6a, the target and HIB parameter are selected so that all the HIB particles deposit their energy at the outer higher-density Al layer outside of the Al foam layer in order to present a fuel preheating. The heated Al layer produces the radiation energy. The radiation energy is confined in the foam layer, and smooths the HIB illumination non-uniformity. To check the radiation transport effect on the implosion non-uniformity smoothing, we compare the results for the cases with the radiation transport (ON) and without the radiation transport (OFF).

The mean density and the radiation temperature averaged over the θ direction at (a) 0.29 ns, (b) 40.4 ns, and (c) 44.6 ns in the case of the 0.5 mm foam.

Figures 7a and 7b show the target materials in the case of the radiation transport ON at 42 ns and 46 ns, respectively. Figures 7c and 7d present the target materials in the case of the radiation transport OFF at 42 ns and 46 ns, respectively. In Figure 7, the number 1, 2, and 3 represent the DT fuel, Al and Pb, respectively. From Figure 7, we can confirm that the more uniform implosion is realized in the case of the radiation transport ON compared with the case of the radiation transport OFF. Especially, the fuel DT is compressed uniformly near the void close in the case of the radiation transport ON. To confirm the radiation transport effect on the implosion non-uniformity smoothing, we pick up the radiation temperature profiles at 34 ns and 42 ns as a function of the θ angle in the cases with the 0.5 mm foam (radiation transport ON and OFF) and without the foam (see Fig. 8). The radiation temperature large non-uniformity in the θ direction can be seen in the case of the radiation transport OFF and the case without the foam. In Figure 8, the radiation transport effect is included in the case without the foam. Therefore, the high-order ripple modes are smoothed by the radiation transport effect in the case without the foam compared with the case of the radiation transport OFF. On the other hand, the radiation non-uniformity becomes small in the case of the radiation transport ON compared with the case of OFF. From the above results, we can also confirm that the non-uniformity is smoothed by the radiation transport effect.

Figures (a) and (b) show the target materials in the case of the radiation transport ON at 42 ns and 46 ns, respectively. Figures (c) and (d) present the target materials in the case of the radiation transport OFF at 42 ns and 46 ns, respectively.

The radiation temperature profile at 34 ns and 42 ns as a function of the θ angle in the cases of the 0.5 mm foam (radiation transport ON and OFF) and without the foam.

Figure 9 presents the time dependence of the RMS non-uniformity of the radiation temperature at the ablation front in the cases of the radiation transport ON and OFF. From Figure 9, we can see that the implosion non-uniformity at the ablation front becomes small effectively by the main pulse in the case of the radiation transport ON. The foam layer is compressed gradually during the main pulse. During the main pulse and the compression of the foam layer, the implosion non-uniformity can be smoothed by the radiation transport effect.

The time dependence of the RMS non-uniformity of the radiation temperature at the ablation front in the cases of the radiation transport ON and OFF.

Figures 10 present (a) the gain curve, (b) the mean ρR, and (c) the maximum ion temperature versus dz of the target displacement in the cases of radiation transport ON, OFF, and without the foam, respectively. As described in the Introduction, the pellet gain must be larger than 30 in order to obtain the sufficient energy production in HIF. In our calculation results, the pellet gain is ∼23 in the case of dz = 0 without the foam. Moreover, the gain decreases dramatically with the increase in the pellet displacement in the case without the foam. Therefore, it may be difficult to use a fusion electric power generation system in the case without foam. On the other hand, we can confirm that the pellet gain in the case with the foam is larger than 30 up to dz of about ∼300 μm pellet displacement. However, the gain becomes smaller with the increase in the pellet displacement in the cases of the radiation transport OFF and without the foam. The maximum ion temperature and the mean ρR decrease for a large pellet displacement in the case of the radiation transport OFF. On the other hand, the mean ρR and the maximum ion temperature in the case of the radiation transport ON are still large compared with those in the cases of the radiation transport OFF and without the foam. From these results, the radiation transport at the low density region plays an important role to release the effective power production by ICF. In ICF, the tolerable pellet displacement from the fusion reactor center was about 20 μm for direct-driven implosion and about 100 μm for indirect-driven implosion, respectively (Goodin et al., 2001; Petzoldt et al., 2003; Someya et al., 2004). From our results, the allowable dz in the direct-indirect mixture drive mode in HIF is about 300 μm.

Figures (a), (b), and (c) present the pellet gain, the mean ρR and the maximum ion temperature as a function of the pellet displacement dz from the chamber center in the cases of the radiation transport ON, OFF and without the foam.

Figure 11 shows the implosion non-uniformity of (a) the target density, (b) the total pressure, (c) the ion temperature, and (d) the radial velocity at the void close time as a function of the pellet displacement dz in the cases of the radiation transport ON, OFF, and without the foam. From Figure 16, the implosion non-uniformity becomes large in the cases of the radiation transport OFF and without the foam compared that with the radiation transport ON case. These results also indicate that the radiation transport effect at the low density region can relax the non-uniform implosion. Especially at the maximum ρR, the non-uniformity is small compared with that at the void close time. This result shows that an effective fuel burning can be realized in spite of the large pellet displacement of dz ∼ 300 μm.

The implosion non-uniformity of (a) the target density, (b) the total pressure, (c) the ion temperature, and (d) the radial velocity at the void close time as a function of dz in the cases of the radiation transport ON, OFF and without the foam.

3.3. Effect of foam thickness

In this section, the effect of foam thickness on the direct-indirect mixture implosion is presented. We employ the target with the 1.0 mm thickness foam as shown in Figure 2c. Figure 12 presents the radiation temperature at the ablation front as a function of θ angle at the (a) 34 ns and (b) 42 ns in the cases of 1.0 mm and 0.5 mm foams, respectively. The radiation non-uniformity in the case of the 1.0 mm foam is almost the same in the case of the 0.5 mm foam. Figure 13 shows the time dependence of the RMS non-uniformity of the radiation temperature at the ablation front in the cases of 1.0 mm and 0.5 mm foams. From Figure 13, we can see that the radiation temperature non-uniformity at the ablation front becomes small effectively at the main pulse region in both the cases.

The radiation temperature at the ablation front as a function of θ angle at the (a) 34 ns and (b) 42 ns in the cases of 1.0 mm and 0.5 mm foams.

The time dependence of the RMS non-uniformity of the radiation temperature at the ablation front in the cases of 1.0 mm and 0.5 mm foams.

Figure 14 displays the time dependence of the radiation energy confined at the low density region in the cases of the 1.0 mm foam, the 0.5 mm foam and without the foam. The peak conversion efficiencies of the HIB total energy to the radiation energy are ∼4.5% in the case of the 1.0 mm foam, ∼4.5% in the case of the 0.5 mm foam and ∼1.5% in the case without the foam. From these results, we find that the implosion mode in the case with the foam is a mixture of direct- and indirect-driven modes.

The time dependence of the radiation energy confined at the low density region in the cases of the 1.0 mm foam, the 0.5 mm foam and without the foam.

Figures 15 show (a) the gain curve, (b) the mean ρR, and (c) the maximum ion temperature in the cases of 1.0 mm and 0.5 mm foams, respectively. We can see that the required pellet gain is satisfied in the cases of 1.0 mm and 0.5 mm foams for the displacement of dz = 0. However, the pellet gain is small in the case of the 1.0 mm foam compared with that in the case of the 0.5 mm foam. The implosion velocity is not high enough to ignite the DT fuel efficiently because the 1.0 mm foam thickness was too thick to create a sufficient implosion driving pressure. Therefore, the pellet gain decreases for the large pellet displacement in the case of the 1.0 mm foam.

Figures (a), (b), and (c) present the pellet gain, the mean ρR and the maximum ion temperature as a function of the pellet displacement dz from the chamber center in the cases of 1.0 mm and 0.5 mm foams.

Figure 16 shows the implosion non-uniformity of (a) the target density, (b) the total pressure, (c) the ion temperature, and (d) the radial velocity at the void close time as a function of dz in the cases of the 1.0 mm foam, the 0.5 mm foam, and without the foam. The implosion non-uniformity in the case without the foam becomes large for the large pellet displacement. In the case of the 1.0 mm foam, the non-uniformity is also small. However, the pellet gain is small compared with that in the 0.5 mm foam case as described above. These results indicate that the foam thickness is important to obtain a sufficient fusion energy output. These results indicate that the foam thickness is important to obtain a sufficient fusion energy output.

5. CONCLUSIONS

In this paper, we discuss the target implosion using the 32-HIBs illumination system. The direct-driven fuel target implosion is weak against the beam non-uniformity. However, in the low density foam region, the radiation energy can be confined and the implosion non-uniformity is smoothed. Therefore, we employ the foam layer for the fuel target in order to increase the radiation energy confined and to expect a uniform target implosion. In our target with the foam, the direct-indirect mixture implosion mode is realized. From our calculation results, the trapped radiation energy at the low density region in the case with the foam (direct-indirect mixture mode) is large compared with that in the case without the foam (direct-driven mode). The peak conversion efficiencies are ∼4.5% in the case of the 1.0 mm foam, ∼4.5% in the case of the 0.5 mm foam, and ∼1.5% in the case without the foam. The foam thickness is important to release sufficient fusion energy. For the 0.5 mm thickness foam case, the implosion non-uniformity is suppressed effectively and a sufficient fusion energy is obtained in HIF. It was also found that the direct-indirect mode target is robust against the target displacement of dz. Our results present that a large pellet displacement of ∼300 μm is allowed in order to obtain a sufficient fusion energy in HIF.

ACKNOWLEDGMENTS

This work was partly supported by the JSPS (Japan Society for the Promotion of Science) and MEXT (Ministry of Education, Culture, Sports, Science and Technology). We would also like to present our thanks to colleagues in the Japan and US HIF VNL research groups for their fruitful discussions on this subject.

References

REFERENCES

Barnard, J.J., Ahle, L.E., Bieniosek, F.M., Celata, C.M., Davidson, R.C., Henestroze, E., Friedman, A., Kwan, J.W., Logan, B.G., Lee, E.P., Lund, S.M., Meier, W.R., Sabbi, G.-L., Seidl, P.A., Sharp, W.M., Shuman, D.B., Waldron, W.L., Qin, H. & Yu, S.S. (2003). Integrated experiments for heavy ion fusion. Laser Part. Beams 21, 553–560.

Basko, M.M. (1993). Simple spherical D-T targets for heavy-ion beam fusion. Laser Part. Beams 11, 733–750.

Bell, A.R. (1981). New equations of state for MEDUSA. Rutherford Lab. Report. RL-80-091.

Callahan, D.A. (1995). Interaction between neighboring beams in heavy ion fusion reactor chamber. Appl. Phys. Lett. 67, 3254–3256.

Callahan, D.A., Herrmann, M.C. & Tabak, M. (2002). Progress in heavy ion target capsule and hohlraum design. Laser Part. Beams 20, 405–410.

Davidson, R.C., Kaganovich, I.D., Lee, W.W., Qin, H., Startsev, E.A., Tzenov, S., Friedman, A., Barnard, J.J., Cohen, R.H., Grote, D.P., Lund, S.M., Sharp, W.M., Celata, C.M., De Hoon, M., Henestroza, E., Lee, E.P., Yu, S.S., Vay, J.-L., Welch, D.R., Rose, D.V. & Olson, C.L. (2002). Overview of theory and modeling in the heavy ion fusion virtual national laboratory. Laser Part. Beams 20, 377–384.

Emery, M.H., Orens, J.H., Gardner, J.H. & Boris, J.P. (1982). Influence of nonuniform laser intensities on ablatively accelerated targets. Phys. Rev. Lett. 48, 253–256.

Emery, M.H., Gardner, J.H., Lehmberg, R.H. & Obenschain, S.P. (1991). Hydrodynamic target response to an induced spatial incoherence-smoothed laser beam. Phys. Fluids B 3, 2640–2651.

Goodin, D.T., Alexander, N.B., Gibson, C.R., Nobile, A., Petzoldt, R.W., Siegel, N.P. & Thompson, L. (2001). Developing target injection and tracking for inertial fusion energy power plants. Nucl. Fus. 41, 527–535.

Hogan, W.J., Bangerter, R. & Kulcinski, G.L. (1992). Energy from inertial fusion. Phys. Today 45, 42–50.

Kawata, S. Someya, T., Nakamura, T., Miyazaki, S., Shimizu, K., &Ogoyski, A.I. (2002). Heavy ion beam final transport through an insulator guide in heavy ion fusion. Laser Part. Beams 21, 27–32.

Kikuchi, T., Someya, T. & Kawata, S. (2005). Beam pulse duration dependence on target implosion in heavy ion fusion. IEE. Jpn. 125, 515–520.

Lindl, J.D., Morory, R.W. & Campbell, M. (1992). Progress toward ignition and burn propagation in inertial confinement fusion. Phys. Today 45, 32–40.

Ogoyski, A.I., Someya, T. & Kawata, S. (2004). Code OK1—Simulation of multi-beam irradiation on a spherical target in heavy ion fusion. Comp. Phys. Comm. 157, 160–172.

Petzoldt, P.W., Alexander, N.B., Drake, T.J., Goodin, D.T., Jonestrask, K. & Stemke, R.W. (2003). Experimental target injection and tracking system. Fusion Sci. Tech. 44, 138–141.

Qin, H., Davidson, R.C., Lee, W.W. & Kolesnikov, R. (2001). 3D multispecies nonlinear perturbative particle simulations of collective processes in intense particle beams for heavy ion fusion. Nucl. Instr. Meth. Phys. Res. A464, 477–483.

Someya, T., Ogoyski, A.I., Kawata, S. & Sasaki, T. (2004). Heavy-ion beam illumination on a direct-driven pellet in heavy-ion inertial fusion. Phys. Rev. ST-AB 7, 044701.

Tabak, M. & Miller, D.C. (1998). Design of a distributed radiator target for inertial fusion driven from two sides with heavy ion beams. Phys. Plasmas 5, 1895–1900.

Turner, N.J. & Stone, J.M. (2001). A module for radiation hydrodynamics calculations with ZEUS-2D using flux-limited diffusion. The Astrophys. J. Supp. 135, 95–107.

Welch, D.R., Rose, D.V., Oliver, B.V., Genoni, T.C. & Clark, R.E. (2002). Simulation of intense heavy ion beams propagating through a gaseous fusion target chamber. Phys. Plasmas 9, 2344–2353.

Xiao, F. (2001). Implementations of multi-fluid hydrodynamic simulations on distributed memory computer with a fully parallelizable preconditioned Bi-CGSTAB method. Comp. Phys. Comm. 137, 274–285.