2. FUSION ENERGY

In order to gain safe, clean, unlimited, and very low cost energy from nuclear fusion of Deuterium (D) and Tritium (T) or other light nuclear reactions, these are extensively studied. These reactions were a fully unexpected process occurring at collisions between nuclei at 10 keV energy or even less because the usual collision energy for reacting nuclei is above MeV in order to overcome the Coulomb repulsion, and to get the colliding nuclei into the distance close to their diameter of femtometers. It was the fully unexpected discovery of Cockroft et al. (1933) and Oliphant et al. (1934) that DD reactions occurred at distances 100 times larger than the nuclear size. These fusion reactions cannot be simply explained by Gamov factors which would be much less than 10⁻⁴⁰ and a resonance processes was generally suggested, but a consequent theory was not available until the work by Li et al. (2000, 2004) for the DT reaction and for the DD, and other reactions to reproduce the cross sections in highly accurate agreement with measurements based on a transparent model with a Schrödinger potential having an imaginary part. Before, only numerical fitting, e.g., with five numerical factors (Clark et al., 1978) or similar were available for reproducing the measured cross sections.

These hot fusion reactions at particle energies in the scale of 10⁴ eV (about 100 Million Kelvin) are of interest for fusion power stations in the future. Most investment in research during the past 50 years went to the ITER magnetic confinement reactor proposal which—if it would be decided next to be built for about $10 Billion—should by 2015 produce discharges of 1000 seconds duration producing 500 MW fusion energy from an input of 500 MW electrical energy (Hora, 2004). This corresponds to a gain of electrical energy per input energy of 0.3 only. One of the key problems not yet solved is the wall erosion needing a replacement of the wall every one to two years. An alternative was opened since the discovery of the laser to be used for driving fusion reactions. Fusion neutrons were measured since 1968–1969 (Hora, 1991). The biggest lasers, NIF and LMJ, being half finished are to demonstrate ignition by about 2010. For laser fusion based on volume ignition (Hora & Ray, 1978), these type of lasers with 5 MJ-nanosecond pulses and compression to twice the measured values of 2000 times the solid state (Azechi et al., 1991) may reach 120 times fusion energy per total electric energy input, i.e., a gain of electricity per input energy of about 30 (Hora et al., 2003, see Miley et al., 2005; Osman et al., 2005). Facilities like NIF or LMJ need an enormous reduction in size, costs, and improvement e.g., in laser pulse repetition, but basically there may not be a physics limit for such developments.

In contrast to this scheme with 10 MJ-ns laser pulses, solidly based on present achievements, an alternative for laser fusion may be possible to be explored now by using the new developments of petawatt-picosecond laser pulses (Perry & Mourou, 1994) to aim the “fast ignitor” (Tabak et al., 1994). This was initiated by Campbell et al.(2000) (Osman et al., 2005) when he realized from the measurements of Azechi et al. (1991) since about 1985 that the laser compression of a carbon polymer was well reaching the density of 2000 g/cm³ (about 2000 times the solid state) but the temperature was unexpectedly low, only about 3 Million Kelvin. In order to reach fusion, Campbell et al. (2000) envisaged that the addition of the necessary heating by depositing kJ energy from a ps pulse to the center of DT, compressed to 3000 times the solid state should result in very high gain fusion energy. This scheme has reached interesting neutron gains (Hora et al., 1998; Kodama & Fast Ingitor Consortium, 2002) and wide range studies are on the way.

The difficulties in these fast ignitor studies consist in the fact that the ps laser pulses with powers above TW resulted in numerous unexpected relativistic effects and an estimation of such effects may (instead of reaching spark ignition) lead to volume ignition (Hora et al., 1998). One remarkable alternative is the use of peripheral ignition of a highly precompressed plasma (Hain & Mulser, 2001; Mulser & Bauer, 2004; Mulser & Schneider, 2004; Deutsch, 2004) or the generation of very high density 5 MeV electron beams from petawatt irradiation of a high density precompressed DT plasma, where the electron beam will ignite a controlled fusion reaction wave in a large amount of nearly uncompressed DT fuel producing a very high gain (Nuckolls & Wood, 2002).

It was an early attempt for laser fusion (Bobin, 1971; Chu, 1972) to consider the ignition of a fusion reaction wave front in uncompressed DT by a laser or particle beam pulse, Figure 1. It turned out that the following conditions A and B had to be fulfilled if light DT ion beams of the optimum energy of 80 keV (at the maximum cross section for resonance, Li et al. (2000)) are incident on solid state DT: the ion current density, j, had to be at least (Bobin, 1971, 1974: Table I; Brueckner & Jorna, 1974)

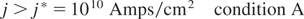
Fusion scheme where a laser beam irradiates solid DT producing a block of plasma moving against the laser light and another block moving into the target. Ignition requires extremely high DT current densities and energy fluxes of the blocks, Eqs. (1) and (2).

and the energy flux density E had to be larger than E*

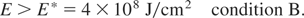
These values were completely out of reach for ion beams in the 1970s though a relaxation of the condition can be expected due to collective effects (Gabor, 1953) by interpenetration (Hora, 1983). However, after the experiments of Badziak et al. (1999, 2003, 2004a, 2004b) and the theory of the skin layer acceleration (Hora et al., 2002; Hora, 2003; Miley et al., 2003, 2004; Osman et al., 2004a, 2004b; Hora, 2004), the ps laser pulses in the TW to few PW range may provide the conditions A and B as explained in Section 4.

3. DISTINGUISHING RELATIVISTIC FROM SUBRELATIVISTIC TW-PS LASER-PLASMA INTERACTION

The theoretical description of laser-plasma interaction (Hora, 1991, Sections 2 to 4) depends on the conditions of the plasma whether the following models can be applied:

Method (a) (Kruer, 1988) arrives at the most general description of numerous effects especially where no thermal equilibrium is reached between the particles but where the limitations even of the largest available computers does not permit the general inclusion of the long range Coulomb forces for collisions and the exchange mechanisms for reaching or going to reach thermal equilibrium. Method (b) again was very successful but not as general by lost of information to describe numerous plasma phenomena simplifying methods a, however without a complete cover of the collisions, since the Boltzmann collision term has not yet been discovered apart from approximations. Hydrodynamics (c) can explain many phenomena including complete inclusion of collisions covering equi-partition and transport processes but based on quasi thermal equilibrium conditions of the fluids only.

One advantage is the development of method (a) to combine with method (b) as the particle in cell (PIC) technique for a more economic and efficient single-particle description including phase space as successfully used in laser-plasma interaction (Wilks et al., 1992) however still not directly covering collisions. One precondition for the hydrodynamics is that the Debye length is sufficiently short compared with the grids in the hydrodynamics. If this is not the case, the collisionless description of the single particle motion and the macroscopic electric fields between the particles is the domain of the PIC method. In the PW-ps laser plasma interaction both methods, hydrodynamics and PIC are to be separated from case to case but there are examples also where there is a rather good agreements between the results of both methods.

A strong relativistic effect was self-focusing which general formulation (Hora, 1975) producing very highly charged ions of up to few hundred MeV energy in full agreement with the theory (Hora, 1991, 2000) was working even at laser intensities up to 1000 times lower values than the relativistic threshold intensity I_rel where the quiver energy is mc² (in cgs units)

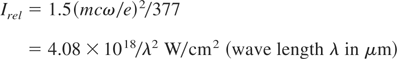
For the subrelativistic approximation, the relativistic self-focusing was derived by several authors with the same result (Hora, 1991). For the subrelativistic and relativistic range (Hora, 1975, 2003), Figure 2, a plane wave front Gaussian laser beam hitting uniform plasma shrinks to a diameter of δλ because the relativistic change of the mass of the quivering electron has a shorter effective wave length at higher laser than at lower laser intensity. If the Debye length is less than 0.1,λ, the energy ε_i of Z times charged ions is

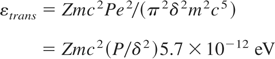
Relativistic self-focusing of a laser beam of radius do /2 of Gaussian intensity profile hits a plane plasma surface. Due to relativistic mass change of the quivering electron, the effective wave length is shorter at central highest laser intensity than outside causing the bending of the plane wave front until the beam receives the diffraction limited diameter of about a wave length (Hora, 1975).

where the laser power P is in Watts and the beam diameter δ is in multiples of the wave length (between 0.6 and 1). One example is that 13 times ionized copper achieves about 22 MeV energy with a laser power of 0.5 TW as observed under usual conditions of relativistic self focusing. The ions are accelerated at the origin by the nonlinear (ponderomotive) force nearly spherically symmetric with a small deviation as explained (Häuser et al., 1992), but appear with a wide cone against the laser light due to slowing down in the target. The measured number of these fast ions from relativistic self-focusing per interaction is 10¹⁴ or more in agreement with the theory.

The emission of fast ions in laser produced plasmas was of interest from early research as far as only laser pulses of less than MW power produced classical plasma heated thermal ion emission in the 10 eV range. At higher powers, the 10 keV ions were due to ponderomotive self-focusing (Hora, 1969, 1991), while the measurements of Ehler (1975) showed three groups of ions, the Z-separated fast group following relativistic self-focusing and subsequent nonlinear (pondermotive) force acceleration, a second fast Z-separated group and the third group of thermal emitted plasma as seen in many repeated experiments later (Woryna et al., 2000; Wolowski et al., 2002, 2003). There is also a Z-separated ion group from ambipolar separated ions from the thermal plasma surface processes (Wägli & Donaldson, 1978) where the number of ions is so small that this group usually is not detected. The second fast group (Ehler, 1975; Woryna et al., 2000) is clearly the result of ambipolar acceleration of the hot X-ray group according to Gitomer et al. (1986), where the energetic quivering electrons are etherealized—confirming anomalous resistively expressed a quantum modified collisions (Haseroth & Hora, 1996)—with subsequent ambipolar acceleration (Hora, 2003).

Within this rather complex situation, the ps-TW interaction produces a further complexity due to the mentioned conditions that the Debye length can be too large for applying the mentioned models and PIC (Wilks et al., 1992; Shorokhov & Pukhov, 2004; Greschik & Kull, 2004) or other methods need to be applied.

The first significant measurement was that with 30 TW, 400 fs laser pulses (Umstadter, 1996) where 10⁸ electrons of 30 MeV energy were emitted within a cone. This was in contrast to the beat-wave and wakefield accelerations (Balakirev et al., 2004) where the acceleration (Kitagawa et al., 1992) did not result in the expected large number of accelerated electrons. The mechanism in the case of the Umstadter experiment was obviously that there was a ponderomotive acceleration of free electrons (Häuser et al., 1994; Wang et al., 1998; Lefebvre et al., 1998; Hartemann et al., 1998; Malka & Fritzler, 2004) confirming the 30 MeV electrons and the angle of the emission cone (Hora et al., 2000) while the number of electrons was reproduced by the volume of relativistic self-focusing which for the 400 fs was applicable because of the short range of mechanical motion during this period.

The measurements after that of Umstadter (1996) with ps or shorter laser pulses of TW to PW power showed then a rich field of relativistic effects (Roth et al., 2001; Schwoerer et al., 2001; Hoffmann et al., 2005) with pair production, gamma radiation for subsequent nuclear transmutations (Ledingham et al., 2000; Magill et al., 2003), ions with nearly GeV energy (Clark et al., 2001) analyzed as different group processes (Hora, 2003) and alternative electron acceleration mechanisms up to GeV energy. The explanation of the measured 5 MeV proton beams (Roth et al., 2000, 2001; Osman et al., 2004a; Hoffmann et al., 2005) by a target normal sheath acceleration mechanisms (TNSA) was derived from PIC computations (Wilks et al., 2001). PIC computations for 10²⁴ W/cm² laser intensities arrived at the nonlinear force acceleration of plasma blocks (Esirkepov et al., 2004) easily covering the conditions on how to ignite uncompressed solid state density DT fusion fuel, Eqs. (1) and (2).

Within these numerous new aspects, it seems to be a drastic alternative, how the subrelativistic interaction occurs as a skin layer acceleration (SLA) mechanism detailed evaluated experimentally from ion emission (Badziak et al., 1999, 2003, 2004a) and recognized as the skin layer process (Hora & Wang, 2001; Hora et al., 2002; Hora, 2003) after the importance of the prepulse was known (Zhang et al., 1998) for avoiding relativistic self focusing and as seen before from the KrF ps-TW interaction with ideal plane geometry nonlinear force acceleration (Sauerbrey, 1996). This all was reproduced from numerical simulations with the then fully permitted genuine two fluid computations (Badziak et al., 2004a, 2004b; Cang et al., 2005).

PIC is now a broad stream development (Wilks et al., 1992, 2001; Esirkepov et al., 2004) not only for exploring the relativistic effects of PW-ps laser plasma interaction. The whole physics of high electric fields (Hartemann, 2002)—initially derived from the electron acceleration by lasers in vacuum (Hora, 1988; Scheid & Hora, 1989; Häuser et al., 1994; Hartemann et al., 1998)—opens a new development in physics. The properties of the double layer on all laser produced plasmas expanding into vacuum characterized by a Debye length are the essential mechanism for Wilks' (Wilks et al., 2001) TNSA proton acceleration. This is the reason why these double layers produce surface tension (Hora et al., 1984; Eliezer & Hora, 1989) surface tension in plasmas and produce a stabilization of surface waves working against Rayleigh–Taylor instabilities, a result which has not been exhausted by theory which always results in worse instabilities than measured. Generalizing this to the electrons in metal by using their Fermi energy instead of a temperature in the Debye length results the double layer expressing the work function of metals and offering a consequent quantum theory of surface tension and surface energy as measured (Hora et al., 1989). Generalizing this to the hadrons of nuclei, results in a theory of the forces, confining a nucleus at the well known diameters, and the transition into quark-gluon plasmas (Hora et al., 2005). This affinity to the TNSA model is the reason why these questions were discussed in this connection (Osman et al., 2005).

4. INITIAL DEVELOPMENT OF SUBRELATIVISTIC PLASMA BLOCK GENERATION

It was one of the main motivations for the UWS International Workshop “Fast high Density Plasma Blocks Driven by Picosecond Terawatt Lasers” to clarify the differences between the relativistic and subrelativistic laser-plasma interaction in this range as explicitly outlined by presented contributions. It seems to be indicated to summarize the following background facts for underlining the skin layer acceleration (SLA) process.

For understanding the skin layer laser plasma interaction theory with plane waves geometry we explain the nonlinear (ponderomotive) force as the main driving process in the following numerical results The force density in plasmas (Hora, 1991) f = f_th + f_NL consisting in the thermokinetic force f_th = −∇p given by the gas dynamic pressure p and the general transient (Hora, 1985) nonlinear force

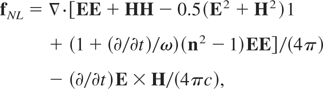
where 1 is the unity tensor, ω the laser frequency, and n is the (complex) refractive index. This can be reformulated into

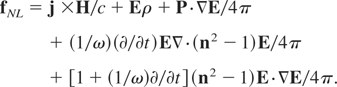
It was shown that these algebraically identical formulations are Lorentz and gauge invariant and are the complete description of the force density in the plasma due to electric and magnetic fields. The formulation (5) is that of the Maxwellian stress tensor including the dielectric response and transient (time dependent) behavior of the fields. The formulation (6) explains the parts acting in the nonlinear force. Here one recognizes on the right-hand side first the Lorentz term f_Lorentz = j × H/c with the plasma current density j and the vacuum velocity of light c, then the Coulomb term Eρ with the electric charge density ρ and as the third term the Kelvin ponderomotive term (Hora, 2000, see Eq. (1))

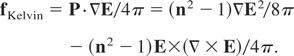
The remaining terms in Eq. (6) are new nonlinear terms which were derived for the general equation of motion in plasmas from the studies of laser interaction. The proof for the final generality of Eq. (6) was given by momentum conservation for the nontransient case (∂/∂t = 0) and for the transient case by symmetry (Hora et al., 1984) of the terms and from gauge and Lorentz invariance.

For the correct interpretation it is necessary to mention that Kelvin's ponderomotive force is identical with the nonlinear Schlüter term

remembering the definition of the electric polarization P and the refractive index without collisions

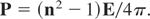
From Kelvin's ponderomotive force (7) follows formally an expression of the “field gradient force” or the electrostriction for collisionless plasma (n without imaginary part)

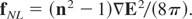
This can be used for the case of perpendicular incidence of plane laser waves on an inhomogeneous plasma of one-dimensional geometry e.g., along the coordinate x. For the same conditions, the stress tensor description produces a force density into the x-direction of

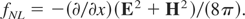
Formulation (10) led to the common expression of “ponderomotive force” for (1). As is known for (plane wave) perpendicular incidence of laser radiation on plasma, the Schlüter term is then zero. Nevertheless there is a force of the form of Eq. (10). In this case, however, the nonlinear force f_NL is the result of the Lorentz term in Eq. (6). This confusion of the definitions is avoided if one uses the general expression of the nonlinear force (6) for the electrodynamic part of the force density in plasma. This is valid for any incidence, for plasma with collisions, and including time dependence of the fields.

The nonlinear force (5) or (6) was the first inclusion of the dielectric plasma properties into the electrodynamic interaction of (laser) fields with plasma where the first step was for the simplified case of perpendicular incidence while the ponderomotive interaction of electromagnetic waves on free electrons without dielectric effects for plasma confinement was discussed before (Weibel, Kibble, and others, see Hora, 1991). The proof that (5) and (6) are the general solution for the non-transient (stationary laser) case (∂/∂t = 0) was given from momentum conservation for the collisionless case where nonlinear terms were derived as necessary addition for completion of Schlüter's two-fluid equation of motion leading to the general transient case (Hora, 1985).

The action of the nonlinear force at the plane wave geometry can be seen as shown in Figure 4-1 of Hora (2000). An electromagnetic wave incident from vacuum for x > 0 on a plasma with (initially) monotonous increase of electron density n_e(x) from x = 0 will cause an increase of the electromagnetic field energy density (E² + H²)/(8π) up to a maximum close before the density reaches the value of the critical electron density n_ec (where the plasma frequency ω_p = (4πe²n_e /m)^1/2 is equal to the laser frequency ω). For further increasing x, the energy density will exponentially drop to zero in the overdense plasma (ω_p > ω) within the skin depth similar to metal optics due to the plasma collisions. The negative gradient of the energy density results in the nonlinear force (11) driving the plasma corona as a whole blocks (John Nuckolls said like gravitation) toward the vacuum. The plasma block between the maximum of the energy density and its vanishing value in the skin layer is driven into the plasma interior. This is identical with the result of the dielectric increase of the electric field |E| = E_v /|n|^1/2 expressed by its vacuum amplitude E_v and the oscillating cos-function of the wave in the inhomogeneous plasma.

Numerical cases of the real plasma dynamics with nonlinear plasma collisions and numerically detailed wave optical calculations of the laser field for each time step during the time dependent variation of the plasma density and temperature were performed for neodymium glass laser intensities between 10¹⁴ and 10¹⁸ W/cm² for times up to few ps using a single fluid hydrodynamic code (see Figs. 4-13 to 4-16 in Hora, 2000). Within this short time, velocities of the Deuterium plasma blocks of up to nearly 10⁹ cm/s resulted. An example for plasma of initially double-Rayleigh profile of 100 μm thickness corresponding to 95 vacuum laser wave lengths (Fig. 10.17 in Hora, 1991) for minimizing initial optical reflection for Deuterium plasma with central maximum density very close to the critical density and an initial temperature of 100 eV is shown in Figure 3. Irradiating 10¹⁸ W/cm² neodymium glass laser radiation from the right-hand side, we see after 1.5 ps that the light does not penetrate up to the maximum initial density at x = 0 but only to about 37 μm due to the (weak) collision absorption shown from the spatial distribution of the electromagnetic energy density (E² + H²)/8π. This energy density as negative gradient produces the forces, Eq. (11), to move a block of Deuterium plasma between 40 and 63 μm against the laser light with velocities of up to 10⁹ cm/s, while a block of plasma of similar thickness is moving with velocities up to 3 × 10⁸ cm/s toward the plasma interior. The initial conditions were chosen in such a way that the block motion was possible until the irradiation time of 1.5 ps. At later times or for other initial conditions, the generation of locally reflected waves in the dynamically developing laser field within the driven and thermally expanding plasma causes the well known driving of plasma into the nodes of the partially standing wave field disturbing the smooth motion of the blocks, see Fig. 10.20a of Hora (1991). These calculations were more than 20 years too early in view of the PW-fs laser pulses of today.

Generation of blocks of Deuterium plasma moving against the neodymium glass laser light (positive velocities v to the right) and moving into the plasma interior (negative velocities) at irradiation by a neodymium glass laser of 1018 W/cm2 intensity onto an initially 100 eV hot and 100 μm thick bi-Rayleigh profile (Fig. 19.17 of Ref. Hora, 1991) with minimum internal reflection. The electromagnetic energy density (E2 + H2)/(8π) is shown at the same time of 1.5 ps after begin of the constant irradiation.

Number of (integrated signal) emitted fast ions and thermal ions from a perpendicular irradiated copper target at neodymium glass irradiation for 1.2 ps pulses depending on the laser pulse energy focused to a 30 wavelength diameter beam at the target surface with suppression of a prepulse by 108 for a time less then 100 ps before the main pulse arrived. During the last 100 ps the contrast ratio was about 104 (Badziak et al., 1999).

What was significant about the anomaly of ion emission observed by Badziak et al. (1999) is the measurement of very low maximum ion energies and subsequent measurements which were done after the skin layer model (Hora et al., 2002) were confirmed (Badziak et al., 2003, 2004a, 2004b). Focusing a neodymium glass laser pulse of 1.5 ps duration at power P up to 2.1 × 10¹¹ W produced Cu⁺¹³ ion or up to 450 keV energy. Using the theory of relativistic self focusing, Eq. (4), the ion energy after the usual relativistic self-focusing should have been 22.6 MeV. This was a first indication that relativistic self focusing could not have occurred in this experiment. It is important to note that any prepulse (aspect ratio) was suppressed by a factor 10⁸. Another very strange result is that not any change of the number of the fast ions (to distinguish from the following slow thermal ions) was observed on the variation of the laser power (energy) over a factor 25 (Fig. 4) while the ion velocity increased on a square root law such that the energy of the fastest ions showed the following dependence on the laser intensity I

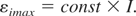
Therefore, the measured fast ions were different from the quiver-collision property (Hora, 2003) but were different also from the relativistic-self-focusing property due to the 50-times too low maximum ion energy. Later, after knowing the skin layer interaction (Hora et al., 2002a, 2002b), measurements were performed (Badziak et al., 2004a, 2004b, 2005) in order to clarify this discrepancy specifically designed for these conditions using the laser system described before. This neodymium glass laser system produced 0.5 ns laser pulses of 1.4 × 10⁹ W/cm² in the focus for irradiation on gold targets at an intensity of 2 × 10¹⁴ W/cm². In other measurements with the same focus geometry and the same pulse has been compressed to 1.2 ps for a power of P = 6 × 10¹¹ W for an intensity of 8 × 10¹⁶ W/cm² on the same gold target. For clarifying the discrepancy between ps and ns irradiation, the whole optical system was identical in both cases of experiments with a short or long pulses where the same laser energy of 0.7 J was incident in both cases. The energy of the emitted ions was measured by the time of flight probes and by ion electrostatic analyzers. A most significant result is that of a maximum ion energy of 0.95 MeV for Au⁺³⁴ produced by the 0.5 ns pulses, while laser pulses of 1.2 ps duration produced fastest 1.03 MeV Au⁺²⁶ ions.

How is it possible that the 30-times ionized gold ions had nearly the same maximum energy of MeV though the irradiation power and the intensity differed by more than 400 between the cases of 0.5 ns and 1.2 ps laser pulse duration? Interestingly the 0.5 ns case is close to the expected ion energy following the relativistic self focusing and nonlinear acceleration mode, Eq. (4), within a factor of about two where experimental error bars and minor simplifications of the model may be ignored when realizing the several hundred times different result for the ps-case. This also clearly confirms the enormous discrepancy in the preceding measurements (Badziak et al., 1999) with the more than 50-times lower maximum ion energy for ps irradiation than with ns irradiation at the same intensities.

From the numerous details of the present measurements, one may mention also the result that maximum X-ray emission depending on the focusing distance from the gold target appeared for the 0.5 ns laser when the target was 280 μm moved away from the focus at vacuum conditions. This may be explained qualitatively as a plasma-optical process that the <10¹¹ W/cm² laser intensity beam hitting the pre-generated plasma was shrinking initially by ponderomotive self focusing (Hora, 1969) within the sufficiently long time and when reaching the necessary minimum intensity for the relativistic self-focusing going to the diameter of about one wave length necessary for the nonlinear-force acceleration of the Au + 30 ions to the observed MeV energy as in all the numerous cases reported before. This all agrees with the measured slight decrease in the average energy of the thermal plasma on increasing laser intensity of the slow thermal group of plasma in the 0.5 ns case.

The uniqueness of the skin layer acceleration by the nonlinear force can be seen also from the direction of the emitted ions, see Figure 6 in Badziak et al. (2004b). As explained before, the ion acceleration by the nonlinear force after relativistic self focusing goes into all directions similar to the ambipolar acceleration in the hot electron mechanism (Gitomer et al., 1986; Haseroth & Hora, 1996; Hora, 2003) as documented also in the just mentioned figure at ns laser pulse interaction. It there is no relativistic self-focusing and the plane geometry nonlinear force acceleration dominates in the skin layer, the plasma blocks move like pancakes against or with the laser beam with a little sidewise stretch. Exactly this was measured.

Summarizing, Figure 5 shows the essential difference between the skin layer acceleration due to suppression of prepulses, and the usual interaction with generation of a preplasma with subsequent relativistic self-focusing leading to the enormously high laser intensities and subsequent numerous relativistic effects.

Usual interaction of a laser pulse with a target in vacuum (a) where a pre-plasma is produced causing relativistic self-focusing with very high laser intensities in the beam squeezed to about one wave length diameter and subsequent very high energy ion emission. If relativistic self focusing is suppressed (b) by avoiding a pre-plasma at very high contrast ratio (suppression of pre-pulse), plane wave geometry nonlinear force acceleration of plasma blocks in the skin layer appears.