Introduction
The idea of achieving a large thermonuclear gain with a laser or particle beam is to create a hot spot from which a thermonuclear burn wave is launched into still unignited thermonuclear material. It can be traced back to the ignition of large thermonuclear explosive devices where the hot spot is created by soft X rays from an exploding fission bomb (Teller–Ulam configuration). It has been proposed that the creation of a hot spot with a laser or particle beam could be achieved by the implosion of a hollow, or even solid, sphere made from frozen deuterium–tritium (DT). But as the Centurion–Halite experiment at the Nevada Test Site has shown, generating a hot spot in this way would require an energy of at least 50 MJ, much larger than the 2 MJ energy of the laser at the National Ignition Facility (NIF). As an analysis by Kidder (Reference Kidder1998) has shown, even a tenfold increase in energy from 2 to 20 MJ would not be enough. The reason for this problem is the Rayleigh–Taylor instability. Because current lasers have difficulty achieving an output of 50 MJ, several alternative concepts have been explored. One promising approach is the ignition of a target with axial symmetry by a multi-mega-ampere GeV proton beam below the Alfvén limit (Winterberg, Reference Winterberg2014a). This may find an interesting application for fusion micro-explosion nuclear rocket propulsion, using the entire spacecraft as a magnetically insulated GeV capacitor in the high vacuum of space (Winterberg, Reference Winterberg2014b), but all these proposals would still be very expensive.
A promising alternative is to replace the small spherical target with a hollow cm-size double cone, made from a ferromagnet as shown in Figure 1 (Winterberg, Reference Winterberg1977). If this target is brought into rapid rotation to an azimuthal velocity of 1 km/s, at the limit of its tensile strength of ~1011 dyn/cm2, then the general theory of relativity predicts in the co-rotating reference frame, a large negative gravitational field mass in the center of the target by the Coriolis force-field. It gravitationally repels the DT plasma toward the inner wall of the target chamber, with a force equal to the centrifugal force. At the same time, the large temperature gradient in the radial outwards direction results in large electric currents by the thermomagnetic Nernst effect, leading to large magnetic fields radially confining the plasma. In addition, the Coriolis force leads to the establishment of a magnetohydrodynamic generator inside the target chamber with closed magnetic field lines, also axially confining the plasma.

Fig. 1. The fusion fuel contained in the rapidly rotating cylinder, with a laser or particle beam heating and ablatively imploding the cylinder.
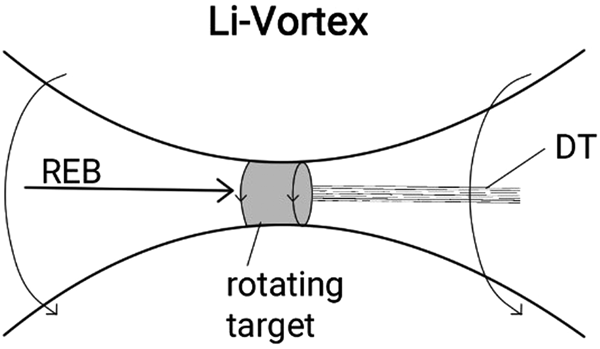
Incorporating this configuration into a working thermonuclear inertial confinement fusion reactor, it is proposed to place the ferromagnetic target made up of a cylinder, filled with DT (Fig. 1), in the center of a liquid lithium vortex tube (Fig. 2), cooling its outer wall and generating tritium by the absorption of neutrons from the DT fusion. The DT is ignited by bombarding the ferromagnetic target with an intense relativistic beam injected into the vortex tube, imploding the target. The implosion leads to the creation of a hot spot from which a propagating thermonuclear burn wave can be launched into a long cylindrical second-stage target place through the other end of the vortex tube. The maximum rotational velocity is obtained from the inequality ρv 2 < σ, ![]() $v\simeq \sqrt {{\rm \sigma} /{\rm \rho}} $, with σ ≃ 1011 dyn/cm2 is the tensile strength of a ferromagnet, and one obtains
$v\simeq \sqrt {{\rm \sigma} /{\rm \rho}} $, with σ ≃ 1011 dyn/cm2 is the tensile strength of a ferromagnet, and one obtains ![]() $v\simeq 1{\kern 1pt} {\kern 1pt} \,{\kern 1pt} {\rm km/s}$.
$v\simeq 1{\kern 1pt} {\kern 1pt} \,{\kern 1pt} {\rm km/s}$.

Fig. 2. The rapidly rotating cylinder is placed in a vortex with a laser or particle beam injected into one end of the vortex to heat and implode the cylinder using additional fuel.
The rotational acceleration of the target must be done by a rotating traveling magnetic wave acting as a small electric motor. After having reached the maximum rotational velocity, the target is ballistically injected into the vortex tube.
In this configuration, three physical principles miraculously work together: Einstein's general theory of relativity, the thermomagnetic Nernst effect, and Elsasser's dynamo theory.
But this is not all. Because of the greatly increased stability of a rapidly rotating target compared with a non-rotating one of spherical symmetry, the 50 MJ minimum ignition energy obtained by the Centurion–Halite experiment can conceivably be reduced to no more than 10 MJ, the value obtained in an early study of relativistic electron beam ignition (Winterberg, Reference Winterberg1968). This is very important because the generation of a 10 MJ electron beam by a Marx generator is orders of magnitude less expensive than the generation of a laser beam of the same energy and power.
Kidder's spherical implosion law and the law for the implosion of a rotating cylinder
Kidder's law is obtained as follows: For an implosion velocity v imp (where for ignition v imp ~ 108 cm/s), and M the mass of density ρ of an imploding spherical mass of radius R, the energy input E for ignition is
for thermonuclear burn in DT one has ![]() ${\rm \rho} R \sim 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm g}/{\rm c}{\rm m}^2$, hence
${\rm \rho} R \sim 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm g}/{\rm c}{\rm m}^2$, hence
but because
where ρ and ρ0 are the final and initial densities reached at R and R 0 the final and initial radii. Hence
or
which means that the ignition energy is very sensitive to the ratio R 0/R, or vice versa, the ratio R 0/R is very insensitive to the energy input and limited to the Rayleigh–Taylor instability.
Repeating the same analysis for a small cylinder of height h, one has
or with M ≅ ρR 2h,
here we have
but for a cylindrical implosion, one has
hence with ρR ≅ 1 g/cm2
which unlike (5) does not depend on R 0/R.
The occurrence of the large negative mass densities in the general theory of relativity
While it is not possible to make a laboratory-size star, it is possible to reach a centrifugal field comparable to the gravitational field of a very dense star, with a density of the same order of magnitude as the density of a neutron star. It is the general theory of relativity (Landau and Lifshitz, Reference Landau and Lifshitz1951) in which the gravitational energy cannot be localized but is described by Einstein's energy-momentum pseudo tensor tik, where the energy and momentum are expressed by a sum of products of Christoffel symbols Γikl, which are the forces. In a non-inertial reference frame, these forces are generally different from zero even in the absence of gravity-producing masses. As it was shown by Hund (Reference Hund1948), for non-relativistic velocities these forces can be obtained by Newtonian mechanics.
In the rotating reference frame inside the rapidly rotating target chamber, the equation of motion for a test particle is given by:
where
is the centrifugal force, and:
the Coriolis force, with ![]() ${\bf \omega} $ the angular velocity vector of rotation. If F is a gravitational acceleration produced by the mass distribution of density ρ as the source of Newton's law of gravity, one has:
${\bf \omega} $ the angular velocity vector of rotation. If F is a gravitational acceleration produced by the mass distribution of density ρ as the source of Newton's law of gravity, one has:
where G is Newton's constant. A centrifugal acceleration is also not free of sources, because of (12) one has
and hence the negative gravitational field mass density
This negative mass is not fictitious and can be felt as the repulsive force in a merry-go-round. For ω = 0.6/s (an example given by Hund), one has ρ = −106 g/cm3, comparable to the positive mass density of a white dwarf star.
The mass density (16) represents a physical reality as the mass density of the electric field E,
While the mass density (17) is positive, because the equal sign charges repel each other, the mass density of a gravitational field g where equal sign masses attract each other, is negative and is
Likewise the mass density of the Coriolis field (13) is
equal to the mass density given by (16). This means the centrifugal force is caused by the negative mass density of the Coriolis force field. By comparison, the negative mass density ![]() $-\,{\bf F}^2/8{\rm \pi} Gc^2$ of the centrifugal force field (12) is smaller by the order v 2/c 2.
$-\,{\bf F}^2/8{\rm \pi} Gc^2$ of the centrifugal force field (12) is smaller by the order v 2/c 2.
Let us compare the negative gravitational field mass density with the positive mass density, ρN = 1014g/cm3, of a neutron star. With ω ≃ v/R 0, where R 0 ≃ 1 cm is the radius of the target chamber and ![]() $v\simeq 1{\kern 1pt} \; {\kern 1pt} {\rm km/s} = {\rm } 10^5{\rm cm/s}$, one finds that
$v\simeq 1{\kern 1pt} \; {\kern 1pt} {\rm km/s} = {\rm } 10^5{\rm cm/s}$, one finds that ![]() ${\rm \omega} = 2.6\; \, \times \,\,10^5{\kern 1pt} /{\rm s}$ and ρ = −1017 g/cm3, absolute three orders of magnitude larger than the mass density of a neutron star.
${\rm \omega} = 2.6\; \, \times \,\,10^5{\kern 1pt} /{\rm s}$ and ρ = −1017 g/cm3, absolute three orders of magnitude larger than the mass density of a neutron star.
In the scientific literature little can be found about the fundamental importance of the Coriolis force in rotating plasmas. However, there are two references, one made by the author (Winterberg, Reference Winterberg1963), to an experimental verification of Elsasser's dynamo theory in rotating liquid metals, and the work by Haverkort and de Blank (Reference Haverkort and de Blank2012).
Nernst effect
In the proposed concept, the plasma is confined by the outwardly directed gravitational force of the negative mass of the Coriolis field, and by the inwardly directed magnetic force from the wall of the target chamber, by the Nernst effect.
With the temperature gradient ![]() $\nabla T$ from the cold wall into the hot plasma and B the magnetic field, the thermomagnetic current by the Nernst effect is for a hydrogen plasma given by Spitzer (Reference Spitzer1962):
$\nabla T$ from the cold wall into the hot plasma and B the magnetic field, the thermomagnetic current by the Nernst effect is for a hydrogen plasma given by Spitzer (Reference Spitzer1962):
with the magnetic force density of the plasma:
or with ![]() $\nabla T$ perpendicular and B parallel to the wall
$\nabla T$ perpendicular and B parallel to the wall
With the magnetohydrodynamic equilibrium condition
where ![]() $p = 2nkT,\; \nabla p = 2nk\nabla T + 2kT\nabla n$, one has
$p = 2nkT,\; \nabla p = 2nk\nabla T + 2kT\nabla n$, one has
which upon integration yields
In a cartesian x, y, z coordinate system with the cold wall at z = 0, and the magnetic field B into the x-direction, the Nernst current density j is in the y-direction, and is
From Maxwell's equations ![]() $4{\rm \pi} {\bf j}/{\rm c} = {\rm curl\;} {\bf B}$ one has
$4{\rm \pi} {\bf j}/{\rm c} = {\rm curl\;} {\bf B}$ one has
Eliminating ![]() ${\bf j}_y$ from (26) and (27) one obtains
${\bf j}_y$ from (26) and (27) one obtains
If in the plasma far away from the wall n = n 0, T = T 0, one has from (25)
Inserting this into (28) one finds
With the boundary condition B = B 0 at z = 0 and T = T 0 at z = ∞, integration of (30) yields
The meaning of (31) is that the magnetic pressure ![]() ${\bf B}_0^2 /8{\rm \pi} $ exerted on the plasma from the wall surface at z = 0 balances the plasma pressure 2n 0kT 0 at z = ∞. With n 0 = 1023/cm3 and T ≃ 108 K, one finds that B 0 ≃ 107 Gauss.
${\bf B}_0^2 /8{\rm \pi} $ exerted on the plasma from the wall surface at z = 0 balances the plasma pressure 2n 0kT 0 at z = ∞. With n 0 = 1023/cm3 and T ≃ 108 K, one finds that B 0 ≃ 107 Gauss.
With the Nernst effect, where according to (25) Tn 4 = constant, the bremsstrahlung losses going in proportion to ![]() $n^2\sqrt T $ (Spitzer, Reference Spitzer1962) are constant across the entire plasma, which for nT = constant would near the wall rise in proportion to T −3/2. The reason are the large thermomagnetic currents set up in between the hot plasma and the cold wall of the target, leading to a large magnetic force repelling the hot plasma from the wall.
$n^2\sqrt T $ (Spitzer, Reference Spitzer1962) are constant across the entire plasma, which for nT = constant would near the wall rise in proportion to T −3/2. The reason are the large thermomagnetic currents set up in between the hot plasma and the cold wall of the target, leading to a large magnetic force repelling the hot plasma from the wall.
For the working of the Nernst effect one must have
Where ω is the electron cyclotron frequency and τ is the electron–ion collision time. At high magnetic fields of the order B ≃ 107 G and temperatures of the order 108 K, with a particle number density n ≃ 1023/cm3, one has ω ≃ 1014/s1, τ ≃ 10−9s (Spitzer, Reference Spitzer1962) and hence ωτ ≃ 105 ≫ 1.
Magnetohydrodynamic dynamo in the target chamber
A magnetohydrodynamic dynamo is ruled first by the equation (generalized Ohm's law in cgs units)
where σ is the electrical conductivity, second, by the Euler equation of motion with the magnetic body force (1/c) j × B where j is the electric current density, neglecting viscous forces, and is given by
in addition to the equation of continuity (mass conservation) and energy. For a uniform rotation, one can write
where ω = (1/2)curlv with (4π/c)j = curlB, one thus has for (34)
Even without solving these equations, a general conclusion can already be drawn: For the buildup of the magnetic field by (33) one must have ∂B/∂t >0, which requires that the second term on the r.h.s of (33) is larger than the first term, or that the magnetic Reynolds number:
where ![]() $R\simeq 1{\kern 1pt} \,{\rm cm}$ is the radius of the target chamber and v the plasma velocity. Instead of (37) one can also write
$R\simeq 1{\kern 1pt} \,{\rm cm}$ is the radius of the target chamber and v the plasma velocity. Instead of (37) one can also write
or that
Setting v = 105 cm/s for the tangential velocity of the target chamber, one finds that σ ≳ 2.5 × 1013/s. On the other hand, the conductivity of a fully ionized plasma for T ≳ 10⁵ K is
which means that for T ≳ 10⁵ K, one has σ ≳ 3 × 1014/s, or that for T ≳ 10⁵ K, σ is larger than the r.h.s. of (39).
With the plasma accelerated by the magnetic forces to a velocity of the order v ~ 10⁸ cm/s, (33) can be approximated extremely well by
The magnetohydrodynamic instabilities arise from the last term on the r.h.s. of (36), at the moment when the magnetic forces overwhelm the fluid stagnation pressure or when B 2/8π ≥ (1/2)ρv 2. For (1/2)ρv 2 ≫ B 2/8π, the magnetic lines of force align themselves with the streamlines of the fluid flow. Then, if likewise the electric current flow lines j align themselves with ω, one has j orthogonal to B, and ω orthogonal to v. With ω = (1/2) curlv and j = (c/4π)curlB one can write for (1/2)ρv 2 ≫ B 2/8π, that
or
where
is the Alfvén velocity. B will eventually reach the value ![]() $B = \sqrt {4{\rm \pi \rho}} v$, where v = v A. In approaching this magnetic field strength, the magnetic pressure forces begin to distort the fluid flow which becomes unstable. In a plasma this leads to the formation of unstable pinch current discharges, where p = B 2/8π. For a hydrogen plasma of temperature T and particle number density n this leads to the Bennett equation
$B = \sqrt {4{\rm \pi \rho}} v$, where v = v A. In approaching this magnetic field strength, the magnetic pressure forces begin to distort the fluid flow which becomes unstable. In a plasma this leads to the formation of unstable pinch current discharges, where p = B 2/8π. For a hydrogen plasma of temperature T and particle number density n this leads to the Bennett equation
The pinch instability can be seen as the breakdown of the plasma into electric current filaments, determined by the B × curlB term, whereas the v × curlv term is responsible for the breakdown of the plasma in vortex filaments. But while the breakdown into current filaments is unstable, the opposite is true for the breakdown into vortex filaments. This can be seen as follows: Outside a linear pinch discharge one has curlB = 0, and outside a linear vortex filament one has curlv = 0. Because of curlB = 0, the magnetic field strength gets larger with a decreasing distance from the center of curvature of magnetic field lines of force. For curlv = 0, the same is true for the velocity of a vortex line. But whereas in the pinch discharge a larger magnetic field means a larger magnetic pressure, a larger fluid velocity means a smaller pressure by virtue of Bernoulli's theorem. Therefore, whereas a pinch column is unstable with regard to its bending, the opposite is true for a line vortex. This suggests that a pinch column places itself inside vortex tube.
What is true for the m = 0 kink pinch instability is also true for the m = 0 sausage instability by the conservation of circulation
And because of the centrifugal force the vortex also stabilizes the plasma against the Rayleigh–Taylor instability.
In the proposed configuration, the plasma is radially confined between the convex centrifugal force in the target, and the concave centripetal magnetic force set up by the thermomagnetic current at the cold wall inside the target. According to Einstein's equivalence principle, the ions and electrons are affected by the centrifugal force in the same way as by the gravitational force in a star, having a stable configuration, but an instability may still arise in the thin boundary layer carrying the thermomagnetic current near the wall of the centrifuge. As Teller has pointed out in a private communication (Reference Teller1969), the instabilities of magnetic confinement configurations are likely to be absent in collision-dominated plasmas, or in plasmas where the mean free path λ is smaller than the linear dimension L of the magnetic confinement configuration. At the temperature T [K] and particle density n, the mean free path is likely given by
For n ≃ 1018/cm3 and T ≃ 108 K, one has λ ≃ 10−2 cm ≪ R ≃ 1 cm. This means that in this range of densities and temperature, the plasma is collision-stabilized.
In the past, rotating plasmas have been extensively studied by (Lehnert, Reference Lehnert1971), but only for densities where the plasma is not “collision dominated.” The proposed novel nuclear fusion concept is unique because it makes use of the self-exciting magnetohydrodynamic dynamo driven by the heat released from thermonuclear reactions in the fusion plasma. But it also has the potential to reach much larger magnetic fields for confinement and particle number densities than are otherwise possible.
This leaves open the question of how to remove heat from the target, even though this problem exists only for the 20% of fusion energy released in the target as charged particles, not for the 80% of the energy going into the kinetic energy of the neutrons, which can be slowed down outside the target over a much larger distance. One possible answer is to place the target in a supersonic potential gas vortex, for example, a vortex of helium gas, with the high velocity vortex core touching the outer surface of the target as a velocity of ~1 km/s, the tangential velocity of the target, with the vortex flow cooling the fusion target.
Ignition
The ignition is achieved by a <50 MJ pulse of an intense relativistic electron beam as it was originally proposed by the author in his 1968 paper published in the Physical Review (Winterberg, Reference Winterberg1968), except that here the beam stopping does not depend on the difficult to achieve two-stream instability, because for MeV electrons the stopping range is determined in the ferromagnetic mantle of the target, which implodes the target. This stopping range is given by (Winterberg, Reference Winterberg2010):
Where ρ is the target density in g/cm3, and E is the electron energy in MeV. For ρ ≃ 10 g/cm3 and E ≃ 10 MeV, one obtains λ ≃ 1 cm, about equal to the linear dimension of the target.
With 10 MJ ≃ 1014 erg, deposited in a volume ![]() $V\simeq {\rm \pi} R_0^2 h \gt 1\,{\kern 1pt} {\rm c}{\rm m}^3$, the temperature given by E ≃ nkT, with n ≃ 1023 particles/cm3, is T ≃ 106 K. The threefold implosion of the DT from
$V\simeq {\rm \pi} R_0^2 h \gt 1\,{\kern 1pt} {\rm c}{\rm m}^3$, the temperature given by E ≃ nkT, with n ≃ 1023 particles/cm3, is T ≃ 106 K. The threefold implosion of the DT from ![]() $R\simeq h\simeq 1{\kern 1pt} $ to
$R\simeq h\simeq 1{\kern 1pt} $ to ![]() $R\simeq h\simeq 0.3{\kern 1pt} \,{\rm cm}$ increases its temperature by the factor of 100, from T ≃ 106 to T ≃ 108 K, meaning T would reach the ignition temperature of the DT reaction at T ≃ 108 K.
$R\simeq h\simeq 0.3{\kern 1pt} \,{\rm cm}$ increases its temperature by the factor of 100, from T ≃ 106 to T ≃ 108 K, meaning T would reach the ignition temperature of the DT reaction at T ≃ 108 K.
Conclusion
While the ignition of a large thermonuclear explosive device with a fission bomb trigger has been achieved more than 50 years ago, the non-fission ignition of thermonuclear micro-explosions is still awaiting its realization. The advent of powerful lasers raised the hope that this could be done by the spherical implosion of a small amount of DT with a powerful laser. However, experiments done at the Nevada Test Site (Centurion–Halite experiment) have shown that this would require a laser energy of about 50 MJ, 25 times more than the 2 MJ delivered by the laser of the NIF, currently the most powerful laser in the world. The analysis by Kidder (Reference Kidder1998) has shown that even a tenfold increase of the laser energy from 2 to 20 MJ would be insufficient. The reason for this problem is the Rayleigh–Taylor instability of spherical implosions. The replacement of lasers by high-voltage pulse power technology for the generation of charged particle beams, proposed by the author in 1964–1968 (Winterberg, Reference Winterberg1968), can reduce this problem, but so far has also failed to reach the ignition of a small thermonuclear target. In either case the idea is to create a hot spot, from which a thermonuclear detonation wave can be launched into still unburnt DT.
Because of the difficulty of creating a hot spot by the radial implosion of a DT sphere, it is proposed here to replace the sphere with a small, rapidly rotating conical target with the DT encased in a target made of ferromagnetic material. This target would have to be rotationally accelerated by an externally applied circular magnetic traveling wave to a velocity of 1 km/s at the limit of the tensile strength of the ferromagnetic material, about equal to 1011 dyn/cm2.
The importance of such a configuration is a consequence of Einstein's general theory of relativity. In a reference system at rest with the rotating cylinder, it leads to a large, negative gravitational field mass from the Coriolis field. In such a configuration, a DT plasma is stably confined by the magnetic field of the thermomagnetic Nernst effect. In the presence of the strong Coriolis field, it acts as a powerful magnetohydrodynamic generator, axially confining the DT plasma. And because of the short stopping length of relativistic electrons in the ferromagnetic material, a 10 MJ intense relativistic electron beam can radially implode the rotating target, circumventing the Rayleigh–Taylor instability. With the DT plasma reaching ignition temperature, it can thus serve as a hot spot for the high gain release of fusion energy.
If experiments can establish the feasibility of this idea, it would imply the large-scale release of energy from nuclear fusion and lead to a breakthrough in developing a nuclear propulsion system without fission products for the manned exploration of the Solar System.
Appendix
In Einstein's general theory of relativity, the motion of a test particle is given by the geodesic equation
where
In the limit of velocities small compared with the velocity of light, (A.1) is reduced to (11). It was shown by Hund (Reference Hund1948) that in this approximation the energy (mass) density of the Coriolis force field obtained from Einstein's energy-momentum pseudotensor must be equal to (19).