1. INTRODUCTION
Interaction of an ultrashort laser pulse with metal surface leads to a
rapid increase in electron temperature, whereas the thermalization between
electron and ion subsystems occurs on a substantially longer time-scale
(Anisimov et al., 1967, 1974). At laser intensities of 1012 to
1015 W/cm2, for pulse duration of a few tens of
femtoseconds, electron temperature Te
typically reaches 1 to 100 eV, while ions remain essentially cold in the
duration of the laser pulse. In that situation, a significant
redistribution occurs of electrons by their energy states. The ensuing
modification of electron charge distribution and lattice potential may
facilitate ultrafast melting, or even result in a nonthermal melting of
the irradiated material. Ultrafast and/or nonthermal melting
facilitated by depopulation of covalent-bonding orbitals was observed in
several semiconductors (Shank et al.,
1983; Tom et al., 1988; Saeta et al., 1991; Sokolowski-Tinten et
al., 1995, 1998;
Siders et al., 1999; Cavalleri et al., 2001; Lindenberg et al., 2005), C (Reitze et al., 1992), and Ga (Uteza et al., 2004), see review by Bennemann
(2004). Ultrafast melting phenomenon was
extensively studied theoretically (Stampfli &
Bennemann, 1992; Rethfeld et al., 2002, 2004), and reproduced
in molecular dynamics simulations (Silvestrelli et
al., 1996; Gambirasio et al.,
2000; Jeschke et al., 2001;
Dumitrica & Allen, 2002). Softening of
phonon modes was observed in Te (Hunsche et
al., 1995) and Bi (DeCamp et al.,
2001). Ultrafast thermal melting of Te was observed in (Ashitkov et al., 2002). Significant
reflectivity increase on a subpicosecond time-scale, incompatible
with Drude model and interpreted as melting, was detected in W (Wang & Downer, 1992). For self-absorption
measurements or short-delay pump-probe absorption measurements, caution
must be exercised to discriminate between suppression of interband
absorption in a solid metal and an ultrafast melting of the metal (Fisher et al., 2002).
Transient increase in Al reflectivity at 800 nm pumping/probing
wavelength was observed by Guo et al. (2000) in pump-probe experiments. Difference in target
damage effect from 800 nm and 400 nm wavelength pulse was also reported
ibidem. An increase in Al reflectivity at 800 nm wavelength, and
absence of such increase at 400 nm wavelength, were observed by Fisher
et al. (2002) in self-absorption
experiments. Two alternative explanations for the experimental findings
were provided in these works. Guo et al. (2000) suggested a nonthermal melting of Al, associated
with pumping of a bonding-to-antibonding-state interband transition, as an
explanation for their experimental results. This hypothesis was further
investigated by Youn et al. (2004).
Fisher et al. (2002) have, on the other
hand, suggested an electron impact broadening of the interband absorption
peak, without a loss of crystalline order, as an explanation for their
experimental results. The fact that the increase in Al reflectivity at 800
nm was observed by Fisher et al. (2002)
to occur on a time-scale of about 50 fs or shorter, at modest laser
intensities, agrees with the impact broadening hypothesis, but can hardly
be explained by a nonthermal melting. The controversy was eventually laid
to rest by the experimental findings of Siwick et al. (2003) that rule out the nonthermal melting hypothesis
of Guo et al. (2000). In Siwick et
al. (2003) the melting of Al heated by a
laser pulse of 800 nm wavelength was found to occur thermally, on a
picosecond time-scale.
As the electron temperature increases, the electron-electron (e-e) and
electron-ion (e-i) energy and momentum relaxation times characteristic of
a periodic-lattice electron behavior must be replaced continuously by the
relaxation times characteristic of a nonideal-plasma electron behavior.
Although that transition was expected in theory (Lee
& More, 1984; Mott, 1990) and
observed in experiment (Milchberg et al.,
1988; Ng et al., 1994; Price et al., 1995), the details of
mechanism, conditions and time-scale of metal-to-plasma electron
transition are not known. In the present work we attempt to fill this
gap.
It is generally accepted that the exceedingly large probabilities for
elastic electron collisions at Te ∼
TF (where TF is
Fermi temperature), at solid metal densities, result in electron mean free
path (MFP) with respect to longitudinal momentum relaxation being of the
same order as the typical interionic distance a. The electron
longitudinal momentum relaxation rate ν is then approaching
ue /a, where
ue is the characteristic electron velocity.
This is the resistivity saturation (also referred to as minimal MFP,
minimal conductivity, or Ioffe-Regel) regime (see Chapter 1.6.3 in Mott, 1990). However, very little is known on the
details of this transition: how the e-ph interaction is replaced by e-i
interaction, how the Umklapp electron-electron scattering dies out, and so
on. Also, the details of the transition from (a relatively low) e-ph
energy exchange rate to (a relatively high) e-i energy exchange rate, as
well as the actual mechanism(s), Te values,
and time-scales on which this transition occurs in various metals remained
largely unknown until recently or until now. Attempts to evaluate
theoretically the e-i energy exchange rate in a solid target with
Te ∼ 1 − 100 eV and
Ti < 1 eV have lead, under different
approximations, to results varying by well over an order of magnitude for
the same conditions (Dharma-wardana & Perrot, 1998, 2001; Hazak et al., 2001; Gericke et al., 2002). The key to
understanding the e-i energy exchange physics, under the conditions
considered is, again, the knowledge of the details of mechanism,
conditions, and time-scale of the gradual transition in the conductivity
electron properties from nearly-free-electron (NFE)-like to
strongly-coupled-plasma-like. As we explain below, this gradual transition
involves usually not only the conductivity electrons, but rather the
core-state electrons as well.
This work is structured as follows. In Section 2 we consider the
mechanisms for lattice periodicity breakdown and for gradual transition
from metal-like to plasma-like electron behavior (electron metal-to-plasma
transition, eMPT) in metal targets subjected to an ultrashort radiative
energy deposition. In Sections 3 to 5, we study in detail the core-state
electron impact ionization and three-body (Auger) recombination processes
which, as we show, dominate the eMPT in most metals. In Sections 6 to 9,
we demonstrate the important differences in eMPT mechanisms between
various metallic elements. Three distinct categories of normal metals are
found with respect to detailed mechanisms of eMPT under ultrashort laser
irradiation. Metals with relatively deep-lying weakest-bound core states
(Li, Be, Na, Mg, Al, K, Ca) form the first category.
“Relatively” here is defined by comparison with the Fermi
energy value in the metal under consideration. Metals with relatively
shallow-lying weakest-bound core states (Zn, Cd, Sn, Pb) form the second
category. Noble metals Cu, Ag, Au, in which d-band states localize with
increasing electron temperature (Fisher et al., 2004, 2005a), form
the third category. Transitional metals and semimetals are not considered
in this work, and will be considered separately. Energy exchange rate
between electron and ion subsystems is discussed in Section 7.
We use cgs units in all expressions. In the text, values of particle
energies and temperatures are given for convenience in units of
electron-volt rather than, respectively, erg or Kelvin.
2. PERIODICITY BREAKDOWN
Fundamental differences exist between electronic properties of a metal
and electronic properties of a plasma, at the same ion number density and
temperature. Electron transport properties and electron-ion energy
exchange rate in metal are governed by lattice periodicity effects on
(quasi-) electron states, so that the energy and momentum exchange occurs
between collective perturbations of conductivity electron distribution
(quasielectrons), and ion distribution (phonons). In plasma, on the other
hand, energy and momentum exchange can be described as occurring between
individual electrons and ions, in pair collisions, with an environment
providing merely a screening background. The key to the transition from
quasiparticle to individual-particle picture lies in the relation of the
quasiparticle decay rate (in energy units) to the quasiparticle energy.
For the quasiparticle picture to be valid, the former must be much smaller
than the latter (Abrikosov, 1972). In other
words, periodic-lattice electron behavior breaks down and eMPT occurs when
(quasi-)electron total collision frequency, in energy units, is no longer
much smaller than the electron Fermi energy.
There are five mechanisms by which the periodic-lattice behavior of
conductivity electrons can break down in femtosecond laser-matter
interaction. The mechanisms are as follows.
(1) Ultrafast isochoric melting. In metals irradiated by an ultrashort
laser pulse the melting may occur either with an expansion of the free
surface of the target (heterogeneous melting), or, provided the
overheating of the solid is substantial, isochorically (homogeneous
melting), see (Rethfeld et al., 2004).
The mechanism we consider in this paragraph is the isochoric, homogeneous
melting; lattice disordering mechanisms involving the free surface are
outlined in paragraph (5) below. In NFE metals, homogeneous melting occurs
as a result of energy transfer from electrons (they are heated by laser
radiation) to lattice ions. As mentioned in the Introduction, in non-NFE
metals and in semiconductors the thermal redistribution of electrons over
energy levels changes the spatial charge distribution in the lattice and
leads to weakening of covalent bonding. The weakened bonding facilitates
ultrafast thermal melting. The spatial charge redistribution can induce
non-thermal melting in not closely packed lattices. For NFE metals, on the
other hand, conductivity electron spatial distribution is much closer to
uniform even at low temperatures. Then, a shift of an ion from its
equilibrium lattice location occurs on the time scale of one or few phonon
periods, 102-103 fs, after isochoric melting ion
temperature has been reached. It is important to stress that melting alone
does not produce an eMPT. It is well known that a room-pressure isobaric
equilibrium melting of a metal does not destroy a short-range lattice
order, and thus produces only a modest increase in ν across the
melting point. Relation ν << ue
/a certainly remains valid. Laser-induced ultrafast isochoric
melting occurs at higher ion temperatures and may have a stronger effect
on the short-range order, eliciting stronger increase in ν. Still, an
eMPT can not be produced by melting alone; the joint action of some (or
all) of the mechanisms listed below is required.
(2) Charge disorder (Fisher et al., 2004, 2005a).
Ionization of localized core states (in simple metals) or localization of
d-band states (in noble metals) with increasing
Te produce ions in a variety of ionization
stages occupying individual lattice sites. Ions remain positioned at their
lattice sites (at least for some time, estimated to be of the order of 100
fs), but their charge states vary from site to site in a random fashion.
Lattice translational symmetry is thus lost even though the geometric ion
ordering persists. This is a solid plasma, a charge-disordered solid
state. At comparable abundances of two or more different ionization
stages, the loss of short-range order is complete. Individual impact
ionization events occur on a time-scale of the knocked-out electron
evacuation from its parent ion potential well, that is,
a/ue ∼ 0.1 fs. However,
charge disorder emerges only when the abundance of the next ionization
stage becomes significant ([gsim ]1%). It may take ∼1 to 100 fs,
depending on ionization rate, after Te
reaches sufficiently high values (1 to 20 eV). The details of this
mechanism are considered in the Sections 3 to 9.
(3) Reduction in conductivity electron MFP due to the increasing
collision rate. A typical linear size L of an electron
wave-packet envelope can not significantly exceed the MFP. The MFP, and
thus L as well, can become as small as a, thereby
destroying Bloch state structure. For ν this phenomenon produces
resistivity saturation. The values of ν and L are determined
by Te and, at Te
[lsim ] 1 eV, also by an ion temperature Ti
(Fisher et al., 2002). In absence of
charge disorder, resistivity saturation occurs usually as
Te approaches Fermi temperature (Milchberg et al., 1988; Price et al., 1995; Fisher
et al., 2002). Time scale for electron MFP reduction is
given by the inverse of the electron total collision frequency, which is
sub-femtosecond in the vicinity of resistivity saturation regime. Time
scale on which Te changes is significantly
longer in most cases, and determines therefore the resistivity saturation
onset time.
The three aforementioned mechanisms can operate equally well in the
metal bulk and on the metal surface, as they involve neither ion density
change nor deviation from a local charge neutrality. There exist another
two mechanisms that can affect the metallic electron properties of the
target. Those two mechanisms involve explicitly the free target
surface.
(4) The local breach of charge neutrality due to the escape of fast
electrons from the target surface into the void, and the associated
production of strong electric and magnetic fields (Gamaly et al., 2002). The effect of the
strong surface fields on the electron states and transport inside the
target, in the laser intensities range considered here (1012
− 1015 W/cm2), remains largely
uninvestigated as far as we know.
(5) An anisotropic expansion of the surface target layers normally to
the free surface of the target (Eliezer, 2002,
2005; Eidmann et
al., 2000). This expansion is driven by the thermal pressure
of conductivity electrons heated by the laser radiation absorption to
temperatures of a few electron-volts or few tens of electron-volts.
Estimates in Fisher et al. (2002) show
that the typical time-scales for this effect, under our conditions, are in
order of
,
where δ is skin layer thickness, and Mi
is ion mass.
In this work we only concentrate on the “bulk,” isochoric
mechanisms (1)–(3). As we said in the Introduction, ultrafast
melting mechanism (1) is important in semiconductors. Charge disorder
mechanism (2) and electron MFP reduction mechanism (3) are dominant in
simple metals. Furthermore, we show that there are two alternative
pathways to charge disorder, one realized by ionization of the core states
and the other realized by localization of the d-band states of noble
metals. After the initial isochoric stage, which lasts several tens or
hundreds of femtoseconds, expansion of the heated layers into the void can
no longer be neglected, and mechanism (5) becomes important in most
systems.
3. IONIZATION OF CORE STATES AND CHARGE
DISORDER
Charge disorder in normal metals is produced by ionization of
localized core electron states. First we consider metals with core states
lying at least several eV below the bottom of the conductivity band. Noble
metals (Cu, Ag, Au), in which the d-band energy lies above the bottom of
the conductivity band but below the Fermi level, or metals with core
states or d-band located close to the bottom of the conductivity band (Zn,
Cd, Sn, Pb), are considered in Sections 8 and 9. The charge disordering
mechanism is more complicated in those metals.
Both in metals and in plasma the ionization of a bound electron state
can occur either by a free electron impact or by photon absorption. At the
laser intensities relevant to this work (below 1015
W/cm2) multiphoton ionization of core states can be
neglected; therefore, for photon energies below the photoionization
threshold (optical laser), the only ionization channel is the electron
impact ionization (EII) of core states by sufficiently energetic
conductivity electrons. For a vacuum-ultraviolet free electron laser (see,
e.g., Lee et al., 2002; Ke Lan & Meyer-ter-Vehn, 2004; Alesini et al., 2004), or any other source of
high-intensity femtosecond/attosecond radiation pulses with photon
energies above the core state photoionization threshold in the irradiated
sample, both EII and photoionization channels must be accounted for.
Finally, in a solid matter bombarded by an intense energetic ion beam
(either laser or accelerator produced, see e.g. Malka
& Fritzler, 2004; Hoffmann et al.,
2005), dynamics of isochoric transition from an ordered solid to a
high-energy-density matter is of significant interest. There, on
sufficiently short time scales, both charge disordering due to interaction
with projectile ions and charge disordering due to EII by hot electrons
are expected.
4. IONIZATION OF CORE STATES BY CONDUCTIVITY
ELECTRON IMPACT
Here we restrict ourselves to consideration of only the
shallowest-lying (weakest-bound) core states of any ion, as core hole
abundances even lower than one per ion are already sufficient for the
eMPT. Core states considered have binding energies in the range of 15 to
100 eV, depending on the chemical element. Deeper-lying core states are
not affected under present conditions. Zero of energy is chosen at the
bottom of conductivity band, so that the core states have negative energy
(i.e., positive binding energy Eb), and
conductivity electron states have positive energy. An EII event occurs
when a sufficiently energetic conductivity electron collides with a
core-state electron, with energy transfer in the collision exceeding the
core state binding energy. Final states of both electrons belong then in
conductivity band, and an ionization degree of the parent ion increases by
unity.
As the gradual eMPT is what we are ultimately interested in, we must
develop a unified description for EII events (their
cross-section, probability, and rate) in metal and in plasma. To the best
of our knowledge, this was never carried out. The weakest-bound core state
in metal is equivalent to an optical electron state of a plasma ion, and
the NFE conductivity-band states in metal are equivalent to free electron
states in plasma. The core state binding energy in metal is therefore
measured relative to the bottom of the conductivity band. Due to
density-dependent screening effects, the binding energy for the same ionic
state in metal and in dilute plasma differ (see, for example, Johansson & Martensson, 1980). The EII cross
section must be scaled to the correct binding energy (Salzmann, 1998). The appropriate expression for the
EII cross-section σEII(E), where
E is the incident electron energy, is presented at the end of
this Section. For now, it is sufficient to state that
σEII(E) is a smooth finite non-negative
function of E, and
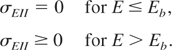
This presumes the absence of excitons in metal under conditions
considered here.
To evaluate the probability (per second) P of ionization of a
core state in a single ion, we use
where Ne is the number density of
conductivity electrons, u(E) is the incident electron
velocity, and the average 〈〉 is over the conductivity electron
energy distribution. Π is a Pauli blocking factor accounting for
reduction in P due to the significant probability of the electron
final state(s) being occupied. The conductivity band is assumed parabolic
in the extended zone scheme,
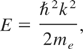
with k denoting the (quasi)electron momentum, and with the
(quasi)electron mass equal to a free electron mass. Then,
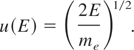
The averaging in Eq. (2) is over the energy distribution
g(E) f (E) of the incident
electron,
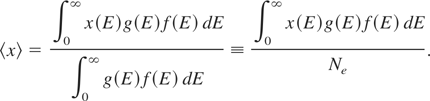
Here
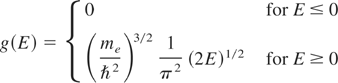
is the conductivity electron density of states (in units of [1
/ erg cm3]) in a NFE band with dispersion relation
(3), and
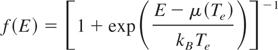
is the Fermi-Dirac distribution function, where
kB is Boltzmann constant, and μ is
electron chemical potential. The values of
μ(Te) are determined implicitly by the
identity
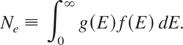
The EII event is only possible when the final states are vacant for
both electrons involved. In contrast to a classical plasma, in
nonclassical plasma or in metal the probability for the final states to be
vacant may be low. Therefore, in the average (in right-hand side of Eq.
(2)) a Pauli blocking factor 0 < Π(E −
Eb) < 1 is included, and the expression
for EII rate becomes
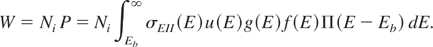
We estimate the blocking factor Π(E −
Eb) in the following way. The total energy of
the two electrons in the final state is E −
Eb > 0. The probability to find the final
state vacant decreases nearly exponentially as the energy of one of the
final states decreases. Thus, the most favorable scattering event with
respect to both final states being vacant is the scattering in which final
energy of both electrons is approximately equal, each one being given then
by (E − Eb)/2. Hence, the
factor Π(E − Eb) may be
approximated by
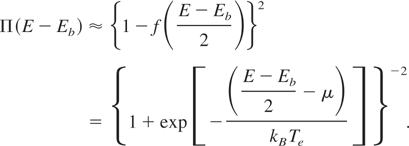
It approaches unity, of course, as E increases. It also
approaches unity for any E at large
Te due to a drop in
μ(Te). In a
low-Te limit,
kBTe <<
μ, Eq. (10) is straightforward to derive; this is done by assuming any
realistic form of differential EII cross-section
dσ/dε (where 0 ≤ ε ≤ E
− Eb is the energy of ejected electron)
and integrating over ε. A prefactor close to unity appears then in the
low-Te limit of the right-hand side of (10).
The prefactor depends on E, Eb,
μ, as well as on the details of the functional form of
dσ/dε. Most important, however, it does
not depend on Te. We neglect the
said prefactor altogether.
We note that Ne does not appear
explicitly in Eq. (9). Instead, it enters implicitly through the value of
μ(Te), which appears in Eq. (7) for
f (E). In classical plasmas f (E)
<< 1 for all E ≥ 0. In that limit we find
Π(E − Eb) ≈ 1 for all
E ≥ Eb, and f
(E) ≈ exp[(μ −
E)/kBTe].
Using the nondegenerate free-electron asymptote
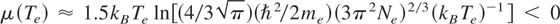
one finds f (E) ∼
NeTe−3/2
exp(−E/kBTe),
hence the familiar explicit factor Ne in EII
probability in classical plasma.
In the above model for P, the use of a constant value for
Eb is only justified as long as the depletion
of the core state is not too large (say, no more than 10% vacancies
abundance in the core state; for example, no less than 5.4 electrons on
average per ion in the 2p state of Al). The abundance of holes (vacancies)
in a core state is defined here as a ratio of the number of vacant
electron states to the total number of electron states. At larger vacancy
abundances, the reduction in nucleus screening for the remaining core
electrons becomes important and Eb increases.
This effect can be accounted for in equilibrium, by the following
extension of the model. The equilibrium core hole abundance
h(Te) is evaluated by including a
narrow core state in the density of states, Eq. (6), and recalculating the
chemical potential from Eq. (8) with Ne now
including the core electrons as well; then h = 1 −
f (−Eb). Values of
Eb(Te) may be
found using INFERNO model (Liberman, 1979, 1982).
For a laser pulse not much longer than the typical equilibration
times, on the other hand, the equilibrium number of vacancies in the core
state is not reached, and the core states are thus overpopulated for the
given Te (i.e., actual vacancy abundance is
lower than h). In the nonequilibrium case it is possible to solve
rate equations for h, and to use
Eb(h) as above; such a procedure,
however, is beyond the scope of the present work. The hole population
equilibration time is estimated in Section 6.
The following point must be clarified. Since the core state is
localized, not all ions have the same number of core electrons.
Consequently, the notion of
Eb(Te) is
meaningful only in the average sense, as explained in the Appendix of
Liberman (1979). Simply put, ions with
K = 1,…,q electrons in the core state have
different binding energies EbK of the core
state. The smaller is K, the larger is
EbK. The average
Eb(Te) increases
with Te following the shift in the ionization
composition of the matter, so that
Eb(Te) is not
far from EbK for the dominant K
value at any given Te. Due to the dependence
of free-electron screening on free electron density and temperature, all
EbK are also functions of
Te. However, the
Te dependence of
EbK is significantly weaker than the
Te dependence of the average
Eb(Te). As we
already said, core-hole ion (K = q − 1) abundance
∼1% in metal is sufficient to produce the charge disorder and the
ensuing eMPT. Thus, for normal metals below we assume
Eb = Ebq, that
is, binding energy is that of an electron in a fully occupied core state,
unless explicitly stated otherwise. For noble metals the situation with
the d-band energy is different, see Section 8.
Let us now turn to the determination of an appropriate expression for
σEII(E). In a single ion, the
cross-section for a direct EII event may be approximated by Lotz
formula,
see e.g., Pal'chikov and Shevelko (1995). Here a0 is Bohr radius,
q is the degeneracy of the core state, and Ry = 13.6 eV
is the binding energy of a ground state of an isolated hydrogen atom. Lotz
formula was obtained semi-empirically to fit the EII cross-sections
measured for multiply charged ions. It was later found to be applicable to
majority of direct EII cross sections in dilute ideal plasmas (including
EII of weakly charged ions and EII from inner shells) (Griem, 1997). However, Lotz formula in its original
form is inapplicable to either metals or dense plasmas. It does not
account for the screening of a momentum transfer between electrons in a
dense conducting medium. It also does not account for the difference in
low-energy conductivity electron wave functions between a condensed matter
and a dilute plasma. The latter problem is especially acute for low
projectile energy values, E ≈ Eb.
The E/Eb >> 1
nonrelativistic asymptotic (Bethe) form of Eq. (11) is applicable to an
atom in dense medium as well as to an atom in dilute plasma. The screening
effect of the medium becomes important either in relativistic limit (Fermi, 1940; Sternheimer &
Peierls, 1971; Inokuti & Smith, 1982)
which is not considered here, or for
(see, for example, Nozieres & Pines (1959)
and Murillo & Weisheit (1998)). In most
metals, the plasma frequency ωpe obeys
ħωpe [lsim ]
Eb. Thus, both the screening and the
continuum wavefunction modification by the dense medium necessitate the
amendment of Eq. (11) at the low (near-threshold) projectile energies,
E ∼ Eb. Under present
conditions, the σEII values in medium tend to be
lower than for an individual ion. We introduce, therefore, an empirical
correction factor (1 − Eb
/E)Y into the EII cross-section,
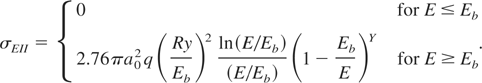
Here Y > 0 is a fitting constant depending on the chemical
element (and possibly on a lattice structure of metal, for elements in
which a number of metallic phases exist). The value of Y can be
found from the room-temperature experimental values of the core hole
lifetimes, as explained in the next Section. Note that in the present
model Y is independent of Te. By
adopting Eq. (12) we therefore neglect the effect on EII cross-section
stemming from changes in electron eigenstates and electron screening with
an increasing electron temperature at a given ion density. This is, of
course, an oversimplification; however, as Te
increases, the dominant contribution to EII comes from larger E
values, and the factor (1 − Eb
/E)Y becomes less important. We stress
that Y is a function of ion density, and may be assumed constant
only as long as ions remain motionless (as in the present case). In
expanding plasmas Y is expected to decrease as
Ni decreases, and to approach zero eventually
when Ni is low enough for the density effects
on EII cross-section to be negligible.
In this work we concentrate on the ionization in metal targets with
Te no larger than, say, 100 eV. This roughly
corresponds to laser intensities below 1015
W/cm2, for a pulse duration of a few tens of femtoseconds.
Rapid ionization of target material at higher laser intensities is
considered, for example, by Kemp et al., (2004).
For completeness, we note that the EII contribution to stopping of a
hot electron in a cold metal, and a related problem of an Auger
lifetime of a core vacancy in metal at room conditions, have been studied
(Almbladh et al., 1989; Schoene et al., 1999; Campillo et al., 2000; Knorren et al., 2001). The results in these
publications are obtained by means of detailed band structure
calculations, and are inapplicable to the systems with
Te comparable with Fermi temperature or
higher.
5. IONIZATION AND RECOMBINATION RATES
The process inverse to EII is the three-body recombination or,
synonymously, an Auger process involving two electrons in a conductivity
band and a core state hole. The three-body recombination probability and
rate are found from the detailed balance requirements for the equilibrium
conditions. We consider the simple case of relatively low abundance of
holes, such that only K = q and K = q
− 1 species are present in the system. That is, abundances of
species with K < q − 1 are negligible. This is
the case relevant to eMPT. The equilibrium core hole abundance h
= 1 − f (−Eb). There are
q core states per ion, and each of those states can be occupied
or vacant. Thus, the probability to have a hole in the core state of a
given ion equals qh, provided the probability to have more than
one core-state hole per ion is negligible. Of course, this approximation
is only accurate for qh << 1. The probability to have no
holes in the core state is then 1 − qh. Rate of EII (in
units of events per second per cm3) is given by
where Nq is the number density of ions
with no core-state holes (i.e., with q electrons in the core
state per ion). In equilibrium,
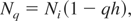
where Ni is the total number density of
lattice ions. Likewise, three-body recombination rate
W3 is expressed via the three-body recombination
probability P3 by
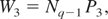
where Nq−1 is the number density of
ions with one core hole per ion. The physical meaning of
P3 is the inverse mean lifetime,
〈τh〉−1 ≡
P3, of a hole in a core state of a lattice ion. For
equilibrium conditions, Nq−1 is given
by
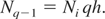
In equilibrium between the core state population and the next
ionization stage ground state population, W3 =
W. Thus, for qh << 1,
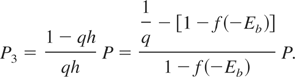
The three-body recombination occurs in an interaction of two
conductivity electrons in presence of an ion with a core-state vacancy.
One of the conductivity electrons makes a transition into the vacant core
state and the other one takes the excess energy. In the limit
kBTe <<
min(Eb,EF),
where EF ≡
kBTF ≡
μ(Te = 0), one should expect
P3 to become independent of
Te, since the energy distribution of
conductivity electrons becomes nearly independent of
Te at
kBTe <<
EF. It is easy to show that Eq. (17) yields
indeed the correct limiting behavior:
limTe→0
P3 = const. The prefactor in Eq. (17) becomes
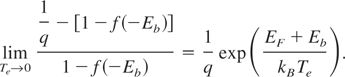
To find the limit limTe→0
P, we must consider two distinct cases:
EF < Eb and
EF ≥ Eb. Let
us first consider the case EF <
Eb. Using Eq. (9) for P and Eq. (7)
for f, we find
In the case under consideration, unity next to exp((E −
μ)/kBTe)
is negligible since
kBTe <<
EF < Eb,
E ≥ Eb, and lim
μ(Te → 0) =
EF. Thus,
independent of Te. For the case
EF ≥ Eb,
which corresponds to a relatively weakly bound (shallow-lying) core state,
one finds in a similar way
independent of Te, too. Thus, for both
cases limTe→0
P3 can be described by a single expression
The value of limTe→0
P3 depends on Ne both via
EF ∼
Ne2/3 and via Y. The
dependence of P3 on Ne in
this degenerate-conductivity-electrons limit is therefore far more
complicated than the trivial P3 ∼
Ne2 dependence encountered in an
ideal classical plasma limit.
Eqs. (18) and (21) show that, despite the Pauli blocking, for
kBTe <<
EF the dominant contribution to EII
probability P comes from slow projectile electrons,
Eb < E ≤
Eb + 2EF. This
underlines the importance of the empirical correction factor (1 −
Eb /E)Y
introduced in the previous Section.
6. RESULTS FOR SIMPLE METALS WITH LARGE
Eb
/EF
We have calculated P(Te) and
P3(Te) for solid-density
Li, Be, Na, Mg, Al, K, and Ca. For these metals the ratio
Eb /EF >
4. Parameters used in the calculations are presented in Table 1. Elements are listed in the order of
increasing atomic number. Values of Ne
include conductivity electrons only. Values of the binding energy with
respect to Fermi level, Eb +
EF, are taken from NIST data tables http://physics.nist.gov/PhysRefData/FFast/Text/Cover.html.
Values of EF are obtained from table values
for Ne using Eq. (8) at
Te = 0. Values of room-temperature hole
lifetimes 〈τh〉 were found in literature,
as follows. For Li, we adopted the experimental value of
〈τh〉 = ħ/Γ ≈ 20 fs as
reported by Citrin et al. (1979), where
Γ is the lifetime broadening of the core hole state. For Be, no
experimental data were found, so we used the value of
〈τh〉 ≈ 16 fs obtained by band
structure calculations (Almbladh et al.,
1989). For Na and Mg we adopted the
〈τh〉 experimental values of ≈70 fs
and ≈30 fs, respectively (Citrin et al.,
1979; Neddermeyer, 1976). For Al, we
adopted the experimental value of 〈τh〉
≈ 20 fs reported by Theis and Horn (1993),
see also, Almbladh et al. (1989) and
Citrin et al. (1979). For K,
experimental 〈τh〉 ≈ 44 fs (First et al., 1988). All the above
〈τh〉 data are typically accurate to
within a factor of 2. Datum for K is accurate to within 15%. For Ca no
data were found either experimental or theoretical, so we used a typical
value 〈τh〉 ≈ 20 fs; this is merely an
order-of-magnitude “guesstimate.” Table
1 lists also the fitted Y values for room-density metallic
state of Li, Be, Na, Mg, Al, K, and Ca. The Y values were
determined by equating the
limTe→0
P3 value, Eq. (21), to
〈τh〉−1 for each of the
elements. We note the ostensible regularity in Y: the latter
seems to grow nearly monotonously with the increasing atomic number.
Parameters of weakest-bound core states for several
metals
Calculation results for EII probability P in the
aforementioned metals are presented in Table 2.
Data are only given for P > 106
s−1. Figure 1 shows
P(Te) for the same metals. Figure 2 shows calculation results for
P3(Te) in the same
metals, up to qh = 0.1. One can see that P3
decreases with increasing temperature. It is important to note that
constant Eb and
Ne were assumed in the above calculations,
which corresponds to core-ionized ion abundance much smaller than unity.
As we said, under equilibrium conditions the present values of
P(Te) and
P3(Te) are only valid for
Te such that the equilibrium core-ionized ion
abundance qh(Te) << 1. For
very short pulses, as long as the hole abundance is substantially lower
than in equilibrium, present values of
P(Te) can be used at higher
Te as well (provided the
conductivity electrons are thermalized between themselves, i.e.,
the conductivity electron distribution function can be approximated by Eq.
(7)).
Calculated probabilities of core state electron impact ionization for
several metals
Calculated probabilities of core state electron impact ionization for
several metals.
Calculated probabilities of core vacancy 3-body recombination for
several metals.
Rate with which an equilibrium value h of the core hole
abundance is approached, for a given electron temperature
Te, is easy to evaluate. Assuming, as above,
that only K = q and K = q − 1
species are present in the system, for Nq and
Nq−1 the following rate equations are
readily written down:
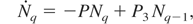
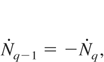
with the initial condition Nq(t
= 0) = Nq0,
Nq−1(t = 0) =
Nq−10 =
Ni −
Nq0. The solution is
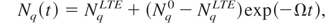
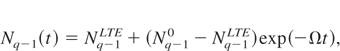
where
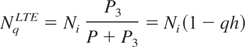
and
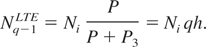
The hole abundance relaxes to its equilibrium value h at the
rate Ω which is given by
Ω values vary between 1013 and 1015
s−1 for the metals considered in this Section.
For a short-range lattice order to be destroyed by charge disordering,
the fraction Nq−1
/Ni of core-ionized ions in the medium
must be in excess of, say, 0.1/n ∼ 0.01. Here n
is the number of near neighbors of a given ion in the lattice, typically
between 4 and 12. To attain these values of
Nq−1
/Ni by means of ultrashort optical laser
energy deposition one needs, first of all, to reach
Te such that
qh(Te) [gsim ] 0.01. Furthermore, to
attain these values of Nq−1
/Ni on a 100-fs scale or faster, one
needs the EII rate P > 1011 s−1,
see Eq. (22). Temperatures at which qh equals 0.001, 0.01, and
0.1 are listed in Table 3. For readers'
convenience, Fermi energies of the elements are listed again in Table 3. By looking at Tables 2 and 3, one can immediately
see that the charge disorder emerges at Te
≈ (0.5 − 2)TF. That is, the same
temperature range as for the minimal conductivity regime. For that reason,
it is hard (if at all possible) to detect charge disorder by
self-absorption or pump-probe measurements of optical properties of the
metals considered in this section. This confirms the conclusion drawn by
Fisher et al. (2002) that for 50-fs
laser pulse irradiation of Al targets at intensities below 1015
W/cm2, at 1.5 eV and 3 eV photon energies, the core state
ionization does not affect appreciably the laser pulse absorption
coefficient.
Temperature values corresponding to specified equilibrium core-ionized
ion abundances qh
Charge disorder can also be produced, temporarily, by a hard
ultraviolet or X–ray laser irradiation of a metal sample. To produce
an observable charge disorder effect in a relatively cool metal, photons
with energy close to the photoionization threshold
Eb + EF are
required. Tunability of a free electron laser presents a great advantage
in this case. The optimal laser energy deposition should be such that the
Nq−1
/Ni value produced is in the range 0.01
− 0.1. Lower core hole populations are harder to observe, while
higher core hole populations yield, upon recombination to equilibrium hole
abundances, Te values that are too high
(close to Fermi temperature). At Te ≈
TF or higher, the ν values, as we said,
are close to minimal conductivity value anyway, and the charge disorder
effect is not manifested in optical properties. Core hole population
thermalization is expected to occur, under the conditions relevant to
X–ray induced charge disorder, at a rate of (1 − 5) ×
1013 s−1, that is, on a time scale of tens of
femtoseconds, see Figure 2.
7. ENERGY COUPLING BETWEEN ELECTRON AND ION
SUBSYSTEMS
It is important to stress that the charge disorder being hard to
detect optically in metals listed in Tables 1, 2, and 3 does not imply that charge disorder is hard to
detect at all in these metals. Charge disorder produces a
significant increase in electron-ion energy coupling (Fisher, 2005b). Indeed, a solid-density
medium with partially degenerate conductivity electrons and
identical ions in a short-range order may have an e-i energy
coupling coefficient significantly lower than a strongly-coupled plasma
under the same conditions. The plasma lacks a short-range order by virtue
of its ionization composition, and is characterized by Braginsky e-i
coupling value (Braginskii, 1965); originally
derived by Kogan (1959). Plasma e-i coupling
value is limited by the maximal possible coupling constraint (Fisher, 2005b) due to a limit on energy
transfer in a single e-i collision. (The maximal possible coupling value
is evaluated by simply assuming a large-angle elastic scattering of
electrons on ions, with a MFP equal to the interionic distance). As the
plasma e-i energy coupling constant is typically an order of magnitude
larger than e-i (or, more accurately, e-ph) energy coupling constant of a
simple metal, one would expect a notable shortening in ultrafast melting
times of a charge-disordered metal in comparison to a model in which the
charge disorder is disregarded. A comparison for Cu between melting times
with and without an account for the charge disorder is given in Figure 1 of (Fisher,
2005b). Charge disorder in Cu is discussed in the next
Section.
8. CHARGE DISORDER IN NOBLE METALS
The occurrence of charge disorder was first predicted by Fisher et
al. (2004, 2005a, 2005b) for noble metals under ultrashort
pulse laser irradiation. In noble metals (Cu, Ag, Au) the charge disorder
is brought along by a mechanism that is somewhat different from that in
the normal metals described above. In normal metals, charge disorder is
brought along by core state vacancies production, the core state being
localized throughout the Te range considered.
In noble metals, on the other hand, charge disorder is brought along by
d-band state localization which occurs at Te
values of a few electron-volts. At room temperature, d-band hole is
mobile, similar to a conductivity-band hole, rather than localized in a
single ion potential well. The criterion for mobile versus
localized holes is according to the relationship between (A) hole
tunneling rate out of the resonance and (B) the hole inverse lifetime with
respect to inelastic processes. At room temperature, in d-bands of noble
metals the typical hole inelastic lifetimes (dominated by three-body
recombination) are 5 − 50 fs, see for example, Zhukov et
al. (2003). We estimate the
room-temperature tunneling time to be of order of 1 fs, so the holes are
not localized. As Te increases, binding
energy of the d-band increases with it, and the d-hole tunneling rate
between individual ion sites drops. This leads to localization of the
d-holes at individual lattice sites. In the localization
Te domain, Te of
a few eV, the d-band hole concentration is already large. It exceeds one
hole per ion at Te [gsim ] 3 eV, see Table 4. Thus, the charge disorder follows directly
from d-band localization. In other words, in noble metals charge disorder
is brought along by a collective process (band structure evolution with
increasing Te) rather than by inelastic pair
collisions (EII events) as in normal metals. As the result, in noble
metals the parameters governing the eMPT are the energy
E(Te) and the lifetime width of the
d-band, while in normal metals the parameter governing eMPT is the
core-state vacancy abundance. Moreover, during a femtosecond laser
irradiation of normal metals with large Eb,
the core state population is not necessarily in thermal equilibrium with
the conductivity-band electrons. In that case, the core-state vacancy
abundance depends on time explicitly (and not via
Te), and is determined by the ionization
rate.
Equilibrium number of electrons per ion in d-bands of noble metals, as
a function of electron temperature at solid density, evaluated using
INFERNO model
9. INTERMEDIATE CASES
The metals Zn, Cd, Sn, and Pb represent an intermediate case between
noble metals on one hand and normal metals on the other. The d-bands of Zn
and Cd are located close to the bottom of the conductivity band, and are
localized in the above sense even at room temperature. In the case of Zn
and Cd Eq. (12) is inapplicable. In Sn (white tin) and in Pb, the fully
occupied d-bands are located several electron-volts below the bottom of
the conductivity band, Eb ≈
EF ≈ 10 eV. For Sn and Pb, Eq. (12) can be
applied, provided an amenable Y calibration is carried out. Such
a procedure is, however, largely unnecessary. Indeed, due to the relative
proximity in energy between the d-band and the conductivity band one can
assume that, at least on a time scale of 10 fs or longer, the d-band hole
population is in thermal equilibrium with the conductivity electrons.
INFERNO model calculation results for average fraction of core-ionized
lattice ions, Nq−1
/Ni = qh, in 4d band of Sn and
in 5d band of Pb are given in Table 5. One can
see that the charge disorder onset is expected at
Te ≈ 3 eV. At
Te = 5 eV the loss of short-range order is
complete. These temperatures are by a factor of 2 − 3 lower than the
Fermi temperatures of Sn and Pb.
Equilibrium fraction of core-ionized ions in Sn and Pb at solid
densities
INFERNO model calculation results for average equilibrium fraction of
core-ionized lattice ions qh in 3d band of Zn and in 4d band of
Cd are given in Table 6. The core-ionized ion
abundance in metallic Zn and Cd becomes significant at
Te as low as 1 − 2 eV. A complete
charge disorder is expected at Te ≥ 2 eV.
For comparison, Fermi energy of Zn is 9.4 eV. Zn thus seems to be the best
candidate for charge disorder effect observation using optical lasers. The
Fermi energy of Cd is 7.5 eV, so Cd should also exhibit clearly the
optical properties characteristic of charge disorder (resistivity
saturation) at Te ≥ 2 eV.
Equilibrium fraction of core-ionized ions in Zn and Cd at solid
densities
10. DISCUSSION AND CONCLUSIONS
Transition from metallic to plasma electron transport properties,
eMPT, has been studied in metals undergoing ultrashort pulse
electromagnetic energy deposition. The mechanisms contributing to eMPT
have been discussed, and the role of charge disorder phenomenon in the
eMPT has been determined. Approximate analytic expressions for
cross-section, probability, and rate of EII of core states, applicable to
both metals and plasmas, have been derived. Probability of three-body
recombination was determined through detailed balance. Calculations were
carried out for a number of normal metals.
It was shown that the charge disorder occurs at room densities in all
metals considered. Under equilibrium conditions for core population, in
Li, Be, Na, Mg, Al, K, and Ca the charge disorder occurs at temperatures
close to Fermi temperature, when the electron momentum relaxation rate is
already close to resistivity saturation limit. The resistivity saturation
in those metals is reached, with rising electron temperature, due to an
increasing electron elastic collision rate. For Zn, Cd, Sn, and Pb the
charge disorder occurs at temperatures a few times lower than the Fermi
temperature, with charge disorder leading to resistivity saturation. For
noble metals, resistivity saturation is also reached through charge
disorder. In the case of noble metals, in contrast to simple metals,
charge disorder occurs due to d-band sinking and localization, rather than
due to core state ionization. It was concluded that effect of charge
disorder on visible or near-infrared femtosecond laser absorption
coefficient should be pronounced in Zn, Cd, Sn, Pb, Cu, Ag, Au, and
probably can not be detected in Li, Be, Na, Mg, Al, K, and Ca. Charge
disorder produced directly by energetic photon ionization of core states
was also considered. Core hole lifetimes (with respect to recombination
from conductivity band) were found to be 10 − 100 fs for
Te = 0 − 20 eV and
Eb = 15 − 100 eV.
Differences in experimentally determined optical properties of Cu and
Al near the resistivity saturation domain were noted by Price et
al. (1995), and the shift of Cu d-band was
proposed as an explanation. Lack of detectable effect of core ionization
on optical properties of Al was determined both experimentally and
theoretically by Fisher et al. (2002).
In both works, the absorption of visible or near-infrared femtosecond
laser pulses was used both to heat the target and to probe its electron
transport properties. Unfortunately, we are not aware of any detailed
experiment on the femtosecond laser absorption in Zn, Cd, Sn, or Pb that
would allow to test the predictions of the present work.
In noble metals, as we said, the charge disorder is expected to
increase the value of electron-ion energy coupling coefficient g
and thus to reduce melting time. The charge disorder at sub-Fermi
temperatures also affects optical properties of the noble metals, although
that effect may be somewhat harder to single out. Pump-probe results for
Cu were reported in several works. In the pioneering study of Elsayed-Ali
et al. (1987) Fermi level smearing
effect with increasing Te was demonstrated,
for Te ≤ 0.2 eV. In a recent study (Sandhu et al., 2005) detailed pump-probe
results for Cu and Al are presented for pump intensity of 3 ×
1015 W/cm2, showing a transition to plasma
regime. This intensity produces peak Te
several times higher than the Fermi temperature. For the present purpose
(to study the specifics of the eMPT, that is), this temperature is too
high. Experiments at 10–100 times lower intensities are needed. In
Wang et al. (1994) an increase in
g was indeed observed by means of a two-pulse thermionic
emission, for Au at modest laser intensities
(Te of about 1 eV or even lower). This result
is suggestive of a charge disorder effect, however, the temperature seems
too low. Thus, the experimental evidence for charge disorder in the noble
metals remains inconclusive so far.
Several experiments can be carried out to test the predictions made in
this work. First of all, pump-probe or self-absorption ultrashort laser
experiments can be carried out on Zn targets in visible or near infrared
range. Excessive electron momentum relaxation rate at
Te > 1 eV, and resistivity saturation at
Te
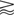
2 eV are predicted as a result of charge disorder. Similar experiments on
Cd are also possible, as explained in the previous Section. For Sn and Pb,
the charge disorder is predicted to cause resistivity saturation at
Te
3 eV. Experiments with probe wavelength near parallel-band interband
absorption peak (the peak being produced by conductivity band splitting at
Brillouin zone boundary (Ashcroft & Sturm,
1971)) should be particularly conclusive, since the peak is
destroyed by the loss of short-range order in a charge disordered solid.
Note that, by contrast, an interband absorption peak produced by electron
excitation from a core state or from a d-band to the Fermi surface is not
likely to be destroyed by charge disorder. It is subjected, however, to an
increased lifetime broadening as a result of an increased electron
collision rate; it is also broadened by Fermi level smearing.
Another possibility is to detect the charge disorder effect in
ultrafast melting experiments. The X-ray probe experiments (see Siders et al., 1999; von
der Linde et al., 2001; Lindenberg
et al., 2005) or electron-beam probe experiments (Siwick et al., 2003) allow to directly probe
the ion spatial arrangement and to resolve the ultrafast homogeneous or
heterogeneous melting dynamics. Those are especially relevant for noble
metals where a significant difference in melting times with and without
charge disorder is predicted; and for normal metals where, at
Te close to Fermi temperature, various
theoretical predictions for electron-ion coupling coefficient value differ
substantially.
ACKNOWLEDGMENTS
The authors thankfully acknowledge discussions with Z. Zinamon, S.I.
Anisimov, N.A. Inogamov, and S.N. Gordienko.
