Laboratory laser intensities have grown remarkably during recent years due to the method of chirped pulse amplification (CPA) (Strickland & Mourou, 1985). Ultrashort intense lasers lead to a new field of physics, known as high-field science (Batani & Wootton, 2004; Honrubia & Tikhonchuk, 2004), which studies the interaction between ultra-intense radiation and matter (Magunov et al., 2003; Chirila et al., 2004; Fukuda et al., 2004; Limpouch et al., 2004).

In CPA, optical gratings are used to chirp and stretch a short pulse. A broadband optical amplifier is then employed to amplify the chirped low-power stretched signal. Finally, complementary gratings then recompress the original, but now highly amplified, signal. Nowadays, a strong motivation for development of the next generation of high-energy petawatt (HEPW) lasers exists. Production of HEPW pulses remains a technical challenge, the primary concern being the high fluence and short-pulse width experienced by the final HEPW optics, i.e., the final compressor grating and beam transport and focusing optics. For the subpicosecond intense laser pulses, the damage threshold (DT) of dielectric (e.g., fused silica) is about 2 J/cm² (Perry et al., 1999a, 1999b; Gamaly et al., 2002; Jovanovic et al., 2004), and the DT of metal (e.g., gold) is about 0.5 J/cm² (Gamaly et al., 2002).

Recently, plasma medium was used to focus an ultrashort intense laser pulse and meanwhile improve its temporal contrast by so-called “plasma mirror” (Kapteyn et al., 1991; Backus et al., 1993; Gold, 1994; Perry et al., 1999a, 1999b; Doumy et al., 2004). It is also proposed to generate ultrahigh intense light fields by superradiant Compton scattering (Shvets et al., 1998; Dreher, 2004), Raman-scattering amplification (Malkin et al., 1999; Ping et al., 2004), quasi-soliton amplification between two foils (Shen & Yu, 2002), pulse focusing by relativistic plasma waves (Bulanov et al., 2003), and self-compression of laser pulses (Shorokhov et al., 2003). The main advantage of the plasma medium for these novel applications is that it has no thermal DT and can sustain extremely high intensities. Most recently, plasma Bragg grating (PBG) induced by two intersecting laser pulses at intensities of about 10¹⁵ W/cm² is well established theoretically by Sheng et al. (2003). The ponderomotive force of the interference fields of the two pump pulses pushes the electrons, which further drag the heavy ions through Coulomb force. Finally, an electrically neutral PBG forms, which can last as long as a few picoseconds.

Another similar structure, fiber Bragg gratings (FBGs), was widely investigated (Agrawal, 2001). FBGs have wide applications in wave filtering (Longhi et al., 1997), optical switching (Broderick et al., 1998; Taverner et al., 1998), and pulse compression (Winful, 1985; Eggleton et al., 1996, 1997). These periodic structures have a photonic band gap, around which there is strong dispersion. The grating dispersion dominates the dispersion of background medium by several orders of magnitude. The PBG demonstrates similar properties as the FBG as shown in the following. Moreover, the photonic band gap of the PBG is three orders wider than that of a typical FBG (Eggleton et al., 1996, 1997; Agrawal, 2001). Though the PBG have no thermal DT, it can be damaged by the laser ponderomotive force. We find that, for laser pulse with duration of around 100 fs, the ponderomotive DT of the PBG is about a few 10³ J/cm², which is three orders higher than that of the ordinary optical elements made of metal or dielectric. Due to its ultrawide band gap and high DT, the PBG can be a novel device for controlling the femtosecond intense laser pulses. In this paper, we study a few interesting phenomena in the PBG, such as light speed reduction, pulse stretching, chirped-pulse compression.

Figure 1 illustrates the electron density evolution of a part of PBG obtained in our one-dimensional (1D) particle-in-cell (PIC) simulations (Sheng et al., 2003). The rest is the same as the shown part and the ion density evolution is completely identical to the electron density. The PBG with the length 100λ₀ in 0 ≤ z ≤ 100λ₀ are induced by two counter propagating flat-topped pulses with amplitudes a = 0.03 and durations 200λ₀, where λ₀ is wavelength of the pump pulses in vacuum, and a is the normalized vector potential relating to the laser intensity by Iλ₀²/a² = 1.37 × 10¹⁸ Wcm⁻² μm². The pump pulses simultaneously reach the right-and-left boundaries of the initial uniform plasma slab at t = 0. Its initial electron density is n₀ = 0.3n_c, where n_c = πm_e /e²τ₀² is the critical density for the pump pulses is, and τ₀ = λ₀ /c is a light cycle. Obviously, the induced PBG is centrosymmetrical against z = 50λ₀. The PBG begins to build up at t = 300τ₀ and stays at the deepest modulation almost unchanged during 700τ₀ < t < 1300τ₀. The PBG begins to attenuate after t = 1600τ₀, and completely disappears at t = 2000τ₀. The maximum electron density of the PBG can be up to n_max = n_c, as shown in Figure 1. If not particularly mentioned, we take the initial electron and ion temperatures to be T_e = 10 eV and T_i = 1 eV, respectively, the mass ratio of ions to electrons ZM_i /m_e = 5508 with Z = 1 being the ion charge number in the simulations.

Spatio-temporal plot (part) of electron density n/nc of the PBG induced by two counter propagating laser pulses with amplitudes a = 0.03 and durations 200λ0 in uniform plasma with density 0.3nc.

It is apparent that the period of the PBG is Λ = λ₀ /2N₀, where the refractive index of the background plasma is

, the refractive index of the background plasma. According to the well-known Bragg principle, incident light with the Bragg frequency ω_B = 2πc/λ₀, i.e., the pump light frequency for the PBG is fully reflected by the PBG. The key property of a grating is that Bragg reflection occurs over a range of frequencies centered about the Bragg frequency ω_B (Eggleton et al., 1996, 1997; Agrawal, 2001). At frequencies far away from ω_B, the reflectivity becomes small. The grating transmission spectrum shown in Figure 2 is obtained by injecting the signal light of different frequencies through the PBG shown in Figure 1. The transitivity suggests that the PBG have an ultrawide band gap about 0.12 ω_B, i.e., 96 nm for λ₀ = 800 nm. The PBG can be a wave filter since the light detuned with frequencies inside the band gap cannot propagate through the grating. The light with frequencies near the band gap edges can propagate, but suffers strong dispersion from the PBG.

Transitivity as a function of the signal light frequency through the PBG shown in Figure 1.

To describe the propagation of a signal pulse in the PBG, we start from the 1D wave equation in underdense plasma (Esarey et al., 1997)

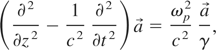
where

is the normalized vector potential, γ the relativistic factor of the electrons,

the plasma frequency, and n the electron density. One can write

for the light field, where k_B is Bragg wave number, a_± are the envelopes of the forward and backward propagating modes. For a weakly relativistic laser pulse,

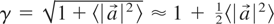
, where 〈〉 represents the time-average over a light cycle. The electron density of the PBG can be written as Fourier series:

, where δn_m is Fourier component with the spatial period Λ/m. The average of δn₁ between 700τ₀ < t < 1300τ₀ for the PBG in Figure 1 is δn₁ ≈ 0.13n_c, indicating that our PBG is a deep modulated grating (δn₁ << n₀ corresponding to a shallow grating).

Substituting the above terms into Eq. (1) under the slowly-varying-envelope approximation, we obtain the following nonlinear coupled-mode equations (NLCME)

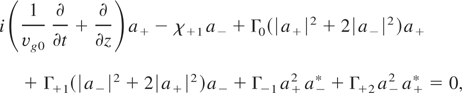
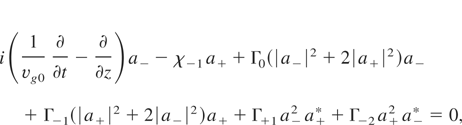
where χ_±1 = (ω_B /2v_g0)(δn_±1 /n_c) is coupling coefficients, v_g0 = N₀ c is group velocity, and Γ_m = (ω_B /8v_g0)(δn_m /n_c). Since δn_m = δn_−m, one can simply define χ ≡ χ_±1, Γ_|m| ≡ Γ_m. The second terms on the left-hand sides of Eqs. (2) and (3) are the coupling terms, which lead to the grating dispersion. The third and latter terms refer to the nonlinearity owing to the relativistic electron motion. Generally, since Γ₀ > Γ₁ > Γ₂, the effect of these nonlinear terms reduces in turn. When the transitivity is high, i.e., a₋ << a₊, neglecting |a₋|²a₊ and Γ_1,2 terms in Eqs. (2) and (3), the remainder Γ₀|a₊|²a₊ corresponds to self-phased modulation (SPM) for the forward propagating mode. Eqs. (2) and (3) can also apply to the deep grating structure (Iizuka & Sterke, 2000; Haus et al., 2002). When neglecting Γ_1,2 terms, the left equations can well describe the nonlinear pulse propagation for the shallow grating case (Eggleton et al., 1996, 1997; Agrawal, 2001).

The dispersion relation in the PBG can be obtained by inserting the plane-wave solutions a_± = C_± exp[i(qz − Δωt)] into the linearized Eqs. (2) and (3), where q = k − k_B, Δω = ω − ω_B represent the detuning between the wave number (frequency) of the incident light, and the Bragg wave number (frequency) of the grating. This substitution leads to the linear dispersion relation

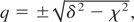
where δ = Δω/v_g0. This dispersion relation indicates that the PBG has a photonic band gap, i.e., −χ < δ < χ, inside which the light cannot propagate because of imaginary q. The band gap width is found explicitly to be ω_Bδn₁ /n_c. For the PBG given in Figure 1 (δn₁ ≈ 0.13n_c), the band gap width is about 0.13ω_B. This agrees well with the transmission spectrum given in Figure 2.

The group velocity of the signal pulse in the grating is found by calculating V_g = dω/dk from Eq. (4), leading to

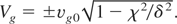
Eq. (5) indicates that the speed of light decreases to zero at the band gap edges. Eq. (5) (solid line) agrees well with 1D PIC simulation results as displayed in Figure 3. For example, the signal light with ω = 0.93ω_B propagates in the PBG at a group velocity of 0.34c only, which corresponds to 40% of the speed of light in the uniform plasma, i.e., no grating (NG) case.

Group velocity of the signal pulses around the photonic band gap. The group velocity in uniform plasma is also shown by the dashed line.

The group-velocity dispersion (GVD) β₂^g = d²k/dω² is found to be

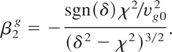
Eq. (6) indicates that on the lower branch (δ < −χ) of the band gap, the grating dispersion is normal (β₂^g > 0); on the upper branch (δ > χ), the dispersion is anomalous. Moreover, the grating dispersion approaches infinite at the band gap edges. For a signal light of ω = 0.9ω_B propagating in the PBG given in Figure 1, for example, one obtains β₂^g = 1.6 × 10⁴ fs²/mm, much larger than the GVD β₂ ≡ −(c²v_g³ω)(n/n_c) = 1.2 × 10³ fs²/mm in the uniform plasma, which is naturally anomalous. Therefore, the grating formation reverses the plasma medium dispersion from anomalous to normal on the lower branch of the band gap, and largely strengthens the anomalous dispersion on the upper branch. Owing to the strong dispersion, the PBG can be a novel dispersion element. Also one can obtain the third-order dispersion (TOD) β₃^g = (3|δ|χ²/v_g0³)/(δ² − χ²)^5/2, which is always positive and becomes infinitely large at the band gap edges. The positive TOD induces fluctuant structures at the trailing edge of the light pulse (Agrawal, 1995). TOD is the main factor for limiting the pulse compression in the grating (Agrawal, 2001).

Figure 4 shows pulse stretching [(a) and (b)] and chirped-pulse compression [(c) and (d)] in the PBG given Figure 1. In both cases, the central frequency of the signal pulses is on the lower branch of the band gap, where the grating dispersion is normal. The incident pulses have the Gaussian envelope a₀ exp[−(1 + iC)t²/T₀²], where C is the chirp factor. In the pulse stretching case, the incident pulse is with C = 0, a₀ = 0.04, and T₀ = 10τ₀, which reaches the left boundary of the PBG at t = 795τ₀. Figure 4a shows that the pulse is stretched faster when the light frequency is closer to the band gap edge (ω = 0.935ω_B). This is due to the increasing dispersion at the band gap edge as predicted by Eq. (6). For the NG case, the signal light of ω = 0.92ω_B propagates through the uniform plasma almost with a constant duration, indicating a very small dispersion as compared with the PBG case. Figure 4b shows the output pulse at the right boundary for ω = 0.92ω_B. PIC simulation (solid line) is recovered by the coupled-mode theory (dashed line) by numerically solving Eqs. (2) and (3) (Sterke et al., 1991), using δn₁ ≈ 0.13n_c and δn₂ ≈ 0.08n_c for the PBG as shown in Figure 1.

(a) Pulse stretching as a function of the propagating distance because of PBG's strong dispersion. The numerical labels indicate the frequencies; (b) Stretched pulse shapes found from PIC simulation and model calculation for ω = 0.92ωB; (c) Compression of chirped pulses as a function of the propagating distance because of PBG's strong dispersion. The numerical labels indicate the frequencies; (d) Compressed pulse shapes found from PIC simulation and model calculation for ω = 0.9ωB.

In the case for chirped-pulse compression, the incident pulse has a negative chirp factor C = −4, an amplitude a₀ = 0.01, and a duration T₀ = 50τ₀, which reaches the left boundary at t = 915τ₀. As shown in Figure 4c, the chirped pulse is compressed faster when the light frequency is closer to the band gap edge. The reason is the same as for the pulse stretching. For the NG case, the signal light of ω = 0.9ω_B is slightly stretched because of anomalous dispersion of the uniform plasma. The compression of the negatively chirped pulse indicates that here the grating dispersion is normal. Figure 4d shows the output pulse for ω = 0.9ω_B. Again the coupled-mode theory is well consistent with the PIC simulation. The little fluctuation at the trailing edge of the pulse is due to the TOD effect, as mentioned above.

Both pulse stretching and chirped-pulse compression are linear propagation in PBG. We also study the nonlinear propagation of weakly relativistic laser pulse in PBG (Wu et al., 2005), and observe the compression of Bragg grating soliton (BGS) (Eggleton et al., 1996, 1997; Agrawal, 2001). Eqs. (2) and (3) also qualitatively agree with the PIC simulation results. The BGS compression is much faster than the self-compression of the pulse in the uniform plasma (Shorokhov et al., 2003). The fast BGS compression can be used to generate powerful laser pulses with the duration of about 10 femtosecond.

In conclusion, the propagation of the ultrashort intense laser pulses in a PBG induced by intersecting laser pulses was studied. The PBG shows an ultrawide photonic band gap, near which strong dispersion appears. Both theory and PIC simulations suggest that the PBG is a simple and novel element for light speed reduction, pulse stretching, chirped pulse compression, and fast compression of BGS (Wu et al., 2005). Because of its ultrahigh DT, three orders higher than that of the ordinary optical elements, it opens a way to manipulate femtosecond laser pulses in the high intensity regime, and may have important applications in generating femtosecond HEPW laser pulse in the future HEPW lasers.