Introduction
Ultrashort pulse lasers (USPL) have numerous advantages over longer pulse laser when it comes to materials ablation for various applications. A distinctive feature of ultrashort pulse ablation is that laser–material interaction is separated in time from the actual removal of material. Therefore, the laser pulse energy is directly deposited into the solid target without self-shielding from the ablated plume typical for longer pulse lasers. Thus, ultrashort pulses provide a way of creating extremely higher energy densities in condensed matter with precise control over the ablated region. The combination of high power and extremely short pulse duration results in unique characteristics of the USPL–material interaction such as reduced heat affected zone (HAZ), ignition of ultrafast electron dynamics, and rapid formation and expansion of a strong plasma (Hypsh et al., Reference Hypsh, Shannon and Shannon2015).
However, the basic mechanisms leading to USPL induced ablation are poorly understood primarily due to extremely challenging experimental conditions, that is, time scales of the laser–matter interaction and complexity of physical processes needed to be considered for accurate computer simulation. Despite such difficulties, significant research efforts have been focused on developing a variety of simulation models with the aim of gaining a better understanding of the physical processes involved in the laser–matter interaction and their role in the different ablation mechanisms. Molecular-dynamics simulations (Perez & Lewis Reference Perez and Lewis2003; Hirayama & Obara Reference Hirayama and Obara2005; Lewis & Perez Reference Lewis and Perez2009) and hydrodynamic modeling (Eidmann et al., Reference Eidmann, Meyer-ter-Vehn, Schlegel and Hüller2000; Colombier et al., Reference Colombier, Combis, Bonneau, Le Harzic and Audouard2005) are often used to qualitatively describe USPL–solid target interaction. Different ablation mechanisms such as spallation, explosive boiling (phase explosion - PE), fragmentation, and vaporization have been identified and explored. Quantitative models applied to describe the experimental results are usually based on two-temperature model (TTM) (Anisimov et al., Reference Anisimov, Kapeliovich and Perelman1974). Utilization of TTM allows to simulate the target thermodynamic evolution, which is not easily accessible through experiment. The knowledge of the thermodynamic evolution is a critical parameter to identify different USPL ablation regimes and mechanisms. In the present paper, we report experimental results on the interaction of femtosecond pulse laser with metal targets at laser intensities up to 1014 W/cm2. In this laser intensity range, phase explosion (Miotello & Kelly Reference Miotello and Kelly1995) is commonly considered as primary ablation mechanism for USPL with spallation potentially playing an important role (Zhigilei et al., Reference Zhigilei, Ivanov, Leveugle, Sadigh and Bringa2004, Reference Zhigilei, Lin and Ivanov2009; Lewis & Perez Reference Lewis and Perez2009). Numerical computations were carried out using our newly developed FEMTO-2D computer simulation code based on solving TTM (Suslova & Hassanein Reference Suslova and Hassanein2017a, Reference Suslova and Hassaneinb). We took great care to account for the strong temperature dependence of the material optical and thermodynamic properties under the condition of strong thermal non-equilibrium.
Model description
Theoretical analysis of femtosecond pulse laser interaction with metals applied in the FEMTO-2D simulation package is based on TTM model written for axially symmetric 2-D cylindrical coordinates (Suslova & Hassanein Reference Suslova and Hassanein2017b):
$$C_{\rm e}\displaystyle{{\partial T_{\rm e}} \over {\partial t}} = \; \displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\left( {k_{\rm e}r\displaystyle{{\partial T_{\rm e}} \over {\partial r}}} \right) + \displaystyle{\partial \over {\partial z}}k_{\rm e}\displaystyle{{\partial T_{\rm e}} \over {\partial z}} - G\left( {T_{\rm e} - T_{\rm l}} \right) + S(r,z,t)$$
$$C_{\rm l}\displaystyle{{\partial T_{\rm l}} \over {\partial t}} = \; \displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\left( {k_{\rm l}{\rm r}\displaystyle{{\partial T_{\rm l}} \over {\partial r}}} \right) + \displaystyle{\partial \over {\partial z}}k_{\rm e}\displaystyle{{\partial T_{\rm e}} \over {\partial z}} + G\left( {T_{\rm e} - T_{\rm l}} \right)$$where r is the radial distance from the center of the beam and z is the coordinate normal to the sample surface with the origin at the surface.
The main laser absorption mechanism in metals is inverse bremsstrahlung absorption by free electrons (Zhao Reference Zhao2014) followed by the rapid increase in electron temperature while lattice remains relatively cold, and the target density is unchanged during the laser pulse (Gamaly Reference Gamaly2011). The laser heat source component within the film layer was modeled using Gaussian temporal and spatial (radial) profiles, and an exponential attenuation of the laser intensity with depth according to the Beer–Lambert law (Suslova & Hassanein Reference Suslova and Hassanein2017b):
$$\eqalign{ &S{\left( {z,r,t} \right) }\cr &\quad= \sqrt {\displaystyle{{\rm \beta} \over {\rm \pi}}} \displaystyle{{\left( {1 - R} \right){\rm \;}} \over {t_{\rm p}{\rm \alpha} _{{\rm opt}}}}{\rm \;} I_0{\rm \;} exp\left[ { - ({\rm \;} \displaystyle{z \over {{\rm \alpha} _{{\rm opt}}}}{\rm \;} )} \right]exp\left[ { - \displaystyle{{r^2} \over {2{\rm \sigma} ^2}}} \right]exp\left[ { - {\rm \beta} {\rm {^\ast}}{({\rm \;} \displaystyle{{t - 2t_{\rm p}} \over {t_{\rm p}}}{\rm \;} )}^2} \right]}$$where, I 0 is the laser pulse peak intensity, R is the temperature dependent reflectivity, αopt is the temperature dependent optical penetration depth, t p is the laser pulse full width at half-maximum, σ is profile parameter, and parameter β = 4 ln (2).
Optical and thermophysical properties of target materials were defined as temperature dependent parameters; a detailed description of the analytical models was provided in Suslova and Hassanein (Reference Suslova and Hassanein2017a, Reference Suslova and Hassaneinb). For electron subsystem, electron heat capacity (C e) and thermal conductivity (k e) were defined via smooth interpolation between two polar states of the material, that is, the cold solid state and hot dense plasma state as following:
$$C_{\rm e} = \; n_{\rm e}k_{\rm B}\displaystyle{{3{\rm \pi} ^2T_{\rm e}} \over {\sqrt {36T_{\rm F}^2 + 4{\rm \pi} ^4T_{\rm e}^2}}} $$
$$k_{\rm e} = \sqrt {{\left( {\displaystyle{{C_{\rm e}{\rm \upsilon} _{\rm F}^2} \over {3{\rm \nu} _{{\rm eff}}}}} \right)}^2 + {\left( {\displaystyle{{128\; (0.24 + Z)n_{\rm e}T_{\rm e}} \over {3{\rm \pi} \left( {4.2 + Z} \right)m_{\rm e}(v_{{\rm e} - {\rm i}}\; + \; {\rm \nu} _{{\rm e} - {\rm e}})}}} \right)}^2} $$where v e−i, νe−e are electron–ion and electron–electron collision frequencies, n e = Zn i is electron density, Z is the average charge state at given T e, n i is the ion density, T F is Fermi temperature, υF is Fermi velocity, and k B is Boltzmann constant. Details of the applied collision theory and its role in the calculation of electron and lattice thermodynamic properties, and material optical properties were given in (Suslova & Hassanein Reference Suslova and Hassanein2017b).
The lattice heat capacity was considered as constant (Cl(Cu) = 3.5 J/cm3K) because of its weak dependence on the lattice temperature.
The lattice heat conductivity was approximated based on the collisional theory as follows:
$$k_{\rm l}\; = \displaystyle{1 \over 3}C_{\rm l}\displaystyle{{{\rm \vartheta} _{\rm i}^2} \over {{\rm \nu} _{{\rm i} - {\rm i}}}}$$where
$${\rm \vartheta} _{\rm i} = \; \sqrt {\displaystyle{{2k_{\rm B}T_{\rm i}} \over {m_{\rm i}}} + C_{\rm s}^2}$$
is the ion/phonon velocity at given lattice temperature, and 
${\rm \nu} _{{\rm i} - {\rm i}} = \; n_{\rm i}{\rm \pi} (2r_0)^2{\rm \vartheta} _{\rm i}$ is the ion–ion collisional frequency calculated based on hard sphere model, m i is atomic mass, and r 0 is the atomic radius.
The temperature dependent electron–phonon coupling factor was adopted from recent theoretical model (Lin Reference Lin2007; Lin et al., Reference Lin, Zhigilei and Celli2008) that takes into account the electron density of states in the material, since it has been shown that electron–phonon coupling factor is very sensitive to details of the electronic structure of the material. For the electron temperature range above 4.3 eV, the model was further extended to higher electron temperature range with the formula for electron–ion coupling in plasma:
$$G = 3\displaystyle{{m_{\rm e}} \over {m_{\rm i}}}{\rm \nu} _{{\rm e} - {\rm i}}Zn_{\rm i}k_{\rm B}.$$The following initial and boundary conditions were applied to solve Eqns. (1) and (2). The simulation started at time t = 0. The initial temperature for electrons and lattice, as well as the temperatures far away from the exposed surface in the z-direction and far from the center in r-direction at any time step, are set at the ambient temperature (300 K). Thermal emission from the surface of the target during simulation was accounted for with the Stefan–Boltzmann law. For the other outer boundaries, zero heat losses to the surrounding vacuum were assumed during the entire calculation time:
$$\left. {\displaystyle{{dT_{\rm e}} \over {dr}}} \right \vert _0 = \left. {\displaystyle{{dT_{\rm l}} \over {dr}}} \right \vert _0 = \left. {\displaystyle{{dT_{\rm e}} \over {dr}}} \right \vert _{\rm r} = \left. {\displaystyle{{dT_{\rm l}} \over {dr}}} \right \vert _{\rm r} = 0,$$and
$$\left. {\displaystyle{{dT_{\rm e}} \over {dz}}} \right \vert _z = \left. {\displaystyle{{dT_{\rm l}} \over {dz}}} \right \vert _z.$$Phase transformations from solid to liquid and from liquid to solid were treated as isothermal phase changes. The lattice temperature remained constant (T l = T melt) during the phase change process until the transformation is completed. The phase transformation was considered completed when the net heat absorbed (for melting) or released (for solidification) within the control volume became equal to the fusion latent heat:
$${\rm \rho} _{\rm l}H_{\rm m} = \mathop \int \limits_{t_{{\rm chst}}}^{t_{{\rm chfn}}} \left[ {\displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\left( {k_{\rm l}{\rm r}\displaystyle{{\partial T_{\rm l}} \over {\partial r}}} \right) + \displaystyle{\partial \over {\partial z}}k_{\rm l}\displaystyle{{\partial T_{\rm l}} \over {\partial z}} + G\left( {T_{\rm e} - T_{\rm l}} \right)} \right]dt$$where t chst is a time when phase transformation begins and t chfn is a time when phase transformation fully completed. Once melting begins, the two phases exist simultaneously separated by a moving interface. The location of the solid–liquid interface was tracked, and interphase velocity was calculated based on the energy balance equation at the interface (Hassanein Reference Hassanein1983):
$$\left[ {1 + {\left( {\displaystyle{{\partial z_{\rm m}} \over {\partial r}}} \right)}^2} \right]\left[ {k_{\rm l}^{\rm s} \displaystyle{{\partial T_{\rm l}^{\rm s}} \over {\partial z}} - k_{\rm l}^{\rm l} \displaystyle{{\partial T_{\rm l}^{\rm l}} \over {\partial z}}} \right] = {\rm \rho} _{\rm l}H_{\rm m}u_{{\rm sl}}$$where z m is the location of the interface, usl is the interface velocity, upper case s denotes a solid state and upper-case l stays for a liquid phase.
The location of the liquid phase–solid interface has been tracked through the simulation time to estimate the melted zone, assuming no material removal may originate from outside of the melted pool.
Two material removal mechanisms were considered for the model. Material removal via normal evaporation was estimated by considering receding surface at the interphase between vapor and solid or liquid. The velocity of the receding interface is a highly non-linear function of temperature and calculated with following equation (Hassanein et al., Reference Hassanein, Kulcinski and Wolfer1984):
$${\rm \vartheta} _{{\rm surface}}\left( {r,t} \right) = 0.058\displaystyle{{\sqrt A P_{\rm V}\left( {T_{\rm V}} \right)} \over {{\rm \rho} _{\rm V}\left( {T_{\rm V}} \right)\sqrt {T_{\rm V}}}} $$
$$P_{\rm V} = P_0{\rm exp}( - \displaystyle{{H_{\rm V}} \over {k_{\rm B}T_{\rm V}}})$$where A is atomic mass number, P V is vapor pressure as a function of vapor temperature, and latent heat of vaporization HV, TV is target temperature at the surface, ρV target density at given temperature, and P0 is the reference pressure.
The second ablation mechanism considered is explosive boiling (phase explosion). Phase explosion takes place when the material is superheated to the thermodynamic equilibrium critical temperature point Tcr due to rapid laser energy absorption by electrons and following heat transfer to the lattice on the time scale shorter than the time required for a normal boiling to occur (Sokolowski-Tinten et al., Reference Sokolowski-Tinten, Bialkowski, Cavalleri, Von der Linde, Oparin, Meyer-ter-Vehn and Anisimov1998; Bulgakova & Bourakov Reference Bulgakova and Bourakov2002; Lewis & Perez Reference Lewis and Perez2009). The typical time span for the normal boiling is in the range of 100 ps (Yang et al., Reference Yang, Zhao and Zhu2007). For the phase explosion, we considered the commonly applied (Chicbkov et al., Reference Chicbkov, Momma, Nolte, Yon Alvensleben and Tiinnermann1996; Chen & Beraun Reference Chen and Beraun2003; Yang et al., Reference Yang, Zhao and Zhu2007; Li et al., Reference Li, Lao, Lin, Chen and Chen2011; Wang et al., Reference Wang, Ren, Cheng, Chen and Tzou2013) condition for the lattice temperature reaching 0.9 T cr.
Experimental details
The experimental work was conducted at the Center for Materials Under eXtreme Environment (CMUXE) in the High Energy Density Physics laboratory (HEDP Lab) with chirped pulse amplified Ti:Sapphire femtosecond laser system operating at 800 nm wavelength. The contrast of the laser system is ~10−7. The following laser system parameters were used during the experiment: minimum pulse duration – 40 fs, repetition rate – 1 Hz, beam diameter on the target – 100 µm, the laser pulse energy range – from 140 µJ to 770 µJ (corresponds to laser intensity ranges from 2 × 1013 W/cm2 to 1.1 × 1014 W/cm2). All experiments were conducted at normal incidence at the base pressure of ~ 10−5 Torr.
Targets were made of commercially available copper samples mechanically polished to a mirror-like surface. Due to slow ablation rate at low laser fluence, the experiments were performed with 20 laser shots, and the ablation rate was then defined as the maximum crater depth per laser shot. The accumulation of the residual heat was assumed to have a negligible effect because of the extremely short pulse duration compared with the cooling time between pulses.
After irradiation, samples were imaged with scanning electron microscope (SEM); ablation profiles were characterized with optical microscope profilometer and with cross-sectional SEM images obtained with FIB SEM. For the optical profilometer, lateral resolution was ~ 2 µm and depth resolution was ~1 nm.
Results and discussion
Analysis and comparison of FEMTO-2D simulation with the experimental data
The aim of this work was to test our developed simulation package for USPL–matter interaction to predict laser-induced ablation and to gain a better understanding of the material removal processes through careful analysis of experimental data and simulated results. Copper was chosen as target material for being affordable, available, and extensively studied.
First, we have determined target melting threshold in given experimental setup, since no material removal is possible before enough energy has been supplied to the target and melting occurs. FEMTO-2D simulation predicted the melting threshold for copper at laser fluence around 0.6 J/cm2 which corresponds to about 0.045 J/cm2 of absorbed energy density.
The absorption efficiency is one of the parameters that should be carefully analyzed when investigating the interaction of the USPLs with condensed matter. Many analytical models and experimental work (Preuss et al., Reference Preuss, Demchuk and Stuke1995; Price et al., Reference Price, More, Walling, Guethlein, Shepherd, Stewart and White1995; Fisher et al., Reference Fisher, Fraenkel, Henis, Moshe and Eliezer2001, Reference Fisher, Fraenkel, Zinamon, Henis, Moshe, Horovitz, Luzon, Maman and Eliezer2005; Kirkwood et al., Reference Kirkwood, Tsui, Fedosejevs, Brantov and Bychenkov2009; Loboda et al., Reference Loboda, Smirnov, Shadrin and Karlykhanov2011) have demonstrated that the material optical properties are defined by the collisional processes inside the material. The absorption efficiency as a function of laser fluence in copper was calculated based on FEMTO-2D simulations and compared with available experimental data in Suslova and Hassanein (Reference Suslova and Hassanein2017b). Figure 1 shows how the absorption efficiency of copper changes as a function of the incident laser pulse fluence in the range considered for this work compared with the fixed value determined at room temperature.
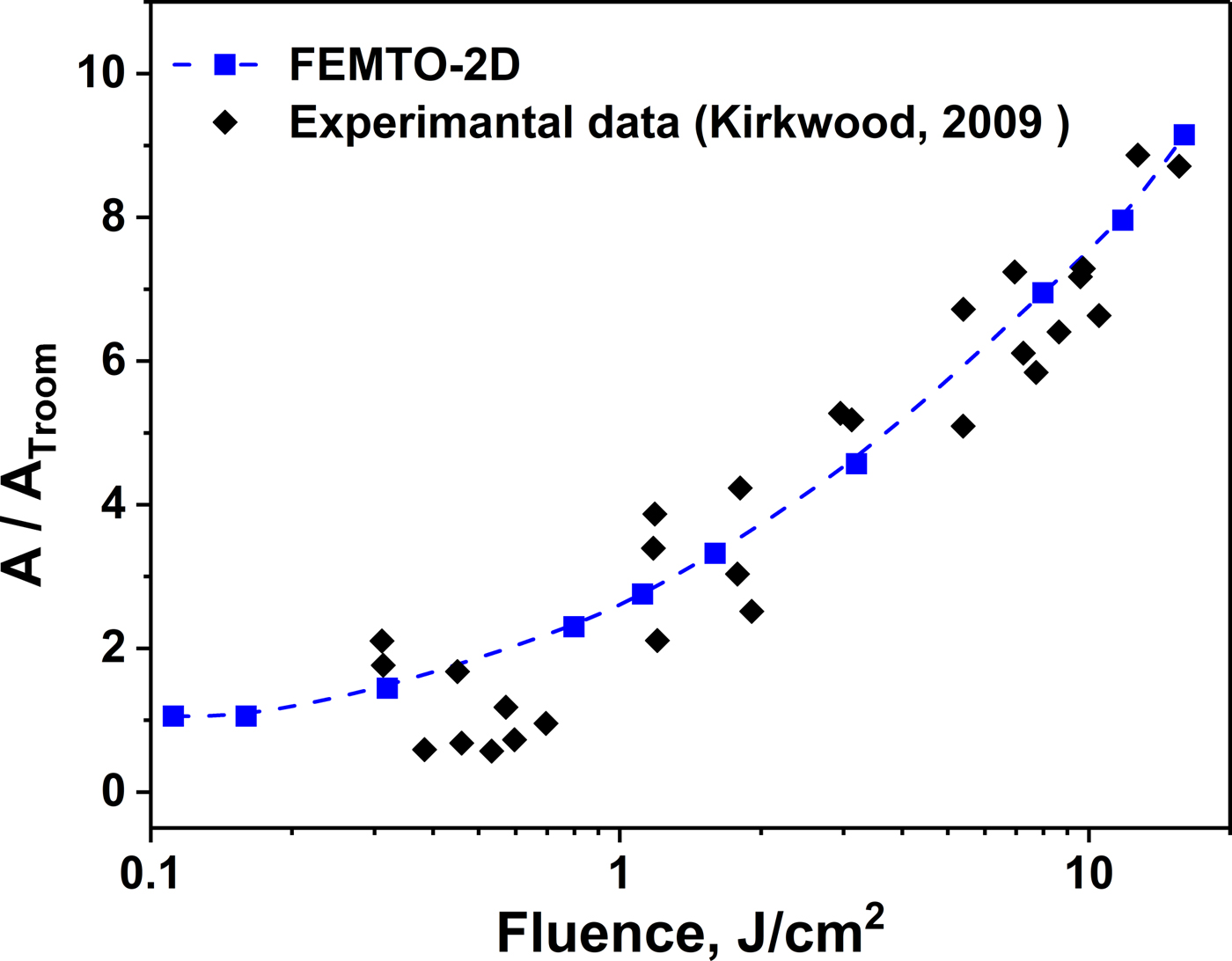
Fig. 1. Copper absorption normalized to the constant value at room temperature as function of the laser fluence. Comparison of FEMTO-2D simulations to experimental data by Kirkwood et al. (Reference Kirkwood, Tsui, Fedosejevs, Brantov and Bychenkov2009).
As seen from Figure 1, absorption efficiency for copper target increases by an order of magnitude within the laser fluence range considered in our work. Therefore, to account for changes in optical properties and its effect on the ablation, we consider absorbed laser fluence for further analysis.
Next, an ablation threshold fluence of 0.27 J/cm2 was defined for explosive boiling based on our simulations as the fluence at which the maximum lattice temperature at the surface reaches the temperature criterion for phase explosion (0.9T cr). Based on this parameter, we concluded that all except one of our experimental data correspond to the ablation regime with explosive boiling.
FEMTO-2D simulation predictions of the ablation and melted zone profiles were compared with ablation profiles from experiment measured using optical microscope profilometer for four laser energies: 0.14 mJ (corresponds to 0.2 J/cm2 absorbed fluence), 0.2 mJ (corresponds to 0.28 J/cm2 absorbed fluence), 0.4 mJ (corresponds to 0.91 J/cm2 absorbed fluence), and 0.77 mJ (corresponds to 2.37 J/cm2 absorbed fluence) as shown in Figure 2. At lowest laser fluence, FEMTO-2D predicts extremely shallow ablation profile solely due to evaporation; therefore, the additional scale was used for simulated ablation depth for 0.14 mJ laser pulse.
Fig. 2. Comparison of simulated melted zone profiles (dash-dotted green line), ablation via evaporation (purple line) for (a) −0.2 J/cm2, and ablation via pure phase explosion (red solid line) profiles for (b) −0.28 J/cm2, (c) −0.91 J/cm2, and (d) −2.37 J/cm2 with experimental data by optical profilometer (blue dots).
Analysis of the FIB cross-sectional SEM image of ablation profiles for 0.2 J/cm2 and 0.28 J/cm2 laser pulses (Fig. 3) confirms the measured maximum depth of the ablated crater. It also reveals the effect of the poor lateral resolution of the optical profilometer. Cross-sectional SEM images show very localized damage induced by USPLs with no cracks observed at the samples’ surfaces and underneath.
Fig. 3. Comparison of experimentally measured profiles (FIB-SEM and profilometer) with simulated predictions for (a) 0.20 J/cm2 and (b) 0.28 J/cm2 laser pulses.
In Figure 4, FEMTO-2D simulation predictions of ablation rate and melted pool depth for a single pulse as a function of absorbed laser fluence were compared with the experimental results predicted based on optical profilometry measurements. For convenience, logarithmic and semi-logarithmic scales were used.
Fig. 4. Comparison of experimental ablation rate to simulated ablation rate and melted pool depth: (a) – logarithmic scale, (b) – semi-logarithmic scale.
The first observation from Figures 2 and 4 is that our simulation predictions tend to underestimate the ablation rate in the given range of laser fluences. As described, FEMTO-2D accounts for two material removal mechanisms: evaporation and phase explosion, with the later proven to be dominant at the fluences above the phase explosion ablation threshold (simulated absorbed fluence of 0.27 J/cm2). However, in reality, several different material removal mechanisms identified for USPL induced ablation contribute to the final ablation rate (Price et al., Reference Price, More, Walling, Guethlein, Shepherd, Stewart and White1995; Perez & Lewis Reference Perez and Lewis2002). Several MD simulations (Perez & Lewis Reference Perez and Lewis2003; Lewis & Perez Reference Lewis and Perez2009; Zhigilei et al., Reference Zhigilei, Lin and Ivanov2009) demonstrated that at laser fluence just above the damage (melting) threshold, spallation is a dominating ablation mechanism. The spallation regime requires satisfaction of the requirement of stress confinement (for pulses below 1 ps pulse duration), and it is identified by significant melting and material removal in the form of large droplets. The transition from spallation to explosive boiling happens at higher laser intensities, and phase explosion becomes dominant. In FEMTO-2D simulations, phase explosion is considered as ‘pure’ explosive boiling solely based on the thermal criterion since TTM does not provide a way to account for the stress confinement induced by the USPLs. It was pointed out that phase explosion occurring under conditions of stress confinement takes place simultaneously with the relaxation of the laser-induced stresses, resulting in a more vigorous material ejection and higher ablation yields as compared to a “pure” phase explosion (Zhigilei et al., Reference Zhigilei, Lin and Ivanov2009). Therefore, it was expected to have lower ablation rate based on the simulations compared with experimental results. Based on the observation that the material removal depth in experiment never went beyond the simulated depth for a liquid phase at any considered laser intensity, FEMTO-2D proved to be useful for simulation and analysis of USPL induced ablation.
The second observation is that like many reported experimental results for USPL induced ablation, our experimental data clearly show two ablation regimes (Preuss et al., Reference Preuss, Demchuk and Stuke1995; Furusawa et al., Reference Furusawa, Takahashi, Kumagai, Midorikawa and Obara1999; Hashida et al., Reference Hashida, Semerok, Gobert, Petite, Izawa and Wagner2002; Colombier et al., Reference Colombier, Combis, Bonneau, Le Harzic and Audouard2005; Hirayama & Obara Reference Hirayama and Obara2005; Wang et al., Reference Wang, Ren, Cheng, Chen and Tzou2013). In literature, the first ablation regime at lower laser fluence is usually associated with the skin depth. It is assumed that due to low free electron density the energy transfer occurs only within the area characterized by the skin depth (an effective absorption depth) d (Furusawa et al., Reference Furusawa, Takahashi, Kumagai, Midorikawa and Obara1999). The ablation rate can then be fitted with the following logarithmic function: 
$L = \; d\; {\rm ln}(F/F_{{\rm th}}^{{\rm skin}} )$. Fitting our experimental data into the equation predicts d = 50 nm and 
$F_{{\rm th}}^{{\rm skin}} \approx 2F_{{\rm melt}} = 0.09\; J/cm^2$. For metallic targets, the skin depth is often referred as combination of the optical penetration depth and ballistic electron range, and it represents the depth of laser energy deposition inside the target (Wellershoff et al., Reference Wellershoff, Hohlfeld, Güdde and Matthias1999; Hohlfeld et al., Reference Hohlfeld, Wellershoff, Güdde, Conrad, Jähnke and Matthias2000; Schmidt et al., Reference Schmidt, Husinsky and Betz2002). The capability of FEMTO-2D simulation package to account for ballistic heat transfer and to predict the heat flux penetration profile was discussed in Suslova and Hassanein (Reference Suslova and Hassanein2018). An effective absorption depth was defined right after the laser pulse as the depth where maximum electron temperature (offset by 300 K) drops by a factor of e. The effect of ballistic electrons on the heat flux deposition profile is significant at low laser fluences and reduces considerably as the laser fluence increases due to higher electron density (Furusawa et al., Reference Furusawa, Takahashi, Kumagai, Midorikawa and Obara1999). Recent experimental work (Chen et al., Reference Chen, Sametoglu, Tsui, Ao and Ng2012) and our recent simulation results (Suslova & Hassanein, Reference Suslova and Hassanein2018) demonstrated that the ballistic component of the heat transfer becomes negligible above particular laser fluence. Based on the FEMTO-2D simulations for copper presented in Figure 5, the role of the ballistic heat transport in the initial heat distribution inside the target diminishes for the absorbed fluence range from melting threshold to around 0.9 J/cm2. The latter marks the upper limit for ballistic heat transport effect and corresponds to the end of the first ablation regime observed experimentally. Figure 5 shows how the effective laser abortion depth is determined right after the laser pulse, simulated temperature dependent optical penetration depth, and calculated ballistic range change with laser fluence in the low range of the fluences considered in this work.
Fig. 5. FEMTO-2D simulation of the effective absorption depth of the laser pulse in copper.
The maximum effective absorption depth for the laser intensity range between melting threshold and the end of the first ablation regime is 45 nm which close to the theoretically calculated electron mean-free path in copper at room temperature (42 nm) (Byskov-Nielsen et al., Reference Byskov-Nielsen, Savolainen, Christensen and Balling2011), optical penetration depth (42.7 ± 0.85 nm) determined based on the experimental results in Mannion et al. (Reference Mannion, Magee, Coyne, O'Connor and Glynn2004), and to the fitted value for d based on our experimental data. At laser fluences above 0.9 J/cm2, the estimated ballistic range remains at an almost constant value of 15 nm. This value for the ballistic range is commonly used to account for ballistic electron heat transport in copper (Byskov-Nielsen et al., Reference Byskov-Nielsen, Savolainen, Christensen and Balling2011; Cheng & Chen Reference Cheng and Chen2016). Thus, although FEMTO-2D is not designed to quantitatively predict the ablation profile due to the complexity of different ablation mechanisms, it confirms that the first ablation regime is related to the depth of the initial heat deposition when ballistic heat transport dominates over diffusive transport.
The second ablation regime is commonly referred to the case when hot electrons penetrate significantly deeper than skin layer before transferring their energy to the lattice. In literature, the second ablation regime is usually fitted with a function similar to the low fluence regime logarithmic function: 
$L = \; l\; {\rm ln}(F/F_{{\rm th}}^{{\rm td}} )$, where l corresponds to the electron thermal diffusion length. For copper, l found to be equal 80 nm at the threshold fluence of 1 J/cm2 (Hashida et al., Reference Hashida, Semerok, Gobert, Petite, Izawa and Wagner2002). In the fluence range from 1.26 J/cm2 to 2.36 J/cm2, the fitting function is in a good correlation with our experimental results (Fig. 2).
In addition, FEMTO-2D simulation results of ablation rate due to the phase explosion for the considered range of the laser intensities can also be fitted with logarithmic function 
$L = \; l\; {\rm ln}(F/F_{{\rm th}}^{{\rm pe}} )$, where l is the fitting parameter representing thermal conduction depth, and 
$F_{{\rm th}}^{{\rm pe}} $ is simulated threshold for explosive boiling. The best fit was achieved with l equal 80 nm. This was expected since phase explosion is purely temperature controlled ablation mechanism defined by the heat propagation dynamics.
Analysis of material ablation dynamics for two ablation mechanisms: spallation and explosive boiling
Despite FEMTO-2D ability to match the experimental results, the logarithmic fitting model discussed above does not provide detail information on the physical mechanisms of the material removal. Moreover, the fitting parameters are often determined based on the experimental data without clear theoretical explanation. To gain more understanding of the material removal dynamics, we have analyzed SEM images of four laser shots in our experiment considering MD simulation results presented in (Zhigilei et al., Reference Zhigilei, Lin and Ivanov2009) and our FEMTO-2D predictions (Fig. 6).
Fig. 6. SEM images of the central spot of the laser for (a) −0.20 J/cm2, (b) −0.28 J/cm2, (c) −0.91 J/cm2, (d) −2.37 J/cm2. Central column images were taken at 52o sample stage tilt.
FEMTO-2D simulations predict no material removal via phase explosion at laser fluences below 0.27 J/cm2. The transition from spallation to explosive boiling can be characterized by the change in the composition of the ejected ablated plume, that is, from large liquid droplets to a mixture of the small droplets and vapor-phase atoms (Zhigilei et al., Reference Zhigilei, Lin and Ivanov2009). Comparing two SEM images of the center spots of the laser shots at 0.20 J/cm2 (0.14 mJ) and 0.28 J/cm2 (0.20 mJ), we observed very few ‘loose’ particles at the lowest laser energy below the phase explosion threshold. However, at laser fluence right above the threshold (F th = 0.27 J/cm2), the particles density increases more than twice (Fig. 7) with the particles minimum size decreasing more than twice (Fig. 8) from around 80 nm to around 30 nm (based on the analysis of three different laser spots for each fluence). We attribute the drop in the minimum particle size to initiation of ablation via phase explosion. Further analysis showed that the minimum particles size at all fluences above the threshold for explosive boiling remained nearly the same. The analysis of the particle size distribution (Fig. 9) also shows an increasing fraction of the smaller particles at higher laser fluences. The observed particles density in the central region is linearly increasing as a function of the laser fluence up to 1 J/cm2. At the higher laser intensity, the role of the explosive boiling in the total ablation is increasing significantly and becomes dominant; therefore, the smaller fraction of the ablated material is redeposited in the central region in form of droplets or small particles. Extrapolating the linear trend to the lower laser fluence gives as an ablation threshold fluence in our experiment which is the same value for the spallation ablation threshold as estimated from the logarithmic fitting function 
$F_{{\rm th}}^{{\rm skin}} \approx 2F_{{\rm melt}} = 0.09\; J/{\rm c}{\rm m}^2$.
Fig. 7. Average particles density versus laser fluence.
Fig. 8. Size of the smallest particles at different laser fluences.
Fig. 9. Normalized particles size distribution.
The role of electron heat conduction and electron-lattice heat transfer dynamics at different ablation regimes
Another aspect of laser–material interactions, considered in this work is the interplay between electron–lattice coupling and hot electron heat transport during thermalization time. These two simultaneous processes are main factors that determine the material ablation rate and specific removal depth. The specific removal depth in this work is defined as the depth removed per unit incident fluence. Figure 10a shows how specific removal depth changes as a function of the laser fluence. We have identified three regions: first region characterized by extremely small specific removal depth due to evaporation; the second region coincides with the first ablation regime; and the third region coincides with the second ablation regime. The second region is characterized by rapidly increasing specific removal depth which reaches the maximum at around 1 J/cm2. In the third region, the specific removal depth starts decreasing, indicating reduced laser ablation efficiency. Similar trends were observed in several experimental works (Colombier et al., Reference Colombier, Combis, Bonneau, Le Harzic and Audouard2005; Polek Reference Polek2015).
Fig. 10. (a) Specific removal depth versus laser fluence; (b) Temperature dependence of coupling factor and electron thermal conductivity normalized to corresponding room temperature values.
Next, we have compared the behavior of the coupling factor and the hot electron conductivity (considering also a contribution from ballistic electrons) as a function of the electron temperature. To directly compare these two parameters, we have normalized them to their room temperature values. Three regions discussed in Figure 10a were identified on the Figure 10b with respect to the maximum electron temperature at given laser fluence. Based on the scope of this work, we focused on the regions II and III. As one can see from Figure 10b, region II corresponds to the electron temperature diapason where electron thermal conductivity has increased slightly more than coupling factor compared with their room temperature values. This means hot electrons can travel deeper into the target before depositing their energy to the lattice. As the electron temperature decreases, the coupling of electron energy to lattice is still taking place but at a slower rate. However, this region also coincides with the range where ballistic electrons play a significant role in the heat transfer and define the ablation profile. The third region is characterized by significantly faster-increasing coupling factor compared with the increase in thermal conductivity. Therefore, due to decreasing thermalization time, the distance that hot electrons can travel before reaching thermal equilibrium with lattice is increasing slower than in the second region. It is not very clear if such coincidence of regions for different specific removal depth trends, the transition between two discussed ablation mechanisms, and two ablation regimes indicate a direct connection to the material thermodynamic properties. More careful experimental and analytical analysis is required for different target materials to draw a conclusion.
Conclusion
Simulation results of femtosecond laser ablation of copper were compared with new experimental data. The numerical analysis was performed using our newly developed FEMTO-2D computer package based on the solution of the two-temperature model. Based on the analysis of the experimental results, we conclude that more than one ablation mechanism is contributing to the total material removal at the considered laser intensities in this study. Even though explosive boiling is commonly considered as dominant ablation mechanism for the USPL induced ablation, the ‘pure’ phase explosion simulated based on the temperature profiles underestimates the total material removal. We attributed that to the expected enhancement of the explosive boiling ablation under the condition of the stress confinement satisfied for sub-picosecond laser pulses. With FEMTO-2D simulation package, based on the solution of the two-temperature model, we could estimate the maximum possible ablation depth by simulating the melted pool profile. However, predicted ablation profile based on the phase explosion criterion slightly underestimates material removal rate at the investigated laser intensities. Another factor that might have also contributed to the difference in ablation profiles between experiment and computer simulation is due to multiple shots used during experiment versus single shot predictions from simulations. Multiple shots were used in our experiment because of very low ablation rate at the given laser fluences such that ablation from the single shot near threshold fluence would be comparable, for example, to the surface morphology resulted from polishing. Further investigation on the effect of a number of pulses on ablation depth at different laser fluence is required to evaluate the significance of this factor. Nevertheless, FEMTO-2D simulations provided additional details to enhance our understanding of the ablation mechanisms in metals during femtosecond laser interactions with materials.
We found that during the fast ablation regime, that is, when the ablation rate increases significantly with the laser intensity at low laser fluence, can be correlated with the intensity range were ballistic electrons play a dominant role in heat transfer. Simulated laser intensity limit for ballistic electrons domination corresponds to the upper limit of the first ablation regime where material removal depth is associated with the skin layer depth. The predicted maximum effective laser deposition range (can be interpreted as skin layer depth) is similar to the fitting parameter for the first ablation regime based on our experimental data. We also observed a rapid growth of specific removal depth with increasing absorbed laser fluence for laser intensity range corresponding to the fast ablation regime. After the transition to the second ablation regime, specific removal depth starts to decrease with increasing absorbed laser fluence. We have demonstrated that by analyzing the relation between electron thermal conductivity and electron–lattice coupling factor calculated using FEMTO-2D, it is possible to predict the transition zone between two ablation regimes. This allows predicting laser parameters corresponding to the maximum efficiency of laser-induced ablation (depth removed per energy unit). Our experimental results demonstrate that two ablation mechanisms (spallation and phase explosion) may simultaneously contribute to the total material ablation in the first ablation regime with a significant increase of phase explosion role with laser intensity.
For the second ablation regime, experimental data for different laser intensities follows the same trend as simulated ablation rate for explosive boiling and they both can be fitted with the well-known logarithmic function. The explanation is that the second ablation regime is associated with the hot electron diffusion depth, which is directly defined by the electron temperature. The phase explosion – a purely temperature controlled ablation mechanism, is defined by heat propagation dynamics. The simulation data show that laser ablation efficiency for the second ablation regime is lower than the first ablation regime. We attributed that to faster increasing coupling factor compared with the electron thermal conductivity. High coupling factor results in a rapid heating, which is the main reason for the phase explosion. Analysis of SEM images from our experiments also supports the hypothesis that phase explosion is a dominant ablation mechanism for the second ablation regime.
Acknowledgments
This work is partially supported by the NSF, PIRE project.
