Introduction
With the advent of high-power lasers, generation of high energetic ions has become possible by the interaction of high-intensity laser pulses with plasmas. Ion acceleration has become an interesting and active area of research due to its numerous applications such as fast ignition scenarios (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001), proton radiography (King et al., Reference King, Ables, Adams, Alrick, Amann, Balzar, Barnes, Crow, Cushing, Eddleman, Fife, Flores, Fujino, Gallegos, Gray, Hartouni, Hogan, Holmes, Jaramillo, Knudsson, London, Lopez, McDonald, McClelland, Merrill, Morley, Morris, Naivar, Parker, Park, Pazuchanics, Pillai, Riedel, Sarracino, Shelley, Stacy, Takala, Thompson, Tucker, Yates, Ziock and Zumbro1999), proton imaging techniques (Borghesi et al., Reference Borghesi, Schiavi, Campbell, Haines, Willi, Mackinnon, Patel, Galimberti and Gizzi2003), nuclear physics (Bychenkov et al., Reference Bychenkov, Tikhonchuk and Tolokonnikov1999), cancer therapy (Khoroshkov and Minakova, Reference Khoroshkov and Minakova1998; Bulanov et al., Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro2002), as well as in astrophysics (Remington et al., Reference Remington, Drake and Takabe2000). Multi-MeV ions generated experimentally (Clark et al., Reference Clark, Krushelnick, Davies, Zepf, Tatarakis, Beg, Machacek, Norreys, Santala, Watts and Dangor2000; Maksimchuk et al., Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov2000; Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Fuchs et al., Reference Fuchs, Antici, d'Humieres, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2006) can be explained via The target normal sheath acceleration (TNSA) (Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001; Mora, Reference Mora2003) mechanism in which the ions are accelerated from the target rear side by a sheath field generated by a cloud of hot electrons. The hot electrons generated by the high-intensity laser at the target front-side travel through the target and on reaching the target rear side form a highly negatively charged sheath whose electric field accelerates the ions in the target normal direction. Ions can be accelerated more effectively by the laser ponderomotive force to high energies from the target front side by using ultra intense circularly polarized (CP) laser pulses via radiation pressure acceleration (RPA) (Naumova et al., Reference Naumova, Schlegel, Tikhonchuck, Labaune, Sokolov and Mourou2009; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuck, Labaune, Sokolov and Mourou2009).
Most of the ion acceleration experiments deal with solid target interactions. Near-critical plasmas such as cluster gas targets and foam targets can also be used to accelerate ions efficiently up to multi-MeV energies and also to enhance the collimation of energetic ion beam. Collimation is a very essential characteristic of accelerated ions which should be enhanced as the lack of collimation limits the use of high energetic ions for potential applications. Replenishable cluster targets facilitate high repetition rate of accelerated ions which are free from plasma debris and are highly collimated (Fukuda et al., Reference Fukuda, Faenov, Tampo, Pikuz, Nakamura, Kando, Hayashi, Yogo, Sakaki, Kameshima, Pirozhkov, Ogura, Mori, Esirkepov, Koga, Boldarev, Gasilov, Magunov, Yamauchi, Kodama, Bolton, Kato, Tajima, Daido and Bulanov2009). The motion of a laser pulse through near-critical plasma targets can lead to the formation of magnetic dipole structure which can accelerate the ions efficiently from the target rear side via magnetic vortex acceleration (MVA) (Bulanov and Esirkepov, Reference Bulanov and Esirkepov2007; Fukuda et al., Reference Fukuda, Faenov, Tampo, Pikuz, Nakamura, Kando, Hayashi, Yogo, Sakaki, Kameshima, Pirozhkov, Ogura, Mori, Esirkepov, Koga, Boldarev, Gasilov, Magunov, Yamauchi, Kodama, Bolton, Kato, Tajima, Daido and Bulanov2009; Bulanov et al., Reference Bulanov, Bychenkov, Chvykov, Kalinchenko, Litzenberg, Matsuoka, Thomas, Willingale, Yanovsky, Krushelnick and Maksimchuk2010; Nakamura et al., Reference Nakamura, Bulanov, Esirkepov and Kando2010a) generating collimated energetic ions. Moreover, near-critical targets support the formation of plasma waveguide which makes it possible for the laser pulse to penetrate deeper into the plasma and generate abundant number of hot electrons. Nakamura et al. (Reference Nakamura, Tampo, Kodama, Bulanov and Kando2010b) have reported experimental results on ion acceleration from SiO2 foam attached with a thin Al target. They have observed that the bulk electrons inside the foam region are heated up to MeV energies and abundant number of hot electrons are generated which increases the laser–plasma energy coupling and enhances the maximum ion energy. Bin et al. (Reference Bin, Ma, Wang, Streeter, Kreuzer, Kiefer, Yeung, Cousens, Foster, Dromey, Yan, Ramis, Meyer-ter-Vehn, Zepf and Schreiber2015) have reported experimental results supported by three-dimensional (3D) particle-in-cell (PIC) simulations on accelerating ions from carbon nanotube foams attached with thin diamond-like carbon targets. They have observed that the high-intensity laser pulse on propagating through the near-critical carbon nanotube region undergoes relativistic self-focussing resulting in an extremely steep rising edge laser pulse profile which causes a significant enhancement in the carbon ion energies consistent with a transition to RPA. Willingale et al. (Reference Willingale, Mangles, Nilson, Clarke, Dangor, Kaluza, Karsch, Lancaster, Mori, Najmudin, Schreiber, Thomas, Wei and Krushelnick2006) have reported an experimental observation of a collimated He2+ ion beam generated via TNSA mechanism having a maximum energy of 40 MeV by a petawatt-class laser from a gas jet target. Ions can also be accelerated to multi-MeV energies from underdense plasmas (Krushelnick et al., Reference Krushelnick, Clark, Najmudin, Salvati, Santala, Tatarakis, Dangor, Malka, Neely, Allott and Danson1999). A very high-intensity laser on propagation through the underdense plasma causes a ponderomotive expulsion of electrons from the high-intensity region at the central axis along the radial directions which create a central ion channel. Thus, a large space-charge field is generated which accelerates the ions along transverse directions via Coulomb explosion (Sarkisov et al., Reference Sarkisov, Bychenkov, Novikov, Tikhonchuk, Maksimchuk, Chen, Wagner, Mourou and Umstadter1999). Ions can also be accelerated from underdense plasmas via collisionless shock acceleration (Wei et al., Reference Wei, Mangles, Najmudin, Walton, Gopal, Tatarakis, Dangor, Clark, Evans, Fritzler, Clarke, Hernandez-Gomez, Neely, Mori, Tzoufras and Krushelnick2004). However, these accelerated ions have poor collimation due to high transverse momentum. Willingale et al. (Reference Willingale, Nagel, Thomas, Bellei, Clarke, Dangor, Heathcote, Kaluza, Kamperidis, Kneip, Krushelnick, Lopes, Mangles, Nazarov, Nilson and Najmudin2009) have reported experimental observations on the propagation of a high-intensity laser in foam targets generating energetic proton beams in the relativistic transparent regime. They have observed that the laser beam propagates deeper into the target due to its relativistic propagation and results in greater collimation of the hot electrons which enhances the rear surface accelerating field and hence increases the efficiency of acceleration.
Generation of ultra-strong magnetic fields has gained a lot of interest recently. Magnetic fields of the order of 100 T sustainable up to longer time duration can now be readily produced using conventional techniques (Sims et al., Reference Sims, Rickel, Swenson, Schillig and Ammerman2008; Debray and Frings, Reference Debray and Frings2013). Higher strength fields operating at shorter timescales are also produced (Schmit et al., Reference Schmit, Knapp, Hansen, Gomez, Hahn, Sinars, Peterson, Slutz, Sefkow, Awe, Harding, Jennings, Chandler, Cooper, Cuneo, Geissel, Harvey-Thompson, Herrmann, Hess, Johns, Lamppa, Martin, McBride, Porter, Robertson, Rochau, Rovang, Ruiz, Savage, Smith, Stygar and Vesey2014). Interaction of intense ultrashort laser pulses with dense plasmas can lead to the generation of huge magnetic fields of the order of 108 G (Wilks et al., Reference Wilks, Kruer, Tabak and Langdon1992; Sandhu et al., Reference Sandhu, Dharmadhikari, Rajeev, Kumar, Sengupta, Das and Kaw2002; Tatarakis et al., Reference Tatarakis, Watts, Beg, Clark, Dangor, Gopal, Haines, Norreys, Wagner, Wei, Zepf and Krushelnick2002; Mondal et al., Reference Mondal, Narayanan, Ding, Lad, Hao, Ahmad, Wang, Sheng, Sengupta, Kaw, Das and Kumar2012). Magnetic fields of the order of kT can be produced experimentally in the interaction of kilo-Joule high-power lasers with a capacitor-coil target (Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013; Santos et al., Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d'Humieres, Hulin, Ishihara, Kojima, Loyez, Marques, Morace, Nicolai, Peyrusse, Poye, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey2015) which is significant for a number of applications such as inertial confinement fusion (Wang et al., Reference Wang, Gibbon, Sheng and Li2015). These magnetic fields can play a significant role in the high-energy electron flow induced during intense laser–plasma interactions and hence has attracted the attention of a lot of researchers working in this field. Hosokai et al. (Reference Hosokai, Kenishita, Zhidkov, Maekawa, Yamazaki and Uesaka2006) have experimentally observed that the emittance and total charge of electron beams generated by laser-wakefield acceleration gets significantly enhanced on applying a static magnetic field directed along the laser axis of propagation. The formation of solitons during the interaction of an intense laser pulse with plasma in the presence of a strong magnetic field has been studied (Farina et al., Reference Farina, Lontano and Bulanov2000; Borhanian et al., Reference Borhanian, Kourakis and Sobhanian2009). Bulanov et al. (Reference Bulanov, Esirkepov, Kando, Koga, Hosokai, Zhidkov and Kodama2013) have presented an analytical description of the strongly non-linear oscillations in magnetized plasmas, which show that the magnetic field prevents the closing of the cavity formed behind the laser pulse. Yang et al. (Reference Yang, Yu, Xu, Yu, Ge, Xu, Zhuo, Ma, Shao and Borghesi2015) have shown that the plasma transparency in the presence of magnetic field gets enhanced in case of a right circularly polarized (RCP) light, which is beneficial for plasma acceleration. Wilson et al. (Reference Wilson, Li, Weikum and Sheng2017) have presented an analytical description as well as 1D and 3D-PIC simulation results on the influence of externally applied strong magnetic fields on laser pulse propagation in an underdense plasma and have shown that the electron motion gets dramatically enhanced in case of an RCP light, whereas in case of a left circularly polarized (LCP) light, the electron motion gets dampened and causes a reduction in instability growth. Sharma et al. (Reference Sharma, Liu and Tripathi2010) have analytically investigated the acceleration of ions from an overdense plasma target and have shown that RCP and LCP lasers act differently towards acceleration due to a change in dielectric constant because of cyclotron effects which in turn enhance or reduce the ponderomotive force. Kuri et al. (Reference Kuri, Das and Patel2017) have presented 3D-PIC simulation results where they have shown that the axial magnetic field favors acceleration by TNSA in case of an RCP laser, whereas protons get accelerated more effectively to higher energy by RPA in case of a LCP laser. Gong et al. (Reference Gong, Cao, Pan, Xiao, Wu, Zheng, Liu and He2017) have investigated the acceleration of protons by an RCP laser from a cone target in the presence of a 50 000 T longitudinal magnetic field via 2D-PIC simulations. They have shown that both the energy and yield of the sheath-accelerated protons at the target rear side increase remarkably due to enhanced coupling efficiency from RCP laser energy to electrons.
In the present work, we investigate the role played by an axial magnetic field in accelerating protons and most importantly in enhancing the collimation of the accelerated protons from a near-critical plasma target by linearly polarized (LP) and CP laser pulses with the help of 3D-PIC simulations using the code Picpsi-3D (Upadhyay et al., Reference Upadhyay, Patel, Rao, Naik and Gupta2012). It is observed that the collimation of proton beams increases significantly in the presence of an axial magnetic field. Collimation is observed to be highest in case of a LP laser in the presence of magnetic field. However, protons accelerated by an RCP laser are not only highly collimated but are also highly energetic having highest axial momentum. The paper is organized as follows. “The 3D-PIC simulation model” section represents the detailed parameters of 3D-PIC simulation. Detailed analysis of proton acceleration and beam collimation has been presented in “Generation of collimated proton beams” section. The conclusions are presented in “Conclusion” section.
The 3D-PIC simulation model
A laser of wavelength λ = 1 μm, normalized electric field amplitude a 0( = eE 0/m eωc) ≈ 6 which corresponds to an intensity of 5 × 1019 W/cm2, pulse duration τ = 50 fs (FWHM) is incident on a near-critical plasma target of density 3.35 × 1021 cm−3 (3n c). Here, n c = m eω2/4πe 2 is the critical density, where e and m e are the charge and mass of an electron, respectively, ω is the laser frequency, E 0 is the laser electric field amplitude, and c is the speed of light. The spot size of the laser pulse is 3 µm (FWHM) and the laser period T 0( = λ/c) is 3.3 fs. A simulation box of dimensions 14 µm × 14 µm × 25 µm consisting of 140 × 140 × 250 cells has been used. The near-critical plasma of height and width 10 µm and thickness 18 µm is sharply edged and is located at a distance of 2 µm from the left boundary of the simulation box as shown in Figure 1. The plasma thickness of 18 µm is chosen to ensure complete laser penetration. Since, the length ( = cτ) of the laser pulse is 15 µm, the plasma thickness should be at least of the order of laser pulse length in order to achieve maximum penetration. This deep penetration results in volumetric heating of the plasma slab generating large number of hot electrons which can create strong electric fields. A magnetic field of B = 50 MG (ωce/ω ≈ 0.5) is applied along Z which is the axial direction. The simulations have been done for five different cases (i) CP with B = 0 G, (ii) RCP with B = 50 MG, (iii) LCP with B = 50 MG, (iv) LP with B = 0 G, and (v) LP with B = 50 MG. A vacuum gap of 5 µm is maintained across the target rear side in all cases. Absorbing boundary conditions has been incorporated along all the three directions. The simulations are done with 25 macroparticles per cell. The ions considered in these simulations are protons with mass m i = 1836 m e . ![]() ${\rm \omega} _{{\rm pe}} = \sqrt {4{\rm \pi} n_{\rm e}e^2/m_{\rm e}} $ and ωce = eB/m ec are the electron plasma frequency and electro cyclotron frequency, respectively, where n e is the electron plasma density. The plasma is initially assumed to be cold with T e = T i = 0, where T e and T i are the electron and ion temperatures, respectively.
${\rm \omega} _{{\rm pe}} = \sqrt {4{\rm \pi} n_{\rm e}e^2/m_{\rm e}} $ and ωce = eB/m ec are the electron plasma frequency and electro cyclotron frequency, respectively, where n e is the electron plasma density. The plasma is initially assumed to be cold with T e = T i = 0, where T e and T i are the electron and ion temperatures, respectively.
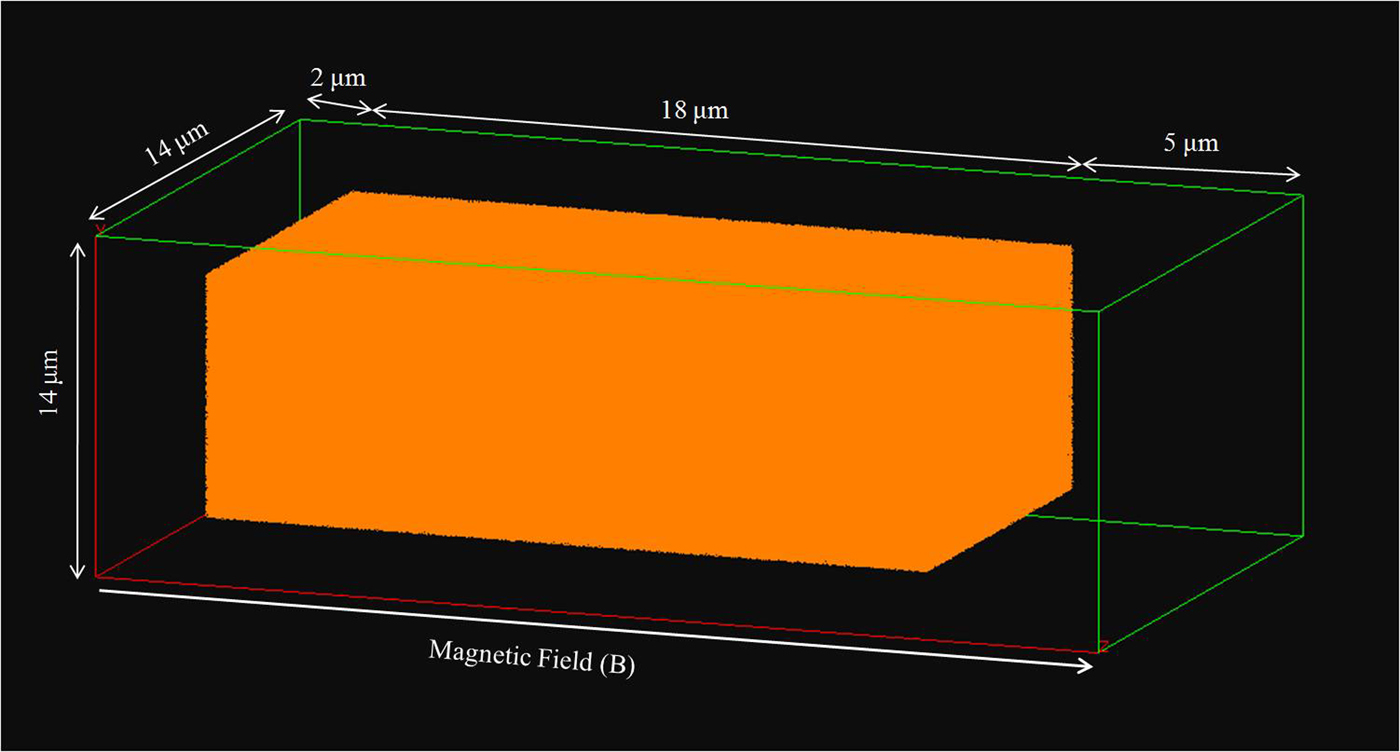
Fig. 1. The 3D-PIC geometry of the simulation box.
Generation of collimated proton beams
The cyclotron effects play an important role in the generation of hot electrons. An RCP laser and a LCP laser act differently on electrons in the presence of an axial magnetic field due to cyclotron effects. In case of an RCP laser, the direction of rotation of electrons by the laser electric field and the direction of electron gyrations by an axial magnetic field are same, which enhances the effect of the laser ponderomotive force. Hence, the electrons gain more energy in case of an RCP laser. On the other hand, in case of a LCP laser, the direction of electron rotations by the laser electric field and the axial magnetic field gyrations is opposite which reverses the cyclotron effects. This opposes the electron motion and causes a reduction in the electron energy. Thus, the electrons move longer distances on gaining higher energy in case of an RCP laser. Whereas, in case of a LCP laser, the electrons tend to get accumulated at the tip of the laser pulse, which may increase the local electron density at the laser pulse front (Kuri et al., Reference Kuri, Das and Patel2017).
The hot electrons reach the target rear side and form a hot electron sheath which accelerates the protons from the target rear side via TNSA mechanism as shown in Figure 2. Since, the electrons gain more energy by an RCP laser in the presence of an axial magnetic field, the hot electrons reach the target rear side quickly and form the hot electron sheath. The axial sheath electric field is strongest in case of an RCP laser as compared with all the other cases at time 101 T 0 as shown in Figure 2(b2). Comparing Figure 2(b1) and 2(b4), it can be observed that in the absence of magnetic field, the sheath field by a CP laser is stronger than that by a LP laser. This might be due to the dominant effect of radiation pressure as the oscillatory component of the ponderomotive force is absent in case of a CP laser. Since, the transverse motion of the hot electrons generated by a LP laser gets restricted in the presence of an axial magnetic field, the hot electron number as well as the energy along the axial direction is increased which makes the sheath field stronger as shown in Figure 2(b5).
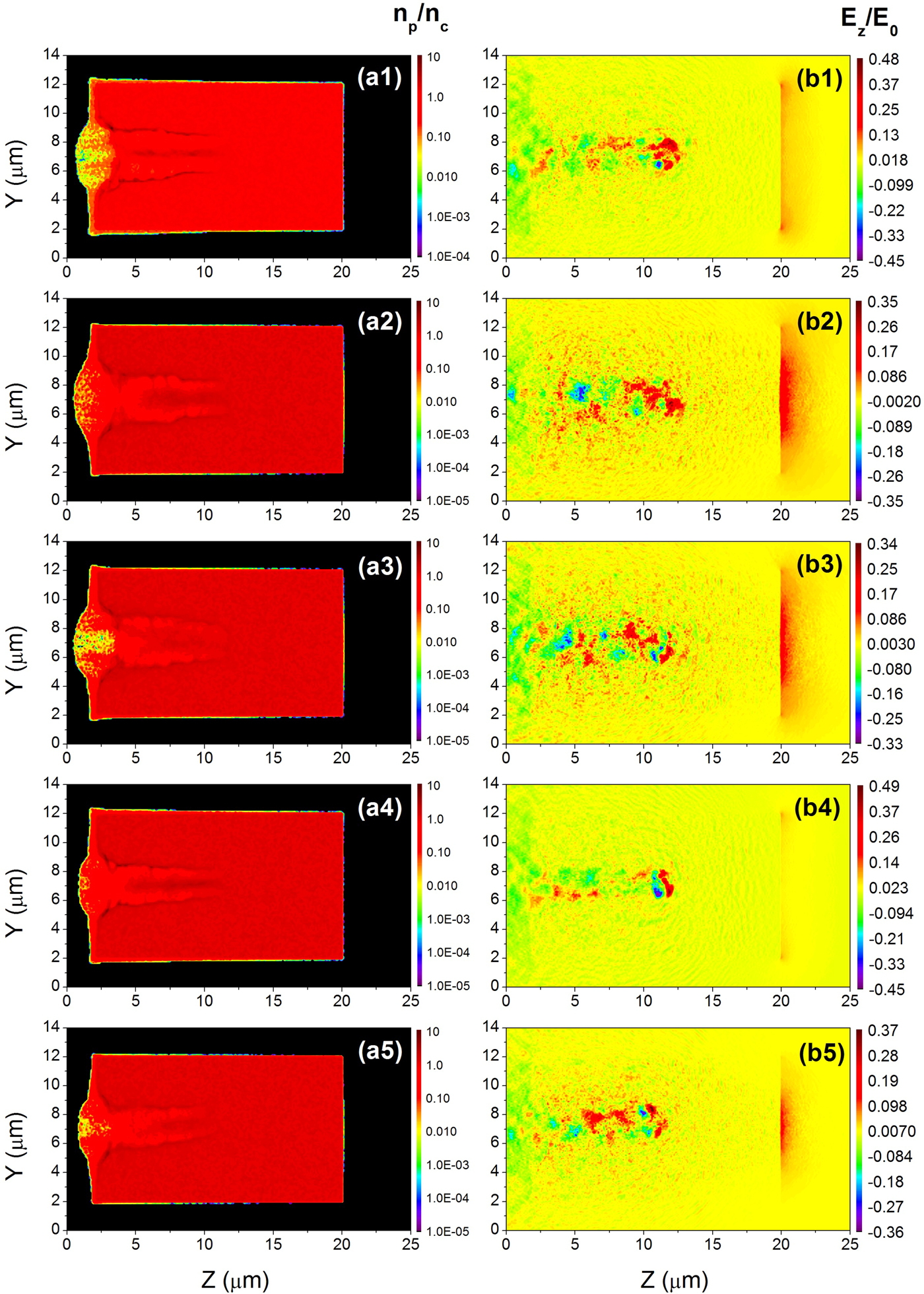
Fig. 2. Proton density distribution (a1–a5) and axial electric field (b1–b5) in the central YZ plane (X = 7 µm) at time 101 T 0, respectively, for (a1, b1) CP with B = 0 G; (a2, b2) RCP with B = 50 MG; (a3, b3) LCP with B = 50 MG; (a4, b4) LP with B = 0 G; and (a5, b5) LP with B = 50 MG. The proton density n p is normalized by the critical density n c = 1.12 × 1021 cm−3 and the axial electric field E z is normalized by the laser electric field E 0.
Comparing all the five cases at time 101 T 0, it can be observed that the protons gain highest momentum at the target rear side in case of an RCP laser in the presence of an axial magnetic field due to efficient hot electron generation as shown in Figure 3(b). However, it can also be observed that the forward momentum gained by the protons at the target front side is higher in case of a CP laser in the absence of magnetic field and a LCP laser in the presence of magnetic field as shown in Figure 3(a) and 3(c) respectively. Since, the oscillatory component of the laser ponderomotive force is absent in case of a CP laser, the radiation pressure can effectively form an electrostatic charge separation region at the target front side and accelerate protons in the forward direction. In case of a LCP laser, due to reverse cyclotron effects, there might be an electron accumulation at the laser pulse front which can strengthen the electrostatic charge separation region at the target front side and accelerate protons effectively in the forward direction. Thus, traces of RPA-accelerated protons are also observed in these two cases but TNSA overtakes the acceleration process eventually. Since, the ponderomotive force gets enhanced in case of an RCP laser, the electrons gain high energy and move fast across the target rear side which accelerates the protons via TNSA mechanism. Thus, front-side acceleration is least and rear-side acceleration is highest in case of an RCP laser in the presence of an axial magnetic field. In case of a LP laser, the protons gain more momentum at the target rear side in the presence of an axial magnetic field as the transverse hot electron motion is restricted due to cyclotron effects resulting more number of hot electrons to flow along the axial direction and generate stronger sheath field which enhances the acceleration as shown in Figure 3(e).

Fig. 3. Normalized proton axial momentum p z/m ic phase space for (a) CP with B = 0 G, (b) RCP with B = 50 MG, (c) LCP with B = 50 MG, (d) LP with B = 0 G, and (e) LP with B = 50 MG at time 101 T 0.
The acceleration of protons at time 147 T 0 is shown in Figure 4. The transverse motion of protons gets considerably reduced in the presence of an axial magnetic field due to cyclotron effects as observed from the proton density plots shown in Figure 4(a1–a5). The protons gain highest forward momentum along the axis at the target rear side in case of an RCP laser as shown in Figure 4(b2). As evident from the proton axial momentum phase space plots, the protons are accelerated mainly via TNSA mechanism. It can also be observed from the proton density plots that the laser penetrates deeper into the plasma in the absence of magnetic field. Since, the plasma can expand freely in the absence of magnetic field, the laser penetration does not get affected. The penetration decreases in the presence of magnetic field due to restricted transverse electron motion which causes more number of hot electrons to be present along the axial direction. These hot electrons restrict laser pulse penetration.

Fig. 4. Proton density distribution (a1–a5) in the central YZ plane (X = 7 µm) and normalized proton axial momentum p z/m ic phase space (b1–b5) at time 147 T 0, respectively, for (a1, b1) CP with B = 0 G; (a2, b2) RCP with B = 50 MG; (a3, b3) LCP with B = 50 MG; (a4, b4) LP with B = 0 G; and (a5, b5) LP with B = 50 MG. The proton density n p is normalized by the critical density n c = 1.12 × 1021 cm−3.
A CP laser on propagation through an underdense plasma can generate an axial magnetic field via inverse Faraday effect (Steiger and Woods, Reference Steiger and Woods1972; Bychenkov and Tikhonchuk, Reference Bychenkov and Tikhonchuk1996; Berezhiani et al., Reference Berezhiani, Mahajan and Shatashvili1997; Gorbunov and Ramazashvili, Reference Gorbunov and Ramazashvili1998; Naseri et al., Reference Naseri, Bychenkov and Rozmus2010). The direction of such magnetic fields in case of an RCP and a LCP laser is opposite to each other (Naseri et al., Reference Naseri, Bychenkov and Rozmus2010). These magnetic fields are localized within the laser pulse and do not penetrate in the surrounding plasma. The amplitude is highest along the laser axis and decreases along the transverse directions. These quasistationary magnetic fields are generated in a short time scale ![]() ${\rm \Delta} t = r_0^2 /c^2{\rm \tau} $ (Bychenkov and Tikhonchuk, Reference Bychenkov and Tikhonchuk1996) where r 0 is the radius of the laser pulse. For the present simulation parameters, we have
${\rm \Delta} t = r_0^2 /c^2{\rm \tau} $ (Bychenkov and Tikhonchuk, Reference Bychenkov and Tikhonchuk1996) where r 0 is the radius of the laser pulse. For the present simulation parameters, we have ![]() ${\rm \Delta} t \approx 0.5{\kern 1pt} \hbox{fs}$ which is a very short time scale as compared with the acceleration time 147 T 0 which corresponds to
${\rm \Delta} t \approx 0.5{\kern 1pt} \hbox{fs}$ which is a very short time scale as compared with the acceleration time 147 T 0 which corresponds to ![]() $ \approx 0.5{\kern 1pt} \,\hbox{ps}$. Hence, the effect caused by these quasistatic short-scale magnetic fields on the acceleration process would be negligible as compared with that caused by the static magnetic field. Moreover, unlike these quasistatic magnetic fields which exist only inside the laser pulse, the applied static magnetic field is present throughout the plasma which is essential for proper guiding of the hot electrons along the laser axis towards the target rear surface.
$ \approx 0.5{\kern 1pt} \,\hbox{ps}$. Hence, the effect caused by these quasistatic short-scale magnetic fields on the acceleration process would be negligible as compared with that caused by the static magnetic field. Moreover, unlike these quasistatic magnetic fields which exist only inside the laser pulse, the applied static magnetic field is present throughout the plasma which is essential for proper guiding of the hot electrons along the laser axis towards the target rear surface.
The axial and transverse momentum phase space plots for all the cases are shown in Figure 5. It can be observed that the axial magnetic field significantly reduces the transverse momentum of the accelerated protons. The protons gain more momentum along the laser axis in the presence of an axial magnetic field which also causes an increase in the collimation of energetic protons. As the sheath electric field is built up at the target rear side and the protons start getting accelerated, they gain momentum both along the transverse and axial directions. This causes the transverse proton momentum to rise suddenly at the target rear side in all the cases which causes the formation of wing-shaped patterns in the phase space as shown in Figure 5(a1–a5). Since the transverse proton motion throughout the target is significantly reduced in the presence of magnetic field, the transverse momentum seem to rise sharply at the target rear side in this case. This rise in transverse proton momentum experiences a sharp fall making the wing-shaped patterns more prominent and the protons emerge out as a highly collimated beam from the target rear side with remarkably reduced values of transverse momentum. Collimation of protons accelerated by a LP laser in the presence of magnetic field appears to be highest due to smallest spot size among all the cases as shown in Figure 6. However, the axial momentum is observed to be higher in case of an RCP laser as can be concluded by comparing Figure 5(b2) and 5(b5). Moreover, the energy spectrum plotted in Figure 7 shows that the protons accelerated by a LP laser though more collimated but are less energetic than those accelerated by an RCP laser in the presence of magnetic field. In case of a LCP laser, the proton beams seem to be collimated but the number of protons having transverse momentum is also high as shown in Figure 5(b3). Hence, collimation in case of a LCP laser is not as effective as compared with that of an RCP laser. Moreover, the maximum proton energy obtained in case of a LCP laser is also lower than that of an RCP laser. Since in the absence of magnetic field, the plasma does not experience any restriction in expansion along transverse directions, it becomes possible for the laser pulse to penetrate deeper and generate more number of energetic protons having higher values of transverse momentum. As the transverse motion of protons is restricted in the presence of magnetic field, the number of protons having transverse momentum values is low. Since, the transverse momentum contributes significantly towards increasing the total energy of protons, the maximum proton energy is less in the presence of magnetic field. The proton energy is thus observed to be highest in case of a CP laser in the absence of magnetic field. The presence of magnetic field thus improves the beam collimation but in turn reduces the maximum energy.

Fig. 5. Normalized proton momentum phase space (a1–a5) p y/m ic versus Z (μm) and (b1–b5) p y/m ic versus p z/m ic at time 147 T 0, respectively, for (a1, b1) CP with B = 0 G; (a2, b2) RCP with B = 50 MG; (a3, b3) LCP with B = 50 MG; (a4, b4) LP with B = 0 G; and (a5, b5) LP with B = 50 MG.

Fig. 6. Proton density distribution in the XY plane (Z = 23.6 μm) for (a) RCP with B = 50 MG at time 147 T 0, (b) LCP with B = 50 MG at time 150 T 0, and (c) LP with B = 50 MG at time 154 T 0. The proton density n p is normalized by the critical density n c = 1.12 × 1021 cm−3.

Fig. 7. Proton energy spectrum for CP with B = 0 G (red solid), RCP with B = 50 MG (green solid), LCP with B = 50 MG (blue solid), LP with B = 0 G (pink solid), and LP with B = 50 MG (orange solid) at time 147 T 0. The proton number N is normalized by the total number of protons N 0 in each case.
The effect of an axial static magnetic field was also studied by Kuri et al. (Reference Kuri, Das and Patel2017), where the simulations were done for a comparatively dense target and it was observed that both RPA and TNSA were the actively participating mechanisms in the acceleration process. The axial magnetic field causes a synergy in these two processes which can be controlled by either using an RCP or a LCP laser. It was observed that RCP favors TNSA and LCP favors RPA. However, RPA was observed to be the dominating acceleration mechanism in case of dense targets. A minor enhancement of collimation was also observed. In the present work, since the plasma is near-critical, the laser is able to penetrate longer distance inside the plasma and TNSA is the dominating acceleration mechanism. Thus, the cyclotron effects are carried by the laser pulse itself deeper into the plasma which is responsible for the collimation. In case of a dense target as shown by Kuri et al. (Reference Kuri, Das and Patel2017), the cyclotron effects are carried on by the laser pulse up to the hole-boring depth. Beyond this depth, the cyclotron effects are carried forward into the upstream region by the hot electrons generated at the target front surface. Hence, though a significant enhancement in the proton energy was observed, the collimation as speculated from the proton beam spot size was not significant as such.
Creation of a strong magnetic field of the order of 50 MG might seem to be difficult via conventional techniques. However, it is to be noted that the maximum proton energy in our simulations is obtained at a time ≈0.5 ps. Thus, instead of having a constant source of magnetic field, production of a high-amplitude static magnetic field sustainable at least up to a time duration of ≈0.5 ps should serve the purpose of collimation as shown in our simulations.
Conclusion
The effect of an axial magnetic field on enhancing the collimation of the energetic proton beams generated from a near-critical plasma target has been investigated with the help of 3D-PIC simulations. The effect of laser pulse polarization combined with the cyclotron effects has also been studied by using both LP and CP laser pulses. The conclusions drawn from the above discussions can be summarized as follows:
(i) Protons are observed to get accelerated via TNSA mechanism and the acceleration is higher in case of a CP laser than that of a LP laser.
(ii) Presence of an axial magnetic field reduces the transverse motion of protons and enhances the axial momentum due to cyclotron effects.
(iii) Traces of RPA protons are also observed in case of a CP laser in the absence of magnetic field and LCP laser in the presence of magnetic field. However, TNSA appears to be enhanced in case of an RCP laser in the presence of magnetic field.
(iv) In case of a LP laser, the presence of an axial magnetic field increases the acceleration as the transverse hot electron motion is reduced due to cyclotron effects and the hot electron flow across the rear side along the axis is increased resulting stronger sheath formation and hence enhanced acceleration.
(v) Presence of an axial magnetic field significantly enhances the collimation of proton beams. Collimation appears to be highest in case of a LP laser in the presence of magnetic field due to its smallest spot size. However, proton axial momentum is observed to be highest with good collimation in case of an RCP laser in the presence of magnetic field.
(vi) When the acceleration process starts, transverse proton momentum rises sharply at the target rear side. In the presence of magnetic field, the transverse momentum after rising falls sharply due to cyclotron effects and the proton beams emerge out into the vacuum with very low values of transverse momentum and are therefore highly collimated.
(vii) It is observed that though the presence of magnetic field enhances collimation, it in turn reduces maximum proton energy. This might be due to reduction in transverse momentum which has a significant contribution in the total proton energy.
Acknowledgments
The authors are thankful to the Board of Research in Nuclear Sciences (BRNS), Department of Atomic Energy (DAE), Government of India for providing us the financial support via Project No. 2012/34/61/BRNS.









