Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T08:11:58.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherently enhanced radiation reaction effects in laser-vacuum acceleration of electron bunches

Published online by Cambridge University Press:  19 October 2010

P.W. Smorenburg ,
L.P.J. Kamp ,
G.A. Geloni  and
O.J. Luiten
P.W. Smorenburg*
Affiliation:
Eindhoven University of Technology, Department of Applied Physics, Eindhoven, The Netherlands
L.P.J. Kamp
Affiliation:
Eindhoven University of Technology, Department of Applied Physics, Eindhoven, The Netherlands
G.A. Geloni
Affiliation:
European XFEL GmbH, Hamburg, Germany
O.J. Luiten
Affiliation:
Eindhoven University of Technology, Department of Applied Physics, Eindhoven, The Netherlands
*
Address correspondence and reprint requests to: P.W. Smorenburg, Eindhoven University of Technology, Department of Applied Physics, CQT Group P.O. Box 513, 5600 MB, Eindhoven, The Netherlands. E-mail: p.w.smorenburg@tue.nl
Rights & Permissions [Opens in a new window]

Abstract

The effects of coherently enhanced radiation reaction on the motion of subwavelength electron bunches in interaction with intense laser pulses are analyzed. The radiation reaction force behaves as a radiation pressure in the laser beam direction, combined with a viscous force in the perpendicular direction. Due to Coulomb expansion of the electron bunch, coherent radiation reaction takes effect only in the initial stage of the laser-bunch interaction while the bunch is still smaller than the wavelength. It is shown that this initial stage can have observable effects on the trajectory of the bunch. By scaling the system to larger bunch charges, the radiation reaction effects are strongly increased. On the basis of the usual equation of motion, this increase is shown to be such that radiation reaction may suppress the radial instability normally found in ponderomotive acceleration schemes, thereby enabling the full potential of laser-vacuum electron bunch acceleration to GeV energies. However, the applicability of the used equation of motion still needs to be validated experimentally, which becomes possible using the presented experimental scheme.

Keywords

ClustersCoherent effectsLaser-vacuum accelerationRadiation reactionThomson scattering
Type
Research Article
Information
Laser and Particle Beams , Volume 28 , Issue 4 , December 2010 , pp. 553 - 562
Copyright
Copyright © Cambridge University Press 2010

1. INTRODUCTION

The recent availability of ultra-intense laser pulses has led to increased efforts to develop novel compact acceleration schemes for electron beams. These include wakefield accelerators (Tajima & Dawson, Reference Tajima and Dawson1979; Leemans et al., Reference Leemans, Nagler, Gonsalves, Tóth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006; Malka et al., Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc2008; Schlenvoigt et al., Reference Schlenvoigt, Haupt, Debus, Budde, Jäckel, Pfotenhauer, Schwoerer, Rohwer, Gallacher, Brunetti, Shanks, Wiggins and Jaroszynski2008), thin foil irradiation schemes (Maksimchuk et al., Reference Maksimchuk, Gu, Flippo and Umstadter2000; Borghesi et al., Reference Borghesi, Fuchs, Bulanov, Mackinnon and Patel2006), and laser-vacuum acceleration concepts (Stupakov & Zolotorev, Reference Stupakov and Zolotorev2001; Wang et al., Reference Wang, Shi, Lukyanchuk, Sheppard and Chong2008). Most studies so far have concentrated on the dynamics of the individual electrons in the considered electron bunches under the action of the externally applied electromagnetic fields, while consideration of the self-interaction of the bunches is limited to space-charge effects. Self-interaction due to the radiation emitted by the bunch itself is often ignored. Neglect of this collective radiation reaction is well-justified if the electron density is not too high and the electron bunch size exceeds the laser wavelength used.

In recent years, however, the interaction of intense laser light with nanometer to micrometer sized atomic clusters of near solid state density has become the subject of thorough investigation (Saalmann et al., Reference Saalmann, Siedschlag and Rost2006; Krainov & Smirnov, Reference Krainov and Smirnov2002). This has led to the observation of large numbers of electrons emitted from such clusters (Shao et al., Reference Shao, Ditmire, Tisch, Springate, Marangos and Hutchinson1996; Springate et al., Reference Springate, Aseyev, Zamith and Vrakking2003; Fennel et al., Reference Fennel, Döppner, Passig, Schaal, Tiggesbäumker and Meiwes-Broer2007; Chen et al., Reference Chen, Park, Hong, Choi, Kim, Zhang and Nam2002). In particular, under suitable conditions the production of dense, attosecond electron bunches from laser-irradiated clusters has been observed both numerically (Liseykina et al., Reference Liseykina, Pirner and Bauer2010) and experimentally (Fennel et al., Reference Fennel, Döppner, Passig, Schaal, Tiggesbäumker and Meiwes-Broer2007; Fukuda et al., Reference Fukuda, Akahane, Aoyama, Hayashi, Homma, Inoue, Kando, Kanazawa, Kiriyama, Kondo, Kotaki, Masuda, Mori, Yamazaki, Yamakawa, Echkina, Inovenkov, Koga and Bulanov2007). Also the creation of ultrashort bunches from laser-irradiated foils is actively studied (Meyer-ter-Vehn & Wu, Reference Meyer-ter-Vehn and Wu2009; Wu & Meyer-ter-Vehn, Reference Wu and Meyer-ter-Vehn2009; Qiao et al., Reference Qiao, Zepf, Borghesi, Dromey and Geissler2009). In view of these developments, collective radiation reaction effects may become an important factor in the dynamics of dense electron bunches and should be taken into account. It was realized already many years ago (Veksler, Reference Veksler1957) that these effects can even dominate the bunch dynamics and may be exploited as a collective acceleration mechanism. More recently, the ultra-intense field regime in which radiation reaction effects become dominant has been analyzed (Bulanov et al., Reference Bulanov, Esirkepov, Koga and Tajima2004) and the acceleration of plasma sheets assisted by radiation reaction has been considered (Il'in et al., Reference Il'in, Kulagin and Cherepenin2001; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004) in the context of current technological possibilities.

In the present paper, we consider the effect of collective radiation reaction on a dense subwavelength electron bunch in interaction with a laser pulse. It is shown that the interaction can be modeled by a particularly simple picture of radiation pressure in the direction of the laser beam on a coherently enhanced effective cross section, in combination with a viscous force perpendicular to the laser propagation direction. Thus, collective radiation reaction may be exploited in acceleration schemes as an additional accelerating force as well as a stabilizing force in the transverse direction.

Classically, the net radiative effect of the interaction of charged particles with an electromagnetic wave is described by Thomson scattering. This is the production of secondary dipole radiation by charges that oscillate due to the electric field of an incident radiation wave, which can be seen as scattering of part of the incident radiation by the charges. In case of an electron bunch of charge q = Ne and radius R 0 much smaller than the wavelength λ of the incident radiation, the N electrons in the bunch will essentially perform an identical oscillation, yielding coherently amplified secondary radiation that is identical to the radiation a point charge of magnitude q would produce. Hence the dynamics of the bunch as a whole can be modeled by such a point charge, as long as R 0 ≪ λ is fulfilled. The classical Thomson cross section, defined as the ratio of scattered power to incident intensity I in the non-relativistic limit, is σT = N 2(8π/3)r 02, with r 0 = e 2/(4πε0m ec 2) the classical electron radius (Panofsky & Phillips, Reference Panofsky and Phillips1962). The factor N 2 shows the coherent enhancement of the cross section compared to that of a single electron. Since directed momentum of the incident radiation is scattered into dipole radiation with zero net momentum, momentum is transferred to the electron bunch at a rate σTI/c ≡ F T. This means that the effective force per electron F T/N is proportional to N, and can therefore become significant for dense bunches. It is instructive to compare F T to the ponderomotive force FP = −Ne 2∇I/(2ε0m ecω2) in a laser pulse, which is conventionally used to accelerate charges in laser-vacuum acceleration schemes. Using a typical laser pulse with λ = 1 µm and 100 fs pulse length, the ratio F T/F P becomes on the order of unity for a bunch of N = 106 electrons. Assuming a laser intensity of I = 1 × 1019 W/cm2, this corresponds to a force of F T = 22 mN, which is equivalent to an electric field of F P/(Ne) = 0.14 TV/m in the laser propagation direction. This field already compares to the accelerating fields produced in wakefield accelerators, and increases to well above 1 TV/m for larger numbers of electrons.

Hence, radiation reaction is important for bunches containing ≳106 electrons within a size ≪λ, that is, for bunches with a charge density close to solid state density. These electron bunches could only recently be extracted from atomic clusters by irradiation with an intense laser pulse. Of course, such dense electron bunches quickly expand beyond R = λ due to the strong Coulomb repulsion, so that they will scatter radiation coherently only for a brief period of time after creation. Therefore, coherent Thomson scattering will not in itself be an efficient driving mechanism for electron bunch acceleration. However, it will be shown in this paper that even a short initial period of radiation reaction dominated interaction can have observable effects.

Collective radiation reaction of subwavelength electron bunches is, in some respects, the coherently enhanced version of the radiation reaction of a point charge. The latter has been a subject fundamental to the understanding of elementary particles and early electron theory, and played a role in the development of quantum theory (Lorentz, Reference Lorentz1916; Abraham, Reference Abraham1923; Dirac, Reference Dirac1938). It has always been a purely academic subject due to the smallness of the effect, however, and is only now coming within experimental reach due to the availability of ultra-intense fields (Bulanov et al., Reference Bulanov, Esirkepov, Koga and Tajima2004). We suggest that an interesting alternative may now be offered by electron bunches of subwavelength size. As explained above, for bunches, the enhanced radiation reaction effects are much stronger so that they are accessible already using moderate laser intensities. Furthermore, also the characteristic time scale on which radiation reaction effects play a role (as measured by the quantity τe introduced below) is coherently prolonged, bringing these effects into the experimental attosecond regime. Thus, the coherent enhancement of radiation reaction by electron bunches yields interesting possibilities to investigate this fundamental subject by experimental techniques.

In Sections 2–4, the bunch dynamics are analyzed treating the radiation reaction force in a perturbative way. In section 2, multiple-scale analysis and averaging over the laser optical time scale are applied to the equation of motion including radiation reaction, yielding a cycle-averaged description of the bunch dynamics. The results are applied to the case of a laser pulse in Section 3, validating the averaged description and our numerical calculations. Subsequently, in Section 4, the theoretical results are placed in an experimental context by exploring the possibility of having subwavelength electron bunches in the first place. Both the time in which electron bunches Coulomb expand beyond the wavelength and the production of dense bunches in laser-cluster interactions are addressed. Using accordingly realistic electron bunches, the observable effects of coherent radiation reaction on the bunch trajectory are calculated. Finally, in Section 5, the theoretical and numerical results are tentatively extrapolated to the non-perturbative regime of highly charged electron bunches. It is shown that ponderomotive acceleration of electron bunches by laser pulses may be stabilized by radiation reaction.

2. AVERAGED RADIATION REACTION FORCE

Suppose that an electron bunch of charge q = Ne, mass m = Nm e, and radius R 0 ≪ λ oscillates due to the Lorentz force FL of plane wave radiation propagating in the z-direction with electric field E = E 0sin (ωt − kz)ex. The oscillatory quiver motion of the bunch (henceforth modeled by a point charge q) is a “figure-of-eight”-cycle in the (x,z)-plane in the Lorentz frame in which the charge is at rest on average (Landau & Lifshitz, Reference Landau and Lifshitz1975). In the course of each cycle, the accelerating charge continuously radiates and exchanges energy with its periodically changing Coulomb field, thereby experiencing an additional radiation reaction force FR. The detailed description of FR has been discussed intensively in the literature (Rohrlich, Reference Rohrlich2007), in which the covariant equation of motion for a point charge (Lorentz, Reference Lorentz1916; Abraham, Reference Abraham1923; Dirac, Reference Dirac1938),

(1)
{\dot p}^{\rm \mu} = F_L^{\rm \mu} + F_R^{\rm \mu} = qF^{\rm \mu \nu} {\,p_{\rm \nu} \over m} + {\rm \tau}_e \lpar \dot{\,p}^{\rm \lambda} {\dot p}_{\rm \lambda} p^{\rm \mu}/ \lpar mc \rpar ^2 + {\ddot p}^{\rm \mu} \rpar \comma

has played a central role. In Eq. (1), dots denote differentiation with respect to proper time, F μν is the electromagnetic field tensor of the incident radiation, τe = N(2r 0)/(3c) is the characteristic time for radiation reaction, and the metric signature (+, − , − ,−) has been adopted. The first term in brackets equals the covariant Larmor power and represents the recoil of the charge caused by emission of radiation, that is, by the irreversible loss of four-momentum detaching from the charge and propagating toward infinity. The second term is referred to as the “Schott term” and is associated with the reversible exchange of four-momentum with the Coulomb or velocity field, that is, with the part of the electromagnetic field bound to the charge that does not give rise to radiation (Teitelboim, Reference Teitelboim1970; Heras & O'Connell, Reference Heras and O'Connell2006). In the usual incoherent case N = 1, the bracketed terms can be neglected because of the smallness of τe. However, in the present case, τe is N times larger and p μ ∝ m ≡ Nm e, so that F μR ∝ N 2. This shows again that the radiation reaction force is coherently enhanced and can become very relevant. Two regimes may be identified: the perturbative regime in which the radiation reaction parameter ωτe ≪ 1 and the radiation reaction dominated regime in which ωτe≳1 (Bulanov et al., Reference Bulanov, Esirkepov, Koga and Tajima2004). In the perturbative regime, the Thomson cross section is by definition much smaller than the physical bunch size, and F R ≪ F L. This is the regime studied in this and the next two sections. In Section 5, laser-vacuum acceleration in the radiation reaction dominated regime is considered.

The two-dimensional (2D) “figure-of-eight”-motion in the (x, z)-plane due to the linearly polarized incident radiation does not induce any y-component of acceleration in Eq. (1), so that the motion of the charge remains 2D throughout. Assuming F R ≪ F L, the radiation reaction force FR affects the quiver motion negligibly on time scales ~ω−1. However, its cumulative effect over many cycles is to accelerate the charge, so that it gains a slowly varying average momentum $ \overline{\bi p}$ superimposed on the quiver motion. To study $ \overline{\bi p}$, it is instructive to derive averaged equations of motion from Eq. (1) by means of a multiple-scale expansion. For this purpose, define a fast dimensionless time scale T ≡ ωt and a slow dimensionless time scale εT ≡ (ωτe)T. The latter equals the time scale of radiative damping of a charged harmonic oscillator (Panofsky & Phillips, Reference Panofsky and Phillips1962) so that this is the time scale on which $ \overline{\bi p}$ will change appreciably. Hence, the dimensionless momentum (γ, P x, P y, P z) = P μ ≡ p μ/(mc) may be written as the sum of a slowly varying part $ \overline{P}^{\rm \mu}\lpar {\rm \epsilon} T\rpar \equiv\langle P^{\rm \mu}\rangle$ and a rapidly varying part ${\tilde P}^{\rm \mu}\lpar {\rm \epsilon} T\comma \; T\rpar = P^{\lpar 0\rpar {\rm \mu}} \lpar {\rm \epsilon} T\comma \; T\rpar + {\rm \epsilon} P^{\lpar 1\rpar {\rm \mu}}\lpar {\rm \epsilon} T\comma \; T\rpar + O\lpar {\rm \epsilon}^2\rpar $, where 〈·〉 denotes the average over an optical period. Incidentally, the quiver motion in a plane wave turns out to be more easily described in terms of the laser phase η ≡ T − kz rather than the time T explicitly (Landau & Lifshitz, Reference Landau and Lifshitz1975). Anticipating this fact by changing the fast coordinate from T to η, time-differentiation takes the form

(2)
{\rm \gamma} {d \over dT} P^{\rm \mu} \lpar {\rm \epsilon} T \comma \,{\rm \eta} \rpar = \left({\rm \epsilon \gamma} {\partial \over \partial \lpar \epsilon T \rpar} + \lpar {\rm \gamma} - P_z \rpar {{\rm \partial} \over \partial {\rm \eta}} \right)P^{\rm \mu} \lpar {\rm \epsilon} T \comma \,{\rm \eta} \rpar \comma

where γ2 = 1 + P x2 + P z2 is the usual Lorentz factor. Substituting the sum $P^{\rm \mu} = \overline{P}^{\rm \mu} + {\tilde P}^{\rm \mu}$ in the space and time components of Eq. (1), using Eq. (2), and collecting equal powers of ε, yields the zeroth-order equations

(3)
P_x^{ \lpar 0 \rpar } = -a\cos {\rm \eta}\comma \;
(4)
P_z^{\lpar 0 \rpar } = {\rm \gamma}^{\lpar 0 \rpar} = - {a \overline{P}_x\cos {\rm \eta} \over \overline{\rm \gamma} - \overline{P}_z} + {a^2\cos 2{\rm \eta} \over 4 \lpar \overline{\rm \gamma} - \overline{P}_z \rpar}\comma \;
(5)
\overline{\rm \gamma}^2 = 1 + a^2/2 + \overline{P}_x^2 + \overline{P}_z^2 \comma

where a ≡ (eE 0)/(m ecω) is the dimensionless field strength. Eqs. (3–4) give the well-known plane wave quiver motion with average momentum $ \overline{\bi p}$ (Salamin & Faisal, Reference Salamin and Faisal1996). Eq. (5) shows that the oscillating charge behaves like a particle with effective mass $m\sqrt{1 + a^2/2}$ due to the energy contained in the quiver motion (Kibble, Reference Kibble1966). Expanding next the components of Eq. (1) to first order in ε, substituting the zeroth-order results Eqs. (3–5), and averaging over the fast time scale, one finally obtains

(6)
{d \overline{P}_x \over dT} = -{{\rm \omega \tau}_e a^2 \over 2}\lpar \overline{\rm \gamma} - \overline{P}_z \rpar^2 { \overline{P}_x \over \overline{\rm \gamma}}\semicolon \;
(7)
{d \overline{P}_z \over dT} = {{\rm \omega\tau}_e a^2 \over 2} \lpar \overline{\rm \gamma} - \overline{P}_z \rpar^2 \left(1 - { \overline{P}_x^2 \over \overline{\rm \gamma} \left(\overline{\rm \gamma} - \overline{P}_z \right)} \right).

The averaged dimensionless position $ \overline{\bi X}\equiv k \overline{\bi x}$ is calculated from

(8)
{d \overline{{\bi X}} \over dT}\equiv \overline{{\bf \beta}}={ \overline{\bi P} \over \overline{\rm \gamma}} .

Eqs. (5–8) now give the evolution of the averaged position $ \overline{\bi X}$ and momentum $ \overline{\bi P}$ of the charge in the plane wave. First, consider the special case $ \overline{P}_x=0$. Then Eqs. (6–7) reduce, after multiplication by m ecω, to

(9)
{d{ \overline{\bi p}} \over dt}={\rm \sigma}_T{I \over c} \overline{\rm \gamma}^2 \lpar 1- \overline{\rm \beta}_z\rpar^2{\bi e}_z\comma

where I = ε0cE 02/2 is the intensity of the incident plane wave. This clearly shows that the averaged reaction force takes the classical form of a radiation pressure I/c on an effective cross section σT, corrected by a Doppler factor $ \overline{\gamma}^2 \lpar 1- \overline{\beta}_z\rpar ^2$. This Doppler factor reflects the fact that plane wave appears Doppler-shifted in the frame of the charge, with a corresponding change in radiation pressure. Eq. (9) may also be obtained by Lorentz-transformation of the non-relativistic force σTI/c (Landau & Lifshitz, Reference Landau and Lifshitz1975). In the more general case $ \overline{P}_x\ne 0$, the direction of the radiation pressure is no longer along the propagation direction of the incident wave. This is because the secondary, scattered radiation produced by the charge is Lorentz boosted along $ \overline{\bi P}$, so that the recoil from this radiation has a net transverse component when $ \overline{P}_x\ne 0$. The latter appears in Eqs. (6–7) as the additional factors involving $ \overline{P}_x$ on the very right. Effectively, in the transverse direction, the averaged reaction force appears as a frictional force proportional to the velocity, which will be important below. Effective forces similar to Eqs. (6–7) have been obtained earlier for a one-dimensional plasma sheet (Il'in et al., Reference Il'in, Kulagin and Cherepenin2001).

A typical experiment will involve the use of a high-intensity laser pulse of length τL focused to a waist of size w 0. Due to the intensity gradients in such a pulse, on average the electron bunch will experience ponderomotive forces in addition to the radiation reaction forces. In absence of the latter, the ponderomotive force takes the simple form

(10)
{{\bi F}_P \over m_ec\omega}=-{ \lpar k^{-1}\nabla \rpar \lsqb a^2 \lpar \overline{\bi X}\comma \; T \rpar \rsqb \over 4 \overline{\rm \gamma}},

which can be derived by means of a separate multiple-scale analysis, using the small parameters λ/(cτL) and (kw 0)−1 (Quesnel & Mora, Reference Quesnel and Mora1998). The combined effect of radiation reaction and gradients may be derived formally using a multiple-scale analysis in terms of all three small parameters ωτe, λ/(cτL), and (kw 0)−1. This is possible provided that these parameters are all on the same order of magnitude.

However, mixed expansion terms that involve products of the parameters appear only from the second order onward, so that to first order the radiation reaction and ponderomotive effects remain separated throughout the analysis. Hence, the averaged reaction force is still given by Eqs. (6–7), but now with the dimensionless field strength $a\lpar \overline{\bi X}\comma \; T\rpar $ evolving according to the laser pulse shape. Furthermore, Eqs. (6–7) are supplemented with the effects of intensity gradients by simply adding the ponderomotive force Eq. (10) to the right-hand sides. Carrying out the full three-parameter multiple-scale analysis to first order confirms these results. In the numerical calculations below, Eqs. (6–7) will always be used with the force Eq. (10) included.

Rather than using averaged equations, the detailed trajectory of the electron bunch may be calculated by direct integration of Eq. (1). However, it is well-known that this equation yields unphysical runaway solutions, which may be disposed of by substituting the applied Lorentz force ${\dot p}^{\rm \mu}\approx F^{\rm \mu}_L$ in the right-hand side of Eq. (1). This yields the space component (Landau & Lifshitz, Reference Landau and Lifshitz1975; Jackson, Reference Jackson1999; Ford & O'Connell, Reference Ford and O'Connell1993)

(11)
{d{\bi p} \over dt} = {\bi F}_L + \tau_e \left[{\rm \gamma}{d{\bi F}_L \over dt} - {{\rm \gamma}^3 \over c^2} \left({d{\bi v} \over dt} \times \lpar {\bi v}\times {\bi F}_L \rpar\right)\right].

This expression can also be derived from quantum mechanical arguments (Ford & O'Connell, Reference Ford and O'Connell1991, Reference Ford and O'Connell1993).

3. RADIATION REACTION IN A LASER PULSE

In this section, the results of the previous section will be applied to concrete examples of laser-vacuum experiments. First, however, it should be stressed that an accurate calculation of the detailed charge trajectory in a laser pulse requires the field of the pulse to be described in more detail than the usual paraxial approximations (Hora et al., Reference Hora, Hoelss, Scheid, Wang, Ho, Osman and Castillo2000) even in the absence of radiation reaction forces. Quesnel and Mora (Reference Quesnel and Mora1998) use a laser field representation in terms of Fresnel-type integrals to calculate detailed charge trajectories in a laser pulse, which are then compared with averaged trajectories calculated from the ponderomotive force Eq. (10) using the laser field in paraxial approximation. The agreement between the two results was found to be excellent except for highly relativistic initial velocities. In this paper, we will adopt the same approach, using the detailed field representation of Quesnel and Mora (Reference Quesnel and Mora1998) when evaluating the Lorentz force FL in Eq. (11), while taking the simpler paraxial approximation to evaluate the field intensity a 2 in the averaged Eqs. (5–10). As a reference, both field representations are shown in the Appendix.

To validate the results of the previous section and to illustrate the effect of the effective radiation pressure produced by radiation reaction, we consider an intense laser pulse propagating in the z-direction and polarized in the x-direction, which has wavelength λ = 1 µm, peak intensity I = 1 × 1019 W/cm2 and pulse length τL = 200 fs, focused to a relatively large waist of size w 0 = 10λ. This pulse contains 2.3 J of energy and has a peak dimensionless field strength a max = 2.7. An electron bunch of radius R 0 ≪ λ and radiation reaction parameter ωτe = 0.03 is considered, corresponding to a bunch charge of q = 0.4 pC. For these parameters, λ/(cτL) ~ (kw 0)−1 ~ ωτe so that the averaged description is valid. The electron bunch is placed at rest at the initial position x0 ≡ (x 0, z 0) = (λ, 0) prior to arrival of the laser pulse, deliberately at an off-axis position arbitrarily set to one wavelength, in order to study the radial acceleration as well. In this (unrealistic) first example, we disregard the Coulomb expansion of the bunch and assume that it retains its coherent Thomson cross section during the entire interaction.

Figure 1 shows the trajectory of the bunch and its momentum as a function of time as it is overtaken by the laser pulse, calculated using both the averaged description Eqs. (5–10) and the detailed description Eq. (11). Clearly, the agreement between the averaged and the detailed description is excellent, validating the multiple-scale analysis, the applicability of Eq. (11), and our numerical calculations. The figure also shows the trajectory and the momentum in the absence of radiation reaction, that is, in case of conventional ponderomotive acceleration. In the latter case, the charge is quickly expelled in the radial direction because of the large radial intensity gradient, which is a well-known instability that so far has limited the applicability of ponderomotive acceleration schemes (Stupakov & Zolotorev, Reference Stupakov and Zolotorev2001). The theoretical escape angle θ for ponderomotive acceleration of a charge initially at rest by a radiation pulse, is related to the final Lorentz factor γf by (Hartemann et al., Reference Hartemann, Fochs, Le Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995)

(12)
{\rm \theta} = \arccos \sqrt{{\rm \gamma}_f-1 \over {\rm \gamma}_f + 1}.

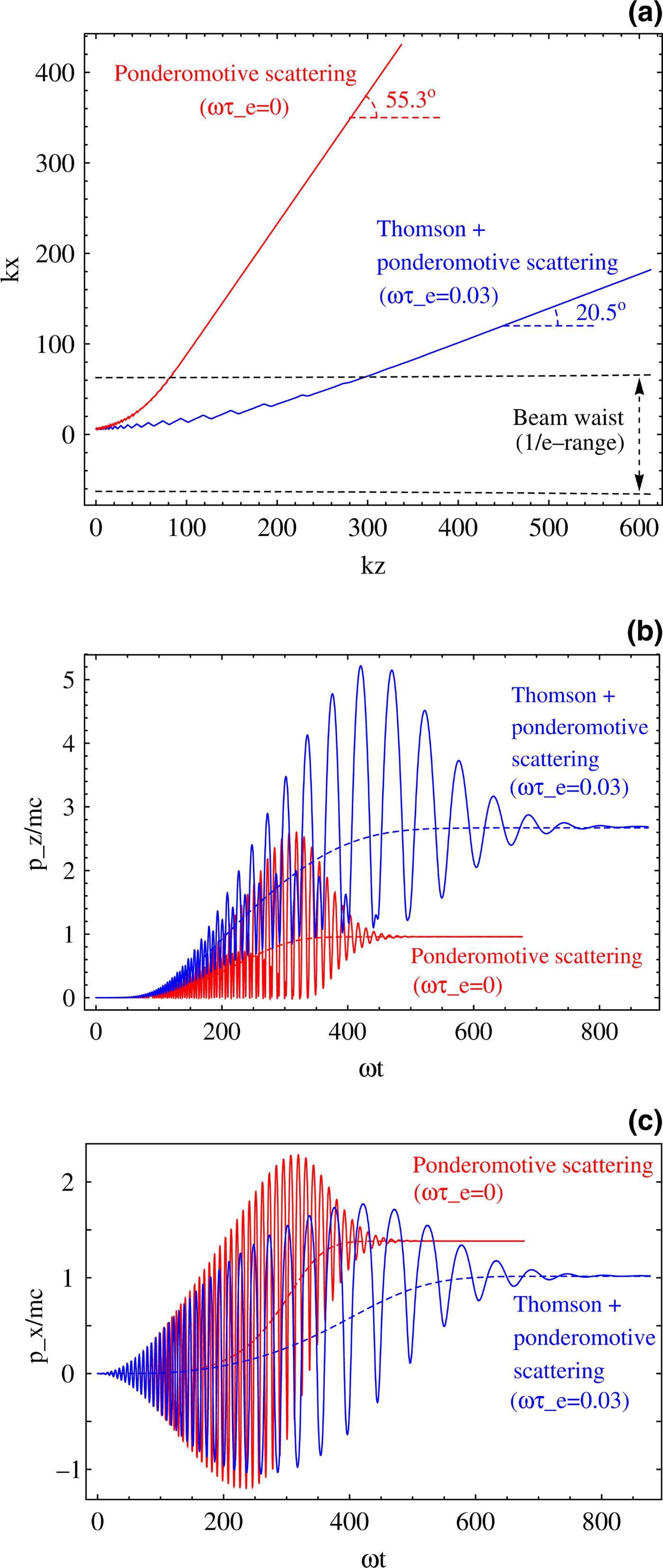
Fig. 1. (Color online) (a) Trajectory of an electron bunch accelerated by a laser pulse with parameters λ = 1 µm, I = 1 × 1019 W/cm2, τL = 200 fs, and w 0 = 10λ; (b) Longitudinal momentum of the bunch as a function of time; and (c) Transverse momentum of the bunch as a function of time, calculated for the case including radiation reaction (Thomson + ponderomotive scattering, ωτe = 0.03) and for the case without radiation reaction (ponderomotive scattering, ωτe = 0). The solid lines have been calculated using Eq. (11) with FL = q(E + v × B), taking for E and B Eqs. (A.1–A.4). The dashed lines have been calculated using Eqs. (5–10), taking a 2 according to Eq. (A.5). The initial position was x0 = (λ, 0) and the initial velocity was zero.

In the present example γf = 1.96, yielding a theoretical escape angle of 55.3° in excellent agreement with the numerically calculated result. In contrast to the purely ponderomotive case, in the case including coherent Thomson scattering, the acceleration in the radial direction is markedly suppressed. This stabilizing effect is due to the average frictional force shown by Eq. (6), which opposes the tendency to radial acceleration. Meanwhile, the charge stays in the beam longer and is accelerated in the forward direction for a longer time by both the radiation reaction pressure and ponderomotive forces, leading to a higher final energy and a smaller escape angle.

4. REALISTIC ELECTRON BUNCHES

We now consider the more realistic case of an electron bunch that expands due to Coulomb repulsion. The time after which the Thomson cross section fails to be coherent, that is, the time it takes the bunch to expand to R(t) = λ, depends on the charge and the initial size of the bunch. To obtain realistic values for these initial parameters, we first make some estimates concerning the method to produce dense electron bunches mentioned in the introduction.

Rather than irradiating a pre-existing electron bunch, an electron bunch may be created in practice by irradiating a subwavelength atomic cluster. When the laser pulse is sufficiently strong, the electron bunch will be emitted from the cluster somewhere in the leading edge of the pulse, after which it is available to be accelerated by the remainder of the pulse as has been analyzed in the previous section. Many different mechanisms play a role in laser-cluster interaction (Saalmann et al., Reference Saalmann, Siedschlag and Rost2006; Krainov & Smirnov, Reference Krainov and Smirnov2002) and it is beyond the scope of this paper to analyze this interaction in detail. Instead, we use a strongly simplified model of the cluster suggested by Parks et al. (Reference Parks, Cowan, Stephens and Campbell2001) to obtain order-of-magnitude estimates for the initial parameters of the electron bunch. Accordingly, at some point in the leading edge of the pulse the field strength becomes such that all atoms in the cluster are ionized almost instantaneously, changing the neutral cluster into a dense plasma ball. Subsequently, this plasma ball is modeled as a spherical rigid electron bunch, interpenetrating with and moving through a practically immobile oppositely charged ion bunch, under the action of both the driving laser electric field and the restoring Coulomb force of the ion cloud. As the rising edge of the laser pulse advances, the electron bunch oscillates around the ion bunch center with increasing amplitude. At a critical laser field strength the electron bunch breaks free and escapes the ion bunch within a fraction of an optical period, yielding the free, dense electron bunch we will now use as an input for our calculation.

The critical dimensionless field strength at which the electron bunch is liberated may be estimated as (Parks et al., Reference Parks, Cowan, Stephens and Campbell2001)

(13)
a_{\rm crit} = {15 \over 96} \left({{\rm \omega}_p \over {\rm \omega}} \right)^2kR_0\comma

where ${\rm \omega}_p = \sqrt{3Ne^2/\lpar 4{\rm \pi} {\rm \epsilon}_0m_eR_0^3\rpar }$ is the electron plasma frequency of the ionized cluster of size R 0 consisting of N atoms. The electron bunch leaves the cluster at the maximum of an optical cycle. The time this takes is on the order t esc ~ ωp−1 (Parks et al., Reference Parks, Cowan, Stephens and Campbell2001), so that the escaping electron bunch will have a velocity of approximately

(14)
{\rm \beta}_{\rm esc} c \approx {\rm \omega}_p R_0

in the direction of the laser polarization. Incidentally, note that the coherent radiation reaction parameter can be expressed in terms of the cluster parameters as ωτe = (2/9)(ωp/ω)2(kR 0)3, by which the validity condition ωτe ≪ kR 0 of Section 2 automatically implies that βesc < 1. After leaving the cluster, the electron bunch will start to expand. It can be shown straightforwardly that, after a short period of slow expansion, the expansion rate increases to the constant value (Ammosov, Reference Ammosov1991)

(15)
{dR \over dt} \approx {\sqrt{{2 \over 3}}{\rm \omega}_pR_0 \over \sqrt{1 + P_{\rm esc}^2 + {a_{\rm crit}^2 \over 2}}}.

In Eq. (15), it has been used that the expanding electron bunch will be in quiver motion immediately after leaving the cluster, so that it will move with an average Lorentz factor according to Eq. (5). This reduces the expansion rate by a factor $ \overline{\gamma} = \sqrt{1 + P_{\rm esc}^2 + a_{\rm crit}^2/2}$.

As an example, we take an R 0 = 16 nm cluster with an electron density of 5 × 1028 m−3, which can be routinely made using a supersonic gas jet (Krainov & Smirnov, Reference Krainov and Smirnov2002) irradiated by the same laser pulse as in the previous example. With these numbers, the other parameters are kR 0 = 0.1, ωp/ω = 6.6, ωτe = 0.01, and a crit = 0.68 and βesc = 0.66 according to Eqs. (13–14). The last two numbers roughly compare to the field strengths used and electron velocities obtained by Liseykina et al. (Reference Liseykina, Pirner and Bauer2010) and Fukuda et al. (Reference Fukuda, Akahane, Aoyama, Hayashi, Homma, Inoue, Kando, Kanazawa, Kiriyama, Kondo, Kotaki, Masuda, Mori, Yamazaki, Yamakawa, Echkina, Inovenkov, Koga and Bulanov2007). Assuming the expansion rate Eq. (15), the bunch grows larger than the wavelength after a time 8.3ω−1, that is, after no more than 1.3 optical cycles following the moment of escape from the cluster. Thus, coherent Thomson scattering will only occur for a brief initial period. Nevertheless, even such a brief period can have an observable effect on the trajectory of the electron bunch in interaction with the laser pulse.

Figure 2 shows the trajectory of the bunch, both for the case without the radiation reaction force (ωτe = 0) and for the case including the radiation reaction force (ωτe = 0.01) during the initial period 0 ≤ ωt ≤ 8.3. In the latter case, the decrease in coherent radiation reaction was modeled by a sudden switch-off, setting ωτe = 0 at the somewhat arbitrary time ωt = 8.3. Again, the results of Figure 2 were calculated both using the averaged description Eqs. (5–10) and the detailed description Eq. (11). In both cases, the initial position was x0 = (−λ, 0) and the initial velocity was βescc ex. The initial position of the laser pulse along the z-axis was chosen such that a = a crit at x0, and the optical phase offset ϕ0 was chosen such that the optical cycle was at its maximum at t = 0. This time, the escape angle for the case without radiation reaction does no longer agree with Eq. (12) or its generalization for a nonzero initial velocity (Hartemann et al., Reference Hartemann, Fochs, Le Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995). This may be caused by the sudden injection into the radiation field at t = 0, which is not considered in the derivation of Eq. (12). The good agreement between the averaged and detailed descriptions is remarkable here, considering the fact that the concept of averaging the equation of motion over the optical time scale is not a priori valid when applied to the initial period, which is as short as the optical period itself.

Fig. 2. (Color online) Trajectory of an electron bunch accelerated by a laser pulse, calculated for the case including radiation reaction (Thomson + ponderomotive scattering, ωτe = 0.01) during the initial period 0 ≤ T ≤ 8.3, and for the case without radiation reaction (ponderomotive scattering, ωτe = 0). See Fig. (1) for details about the calculation and laser parameters. The dash-dotted lines show the error margins for the case ωτe = 0 corresponding to a hypothetical uncertainty of magnitude λ in the initial position, calculated using the averaged description. The initial position was x0 = (−λ, 0) and the initial velocity was according to Eq. (14).

From the figure it is clear that the initial period of radiation reaction still reduces the escape angle observably, but much less than in the previous example because the radiation reaction force is switched off at an early stage. To put the 1.3° of reduction in angle in perspective, the figure also shows the error margins around the trajectory without radiation reaction, which would be caused by an uncertainty of magnitude λ in the initial position x0. The deviation caused by radiation reaction is clearly outside these error margins.

As another example, we show how the initial period of coherent Thomson scattering may even change the behavior of the bunch completely. Figure 3 shows the trajectory of the bunch, using the same laser parameters and initial conditions as in the previous example, only now with the initial position changed to x0 = (−7.1λ,0). This time the effect of radiation reaction is such that the bunch is deflected by the laser pulse in the negative x-direction instead of the positive x-direction. Under the initial conditions of this example, the bunch is produced much further from the laser beam axis and is therefore decelerated in the negative x-direction by the radial ponderomotive force of Eq. (10) for a longer time. Without the action of the radiation reaction force, the bunch just makes it across the laser axis (where the ponderomotive potential is maximum), after which it is accelerated in the positive x-direction. Including radiation reaction, however, in the initial stage, the bunch is additionally decelerated by the frictional force of Eq. (6). Furthermore, it is additionally accelerated in the positive z-direction by the radiation pressure of Eq. (7), so that it keeps up with the laser pulse and is under the action of the decelerating radial ponderomotive force for a somewhat longer time. Both effects are only small, but in this case just enough to prevent the bunch from passing the beam axis. It is to be noted that in this example whether or not the bunch will pass the beam axis is very sensitive to the initial parameters. This is an additional reason why the averaged description cannot be used here to reproduce the trajectories of Figure 3, since the small differences between the two descriptions in the initial part of the trajectory affect the final behavior strongly. Still, it is clear that radiation reaction can play an important role in laser-vacuum experiments.

Fig. 3. (Color online) See Figure 2, with the initial position changed to x0 = (−7.1λ, 0).

5. THE RADIATION REACTION DOMINATED REGIME

In the previous section, relatively small electron bunches were considered leading to modest values for the bunch charge, and for the radiation reaction parameter (ωτe ≪ 1), thereby staying well inside the perturbative regime mentioned in Section 2. Much stronger radiation reaction effects could be expected when scaling the system to larger bunches. In the introduction, the magnitude of the effective radiation reaction force was estimated assuming a wavelength of 1 µm. Taking now, for instance, a CO2 laser with a wavelength of 10 µm, 10 times larger bunches still scatter light coherently. Since the coherent Thomson cross section scales as σT ∝ N 2 ∝ R 6, in that case an effective force F T = σTI/c on the order of kN rather than mN may be expected, equivalent to accelerating fields F P/(Ne) approaching PV/m rather than TV/m. Thus, the radiation reaction force in this case completely dominates the bunch dynamics. In this radiation reaction dominated regime ωτe ~ 1, the averaged description Eqs. (5–10) is no longer valid, and analysis of the dynamics is restricted to the instantaneous equations of motion (1) or (11). However, in this regime, the validity of these equations is at issue. Eq. (1) can be shown to be valid for a subwavelength but finite charged body when the mass equivalent of its electrostatic energy U/c 2 ~ (Ne)2/(ε0Rc 2) is less than its mechanical mass Nm e (Medina, Reference Medina2009). From the definition of τe, this requirement is equivalent to ωτe < kR, in which case Eq. (11) is valid as well (Rohrlich, Reference Rohrlich2001, Reference Rohrlich2002). But in the present case, this requirement is not satisfied, as ωτe ~ 1 ≫ kR here. Thus the experiment in the radiation reaction dominated regime can provide valuable insights, as the departure from known equations can be controlled and studied.

We now give an example of acceleration using radiation reaction in the regime ωτe ~ 1, as it would result according to the equation of motion (11). As before, the action of the radiation reaction force is restricted to the initial period following the creation of the electron bunch, while the bunch is still smaller than the wavelength. Therefore, the large accelerating fields mentioned above are not effective as a driving acceleration mechanism. However, the initial radiation reaction dominated phase pre-accelerates and redirects the velocity of the bunch, which serves to stabilize subsequent ponderomotive acceleration. Consider the same laser pulse as used in the previous examples, but scaled 10 times in all directions so that λ = 10 µm, τL = 2 ps, and w 0 = 10λ. This CO2 laser pulse contains 2.3 kJ of energy and has a peak dimensionless field strength a max = 27, which is presently available. The increased wavelength allows an electron bunch of initial size R 0 = 160 nm containing N = 8.5 × 108 electrons, resulting as before in kR 0 = 0.1, but this time in a much bigger value ωτe = 1. The non-relativistic cluster model of (Parks et al., Reference Parks, Cowan, Stephens and Campbell2001) does not apply for such a large amount of charge. We assume a relativistic initial electron bunch velocity of β0 = 0.9 instead, as is also indicated by Liseykina et al. (Reference Liseykina, Pirner and Bauer2010). Substituting $P_{\rm esc}\equiv {\rm \beta}_0/\sqrt{1 - {\rm \beta}_0^2}$ and a crit ≡ a max in Eq. (15), the resulting expansion rate is such that the bunch stays smaller than the wavelength for about one optical cycle, just as in the previous examples.

Figure 4 shows the trajectory and momentum of this electron bunch in the laser pulse. The initial bunch position was set to x0 = (λ, 0), the initial position of the laser pulse along the z-axis was chosen centered around x-axis so that the bunch started its movement at the pulse maximum, and the optical phase offset ϕ0 was chosen such that the optical cycle was at its maximum at t = 0 and x0. From the figure the effect of the initial period of radiation reaction is evident: the large radial velocity of the bunch is suppressed immediately preventing an early escape from the beam waist, after which the bunch is strongly accelerated in the direction of propagation of the laser pulse. The inset of the p z-panel of Figure 4 shows the long-term evolution of the momentum in this direction. The bunch is first accelerated by the leading edge of the laser pulse and then decelerated by the trailing edge, as is characteristic for laser-vacuum acceleration. The energy of the bunch is increased to γ ≈ 600, corresponding to an energy of 0.3 GeV per electron. In the case without radiation reaction, the bunch is quickly expelled from the laser beam. Consequently, the energy gained is much less. The cusp-like features in the corresponding p z- and p x-plots of Figure 4 agree with previous results (Dodin & Fisch, Reference Dodin and Fisch2003; Galkin et al., Reference Galkin, Egorov, Kalashnikov, Korobkin, Romanovsky, Shiryaev and Trofimov2009) in comparable cases of ponderomotive scattering.

Fig. 4. (Color online) (a) Trajectory of an electron bunch accelerated by a laser pulse with parameters λ = 10 µm, I = 1 × 1019 W/cm2, τL = 2 ps, and w 0 = 10λ; (b) Longitudinal momentum of the bunch as a function of time; and (c) Transverse momentum of the bunch as a function of time, calculated for the case including radiation reaction (Thomson + ponderomotive scattering, ωτe = 1) during the initial period 0 ≤ T ≤ 2π and for the case without radiation reaction (ponderomotive scattering, ωτe = 0). The solid lines have been calculated using Eq. (11) with FL = q(E + v × B), taking for E and B Eqs. (A.1–A.4). The inset of the middle panel shows the long-term behavior of the longitudinal momentum for the case including radiation reaction. The inset of the lower panel is a close-up of the first optical period; the slope of the dashed line is according to Eq. (16). The initial position was x0 = (λ, 0) and the initial velocity was β0 = 0.9ex.

In the case including radiation reaction, it may seem strange that the bunch starts, at t = 0, with a downward radial acceleration while the laser electric field points upward at that moment. This, however, is a consequence of the large value of ωτe as can be inferred from Eq. (11). Namely, at t = 0 the optical field at the bunch position is maximum, so that

qE_x = qcB_y = m_{ec} \omega a_{\max}\semicolon \;
{d{\bi F}_L \over dt} = q{d{\bi v} \over dt} \times {\bi B}\comma

while p z = 0. Substituting the above in the x- and z-components of Eq. (11), writing d v/dt in terms of the momentum p = γm v, and rearranging, one finds in dimensionless form the x-component

(16)
\left.{dP_x \over dT}\right\vert_{t=0}=a_{\max}{1-{\rm \omega\tau}_ea_{\max}{\rm \gamma}_0^2{\rm \beta}_0 \over 1+{\rm \gamma}_0^2 \lpar {\rm \omega\tau}_ea_{\max} \rpar ^2}\approx-{{\rm \beta}_0 \over {\rm \omega\tau}_e} \comma

where γ0 ≡ (1 − β02)−1/2. On the right hand side it has been used that ωτea maxβ0 ≫ 1 in the example of Figure 4. In the inset of the p x-panel of Figure 4, the initial acceleration Eq. (16) is indicated by the sloped line.

Eq. (16) suggests that the initial velocity of the bunch can be redirected by means of a short period of radiation reaction choosing favorable parameters a max and ωτe, which may be exploited to efficiently accelerate the bunch into the direction of propagation of the laser. Whether this scheme, and the results of this section in general, are realistic depends on the way the validity of Eq. (11) extends into the present radiation reaction dominated regime. This may be studied by means of the proposed setup, which also may offer further opportunities to experimentally test radiation reaction theories.

6. CONCLUSION

The current developments in laser technology make it possible to obtain subwavelength electron bunches of very high charge density. With that, a qualitatively new regime is accessed in which coherently enhanced radiation reaction effects become significant. In this paper, we have analyzed some of these effects in the context of laser-vacuum experiments. It has been shown that the radiation reaction force affects the bunch dynamics notably, even if the radiation reaction can still be treated as a small perturbation on the optical time scale. Considering larger bunches containing more charge, we demonstrated that the radiation reaction effects may even become strong enough to be exploited in effective bunch acceleration schemes, although this is also where the theory is still controversial and needs further development. It is clear that the coherently enhanced radiation reaction of high-density electron bunches offers interesting new possibilities, both as a technological tool in the development of novel acceleration schemes, and as an experimentally accessible system to study the fundamental topic of radiation reaction.

APPENDIX: LASER FIELD REPRESENTATIONS

In this paper, when evaluating the Lorentz force FL in Eq. (11), the following fields are used (Quesnel & Mora, Reference Quesnel and Mora1998):

(A.1)
{qE_x \over m_ec{\rm \omega}} = {\lpar kw_0\rpar ^2a_{\max} \over 4} \left(I_1 + {I_2 \over X} \right)\semicolon \;
(A.2)
{qE_z \over m_ec{\rm \omega}} = {\lpar kw_0\rpar ^2a_{\max} \over 4} I_4\semicolon \;
(A.3)
{qB_y \over m_e{\rm \omega}} = {\lpar kw_0\rpar ^2a_{\max} \over 4} \left(I_1 - {I_2 \over X} + I_3\right)\semicolon \;
(A.4)
E_y = cB_x = cB_z = 0\semicolon \;
I_1 \equiv \,\vint_0^1 \exp \left(- {\lpar kw_0\rpar ^2b^2 \over 4}\right)\left(1 + \sqrt{1 - b^2} \right)\sin{\rm \phi} J_0 \lpar Xb \rpar bdb\semicolon \;
I_2 \equiv \,\vint_0^1 \exp \left(- {\lpar kw_0\rpar ^2b^2 \over 4} \right){1 \over \sqrt{1-b^2}} \sin {\rm \phi} J_1 \lpar Xb \rpar b^2db\semicolon \;
I_3 \equiv \,\vint_0^1 \exp \left(- {\lpar kw_0\rpar ^2b^2 \over 4} \right){1 \over \sqrt{1 - b^2}} \sin {\rm \phi} J_0 \lpar Xb \rpar b^3db\semicolon \;
I_4 \equiv \,\vint_0^1 \exp \left(- {\lpar kw_0\rpar ^2b^2 \over 4}\right)\left(1 + {1 \over \sqrt{1 - b^2}} \right)\cos {\rm \phi} J_1 \lpar Xb \rpar b^2db\semicolon \;
{\rm \phi} \equiv T - Z \sqrt{1 - b^2} + {\rm \phi}_0 \comma

where ϕ0 is the phase offset of the optical field. These expressions describe a Gaussian beam which propagates along the z-direction, is polarized in the x-direction, and is focused to a waist of size w 0. The fields above are multiplied by an envelope function cos2(πη/(2ωτL)) to obtain a laser pulse of length τL instead of a full beam. To evaluate the field intensity a 2 in the averaged equations (5–10), the simpler paraxial approximation is used according to

(A.5)
a^2 = \left[a_{\max} {w_0 \over w}\exp \left(- {w_0^2 \over w^2} X^2 \right)\cos^2 \left({{\rm \pi \eta} \over 2{\rm \omega \tau}_L} \right)\right]^2\semicolon \;
w \equiv w_0\sqrt{1 + 4{Z^2 \over \lpar kw_0 \rpar^4}}.

References

REFERENCES

Abraham, M. (1923). Elektromagnetische Theorie der Strahlung. Leipzig: Teubner.Google Scholar
Ammosov, M.V. (1991). Influence of the Coulomb repulsion between electrons on their energy spectrum in the case of the nonlinear surface photoeffect. J. Opt. Soc. Am. B 8, 2260–2264.CrossRefGoogle Scholar
Borghesi, M., Fuchs, J., Bulanov, S.V., Mackinnon, A.J. & Patel, P.K. (2006). Fast ion generation by high-intensity laser irradiation of solid targets and applications. Fusion Sci. Technol. 49, 412–439.CrossRefGoogle Scholar
Bulanov, S.V., Esirkepov, T.Z., Koga, J. & Tajima, T. (2004). Interaction of electromagnetic waves with plasma in the radiation-dominated regime. Plasma Phys. Reports 30, 196–213.CrossRefGoogle Scholar
Chen, L.M., Park, J.J., Hong, K.-H., Choi, I.W., Kim, J.L., Zhang, J. & Nam, C.H. (2002). Measurement of energetic electrons from atomic clusters irradiated by intense femtosecond laser pulses. Phys. Plasmas 9, 3595–3599.CrossRefGoogle Scholar
Dirac, P.A.M. (1938). Classical theory of radiating electrons. Proc. Royal Soc. London A 167, 148–169.Google Scholar
Dodin, I.Y. & Fisch, N.J. (2003). Relativistic electron acceleration in focused laser fields after above-threshold ionization. Phys. Rev. E 68, 056402.CrossRefGoogle ScholarPubMed
Fennel, T., Döppner, T., Passig, J., Schaal, C., Tiggesbäumker, J. & Meiwes-Broer, K.-H. (2007). Plasmon-enhanced electron acceleration in intense laser metal-cluster interactions. Phys. Rev. Lett. 98, 143401.CrossRefGoogle ScholarPubMed
Ford, G.W. & O'Connell, R.F. (1991). Radiation reaction in electrodynamics and the elimination of runaway solutions. Phys. Lett. A 157, 217–220.CrossRefGoogle Scholar
Ford, G.W. & O'Connell, R.F. (1993). Relativistic form of radiation reaction. Phys. Lett. A 174, 182–184.CrossRefGoogle Scholar
Fukuda, Y., Akahane, Y., Aoyama, M., Hayashi, Y., Homma, T., Inoue, N., Kando, M., Kanazawa, S., Kiriyama, H., Kondo, S., Kotaki, H., Masuda, S., Mori, M., Yamazaki, A., Yamakawa, K., Echkina, E.Yu., Inovenkov, I.N., Koga, J. & Bulanov, S.V. (2007). Ultrarelativistic electron generation during the intense, ultrashort laser pulse interaction with clusters. Phys. Lett. A 363, 130–135.CrossRefGoogle Scholar
Galkin, A.L., Egorov, V.A., Kalashnikov, M.P., Korobkin, V.V., Romanovsky, M.Yu., Shiryaev, O.B. & Trofimov, V.A. (2009). Energy distribution of electrons expelled from relativistically intense laser beam. Contrib. Plasma Phys. 49, 544–549.CrossRefGoogle Scholar
Hartemann, F.V., Fochs, S.N., Le Sage, G.P. Jr., Luhmann, N.C., Woodworth, J.G., Perry, M.D., Chen, Y.J. & Kerman, A.K. (1995). Nonlinear ponderomotive scattering of relativistic electrons by an intense field at focus. Phys. Rev. E 51, 4833–4843.CrossRefGoogle ScholarPubMed
Heras, J.A. & O'Connell, R.F. (2006). Generalization of the Schott energy in electrodynamic radiation theory. Am. J. Phys. 74, 150–153.CrossRefGoogle Scholar
Hora, H., Hoelss, M., Scheid, W., Wang, J.W., Ho, Y.K., Osman, F. & Castillo, R. (2000). Principle of high accuracy for the nonlinear theory of the acceleration of electrons in a vacuum by lasers at relativistic intensities. Laser Part. Beams 18, 135–144.CrossRefGoogle Scholar
Il'in, A.S., Kulagin, V.V. & Cherepenin, V.A. (2001). Acceleration of dense electron bunches at the front of a high-power electromagnetic wave. Plasma Phys. Reports 27, 1048–1056.CrossRefGoogle Scholar
Jackson, J.D. (1999). Classical Electrodynamics, 3rd ed.. New York: Wiley & Sons.CrossRefGoogle Scholar
Kibble, T.W.B. (1966). Mutual refraction of electrons and photons. Phys. Rev. 150, 1060–1069.CrossRefGoogle Scholar
Krainov, V.P. & Smirnov, M.B. (2002). Cluster beams in the super-intense femtosecond laser pulse. Phys. Reports 370, 237–331.CrossRefGoogle Scholar
Kulagin, V.V., Cherepenin, V.A. & Suk, H. (2004). Compression and acceleration of dense electron bunches by ultraintense laser pulses with sharp rising edge. Phys. Plasmas 11, 5239–5249.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.M. (1975). Classical Theory of Fields, 4th rev. ed. Oxford: Pergamon.Google Scholar
Leemans, W.P., Nagler, B., Gonsalves, A.J., Tóth, CS., Nakamura, K., Geddes, C.G.R., Esarey, E., Schroeder, C.B. & Hooker, S.M. (2006). GeV electron beams from a centimetre-scale accelerator. Nature Phys. 2, 696–699.CrossRefGoogle Scholar
Liseykina, T.V., Pirner, S. & Bauer, D. (2010). Relativistic attosecond electron bunches from laser-illuminated droplets. Phys. Rev. Lett. 104, 095002.CrossRefGoogle ScholarPubMed
Lorentz, H.A. (1916). The Theory of Electrons. Leipzig: Teuber.Google Scholar
Maksimchuk, A., Gu, S., Flippo, K. & Umstadter, D. (2000). Forward ion acceleration in thin films driven by a high-intensity laser. Phys. Rev. Lett. 84, 4108–4111.CrossRefGoogle ScholarPubMed
Malka, V., Faure, J., Gauduel, Y.A., Lefebvre, E., Rousse, A. & Phuoc, K.T. (2008). Principles and applications of compact laser-plasma accelerators. Nature Phys. 4, 447–453.CrossRefGoogle Scholar
Medina, R. (2009). Radiation reaction of a classical quasi-rigid extended charge. J. Phys. A: Math. Gen. 39, 3801–3816.CrossRefGoogle Scholar
Meyer-ter-Vehn, J. & Wu, H.-C. (2009). Coherent Thomson backscattering from laser-driven relativistic ultra-thin electron layers. Eur. Phys. J. D 55, 433–441.CrossRefGoogle Scholar
Panofsky, W.K.H. & Phillips, M. (1962). Classical Electricity and Magnetism, 2nd ed. Reading, MA: Addison-Wesley.Google Scholar
Parks, P.B., Cowan, T.E., Stephens, R.B. & Campbell, E.M. (2001). Model of neutron-production rates from femtosecond-laser-cluster interactions. Phys. Rev. A 63, 063203.CrossRefGoogle Scholar
Qiao, B., Zepf, M., Borghesi, M., Dromey, B. & Geissler, M. (2009). Coherent x-ray production via pulse reflection from laser-driven dense electron sheets. New J. Phys. 11, 103042.CrossRefGoogle Scholar
Quesnel, B. & Mora, P. (1998). Theory and simulation of the interaction of ultraintense laser pulses with electron in vacuum. Phys. Rev. E 58, 3719–3732.CrossRefGoogle Scholar
Rohrlich, F. (2001). The correct equation of motion of a classical point charge. Phys. Lett. A 283, 276–278.CrossRefGoogle Scholar
Rohrlich, F. (2002). Dynamics of a classical quasi-point charge. Phys. Lett. A 303, 307–310.CrossRefGoogle Scholar
Rohrlich, F. (2007). Classical Charged Particles, 3rd ed. Singapore: World Scientific.CrossRefGoogle Scholar
Saalmann, U., Siedschlag, CH. & Rost, J.M. (2006). Mechanisms of cluster ionization in strong laser pulses. J. Phys. B 39, R39–R77.CrossRefGoogle Scholar
Salamin, Y.I. & Faisal, F.H.M. (1996). Harmonic generation by superintense light scattering from relativistic electrons. Phys. Rev. A 54, 4383–4395.CrossRefGoogle ScholarPubMed
Schlenvoigt, H.-P., Haupt, K., Debus, A., Budde, F., Jäckel, O., Pfotenhauer, S., Schwoerer, H., Rohwer, E., Gallacher, J.G., Brunetti, E., Shanks, R.P., Wiggins, S.M. & Jaroszynski, D.A. (2008). A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nature Phys. 4, 130–133.CrossRefGoogle Scholar
Shao, Y.L., Ditmire, T., Tisch, J.W.G., Springate, E., Marangos, J.P. & Hutchinson, M.H.R. (1996). Multi-keV electron generation in the interaction of intense laser pulses with Xe clusters. Phys. Rev. Lett. 77, 3343–3346.CrossRefGoogle ScholarPubMed
Springate, E., Aseyev, S.A., Zamith, S. & Vrakking, M.J.J. (2003). Electron kinetic energy measurements from laser irradiation of clusters. Phys. Rev. A 68, 053201.CrossRefGoogle Scholar
Stupakov, G.V. & Zolotorev, M.S. (2001). Ponderomotive laser acceleration and focusing in vacuum for generation of attosecond electron bunches. Phys. Rev. Lett. 86, 5274–5277.CrossRefGoogle ScholarPubMed
Tajima, T. & Dawson, J.M. (1979). Laser electron accelerator. Phys. Rev. Lett. 43, 267–270.CrossRefGoogle Scholar
Teitelboim, C. (1970). Splitting of the Maxwell tensor: radiation reaction without advanced fields. Phys. Rev. D 1, 1572–1582.CrossRefGoogle Scholar
Veksler, V.I. (1957). The principle of coherent acceleration of charged particles. Sov. Atom. Energy 2, 525–528.CrossRefGoogle Scholar
Wang, H.F., Shi, L.P., Lukyanchuk, B., Sheppard, C. & Chong, C.T. (2008). Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nature Photonics 2, 501–505.CrossRefGoogle Scholar
Wu, H.-C. & Meyer-ter-Vehn, J. (2009). The reflectivity of relativistic ultra-thin electron layers. Eur. Phys. J. D 55, 443–449.CrossRefGoogle Scholar
Yaghjian, A.D. (2006). Relativistic Dynamics of a Charged Sphere. New York: Springer.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) (a) Trajectory of an electron bunch accelerated by a laser pulse with parameters λ = 1 µm, I = 1 × 1019 W/cm2, τL = 200 fs, and w0 = 10λ; (b) Longitudinal momentum of the bunch as a function of time; and (c) Transverse momentum of the bunch as a function of time, calculated for the case including radiation reaction (Thomson + ponderomotive scattering, ωτe = 0.03) and for the case without radiation reaction (ponderomotive scattering, ωτe = 0). The solid lines have been calculated using Eq. (11) with FL = q(E + v × B), taking for E and B Eqs. (A.1–A.4). The dashed lines have been calculated using Eqs. (5–10), taking a2 according to Eq. (A.5). The initial position was x0 = (λ, 0) and the initial velocity was zero.

Figure 1

Fig. 2. (Color online) Trajectory of an electron bunch accelerated by a laser pulse, calculated for the case including radiation reaction (Thomson + ponderomotive scattering, ωτe = 0.01) during the initial period 0 ≤ T ≤ 8.3, and for the case without radiation reaction (ponderomotive scattering, ωτe = 0). See Fig. (1) for details about the calculation and laser parameters. The dash-dotted lines show the error margins for the case ωτe = 0 corresponding to a hypothetical uncertainty of magnitude λ in the initial position, calculated using the averaged description. The initial position was x0 = (−λ, 0) and the initial velocity was according to Eq. (14).

Figure 2

Fig. 3. (Color online) See Figure 2, with the initial position changed to x0 = (−7.1λ, 0).

Figure 3

Fig. 4. (Color online) (a) Trajectory of an electron bunch accelerated by a laser pulse with parameters λ = 10 µm, I = 1 × 1019 W/cm2, τL = 2 ps, and w0 = 10λ; (b) Longitudinal momentum of the bunch as a function of time; and (c) Transverse momentum of the bunch as a function of time, calculated for the case including radiation reaction (Thomson + ponderomotive scattering, ωτe = 1) during the initial period 0 ≤ T ≤ 2π and for the case without radiation reaction (ponderomotive scattering, ωτe = 0). The solid lines have been calculated using Eq. (11) with FL = q(E + v × B), taking for E and B Eqs. (A.1–A.4). The inset of the middle panel shows the long-term behavior of the longitudinal momentum for the case including radiation reaction. The inset of the lower panel is a close-up of the first optical period; the slope of the dashed line is according to Eq. (16). The initial position was x0 = (λ, 0) and the initial velocity was β0 = 0.9ex.