Published online by Cambridge University Press: 06 March 2006
We will consider relativistic electron beam interacting with plasma and study the electromagnetic instabilities obtained for arbitrarily oriented wave vectors ranging from two-stream to filamentation instabilities. For these unstable modes, we will study every temperature effects, namely beam and plasma normal, and parallel temperatures. Temperatures are supposed to be non-relativistic and modeled through water bag distributions. It is found that only normal beam temperature and parallel plasma temperature have a significative influence over the growth rates for wave vector making an angle with the beam larger than a critical angle θc which is determined exactly. The largest growth rate being reached for a wave vector making an angle with the beam smaller than θc, it is not damped by any kind of temperatures. We finally explore collisions effects and show they can reduce the largest growth rate.
Beam plasma interaction plays an important role in many areas of physics (Umstadter, 2003) and received a renewed interest in recent years with inertial confinement fusion. In the fast ignition scenario for example (Mulser & Bauer, 2004; Deutsch et al., 2005), an ultra short laser pulse is supposed to generate a relativistic electron beam (Tabak et al., 1994; Koch et al., 1998) which ignites the Deuterium Tritium (DT) core (Deutsch, 2003; Deutsch et al., 1997). The electron beam quickly creates a return current in the target plasma so that one eventually ends up with a very classical two-stream configuration. This system is known to be sensitive to various electromagnetic instabilities which can be classified according to their origin. The two-stream and filamentation instabilities are beam dependant so that they need the beam to exist. The first one is longitudinal with a wave vector aligned with the beam, the second one is transverse with a wave vector normal to the beam, but both disappear when the beam is removed. The Weibel instability (Weibel, 1959), on the other hand, arises from a temperature anisotropy in the plasma. Although the presence of the beam may slightly affects its growth rate, it does not depend on the beam so that a strongly anisotropic plasma shall be Weibel unstable whether there be a beam or not, whereas an isotropic plasma shall be Weibel stable, with or without a beam.
Indeed, the most important issue is not so much to study a given instability than to search for the most unstable mode of the system. It means that a thorough investigation of one given instability may not be relevant if it turns out that elsewhere in the spectrum of unstable waves, one mode has a much more important growth rate. Where in the k space could such a mode be found? In the part of the space which is left unexplored once two-stream and filamentation instabilities have been checked, which means for wave vectors arbitrarily orientated with respect to the beam. Performing such an investigation in a previous paper (Bret et al., 2005), we unravelled two oblique interesting effects: The existence of a critical angle in the k space in which direction waves are unstable at any k, and an absolute maximum growth rate found for a wave vector making an oblique angle with the beam. The model requirements to obtain these two effects are minimal for they appear as soon as the beam is relativistic (even if it is cold) and the plasma hot in the transverse direction. Since a mixed two-stream/filamentation mode with maximum growth rate was clearly identified, our goal is to investigate temperature as well as collisions effects on this mode. This paper is therefore structures as follow: We start exposing our formalism and then turn to temperature effects. Since we want to study every potential temperatures, we shall add one temperature at a time before we analyze the full problem. We then turn to collisions effects before reaching our conclusions.
We consider an infinite and homogenous unmagnetized plasma of electronic density ne interacting with an infinite and homogenous beam of electronic density nb and relativistic velocity Vb. The z axis is set along the beam velocity and the angle θk measure the angle between the wave vector and the beam. Two-stream instability corresponds therefore to θk = 0 and filamentation to θk = π/2. One of the specificities of the problem is that an approximation such as the longitudinal approximation cannot be used here because we need to analyze transverse modes as well as longitudinal modes with the same formalism. We therefore used the Maxwell equations together with the relativistic Vlasov equation in the linear regime to derive the dielectric tensor and the dispersion equation. This equation is found to be amenable to the form (Bret et al., 2004) P(k,ω)Q(k,ω) = 0 with (η ≡ ω/c),
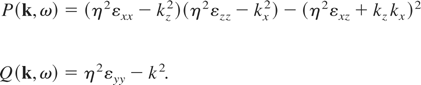
We will focus here on the first equation, for this is the one bearing the two-stream and filamentation instabilities. Interestingly, Weibel modes can be found on both branches according to the direction of the plasma temperature anisotropy. As far as temperature and distribution functions are concerned, we choose water bag instead of Maxwellian distributions. This simple distribution can model a thermal velocity spread and leads to calculable quadratures more frequently than the Maxwellian. The beam distribution is therefore considered as a rectangular window centered around momentum Pb = γb mVb with a thermal spread Ptb∥ along the beam axis and Ptb⊥ along the x and y axis. In a similar way, the plasma distribution is centered around momentum Pp = −mVp with a thermal spread Ptp∥ along the beam axis and Ptp⊥ along the x and y axis. One will notice that if the beam is treated as a perturbation (nb << np) and the equilibrium is current neutralized (nbVb = npVp), then the velocity of the return current is non relativistic. Since we will consider non-relativistic temperatures as well, the beam velocity is eventually the only relativistic velocity of the problem. This will be proved useful since the reduced velocities which appear naturally in the equations,
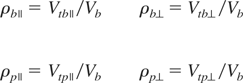
are small parameters. The other reduced parameters involved here are
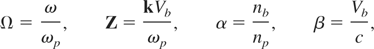
where ωp is the plasma frequency.
Starting therefore from a cold relativistic beam and hot plasma in the transverse direction, one can derive the growth rate map displayed on Figure 1. One can notice the two-stream profile along the beam axis as well as the filamentation profile along the normal axis. Looking only in these directions, one could think the system is stable at high k whereas looking in the θc direction with (Bret et al., 2005)
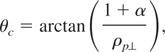
one finds out the system is unstable for every k. Also, it is clear that the absolute maximum growth rate δmTSF is now found off axis with,
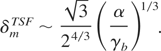
Knowing that the two-stream and filamentation maximum growth rates are scaled like

, respectively, it is obvious that δmTSF will be all the more dominant than the beam is relativistic.

Basic model displaying the main oblique effects. Parameters are γb = 4, α = 0.05 and ρp⊥ = 0.1. The beam velocity Vb is along the Zz axis.
Having introduced the basic model, our intend from now on is to add one temperature at a time and carefully analyze its effects before we investigate collisions influence on the maximum growth rate.
This first temperature we introduce is very interesting for it is already known that transverse beam temperature can strongly damp, and even cancel, the filamentation instability (Silva et al., 2002). On the other end, it may be easily checked that effect on the two-stream instability is rigourously zero. This comes from the fact that two-stream modes are longitudinal with an electric field aligned with the beam. The electrons which are added with transverse beam temperature are therefore unable to interact with these modes. Having no effect for θk = 0 and a strong effect for θk = π/2, the question comes immediately to know where, in terms of θk, starts the influence. The calculation of the growth rate all over the two-steam/filamentation (TSF) branch displayed in Figure 2 clearly answers: modes are damped beyond the critical angle and almost unaffected below. Indeed, modes located in the two-stream zone, below θc, tend to behave as the two-stream ones whereas those located beyond behave like filamentation modes. The concepts of two-stream and filamentation zones are really useful to evaluate any kind of property in the analytically almost inaccessible region of oblique angles.

Transverse beam temperature effect. Parameters are γb = 4, α = 0.05 and ρb⊥ = ρp⊥ = 0.1.
The situation is almost symmetric with respect to the previous one since we now add electrons going along the main beam direction. As far as filamentation instability is concerned, some easy (though lengthy) calculations show that this temperature has a limited effect on the instability. Although the electrons which are added can still interfere with filamentation modes (since these modes have also E∥Vb), it is found that a parallel velocity spread poorly affects them. This can be mainly understood in terms of their phase velocity. It can be shown easily that they correspond to a solution of the dispersion equation with a real part that is zero. These modes are therefore not traveling and for them, the beam electrons have almost the same parallel velocity as long as the parallel thermal spread is not relativistic. Additionally, another effect we will study now with the two-stream instability still reduces this temperature influence.
Surprisingly, parallel beam temperature also affects poorly the two-stream instability. Yet, it is known that influence is important for a non relativistic beam (Mikhailovskii, 1974), since we are adding electrons which are co-moving with the unstable modes. However, the dispersion equation, which is easily calculated with a water bag, shows the parameter involved when Vb ∼ c is no longer ρb∥ but ρb∥ /γb3. Indeed, if one considers a thermal momentum spread Pb∥, the corresponding thermal velocity spread is only Pb∥ /mγb3 so that relativistic effects dramatically shrink the thermal velocity spread. If the beam electrons are already almost at c, there cannot be a significative velocity spread around this value, although the momentum spread can be arbitrary. And since instabilities are very sensible to velocity spread, the thermal momentum spread has little influence over them. This is eventually confirmed comparing Figure 3 with Figure 1 and we can conclude parallel beam temperature overall impact is negligible.

Parallel beam temperature effect. Parameters are γb = 4, α = 0.05 and ρb∥ = ρp⊥ = 0.1.
Starting with the two-stream instability, the dispersion equation is again easy to compute and shows that thermal electrons centered around the return current interact poorly with two-stream modes moving at the beam velocity. Turning to the effects on filamentation instability, we encounter a much more interesting situation. Since our base model already contains a transverse plasma temperature, we can now model the isotropic plasma. For such a plasma with ρp∥ = ρp⊥ = ρp, it is found that the maximum filamentation growth rate is very well fitted by
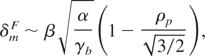
so that plasma temperature slightly damps the instability. Situation becomes very interesting when considering plasma with a high parallel temperature. In the regime ρp∥ >> ρp⊥ the growth rate is found to behave as
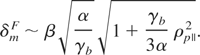
In the high ρp∥ limit, this quantity tend to
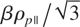
which, unlike Eq. (6), no longer depends on the beam density. As we can see, we are here in the presence of a very interesting transition between filamentation and Weibel instability. As was said previously, this instability arises from a temperature anisotropy in the plasma, whether there be a beam or not. Furthermore, Weibel unstable modes are transverse and have their wave vector normal to the high temperature axis. If we now consider our present situation, we see that we are dealing with plasma with a high temperature in the beam direction. If this plasma becomes Weibel unstable because of a high parallel temperature, the corresponding Weibel modes should be found transverse and with a wave vector in the transverse direction. It means the Weibel modes we expect to see are really similar to the beam based filamentation instability; both are transverse, and both have θk = π/2. The only remaining difference between the two is that one is suppressed when the beam is removed while the other one remains unchanged. Looking at Eq. (7) in the high ρp∥ limit to check this important property of the growth rate, one sees that we just found the Weibel modes we are looking for. There is a continuous transition between filamentation and Weibel modes, and the growth rate reached at high ρp∥ is independent of the beam and is exactly the one which is found when calculating Weibel growth rate with water bag distributions (Bret et al., 2005).
Turning now to arbitrarily oriented wave vectors, parallel plasma temperature introduces an additional critical angle with
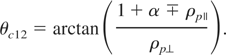
Figure 4 display the growth rate calculated for an isotropic plasma (Fig. 4a) and an anisotropic one (Fig. 4b). The two critical angles are clearly visible together with the transition to the Weibel regime for (Fig. 4b). As far as the absolute maximum growth rate is concerned, one can check it is still located in the two-stream region and is therefore poorly affected. It is possible for the Weibel/filamentation growth rate to compete with the maximum of the basic model, especially for low beam density or high γb, but in a fast ignition scenario setting for example, the plasma is expected to be roughly isotropic, namely Weibel stable, so that the absolute maximum should stay the same.

Parallel plasma temperature effect. Parameters are γb = 4, α = 0.05 and ρp∥ = ρp⊥ = 0.1 for (a). Plasma is Weibel unstable in (b) with ρp∥ = 0.2 and ρp⊥ = 0.05.
We are now gathering all previous results to analyze the situation when every temperatures are accounted for together. As far as two-stream instability is concerned, we found that temperatures will not significantly affect it as long as they are non-relativistic. Our temperature parameters remaining small, the overall effect will also be negligible. The case of filamentation instability is much more interesting for we found two temperatures having two potentially opposite effects on it. On one hand, transverse beam temperature tend to damp it while on the other hand, parallel plasma temperature can boost it. It is therefore especially interesting to combine these two and see which effect overcomes the other. We can start simplifying the problem setting beam parallel temperature to zero since its effects are really negligible on filamentation. We then search under which condition transverse beam temperature can cancel the instability. To do so, we start noting the system is unstable if D0 = P(k,ω = 0) > 0 (see Eq. (1) for the definition of function P). The quantity D0 is a function of Zx and calculation shows straightforwardly that D0 ∝ Zx2. This means the system is always stable for Zx = 0. To find to largest unstable wave vector Zxm, one needs to solve the equation D0(Zxm)/Zxm2 = 0 where the root at Zx = 0 is eliminated. If the instability must be totaly cancelled, we have Zxm = 0 which means 0 must be a root of D0(Zx)/Zx2 = 0. All the equations being polynomial with the water bag distribution, this quantity may be expressed easily and one finds Zx = 0 can be a root of the required equation if
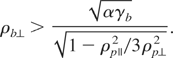
This equation clearly shows a threshold for

. As long as ρp∥ is smaller than the threshold value, filamentation instability can be cancelled for a value of ρb⊥ high enough. Let us notice than the threshold is even lower than
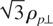
since ρb⊥ cannot be larger than 1. On the other hand, when the threshold is exceeded, transverse beam temperature can no longer cancel the filamentation instability because it has entered the Weibel regime where it is disconnected from the beam and just relies on the plasma anisotropy.
As far as the critical angles and oblique wave vectors are concerned, the most general expression for the two critical angles is
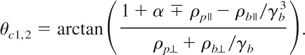
Figures 5 display the growth rate calculated for an isotropic (Fig. 5a) and an anisotropic plasma (Fig. 5b). Every effects previously investigated are clearly visible; the two critical angles, the transverse beam temperature damping beyond the critical angles as well as the filamentation boosting from plasma anisotropy. Still, in both cases, the maximum growth rate located in the two-stream region is still more than 90% of the basic model value so that it can be considered as almost unsensible to any kind of temperature. Since this most unstable mode shares its properties with the usual two-stream instability, we need to find what damps the two-stream instability. We could check here that temperatures shall not do it as long as they are non-relativistic. That is why it is important to evaluate the effect of collisions.

All temperature effects for an isotropic plasma (a) with ρp⊥ = ρp∥ = 0.15. For an anisotropic plasma (b) with ρp⊥ = 0.05 and ρp∥ = 0.2. Other parameters are α = 0.05, γb = 4 and ρb⊥ = ρb∥ = 0.1 for both plots.
There are many ways to modify the Vlasov equation in order to take accounts of collisions. A classical method consist in adding a “Krook” collision term to the equation such as
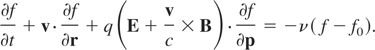
One of the main drawbacks of this equation is that it does not relax to a Maxwellian. However, it leads to calculable quadratures and that is why it is often used. Calculation of the dielectric tensor through this equation and Maxwell equations yields the following dielectric tensor elements
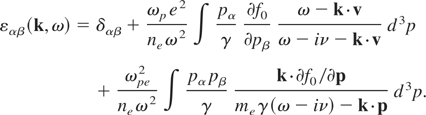
If we set ω′ = ω − iν the general dispersion equation reads (Bret et al., 2005)
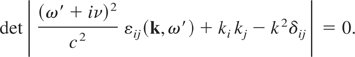
Let ω0 be a complex root of the collisionless dispersion equation and ων the corresponding root of the collisional problem, so that limν→0 ων = ω0. If ν << |ω0|, then one can set ω′ + iν ∼ ω′ and the resulting dispersion equation for ω′ is exactly the one for ω. The roots will therefore be the same with ων′ ∼ ω0, yielding
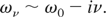
We therefore find a very simple result which is valid for a wide class of distribution functions: as long as the collision frequency is small, the effect of collisions simply consists in subtracting the collisions frequency to the collisionless growth rate. However, the validity condition of this result varies with k since ω0 is a function of k. The proper frequency ω0(k) can be expressed through its real and imaginary parts as ω0(k) = ω0r(k) + iδ0(k). We know from previous studies (Bret et al., 2005) that ω0r(k)/ωp ∼ Z cos θk = Zz. As far as the imaginary part, namely the growth rate, is concerned, all that can be said is that it is much smaller than the plasma frequency but there is no general analytical formula for it all over the k space. We can see straightforwardly than due to the expression of ω0r(k), the range of validity of Eq. (14) will be limited to some given region of the k space. If we restrict to the region where the maximum growth rate is located, we set Zz ∼ 1 to obtain the real part of the proper frequency and replace the imaginary part by Eq. (5). This yields the condition under which our approximation is valid for the maximum growth rate,
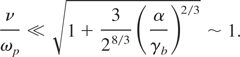
Interestingly this condition is none other than the weakly collisional regime hypothesis. Figures 6(a–d) display an evaluation of the growth rate in the collisional regime. Parameters are α = 0.05, γb = 4 and ρp⊥ = 0.1. The quantity plotted on these figures is not the collisional growth rate itself but Δ = (δν=0 − δν)/ν which is 1 when Eq. (14) is fulfilled. The result is as expected; as long as the collision frequency is kept small, Δ is found almost equal to 1 where the growth rate is important and in particular, for the maximum growth rate. As the collisions frequency approaches ωp, Δ departs from 1 and becomes smaller, which shows growth rate reduction is eventually smaller than the one predicted by the simple formula δν ∼ δν=0 − iν.

Collisions effects on the growth rate for various collisions frequency. The quantity plotted is Δ = (δν=0 − δ)/ν. Parameters are α = 0.05, γb = 4 and ρp⊥ = 0.1. Collision frequency ν is (a) 0.01ωp, (b) 0.1ωp, (c) 0.2ωp, (d) 0.3ωp.
We have investigated the role of transverse and parallel beam and plasma temperatures on electromagnetic instabilities in the k space. Various important effects can be highlighted whether we focus on the map or on the absolute maximum growth rate. We find that the wave vector space is divided into two regions delimitated by a critical angle θc with the beam. Modes having their wave vector below this angle are poorly affected by any kind of temperature and are almost longitudinal (Bret et al., 2004), like the usual two-stream modes. Modes located beyond the critical angle can be damped by transverse beam temperature and boosted by parallel plasma temperature. When these two temperatures are accounted for together, it is found that filamentation instability can be cancelled by transverse beam temperature as long as parallel plasma temperature is not too high, namely
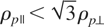
. Beyond this limit, filamentation instability enters a Weibel regime where it mostly relies on the plasma temperature anisotropy and is disconnected from the beam. Therefore, it can no longer be suppressed by beam temperature. As far as the maximum growth rate is concerned, no temperature of any kind can significantly affect it (at least non relativistic temperatures) because it is found in the two-stream region, bellow the critical angle.
We therefore turn to a simple model of a collisional plasma to investigate collisions effects on the maximum growth rate. We proved that as long as collision frequency is small enough, the collisional growth rate can be found from the collisionless one just subtracting the collision frequency. This results therefore in a damping of the instability. For larger collision frequencies, it is found that the damping becomes weaker. It is therefore proved that while non relativistic temperatures failed to damp to all k maximum growth rate, collisions can succeed.
One of us (A. Bret) wishes to thank the Laboratoire de Physique des Gaz et des Plasmas at Orsay University for allowing him to start this work. The work has been partially achieved under project FTN2003-00721 of the Spanish Ministerio de Educación y Ciencia.

Basic model displaying the main oblique effects. Parameters are γb = 4, α = 0.05 and ρp⊥ = 0.1. The beam velocity Vb is along the Zz axis.

Transverse beam temperature effect. Parameters are γb = 4, α = 0.05 and ρb⊥ = ρp⊥ = 0.1.

Parallel beam temperature effect. Parameters are γb = 4, α = 0.05 and ρb∥ = ρp⊥ = 0.1.

Parallel plasma temperature effect. Parameters are γb = 4, α = 0.05 and ρp∥ = ρp⊥ = 0.1 for (a). Plasma is Weibel unstable in (b) with ρp∥ = 0.2 and ρp⊥ = 0.05.

All temperature effects for an isotropic plasma (a) with ρp⊥ = ρp∥ = 0.15. For an anisotropic plasma (b) with ρp⊥ = 0.05 and ρp∥ = 0.2. Other parameters are α = 0.05, γb = 4 and ρb⊥ = ρb∥ = 0.1 for both plots.

Collisions effects on the growth rate for various collisions frequency. The quantity plotted is Δ = (δν=0 − δ)/ν. Parameters are α = 0.05, γb = 4 and ρp⊥ = 0.1. Collision frequency ν is (a) 0.01ωp, (b) 0.1ωp, (c) 0.2ωp, (d) 0.3ωp.