1. INTRODUCTION
Turbulent mixing driven by the Rayleigh–Taylor (RT) instability
is an important physical process in a number of environments, including
inertial confinement fusion (Lindl, 1995).
Perturbations at an accelerated material interface grow by the RT
instability when the direction of acceleration is from the lighter
material toward the heavier material. If perturbations are small in
amplitude compared to wavelength, then the growth is described by
linear theory, giving the amplitude of a perturbation of wavenumber,
k, varying with time, t, as
ak ∝
eγt, where the growth rate γ =
(Agk)1/2. Here, g is the acceleration,
A = (ρh −
ρl)/(ρh −
ρl) is the Atwood number, and
ρh and ρl are the
densities of the heavy and light fluids (Rayleigh,
1900; Taylor, 1950). When
kak ∼ 1, nonlinear effects become
important. These include coupling of different wavelengths, changes in
shape of the modulation, and reduction in the rate of growth below
exponential. A surface with multiwavelength initial perturbations
eventually will develop into a mixing zone of turbulent, multiscale
structure. Experiments (Read, 1984),
simulations, and scaling arguments (Annuchina et
al., 1978; Youngs, 1984) indicate
that the mixing region should grow with time in a self-similar fashion,
and that the total mixing extent should increase as h =
αAgt2.
Two-dimensional (2D) and three-dimensional (3D) simulations of this
process have been presented by a number of authors (including Youngs, 1994; Hecht et
al., 1995; Cook and Dimotakis,
2001; Glimm et al., 2001;
Young et al., 2001). Fits to the
parameter, α, vary, but the simulated problems and analysis methods
also differ. For this reason, a test problem was proposed (Dimonte et al., 2003) to permit
comparisons between codes for identical conditions. This article
reports only upon our own work; results of other groups, comparisons,
and general conclusions are presented elsewhere (Dimonte et al., 2003). The problem
specifies constant acceleration, compressible γ-law gases, and
defines the mesh and the initial interface perturbation.
We present simulations of the “α group” test problem
(Dimonte et al., 2003) employing an
arbitrary Lagrange–Eulerian (ALE) code, HYDRA (Marinak et al., 1996). HYDRA incorporates
interface reconstruction, but the full problem has only been run
without this. We have also run smaller simulations, either
1282 × 256 or 1282 × 512, and either
with and without interface reconstruction. We find that interface
reconstruction gives only slightly larger penetration distances, and
little difference in the energy dissipation rate.
We have performed 2D simulations with meshes of 256 × 512, 512
× 1024, and 1024 × 2048, using a cut of the 3D initial
perturbation. The initial modulation was held constant while the mesh
size increased, so that the larger problems better resolve the initial
structure. Although the nominal problem greatly undercalculated the
linear growth rates of the initial perturbations, the mix extent at
late times differed little between these resolutions.
2. PROBLEM DEFINITION
The test problem specifies perfect gases of γ = 5/3 in a box
of width and depth, L = 10 cm, and height 2L. The
light and heavy layers have heights 17L/16 and
15L/16. Gravity is taken to be in the z
direction. The initial density distribution is
where P0 = 500 dyne/cm2,
ρ0 = 3 g/cm3 for the top fluid,
ρ0 = 1 g/cm3 for the lower fluid, and
g = 2 cm/s2. The mesh is 2562
× 512. The initial perturbations have a random spectrum in an
annulus in k space spanning 32–64 wavelengths across the
box width. The modal amplitudes are selected from a Gaussian of rms 0.1
cm. The surface was intended to be the same for all simulations. The
upper and lower boundaries are rigid walls.
The original surface was created for use with periodic spanwise
boundaries. Thus, it was constructed of modes having random phases with
respect to the boundaries. The ALE code that we have used, HYDRA, did
not provide periodic boundary conditions (bc) at the time we began this
study, but they were added later. The modes supported on a square
domain with reflection boundaries are
cos(πnx/L)cos(πmy/L).
If the original surface is evolved with reflection boundary conditions,
the modes with sine components are aliased into cosine modes, creating
higher spatial frequencies. Equivalently, treating the sine modes as
reflection symmetric results in a cusp at the boundary. This yields
apparently spurious growth at the boundaries, even in the linear
regime.
Consequently, Youngs (2001, pers. comm.) provided an alternative
surface of otherwise equivalent statistics made up of normal modes for
reflection boundaries. The number of modes in the k space
annulus is equal to that for the periodic case because modes may have a
half-integer number of wavelengths across the domain. The two initial
surfaces and resulting early evolution appear very similar.
HYDRA (Marinak et al., 1996) is an
ALE code with interface reconstruction. Because the two materials have
the same γ, we can treat them either as the same fluid starting at
different adiabats or as two fluids. In the second case, interface
reconstruction is performed, whereas in the first case, it is not.
Without interface reconstruction, advection of the interface results in
mixing of the two materials.
3. RESOLUTION ISSUES
The resolution of the initial perturbations of 4–8 zones per
wavelength significantly affects the accuracy of the results.
Underresolution acts like a viscosity, slowing the growth of shorter
wavelengths. This choice of modes resulted from a trade-off between
resolution and dynamic range in wave number. Youngs (1994) found that this resolution appeared to give
convergence in the growth of mix width.
Figure 1 shows the ratio of the growth rate
in the linear regime to the analytic value
(gkA)1/2. In the 2D runs, the initial
perturbations grow at 15–40% of the analytic rate. In 3D, modes
with k oblique to the mesh grow even more slowly, down to 5%
of the analytic rate. As a consequence of this orientation dependence,
the perturbation evolves from random in the x–y
plane to a checkerboard pattern of prominent bubbles during linear
growth. Mesh alignment is not apparent in later stages in the flow.
Ratio of linear growth rate to classical incompressible value versus
mode number, that is, number of wavelengths in L = 10 cm. xs
are results from 2D single-mode simulations, and other symbols are from
the near-linear regime of 3D multimode simulations; +: modes with
k nearly parallel to the boundaries, ○: k near
diagonal to boundaries, ·: intermediate angles.
Youngs (2001, pers. comm.) noted that terminal bubble velocities,
which may be more relevant to self-similar growth, converged more
rapidly with zoning than linear growth rates. Figure
2 shows bubble rise velocities for simulations of a 3D single
bubble in a square box. Convergence in terminal bubble velocity is seen
by 8 zones per wavelength, but the time needed to reach terminal
velocity depends on resolution.
Bubble rise velocity (cm/s) versus
Agt2/L for single 3D bubbles in a 10
× 10 cm box, for different mesh resolutions.
We have carried out a zoning refinement study in 2D simulations, with
meshes of 256 × 512, 512 × 1024, and 1024 × 2048. The
initial perturbation was the same cut of the 3D case for all three
runs. Rigid boundaries were employed, resulting in artifacts that will
be discussed later.
Figure 3 shows bubble and spike penetration
versus time, taken as 1% and 99% volume fraction of the light material,
respectively. No trend with zoning refinement is apparent. Noise is
present in any particular simulation because there are a finite number
of bubbles and spikes in any particular statistical realization. The
number of features becomes smaller with time because of the inverse
cascade. This has been noted and examined by Clark and Harlow (2002). The noise is larger in two dimensions than
in three dimensions because the number of features of given size is
smaller.
a: Bubble height/L, L = 10 cm versus
Agt2/L, from 2D simulations of
different meshes, 1x: 256 × 512 (thin solid), 2x: 512 ×
1024 (dotted), 4x: 1024 × 2048 (thick solid); b: similar, but for
spikes. Dashed curves are lines of constant α, slope
αb = 0.027 for bubbles,
αs = 0.035 for spikes.
4. THREE-DIMENSIONAL SIMULATIONS
Three-dimensional simulations were carried out both for the nominal
2562 × 512 problem (case A) and for smaller problems
of either 1282 × 512 (case B) or 1282
× 256 (case C). Cases B and C have been run both with and without
interface reconstruction, whereas the full-scale problem has been run
only without interface reconstruction because of computational cost.
Case B used one quadrant of the initial perturbations of the full
problem, in a 5 × 5 cm spanwise domain, whereas case C also used
a quadrant of case A perturbations, but in a 10 × 10 cm box and
with doubled initial amplitudes and wavelengths. Case A has been
simulated both with reflection and with periodic spanwise bc, whereas
case B has been run only with reflection bc, and case C only with
periodic bc.
Our initial simulations were performed with reflection spanwise
boundary conditions (rigid walls). We observed that the most
penetrating features at late times were always found on the boundaries,
especially on the corners. It seems likely that the higher symmetry of
the flow forced by the bc caused greater mix penetration near the
boundaries. Later simulations employed periodic spanwise boundary
conditions. We found that the mix penetration away from the reflection
boundaries agreed well with the penetration calculated with periodic
boundaries. The penetration for the full span using reflection
boundaries exceeded that with periodic boundaries by as much as 30%.
Simulations with and without interface reconstruction differ little
in penetration distance, although density structure in the two cases
differs vastly. Figure 4 compares densities
on cuts parallel to the x–z plane for case C,
with and without interface reconstruction. The total mixing extent is
very similar for the two cases. However, with interface reconstruction,
large-scale features are broken into small droplets in which the two
original fluids remain distinct, whereas without interface
reconstruction, large structures are composed of mixed fluid of
intermediate density. The penetration with interface reconstruction is
consistently greater by ∼5% than that without it. Spanwise-averaged
volume fraction profiles are also close for both cases.
Density (x, z) from case C simulations with
periodic bc, on the plane y = 2.85 cm at a time of 8 s. a:
simulation without interface reconstruction, b: simulation with
interface reconstruction.
Figure 5 shows bubble and spike height
versus Agt2/L, for 3D simulations
without interface reconstruction and for all three meshes. Cases A and
B have the same initial perturbations, so they evolve very similarly
until the growth is affected by the boundaries. The bubble histories
for cases A and B nearly overlay, but the spike growth appears to be
less affected by the boundaries, so scaling by L does not
cause the spike growth histories to collapse. The bubble and spike
penetrations for case C grow initially at the same rates as in the
other two cases, but show a slower decrease in growth rate with
increasing time, resulting in greater penetration at later times. The
difference between this simulation and the other two must result from
the longer wavelengths of the initial interface perturbation.
a: Bubble amplitude/L versus
Agt2/L for case A (L = 10 cm,
solid), case B (L = 5 cm, dot-dashed), and case C (L
= 10 cm, dashed) simulations without interface reconstruction. Circles
are LEM data of Dimonte and Schneider (2000).
b: Spike amplitudes/L, similarly.
Bubble and spike penetrations without interface reconstruction and at
volume fractions of 5% and 95% are smaller than those at volume
fractions 1% and 99% by a factor of ∼0.75. There is less reduction
for the case with interface reconstruction, by factors of 0.88 for the
bubbles and 0.8 for the spikes. Most of the literature presents mix
extents to the extremes of the mix region, more nearly represented by
the 1% to 99% limits.
Figure 6 shows the instantaneous α,
that is, the slope of h(Agt2), versus
time. All cases show a monotonic (other than what appears to be
statistical noise) decrease of α versus time. If the
self-similarity hypothesis is correct, the slope should approach an
asymptotic constant, which would be the true α of the self-similar
regime. It is not convincing that the simulations exhibit an approach
to self-similarity. Allowing for the possibility of a time offset, that
is, h = αAg(t −
t0)2, does not change the conclusion.
The limited range in wavelengths, constrained on one end by grid
resolution and on the other by the domain size, may prevent the
achievement of a self-similar growth range. It may be tempting to take
the late-time slope as the asymptotic limit. However, the boundaries
constrain the growth of bubbles and may depress the late-time growth
rate. We believe that the slower drop in
α(Agt2) of case C is a consequence of the
presence of longer wavelengths in the initial surface.
a: Bubble alpha versus Agt2/L for
case A (L = 10 cm, solid), case B (L = 5 cm,
dot-dashed), and case C (L = 10 cm, dashed) simulations
without interface reconstruction. b: Spike alpha,
similarly.
Bubble and spike penetrations from the Dimonte and Schneider (2000) linear electric motor (LEM) experiment,
constant acceleration A = 0.5 case, are also shown in Figure 5. Note that the scaling between the
simulations and the experiment was based upon the domain width,
L. The other length scales in this problem are the initial
amplitude and wavelength, which are unknown for the LEM experiment. The
fact that data show a nearly constant slope is consistent with the
hypothesis that the initial perturbations do not matter. However, the
simulations do not show a constant slope, so the choice of scaling
affects the fit to the data, and the domain width may not be the best
choice. The data agree most closely with case C, and give a larger
α than the late-time slope of any of the simulations. The
discrepancies could result from weaknesses in the simulations or could
indicate the presence of longer-wavelength perturbations in the (poorly
known) initial surface finish of the experiment.
Comparison of our results for 3D multimode RT instability to others
in the literature is complicated by the fact that different studies
employ different conditions. This fact was the principal reason for the
alpha-group collaboration. Dimonte et al. (2003) present a comparison of results for identical
parameters from several research groups including David Youngs and the
University of Chicago team (Young et al.,
2001). Growth histories agree to within roughly ±10% and
α values fall within the range αb ∼
0.025 ± 0.003, although the other simulations show less evidence
of time variation of α than ours. Cook and Dimotakis (2001) employ the Navier–Stokes equation and
three initial perturbation spectra, all different from the case
considered here. Their shortest wavelength case, that is most similar
to ours, shows an α coefficient that varies in time, but with a
different history than our results, and with a similar time average
αb ∼ 0.03. Glimm et al. (2001) report a substantially larger value of
αb ∼ 0.07 from a front tracking code. Their
initial perturbations are a longer wavelength than those of this study,
10–15 wavelengths across the box width, and also larger in
initial a/λ = 0.1. This difference in
αb is consistent in sense with Cook and
Dimotakis (2001), who find an increase in
αb with the mean wavelength of the initial
perturbations.
An interesting parameter is the molecular mixing fraction,
,
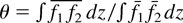
where fi is the volume fraction of fluid
i, and the overbars denote averages over the spanwise plane.
Figure 7 shows θ versus
Agt2/L for cases A and C. The value of
θ shown for case C is an upper limit, as it is does not account
for reconstructed interfaces within zones. Without interface
reconstruction, θ ∼ 0.7, similar to results of Youngs (1994), whereas it is much smaller with interface
reconstruction. Figure 7 also shows the
fraction of the potential energy drop that has been dissipated and the
ratio of the spanwise to streamwise kinetic energy, both for case A.
These ratios are quite similar for all of the simulations, with or
without interface reconstruction.
Atomic mixing parameter, θ, versus
Agt2/L for case A (dashed), and for
case C simulation with interface reconstruction (dotted). Also shown
are the fraction of the potential energy drop that has been dissipated
and the ratio of the kinetic energy in the x (spanwise)
direction to that in the z (streamwise) direction, both for
case A.
5. CONCLUSIONS
We present results of 2D and 3D simulations of growth of the
Rayleigh–Taylor instability for random multimode initial
roughness. The simulations employ meshes up to 2562 ×
512. Linear regime growth rates of the seed modes are well below the
analytic values and are dependent on orientation to the mesh. However,
a 2D convergence study extending to four times the nominal resolution
shows no clear trend in mix extent with improved resolution.
Penetration distance and volume fraction profiles are nearly the same
for simulations with and without interface reconstruction, but the
small-scale structure of the mixing region is quite different. In the
former case, the mixing region consists of small domains of one fluid
or the other, whereas in the latter, most of the fluid in the mixing
region has intermediate density.
Growth of the mix region does not appear to achieve self-similar
h = αAgt2 form in these simulations.
The instantaneous α [slope of
h(Agt2)] decreases with increasing
time. Results for the nominal 2562 × 512 problem and
simulations with smaller meshes and differing initial surfaces do not
overlay. One of the smaller problems gives the best agreement with the
LEM data of Dimonte and Schneider (2000). It
is unclear whether the experiment may have been sensitive to the
initial conditions or whether these calculations do not reach the
self-similar regime.
ACKNOWLEDGMENTS
This work was performed under the auspices of the U.S. Department of
Energy by the University of California, Lawrence Livermore National
Laboratory under contract No. W-7405-Eng-48.
