1. INTRODUCTION
The research about future options for controlled generation of fusion energy for power stations received an essential turning point by interaction of picosecond laser pulses of powers above terawatts with plasmas resulted in ultrahigh acceleration of plasma layers with a thickness of dielectric increased skin depths (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002). These plasma blocks contained directed energetic ions with extremely high ion current densities opening a new way of ignition of fusion by direct laser generation of a fusion flame in uncompressed solid fuel (Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu Hong, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007). This reaction as a kind of side-on ignition was considered before as the following described hydrodynamic Chu-model but only the new experimental results of the plasma blocks provided the necessary conditions for a plane geometry interaction for fusion of deuterium-tritium (DT). Fast ignition was the alternative first formulated by Tabak et al. (Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) and elaborated (Campbell, Reference Campbell2005) following the discussions about the highest DT fusion gains based on shock-free spherical ideal compression at thermal ignition (Yamanaka et al., Reference Yamanaka and Nakai1986; Storm et al., Reference Storm1986; Storm et al., Reference Storm, Lindl, Campbell, Bernat, Coleman, Emmett, Hogan, Horst, Krupke and Lowdermilk1988). The gains of more than 1012 fusion neutrons were significantly higher than all earlier attempts with exploding pushers (Hora et al., Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998), where shocks led to strong degrading deviations from the ideal adiabatic implosion. The ideal adiabatic compression led to the highest gains at volume-burn and the discovery of volume ignition (Hora et al., Reference Hora and Ray1978), confirmed as “Wheeler-modes” (Kirkpatrick et al., Reference Kirkpatrick and Wheeler1981) and then summarized (Hora et al., Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998). The discovery of this shock-free compression was reached systematically by varying the experimental parameters in parallel to computations, which, in contrast to those of exploding pushers, arrived at the highest gains as predicted (Hora et al., Reference Hora and Ray1978), the result (Yamanaka et al., Reference Yamanaka and Nakai1986) of which was called “Yamanka compression.” Gains above 1013 neutrons were achieved (Azechi et al., Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi and Yamanaka1991) and as well as compression to 2000 times that of the solid state, where it was crucial that laser beam smoothing (Kato et al., Reference Kato, Mima, Miyanaga, Arinaga, Kitagawa, Nakatsuka and Yamanaka1984) be used (Hora, Reference Hora2006). Further improvement to gains led to gains of 2 × 1014 neutrons (Soures et al., Reference Soures, Mccrory, Vernon, Babushki, Bahr, Boehli, Boni, Bradlay, Brown, Craxton, Delettrez, Donaldson, Epstein, Jaanimagi, Jacobs, Kearney, Keck, Kelly, Kessler, Kremes, Knauaer, Kumpan, Letzring, Lonobile, Loucks, Lund, Marshall, Mckenty, Meyerhofer, Morse, Okishev, Papernov, Pien, Seka, Short, Shoup Iii, Skeldon, Skoupski, Schmid, Smith, Swmales, Wittman and Yaakobi1996) all with direct drive and volume ignition (Hora et al., Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998) in contrast to about 1000 times lower gains with indirect drive spark ignition (Lindl, Reference Lindl, Hora and Miley2005).
What was most disappointing was the rather low maximum temperature T at highest compression (Azechi et al., Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi and Yamanaka1991) of only about T = 3 × 106 K, while the theory of spherical compression and thermal ignition said it should have reached higher temperatures. Nevertheless, the spherical compression and thermal ignition scheme was followed up by building the $4 Billion laser facility at the National Ignition facility (NIF) under the initial leadership of Campbell (2006) followed by Moses et al. (2006) leading close to the historic first controlled exothermic nuclear fusion reactions (Glenzer et al., Reference Glenzer and Moses2011), while simultaneously it was considered by Tabak et al. (Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) to overcome the problem of the unexpected low temperature at compressions (Azechi et al., Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi and Yamanaka1991) by “fast ignition.” The scheme at the first discussions (2006) was to use the spherical plasma compression to more than 1000 times the solid state density and to produce an additional heating of the center area by an additional laser pulse of picoseconds duration with energy in the range above 105 J. In order to produce laser pulses of this short duration and power above terawatt (TW) and up to more than petawatt (PW), the chirped pulse amplification (CPA) (Strickland et al., Reference Strickland and Mourou1985; Mourou et al., Reference Mourou, Tajima, Tanaka, Meyerhofer and Meyer-ter-Vehn2002) was invented for solid state lasers. Another method is the dye laser pulse amplification by KrF lasers known as the Szatmari-Schäfer method (Szatmari et al., Reference Szatmari and Schäfer1988; Szatmari, Reference Szatmari1994).
These developments were leading to a modification or an alternative to the fast ignition. Ultrahigh accelerations of plasma by lasers were discovered from direct Doppler measurements by Sauerbrey (Reference Sauerbrey1996), which were more than 10,000 times higher than any known from thermal driven gas dynamic accelerations from the laser-plasma interaction. This was a unique new effect in contrast to the usual broad stream thermal acceleration processes. In the following, this observation of ultrahigh acceleration is summarized (Section 2). Theses accelerations were measured exactly as predicted from the theory of nonlinear effects of laser-plasma interaction made much earlier. This was recognized as a crucial new effect of the laser for which nearly instant 100% efficient non-thermal conversion of optical energy into mechanical energy of the plasma occurred. In support of the Doppler effects measurements of highly directed plasma blocks by Sauerbrey (Reference Sauerbrey1996), Section 3 presents an analysis at subsequent measurements of plasma acceleration with the similar system of sub-picosecond dye laser pulses amplified in inverted excimer plasma (Szatmari et al., Reference Szatmari and Schäfer1988; Szatmari, Reference Szatmari1994) up to nearly TW laser power. These confirmed plasma blocks of ultrahigh acceleration (Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu Hong, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) with highly directed and extremely high ion current densities. Section 4 reports the application of these results for igniting solid state density of modestly compressed fusion fuel by side-on laser irradiation for generating a fusion flame following an updating of the scheme of Chu (Reference Chu1971) and Bobin (Reference Bobin, Schwarz and Hora1974) for DT and for the fusion of proton-11B (HB11). The following discussion in Section 5 focuses on some next questions to be studied.
2. SAUERBREY'S EXPERIMENTAL DISCOVERY OF ULTRA-HIGH LASER ACCELERATION OF PLASMA BY NONLINEAR FORCES
Sauerbrey's (Reference Sauerbrey1996) measurement of ultrahigh acceleration of plasma blocks by lasers turned out to be basically a non-thermal interaction process for which clarification was needed and developed in due course, as the problems were of a rather complicated nature. First we give the final short-cut result before going into details. The final result in hydrodynamic plasma theory is based on the force density f in a plasma to be determined by the gas-dynamical pressure p = 3n pkT/2 where n p is particle density, k is Boltzmann's constant and T the temperature, and by the present electric and magnetic fields E and H.
$${\bf f} = - \nabla_{p} + {\bf f}_{\rm NL}.$$For fields of a laser of frequency ω defining a complex optical constant n in the plasma, the nonlinear force with the unity tensor 1 is
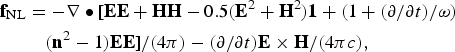$$\eqalign{ {\bf f}_{\rm NL} &= - \nabla \bullet [ {\bf EE}+{\bf HH} - 0.5 \lpar {\bf E}^{2} + {\bf H}^{2}\rpar {\bf 1} + \lpar 1+\lpar \partial/\partial t\rpar /{\rm \omega}\rpar \cr & \quad \lpar {\bf n}^{2}-1\rpar {\bf EE}\rsqb /\lpar 4{\rm \pi}\rpar - \lpar \partial/\partial t\rpar {\bf E}\times{\bf H}/\lpar 4{\rm \pi} c\rpar \comma \; }$$which is dominant over the gas dynamic force (also called the thermo-kinetic force fth = −∇p) if the quiver energy of the electrons in the laser field is larger than the energy of thermal motion (Hora, 1969;1985; see Eqs. (8.87) and (8.88) of Hora (Reference Hora1991)). For simplified one-dimensional geometry and perpendicular laser irradiation, the force (Eq. (2)) can be reduced to the time averaged value (Chen Reference Chen, Schwarz and Hora1974)
$$\eqalign{ {\bf f}_{\rm NL} &= -\lpar \partial/\partial x\rpar \lpar {\bf E}^{2}+{\bf H}^{2}\rpar /\lpar 8{\rm \pi}\rpar \cr &= -\lpar {\rm \omega}_p/{\rm \omega}\rpar ^{2}\lpar \partial/\partial x\rpar \lpar E_{v}^{2}/{n}\rpar /\lpar 16{\rm \pi}\rpar \comma \; }$$where Ev is the amplitude of the electric field of the laser in vacuum. The second expression corresponds to the formulation of the ponderomotive force in electrostatics while the first expression includes identities from the later Maxwellian theory with the magnetic field as shown before (Hora, Reference Hora1991).
Computations for plane geometry interaction with inclusion of the nonlinear force interaction, with thermal laser absorption by collisions, and equi-partition processes in the dynamically developing optical plasma properties for interaction of neodymium glass laser irradiation of 1018 W/cm2 intensity on deuterium having an initial double-Rayleigh density profile (see Hora (Reference Hora1981), Fig. 10.18a and 10.18b), arrived at a velocity distribution and an electromagnetic energy density as shown in Figure 1 after 1.5 ps interaction time. The laser was irradiating from the right-hand side and a plasma block was moving against the laser light and another one into the deeper target. The velocity at this very short time at the closest part to the laser was more than 109 cm/s. This corresponds to an average acceleration of more than 5 × 1020 cm/s2.
Fig. 1. Hydrodynamic computations in 1978 using 1018 W/cm2 laser irradiation on deuterium close to the critical density resulted in a plasma block moving to the right against the laser light after 1.5 ps showing an acceleration of about 1020 cm/s2 (see Fig. 1 of Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu Hong, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007 from Fig. 10.18a and 10.18b of Hora, 1971).
These results of the computation were initially published in 1978 (see references Hora, Reference Hora1981) but it took a long time (Sauerbrey, Reference Sauerbrey1996) before an experimental confirmation of these ultrahigh accelerations were measured. The reason was not only the question how to produce the ps laser pulses up to the range of TW power, but there was the difficulty of relativistic self-focusing (Hora, Reference Hora1975). Each laser pre-pulse produced a plasma plume where any very intense laser beam which was relativistically squeezed to less than wave length diameter (Fig. 2), producing very high intensities resulting in emission of highly charged ions to energies far above MeV and extremely intense very short wave length X-rays. These extreme mechanisms due to relativistic self-focusing had to be suppressed for verifying the plane geometry of the early computations and also to provide the conditions that the ultrahigh acceleration could be detected directly by Doppler effect.
Fig. 2. Relativistic self-focusing of a laser beam from the left with a dashed Gaussian intensity profile and radius d 0/2 moves into plasma right from the vertical line. Due to the relativistic change of the electron mass at the quiver motion, the effective wave length within the plasma is dielectrically shorter at higher intensity then at lower causing a concave bending of the initially plane wave front with shrinking of the beam to less than wave length diameter (Hora, Reference Hora1975; Cicchiteli et al., Reference Cicchitelli, Hora and Postle1990; Häuser et al., Reference Häuser, Scheid and Hora1992).
A confirmation of these conditions in the measurements of Sauerbrey (Reference Sauerbrey1996) and the non-thermal processes was supported by following experiments (Zhang et al., Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998; Badziak et al., Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999), after similar measurements led to the conclusion that relativistic self-focusing was suppressed and shown from further related experiments (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002; Reference Hora, Badziak, Read, Li, Liang, Liu Hong, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007; Hora, Reference Hora2003). This was in drastic contrast to the usual experiments with ps-TW and few PW laser pulses studied by the broad stream of experiments after Cowan et al. (Reference Cowan, Parry, Key, Dittmire, Hatchett, Henry, Mody, Moran, Pennington, Phillips, Sangster, Sefcik, Singh, Snavely, Stoyer, Wilks, Young, Takahashi, Dong, Fountain, Parnell, Johnson, Hunt and Kuhl1999) observed high acceleration of ions and electrons, pair production, gamma rays with subsequent nuclear transmutations etc.
The characteristic for the very rare experiments of Sauerbrey (Reference Sauerbrey1996), Zhang et al. (Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998), and Badziak et al. (Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999), see also Hora et al. (Reference Hora, Badziak, Read, Li, Liang, Liu Hong, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) is the use of the extremely high contrast ratio above 108 for the suppression of the relativistic self-focusing for achieving the enormous suppression of laser pre-pulses before the arrival of the main pulse on the targets. The reason for this was a specific need with the unique KrF laser pulses used by Sauerbrey (Reference Sauerbrey1996) where sub-picosecond laser pulses from dye lasers propagated in an inverted KrF laser gas for pulses reaching nearly TW power (Szatmari et al., Reference Szatmari and Schäfer1988; Szatmari, Reference Szatmari1994). The KrF excimer wave length of 248 nm — in contrast to the longer laser wave lengths of the usually applied lasers – was disturbing the experiments by the amplified spontaneous emission (ASE) radiation where the short wave length was pre-ionizing the target too much. It was therefore highly necessary to reduce the ASE to a sufficient degree by suppression of any pre-pulse using plasma mirrors and other techniques for this type of lasers (Szatmari, Reference Szatmari1994).
Sauerbrey therefore used lasers with a cut-off of the pre-pulses by a factor above 108 (contrast ratio), and had an interaction of the plane one-dimensional wave front of the interacting laser avoiding any self-focusing. The resulting plane wave front geometry provided then for the very first time the conditions for which the interaction was calculated before (Fig. 1). Sauerbrey measured an acceleration of the plane plasma fronts perpendicular to the target of 1020 cm/s2 against the laser as immediately given from the Doppler shift. This was in full agreement with the nonlinear force acceleration as computed before. Variations with respect to experimental accuracy were of minor nature for comparison in view of the significant fact that these ultrahigh accelerations were 100,000 times higher than the thermal pressure acceleration with the largest NIF laser (Park et al., 2010) using nanosecond laser pulses.
3. ANALYSIS OF ACCELERATION MEASUREMENTS WITH DOPPLER EFFECT
Compared with the Doppler experiments with KrF lasers, the continuation with solid state lasers indicated a number of complexities which still have to be studied. It was possible (Yang et al., Reference Yang, Miley, Flippo and Hora2011) that a suppression of relativistic self-focusing for generation of plane plasma blocks as known from the numerous experiments with solid state lasers by Badziak et al. (Reference Badziak, Glowacz, Jablonski, Paris, Wolowski, Kraska, Laska, Rohlena and Hora2004; Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005) was possible by the proof of very low emission of X-rays (K. Flippo, private communication, 2011) following the method of Zhang et al. (Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998). Doppler experiments were performed with KrF ps laser pulses (Földes et al., Reference Földes, Bakos, Gal, Juhasz, Kedves, Kocsis, Szatmari and Veres2000; Reference Földes and Szatmari2008; Veres et al., Reference Veres, Kocsis, Racz and Szatmari2004) which are now discussed in view of the later reached clarification between thermal and nonlinear force acceleration processes.
Figure 3 shows the measured plasma block velocities from the Doppler effect at varying KrF laser intensities for 700 fs laser pulses with sufficiently high contrast ratio to suppress the ASE. The laser pulse of 2.6 × 1015 W/cm2 intensity produced a velocity of 1.25 × 107 cm/s of the plasma at irradiation of aluminium (Földes et al., Reference Földes, Bakos, Gal, Juhasz, Kedves, Kocsis, Szatmari and Veres2000). This corresponds to an acceleration of 1.6 × 1019 cm/s2. The question is then, how fast the laser energy can be converted into plasma motion. At this intensity, the quiver energy of electrons
$$\varepsilon_{\rm osc}=e^{2}{\bf E}_{\rm v}^{2}/\lpar 2m_{\rm e}{\rm \omega}^{2}\rpar \comma \;$$using the electron mass m e is 31.2 eV with the electric field amplitude Ev of the laser in vacuum for the KrF laser. This is sufficient to produce plasma electrons in the target within about a laser period by the electrons impacting in the target and with other aluminium ions to be ionized. The generation of an inhomogeneous plasma density in the interaction region can well be assumed to be within this very short time to produce a dielectric swelling S = 3 which determines the electric field E by dielectric properties given by the temporary and spatially change during the interaction dynamics by the absolute value of the refractive index n
$${\rm E}^{2}{\kern 1pt} ={\kern 1pt} {\rm E}_{\rm v}^{2}/{\bf n} \quad \quad {\rm S}{\kern 1pt}={\kern 1pt}1/{\bf n}.$$
Fig. 3. Intensity dependence of the velocity of the plasma front from the Doppler shift of the reflected 700 fs KrF laser pulses from Al target (Földes et al., Reference Földes, Bakos, Gal, Juhasz, Kedves, Kocsis, Szatmari and Veres2000).
This number S can be larger or smaller. The experience from the evaluation of the experiments of Badziak et al. (Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999) arrived at a swelling of a value of 3 (Hora, Reference Hora2003). The example of Figure 1 of the numerical velocity of deuterium with an assumed initial Rayleigh density profile had a swelling above S = 15. Swelling by S = 3 produced a quiver energy of the electrons in the considered case for aluminium within fs duration had an energy of 93 eV and may then have produced high ionization Z of the aluminium. The dynamics of the plasma will then be determined by the nonlinear force (3) acting on the electron cloud again within the time of quiver motion to an acceleration whose dynamics will be determined by the inertia of the ion cloud due to electrostatic attraction in the same way as in the example of Figure 1 in agreement with the experiments of Sauerbrey (Reference Sauerbrey1996). Taking full ionization Z = 13, the front of the fastest ions arrives at a velocity of 1.2 × 107 cm/s. In view of a possible higher number S or lower number Z, it is sufficient at this stage only to see that the 700 fs laser interaction is sufficient, to produce the measured acceleration. This is in contrast to any thermal mechanism, where first the quiver energy of the electrons has to be changed by collisions into random motion determining a temperature which then by a rather long equipartition time leads to heat the ions to move with the measured high plasma velocity.
Similar acceleration velocities from Doppler experiments by Veres et al. (Reference Veres, Kocsis, Racz and Szatmari2004) agree with the considered results from aluminium where the intensity dependence in comparison with the experiments of Badziak et al. (Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999) and the difference between irradiation of polystyerene and of aluminium may be interpreted along the discussed results of Földes et al. (Reference Földes, Bakos, Gal, Juhasz, Kedves, Kocsis, Szatmari and Veres2000). At oblique incidence of lasers on the target, the nonlinear force is directed perpendicular to the plasma surface (see Section 11 of Hora (Reference Hora1991)) and the laser field energy density is not drastically modified.
The acceleration of the ions is happening directly by the conversion of the laser field energy into the nonlinear force driven electron cloud driving the ion cloud by electrostatic attraction. This is in contrast to thermal absorption and heating which takes a much longer time than the interaction of the ps laser pulses. Computations at plasma surfaces with similar initial Rayleigh density profiles as in Figure 1 were performed, however using a later developed genuine two-fluid hydrodynamic computation scheme. This code was developed by using the Euler equations of electrons and for ions separately combined by the electric fields given by the Poisson equation. These internal electric fields in the plasmas were eliminated in Schlüter's (Reference Schlüter1950) two-fluid hydrodynamics where the Euler equations were added to arrive at a one fluid plasma equation of motion (1) used in the computations of Figure 1, and where the difference of the of the Euler equations led to a generalized Ohm's law for the plasmas. This elimination of the electric fields was correct for homogeneous, uniform plasmas similar to metals where the electric conductivity is similar to plasmas and where any electric field is decaying in much shorter times than fs. For dimensions where the Debye length is much shorter than the considered length dimensions, the electric fields can well be ignored too. If these fields did appear in extra-terrestrial plasmas as known by Alfven (Reference Alfven1981) and his associates, it was mentioned in a book review about this work by Kulsrud (Reference Kulsrud1983) that “these fields are intuitively not clear.”
In contrast to these general views in plasma theory, the genuine two-fluid hydrodynamics showed the strong appearance of these electric fields especially in the highly inhomogeneous plasmas at very intense laser interaction (Lalousis et al., Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984; see Sections 8.8, 8.9, and 10.7 of Hora (Reference Hora1991)). It was then most interesting to see how these electric fields modify the results of Figure 1. After the genuine two-fluid code was applied to study the experiments of Badziak et al. (Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005) using genuine two-fluid hydrodynamics (Glowacz et al., Reference Glowacz, Badziak, Jablonski and Hora2004; Reference Glowacz, Hora, Badziak, Jablonski, Cang and Osman2006) and other details of the nonlinear force dominating the laser-plasma interaction (Cang et al., Reference Cang, Osman, Hora, Zhang, Badziak, Wolowski, Jungwirth, Rohlena and Ullmschmied2006), a numerical evaluation was achieved for the initially Rayleigh plasma density profiles similar to Figure 1 (Sadighi et al., Reference Sadighi-Bonabi, Yazdani, Cang and Hora2010), where high swelling factors, S, were again the result. It turned out that the net ion motion was not much changed (Fig. 4), compared with Figure 1 due to the fact that there was a dominant non-thermal conversion of laser energy into the macroscopic ion motion by the nonlinear force. The very general code with inclusion of collisions for thermal absorption and equi-partition for ion heating were highly delayed and not strongly affecting the plasma dynamics determined by the ions for the very high laser intensity interactions during pulses in the ps range.
Fig. 4. Ion velocity within an initially bi-Rayleigh α = 9.59 × 103 cm−1 deuterium plasma with initially zero velocity and with 100 eV initial temperature located between x = 10 and +10 µm at neodymium glass laser irradiation from the left hand side of 2 × 1016 W/cm2 intensity during the time between 0 and 750 fs.
4. APPLICATION TO A RADICAL NEW LASER DRIVEN FUSION OF SOLID DENSITY FUEL WITHOUT NUCLEAR RADIATION
What was important with the ultrahigh acceleration, was that extremely high current densities in the highly directed space charge neutral plasma blocks arrived at 1011 Amps/cm2 or more. This is again more than a million times higher than accelerators could provide for ion beam fusion and permitted a comeback of the reaction of solid state — uncompressed or modestly compressed — fusion fuel by side-on ignition of a fusion flame. This was absolutely impossible with the first side-on ignition calculations for solid density fusion fuel (Chu, Reference Chu1971; Bobin, Reference Bobin, Schwarz and Hora1974) but this has changed now with the >PW-ps laser pulses (Cowan et al., Reference Cowan, Parry, Key, Dittmire, Hatchett, Henry, Mody, Moran, Pennington, Phillips, Sangster, Sefcik, Singh, Snavely, Stoyer, Wilks, Young, Takahashi, Dong, Fountain, Parnell, Johnson, Hunt and Kuhl1999; Mourou et al., 2002). It is potentially possible for energy production in power stations to achieve gains of 10,000 similar to the Nuckolls et al. (Reference Nuckolls and Woods2002) scheme using ps-laser produced very high density 5 MeV relativistic electron beams in analogy to the here treated nonlinear force driven plasma blocks based on ions. The theory of Chu (Reference Chu1971) had to be updated (Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008) by the then not known effects of the thermal inhibition factor and by the collective effect of the stopping power (Gabor, Reference Gabor1953).
For laser fusion of DT, extremely clean ps laser pulses with a contrast ratio above 108 may drive the controlled reactions in power stations with pulses in the range of few dozens of PW power (Hora, 2009). These are close to technical realization. What was very surprising, is that the reaction of hydrogen and the boron isotope 11 (HB11) is less than 10 times only more difficult than the DT fusion. This will generate fewer radioactivities in the entire reaction and in the waste than burning coal, per energy production (Hora et al., Reference Hora, Miley, Ghornanneviss, Malekynia, Azizi and He2010; Li, Reference Li2010). In contrast to the need of extremely high fuel compression in the usual thermally ignited laser-fusion schemes, the side-on ignition is simplifying the process and it can be expected that power production can be at considerably lower cost than present lowest cost sources, as today's cost in Eurocents/kWh: nuclear fission 2, coal 5, wind 8, photovoltaics 38.
For the next exploration of the side-on ignition of laser fusion with nonlinear force driven plasma blocks, the initial computations (Hora, 2009; Hora et al., 2009; Reference Hora, Miley, Ghornanneviss, Malekynia, Azizi and He2010) are now generalized to use the genuine two-fluid model (Lalousis et al., 1983; Hora et al., Reference Hora, Lalousis and Eliezer1984) in order to study details of shock generation and very high electric field dynamics in the extremely inhomogeneous plasma in the fusion flame fronts. This is also for preparation of specific experiments with PW-ps lasers of sufficient contrast to explore the revolutionary new scheme. Figure 5 shows results of the ion density of the fusion flame when developing into solid density DT fuel after a ps laser pulse initiated the fusion flame. It is very interesting to see that the local ion density in the thin flame front moves with a velocity of 1.55 × 108 cm/s and the density in the flame front is four times higher than the DT. This is an automatic result of the genuine two-fluid computation and agrees with the Rankine-Hugoniot theory of shock generation.
Fig. 5. Genuine two fluid hydrodynamic computations (Lalousis et al., 1983; Hora et al., Reference Hora, Lalousis and Eliezer1984) of the ion density in solid DT after irradiation of a laser pulse of 1020 W/cm2 of ps duration at the times 22 ps (dashed) and 225ps after the initiation.
5. DISCUSSION AND CONCLUSIONS
What is evident is the measurement of the ultrahigh acceleration of plasmas at interaction with sub-picosecond high intensity laser pulses if relativistic self-focusing is avoided by using very high contrast ratios for suppression of pre-pulses. The high contrast was initially necessary with KrF laser pulses to avoid ASE. The generation of the ultrafast plane highly directed plasma blocks and avoiding relativistic self-focusing was confirmed also by X-ray emission measurements (Zhang et al., Reference Zhang, He, Chen, Li, Zhang, Wong, Li, Feng, Zhang, Tang and Zhang1998) and the properties of the directed ion blocks based on the number of the fast ions limited to the dielectric strongly increased skin depth (Badziak et al., Reference Badziak, Kozlov, Makowksi, Parys, Ryc, Wolowski, Woryna and Vankov1999). The confirmation of the acceleration by the nonlinear (generalized ponderomotive) force in agreement with computed plane geometry conditions (Fig. 1) (Hora, Reference Hora1981; Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu Hong, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007) demonstrated a non-thermal process where the laser energy was nearly completely converted into macroscopic acceleration of the space-charge neutral electron cloud in the plasma and the electrostatically attached ion cloud. These results are basically confirmed and but may need more information about detailed properties.
The use of the ultrafast plasma blocks for side-on ignition of uncompressed (or modestly compressed) solid fusion fuel following the early computations of Chu (Reference Chu1971) are based on hydrodynamic theory leading to ignition of high gain fusion with next available high contrast laser pulses of dozens of PW-ps laser pulses for DT fuel but even for HB11 fuel where less radioactivity is generated than from burning coal per gained energy (Hora et al., 2009; Reference Hora, Miley, Ghornanneviss, Malekynia, Azizi and He2010).
One problem is whether the hydrodynamic treatment for fusion is sufficient and whether not details of particle interpenetration (Hora Reference Hora1983) need to be included as known from Particle in Cell (PIC) computations as discovered by Wilks et al. (1991). A comparison between results from hydrodynamics and PIC evaluations for the range of interesting laser intensities (Limpouch et al., 2006) showed a rather good agreement. Laser generation at thin foils with high contrast ratio was studied in a number of experiments (see e.g., Kaluza et al., Reference Kaluza, Schreiber, Sandala, Tsakiris, Eidmann, Meyer-Ter-Vehn and Witte2004) and may need to be re-considered as in similar cases (Hora, Reference Hora2003) where the interaction by thermal processes need a comparison with nonlinear force effects.
ACKNOWLEDGEMENT
The first author acknowledges numerous valuable contacts about the presented topic with the leading authors of the crucial experiments, Roland Sauerbrey, Scientific Director of the Helmholtz Forschungszentrum Dresden-Rossendorf (HFDR), Jie Zang, President of the Shanghai Jiao Tong University and Jan Badziak at the Kaliski Institute for Plasma Physics and Microfusion, K. Flippo, Los Alamos, P. Lalousis, Heraklion, Crete, Greece, S. Szatmári, Hungary, I.B. Földes, Hungary, R. Castillog, Sydney, Australia, X. Yangb, IL, USA, as well as many colleagues and associates including Dieter Hoffmann, Darmstadt, Klaus Witte, Munich, John H. Nuckolls, Livermore, Mike Campbell, Scott Wilks, Livermore, Shalom Eliezer, Rehovot, Claude Phipps, Santa Fe and Peter Hammerling, San Diego.
