1. INTRODUCTION
The solidification and microstructure development (Duggan et al., Reference Duggan, Tong and Browne2015; Tan & Shin, Reference Tan and Shin2015) in energy-beam keyhole welding process play an important role on the quality after welding. The thermal transport characteristics in the keyhole and its surrounding heat-affected zone significantly influence the solidification and microstructure development. Many efforts have been made to study the heat transfer in the keyhole and its surrounding heat-affected zone for the high-energy beam welding process. During the analytical and computational heat transfer, these studies paid special attention to the determination of keyhole and the temperature field of its fusion zone. The more advanced models fully coupled with the computational heat transfer and fluid flow was developed to enable the dynamic determination of the keyhole shape (Sibillano et al., Reference Sibillano, Ancona, Berardi, Schingaro, Basile and Lugarà2006; Tenner et al., Reference Tenner, Brock, Gürtler, Klämpfl and Schmidt2014).
A high-energy beam with the intensity in excess of 106–107 W/cm2 is focused on the surface of workpieces, melts the irradiated target of the workpiece and then induces vapor. The vapor acts a recoil pressure on the molten layer. Consequently, a deep and narrow vapor-filled hole, or keyhole surrounded by molten material forms in the deep penetration process. Estimated from the theory, the peak intensity of high-peak-power laser can arrive at 1020 W/cm2 in the focal region (Kalashnikov et al., Reference Kalashnikov, Andreev, Ivanov, Galkin, Korobkin, Romanovsky, Shiryaev, Schnuerer, Braenzel and Trofimov2015). The study on ablation of Al or Cu targets was conducted using laser radiation intensity of 1–50 PW/cm2 with focal spot radius 40–100 µm (Gus'kov et al., Reference Gus'kov, Demchenko, Kasperczuk, Pisarczyk, Kalinowska, Chodukowsk, Renner, Smid, Krousky, Pfeifer, Skala, Ullschmied and Pisarczyk2014). The deep penetration is generally defined as a high ratio of depth-to-width for the weld penetration region. The weld depth may be up to ten times greater than the weld width and reaching 25 mm. Deep penetration of high-intensity energy beam (e.g. laser or electron beam) has been widely studied in materials processing. The plasma temperature in deep penetration laser welding was measured using the spectral relative intensity method (Chen et al., Reference Chen, Zhang, Zhao, Zhang and Li2013). Plasma plume oscillation during very short period was presented in the deep penetration process of laser welding (Mrña & Šarborta, Reference Mrña and Šarborta2014). The focal location of the beam significantly influences on the welding of thick workpieces and is preferable below the surface of the workpice. The deep penetration occurs beyond the threshold intensity of high-energy beam due to the structural rearrangement of the thermocapillary flow (Seidgazov, Reference Seidgazov2011). Giedt and Tallerico conducted a study to predict the electron beam deep penetration (Giedt & Tallerico, Reference Giedt and Tallerico1988). The beam focus current was found to be the most critical parameter and the distance between the focus coil and workpiece is significant. Penetration mechanisms of electron beam welding were investigated using a refinement of the X-ray pinhole movie camera technique (Mara et al., Reference Mara, Funk, Mcmaster and Pence1974). Results indicate that the X-ray pinhole camera technique is able to obtain a precise measurement for beam material penetration. A chamber with the low vacuum conditions obtained from rotary pumps was developed (Seiji et al., Reference Seiji, Masami and Yousuke2011). The laser welding of this system can fabricate a deep-penetration weld bead, which is comparable with that of electron beam welding. The effect of focal location on penetration was also studied experimentally. The transition of shallow penetration to deep penetration was reported in the process of electron beam welding (Elmer et al., Reference Elmer, Giedt and Eagar1990). The available empirical relationships were obtained to calculate the wide-range penetration depth.
The focused high-intensity energy beam can deeply penetrate into workpieces, induce the high aspect ratio of fusion zone, and enhance the machining efficiency. The focused energy beam has been applied in many fields such as the focused electron beam etching to modify semi-conductor nanodevices (Shawrav et al., Reference Shawrav, Gökdeniz, Wanzenboeck, Taus, Mika, Waid and Bertagnolli2016), focused electron beam inducing deposition (Béchéa et al., Reference Béchéa, Winkler, Plank, Hoferc and Verbeeck2016), processing of a glass ceramic surface by selective focused beam laser (Basile et al., Reference Basile, Gonon, Petit and Cambier2016), a micron-sized electron column fabricated by focused ion beam (Wicki et al., Reference Wicki, Longchamp, Escher and Fink2016).
The influences of electron-beam welding parameters on the penetration and weld geometry were investigated (Konkol et al., Reference Konkol, Smith, Willebrand and Connor1971). The penetration up to 50.8 mm can be achieved by adjusting the welding parameters. The relation of penetration depth with focal length relative to the surface of workpiece was presented. The weld geometry was changed from convex shape to parallel-sided shape and then v shape for the focal location lowered from above to below the workpiece surface. Joint penetration was studied for electron beam welding by the measurement of welding machine current distributions in the plane of the workpiece surface (Hicken et al., Reference Hicken, Giedt and Bentley1991). The experiment indicates that the focal location of the electron beam significantly influences on the penetration. Beam focusing characteristics affect the distribution of energy absorbed on the wall of welding cavity and apparent absorption in the welding cavity. The energy absorption distribution along the wall of a conical cavity truncated by spherical cap subject to a focused energy beam was investigated (Ho & Wei, Reference Ho and Wei1997). The location of the maximal energy absorption appears at the cavity base for a conical cavity truncated by spherical cap. As the focal location is changed from the workpiece surface to the cavity base, the energy absorption increases at first and then reaches the maximum at the location slightly below the workpiece surface. After the location of maximal absorption is arrived, the energy absorption decreases for continuing to be lowered focal spot of the focused energy beam. The decrease of focal convergence angle and spot size enhances the energy absorption. For the parabolic keyhole (Wei & Ho, Reference Wei and Ho1998), the location of maximal energy absorption after redistribution due to multi-reflections shifts toward the base of cavity when the focal spot of the focused energy beam is lowered from workpiece surface to the cavity base. The apparent absorptivity for a focused energy beam irradiating on a cavity of paraboloid of revolution is higher near or slightly below the workpiece surface than that far away from workpiece surface (Ho, Reference Ho2005a ). Hence, the energy efficiency is also changed by the different focal locations for the incident focused energy beam-induced materials processing. A three-dimensional (3D) thermal model (Wei & Shian, Reference Wei and Shian1993) was employed to investigate the effects of focal location on the penetration depth and fusion zone produced by a focused energy beam (Ho, Reference Ho2005b ). The 3D thermal model (Wei & Shian, Reference Wei and Shian1993) considering a parabolic cavity irradiated by a moving energy beam set the adiabatic condition on the workpiece surface by the image method, which transforms the infinite domain into semi-infinite domain in parabolic coordinate system. The maximal penetration occurs at the incident energy beam-focusing location about 5.588 mm below the workpiece surface. On the other hand, the penetration depth becomes shallow with the increasing distance away from the location 5.588 mm below the workpiece surface. The 3D thermal model (Wei & Shian, Reference Wei and Shian1993) gave some successful predictions for the materials processing of the high-energy beam. Nevertheless, it cannot give a reasonable prediction for the cavity temperatures.
This paper investigates the deep penetration induced by a focused high-energy beam using the 3D thermal model with the adiabatic condition directly set on the workpiece surface instead of the image method. The 3D thermal model (Wei & Shian, Reference Wei and Shian1993) utilized the image method to transform the infinite domain into semi-infinite domain with the adiabatic condition on the workpiece surface. The image method results in the complexity of the model, difficulty in obtaining a closed form solution and deviate predictions from the measured temperatures along the welding cavity (Wei & Shian, Reference Wei and Shian1993). The results calculated by this work are compared with the available measured data. The effects of the focal location, convergence angle, and spot size on the deep penetration are also discussed.
2. GOVERNING EQUATIONS AND BOUNDARY CONDITIONS
For the deep penetration of high-intensity energy beams such as laser (Luo & Shin, Reference Luo and Shin2015), electron beam (Giedt & Tallerico, Reference Giedt and Tallerico1988; Elmer et al., Reference Elmer, Giedt and Eagar1990), and ion beam, the opening diameter of the keyhole induced by high-intensity energy beams is small relative to its penetration depth, so that the fusion zone of high ratio of depth-to-width is obtained. The heat-affected zone produced by the high-intensity energy beam is also small for the reason that rapid penetration achieves the required depth before heat is dissipated into large region. This characteristic is also the reason why laser and electron beam is usually employed to conduct precise machining. It is taken into account in this study that a moving focused energy beam with the intensity of Gaussian distribution irradiates the keyhole of the parabolic shape formed in the wokpiece. The parabolic coordinate system describing the keyhole of the parabolic shape and the heat-affected zone around the keyhole is shown in Figure 1. On the other hand, the nomenclatures of symbols are listed in Table 1.
Fig. 1. Parabolic coordinate system, keyhole, and incident energy beam.
Table 1. Nomenclatures of symbols
The parabolic coordinates near the opening of the welding cavity approximates to horizontal lines in the η-direction (e.g. at ξ = ξe) and vertical lines in the ξ-direction (e.g. at η = η0) for the deep penetration of high-intensity energy beam. Especially, the focused high-intensity energy beam can make the welding cavity and its heat-affected zone more concentrated on a small region. Therefore, in the case of deep penetration induced by the focused high-intensity energy, the heat dissipation into the ambient air from the welding cavity and the fusion zone is negligible on the workpiece surface near the opening due to very small heat-affected zone when compared with the incident high-intensity energy. The adiabatic condition can be directly set on the workpiece surface near the opening of the welding cavity instead of the image method transferring the infinite domain into semi-infinite domain.
$$\displaystyle{{\partial \Theta} \over {\partial {\rm \xi}}} = 0,\quad {\rm at}\quad {\rm \xi} = {\rm \xi} _{\rm e}. $$
The boundary conditions taken into account in this study are sketched in Figure 2. The temperature is finite at the cavity base (ξ = 0) and at the locations away from the keyhole (η → ∞). The energy absorption of the cavity wall (η = η0) for the incident energy beam is balanced by the heat transfer into the wokpiece.
Fig. 2. Boundary conditions.
In this work, the model considers the physical system of welding to be completely at a quasi-steady state. Therefore the observer located on the ground can see that the high-energy beam, the shape of keyhole and molten region move together in a constant speed. However, the observer moving together with the high-energy beam will see the static diagram, including the profile of high-energy beam, the fixed shape of keyhole and molten region. The welding cavity (i.e. paraboloid of revolution-shaped cavity or keyhole) and high-energy beam coexist during quasi-steady state. In the quasi-steady-state welding process, the molten area is almost the same as the solidified area for the observer located on the ground. On the other hand, no melting or freezing is found for the observer moving together with the physical system in a constant speed. Therefore, the latent heat of molten metal can be approximately balanced by the latent heat of solidified metal. Figure 3 shows the schematic diagram of physical system in this study. The quasi-steady-state thermal transport equation with a constant moving velocity of high-intensity focused energy beam relative to the workpiece is written as
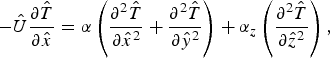$$- {\hat U}\displaystyle{{\partial {\hat T}} \over {\partial {\hat x}}} = {\rm \alpha} \left( {\displaystyle{{\partial ^{\rm 2} {\hat T}} \over {\partial {\hat x}^2}} + \displaystyle{{\partial ^{\rm 2} {\hat T}} \over {\partial {\hat y}^2}}} \right) + {\rm \alpha} _z \left( {\displaystyle{{\partial ^{\rm 2} {\hat T}} \over {\partial {\hat z}^2}}} \right),$$
where
$\hat U$
, α,
${\hat T},$
and α
z
denote the speed of incident energy beam, thermal diffusivity, temperature, and thermal diffusivity in vertical direction, respectively.
$\hat x$
,
${\hat y},$
and
${\hat z}$
are the Cartesian coordinates. The welding cavity is assumed to be a paraboloid of revolution-shaped cavity. Hence, in order to conveniently obtain the closed form solution, the quasi-steady-state thermal transport equation in the Cartesian coordinates is transformed into that expressed by the parabolic coordinate system using the following relationship:
$$x = \displaystyle{{\hat x} \over {{\hat {\rm \sigma}}}} = \displaystyle{{2\sqrt {{\rm \xi} {\rm \eta}} \cos {\rm \phi}} \over {P_{\rm e}}}, $$
$$y = \displaystyle{{\hat y} \over {{\hat {\rm \sigma}}}} = \displaystyle{{2\sqrt {{\rm \xi} {\rm \eta}} \sin {\rm \phi}} \over {P_{\rm e}}}, $$
$$z = \displaystyle{{\hat z} \over {{\hat {\rm \sigma}}}} = \displaystyle{{{\rm (}{\rm \xi} - {\rm \eta} {\rm )}} \over {P_{\rm e} \sqrt S}}, $$
$${\rm \theta} = \displaystyle{{\hat T - \hat T_\infty} \over {\hat T - \hat T_{\rm m}}}, $$
$$\Theta = {\rm \theta} \exp {\rm [}\sqrt {{\rm \xi} {\rm \eta}} \cos {\rm \phi} ],$$
where the Peclet number P
e and the parameter S approximating convection are, respectively, defined as
$\hat U{\hat {\rm \sigma}} /{\hat {\rm \alpha}} $
and
${\hat {\rm \alpha}} /{\hat {\rm \alpha}} _z $
. The thermal diffusivity is considered to be different in the direction of molten metal flow in order to account for the convection effect. For the deep penetration, the ratio of penetration depth to width is high. Therefore, the molten metal flows mainly along the z-direction. In (Gau & Viskanta, Reference Gau and Viskanta1984; Giedt et al., Reference Giedt, Wei and Wei1984), the thermal diffusivity in the direction of molten metal flow is about three to five times of that in other directions.
${\hat {\rm \underline\sigma}} $
is the energy distribution parameter. ξ, η, and ϕ are the parabolic coordinates.
$\hat T_\infty $
is the ambient temperature.
$\hat T_{\rm m} $
is the melting temperature of workpiece; θ is the non-dimensional temperature; and ϕ is the polar angle in the parabolic coordinate system. Consequently, the quasi-steady-state thermal transport equation in the parabolic coordinate system yields
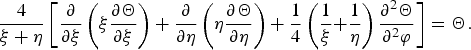$$\displaystyle{4 \over {{\rm \xi} + {\rm \eta}}} \left[ {\displaystyle{\partial \over {\partial {\rm \xi}}} \left( {{\rm \xi} \displaystyle{{\partial \Theta} \over {\partial {\rm \xi}}}} \right) + \displaystyle{\partial \over {\partial {\rm \eta}}} \left( {{\rm \eta} \displaystyle{{\partial \Theta} \over {\partial {\rm \eta}}}} \right) + \displaystyle{1 \over 4}\left( {\displaystyle{{\rm 1} \over {\rm \xi}} {\rm +} \displaystyle{{\rm 1} \over {\rm \eta}}} \right)\displaystyle{{\partial ^2 \Theta} \over {\partial ^2 {\rm \varphi}}}} \right] = \Theta. $$
Based on the parabolic coordinates, the focused incident high-intensity energy beam with the profile of the Gaussian distribution can be expressed as
$$q = \displaystyle{3 \over {A_{\rm n}}} e^{{\rm [} - 3{\rm (}{\rm \beta} {\rm ^{\prime}/}{\rm \beta} {\rm )}^2 {\rm ]}} $$
and
$$A_{\rm n} = 2{\rm \pi} s^2 {\rm (}1 - \cos {\rm \beta} {\rm ),}$$
$$s = \displaystyle{1 \over {\cos {\rm \beta} {\rm ^{\prime}}}}\left[ {\displaystyle{{r_{\rm f}} \over {\tan {\rm \beta}}} + {\rm sign}\left( {\,f + h - \displaystyle{{{\rm \xi} - {\rm \eta} - {\rm \eta} _0} \over {P_{\rm e} \sqrt S}}} \right)} \right],$$
$${\rm \beta} {\rm ^{\prime}} = \tan ^{ - 1} \left\{ {\displaystyle{{2\sqrt {{\rm \xi} {\rm \eta} _0}} \over {P_{\rm e} {\rm [}s_0 - {\rm sign}({\rm \xi} - {\rm \eta} - {\rm \eta} _0 )/P_{\rm e} \sqrt S {\rm ]}}}} \right\},$$
$$h = \displaystyle{{P_{\rm e} r_0^2} \over {4{\rm \eta} _{\rm 0} \sqrt S}}, $$
where r f, β, f, h, η0, and r 0 are the symbols of the non-dimensional focal spot size, convergence angle, focal spot location relative to the workpiece surface, cavity depth, parabolic coordinate of the cavity, and cavity opening radius, respectively. The symbol, sign ≡ (f + h)/|f + h|, is positive for the focal spot above the cavity base or negative for the focal spot below the cavity base. It is assumed in this model that the heat taken away from the vaporization is negligible when compared with the incident heat flux and the incident energy is totally absorbed by the cavity. The energy balance on the wall of paraboloid of welding cavity (η = η0) is as follows:
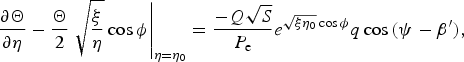$$\displaystyle{{\partial \Theta} \over {\partial {\rm \eta}}} - \displaystyle{\Theta \over 2}\left. {\sqrt {\displaystyle{{\rm \xi} \over {\rm \eta}}} \cos {\rm \phi}} \right \vert _{{\rm \eta} = {\rm \eta} _0} = \displaystyle{{ - Q\sqrt S} \over {P_{\rm e}}} e^{\sqrt {{\rm \xi} {\rm \eta} _0} \cos {\rm \phi}} q\cos {\rm (}{\rm \psi} - {\rm \beta} {\rm ^{\prime}),}$$
where ψ is the angle between horizontal line and the tangent of the cavity wall at location irradiated by the ray of convergence angle β′. The non-dimensional beam power Q is defined as
$\hat Q/\hat k_{\rm l} {\hat {\rm \sigma}} {\rm (}\hat T_{\rm m} - \hat T_\infty {\rm )}$
.
$\hat k_{\rm l} $
is the thermal conductivity of the molten workpiece and
$\hat Q$
is the power of high-energy beam. The momentum balance due to the vapor pressure and surface tension is considered at the base of cavity.
$${\rm \eta} _0 = \displaystyle{{Pe{\rm [}1 + Y{\rm (}{\rm \theta} _{\rm b} - 1{\rm )]}} \over P}e^{{\rm [}H{\rm (}{\rm \theta} _{\rm b} - {\rm \theta} _{\rm B} {\rm )/(}{\rm \theta} _{\rm B} + {\rm \theta} _\infty {\rm )(}{\rm \theta} _{\rm b} + {\rm \theta} _\infty {\rm )]}}, $$
where θB and θb are the non-dimensional temperatures at cavity base and boiling point, respectively. Other non-dimensional parameters in Eq. (15) are
$$Y = \displaystyle{{{\rm (}\hat T_{\rm m} - \hat T_\infty {\rm )}d{\hat {\rm \gamma}} /d\hat T} \over {{\hat {\rm \gamma}} _{\rm m}}}, $$
$$P = \displaystyle{{\hat p_{\rm b} {\hat {\rm \sigma}}} \over {{\hat {\rm \gamma}} _{\rm m}}}, $$
$$H = \displaystyle{{\hat h_{\lg}} \over {\hat R{\rm (}\hat T_{\rm m} - \hat T_\infty {\rm )}}}.$$
In Eqs. (16)–(18),
$\hat p_{\rm b} $
is the vapor pressure at boiling point.
${\hat {\rm \gamma}} $
is the surface tension and
${\hat {\rm \gamma}} _{\rm m} $
is the surface tension at the melting point.
$\hat h_{{\rm lg}} $
is the latent heat of boiling and
$\hat R$
is the gas constant.
Fig. 3. Schematic of physical system in the z–x plane.
3. ANALYTICAL SOLUTION
The separation-of-variables method is employed to solve Eq. (8). After separating variables, three ordinary differential equations are obtained.
$$\displaystyle{{d^2 \Omega} \over {d{\rm \xi} ^2}} + \displaystyle{1 \over {\rm \xi}} \displaystyle{{d\Omega} \over {d{\rm \xi}}} + \left( { - \displaystyle{{m^2} \over {4{\rm \xi} ^2}} + \displaystyle{n \over {\rm \xi}} - \displaystyle{1 \over 4}} \right)\Omega = 0,$$
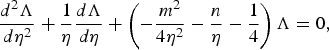$$\displaystyle{{d^2 \Lambda} \over {d{\rm \eta} ^2}} + \displaystyle{1 \over {\rm \eta}} \displaystyle{{d\Lambda} \over {d{\rm \eta}}} + \left( { - \displaystyle{{m^2} \over {4{\rm \eta} ^2}} - \displaystyle{n \over {\rm \eta}} - \displaystyle{1 \over 4}} \right)\Lambda = 0,$$
$$\displaystyle{{d^2 \Pi} \over {d{\rm \varphi} ^2}} + m^2 \Pi = 0.$$
The finite temperature at ξ = 0 indicates that the solution of Eq. (19) should be proportional to Laguerre function
$L_p^m $$
$$\Omega \sim {\rm \xi}^{m/2}e^{ - ({\rm \xi} /2)}L_{\,p - 1}^m {\rm (}{\rm \xi} {\rm )} $$
and the value p (= n − m/2 − 1/2) is determined by the boundary condition ∂Θ/∂ξ = 0 at ξ = ξe. Similarly, Eq. (20) also should satisfy the condition that the temperature is finite at η → ∞, so the form of solution of Eq. (20) is
$$\Lambda \sim{\rm \eta} ^{m/{\rm 2}} e^{ - ({\rm \eta} /2)} \Psi {\rm (}m + p,\;m + 1,\;{\rm \eta} {\rm ),}$$
where the function ψ is the confluent hypergeometric function of the second kind.
The solution of Eq. (21) is the function of cosine due to symmetry relative to the central line of the keyhole of the parabolic shape.
$$\Pi \sim\cos m{\rm \phi} \;(m = 0,\;1,\;2,\;3,\; \ldots ).$$
Therefore, a general solution of Eq. (8) follows as
$$\eqalign{& {\rm \theta} = e^{ - ({\rm \xi} + {\rm \eta} /2)} \sum\limits_{m = 0}^\infty {\sum\limits_{\,p_i} {C_{m{\rm,} p_i} {\rm (}{\rm \xi} {\rm \eta} {\rm )}^{m/2}} L_{\,p_i} ^m} \cr & \quad\quad {\rm (}{\rm \xi} {\rm )}\Psi {\rm (}m + p_i, \;m + 1,\;{\rm \eta} {\rm )}\cos m{\rm \phi} {\rm.}} $$
The coefficient
$C_{m{\rm,} p_i} $
in Eq. (25) can be determined by Eq. (14).
$$\eqalign{& C_{m{\rm,} p_i} = \displaystyle{{{\rm (}1{\rm /2)}^{{\rm \delta} _{m0 - 1}} \int_0^{{\rm \xi} _{\rm o}} {{\rm \xi} ^{m/2} e^{ - ({\rm \xi} /2)} \sqrt {{\rm \xi} /{\rm \eta} _{\rm 0} s + 1} q_j \cos {\rm (}{\rm \psi} _j - {\rm \beta} ^{\prime}_j {\rm )}}} \over {{\rm \pi} e^{ - ({\rm \eta} _{\rm 0} /2)} {\rm \eta} _{\rm 0}^{m{\rm /2}} {\rm [((}m/2{\rm \eta} _{\rm 0} {\rm )} - (1/2){\rm )}\Psi + \left. {(d\Psi /d{\rm \eta} )} \right \vert _{{\rm \eta} = {\rm \eta} _{\rm o}} {\rm ]}}} \cr & \quad\quad\quad \displaystyle{{I{\rm (}\sqrt {{\rm \xi} {\rm \eta} _{\rm 0}} {\rm )}L_{\,p_i - 1}^m {\rm (}{\rm \xi} {\rm )}d{\rm \xi}} \over {{\rm Norm}{\rm (}m,p_i {\rm )}}},} $$
where
$${\rm Norm}{\rm (}m,\;p_i {\rm )} \equiv \int_0^{{\rm \xi} _{\rm 0}} {{\rm \xi} ^m e^{ - {\rm \xi}} {\rm (}L_{\,p_i} ^m {\rm )}^2 d{\rm \xi}}. $$
4. RESULTS AND DISCUSSION
The typical non-dimensional parameters of the focal location, spot size, and convergence angle are correspondingly chosen to be 0, 0.85, and 0.02 for the following figures. Figure 4 presents the comparison between the predicted temperatures for different theoretical models and the measured temperatures for the experiment (Schauer & Giedt, Reference Schauer and Giedt1978) along the wall of the welding cavity from the base to opening. The measured data of the surface temperature in an electron beam welding cavity of aluminum 1100 were obtained using the adaption of a narrow band infrared radiation pyrometer (Schauer & Giedt, Reference Schauer and Giedt1978). The thermal properties of aluminum 1100 used in this calculations were listed in Table 2. The central line labeled by “this work” in Figure 4 indicates the temperatures along the wall of the welding cavity, which are calculated by this model directly setting the adiabatic conditions on the workpiece surface outside the cavity. On the other hand, Wei and Shian's model computed the cavity temperatures using the image method to transform the infinite domain into semi-infinite domain with the adiabatic condition. It is found that the welding cavity temperature predicted by Wei and Shian's model obviously deviates from the experimental data (Schauer & Giedt, Reference Schauer and Giedt1978), which is denoted by the solid line in Figure 4. The cavity temperatures calculated by this work are about 2200°C at the base and 1600°C at the opening along the wall of the welding cavity for Al 1100. These two temperature values are higher than the measured data (Schauer & Giedt, Reference Schauer and Giedt1978), which are about 1900°C at the base and 1500°C at the opening. The possible reasons for the discrepancy are the adiabatic condition on the surface of workpiece outside the welding cavity and vaporization neglect in the welding cavity. The adiabatic condition on the workpiece surface and vaporization neglected in the welding cavity reduce the heat dissipation from the fusion zone into the ambient air. This leads to the higher predicted temperatures than the measured values. It is also seen from Figure 4 that the prediction of the present model for temperatures on the cavity wall approximates that obtained from the line source model. However, the line source model and point source model predicted the infinite temperature at the base of the welding cavity.
Fig. 4. Comparison between predicted temperatures from theoretical models and measured temperatures from experiments along the wall of the welding cavity from the base to opening.
Table 2. Thermophysical properties of materials used in calculations
The relations of the penetration depth to the distance between the focal spot and workpiece surface are shown in Figure 5 for the predicted results from this work and the measured data from the experiments of HY130 steel (Konkol et al., Reference Konkol, Smith, Willebrand and Connor1971) and SS304 (Hicken et al., Reference Hicken, Giedt and Bentley1991). The symbols, circle and diamond, stand for the measured values of the deep and shallow penetration, respectively. On the other hand, the solid lines obtained from this work represent the predictions for the shallow and deep penetration depths. This work utilized the thermal properties of SS304 and HY130 steel in Table 2 to calculate the relation of the penetration depth to the distance between the focal spot and workpiece surface. It is indicated in Figure 5 that the penetration depths calculated by this work agree well with the measured data. The penetration depth almost linearly increases when the focal spot is lowered from the focal location 25.4 mm above the workpiece surface. Then the penetration arrives at the maximal depth at the focal location about 5.588 mm below the workpiece surface for the shallow penetration and 31.75 mm below the workpiece surface for the deep penetration. Finally, the penetration depth begins to decrease as the focal spot of the incident energy beam sequentially descends after the occurrence of the maximal penetration. The distance between focal spot and the base of penetration is also symbolized by the dashed line. The dashed line illustrates the tendency that the focal location closer to the base of penetration leads to the deeper penetration. According to (Ho & Wei, Reference Ho and Wei1997; Wei & Ho, Reference Wei and Ho1998; Ho, Reference Ho2005a ) investigating the absorption of different cavity shapes for the incident focused energy beam, any location on the wall of the cavity absorbs energy reflected from other locations and directly incident on the location. The number of the reflection resulting in energy re-absorption increases at first and then decreases as the focal location is lowered from the workpiece surface toward the cavity base. There exists maximal energy absorption between the workpiece surface and the cavity base. If the focal location approximates the cavity base, most incident energy escapes from the cavity opening after the incident energy beam only experiences one reflection due to the nearly plane base. This is the possible reason why the penetration depth is reduced when the focal location approximates the cavity base. Joint penetration can be determined by current measurements such as inline coherent imaging (Webster et al., Reference Webster, Wright, Ji, Galbraith, Kinross, Van Vlack and Fraser2014) and spectroscopic analysis of optical emission (Sibillano et al., Reference Sibillano, Rizzi, Ancona, Saludes-Rodil, Rodríguez Nieto, Chmelíčková and Šebestová2012). However, the measured relation of penetration to focal location by current measurements is not found. While Hicken et al. (Reference Hicken, Giedt and Bentley1991) employed to validate the predicted variation of joint penetration with focal location by this work is not recent, the tendency of the measured variation of joint penetration with focal location by Hicken et al. (Reference Hicken, Giedt and Bentley1991) is recognized to be applicable data for a focused electron-beam.
Fig. 5. Relation of the penetration depth to the distance between the focal spot and workpiece surface for the measured and predicted data.
The relation of the predicted penetration depth to the convergence angle for different focal locations relative to the workpiece surface is sketched in Figure 6. The focal spot is on the workpiece surface for the case f = 0, which shows that the non-dimensional penetration depth almost linearly decreases with the increasing convergence angle. On the other hand, the two cases f = 63.5 and −63.5 denote the focal spots above and below the workpiece surface, respectively. The penetration depth for the case f = −63.5 is slightly greater than that for the case f = 63.5 and the penetration depth for these two cases increases more quickly as convergence angle decreases from 0.02 to 0. The higher intensity induces the deeper penetration so the smaller convergence angle making the beam more concentrated enhances the penetration depth. When convergence angle approximates 0, the penetration depth for three cases is almost equal independent of the focal location. This is because the electron beam is nearly collimated. The effect of the convergence angle on the penetration depth is more significant for the focal location away from the workpiece surface (f = 63.5 or −63.5) than that at the workpiece surface (f = 0).
Fig. 6. Relation of the penetration depth to convergence angle for the different distances between the focal spot and workpiece surface.
Figure 7 shows the relation of the predicted penetration depth to the focal spot size for different beam focal locations relative to the workpiece surface. The small focal spot size enhances the intensity of the incident energy beam due to the energy concentrated on the small region. The energy beam of the higher intensity induces the deeper penetration. Therefore, the penetration depth decreases with the increase of the focal spot size. The effect of focal spot size on the penetration depth is more obvious for the focal location at the workpiece surface (f = 0) than that away from the workpiece surface (f = 63.5 or −63.5).
Fig. 7. Relation of the penetration depth to focal spot size for the different distances between the focal spot and workpiece surface.
5. CONCLUSIONS
This paper employs a 3D model with the adiabatic condition directly set on the upper surface of the wokpiece instead of using the image method to transform infinite domain into semi-infinite domain. The closed form solution of the quasi-steady-state model describing the parabolic keyhole induced by a moving focused high-energy beam is obtained. This study gives reasonable predictions for the measured cavity temperatures. The calculated relation of the penetration depth to the focal location relative to the workpiece surface agrees with the measured data. As the focal spot is lowered from the workpiece surface to the cavity base, the penetration depth increases first and then decreases after reaching the maximum. The penetration depth decreases with the increase of the convergence angle and focal spot size. The effect of the convergence angle on the penetration depth is more obvious for the focal location away from the workpiece surface than that at the workpiece surface.
ACKNOWLEDGMENT
Support for this work by Hwa Hsia University of Technology under grant no. HWH105-H-003 is gratefully acknowledged.
