INTRODUCTION
If examining the nature of laser interaction with matter, the expansion of laser-created plasma into a vacuum is a topic of long-standing interest. The initiation and development of laser–plasma interactions and of the subsequent processes responsible, for example, for the charge separation and the formation of plasma jets, were investigated with the use of various diagnostics (Mendel & Ohlsen, Reference Mendel and Ohlsen1975; Kasperczuk et al., Reference Kasperczuk, Pisarczyk, Kalal, Martinkova, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2008; Romagnani et al., Reference Romagnani, Borghesi, Cecchetti, Kar, Antici, Audebert, Bandhoupadjay, Ceccherini, Cowan, Fuchs, Galimberti, Gizzi, Grismayer, Heathcote, Jung, Liseykina, Macchi, Mora, Neely, Notley, Osterholtz, Pipahl, Pretzler, Schiavi, Schurtz, Toncian, Wilson and Will2008). To elucidate the ion acceleration, the early stage of freely-expanding collisionless plasma has been described taking into account a space charge distribution at the plasma front composed of an electron cloud followed by an ion front (Crow et al., Reference Crow, Auer and Allen1975; Mora, Reference Mora2003). In particular, the maximum ion energy attainable in the experiments is of central importance for the research of particle acceleration by ultrashort and high-intensity laser pulses focused on thin foils (Betti et al., Reference Betti, Ceccherini, Cornolti and Pegoraro2005; Fuchs et al., Reference Fuchs, Antici, D'Humieres, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2006; Nishiuchi et al., Reference Nishiuchi, Fukumi, Daido, Li, Sagisaka, Ogura, Orimo, Kado, Hayashi, Mori, Bulanov, Esirkepov, Nemoto, Oishi, Nayuki, Fujii, Noda, Iwashita, Shirai and Nakamura2006; Schreiber et al., Reference Schreiber, Bell, Gruener, Schramm, Geissler, Schnuerer, Ter-Avetisyan, Hegelich, Cobble, Brambrink, Fuchs, Audebert and Habs2006). Energy spectra of fast ions, which are generally measured with the use of Thompson parabola type spectrometer equipped with a nuclear track detector (Schreiber et al., Reference Schreiber, Kaluza, Gruner, Schramm, Hegelich, Cobble, Geissler, Brambrink, Fuchs, Audebert, Habs and Witte2004), indicate that the single charge-states of ions carrying energy of several MeV per nucleon form groups separated in space and time due to their differing energy distributions. A classical example of time-of-flight (TOF) spectra showing the clear separation of fast carbon ions with respect to their charge-states was demonstrated in Ehler (Reference Ehler1975). A later evaluation of ion currents showed that a visible separation of ions by their charge-states during their expansion into the vacuum is possible if the center-of-mass energy of ions is more than 50 times higher than their thermal energy (temperature) for all the charge-states generated (Krása et al., Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007).
The above-mentioned analysis of TOF spectra of ions, which makes the determination of ion temperature T and center-of-mass velocity v CM possible, is based on the assumption that the ion current is commonly a sum of partial currents j i of all the ionized species:
The expression for the time-resolved ion collector signal was derived by Kelly and Dreyfus (Reference Kelly and Dreyfus1988). It is based on a velocity distribution ![]() , which determines the number of particles with the velocity in the range (v x, dv x; v y, dv y; v z, dv z). To obtain the number of particles impacting on the detector's area dS = dydz per dt, the velocity space has to be converted into the space-time dependence. Under the assumption that the ion collector is positioned at the distance L on the x-axis and its surface is parallel to y-z directions each velocity vx, vy, and vz is transformed to |dv x| = |d(x/t)| = x/t 2dt, dv y = d(y/t) = dy/t and dv z = d(z/t) = dz/t, respectively. Substituting L/t into
, which determines the number of particles with the velocity in the range (v x, dv x; v y, dv y; v z, dv z). To obtain the number of particles impacting on the detector's area dS = dydz per dt, the velocity space has to be converted into the space-time dependence. Under the assumption that the ion collector is positioned at the distance L on the x-axis and its surface is parallel to y-z directions each velocity vx, vy, and vz is transformed to |dv x| = |d(x/t)| = x/t 2dt, dv y = d(y/t) = dy/t and dv z = d(z/t) = dz/t, respectively. Substituting L/t into ![]() we get the number of particles hitting the detector's area dS per dt, which is then proportional to f(T/t)Lt −4. Since the ion collector detects the current being proportional to the velocity of ions v = L/t, its signal is
we get the number of particles hitting the detector's area dS per dt, which is then proportional to f(T/t)Lt −4. Since the ion collector detects the current being proportional to the velocity of ions v = L/t, its signal is
We should note that the Kelly's Eq. (2) describes the expansion of ions in a three-dimensional (3D) space, while others often used expressions such as
where |dN/dv| and |dN/dE| are velocity and energy distribution functions, respectively, which were derived for ions “expanding” in a one-dimensional (1D) space and, thus, they do not take into account the rarefaction of the plasma which proceeds in the 3D space.
Following Kelly's reasoning (Kelly & Dreyfus, Reference Kelly and Dreyfus1988) to deduce an analytical form of the ion collector's signal, we shell consider the shifted Maxwell-Boltzmann velocity distribution. If we suppose that every ionized species with the atomic number A and the charge-state q flows with the center-of-mass velocity ![]() directed along the x-axis, then Eq. (1) expressing the total current takes a form:
directed along the x-axis, then Eq. (1) expressing the total current takes a form:
![\,j_{IC} \lpar L\comma \; t\rpar = \sum a_{i\comma q} {L^2 \over t^5} \exp \left[-{m_i \over 2kT} \left({{L \over t} - u_{i\comma q}}\right)^2\right]\comma \;](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000238_eqn5.gif?pub-status=live)
where a i,q is the amplitude of the partial ion current j i,q, m i is the mass of the ion species, k is the Boltzmann constant, and T is the temperature.
The center-of-mass velocity and energy of ions are the parameters reflecting the acceleration of ions by electrons due to a dependence on the charge eq. The charge-state dependence of the center-of-mass velocity u(q) of the slow (so-called thermal) carbon ions emitted from a polyethylene plasma, which was obtained after recovering the partial ion currents by a deconvolution of TOF spectra based on Eq. (5), was found to be linear (Krása et al., Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007):
The linear charge-state dependence of center-of-mass velocity reflects the dominant effect of collisions on the slowing down of the ions accelerated by the electric field, because the relative velocity Δu ≡ u 2–u 1 of the species 1 and 2 in the collisional regime is:
where E is the ambipolar electric field and ω is the slowing down collision frequency between the species 1 and 2.
It is generally accepted that at higher densities of laser-produced plasma many collisions occur not only near the target surface but also during the plasma expansion into the vacuum. Nominally, the three-body recombination strongly affects the evolution of the expanding plasma lowering the charge state of ions (Goforth & Hammerling, Reference Goforth and Hammerling1976). That is, the reason for positioning the ion collectors far from the target where the charge states are already “frozen” (Eidmann et al., Reference Eidmann, Amiranoff, Fedosejevs, Maaswinkel, Petsch, Sigel, Spindler, Teng, Tsakiris and Witkowski1984). Nevertheless, the collisions among the charged species form the shape of the TOF spectrum observed at each given distance from the target. A similar situation led likely to a successful deconvolution of TOF spectra of fast carbon ions produced by a CO2 laser in Krása et al. (Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007) using Eq. (5). Although the carbon ions investigated in Ehler (Reference Ehler1975) were the fast ones, the deconvolution of the TOF spectrum gave rise to a linear charge-state dependence of the center-of-mass velocity u(q)∝q as in the case of the slow carbon ions. The most likely reason of the observed dependence is the fact that the center-of-mass velocities of all fast Cq+ (1 ≤ q ≤ 6) ions ranging from 0.97 × 108 cm/s to 2.4 × 108 cm/s, respectively, are just having a velocity of about 1.6 × 108 cm/s, which can be regarded as a dividing line between the slow and the fast ions (Tsakiris et al., Reference Tsakiris, Eidmann, Petsch and Sigel1981).
The latest experiments performed at the PALS Research Center ASCR in Prague (Kasperczuk et al., Reference Kasperczuk, Pisarczyk, Borodziuk, Ullschmied, Krouský, Mašek, Pfeifer, Rohlena, Skála and Pisarczyk2007, Reference Kasperczuk, Pisarczyk, Kalal, Martinkova, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2008) revealed the formation of plasma jets, namely in Cu, Au, and Ta plasmas. It was reported that the plasma jet formation starts at the focal spot radius close to 0.2 mm when it is exposed to the third harmonics (λ = 438 nm) with an energy of 100 J (Kasperczuk et al., Reference Kasperczuk, Pisarczyk, Borodziuk, Ullschmied, Krouský, Mašek, Pfeifer, Rohlena, Skála and Pisarczyk2007), i.e., the value of the similarity parameter Iλ2 should be lower than about 1 × 1014 W cm−2µm2, where I is the laser intensity, and λ is the laser wavelength. In terms of velocity classification of generated ions, we can deduce that the formation of plasma jets correlates with the generation of slow, i.e., thermal ions. Our experiments (Torrisi et al., Reference Torrisi, Margarone, Láska, Krása, Velyhan, Pfeifer, Ullschmied and Ryć2008) devoted to the ion generation under similar experimental conditions—0.5-mm Au foil was irradiated by the third harmonics with an energy of 150 J varying the focus position (FP) in the range of ± 1500 µm with respect to the target surface—proved that the group of fast ions was absolutely dominating while the focus was positioned 200 µm in front of the target surface, i.e., FP = −200 µm. If FP draws away from this optimum position, the slow thermal ions are strongly produced: at the FP-range limit the amplitude of the current of slow ions approaches the value of the current of fast ions and, in addition, the slow ions carry a much higher charge than the fast ones. This experiment and its analysis confirmed that under these experimental conditions, the fast ions are produced due to the self-focusing effect, which occurs if the laser beam is focused at about 200 mm in front of the target surface.
Though the plasma jets were not detected in the polyethylene plasma, the generation of fast carbon ions occurs for similar laser beam intensities and it is followed by new phenomena as the space-time charge separation. It seems to be a general phenomenon following the creation of fast ions. While the TOF spectra of slow ions show a shallow modulation of the pulsed ion current, the TOF spectra of fast ions may exhibit a modulation depth higher than 50% (Ehler, Reference Ehler1975; Eidmann et al., Reference Eidmann, Amiranoff, Fedosejevs, Maaswinkel, Petsch, Sigel, Spindler, Teng, Tsakiris and Witkowski1984; Láska et al., Reference Láska, Krása, Mašek, Pfeifer, Rohlena, Králiková, Skála, Woryna, Parys, Wolowski, Mróz, Sharkov and Haseroth2000; Torrisi et al. Reference Torrisi, Margarone, Láska, Krása, Velyhan, Pfeifer, Ullschmied and Ryć2008). The charge separation in a stream of fast ions of light elements does not mean that the single charge states are completely separated, but that only some of them are partially separated and the others were merged all in together as a single group (Krása et al., Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007). The highly charged fast ions of heavy elements constitute only indistinguishable groups (Picciotto et al., Reference Picciotto, Krása, Láska, Rohlena, Torrisi, Gammino, Mezzasalma and Caridi2006) because the ratio of the neighboring charge states is close to q + 1/q ≈ 1.
In this paper, we report results of the experiments focused on the separation of fast ions emitted from the polytetrafluoroethylene and the polyethylene plasmas. The adopted method of an analysis of TOF spectra based on the shifted Maxwell-Boltzmann velocity distribution is suitable for a separation of the thermal motion of ions from their directed motion due to the fast electrons.
EXPERIMENTAL SETUP
The reported measurements were performed with the high-power iodine laser system at the PALS Research Center ASCR in Prague (τ ≈ 300 ps; λ = 1.315 µm, the focal spot diameter ≈ 70 µm) (Jungwirth et al., Reference Jungwirth, Cejnarová, Juha, Králiková, Krása, Krouský, Krupičková, Láska, Mašek, Mocek, Pfeifer, Präg, Renner, Rohlena, Rus, Skála, Straka and Ullschmied2001). In this experiment, the laser beam stroke the polytetrafluoroethylene (PTFE) or polyethylene (PE) target at an angle of 30° to the target normal. The focus position (FP) was varied in the range from −500 µm to 800 µm, i.e., the spot diameter ranged from 70 µm to 500 µm. The target positioning accuracy was ±20 µm. The maximum focused laser-light intensity was about 4.5 × 1016 W cm−2, which corresponds to an energy of 450 J. A ring ion collector with ∅︀out = 5 cm and ∅︀in = 3.8 cm (IC) and a cylindrical electrostatic energy analyzer (CEA) fitted with a windowless electron multiplier were employed for the measurement of ion currents. Both the detectors were positioned in the far expansion zone along the target surface normal at the distances L IC = 180 cm and L CEA = 258 cm, i.e., IC was placed in front of CEA.
EXPERIMENTAL RESULTS
When the FP was 600 µm and 700 µm below the surface of the PTFE and PE targets, respectively, slow thermal ion groups with maximum velocity of about 1 × 108 cm/s were observed (see Fig. 1), TOF > 1.5 µs. If FP was shifted near to the surface, an irregular train of fast ion subgroups evolved. The number of these fast subgroups increases when moving the PF up to ≈250 µm and 300 µm below the surface of the PTFE and PE target, respectively. At this setting and for the applied laser energy equal to ≈150 J, the highest velocity of ions reached ≈9 × 108 cm/s. The corresponding kinetic energy of carbon and fluorine ions is about 5 MeV and 8 MeV, respectively.

Fig. 1. Time-resolved currents of ions created by laser irradiation of PTFE and PE targets at various focus positions (FP) below the target surface (L IC = 1.8 m, E L ≈ 150 J).
The mass spectra of fast ions emitted by the PTFE and PE plasmas, which were obtained with the use of CEA, are compared with the IC signals in Figure 2. The diagrams show that the fast Cq+ (1 ≤ q ≤ 4) and Fq+ (1 ≤ q ≤ 6) ions are sporadically distributed. The separated peaks in the TOF spectra of PE and PTFE plasmas are constituted mainly by C6+ and C5+, and C6+, C5+, F9+, F8+, and F7+ ions, respectively. The detection of fully stripped and partially recombined carbon and fluorine ions within those separated peaks can indicate an occurrence of non-linear pulse-modulated generation of outburst trains of fully ionized PE and PTFE plasmas during the early stage of plasma expansion into the vacuum. Both the number of generated outbursts (i.e., ion subgroups) and their time-profile depend strongly on the focus position with respect to the target surface. The maximum number of outbursts as well as the maximum velocity of ions emitted from PE and PTFE plasmas can be achieved if PF ≈ 200 µm to 300 µm below the target surface. The fast ion TOF spectra show less regularity in the occurrence of outbursts and a lower reproducibility. Nevertheless, a satisfactory reproducibility of 13 outbursts (subgroups) of fast highly charged tantalum ions and their peak velocities were observed in the PF dependence (Láska et al. Reference Láska, Jungwirth, Krása, Krouský, Pfeifer, Rohlena, Ullschmied, Badziak, Parys, WoLowski, Gammino, Torrisi and Boody2006). The charge-state composition of these outbursts of fast tantalum ions was not analyzed because it is hard to determine due to an overlap of TOF spectra of highly charged ions created in different plasma outbursts, as demonstrated in Picciotto et al. (Reference Picciotto, Krása, Láska, Rohlena, Torrisi, Gammino, Mezzasalma and Caridi2006). It is just the advantage of carbon and fluorine ions that the number of their charge-states in outbursts is very low: 2 to 3 and 3 to 4, respectively.

Fig. 2. (Color online) Comparison of ion collector signals, U IC (bottom curves), with cylindrical electrostatic energy analyzer signals, U CEA (upper curves), induced by ions of PE and PTFE plasmas. The time scale of the CEA signals was re-scaled for the IC distance of 1.8 m from the target. (a) C6+ and C5+ ions dominate the fast ions emitted by the PE plasma; FP = 300 µm, E L = 98 J. Only the ions with energy of q × 200 keV passed through the CEA. (b) H+, Cq+ (4 ≤ q ≤ 6) and Fq+ (6 ≤ q ≤ 9) ions dominate the fast ions emitted by the PTFE plasma; FP = 300 µm, E L = 157 J. Only the ions with energy of q × 80 keV passed through the CEA.
As mentioned above, the formation of TOF spectra of ions due to the nonlinear mechanisms creating the spatial separation of charges depend especially on the conditions under which the electrons leave the ions having lower mobility. If the ions, accelerated by slowing down the electrons in the self-created strong electric field, collide among themselves, the effect of the accelerating electric field is reduced by the collisions between the ion species. Then the center-of-mass velocity is proportional to the charge state, as it follows from Eq. (7), and as it was observed in the case of slow (thermal) ions in Krása et al. (Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007). If higher laser pulse intensity is applied, there is not enough time to establish the thermal equilibrium in the plasma, and the electron distribution function is of two-temperature-type (Gitomer et al., Reference Gitomer, Jones, Begay, Ehler, Kepphart and Kristal1986). But the collisions among ions, which proceed until a significant rarefaction, should affect the ion velocity distribution and, thus, can form the ion TOF spectrum. However, the acceleration of ions by hot electrons would last longer. The resultant charge dependence of the center-of-mass velocity should differ from Eq. (6); in the limit case, the center-of-mass energy will be proportional to the ion charge and the center-of-mass velocity
where U is the effective accelerating voltage, which represents the induced strong charge separation electric field, and U 0 is the voltage representing the initial ion velocity in the direction of observation.
The ions accelerated backwards by the strong electric field at the front of laser-irradiated plasma plume constitute separated outbursts. Since these ion outbursts are separated, they must have been accelerated at different rates. Moreover, the ions contained in each outburst should also be separated, since their acceleration rate in the electric field is proportional to their charge-to-mass ratio, providing that the ion-ion collisions are sufficiently weak. In that case, the PTFE plasma can be analyzed more easily than that of PE, since C6+ and F9+ ions behave as a well distinguishable doublet, whose constant value of the TOF ratio TOFF9+/TOFC6+ = 1.0274 is independent of the accelerating electric field. Peaks of other doublets of ions (e.g., C5+-F8+ and C6+-C5+) can also be used with an advantage for the TOF spectra analysis: TOFF8+/TOFc5+ 1.005 to and TOFc5+/TOFc6+ = 1.0954. To demonstrate this method, we chose a TOF spectrum of PTFE ions showing the fastest ions available when the focus was 300 µm behind the target surface, as shown in Figure 3. The calculation of TOF of C6+, C5+, F9+, and F8+ ions under the assumption that the same voltage U accelerated all these ion species is the basic step of this analysis:

Fig. 3. (Color online) Matching analysis of the ion current emitted from polytetrafluoroethylene plasma: the doublets of C6+-C5+, F9+-F8+, C6+-F9+ and F8+-C5+ ions expanded together starting from the instant of their generation and were accelerated by the same voltage; FP = 200µm, E L = 155 J. Only six four-ion groups (C6+, C5+, F9+, F8+) were chosen for demonstration. Outbursts of slower ion doublets were accelerated by lower voltage, as Figure 4 shows. The widths of single TOF lines were not considered. The comprehensive analysis of a TOF spectrum taking into account the line width is presented in Figure 5.
Having computed the TOF for various ion doublets accelerated by different voltages, and having compared them with peaks occurring in the TOF spectrum of the ion current, we obtained matching values of the effective accelerating voltage, as illustrated in Figure 4. The numerals 1 to 10 were used for numbering the ion outbursts containing doublets of C6+-F9+, C5+-F8+, and C6+-C5+ ions, which were accelerated by the same voltage U and, thus, have energy E = eqU. The total number of the fast ion outbursts investigated was limited to 10, the label “1” belonging to the fastest ion outburst. In contrast to the slower thermal ion group (see Fig. 1, TOF > 1.5 µs), the TOF spectrum of fast ions reveals chaotic variations in the magnitude of current, but not in the positions of peaks.

Fig. 4. Effective voltage U accelerating outbursts of C+6, C+5, F+9, and F+8 ions. Numbering of the ion outbursts started from the fastest one passing the distance of 180 cm at 254 ns, see Figure 3.
Similar conclusions can be drawn for the PE plasma. In this case, however, the peaks in TOF spectra are constituted by mainly C6+, C5+, and H+ ions, which make it possible to deconvolute the TOF spectrum with the use of Eqs (5) and (8):

where i denotes the carbon and hydrogen ions, and a i,q is the amplitude of a partial ion current j i,q. The term U 0 was omitted due to its low value. The temperature T reflects the width of the partial currents created by the ion-ion collisions and the recombination processes of fully stripped carbon ions, which took place in the early stage of the ion acceleration by fast electrons. Thus, there is no causal relationship between T and u, but T is a measure of broadening the TOF spectral lines, which reflect the center-of-mass velocities u.
Figure 5 shows the deconvolution of ion current emitted by the PE plasma for the TOF period ranging from 190 ns to 300 ns, only. The fit is constituted by 9 doublets of C6+-C5+ ions and four peaks of protons. The partial currents of single charge-states were revealed with the use of numerical code (PeakFit 4.11) using the standard least-squares minimization for finding hidden peaks in the TOF spectrum. The voltages accelerating the ion outbursts were assumed to be free parameters. The decrease of this voltage with the increasing number of the carbon ions doublets and the proton peaks is shown in Figure 6. When temperatures T q were fitted as free parameters, their values fluctuated about a mean value. It was a reason why the same T q was next shared for all the doublets of carbon ions as well as for proton peaks. The fitted values of temperature, which can be regarded as average values characterizing the entire revealed ion outbursts, were ≈1.1 keV and ≈2.4 keV for the carbon ions and the protons, respectively. The higher temperature of proton outbursts reflects their broader widths compared with those of the carbon. The highest effective voltage accelerating the carbon ion outbursts reaches ≈800 kV. The corresponding voltage for the proton outburst moving just before the fastest C6+-C5+ outburst is only ≈400 kV. The deconvolution of the TOF spectrum was limited only to the TOF of 300 ns because of the high number of partial ion currents constituting the entire ion current. In particular, the high number of interfering ion outbursts poses a problem for identification and revealing the hidden partial ion currents, whose width increases with decreasing center-of-mass velocity, i.e., with increasing TOF. Nominally, partial currents of C6+ and C5+ ions, which belong to different outbursts, can superimpose, as it is evident in Figure 5 at TOF = 283 ns.

Fig. 5. (Color online) Deconvolution of TOF spectrum of polyethylene ions; E L = 226 J; FP = 250 µm, L = 1.8 m. The doublets of C6+-C5+ ions and eventually triplets of C6+-C5+-C4+ ions expanded together starting from the instant of their generation and were accelerated by the same voltage. Outbursts of slower ions were accelerated by lower voltage, as Figure 6 shows.

Fig. 6. Effective voltage U accelerating doublets of C6+-C5+ ions and protons versus the doublet (outburst) number, which were evaluated by means of TOF spectrum deconvolution shown in Figure 5.
The analysis of TOF spectra showed that the time delay (i.e., temporal separation) between the arriving peaks of partial C6+ ions typically varies from ≈5 ns to ≈15 ns for both the plasmas. The time-delays between neighboring peaks are irregular.
DISCUSSION
The applied analysis based on revealing of partial ion currents in the observed time-resolved current makes it possible to separate the center-of-mass velocity from the thermal motion in the direction of the ion detector. The center-of-mass velocity reflects an acceleration of ions by the fast electrons via its charge dependence. It is evident that the charge dependence can be affected by the applied analysis namely if the hidden peaks are present in the TOF spectrum. In this case, it is difficult to decide which algorithm will be the most successful in their computerized identification so that, generally, the choice is largely a matter of taste. A different situation can occur if the expanding plasma consists of a number of ionized species and ion groups. A comparison of revealed TOF peaks with the experimentally reconstructed ones can help to solve the problem. But their reconstruction with the help, for example, of an ion mass analyzer requires calibration of all the ion detectors employed, as well as a good reproducibility in the plasma generation, because a large number of laser shots are needed. A satisfactory comparison of the revealed and reconstructed partial ion currents was presented for simple plasma formed by Cuq+ (1 ≤ q ≤ 3) ions in Krása et al. (Reference Krása, Lorusso, Doria, Belloni, Nassisi and Rohlena2005). The temperature and center-of-mass energy of freely expanding ions were also evaluated by fitting an analytical dependence to the partial ion currents, which were reconstructed with the use of a cylindrical ion mass analyzer or of an electrostatic quadrupole spectrometer EPQ Hiden 300 type (Torrisi et al., Reference Torrisi, Gammino, Ando and Láska2002; Caridi et al., Reference Caridi, Torrisi, Margarone and Borrielli2008). The use of this method can be limited if the reconstructed partial current consists of ions with the same charge but coming from various outbursts interfering in the TOF spectrum. It can, for example, result in an overestimate of the temperature. Difficulties can arise also in the presented experiments due to the occurrence of C6+, C5+, F9+, and F8+ ions in every outburst of the PTFE plasma: The TOF of F8+ and C5+ ions distinguished just by the charge-to-mass (TOFF8+/TOFC5+ = 1:1.005) obstruct the revealing analysis. Nevertheless, the matching analysis makes it possible to estimate the TOF of every four-ion group (i.e., C6+, C5+, F9+, and F8+) in the TOF spectrum, as Figure 3 shows. In contrast to the PTFE plasma, the expanding PE plasma containing carbon ions and protons whose charge-to-mass ratios are distinctly different can be easily investigated by the revealing analysis. In analogy to the analysis of slow PE ions in Krása et al. (Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007), a group of protons should move just before the fastest C6+-C5+ one and, thus, they differ in temperature and center-of-mass velocity. A slower increase in the current is distinctiveness for protons due to their lower center-of-mass velocity and higher temperature. Both contribute to the broadening of the proton TOF peak, as it is obvious for TOF of 192 ns, 212 ns, and 237 ns in Figure 5. In contrast to protons, the partial currents of carbon ions are narrower, with steep leading edges, which make them better distinguishable in the TOF spectrum. However, the high number of partial ion currents restricts the application of the revealing analysis to a sufficiently long TOF. Not more then revealing of about 22 hidden partial currents of C6+, C5+ ions and protons was possible. In contrast to the matching analysis, the recovering analysis is more convenient for the evaluation because it is able to distinguish more (or all) hidden peaks in a TOF spectrum, as the comparison of numbers of ion outbursts shown in Figures 4 and 6 demonstrates.
Although the revelation of all the hidden peaks can be a methodological problem in respect to the fact that each ion outburst contains not only fully ionized species, the obtained results show that the outbursts, which are gradually collected by an ion collector, had to be accelerated in gradually decreasing electric field. It is evident that a more complex model than the two-temperature model of plasma being used up to now (Gitomer et al., Reference Gitomer, Jones, Begay, Ehler, Kepphart and Kristal1986; Cowan et al., Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernández, Gauthier, Geissel, Hegelich, Kaae, Karsch, Sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pépin and Renard-leGalloudec2004) should be formulated to elucidate the creation of plasma outbursts. Moreover, the phenomena observed in the presented experiments seem to be similar to the gradual generation of subgroups of ultra-fast heavy ions (Láska et al., Reference Láska, Jungwirth, Krása, Krouský, Pfeifer, Rohlena, Ullschmied, Badziak, Parys, WoLowski, Gammino, Torrisi and Boody2006, Reference Láska, Badziak, Boody, Gammino, Jungwirth, Krása, Krouský, Parys, Pfeifer, Rohlena, Ryć, Skála, Torrisi, Ullschmied and WoŁowski2007a, Reference Láska, Badziak, Gammino, Jungwirth, Kasperczuk, Krása, Krouský, Kubeš, Parys, Pfeifer, Pisarczyk, Rohlena, Rosiński, Ryć, Skála, Torrisi, Ullschmied, Velyhan and WoŁowski2007b).
The measured time-delay between the neighboring peaks of partial C6+ ion currents also depends on the distance between the ion collector and the target as TOF ∝ L. If we suppose that the charge separation was over at the end of laser exposure, τELE, then the separation of the neighboring peaks at this instant should be proportional to the distance of the plasma-plume head from the target, δELE, which was reached at τELE. Referring to interferometric observations of laser-produced plasma in Kasperczuk et al. (Reference Kasperczuk, Pisarczyk, Borodziuk, Ullschmied, Krouský, Mašek, Pfeifer, Rohlena, Skála and Pisarczyk2007), we could estimate δELE to be shorter than 0.5 mm. At this distance, the time-delay ranges from ≈4 ps to ≈14 ps. It is noteworthy that this estimated range is comparable with the range of separation of repeated bursts of back-reflected laser emission at 1ω0 and its harmonics from the expanding laser-created plasma (Maddever et al., Reference Maddever, Luther-Davies and Dragila1990a; Hora, Reference Hora2006). Moreover, the intensity threshold below which the bursts of radiation disappear is near 3 × 1014 W/cm2, similarly to the threshold of the fast ion generation (Gitomer et al., Reference Gitomer, Jones, Begay, Ehler, Kepphart and Kristal1986; Krása et al., Reference Krása, Jungwirth, Krouský, Láska, Rohlena, Pfeifer, Ullschmied and Velyhan2007; Láska et al., Reference Láska, Badziak, Boody, Gammino, Jungwirth, Krása, Krouský, Parys, Pfeifer, Rohlena, Ryć, Skála, Torrisi, Ullschmied and WoŁowski2007a). We should notice that the characteristics of pulsations of 1ω0 and its harmonics also depend on the target position with respect to the laser focus (Maddever et al., Reference Maddever, Luther-Davies and Dragila1990a) analogous to characteristics of fast ions shown e.g., in Figure 1. It was assumed that this behavior was mainly due to the stimulated Raman or Brillouin scattering (Maddever et al., Reference Maddever, Luther-Davies and Dragila1990b), nevertheless, later on it has been shown that the contribution of SRS and SBS to the laser beam absorption is not dominant (Labaune et al., Reference Labaune, Fabre, Michard and Briand1985). It seems that there could be a significant correlation between mechanisms of occurrences of ion outbursts and bursts of back-reflected laser emission.
If searching for a phenomenon which could lead to the creation of the outbursts in the ion emission from laser-produced plasma, it is necessary to consider other phenomena in the underdense expanding plasma responsible for seeding instabilities. For example, the formation of hot spots with the radiation intensity many times higher than the average laser beam intensity, can be induced by the filamentation produced by both the thermal and the ponderomotive mechanisms, if a threshold ranging from 7.9 × l013 W/cm2 to 4.5 × 1014 W/cm2 is reached (Coe et al., Reference Coe, Afsharrad and Willi1989). There is probably a correlation between all three above-mentioned instability thresholds. Moreover, the observed outbursts of ions could also be correlated with the interaction of the plasma with the impacting non-smoothed laser pulse (Hora & Aydin, Reference Hora and Aydin1992; Hora, Reference Hora2006).
CONCLUSIONS
Both the matching and deconvolution analyses clearly demonstrate that the current of emitted fast ions from PE and PTFE plasmas can be regarded as a stream of separated outbursts of ions accelerated by the different electric fields. The time-profile of these outbursts can be expressed in terms of the shifted Maxwell-Botlzmann velocity distribution function, as Eq. (10) presents. Eq. (10) joins together two phenomena: (1) Collisional processes at the beginning of the free plasma expansion, where the formed velocity distribution imposes the time-profile of the expanding outburst of ions due to their temperature; (2) Acceleration of ions by the fast electrons in terms of their center-of-mass velocity and the separation of charge states due to the ratio of the center-of-mass energy to the thermal one.
Limiting charge-dependences of the center-of-mass velocity, which can be expressed as either u(q) ∝ q or u(q) ∝ √q, indicate the limits for a strong or insignificant influence of the ion-ion collisions and recombination on the acceleration of ions by fast electrons.
The repeated occurrence of ion outbursts, each containing the fully stripped ion species, gives evidence for a nonlinear mechanism of quasi-periodic plasma outbursts, which are gradually accelerated in a decreasing electric field. The highest effective voltage, which accelerated the ion outbursts in PE and PTFE plasmas, was estimated to ≈800 kV and ≈750 kV, respectively.
ACKNOWLEDGMENT
The support by the Grant Agency of the ASCR (Grant IAA 100100715) and by the Ministry of Schools, Youth and Sports of CR (project LC528) is gratefully acknowledged.


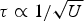 . The repeated occurrence of ion outbursts containing fully ionized ions can be characterized by a set of discrete voltages
. The repeated occurrence of ion outbursts containing fully ionized ions can be characterized by a set of discrete voltages 





