Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-20T22:26:30.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Pulse shape and spectrum of coherent diffraction-limited transition radiation from electron beams

Published online by Cambridge University Press:  01 October 2004

J. VAN TILBORG ,
C.B. SCHROEDER ,
E. ESAREY  and
W.P. LEEMANS
J. VAN TILBORG
Affiliation:
Lawrence Berkeley National Laboratory, University of California, Berkeley, California
C.B. SCHROEDER
Affiliation:
Lawrence Berkeley National Laboratory, University of California, Berkeley, California
E. ESAREY
Affiliation:
Lawrence Berkeley National Laboratory, University of California, Berkeley, California
W.P. LEEMANS
Affiliation:
Lawrence Berkeley National Laboratory, University of California, Berkeley, California
Rights & Permissions [Opens in a new window]

Abstract

The electric field in the temporal and spectral domain of coherent diffraction-limited transition radiation is studied. An electron bunch, with arbitrary longitudinal momentum distribution, propagating at normal incidence to a sharp metal-vacuum boundary with finite transverse dimension is considered. A general expression for the spatiotemporal electric field of the transition radiation is derived, and closed-form solutions for several special cases are given. The influence of parameters such as radial boundary size, electron momentum distribution, and angle of observation on the waveform (e.g., radiation pulse length and amplitude) are discussed. For a Gaussian electron bunch, the coherent radiation waveform is shown to have a single-cycle profile. Application to a novel THz source based on a laser-driven accelerator is discussed.

Keywords

Coherent transition radiationDiffractionElectron beamsRadiation temporal profile
Type
INTERNATIONAL WORKSHOP ON LASER AND PLASMA ACCELERATORS
Information
Laser and Particle Beams , Volume 22 , Issue 4 , October 2004 , pp. 415 - 422
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

With wavelengths smaller than those achieved in electronic circuits, but longer than generated by most optical sources, the terahertz (THz) regime occupies a relatively unexplored part of the electromagnetic spectrum. This lack of scientific attention can partly be attributed to the limited number of available THz sources; however, this does not make this frequency regime less attractive to numerous applications (Mittleman et al., 1999; Orenstein and Millis, 2000; Ferguson et al., 2002). For example, generation and detection of THz radiation find use in medical and biological imaging (Ferguson et al., 2002), as well as material characterization (Li et al., 1999). More recently, applications such as semiconductor imaging (Tae-In Jeon & Grischkowski, 1997), surface chemistry, and high-field condensed matter studies (Orenstein & Millis, 2000) have appeared. Most applications share the need for a source that is externally triggered to allow pump-probe type of measurements. This requirement is naturally satisfied by sources that are triggered by a laser, or sources that are directly produced from a laser. Biased-semiconductor structures have been shown to provide THz pulses with pulse energies on the order of 0.5 μJ per pulse (Budiarto et al., 1996). Another method of THz-generation is based on optical rectification in a nonlinear crystal by a femtosecond laser pulse, generating a pulse train containing millions of THz pulses per second. In these methods, higher pulse energy can be achieved by reducing the repetition rate (Lu et al., 1997).

One of the challenges for the THz community is the realization of bright sources, with peak electric fields that exceed 1 MV/cm, as well as sources with a high average power for rapid multi-dimensional imaging (Ferguson et al., 2002). Particle-based sources are an interesting candidate for achieving high peak power and high average power THz sources. Radiation generation from particle beams can be accomplished by introducing a spatial dependent refractive index (e.g., transition radiation and diffraction radiation), or introducing an external magnetic field (e.g., synchrotron radiation). These various methods of THz radiation generation rely on the coherent superposition of the electric field for wavelengths that are longer than the bunch length. The emitted energy scales quadratically with bunch charge for coherent emission, making these methods attractive candidates for an intense THz source. The work presented in this paper will focus on the radiation emitted when a charged particle passes a boundary with finite radial extent between two media with different indices of refraction. Radiation is emitted in both the forward and backward direction. This mechanism is referred to in this paper as diffraction-limited transition radiation (DLTR).

During the last decade, several research groups in the particle accelerator (e.g., cyclotron, synchrotron, and linac) community have demonstrated the generation of short (sub-ps) electron bunches and applied the characterization of transition radiation as a diagnostic for these bunches (Kung et al., 1994; Leemans, 1997; Catravas et al., 1999; Ricci & Smith, 2000; Lumpkin et al., 2001). Such short relativistic electron beams have relatively small energy spread (δE/E [lsim ] 10−4) and due to space charge effects the charge per bunch is limited to the sub-nC regime. However, for ultra-relativistic electron beams (E > 1 GeV), the space charge limitation on charge density is reduced and short bunches containing charge on the order of several nC can be achieved (Cornacchia et al., 2001). Previous work on detection of transition radiation by these accelerator generated electron beams has primarily focused on deduction of bunch characteristics such as bunch length, bunch shape, and beam divergence (Kung et al., 1994; Shibata et al., 1994; Le Sage et al., 1999). Diffraction was typically not a limitation in these experiments because of the short radiation wavelengths (e.g., optical) and the large transverse size of the optics (diameter on the order of several cm).

Recent experiments at the Lawrence Berkeley National Laboratory (Leemans et al., 2003) have demonstrated a novel method for the generation of DLTR, namely by a laser-driven plasma-wakefield accelerator. In these experiments, an ultra-short intense laser pulse interacts with a plasma and sets up a density oscillation in which background plasma electrons can be trapped and accelerated. As the bunch exits the plasma, the change in index of refraction produces transition radiation, with the transverse plasma size as the diffraction-limiting effect. This method has the advantages that the plasma environment provides shielding for space charge effects in the dense electron bunch (keeping the charge concentrated) and that synchronization of the electron beam with the fs drive pulse occurs naturally. Electron beams in these laser wakefield accelerator experiments can contain up to several nC of charge, while the electron energy distribution is typically described as a 100% energy spread Boltzmann distribution, with temperatures on the order of 3–30 MeV (Leemans et al., 2003). Although the bunch charge is high, the fact that the transverse plasma size is on the order of 100–500 μm imposes a severe limitation on the intensity of the radiation. Theoretical work on the radiation characteristics of this THz source was reported by Schroeder et al. (2004).

Most THz detectors or detection schemes for pulsed sources are either sensitive to total pulse energy or to the spectral energy distribution; however, two recent techniques (Zhang et al., 1990; Bromage et al., 1999) have proven capable of mapping out the temporal electric field using an optical probe pulse. The mechanism behind these detection schemes is the interaction of the THz pulse with an optical probe pulse onto a semiconductor surface (Bromage et al., 1999) or in a nonlinear crystal (electro-optic sampling) (Zhang et al., 1990). In the case of electro-optic sampling, the polarization of an optical probe beam, co-propagating with the THz waveform, experiences linear rotation proportional to the averaged THz electric field upon interaction with the nonlinear crystal. The resolution of such measurements is equal to the pulse length of the optical probe pulse (which is typically on the order of tens of fs). Not only can the power spectrum be derived from the field profile, but also the spectral phase, allowing determination of the real and complex components of the dielectric function of the sample of interest. Electro-optic sampling has been applied to diffraction-limited near-field transition radiation (Yan et al., 2000), although a theoretical model of the temporal field profile has not been reported.

This paper will address such an analysis and include the effects of the electron longitudinal momentum distribution on the temporal waveform. The model is based on electron bunches that propagate at normal incidence through a sharp metal-vacuum boundary. The interface is considered to have a finite transverse extent. Electron energies ranging from non-relativistic to ultra-relativistic are considered, with an arbitrary momentum distribution function. Effects of the bunch length, transverse size of the boundary, and angle of observation on the field amplitude and radiation pulse waveform are investigated.

The paper is organized as follows. Section 2 introduces the general formalism of coherent diffraction-limited transition radiation. Expressions for the angular and spectral energy distribution are presented, as well as the temporal field profile. In Section 3, closed-form solutions for mono-energetic bunches in different regimes are presented, as well as the general solution for bunches with mono-energetic, Gaussian, and Boltzmann momentum distributions. A summary and discussion is presented in Section 4.

2. GENERAL FORMALISM AND ASSUMPTIONS

The theory of transition radiation produce by a single electron was first studied by Ginzburg and Frank (1946), and later extensively treated in the monograph by Ter-Mikaelian (1972). The Coulomb field of a moving charged particle induces a transient polarization at the boundary, and radiation is emitted by the transient polarization current. Consider a sharp (infinite) boundary between medium 1 (ε = ε1 for z < 0) and medium 2 (ε = 1 for z ≥ 0), where ε is the dielectric constant. The Maxwell equations for linear dielectric media can be combined and written as the following wave equation (Jackson, 1975)

with E the electric field, Jb the current of the electron beam, and ω the frequency of the radiation. The radiation fields can be calculated by solving for the wave equation in both media, and applying continuity in the normal electric displacement as well as in the tangential electric field across the boundary. The complete solution to Equation (1) will yield both the particular solution (particle field Ep) as well as the homogeneous solution (radiation field Eh), or E = Ep + Eh, where the homogeneous solution can be rewritten as Eh(ω, k) = E′(ω, k)δ(k2c2 − ω2ε), with k the wave-vector of the radiation. By Fourier space-decomposing Eq. (1) and substituting the Fourier-transformed beam current

the particular solution is found, namely

with vj = (0,0,vj) = cβj and rj the velocity and position at t = 0 of the jth particle, respectively. Electron beam divergence as well as oblique incidence onto the interface are ignored (all particles are assumed to move normal to the z = 0 plane). Furthermore, only a radially symmetric electron beam will be considered.

In the far-field (kR >> 1), and in the limit ε1 >> 1, the homogeneous solution in the region z ≥ 0 is found to be (Schroeder et al., 2004)

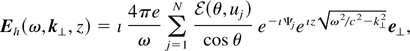
with

and Ψj = k⊥·r⊥,j + ωrz,j /vj. The unit vector e⊥ is directed perpendicular to the vector of observation (k) in the

plane, with

. The ratio kz /|k| is expressed as cos θ, and uj = γj βj with

.

The above model can be extended to dielectrics with a finite transverse boundary. To estimate the effect of diffraction owing to the transverse dielectric boundary, it is assumed that the beam is propagating through the center of the circular boundary of radius ρ, with σr << ρ (where σr is the characteristic transverse extent of the electron distribution). Babinet's principle (Jackson, 1975) relates the electric field of the radiation produced by the finite transverse dielectric to the electric field of an electron bunch passing through an infinite boundary (transition radiation) ETR = Eh, minus the electric field of an electron bunch passing through an aperture with radius ρ (diffraction radiation) EDR. The diffraction radiation in the far-field R >> r⊥ sin θ may be determined by applying Kirchhoff diffraction theory (Jackson, 1975) to the incident particle fields [Eq. (3)], where R2 = x⊥2 + z2 = x2 + y2 + z2 is the observation distance. The total electric field of the diffraction-limited transition radiation is EDLTR = ETR − EDR, or

where (Schroeder et al., 2004)

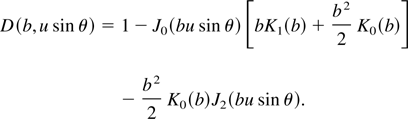
Here Jm and Km are the mth order regular and modified Bessel functions, respectively, and the dimensionless impact parameter b is given by b = kρ/u. In the following sections, the subscript DLTR will be omitted.

2.1. Spectral and angular distribution of coherent diffraction-limited transition radiation

Using the expression for the electric field for the diffraction-limited case Eq. (6), one can derive an expression for the coherent differential energy spectrum. By applying Parseval's theorem one can express the total energy radiated through a z = z0 plane in the far-field as

with E given by Eq. (6). By introducing dkx dky = 2πk⊥ dk⊥ = k2 cos θdΩ it can be shown that

The coherent contribution to the energy are those summation terms where j ≠ m. For N1/2 >> 1 (the ratio of the coherent to incoherent field amplitudes) one can introduce an electron beam distribution f (r,u) and a momentum distribution g(u) = ∫d3rf (r,u), with normalization ∫d3rduf (r,u) = 1. The coherent differential energy spectrum can then be written as

where the angular brackets indicate an average over momentum distribution g(u), D is given by Eq. (7), and the spatial form factor F is given by

For a single electron (N = 1), incident on a boundary with infinite radial extent, it follows that D = F = 1, and Eq. (10) reduces to the well-known result (Ginzburg & Frank, 1946; Ter-Mikaelian, 1972)

Although the above analysis is valid for an arbitrary distribution f (r,u), the remainder of this paper will consider an uncorrelated Gaussian distribution, such that f (r,u) = f (r⊥,z,u) = fz′(z) f⊥′(r⊥)g(u), where fz′(z) and f⊥′(r⊥) are longitudinal and transverse Gaussian distributions [characterized by root-mean square (rms) length and radius, σz and σr, respectively]. For this special case, the form factor is

provided that σr sin θ << σz, where typically θ < 1.

2.2. Temporal electric field profile of coherent diffraction limited transition radiation

The inverse spatial Fourier transform of Eq. (6), substituting the summation with an integral over the distribution function f (r,u), yields

where k⊥ = (ω/c)sin θ. Integrating over φ, where dkx dky = k⊥ dk⊥ dφ, Eq. (14) reduces to

In the far-field, where x⊥·k⊥ >> 1, the Bessel function can be approximated using the asymptotic expansion J0(k⊥ x⊥) ≃ (2/πk⊥ x⊥)1/2 cos(ık⊥ x⊥ − ıπ/4) and the electric field becomes

with

, where H(k⊥) is the Heaviside function [i.e., H(x) = 1 for x ≥ 1 and zero for x < 0] .

Since the imaginary part of the exponent in the first integral of Eq. (16) has a maximum value at k⊥* = kx⊥ /R, the method of stationary phase (Mandel & Wolf, 1995) can be applied. This method approximates the integral by evaluating the integrand around k⊥ = k⊥* (such that k⊥*/k = sin θ = x⊥ /R). Since the imaginary part of the exponent in the second integral of Eq. (16) peaks at k⊥* = −kx⊥ /R, the contribution of this integral can be neglected. Applying the method of stationary phase, the integral in Eq. (16) can be evaluated in the far-field limit (kR >> 1), and has the solution

The temporal electric field for any given electron momentum distribution in the far-field is given by the inverse Fourier-transform integral

where k = ω/c. For a Gaussian form factor F = FG = exp[−(ωσz /v)2/2] ,

with the normalizations ν = βρ/(uσz), τ = β(ct − R)/σz, and η = kσz /β. The parameter ν can be interpreted as the ratio of the long wavelength cut-off in the spectrum due to diffraction (∼βρ/u) to the short wavelength cut-off due to coherence effects (∼σz).

3. RADIATION TEMPORAL WAVEFORMS

In this section, Eq. (18) is examined to determine the resulting temporal waveforms in various parameter regimes. In particular, the dependence of the temporal shape on the normalized momentum u, observation angle θ, transverse dielectric size ρ, and longitudinal electron beam momentum distribution are discussed.

3.1. Infinite transverse boundary

The simplest parameter regime is the case of a single electron (N = 1) passing a boundary with infinite extent (ρ → ∞ such that D = 1). Since there are no bunch effects considered (σz = 0), the form factor reduces to F = 1. With F = 1 and D = 1, it can be shown that Eq. (18) yields

Although the spectrum of this delta function solution contains all frequencies, any physical system will have a long wavelength cut-off due to the physical dimensions of the system, and, for sufficiently high frequency radiation, the assumption of a perfectly conducting dielectric will no longer be valid, providing a short wavelength cut-off.

The above single-electron case can be extended to consider an electron bunch of finite duration. For the case of a Gaussian charge distribution FG crossing a dielectric with an infinite transverse boundary (ρ → ∞ such that D = 1) the expression for the electric field is

with τ = β(ct − R)/σz. In this case, the form-factor FG introduces a high frequency cut-off.

It is interesting to note that Eqs. (20) and (21) are sub-cycle pulses and are therefore unphysical. One consequence is the violation of the Lawson-Woodward-Palmer Theorem (Lawson, 1979; Palmer, 1980), which states that any electromagnetic pulse in vacuum must satisfy

. These unphysical waveforms are the result of the unbounded transverse extent of the dielectric (ρ → ∞). This absence of a long wavelength cut-off allows a DC-component in the spectrum. As shown below, for finite ρ (i.e., D ≠ 1 and diffraction effects are included), the temporal waveform becomes single-cycle with

. Although the spectrum of Eq. (21) has a DC-component, in the large transverse boundary limit b >> 1, Eq. (21) well approximates the transition radiation [with an error of order ∼exp(−b)] .

3.2. Finite transverse boundary and ultra-relativistic beam

In the limit b = kρ/u << 1 (e.g., an ultra-relativistic electron beam with u >> 1), the diffraction function D can be approximated as D ≃ (2 + u2 sin2 θ)b2/4. In this limit (b << 1), integrating Eq. (18) yields

where a Gaussian bunch distribution (FG) is assumed. As can been seen from Equation (22), for a mono-energetic beam, the length of the waveform (i.e., the rms radiation pulse length) is not a function of ρ in this limit. Eq. (22) predicts a single-cycle pulse and satisfies

.

3.3. Waveform for mono-energetic electron beams

In this section, the general solution to Eq. (18) for the electric field of a mono-energetic electron beam is examined numerically. Figures 1(a) and 1(b) show the electric field in both the time domain and frequency domain, respectively, for the parameters u = 10 and θ = 0.1 rad. Here the parameter ν = βρ/(uσz) is varied, while u sin θ is kept constant. The solid curve represents ν = 1.2 (ρ/σz = 12), the dashed curve ν = 0.4 (ρ/σz = 4), and the dotted curve ν = 0.1 (ρ/σz = 1). One can calculate the normalized rms pulse length (στ = βcσt /σz, where σt is the radiation pulse duration) and the normalized frequency bandwidth (

, where σf is the spectral bandwidth). For the radiation pulses shown in Figure 1, στ = 2.59, 1.75, and 1.24, and

, for the solid, dashed, and dotted curves, respectively. As the ratio ρ/σz decreases, low frequency components in the spectrum are reduced and the spectral distribution changes its shape, resulting in an increase of spectral bandwidth. Therefore, one can observe a reduced normalized pulse length for smaller ρ/σz.

Normalized electric field in time-domain (a) and frequency domain (b) for the parameters u = 10, θ = 0.1, and ρ/σz = 12 (solid curve), 4 (dashed curve), and 1 (dotted curve).

Figure 2 shows the electric field in time and frequency domains for the parameters ν = 3 and u = 10. Here the parameters ν and u are fixed, while the observation angle θ is varied. The solid curve represents θ = 0.04, the dashed curve θ = 0.2, and the dotted curve θ = 0.3. Since the angular distribution has a maximum at a specific angle θmax, one can see a lower electric field for both the θ = 0.04 as well as the θ = 0.3 case. For a relativistic electron bunch passing through an infinite boundary, this specific angle is given by θmax ≃ 1/u, but for finite boundaries this angle is also a function of boundary size. The root-mean square for the normalized pulse length (στ) and the normalized frequency bandwidth

for the pulses shown in Figure 2 are στ = 1.45, 2.01, and 2.46, and

, for the solid, dashed, and dotted curves, respectively. For larger observation angles, diffraction effects decrease the width of the spectral distribution and the pulse length increases.

Normalized electric field in time-domain (a) and frequency domain (b) for the parameters ν = βρ/(uσz) = 3, u = 10, and θ = 0.04 (solid curve), 0.2 (dashed curve), and 0.3 (dotted curve).

One can see in Figure 3 the effects of a variation in the mono-energetic beam momentum. The curves represent fixed parameters σz, ρ, and θ (and therefore νu sin θ is constant), but with ν and u sin θ varying: (ν,u sin θ) = (3, 2) for the solid curve, (6, 1) for the dashed curve, and (12, 0.5) for the dotted curve. For sin θ = 0.1, the three cases refer to u = 30 for the solid curve, u = 10 for the dashed curve, and u = 5 for the dotted curve. The normalized rms pulse length (στ) and the normalized frequency bandwidth (

) are calculated for each case, yielding στ = 2.09, 2.00, and 2.21, and

, for the solid, dashed, and dotted curves, respectively. For each choice of the ratio ρ/σz, there is specific umax for which the spectral bandwidth is maximized, resulting in the shortest pulse. For the parameters of Figure 3, this value is found to be umax ≃ 15. Therefore, for both the u = 5 and the u = 30 case, a small increase in pulse length is observed compared to the more optimized u = 10 case.

Normalized electric field in time-domain (a) and frequency domain (b) for fixed νu sin θ = (βρ sin θ)/σz with u = 30 (solid curve), 10 (dashed curve), and 5 (dotted curve).

3.4. Waveform for various momentum distributions

To demonstrate the effect of electron momentum distribution on the electric field waveform, three distributions are considered in this section. Figure 4 displays the waveforms for a Boltzmann momentum distribution, g(u) = (1/utemp)exp(−u/utemp) with temperature utemp = 10 (solid curve), a Gaussian momentum distribution,

with mean umean = 10 and spread urms = 3 (dashed curve), and a mono-energetic momentum distribution, g(u) = δ(u − um) at um = 10 (dotted curve). One can see that the pulse shape is fairly insensitive to the type of momentum distribution. Furthermore, the amplitude of the electric field is weakly influenced by the various momentum distributions.

Normalized electric field in time-domain (a) and frequency domain (b) for the parameters ν = βρ/(uσz) = 6 and u sin θ = 1. The solid line represents a Boltzmann distribution with utemp = 10, the dashed line a Gaussian momentum distribution centered at umean = 10 and urms = 3 and the dotted line represents a mono-energetic bunch at u = 10.

4. SUMMARY AND DISCUSSION

In this paper, the theoretical understanding of diffraction-limited coherent transition radiation (DLTR) has been extended to the time-domain. For arbitrary charge and longitudinal momentum distributions of the electron bunch the spatiotemporal electric field is calculated. The model considers electrons that are incident normal to a sharp (step function) metal-vacuum boundary with finite transverse dimension. The form-factor F of the electron bunch, which is equivalent to the Fourier transform of the charge distribution, and the diffraction function D, determine the spectrum of the electric field. Coherence effects (F) determine the high frequency cut-off, while diffraction effects (D) determine the low frequency cut-off. For a Gaussian charge distribution, characterized by the rms length σz, the coherent electric field in the temporal domain is a single-cycle structure. The pulse shape solely depends on the parameters ν = βρ/(σzu) and u sin θ, while the amplitude of the radiation is a function of ρ/σz, u, and θ. Analysis shows that, for a given mono-energetic momentum distribution, the shortest normalized waveforms are realized at small angles of observation and small values for ρ/σz. The total radiated energy is maximized for a large ratio ρ/σz and a beam with high mean longitudinal momentum.

Recent experiments on DLTR from laser-wakefield accelerated electron beams (Leemans et al., 2003), indicate that a typical bunch contains N = 1010 electrons (1.6 nC), with a mean momentum u = 10 and a bunch length of σz = 10 μm. Since the boundary size is on the order of 500 μm (ν ≃ 5,) the peak electric field, observed at an angle of θ = 0.1 and R = 15 cm from the source, is found to be on the order of 30 kV/cm. Calculation of the root-mean square σt of the waveform yields σt = 63 fs. Future experimental research on this laser-plasma driven radiation source is planned.

ACKNOWLEDGMENTS

This work was supported by the U.S. Department of Energy under Contract No. DE-AC03-76SF0098. J. van Tilborg would like to thank the Techische Universiteit Eindhoven, The Netherlands.

Footnotes

This paper was delivered at the International Workshop on Laser and Plasma Accelerators, held at Portovenere, Italy, September 29 to October 3, 2003.

References

REFERENCES

Bromage, J., Walmsley, I.A. & Stroud, C.R. Jr. (1999). Direct measurement of a photoconductive receiver's temporal response by dithered-edge sampling. Opt. Lett. 24, 1771–1773.Google Scholar
Budiarto, E., Margolies, J., Jeong, S., Son, J. & Bokor, J. (1996). High-intensity terahertz pulses at 1-kHz repetition rate. IEEE J. Quantum Electron. 32, 1839–1846.Google Scholar
Catravas, P., Leemans, W.P., Esarey, E., Zolotorev, M., Whittum, D., Iverson, R., Hogan, M. & Walz, D. (1999). Beam profile measurement at 30 GeV using optical transition radiation. Proc. Part. Accel. Conf., 2111–2113.
Cornacchia, M., Arthur, J., Bentson, L., Carr, R., Emma, P., Galayda, J., Krejcik, P., Lindau, I., Safranek, J., Schmerge, J., Stohr, J., Tatchyn, A. & Wootton, A. (2001). A Sub-Picosecond Photon Pulse Facility for SLAC. Report No. SLAC-PUB-8950. Stanford Linear Accelerator Center.
Ferguson, B., Wang, S., Gray, D., Abbot, D. & Zhang, X.-C. (2002). T-ray computed tomography. Opt. Lett. 27, 1312–1314.Google Scholar
Ginzburg, V.L. & Frank, I.M. (1946). To the Theory of Transition Radiation. Sov. Phys. JETP 16, 15.Google Scholar
Jackson, J.D. (1975). Classical Electrodynamics. New York: Wiley
Kung, P., Lihn, Hung-chi, Wiedeman, H. & Bocek, D. (1994). Generation and measurement of 50-fs (rms) electron pulses. Phys. Rev. Lett. 73, 967–970.Google Scholar
Lawson, J.D. (1979). Lasers and accelerators. IEEE Trans. Nucl. Sci. NS-26, 4217–4219.Google Scholar
Leemans, W.P. (1997). Electron beam monitoring at high frequencies and ultra-fast time scales. Proc. Advanced Accelerator Conf. AIP 398, 23–39.
Leemans, W.P., Geddes, C.G.R., Faure, J., Toth, Cs., van Tilborg, J., Schroeder, D.B., Esarey, E., Fubiani, G., Auerbach, D., Marcelis, B., Carnahan, M.A., Kaindl, R.A., Byrd, J. & Martin, M.C. (2003). Observation of terahertz emission from a laser-plasma accelerated electron bunch crossing a plasma-vacuum boundary. Phys. Rev. Lett. 91, 074802/1–4.Google Scholar
Le Sage, G.P., Cowan, T.E., Fiorito, R.B. & Rule, D.W. (1999). Transverse phase space mapping of relativistic electron beams using optical transition radiation. Phys. Rev. ST Accel. Beams 2, 122802/1–7.Google Scholar
Li, M., Cho, G.C., Ju, T.M., Zhang, X.-C., Wang, S.Q. & Kennedy, J.T. (1999). Time-domain dielectric constant measurement of thin film in GHz-THz frequency range near the Brewster angle. Appl. Phys. Lett. 74, 2113–2115.Google Scholar
Lu, Z.G., Campbell, P. & Zhang, X.-C. (1997). Free-space electro-optic sampling with a high repetition-rate regenerative amplified laser. Appl. Phys. Lett. 71, 593–595.Google Scholar
Lumpkin, A.H., Dejus, R., Berg, W.J., Borland, M., Chae, Y.C., Moog, E., Sereno, N.S. & Yang, B.X. (2001). First observation or z-dependent electron-stream microbunching using coherent transition radiation. Phys. Rev. Lett. 86, 79–82.Google Scholar
Mandel, L. & Wolf, E. (1995). Optical Coherence and Quantum Optics. New York: Cambridge University Press.
Mittleman, D.M., Gupta, M., Neelamani, R., Baraniuk, R.G., Rudd, J.V. & Koch, M. (1999). Recent advances in terahertz imaging. Appl. Phys. B 8, 1085–1094.CrossRefGoogle Scholar
Orenstein, J. & Millis, A.J. (2000). Advances in the physics of high-temperature superconductivity. Science 288, 468–474.CrossRefGoogle Scholar
Palmer, R.B. (1980). A laser-driven grating LINAC. Part. Accel. 11, 81–90.CrossRefGoogle Scholar
Ricci, K.N. & Smith, T.I. (2000). Longitudinal electron beam and free electron laser microbunch measurements using off-phase rf acceleration. Phys. Rev. ST Accel. Beams 3, 032801/1–4.Google Scholar
Schroeder, C.B., Esarey, E., van Tilborg, J. & Leemans, W.P. (2004). Theory of coherent transition radiation generated at a plasma-vacuum interface. Phys. Rev. E 69, 016501/1–12.Google Scholar
Shibata, Y., Takahashi, T., Kanai, R., Ishi, K., Ikezawa, M., Ohkuma, J., Okuda, S. & Okada, T. (1994). Diagnostics of an electron beam of a linear accelerator using coherent transition radiation. Phys. Rev. E 50, 1479–1484.Google Scholar
Tae-In, Jeon & Grischkowski, D. (1997). Characterization of optically dense, doped semiconductors by reflection THz time domain spectroscopy. Phys. Rev. Lett. 78, 1106–1109.Google Scholar
Ter-Mikaelian, T.M. (1972). High-energy electromagnetic processes in condensed media. New York: Wiley.
Yan, X., MacLeod, A.M., Gillespie, W.A., Knippels, G.M.H., Oepts, D., van der Meer, A.F.G. & Seidel, W. (2000). Subpicosecond electro-optic measurement of relativistic electron pulses. Phys Rev. Lett. 85, 3404–3407.CrossRefGoogle Scholar
Zhang, X.-C., Hu, B.B., Darrow, J.T. & Auston, D.H. (1990). Appl. Phys. Lett. 56, 1011–1013.
Figure 0

Normalized electric field in time-domain (a) and frequency domain (b) for the parameters u = 10, θ = 0.1, and ρ/σz = 12 (solid curve), 4 (dashed curve), and 1 (dotted curve).

Figure 1

Normalized electric field in time-domain (a) and frequency domain (b) for the parameters ν = βρ/(uσz) = 3, u = 10, and θ = 0.04 (solid curve), 0.2 (dashed curve), and 0.3 (dotted curve).

Figure 2

Normalized electric field in time-domain (a) and frequency domain (b) for fixed νu sin θ = (βρ sin θ)/σz with u = 30 (solid curve), 10 (dashed curve), and 5 (dotted curve).

Figure 3

Normalized electric field in time-domain (a) and frequency domain (b) for the parameters ν = βρ/(uσz) = 6 and u sin θ = 1. The solid line represents a Boltzmann distribution with utemp = 10, the dashed line a Gaussian momentum distribution centered at umean = 10 and urms = 3 and the dotted line represents a mono-energetic bunch at u = 10.