Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T15:42:03.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Ablation of metals with picosecond laser pulses: Evidence of long-lived non-equilibrium surface states

Published online by Cambridge University Press:  07 June 2005

E.G. GAMALY ,
B. LUTHER-DAVIES ,
V.Z. KOLEV ,
N.R. MADSEN ,
M. DUERING  and
A.V. RODE
E.G. GAMALY
Affiliation:
Laser Physics Centre, Research School of Physical Sciences and Engineering, the Australian National University, Canberra, Australia Centre for Ultra-high Bandwidth Devices for Optical Systems, Australian National University, Canberra, Australia
B. LUTHER-DAVIES
Affiliation:
Laser Physics Centre, Research School of Physical Sciences and Engineering, the Australian National University, Canberra, Australia Centre for Ultra-high Bandwidth Devices for Optical Systems, Australian National University, Canberra, Australia
V.Z. KOLEV
Affiliation:
Laser Physics Centre, Research School of Physical Sciences and Engineering, the Australian National University, Canberra, Australia Centre for Ultra-high Bandwidth Devices for Optical Systems, Australian National University, Canberra, Australia
N.R. MADSEN
Affiliation:
Laser Physics Centre, Research School of Physical Sciences and Engineering, the Australian National University, Canberra, Australia
M. DUERING
Affiliation:
Fraunhofer Institute for Laser Technique, Aachen, Germany
A.V. RODE
Affiliation:
Laser Physics Centre, Research School of Physical Sciences and Engineering, the Australian National University, Canberra, Australia Centre for Ultra-high Bandwidth Devices for Optical Systems, Australian National University, Canberra, Australia
Rights & Permissions [Opens in a new window]

Abstract

Experiments on laser ablation of metals in air, in vacuum, and in similar irradiation conditions, revealed that the ablation thresholds in air are up to three times lower than those measured in vacuum. Our analysis shows that this difference is caused by the existence of a long-lived transient non-equilibrium surface state at the solid-vacuum interface. The energy distribution of atoms at the surface is Maxwellian-like but with its high-energy tail truncated at the binding energy. We find that in vacuum the rate of energy transfer from the bulk to the surface layer to build the high-energy tail, which determines the lifetime of this non-equilibrium state, exceeds other characteristic timescales such as the surface cooling time. This prohibits thermal evaporation in vacuum for which the high-energy tail is essential. In air, however, collisions between the gas atoms and the surface markedly reduce the lifetime of this non-equilibrium surface state allowing thermal evaporation to proceed before the surface cools. It was experimentally observed that the difference between the ablation depth in vacuum and that in air disappears at the laser fluencies 2–3 times in excess of the vacuum threshold value. The material removal at this level of the deposited energy density attains the features of the non-equilibrium ablation similar for both cases. We find, therefore, that the threshold in vacuum corresponds to non-equilibrium ablation during the pulse, while thermal evaporation after the pulse is responsible for the lower ablation threshold observed in air. This paper provides direct experimental evidence of how the transient surface effects may strongly affect the onset and rate of a solid-gas phase transition.

Keywords

AblationNon-equilibrium surface phenomenaPicosecond lasers
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 2 , June 2005 , pp. 167 - 176
Copyright
2005 Cambridge University Press

1. INTRODUCTION

Many experimental and theoretical studies of the ablation threshold and the ablation rate for metals irradiated with short laser pulses clearly demonstrate the presence of two different ablation regimes depending on the pulse duration (Corkum et al., 1988; Stuart et al., 1995, 1996; Nolte et al., 1997; Du et al., 1994; Perry et al., 1999; Malvezzi et al., 1986; Luther-Davies et al., 1992; Eidmann et al., 2000; Gamaly et al., 2002, Semerok et al., 2002; DiBernardo et al., 2003; Ying et al., 2003). For pulses longer than about 100 ps, the surface temperature is determined by the thermal diffusivity of the material, and hence the ablation proceeds in equilibrium conditions. The threshold fluency Fthr, increases with pulse duration, tp, according to the relation Fthr ∝ tp1/2. However, for sub-picosecond pulses ablation proceeds in non-equilibrium conditions because the pulse duration is shorter than both the electron-to-lattice energy transfer time, which is in the order of 1–10 ps, as well as the electron heat conduction time. Hence, the electrons cool without transferring energy to the lattice (Perry et al., 1999; Malvezzi et al., 1986; Luther-Davies et al., 1992; Eidmann et al., 2000; Gamaly et al., 2002). In this regime, the ablation threshold becomes independent of the pulse duration. However, the transition observed experimentally from the ablation threshold expected for the non-equilibrium regime to the thermal regime occurs at unexpectedly large pulse durations, for example, up to ∼100 ps in gold (Stuart et al., 1996; Gamaly et al., 2002). This indicates that for some reason, which is not yet fully understood, the thermal mechanism does not contribute to the ablation rate at fluencies near threshold, as might be expected, even when the pulse-width is up to 10 times longer than the electron-lattice equilibration time (Corkum et al., 1988; Stuart et al., 1996).

In this paper, we report experiments using intermediate duration pulses, 12-ps long, which show that in the same laser illumination conditions the ablation thresholds of metal targets irradiated in air are significantly lower than when the same targets are irradiated in vacuum. To explain this observation, we have developed a model of the single pulse ablation process that indicates that equilibration of the electron and lattice “temperatures” is not the only timescale that must be taken into account. Additionally, the time to establish the high-energy tail of the Maxwellian energy distribution of atoms at the surface must be considered. Specifically, in vacuum, the time needed to transfer energy from the high-energy Maxwellian tail from atoms in the bulk to the atomic layer at the surface (bulk-to-surface energy transfer time tb-s), becomes the crucial parameter that determines the relative contribution of equilibrium (thermal) evaporation and non-thermal ablation to the material removal rate, especially near the ablation threshold. Our analysis, therefore, suggests that thermal ablation will only dominate when the pulse duration is comparable to or longer than the bulk-to-surface energy transfer time. The presence of air speeds up the creation of the Maxwellian distribution at the surface, in effect increasing the role of thermal evaporation, and leading to a reduction in the ablation threshold. Our results may be useful in explaining transition from short pulse to the long pulse ablation regime reported for different materials.

In this paper we first present experimental results on ablation of aluminum, copper, steel, and lead in air and in vacuum using 12 ps 532 nm pulses generated by a 50-W, 4.1 MHz mode-locked Nd:YVO4 laser. We analyze the ablation mechanisms near and above the ablation threshold for these intermediate duration pulses. We demonstrate for the first time, to our knowledge, the importance of the time needed to transfer energy from the high-energy tail of the Maxwellian distribution created in the bulk to the non-equilibrium surface layer in laser ablation with short pulses. We develop a general theoretical model of laser ablation near and above the ablation threshold, based on the process of energy delivery to the atomic surface layer, and applied it to the ablation conditions. The theoretical model is shown to be in good agreement with the experimental data.

2. EXPERIMENTAL RESULTS

2.1. Experimental conditions

The ablation experiments were carried out with laser pulses generated by a 50 W long-cavity mode-locked Nd:YVO4 laser (Kolev et al., 2003; Luther-Davies et al., 2004) using a number of Al, Cu, steel (Fe), and Pb targets. The samples were exposed to 12 ps 532 nm pulses at a pulse repetition rate of 4.1 MHz; the energy per pulse on the target surface was Ep = 6.5 μJ. The use of second harmonic of the fundamental radiation in combination with a number of wavelength separating mirrors guaranteed very high energy contrast of the laser beam, which is important for the ablation experiments near the threshold.

Two sets of experiments were performed: one with the targets in air, and the other in a vacuum of ∼5 × 10−3 Torr. The energy per pulse and the pulse duration were fixed, while the energy density (fluency) was varied by moving the samples away from the focal plane of a 300 mm focusing lens so that the illuminated area was changed from Sf,min = 4.9 × 10−6 cm2 (df = 25 μm FWHM) to Sf,max = 1.2 × 10−4 cm2 (df = 124 μm). This corresponded to a span of fluencies from 5.4 × 10−2 J/cm2 to 1.3 J/cm2 (or, of intensities from 4.2 × 109 W/cm2 to 1.0 × 1011 W/cm2).

To ensure uniformity and to avoid drilling craters in the target material, the beam was scanned with X and Y oscillating mirrors operating at 61 and 59 Hz, respectively, over an area of approximately 17 × 13 mm2. This led to quasi-homogeneous scanning over the ablated area by creating a Lissajous scan pattern.

2.2. Ablation mass, depth and ablation thresholds

Total amount of material ablated over a 60-s period in the ablation experiments was measured by weighting the sample with the accuracy ±10−4 g before and after the ablation. The ablated mass per single pulse, mav, was determined by averaging the mass difference over the 2.46 × 108 pulses. We introduce the ablation depth per single pulse as the follows:

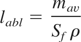
where ρ is the target mass density and Sf is the focal spot area. The measured ablation depths for various ablated materials as a function of the incident laser fluency are shown in Figure 1.

Ablation depth per pulse vs. fluency for (a) Al; (b) Cu; (c) Fe; and (d) Pb in experiments in air (triangles) and in vacuum (circles) using 12 ps 4.1 MHz repetition rate laser. The horizontal lines and the numbers above the lines correspond to inter-atomic distances, while the arrows indicate the ablation threshold. The dashed lines are the upper limits for the ablated depth determined using the energy conservation law.

The ablation threshold was determined as the energy density needed to remove a single atomic surface layer. The threshold introduced by this condition can be justified by comparing the experimental and theoretical results for non-equilibrium ablation using femtosecond pulses (Gamaly et al., 2002). The ablation threshold fluency, Fthr, derived in this manner from the experimental data for different metals is presented in Table 1. We note that the threshold for Cu in vacuum, for example, of 0.41 ± 0.05 J/cm2 is in good agreement with the results of Nolte et al. (1997) (Fthr = 0.375 J/cm2 for 9.6 ps and 0.423 J/cm2 for 14.4 ps pulses).

Threshold fluence for ablation of metals by 12-ps pulses measured in air and in vacuum. In last row is the calculated threshold (see Section 3.7)

Table 1 show that for all the metals studied the ablation threshold in air was found to be noticeably lower than in vacuum. We consider below the physical processes during the pulse and after the end of the pulse in order to understand the influence of air on the ablation rate.

3. DISCUSSION

Two qualitatively different ablation mechanisms must be considered for the intermediate range pulse duration used in these experiments: one is non-thermal ablation; the other is thermal evaporation. Non-thermal ablation occurs when the surface atoms gain an average energy (T) from the laser greater or equal to the binding energy, εb. In such conditions, atoms from the outermost surface layer can leave the surface with kinetic energy equal to T − εb. Note that non-thermal ablation ceases to exist when T < εb. In such conditions, only thermal ablation occurs which involves the escape of atoms whose energy exceeds εb from the high-energy tail of the Maxwellian distribution.

The contribution of thermal evaporation and non-thermal ablation to the total material removed from the surface essentially depends on the duration of the processes of the energy exchange between the electrons and ions (lattice) that is calculated below.

3.1. Electron-to-ion energy-transfer time

The effective electron-ion collision frequency νei for momentum transfer at the electron temperature of a few eV is in the order of magnitude of the electron plasma frequency ωpe: νei ≅ ωpe (Eidmann et al., 2000). The time for energy transfer from electrons to ions is expressed as ten = (νeime /mi)−1. This time, along with the thermal diffusion time tth ≅ ls2/D, for the metal targets used in the experiments is shown in Table 2. It is evident that in all metals except Pb almost all the absorbed laser energy is already transferred to the ions by the end of the 12-ps pulse.

Time for the energy transfer from electrons to the lattice, and thermal diffusion rate

3.2. Temperature in the skin-layer during the pulse

The temperature in the skin-layer during a single laser pulse is calculated using a two-temperature approximation while the heat conduction can be neglected (Kaganov et al., 1957):

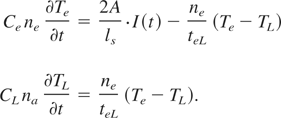
Here, ne and na are, respectively, the electron and the atomic number density, Ce and CL are the heat capacity of the electrons and of the atoms in the lattice, A is the absorption coefficient, ls = c/ωκ is the skin depth (ω is the laser light frequency; κ is the imaginary part of the refractive index; c is the speed of light in vacuum); and I(t) is the laser pulse intensity that has the Gaussian time shape.

The specific heat of degenerate electrons is conventionally expressed as follows (Kittel, 1996):

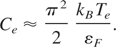
The specific heat for lattice is equal to 3kB per atom at low temperature (T < εb) while at higher temperature, T ≥ εb, is equal to 3kB/2 per atom.

The electron and lattice temperatures in the surface layer for each metal were calculated by the numerical integration of Eq. (4) at the experimentally determined threshold fluency from Table 1 (see Fig. 2).

Calculated electron and lattice temperature in the skin-layer at the ablation threshold in Al, Cu, Fe, and Pb in vacuum and in air, together with the Gaussian profile of the 12-ps laser pulse.

It can be seen from the results that the maximum surface temperature in vacuum is close to the binding energy, thus we can conclude that ablation of metals in vacuum at the ablation threshold starts as a non-equilibrium process. However, the ablation in air starts at a temperature about half the binding energy for Al, Cu, Fe, and 10 times lower for Pb. This is a clear indication of the dominance of the thermal mechanism of evaporation in air. In order to understand the difference we will analyze the energy transfer from the bulk of the heated material to the outermost atomic surface layer where removal of atoms begins. It is also instructive to revisit the conditions and formulae for conventional evaporation in thermodynamic equilibrium, and compare them to the conditions during and after the pulse.

3.3. Thermal evaporation in equilibrium conditions

The pressure, temperature, and chemical potential for both phase states coincide at the solid-vapor interface in conditions of evaporation in equilibrium (Landau & Lifshitz, 1980). The thermal evaporation rate is then defined as follows:

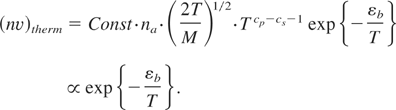
Here cp is a specific heat at a constant pressure for the vapor, cp = cv + 1 = 5/2 (for mono-atomic gas), 3/2 ≤ cs ≤ 3 is the specific heat for a solid (both in units of the Boltzmann constant kB), depending on density; and εb is the heat of evaporation per atom or the binding energy. In conditions close to the critical point, one can take cp − cs ≅ 1. The number density of evaporating atoms in (6), na·exp{−εb /T} coincides with that in the high-energy tail (εb > T) in condition when εb /T ≥ 9 in correspondence to the fact that the equilibrium boiling temperature for majority of solids constitutes Tboil ∼ 0.1εb.

We demonstrate below that these equilibrium formulae can be applied to the ablation by short laser pulses only after the time needed to establish both the main part as well as the high-energy tail of the Maxwellian energy distribution.

3.4. Time to establish the Maxwellian energy distribution in the bulk of a solid

We estimate the time needed to establish a Maxwellian distribution at temperature near, (1/3–1/2) εb, and below the experimentally observed threshold.

The atom-to-atom collision time in a neutral solid is conventionally estimated as tcoll ≅ (naσ0v)−1 ≅ (5 × 1022 cm−3 × 10−15 cm2 × 105 cm/s)−1 ≅ 0.2 × 10−12 s (here σ0 = πr02 ∼ 10−15 cm2 is the cross-section for atomic collisions, and r0 is the atomic radius). Alternatively, in the heated solid density plasma the collision time reads tcoll-p ∼ (nσplv)−1 ∼ T3/2 (Kruer, 1987). Both these times, tcoll and tcoll-p, correspond to the main part of the Maxwellian distribution, tcoll ∼ tmain. However, it was found a long time ago (MacDonald et al., 1957) that the time needed to establish the high-energy tail of the equilibrium distribution in plasma can be estimated for a particular energy in a tail, ε >> T, as ttail ∼ tmain(ε/T)3/2 >> tmain.

In the conditions of our experiments, the temperature is around T ∼ eV. At T ∼1 eV the degree of ionization is only ∼10%. Therefore, we will estimate the time to create the high-energy tail in a neutral solid in conditions where Tmelt << T << εb. The solid is in a disordered state at T >> Tmelt. Thus, the inter-atomic energy exchange occurs due to random collisions. In order to increase the energy of an atom from T to εb, the atom should experience N = εb /ΔT isotropic and statistically independent collisions, each of which increases the atom's energy from T to T + ΔT (ΔT = T/n << T, n >>1). The probability of such energy increase is expressed as follows:

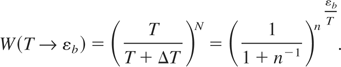
In the limit of n >> 1, that is, taking into account that limn→∞(1 + n−1)n = e, the above formula attains the recognizable equilibrium features:

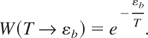
Now, the cross-section to reach energy εb in the conditions T << εb takes the following form:

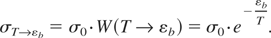
The time to establish the high-energy tail in isotropic conditions characteristic of a bulk solid which has undergone an instantaneous rise in temperature to T << εb then reads:

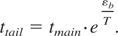
Taking, for example, the average temperature in the skin layer of ∼1 eV, which is close to the threshold conditions with 12-ps pulses, and the binding energy of ∼3 eV, the high-energy Maxwellian tail is established in the bulk in a time of about 20tmain ∼ 4 ps (taking tmain ∼ 0.2 ps).

3.5. Time for the energy transfer from the bulk to the outermost surface layer

The atoms in the outermost surface layer next to the vacuum are in fact in a quite different condition compared to the atoms in the bulk. It is well known that the surface atoms are loosely bound to the bulk making part of bonds dangling or saturated with foreign atoms (Zangwill, 1988; Prutton, 1994). The effects of different bonds leads to decreases in the Debye and melting temperatures; to changes in the bond length and inter-atomic distance as well as the crystalline structure and nature and rate of any phase transition. Moreover, Prutton (1994, p. 155) noticed: “… many surface phases are actually metastable, that is, the surface is not in a true thermodynamic equilibrium.”

This is particularly true in relation to the appearance of the high-energy tail in the energy distribution at ε > εb (while T < εb) of laser-heated atoms in the outermost surface layer. These atoms will immediately leave the solid if their energy instantaneously increases in excess of the binding energy. This is the process of non-equilibrium ablation (Gamaly et al., 2002). Therefore, the presence of the free surface prevents the equilibrium from being established in the surface layer itself, whose thickness is comparable to the mean free path for atomic collision. This thickness is also close to the thickness of a mono-atomic layer. Thermal evaporation from the surface heated to a temperature below the binding energy can, therefore, only proceed when energy is supplied to the surface from the bulk via atom-atom collisions. Thus, the time for the energy to increase from ε = T < εb to ε ≥ εb in the surface layer (that is, the bulk-to-surface energy transfer time, tb-s, and correspondent probability) determines the onset of the thermal evaporation at solid-vacuum interface. The probability of energy transfer from the bulk to the surface can be found from a solution of the time-dependent 2D kinetic equation, which is a formidable problem! However, one can make a reasonable estimate as follows.

It is clear that the probability of the energy transfer in the excess of εb from atoms in the bulk to those at the surface should be lower than that in the bulk due to a decrease in the number of close neighbors capable for such an energy transfer. Indeed, the number of close neighbors equals to six in a closely packed solid. However, any surface atom has only one closest neighbor atom in the bulk while the other four closest neighbors are themselves surface atoms. Therefore, the number of collisions leading to the energy increase in a surface atom, Nsurf, should be larger compared to that in the bulk, Nsurf ∼ b × Nbulk. The decrease in the number of close neighbors allows the above coefficient to be estimated as b ∼ 6. Now using the same arguments as in deriving formulae (7)–(10), one can arrive to the following estimate for the cross-section for the bulk-to-surface energy transfer:

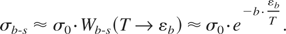
The bulk-to-surface energy transfer time thus reads:

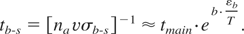
According to Eq. (12), the bulk-to-surface energy transfer time increases dramatically with decreasing temperature. For example, at T ∼ εb /2 tb-s ≈ 1.6 × 105tmain ∼3 × 104 ps. Hence one can see that the bulk-to-surface energy transfer time exceeds markedly the electron-to-lattice thermalization time, and the heat conduction time at fluencies that are below the threshold for nonthermal ablation. In other words, as the surface starts to cool by thermal conduction, the bulk-to-surface energy transfer time increases to such an extent that it makes it impossible for the surface atoms to gain energy above the binding energy. Hence thermal evaporation does not occur.

3.6. Contribution of thermal evaporation at t > tb-S

The total ablation is the sum of contributions from non-equilibrium mechanism at t < tb-s and thermal ablation at t > tb-s if the threshold condition for the nonthermal ablation in vacuum is achieved. The outermost atomic layer, where Tmax ∼ εb, is removed, thus the ablation depth due to non-thermal mechanism equals the thickness of atomic mono-layer, d. Thermal ablation starts after a time tb-s when the energy in excess of the binding energy is delivered to the surface layer from the bulk through atomic collisions. The depth of material removed by thermal evaporation can be expressed through the time- and space-dependent distribution function as follows:

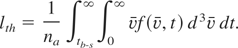
The transient distribution function differs from that in equilibrium only by the high-energy tail. Therefore, the average density and the average velocity are close to their equilibrium values. The number density of evaporating atoms (analogous to the saturated density of vapor in equilibrium) can be approximated as n ≈ na·exp(−b·εb /T). Then the evaporation depth in Eq. (13) is expressed as follows:

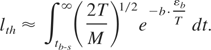
The temperature decreases in accordance with linear heat conduction as T = Tb-s·(tb-s /t)1/2; Tb-s ≡ T(tb-s). Then, Eq. (14) can be immediately integrated to obtain:

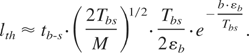
A conservative estimate of Tbs = Tm(tth /(tth + tb-s))1/2 taking Tm ∼ εb; tb-s ∼ 80 ps; tth ∼ 30 ps; v ∼105 cm/s, Tbs = 0.52Tm gives lth ∼ 2 × 10−11 cm << da. Thus, non-equilibrium ablation completely dominates thermal evaporation. Thus, we conclude that in vacuum thermal evaporation at the ablation threshold and below that threshold are completely negligible.

3.7. Ablation threshold in vacuum

The threshold laser fluency for non-thermal ablation can be defined from the condition that the temperature at the end of the pulse equals to the binding energy (Gamaly et al., 2002):

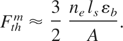
The optical parameters of metals at room temperature are well documented (Bass et al., 2001). However, atoms in the surface skin layer are partially ionized at the temperatures near the ablation threshold, hence the optical properties such as absorption, skin depth, can change, and are difficult to measure during and after the laser pulse (von der Linde & Schuler, 1996; Uteza et al., 2004). We, therefore, calculate these optical properties assuming the existence of hot plasma in the surface layer. These calculations are in agreement with more complicated computer simulations (T. Itina, Private Communication, 2004), which take into account two-temperature hydrodynamics and transient absorption changing from the cold metal to plasma during the laser pulse. The calculated ablation thresholds for a single 12-ps laser pulse (λ = 532 nm) are presented in the last row of Table 1.

The calculated threshold values for Al and Cu are in reasonably close agreement with the experimental data in vacuum. The difference between the calculated single-pulse values and the data taken from the multiple-pulse experiments that is significant for Fe and Pb, most probably relates to the fact that our experiments can be affected by the cumulative action of successive laser pulses following. We will return to this point later. However, the most significant differences exist between the ablation thresholds in air and in vacuum. In order to understand these differences, we will consider how the presence of air can effect thermal evaporation that is the only process that can occur below the vacuum ablation threshold. The question is how is thermal evaporation “turned on” by the presence of air when we concluded it is negligible in vacuum?

3.8. Thermal ablation in air after the pulse

After the laser pulse, the air next to the heated surface layer gains energy through collisions with the solid target. This results in the establishment of a Maxwellian distribution in the air near the air-solid interface. Hence, it is possible for the air to play the same role as the saturated vapor in classical thermal evaporation. The presence of air introduces a new pathway allowing the creation of the high energy tail of the Maxwellian distribution in the surface layer augmenting the bulk-to-surface energy transfer process discussed earlier. Thus there are now three processes acting at the same time which determine the ablation conditions at the solid-air interface: (1) evolution of the atomic energy distribution at the surface due to air-solid collisions; (2) evolution of the atomic energy distribution at the surface due to bulk-to-surface energy transfer; and (3) cooling of the surface layer by heat conduction. Whereas we concluded that mechanism (2) was too slow to result in thermal evaporation when T < εb the role of the air could be to significantly increase thermalization at the surface allowing thermal evaporation to takes place after the air-solid equilibrium has become established. The ablation rate then can be calculated using thermodynamic phase equilibrium relations, which link the saturated vapor density (pressure) to the vapor temperature. Let's consider all these processes in sequence.

The air-solid equilibrium energy distribution is established by collisions of air molecules with the solid. The gas-kinetic mean free path in air in standard conditions is lg-k = 6 × 10−6 cm (Zel'dovich & Raizer, 2002). Therefore, the equilibration time teq needed to establish a Maxwellian distribution in the gas can be estimated as teq ∼ lg-k /vth ∼ 1.8 × 10−10 s, where vth is the average thermal velocity in air (vth = 3.3 × 104 cm/s). The bulk-to-surface energy transfer time calculated by Eq. (12) at the maximum temperature (Tmax ∼ εb/2) for conditions equal to the threshold fluency in air constitutes tb-s ≈ tmain·e12 ∼ 30 ns >> teq for Cu, Al, and Fe after the pulse. Thus, only the air-surface collisions could lead to the formation of high-energy Maxwellian tail, and therefore to thermal evaporation from the surface.

The evaporation rate can be calculated in the following way. The solid-air temperature equilibration is completed when the surface temperature has dropped due to thermal conduction to Teq = Tm(tp /teq)1/2. Thermal evaporation starts after the equilibration time t > teq and the temperature at the solid-air surface continues to decrease in accordance to the linear heat conduction law. We suggest that thermal evaporation proceeds at a vapor density corresponding to the temperature at the solid-air interface. The number of atoms ablated per unit area after establishing the Maxwellian equilibrium can be estimated with the help of Eq. (6) as follows:

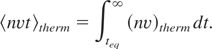
A reliable estimate of the evaporation rate can be obtained with the numerical coefficients extracted from the known experimental data for Cu (Weast & Astle, 1980) at the temperature T = 0.25 eV (≅ 2,850 K) close to our experimental conditions. The saturated vapor pressure and density are, respectively, 107 erg/cm3 and 2.67 × 1019 cm−3 in these conditions. One can calculate the total ablation from unit area using two different interpolation formulae for evaporation rate from (Weast & Astle, 1980) and integrating (17) with these formulae. Such integration yields an ablation rate for Cu of (4.77 ± 0.5) × 1015 cm2.

Thermal ablation rates for Al, Fe, Cu, and Pb can be estimated assuming that the equilibrium in the vapor-air mixture with a predominance of air plays a role in the saturated vapor over the ablated solid. Then one can estimate Eq. (17) as follows:

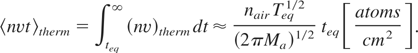
The resulting values should be compared to the corresponding area number density na × dmono in the atomic monolayer. Both values are presented in Table 3 for all the metals studied. One can see that the number of the thermally ablated atoms is close to the number of atoms in a mono-atomic layer.

Thermal evaporation after the pulse end and after establishing the Maxwellian distribution

These calculations suggest that thermal evaporation well after the end of the laser pulse at fluencies corresponding to the threshold measured in air can be responsible for the removal of a mono-atomic layer for Al, Cu, and Fe. This is in a good agreement with the experiments, as the threshold fluency was introduced as the fluency needed to remove a single atomic layer. Therefore, we can conclude that the presence of air decreases the single pulse ablation threshold by approximately a factor of two due to the contribution of thermal ablation assisted by the presence of the air well after the end of the pulse.

The measured ablation thresholds for Pb in air and in vacuum differ by an order of magnitude and the calculated results for Pb are significantly different from the measured results. A possible explanation for this difference may relate to the unknown optical properties of Pb as a function of temperature, as well as to a more pronounced cumulative effect of consecutive pulses (as will be discussed next). As one can see from Eq. (18), the ablation threshold is a function of absorption coefficient, which is temperature-dependent. For example, the use of optical characteristics for cold Al can lead to an order of magnitude difference in the expected ablation threshold.

3.9. Multi-pulse thermal ablation in vacuum

As demonstrated in the previous Section, the presence of a gas next to the solid surface increases the ablation rate due to thermal evaporation after the pulse. A similar effect may take place when a high repetition rate laser is used for ablation because of the accumulation of a dense vapor in front of the solid target surface from successive pulses

One can estimate the conditions for such accumulation effects as follows. Thermal ablation can be efficient once a Maxwellian distribution between the vapor and the solid has been established. Thus, the first condition for cumulative evaporation is that the equilibration time should be shorter than the time gap between the pulses, teq = (nσv)−1 < Rrep−1. From this condition, the vapor density should comply with condition n > (Rrep /σv). Thus, taking the experimental conditions: Rrep = 4.1 × 106 s−1; σ ∼ 10−15 cm2; and vth ∼ 105 cm/s, the vapor density should be na > 4 × 1016 cm−3. Thus, for the vacuum ablation in our experiments at P = 3 × 10−3 Torr (na = 1.8 × 1014 cm−3), the density near the ablated surface should increase more than 200 times due to the action of many consecutive pulses.

Let's consider the conditions for such density build-up. Entropy and the energy are conserved after the pulse. Therefore the plume expands adiabatically. The specific features of the isentropic expansion are the follows: the density and the temperature of a plume go to zero at the finite distance from the initial position (in contrast to isothermal expansion), while the velocity is at maximum (Zel'dovich & Raizer, 2002). Therefore, the density next to ablation surface has a steep gradient. The size of the expanding plume grows linearly with time, Rmax = vth /Rrep, which is ∼250 microns in experiments. The experimental data of Figure 1 indicate that slow non-equilibrium ablation does take place when the surface temperature is as little as half the ablation threshold. This is plausible because only a few collisions can lead to some atoms gaining enough energy to exceed the binding energy. Thus the number of ablated atoms below threshold for a single pulse is several times lower than the number of atoms in a monolayer. Thus, the density increase after the single pulse comprises n1 ∼ 3Nabl /4π(Rmax)3 ≅1.5 × 1013 cm−3 in the conditions of our experiments. Hence, more than 103 pulses are needed to create a vapor dense enough to “switch on” thermal evaporation in the manner invoked in the presence of air. In fact, in our experiments, around a thousand pulses on average dwell at the same spot on the target and this may be sufficient to cause some change of the ablation threshold because of an increased level of thermal ablation. The difference between the single pulse and the multiple pulse thresholds is, however, in a range of experimental error in the case of Al, Cu, and Fe. However, the difference for Pb is large and it might be explained by the accumulation effect, although as pointed out earlier the physical parameters for Pb are not well known especially at elevated temperatures. Evidently, more experimental and theoretical studies are needed to understand the difference between the single-pulse and the high-repetition rate multiple-pulse ablation threshold.

4. CONCLUSIONS

Experiments on the ablation of metals in air and in vacuum by 4.1 MHz repetition rate laser revealed that the presence of air results in a significant reduction in the ablation threshold. In order to explain this observation we analyzed in detail the role of non-thermal ablation and thermal evaporation for the intermediate duration pulses (12 ps) used in the experiments.

Our analysis shows that for materials like Al, the single pulse threshold in vacuum agrees with the threshold for non-thermal ablation that is the well-accepted mechanism applying to ultra-short pulses. This implies that in vacuum there is a negligible contribution from thermal evaporation both during and after the pulse. The threshold condition then corresponds to the surface atoms receiving energy directly from the laser equal to their binding energy.

The somewhat unexpected conclusion that thermal evaporation is negligible led us to examine in detail the characteristic timescales for energy transfer within the laser-heated layer. In previous models, only the electron-to-lattice energy transfer time, and the thermal conduction time were regarded as important. For the materials that were studied, we find that, generally, the electron and lattice energies equilibrate close to the end of the 12 ps laser pulse, and the heat conduction time is usually several times longer than the pulse duration, in agreement with previous work. However, when the laser fluency is below the threshold for non-thermal ablation, thermal evaporation will occur only if a Maxwellian distribution of atom energies can be established at the target surface. We show that the time needed to create the Maxwellian distribution at the surface is surprisingly long and is determined by the bulk-to-surface energy transfer time due to collisions between the surface atoms, and those in the bulk. In fact the time to equilibrate the surface is at least an order of magnitude longer than in the bulk material and is strongly dependent on the layer temperature.

Thus, for example, when the laser imparts energy to the surface atoms corresponding to half their binding energy, the thermalization time at the surface approaches 100 ps compared with only 1 ps in the bulk. Since the surface thermalization time is now longer than the cooling time of the surface, it becomes impossible for thermal evaporation to contribute to material removal at fluencies below the threshold for non-thermal ablation. This is a new result that can explain why the transition from non-thermal to thermal ablation observed in experiments (Corkum et al., 1988; Stuart et al., 1996) occurs at pulse durations much longer than it should be if the electron heat conduction is a major mechanism for this transition to occur.

The clue to understanding why the ablation threshold is lower in air than in vacuum also stems from the need to create a Maxwellian distribution of energies at the surface for thermal evaporation to occur. In this case, collisions between the air and the laser-heated surface create a new pathway by which the surface can thermalise; in fact, the air replaces the role of the saturated vapor in the classical model of thermal evaporation. While it takes up to 1 ns for the air to thermalise with the surface, once this occurs, thermal evaporation will still result in the removal of a mono layer from the surface at fluencies between two and three times lower than the threshold in vacuum. Hence one concludes that the presence of a gaseous atmosphere switches on thermal evaporation that was negligible in vacuum.

It follows from this explanation that the presence of any vapor near the target surface could result in a decrease in the ablation threshold via the same mechanism. We consider the case of the vapor produced when a high repetition rate laser such as used in these experiments is used to continuously evaporate the target. The analysis indicates that the vapor accumulated from multiple pulses hitting the same spot on the target has a density close to the value that might reduce the ablation threshold in our experiments. In particular in the case of Pb this might provide a reason for the larger discrepancy between the measured and calculated threshold values.

Further experimental studies, including time-resolved measurements of the dielectric properties, that is, real and imaginary parts of the dielectric function during the pulse and after the pulse will allow one to gain complete understanding of the ablation processes near and above the ablation threshold.

ACKNOWLEDGMENTS

The support of the Australian Research Council through its Centre of Excellence and Federation Fellowship programs is gratefully acknowledged.

Footnotes

This paper was presented at the 28th ECLIM conference in Rome, Italy.

References

REFERENCES

Bass, M., Van Stryland, E.W., Williams, D.R. & Wolfe, W.L., Eds. (2001). Handbook of Optics, Vol. 2. New York: McGraw-Hill.
Born, M. & Wolf, E. (2002). Principles of optics: Electromagnetic theory of propagation, interference, and diffraction of light. 7th Ed., pp. 746. Cambridge: Cambridge University Press.
Corkum, P.B., Brunel, F., Sherman, N.K. & Srinivasan-Rao, T. (1988). Thermal response of metals to ultra-short pulse laser excitation. Phys. Rev. Lett. 61, 2886–2889.CrossRefGoogle Scholar
DiBernardo, A., Courtois, C., Cros, B., Matthieussent, G., Batani, D., Desai, T., Strati, F. & Lucchini, G. (2003). High-intensity ultrashort laser-induced ablation of stainless steel foil targets in the presence of ambient gas. Laser Part. Beams 21, 59–64.Google Scholar
Du, D., Liu, X., Korn, G., Squier, J. & Mourou, G. (1994). Laser-induced breakdown by impact ionisation in SiO2 with pulse width from 7 ns to 150 fs, Appl. Phys. Lett. 64, 3071–3073.Google Scholar
Eidmann, K., Meyer-ter-Vehn, J., Schlegel, T. & Huller, S. (2000). Hydrodynamic simulation of subpicosecond laser interaction with solid-density matter. Phys. Rev. E 62, 1202–1214.Google Scholar
Gamaly, E.G., Rode, A.V., Luther-Davies, B. & Tikhonchuk V.T. (2002). Ablation of solids by femtosecond lasers: ablation mechanism and ablation thresholds for metals and dielectrics, Phys. Plasmas 9, 949–957.CrossRefGoogle Scholar
Kaganov, M.I., Lifshitz, I.M. & Tanatarov, L.V. (1957). Relaxation between electrons and the crystalline lattice. Sov. Phys. JETP 4, 173–178.Google Scholar
Kittel, C. (1996). Introduction to solid state physics. New York: Wiley & Sons.
Kolev, V.Z., Lederer, M.J., Luther-Davies, B. & Rode, A.V. (2003). Passive mode-locking of a Nd:YVO4 laser with an extra-long optical resonator, Optics Lett. 28, 1275–1277.Google Scholar
Kruer, W.L. (1987). The physics of laser plasma interaction. New York: Addison Wesley.
Landau, L.D. & Lifshitz, E.M. (1980). Statistical physics, Oxford: Pergamon Press.
Luther-Davies, B., Gamaly, E.G., Wang, Y., Rode, A.V. & Tikhonchuk, V.T. (1992). Matter in ultra-strong laser fields. Sov. J. Quantum Electron. 22, 289–325.CrossRefGoogle Scholar
Luther-Davies, B., Kolev, V.Z., Lederer, M.J., Madsen, N.R., Rode, A.V., Giesekus, J., Du, K.-M. & Duering M. (2004). Table-top 50 W laser system for ultra-fast laser ablation. Appl. Phys. A 79, 1051–1055.CrossRefGoogle Scholar
Malvezzi, M., Bloembergen, N. & Huang C.Y. (1986). Time-resolved picosecond optical measurements of laser-excited graphite. Phys. Rev. Lett. 57, 146–149.CrossRefGoogle Scholar
MacDonald, W.M., Rosenbluth, M.N. & Chuck, W. (1957). Relaxation of a system of particles with coulomb interactions. Phys. Rev. 107, 350–359.CrossRefGoogle Scholar
Nolte, S., Momma, C., Jacobs, H., Tünnermann, A., Chichkov, B.N., Wellegehausen, B. & Welling, H.J. (1997). Ablation of metals by ultrashort laser pulses. Opt. Soc. Am. B 14, 2716–2722.CrossRefGoogle Scholar
Perry, M.D., Stuart, B.C., Banks, P.S., Feit, M.D., Yanovsky, V. & Rubenchik, A.M. (1999). Ultra-short laser machining of dielectric materials. J. Appl. Phys. 85, 6803–6810.CrossRefGoogle Scholar
Prutton, M. (1994). Introduction to surface physics. Oxford: Clarendon Press.
Raizer, Yu.P. (1977). Laser-induced discharge phenomena. New York: Consultant Bureau, p. 91.
Semerok, A., Salle, B., Wagner, J.-F. & Petite, G. (2002). Femtosecond, picosecond, and nanosecond laser microablation: Laser plasma and crater investigation. Laser Part. Beams 20, 67–72.CrossRefGoogle Scholar
Stuart, B.C., Feit, M.D., Rubenchik, A.M., Shore, B.W. & Perry, M.D. (1995). Laser-induced damage in dielectrics with nanosecond to subpicosecond pulses. Phys. Rev. Lett. 74, 2248–2251.CrossRefGoogle Scholar
Stuart, B.C., Feit, M.D., Herman, S., Rubenchik, A.M., Shore, B.W. & Perry, M.D. (1996). Optical ablation by high-power short-pulse lasers. J. Opt. Soc. Am. B. 13, 459–468.CrossRefGoogle Scholar
Uteza, O.P., Gamaly, E.G., Rode, A.V., Samoc, M. & Luther-Davies, B. (2004). Gallium transformation under femtosecond laser excitation: Phase coexistence and incomplete melting. Phys Rev B. 70, 054108.CrossRefGoogle Scholar
von der Linde, D. & Schuler, H. (1996). Break down threshold and plasma formation in femto-second laser-solid interaction, JOSA B 13, 216–222.Google Scholar
Weast, R.C. & Astle, M.J., Eds. (1980). CRC Handbook of Chemistry and Physics. 60th Edition. Boca Ralton: CRC Press.
Ying, M., Xia, Y., Sun, Y., Zhao, M., Ma, Y., Liu, X., Li, Y. & Hou, X. (2003). Plasma properties of a laser-ablated aluminum target in air. Laser Part. Beams 21, 97–101.CrossRefGoogle Scholar
Zangwill, A. (1988). Physics at surfaces. New York: Cambridge University Press.CrossRef
Zel'dovich, Ya.B. & Raizer, Yu.P. (2002). Physics of shock waves and high-temperature hydrodynamic phenomena. New York: Dover.
Figure 0

Ablation depth per pulse vs. fluency for (a) Al; (b) Cu; (c) Fe; and (d) Pb in experiments in air (triangles) and in vacuum (circles) using 12 ps 4.1 MHz repetition rate laser. The horizontal lines and the numbers above the lines correspond to inter-atomic distances, while the arrows indicate the ablation threshold. The dashed lines are the upper limits for the ablated depth determined using the energy conservation law.

Figure 1

Threshold fluence for ablation of metals by 12-ps pulses measured in air and in vacuum. In last row is the calculated threshold (see Section 3.7)

Figure 2

Time for the energy transfer from electrons to the lattice, and thermal diffusion rate

Figure 3

Calculated electron and lattice temperature in the skin-layer at the ablation threshold in Al, Cu, Fe, and Pb in vacuum and in air, together with the Gaussian profile of the 12-ps laser pulse.

Figure 4

Thermal evaporation after the pulse end and after establishing the Maxwellian distribution