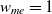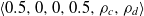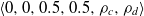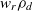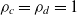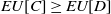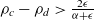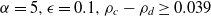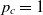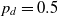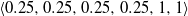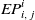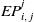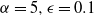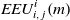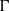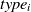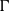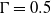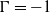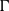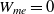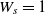2 Related work

Given the rapid increase in user interest and participation in online social networks, researchers are focusing on understanding how interactions between individuals lead to emergent social structures and phenomena (David & Jon, Reference David and Jon2010; Baetz, Reference Baetz2015; Barabasi, Reference Barabasi2016), such as how individuals influence and are influenced by other users they are connected to Cha et al. (Reference Cha, Haddadi, Benevenuto and Gummadi2010). Other researchers have used agent-based models and simulations to explore how behavioral traits and strategic interaction decisions can influence social network dynamics such as change in topologies (Galán et al., Reference Galán, Łatek and Rizi2011), information flow (Tsang & Larson, Reference Tsang, Larson and Richland2014), or to characterize the emergence of conventions or norms (Epstein, Reference Epstein2001; Delgado, Reference Delgado2002) or cooperative behavior (Mahmoud et al., Reference Mahmoud, Miles and Luck2016). Some of these projects are formal studies to prove convergence derive rational agent behaviors (Brooks et al., Reference Brooks, Iba and Sen2011). Others utilize extensive experimental evaluations to characterize the nature of emerging behaviors and topologies in networks of self-interested agents (Delgado, Reference Delgado2002; Peleteiro et al., Reference Peleteiro, Burguillo, Chong and Richland2014; Mahmoud et al., Reference Mahmoud, Miles and Luck2016).

Some of these research investigate how the network topology changes based on strategic or exploratory rewiring of connections by agents seeking relationships that produce higher payoffs (Peleteiro et al., Reference Peleteiro, Burguillo, Chong and Richland2014). Interaction between network neighbors are often represented as a stage game (Epstein, Reference Epstein2001; Delgado, Reference Delgado2002), for example, in studies on the emergence of conventions, the chosen stage games are symmetric coordination games with multiple Nash equilibria.

The behavioral traits of sympathy, parity and reciprocity have been inspired by a study involving human subjects (Güth & Yaari, Reference Güth and Yaari2004) on the Prisoners Dilemma game (Roth, Reference Roth, Kagel and Roth1995). The basic premise of the paper is that people do not necessarily try to maximize their own payoff from interactions with others. Other motivational forces, that take into consideration the payoffs received by interaction partners, have been repeatedly observed to have a key influence on human decision making. As a result, researchers have found notable departures of human actors from self-seeking behaviors (Dawes & Thaler, Reference Dawes and Thaler1988; Sally, Reference Sally1995). While some researchers have observed considerations of parity or inequality aversion when a user is in a disadvantageous position, others have found its use in situations without power imbalance (Bolton, Reference Bolton1991; Bolton & Ockenfels, Reference Bolton and Ockenfels2000). Sympathy, which suggests the ability to put oneself in the position of one’s partner, has been traditionally used to explain cooperative behavior that cannot be rationalized by self-interest (Dawes & Thaler, Reference Dawes and Thaler1988). Social scientists have devoted considerable attention to a somewhat extreme and paradoxical form of sympathy, altruism, where benefits to others is given exclusive consideration (Krebs, Reference Krebs1970; Taylor, Reference Taylor1992; Badhwar, Reference Badhwar1993; Schmitz, Reference Schmitz1993; Day & Taylor, Reference Day and Taylor1998). Reciprocity (Goranson & Berkowitz, Reference Goranson and Berkowitz1966), that is, the desire to do to others as they do to you or applying measure for measure, has also been recognized as a driving force behind human decision making (Martinez-Coll & Hirshleifer, Reference Martinez-Coll and Hirshleifer1991; Rabin, Reference Rabin1993; Fehr et al., Reference Fehr, Gächter and Kirchsteiger1997). For example, experiments with human subjects on sequential social dilemma games show that subjects will incur personal costs to penalize norm violators or reward norm upholders (Fehr & Fischbacher, Reference Fehr and Fischbacher2003). Additionally, some of the experiments are carried out in public goods game scenarios. In contrast, we study simultaneous move game in societies without the background of existing norms and interactions produce private payoffs only. Others have used centralized monitoring and penalty mechanisms to ensure fair access to resources in a society (Danassis & Faltings, Reference Danassis and Faltings2019). We do not assume the presence of any mediating agents or capability to impose direct monetary punishment for individuals for aberrant behavior.

Researchers have looked at local Nash Equilibrium in structured populations, for example, social networks, and the resultant effects on the distribution of defectors and cooperators in social dilemma games such as the Prisoner’s dilemma as well as the evolution of stable strategies (Zhang et al., Reference Zhang, Aziz-Alaoui, Bertelle and Guan2014). In contrast to this work, our agents can change their connections but do not change their strategies.

Güth & Yaari (Reference Güth and Yaari2004) attempt to explain human considerations of sympathy, parity, and reciprocity when departing from self-seeking behavior. In contrast, they try to characterize scenarios where consideration of partner payoffs can maximize utility for self-seeking autonomous agents, trying to maximize cumulative interaction payoffs from their partners. Social networks where an agent’s utility depended on their neighbors’ payoffs have been studied in the context of social choice (Salehi-Abari & Boutilier, Reference Salehi-Abari, Boutilier and Richland2014). The focus of this work is on better social choice mechanisms rather than the viability of individual agent types as is the case in our work. Various computational approaches have studied a certain form of reciprocity, mimicking an opponent’s past action, in promoting cooperation in repeated game scenarios and in multiagent societies (de Vos & Zeggelink, Reference de Vos and Zeggelink1994; Ferriere & Michod, Reference Ferriere and Michod1996; Sen, Reference Sen1996). In this paper, a more strategic form of reciprocity is used that takes into consideration partner payoffs to determine strategy. More specifically, a unified computational framework for decision making, that incorporates sympathy, parity, and reciprocity considerations, together with payoff to self, is used to select actions. To the best of our knowledge, such unified treatment has not been attempted before.

3 Model

This section describes the game scenario used in this paper to represent the interaction between two players, the player types, and strategic decision making framework, including actions for severing and forming social network connections. The agents (players) are situated on a social network, where each agent corresponds to a node and edges connect agents to other agents they can interact (play) with.

To initialize, a Watts-Strogatz model (Watts & Strogatz, Reference Watts and Strogatz1998) is used to generate a small world network with agents allocated to randomly selected nodes. A simulation run consists of repeated rounds numbering R. Every round, each agent is called upon to initiate an interaction (a game) with another agent, which it selects uniformly from all of its neighbors. When an agent initiates an interaction, it will be the first to make its strategy choice. The players move in turns: in a sequential two-player, two-action game, the first player’s strategy choice is visible to the second player when the latter chooses its action. An agent is not exempt from being part of another interaction in the same round should a different agent initiate an interaction upon it (although it will be the second player in these instances).

In addition, after $R_{\overline{r}}$ rounds, each interaction phase will be followed by a rewiring phase. The rewiring phase grants each agent two opportunities: to form and sever a connection with other agents in the network. Agents connect to previously unknown agents via the recommendation of their most favored partner, and disconnect from agents based on a global connection cost constant $\Gamma$ .

3.1 Game

The games used in this paper are based on sequential variants of the Prisoner’s Dilemma and Battle of Sexes games. The Prisoner’s Dilemma payoff matrix for two interacting agents is presented in Table 1, where $\alpha>0$ , $\epsilon>0$ (we use $\alpha >> \epsilon$ following Güth & Yaari (Reference Güth and Yaari2004)). The first value of each pair, x, is the row (first) player’s pay off, and the second value, y, is the column (second) player’s pay off. Similarly, the payoff matrix for the Battle of Sexes is presented in Table 2.

Table 1 Raw Payoffs in a Prisoner’s Dilemma game (default values used (Güth & Yaari, Reference Güth and Yaari2004): $\alpha=5, \epsilon=0.1$ )

Table 2 Raw Payoffs in a battle of sexes game

The utility to an agent for a particular outcome depends on the payoff of both players as the players are not only self-seeking but are also influenced by sympathy, parity, and reciprocity considerations. The utility of a player who receives a payoff x when the other player receives a payoff of y from an interaction is calculated as

\begin{equation*}u(x, y)=w_{me} x+w_s y-w_p |x-y|+w_r ({\mathcal C} \rho_c -(1-{\mathcal C}) \rho_d) y\end{equation*}

where ${\mathcal C}$ is 1 or 0 depending on if the other player cooperates or defects respectively, $\rho_c$ and $\rho_d$ are the fraction of the other player’s payoff used by a reciprocative player when the opponent cooperates and defects respectively.

Table 3 Weight vectors of each of the four agent types

Table 4 Utility to different player types for all possible Prisoner’s Dilemma game outcomes (with the first and second letters representing the strategy choices of that row’s type and its partner respectively)

We define an agent type, $\tau$ , as a vector of six parameters:

\begin{equation*}\tau=\left\langle w^{\tau}_{s},w^{\tau}_{p},w^{\tau}_{r},w^{\tau}_{me},\rho_c,\rho_d\right\rangle\end{equation*}

where the first four parameters represent the relative influences of sympathy, parity, reciprocity and selfishness, respectively, on the agent, and the last two deal with weights toward reciprocating cooperation and defection respectively, if an agent type makes use of reciprocity. The weights normalize the influences on utility, that is, $w_s+w_p+w_r+w_{me}=1$ . We experimented with six types of agents; the corresponding weight vectors are presented in Table 3. The Utility matrix for each of these player types for each of the outcomes is presented in Table 4 for the Prisoner’s Dilemma game. An outcome is characterized by the strategy combination played, where the first letter is the strategy used by the current agent and the second letter is the strategy chosen by its opponent.

3.3 Strategy decision

Every time a player interacts with another player, it records the other player’s strategy and uses this historical record the next time it interacts with the same player to estimate the probability the other player cooperates or defects. Suppose, an opponent is observed to have cooperated $t_c$ times and defected $t_d$ times with this player. Then the next interaction with this player, it assumes that the player will cooperate with a probability, $P_c=t_c/(t_c+t_d)$ and defects with a probability, $P_d=t_d/(t_c+t_d)$ . In the special case of no knowledge (i.e., the very first move), $P_c=P_d=0.5$ is assumed.

The strategy chosen by a player, when making the first move, depends on its expected utility value of cooperating, EU[C], and defecting, EU[D], given the expected move of its opponent, and is calculated as follows:

\begin{equation*} EU[C] = P_c u(CC) + P_d u(CD) \end{equation*}

\begin{equation*} EU[D] = P_c u(DC) + P_d u(DD)\end{equation*}

If the player is the second player, then its expected utility for its actions is calculated from its utility value for corresponding outcomes because the opponent’s strategy is already known. So the utility for the second player in the first interaction is calculated as $EU[C]=u(CC)$ or $EU[D]=u(DC)$ when the other player cooperates, and $EU[C]=u(CD)$ or $EU[D]=u(DD)$ , when the other player defects. A player decides to cooperate when $EU[C]\ge EU[D]$ and defects otherwise. The raw expected utility that a player has for an interaction is $EU=\max\{EU[C], EU[D]\}$ .

3.4 Network and connections

Except for the experiments on pairwise agent interactions, all other networks are initialized using the Watts-Strogatz network small-world generation algorithm (Watts & Strogatz, Reference Watts and Strogatz1998). The Watts-Strogatz algorithm initially places agents on a ring-structured network where each node has degree n, and then randomly reconnects each edge on the network with probability p (we use $n=4$ and $p=0.01$ ). The parameters for the algorithm were chosen so that the network was well-connected for agents to have flexibility in choosing their neighbors, while still representing a realistic structure. A small-world network was ideal for these experiments since all agents initially have approximately equal influence. Only once the rewiring phase of the simulation begins (unrelated to Watts-Strogatz reconnection/rewiring), will the influences of the agents in the network begin to differ.

After $R_{\overline{r}}=100$ iterations of the interaction stage of the algorithm, each agent is given the choice to connect to a new agent and disconnect from an undesirable, existing neighbor. The motivation behind this process is that by 100 iterations, the agents would have had time to interact with all the types of agents and realize which types of agents will be helpful and which types will hurt them in an interaction, and can thus seek new connections that could replace these ‘uncooperative’ individuals.

During the connection phase, an agent a requests a recommendation from its ‘preferred partner’ that is, the neighbor it has the highest expected utility for, $EU=\max\{EU[C], EU[D]\}$ , as the first player in the game. This ‘highest expected utility’ is equivalent to a trust value for the agent (Gambetta, Reference Gambetta1988; Sen, Reference Sen and Richland2013): the higher the expected utility, the more the agent trusts their partner to play a strategy that is mutually rewarding. The preferred partner agent, b, recommends another agent c using a weighted sample based on expected utility (with negative EU partners discarded) from b that is not connected to a. b reports the expected utility it has for c, to a. Agent a will trust this estimate of c unless a has prior experience with c, in which case it will use the information from its prior experience to determine its own expected utility.

Following this recommendation stage, a elects to form a new connection with this neighbor if and only if the expected utility is higher than the connection cost parameter $\Gamma$ . The connection cost is the cost of forming or maintaining social relationships on the network. It can be interpreted as a ‘cognitive load’ on the agent, such that interactions with others only pay dividends when the reward outweighs the cognitive cost.

Table 5 Notation

Disconnecting works as follows: after the recommendation and connection stages, each agent is given the choice to disconnect from their ‘least preferred’ partner, d, which is their partner with the lowest expected utility, EU. If $EU\leq\Gamma$ , the agent will disconnect from this partner. Otherwise, the agent will keep all existing connections.

We summarize the notations introduced herein for easy reference in Table 5.

4 Experimental results

Unless otherwise stated, all games have been simulated with 100 agents for $R=R_r+R_{\overline{r}}=250$ iterations, allowing re-wiring only after $R_{\overline{r}}=100$ iterations.

The results of the Prisoner’s Dilemma game are presented in greater depth as the Battle of Sexes game was used primarily as a means to compare and contrast the results obtained with the Prisoner’s Dilemma game to those in a different domain.

4.1 Pairwise interactions in one-on-one games

It is important to understand the convergence in players’ strategies in repeated binary interactions, because those equilibrium strategy profiles will also be observed across the population when agents repeatedly interact with their neighbors on a social network. Convergence here refers to an equilibrium, understood as a state where every interaction afterward will produce the same outcome. The corresponding convergence strategy utilities for Strict reciprocity and Considerate reciprocity are shown in Figure 1. The convergence strategy profile for Considerate Reciprocity agents differed from the other case only in the following ways: Reciprocity to Parity is CC instead of DD and Reciprocity to Reciprocity is CC instead of DD. These two changes occur because considerate reciprocative opens with C when it goes first, and strict reciprocative opens with D: behaviors forced due to our intentional selection of $\rho_d$ and $\rho_c$ values.

Figure 1 Prisoner’s Dilemma: Equilibrium strategies with (a) Strict Reciprocity and (b) Considerate Reciprocity agents. Edges originating from $type_i$ to $type_j$ represent the equilibrium utilities when $type_i$ plays the first move

4.2 Pairwise interactions in larger groups

To understand the nature of pairwise interactions on social networks, a group of 50 agents of one type are played against another group of 50 agents of another type. To observe which group (multiple players of one type) does better than the other, two groups of every type pair were played against each other and the average payoffs were recorded. The difference in this simulation from the two player simulation is that here not only can a player interact with a player of the other type but it can also interact with other players of its own type.

For the Prisoner’s Dilemma game, these simulations showed that there can be cyclic patterns in the dominance order of agent types in terms of who received the higher payoff in these head-to-head matches. In all cases, the Mixed type dominates other agents influenced primarily by one social consideration as well as the selfish agents. Strict reciprocative players tied with parity and selfish players; all three types having an equal payoff when played against each other. However, parity and strict reciprocative agents performed worse than sympathy in pairwise interactions, while selfish agents performed better than sympathetic and the latter in turn performed better than parity players (see Figure 2(a)). In the case where reciprocative players were considerate, sympathetic players performed rather poorly, only dominating the parity agents (causing a cyclic pattern with selfish, parity, and sympathy agents). Considerate reciprocative agents performed better than all but the Mixed agent in this case (see Figure 2(b)), an incredible improvement over the strict variant. These improvements result because like sympathy and mixed, considerate reciprocity converges to CC with itself, a trait that is not present in strict reciprocity. Yet considerate reciprocity still maintains the punitive aspect of strict reciprocity, by converging to DD with selfish, and DD with parity when parity plays first (opens with a D), CC when it plays second (reciprocity opens with a C).

Figure 2 Prisoner’s Dilemma: Dominance pattern in Head-to-Head interactions for (a) Strict Reciprocity and (b) Considerate Reciprocity. The numbers next to an agent type on an arrow represent the fraction of simulations where the average payoff of agents of that type that performed better than agents of the other type in the population (Note that the fractions on both ends of an arrow need not be 1 as the average payoff to both agent types may be identical in some runs.).

4.2.1 Strict reciprocity

Reciprocity, parity, and selfish players perform the same because they all converge to Defect-Defect strategy profiles, which give 0 payoffs. This happens because all three types have $EU[D]>EU[C]$ as a first player and hence defects for the first move in the game. Also, as the second player, all three types defect as a response to the first player defecting. Defect-Defect is then the equilibrium strategy profile which results in a payoff of 0 for all parties involved.

Sympathy, on the other hand, always cooperates regardless of the other player’s strategy. Therefore, it converges to a state of CC with parity, reciprocity and other sympathy players. All three of these groups cooperate as second players in response to a first player cooperating. The reason reciprocity and parity converge to this state instead of defecting with sympathy is that $EU[D]<EU[C]$ for both. Sympathy receives a higher payoff because it can additionally cooperate with other sympathy players and receive a higher payoff than what parity and reciprocity receive for interacting with their own types (0 payoffs from Defect-Defect outcomes).

4.2.2 Considerate reciprocity

The only difference here is that reciprocity performs better than parity and selfish players because considerate reciprocity players cooperate as the first player. In a group with parity players, the reciprocity players have CC outcome with themselves and CC with parity players, whereas parity players will have DD outcomes with themselves and with reciprocity players, thus receiving a lower payoff than reciprocity. When interacting with selfish players, reciprocity initially tries to cooperate, but chooses to defect when they find the selfish always defect. This way the only payoffs received apart from 0 payoff is when reciprocity interact with their own type and hence receive a higher payoff than selfish players. With sympathy players, the two types perform equally well because they CC with players of the same kind and the other kind.

In terms of the Battle of Sexes game, for both Strict reciprocity and Considerate reciprocity, selfish and parity agents performed worst with selfish outperforming parity. The difference lies in the fact that sympathy underperformed to Strict reciprocity but outperformed Considerate reciprocity, as shown in Figure 3. It is clear to see that the head-to-head dominance patterns for the two games differ drastically, not only in terms of order but also in terms of the structure of the dominance pattern as there are no cyclic patterns seen in the Battle of Sexes game.

Figure 3 Battle of Sexes: Dominance pattern in Head-to-Head interactions for Strict Reciprocity (a) and Considerate Reciprocity (b)

Figure 4 Prisoner’s Dilemma: Dominance pattern for Heterogeneous communities with Strict Reciprocity (a) and Considerate Reciprocity (b).

4.3 Heterogeneous communities

To study more realistic scenarios, we experiment with social networks where players of diverse types interact.

4.3.1 Heterogeneous communities (Prisoner’s Dilemma scenario)

Dominance patterns in populations of sympathetic, strict reciprocating, parity and selfish agents: When a social network contains equal distributions of each of these four groups, there is a clear order of dominance seen for the Prisoner’s Dilemma game, as shown in Figure 4(a). The degree of each agent type reveals whom they interact with and why they gain such payoffs. For sake of conciseness, Figure 7 shows only the total degree of each agent type. It can be seen that Sympathy agents have the highest degree while Selfish the lowest and despite this Selfish agents perform better than Parity and Reciprocity. The reason behind this is, although all agents try to cut off all connections except those with Sympathy, the Selfish agents stand to gain a higher payoff in each interaction with Sympathy agents. Strict Reciprocative agents also gain higher than Parity agents in interactions with Sympathy agents but they lose out by remaining connected to some Reciprocative agents.

Dominance patterns in populations of sympathetic, considerate reciprocating, parity and selfish agents: The dominance pattern of these four groups, shown in Figure 4(b), is similar to the case with Strict Reciprocity except that Considerate Reciprocity now outperforms all other agent types. Such dominance can be attributed to the fact that Considerate Reciprocity players, unlike in the case of Strict Reciprocity, gain a high payoff from self-play. This, added to the payoffs received when interacting with Sympathy players, results in them gaining the highest payoffs compared to the other three agent types.

Cumulative payoffs: The graphs in Figure 5 show the average cumulative payoffs for each agent type over the rounds, averaged over ten trials, in a heterogeneous community. The dominance patterns observed in Figure 4 are evident in (a) Strict and (b) Considerate Reciprocity cases here. We observe that the Sympathy agents follow the same linear increase in their cumulative payoff, even when rewiring option becomes available after 100 time steps. All other agent types, however, receive a noticeable utility boost from re-wiring. We observe that agent types with high average cumulative payoffs also tend to have high degrees of connectivity in the network (see Figure 7).

Figure 5 Prisoner’s Dilemma Cumulative Payoffs: Strict Reciprocity (a) and Considerate Reciprocity (b).

We also present results from a second set of experiments in the Prisoner’s Dilemma domain where $\epsilon$ value was increased to 0.5 from 0.1. This means the payoffs for player one would change to: CC = 5, CD = –0.5, DC = 5.5, and DD = 0. The dominance patterns remain unchanged in both cases of Strict and Considerate Reciprocity (Figures 6(a) and (b) respectively), despite the increased $\epsilon$ value.

Figure 6 Prisoner’s Dilemma cumulative payoffs: $\epsilon = 0.5$ and $\alpha = 5$ for Strict Reciprocity (a) and Considerate Reciprocity (b)

Figure 7 Prisoner’s Dilemma: Average degree of agent type for the cases of Strict Reciprocity (a) and Considerate Reciprocity (b).

4.3.2 Heterogeneous communities (Battle of the Sexes scenario)

The dominance patterns for cases of Strict and Considerate Reciprocity in the Battle of Sexes domain are presented in Figure 8. The corresponding cumulative payoff graphs for agents in heterogeneous groups interacting in the Battle of Sexes scenarios are shown in Figures 9.

Figure 8 Battle of Sexes: Dominance pattern for heterogeneous communities with (a) Strict Reciprocity and (b) Considerate Reciprocity.

Figure 9 Battle of the Sexes cumulative payoffs: For Strict Reciprocity (a) and Considerate Reciprocity (b), averaged over ten trials.

The change in domain results in a partial change in the dominance pattern, where Sympathy, Selfish, and Parity agents retain their relative dominance positions in the Prisoner’s Dilemma game (see Figure 4), across both cases of Reciprocity in the Battle of Sexes game. The stark difference in dominance patterns in heterogeneous groups for Battle of Sexes, when compared to that in the Prisoner’s Dilemma scenario, is that here Strict Reciprocity performed best (see Figure 8(a)) as opposed to being the worst performing in Prisoner’s Dilemma (see Figure 4), and the Considerate Reciprocity performed only second best (see Figure 8(b)) compared to being the best in the Prisoner’s Dilemma scenario.

4.4 Effect of connection cost on network topology

Connection cost, $\Gamma$ has a significant impact on the topology of the network. Figure 10 shows the resultant topologies with heterogeneous agent populations for different connection costs in the Prisoner’s Dilemma scenario. The green, red, blue, and black nodes correspond to Sympathy, Reciprocity, Parity, and Selfish agents respectively. A green edge represents a CC outcome, a red edge represents a DD outcome, a blue edge represents a DC outcome, and a black edge represents a CD outcome.

Figure 10 Topologies for increasing connection cost from (a) to (d): (a) Connection cost = −0.05, (b) Connection cost = 1, (c) Connection cost = 3.5, (d) Connection cost = 5.

The topology becomes sparse with higher connection cost (see Figure 10). This is due to the fact that the players break off connections with opponent players when their EU[C] or EU[D] is lower than the connection cost. Increasing the connection cost reduces the incentive or tolerance for remaining connected to opponent players providing lower utilities.

5 Predicting average cumulative payoff for agent types

We now develop an analytical framework to predict average payoffs from interactions in environments containing our six agent types: selfish ( $type_{me}$ or $type_1$ ), sympathetic ( $type_s$ or $type_2$ ), parity ( $type_p$ or $type_3$ ), strict reciprocity ( $type_{sR}$ or $type_4$ ), considerate reciprocity ( $type_{cR}$ or $type_5$ ), and mixed ( $type_{mix}$ or $type_6$ ). The following analysis uses the Prisoner’s Dilemma (PD) game; an identical analysis using the general formulas provided can also be performed for any other game, including the Battle of Sexes (BoS).

There are only two possible equilibria for each matchup, and such an equilibrium will be reached on the first or second interaction. This conclusion can be derived from a tree diagram of all possible outcomes of two interactions given the following observations for our six agent types in the PD: A decision to cooperate or defect is deterministic and depends only upon $P_c$ , the fraction of cooperative responses by an agent’s partner (and $P_d$ , which is simply $1-P_c$ ). If an agent type cooperated on a prior interaction with $P_c = p$ , an agent type will always cooperate for any $P_c \geq p$ . Similarly, if an agent type defected on a prior interaction when $P_c = p$ , an agent type will always defect for any $P_c \leq p$ . Equilibrium strategy outcomes for every combination of agent types are mapped below into $6 \times 6$ matrices ( $EP^i$ and $EP^j$ ) with 1–6 corresponding to agent types selfish, sympathetic, parity, strict reciprocity, considerate reciprocity, and mixed in that order. These outcomes were found by simply playing each matchup through with both orderings and recording the results.

The following four matrices are constructed using values achieved at the two possible equilibria. In the case of payoff at an equilibrium, any particular outcome (CC, CD, DC, DD) will always produce the same payoffs for every interaction, thus there is no dependence on the interaction number m. However, expected utility is a function of m, as agents calculate expected utilities based on $P_c$ and $P_d$ : values determined by outcome histories that differ between m values. In most cases for this particular analysis, both agents will cooperate every interaction or defect every interaction, which eliminates their dependence on m as $P_c$ and $P_d$ will be constants for all m. In the fewer cases where an equilibrium is achieved at interaction 2, expected utilities will depend upon m as $P_c$ and $P_d$ will not be constants for all m. We now introduce some terminology:

• $EP^i_{i,\,j}$ : Equilibrium payoff for type i when i leads in an interaction between types i and j.

• $EP^j_{i,\,j}$ : Equilibrium payoff for type j when i leads in an interaction between types i and j.

  For $\alpha=5, \epsilon=0.1$ , we get

  \begin{equation*}EP^i= \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&5.1&0&0&0&0\\ -.1&5&5&5&5&5\\ 0&5&0&0&0&0\\ 0&5&0&0&0&0\\ 0&5&5&5&5&5\\ 0&5&5&5&5&5\\ \end{array}\right],\quad EP^j=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&-.1&0&0&0&0\\ 5.1&5&5&5&5&5\\ 0&5&0&0&0&0\\ 0&5&0&0&0&0\\ 0&5&5&5&5&5\\ 0&5&5&5&5&5\\ \end{array}\right]\end{equation*}

• $EEU^i_{i,\,j}(m)$ : Equilibrium expected utility for type i at the mth interaction between types i and j that occurs when i leads.

  \begin{equation*}EEU^i(m)= \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&5.1&0&0&0&0\\ 2.5&5&5&5&5&5\\ 0&2.5&0&0&0&0\\ 0&5&0&0&0&0\\ 0&5&5&5&5&5\\ 0&3.75&3.75&3.75&3.75&3.75\\ \end{array}\right]\end{equation*}

• $EEU^j_{i,\,j}(m)$ : Equilibrium expected utility for type j at the mth interaction between types i and j that occurs when i leads.

  \begin{equation*}EEU^j(m)= \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&2.5&0&0&0&0\\ 5.1&5&2.5&5&5&3.75\\[5pt] 0&2.5+\frac{2.5n-2.5}{n}&0&0&0&0\\[8pt] 0&2.5+\frac{2.5n-2.5}{n}&0&0&0&0\\[5pt] \frac{5.1}{n}&5&2.5&5&5&3.75\\[8pt] \frac{5.1}{n}&5&2.5&5&5&3.75\\ \end{array}\right]\end{equation*}

Given these matrices, we can construct two matrices describing the average interaction payoff for each type within every matchup prior to and during the rewiring phase.

Before the rewiring phase, an average interaction payoff can be described as a probabilistic weighting between the two possible equilibria payoffs. The expected interaction payoff without rewiring ( ${\rm EIP}\overline{\rm R}$ ) for $type_i$ being matched with $type_j$ follows:

\begin{equation*}EIP\overline{R}^i_{i,\,j} = Pr(i)EP^i_{i,\,j}+Pr(j)EP^j_{j,i},\end{equation*}

where Pr(i) is the probability that $type_i$ leads.

As it was determined that these two equilibria are determined by whether i or j leads, and because there is no bias in the topology generation process that will lead to some types having higher initial connections than other types, we can assume that each type is equally likely to initially contact the other, giving us $Pr(i)=Pr(j)=0.5$ . This gives us everything we need to construct our matrix of expected interaction payoffs without rewiring:

\begin{equation*}EIP\overline{R}^i=\left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&5.1&0&0&0&0\\ -.1&5&5&5&5&5\\ 0&5&0&0&2.5&2.5\\ 0&5&0&0&2.5&2.5\\ 0&5&2.5&2.5&5&5\\ 0&5&2.5&2.5&5&5\\ \end{array}\right]\end{equation*}

The case after rewiring is a matter of stable connections, which are edges between agent types that both have expected utilities for the other agent that is higher than the connection cost $\Gamma=0.5$ . One or both of them would eventually disconnect otherwise. We make the simplifying and only partially correct assumption that unstable connections are immediately severed when the rewiring stage begins at round $R_{\overline{r}}+1=101$ . This assumption trades off a small degree of accuracy to avoid the great complexity of predicting the most likely sequence of disconnections each type will perform. We use an effective AND gate composed of two Heaviside (unit step) functions, H, that will produce 1 if and only if both agents will stay wired in a particular equilibrium, and 0 otherwise (indicating a disconnection) to compute the matrix for expected interaction payoffs after rewiring at interaction m with connection cost $\Gamma$ :

\begin{equation*}\begin{aligned}EIPR^i_{i,\,j}(m,\Gamma) & = Pr(i)EP^i_{i,\,j}H\big(EEU^i_{i,\,j}(m)-\Gamma\big)H\big(EEU^j_{i,\,j}(m)-\Gamma\big)\\&\quad + Pr(\,\,j)EP^j_{j,i}H\big(EEU^i_{j,i}(m)-\Gamma\big)H\big(EEU^j_{j,i}(m)-\Gamma\big)\end{aligned}\end{equation*}

\begin{equation*}EIPR^i\left(m=2\frac{R_{\overline{r}}}{n},\Gamma=0.5\right)= \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&5.1&0&0&0&0\\-.1&5&5&5&5&5\\0&5&0&0&2.5&2.5\\0&5&0&0&2.5&2.5\\0&5&2.5&2.5&5&5\\0&5&2.5&2.5&5&5\\ \end{array}\right].\end{equation*}

Where interaction count m is assumed to be equal to the expected number of interactions performed at the time of rewiring decision: twice that of the number of pre-rewiring rounds divided by the mean degree n defined in the Watts-Strogatz construction. The factor of 2 comes from two opportunities for a connection in a single round to cause an interaction (one for each agent), and the factor of $\frac{1}{n}$ to give us the chance an opportunity actually causes an interaction (agents select an interaction partner uniformly between connections). When multiplied by our pre-rewiring rounds $R_{\overline{r}}$ , we have the expected number of interactions prior to rewiring.

Our matrix after rewiring is coincidentally equal to the case without rewiring, although this could easily not be the case for different games, agent type definitions, connection costs, or pre-rewiring interaction counts.

These matrices will allow us to construct a formula for the average total payoff for every agent type. Our simplifying assumption is to consider an initially fully connected graph $K_{|\mathcal{A}|}$ of agents $\mathcal{A}$ , whose total type payoff ratios will hopefully be representative of the mean total type payoff ratios resulting from all possible initial topologies. To arrive at expected total payoff for types, we will make use of the discovered expected interaction payoffs before and after rewiring and transform them into expected payoffs for rounds rather than interactions. We will begin with the post-rewiring case, as it turns out its result will inform us of the simpler case of pre-rewiring (where every agent is connected to every other agent). The expected payoff for an agent a of $type_i$ in a round can be divided into two parts: the expected payoff from the one interaction initiated by a and the expected payoff from possible interactions with a initiated by other agents. The total stable connections (SC) an agent has will be necessary to know in order to calculate probabilities for type interactions. We can define the expected SC for an agent a of $type_i$ as:

\begin{equation*}\begin{aligned}SC_i = \sum_{j=1}^{types}.5\left(H\big(EEU^i_{i,\,j}-\Gamma\big)H\big(EEU^j_{i,\,j}-\Gamma\big) + H\big(EEU^i_{j,i}-\Gamma\big)H\big(EEU^j_{j,i}-\Gamma\big)\right)|type_j-\{a\}|\end{aligned}\end{equation*}

An expected payoff for the interaction initiated by agent a of $type_i$ is a linear combination of probabilities of a $type_j$ agent being sampled from a uniform selection of stable connections, multiplied by the expected interaction payoff for $type_i$ being matched with $type_j$ :

(1) \begin{equation}\sum_{j=1}^{types}\frac{|type_j-\{a\}|}{SC_i}EIPR^i_{i,\,j}(m,\Gamma)\end{equation}

The expected payoff for an agent a of $type_i$ received from interactions initiated by other agents is a linear combination of the amount of other agents of $type_j$ , the chance for a to be sampled by a $type_j$ agent ( $SC_j^{-1}$ ), and the expected interaction payoff for $type_i$ being matched with $type_j$ :

(2) \begin{equation}\sum_{j=1}^{types}|type_j-\{a\}|\frac{1}{SC_j}EIPR^i_{i,\,j}(m,\Gamma)\end{equation}

Combining expressions (1) and (2), we find the expected round payoff for an agent a of $type_i$ after rewiring:

\begin{equation*}ERPR_i(m,\Gamma)=\sum_{j=1}^{types}\left(\frac{1}{SC_i}+\frac{1}{SC_j}\right)|type_j-\{a\}|EIPR^i_{i,\,j}(m,\Gamma).\end{equation*}

For the pre-rewiring phase, we know that connection count is equal to $|\mathcal{A} - \{a\}|$ for an agent a regardless of type. This value will assume the roles of $SC_i$ and $SC_j$ which were previously necessary to consider disconnections. Additionally, $EIPR_i^{i,\,j}$ will be swapped for its pre-rewiring counterpart $EIP\overline{R}_i^{i,\,j}$ :

\begin{equation*}\begin{aligned}ERP\overline{R}_i=&\sum_{j=1}^{types}\left(\frac{1}{|\mathcal{A}-\{a\}|}+\frac{1}{|\mathcal{A}-\{a\}|}\right)|type_j-\{a\}|EIP\overline{R}^i_{i,\,j}\\[6pt]=&\sum_{j=1}^{types}\frac{2|type_j-\{a\}|EIP\overline{R}^i_{i,\,j}}{|\mathcal{A}-\{a\}|}\end{aligned}\end{equation*}

Expected total payoff for an agent a of $type_i$ is then equal to the expected total payoffs for each phase’s rounds:

\begin{equation*}ETP_i=R_{\overline{r}}*ERP\overline{R}_i+R_r*ERPR_i\left(m=2\frac{R_{\overline{r}}}{n},\Gamma\right).\end{equation*}

• Equal types: Considering a graph of 60 agents with 10 of each type we get the following expected payoff for different values of $\Gamma$ (row i corresponds to $type_i$ ):

  \begin{equation*}\Gamma=-1\rightarrow\begin{bmatrix}431\\[2pt]2069\\[2pt]845\\[2pt]845\\[2pt]1655\\[2pt]1655\\\end{bmatrix},\Gamma=0.5\rightarrow\begin{bmatrix}1066\\[2pt]2683\\[2pt]1406\\[2pt]1406\\[2pt]2281\\[2pt]2281\\\end{bmatrix},\Gamma=3\rightarrow\begin{bmatrix}171\\[2pt]2668\\[2pt]336\\[2pt]1499\\[2pt]2213\\[2pt]2213\\\end{bmatrix}\end{equation*}
  Generalizations are difficult to claim with certainty as there exist a very large number of variables. Regardless, in proportions of agent types that are equal, sympathy seems to perform well for all $\Gamma$ . Selfish agents have a sweet spot with $\Gamma=0.5$ as they will not stay connected to each other, and will not be disconnected from sympathetic agents. When $\Gamma=-1$ , selfish agents are punished by their own kind, and so is everyone else for staying connected to them and getting fruitless or exploitative outcomes, and when $\Gamma=3$ no one tolerates selfish agents once they have a choice, and the selfish agent receive only what they can glean from the pre-rewiring stage. We now discuss payoffs to different agent types in some diverse population configurations:

• Disproportionately sympathetic: For a graph of 1000 agents with 900 sympathetic and 20 of every other type we get the following expected payoff for different values of $\Gamma$ :

  \begin{equation*}\Gamma=-1\rightarrow\begin{bmatrix}2297\\2249\\2302\\2302\\2400\\2400\\\end{bmatrix},\Gamma=0.5\rightarrow\begin{bmatrix}2373\\2453\\2362\\2362\\2432\\2432\\\end{bmatrix},\Gamma=3\rightarrow\begin{bmatrix}919\\2481\\921\\2391\\2453\\2453\\\end{bmatrix}\end{equation*}
  Every agent type receives incredible payoffs in a highly sympathetic system. All agents seem nearly comparable until $\Gamma=3$ where sympathy agents end their tolerance of selfish free-riding and parity agents fail to see the value in maintaining a connection with anyone (their construction is pessimistic, as the parity factor can only decrease expected utility).

• Disproportionately selfish: Considering a graph of 1000 agents with 900 selfish and 20 of every other type we get the following expected payoff for different values of $\Gamma$ :

  \begin{equation*}\Gamma=-1\rightarrow\begin{bmatrix}51\\203\\100\\100\\198\\198\\\end{bmatrix},\Gamma=0.5\rightarrow\begin{bmatrix}801\\611\\995\\995\\1589\\1589\\\end{bmatrix},\Gamma=3\rightarrow\begin{bmatrix}20\\1821\\40\\1197\\1630\\1630\\\end{bmatrix}\end{equation*}
  Low payoffs are ubiquitous in a predominantly selfish population. Sympathy agents do not have their usual high ranking payoffs in $\Gamma=0.5$ , when they are exploited by the vast selfish majority. As the majority of the population is selfish, they can only exploit a small portion of the total population, which in turn prevents them from achieving higher relative payoffs.