II. Context and Data

French wines capture a large share of the world wine market.Footnote ¹ This sector is prominent in French agriculture. It is the largest agricultural sector in value (15% of the value of production in 2007, INSEE data 2017). The vast majority of wines (80%) are produced under appellations of origin (Table 1), for which production volumes are restricted. These appellations certify the origin of products whose quality and characteristics are tied to their geography, but not only (Economie Rurale, 2000). Few strictly selected terroirs qualify for the appellation of origin label (Hinnewinkel, Reference Hinnewinkel and Hinnewinkel2002), which is based on the respect for local uses, soil, climate, and human know-how.

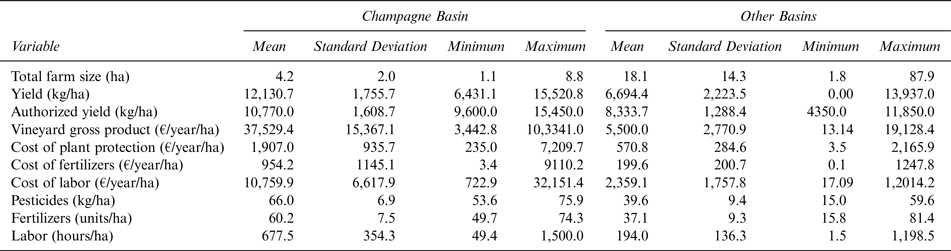
Table 1 Descriptive Statistics

Our analysis is based on data from the European Farm Accountancy Data Network (FADN).^{Footnote 2} This database includes annual farm-level data on surface, yield, value of wine production, working hours, cost of pesticides, fertilizers, and labor. Our dataset consists of a balanced panel of 100 winegrowers in the main French wine production basins and 25 winegrowers in the Champagne region over the 2005–2014 period, which led to a sample of 1,250 observations. This sample includes the most important wine production basins in France: Alsace, Beaujolais, Bordelais, Bourgogne, Languedoc-Roussillon (Lang. Rouss.), Provence-Aples-Côte-d'Azur (PACA), Rhône, Sud-Ouest, Val de Loire, and Champagne. For annual authorized yield figures in each wine production region, we use a database compiled by the French National Institute of Origin and Quality (INAO). Table 1 provides an overview of the data.

III. Theoretical Model

Our empirical specification is based on the assumption that there is uncertainty around the level of output relative to the level of input. We consider a winegrower who makes ex-ante decisions about quantities of inputs. We consider that quantities of pesticides are chosen before output realizations are known. Therefore, we assume that the winegrower maximizes his expected utility of profits with the decisions program given as follows:

(1)$$\mathop {\max} \limits_{x,y} \lcub {E\lpar {U\lpar \pi \rpar } \rpar = E\lpar {U\lpar {\,py-{w}^{\prime}x} \rpar } \rpar } \rcub ,$$

where U(π) is a Von Neumann-Morgenstern utility function form and π = py − ω′x is the profit of the winegrower. y represents output, p denotes the price of output, x a vector of variable inputs, and ω a vector of variable input prices.

We define a multiplicative stochastic production function given by y = f(x)ϵ, where ϵ is a non-negative random term. This random term ϵ represents exogenous shocks that may affect grape production. We assume that E(ϵ) = 1 and Var(ϵ) = σ _ϵ = 2 (Just and Pope, Reference Just and Pope1978). We denote by $\bar{y}$ the ex-ante planned output level.

In this context, the expected utility-maximizer winegrower will choose the quantity of inputs that minimize his cost of producing the expected output level $\bar{y}$. Thenceforth, the ex-ante cost dual to the expected output function is defined as:

(2)$$c\lpar {w,\bar{y}} \rpar = \mathop {\min} \limits_x \lcub {{w}^{\prime}x{:}\;f\lpar x \rpar \ge \bar{y},x \ge 0} \rcub. $$

This cost function represents the minimum factor cost of producing the expected output level y when the input price vector is w. The factor share equations are obtained using Shephard's lemma with s _i = ∂ln(c(w, $\bar{y}$))/∂ln(w _i), where s _i represents the cost share on input i.

As explained earlier, we split the expected utility maximization process into two stages. In the first stage, the winegrower chooses the input level that minimizes his cost of producing the expected output quantity $\bar{y}$. In the second stage, the winegrower chooses the output level $\bar{y}$ that maximizes his expected utility of profit, given the costs computed in the first stage, as follows:

(3)$$\mathop {\max} \limits_{\bar{y} \ge 0} \lcub {E\lpar {U\lpar {\,p\epsilon \bar{y}-c\lpar {w,\bar{y}} \rpar } \rpar } \rpar } \rcub .$$

The first order condition with respect to the planned output $\bar{y}$ is as follows:

(4)$$\displaystyle{{\partial E\lpar {u\lpar \pi \rpar } \rpar } \over {\partial \bar{y}}} = p\theta \lpar. \rpar -\displaystyle{{\partial c(w,{\bar y)}} \over {\partial \bar{y}}} = 0.$$

The function θ($\bar{y}$, w, p) represents the risk preferences function and is defined by θ($\bar{y}$, w, p) = E(U′ϵ)/E(U′), where U′(π) is the marginal utility of profit.

Following Kumbhakar and Tveteras (Reference Kumbhakar and Tveteras2003), we approximate U′(π) by a second-order polynomial at the point (ϵ − 1 = 0). This approximation is made under the assumption that U(π) is continuous and at least twice differentiable. This allows us to rewrite the risk preferences function as a function of the Arrow-Pratt measure of absolute risk aversion (ARA), with the variance of winegrower profit (σ _π² = p ²$\bar{y}$²), the degree of asymmetry or the skewness of the distribution of ϵ (γ = E(ϵ ³)), and the measure of downside risk aversion (DRA = U′′′(π)/U′(π)). Thus, this risk preferences function can be rewritten as follows:

(5)$$\theta \lpar {\bar{y},w,p} \rpar = \displaystyle{{1-ARA\sigma _\pi + 0.5DRA\sigma _\pi ^2 \lpar {\gamma -3} \rpar } \over {1 + 0.5DRA\sigma _\pi ^2}}. $$

The estimation of this risk preferences function requires a parametric form of ARA. Following Kumbhakar and Tveteras (Reference Kumbhakar and Tveteras2003), we define this Arrow-Pratt measure of absolute risk aversion as: ${\rm A}RA = \; \mathop \sum \nolimits_{q = 0}^Q \delta _q\mu _\pi ^q $. This is a flexible parametric function of the winegrower's expected profit μ _π, where q is the order of the polynomial and δ _q are parameters to be estimated. In our case, the winegrower's expected profit is defined as: μ _π = E [pϵ $\bar{y}$ – c(w, $\bar{y}$)], which is equal to μ _π = p $\bar{y}$ – c(w, $\bar{y}$).

The planned output ($\bar{y}$) is not observable. We, therefore, use the appellation yield constraint as a proxy for expected output. In order to rigorously estimate winegrowers gross profit, we assume that the planned output corresponds to the minimum between the yield obtained (y) and the appellation yield constraint ($\hat{y}$). In other words, yield = min (y; $\bar{y}$). Thus, μ _π = p · min (y, $\hat{y}$) – c(w, $\hat{y}$).

The measure of downside absolute risk aversion can be derived from ARA as follows: DRA = − ∂ARA/∂μ _π + ARA ². We simultaneously estimate the factor share parameters s _i and the risk preferences function. A positive sign for the derivative of ARA with respect to μ _π indicates an increasing absolute risk aversion, while a negative sign indicates a decreasing absolute risk aversion. When the derivative is equal to zero, we consider absolute risk aversion as constant. The specifications of the empirical model are further described in Aka, Alonso Ugaglia, and Lescot (Reference Aka, Alonso Ugaglia and Lescot2018).

IV. Results: Risk Attitudes Estimates

Risk attitudes are based on the values of the risk preferences function (θ). However, the ARA and downside risk aversion (DRA) values are more interesting to analyze than the θ-function. Indeed, the magnitude of the risk preferences function is influenced by the output variance, the skewness of output distributions, ARA, and DRA.

A positive ARA indicates risk aversion, and a large positive value signals strong aversion to risk. DRA illustrates the fact that, when choosing between two output distributions with the same mean and variance, winegrowers prefer the output distribution which is less skewed to the left (Kumbhakar and Tveteras, Reference Kumbhakar and Tveteras2003). Intuitively, winegrowers are willing to pay a premium in order to avoid particularly bad outcomes (Koundouri et al., Reference Koundouri, Laukkanen, Myyra and Nauges2009). A positive DRA indicates that individual producers are averse to downside risk.

Another interesting measure of risk aversion is the Relative Risk Premium (RRP), where $RRP = \; \textstyle{{\sigma _\pi ^2 ARA} \over {2\mu}} -\; \textstyle{{\sigma _\pi ^3 \lpar {E\lpar {\epsilon^3} \rpar -4} \rpar DRA} \over {6\mu}} $ (Antle, Reference Antle1987). RRP measures the share of profit that a winegrower is willing to sacrifice to avoid production risk.

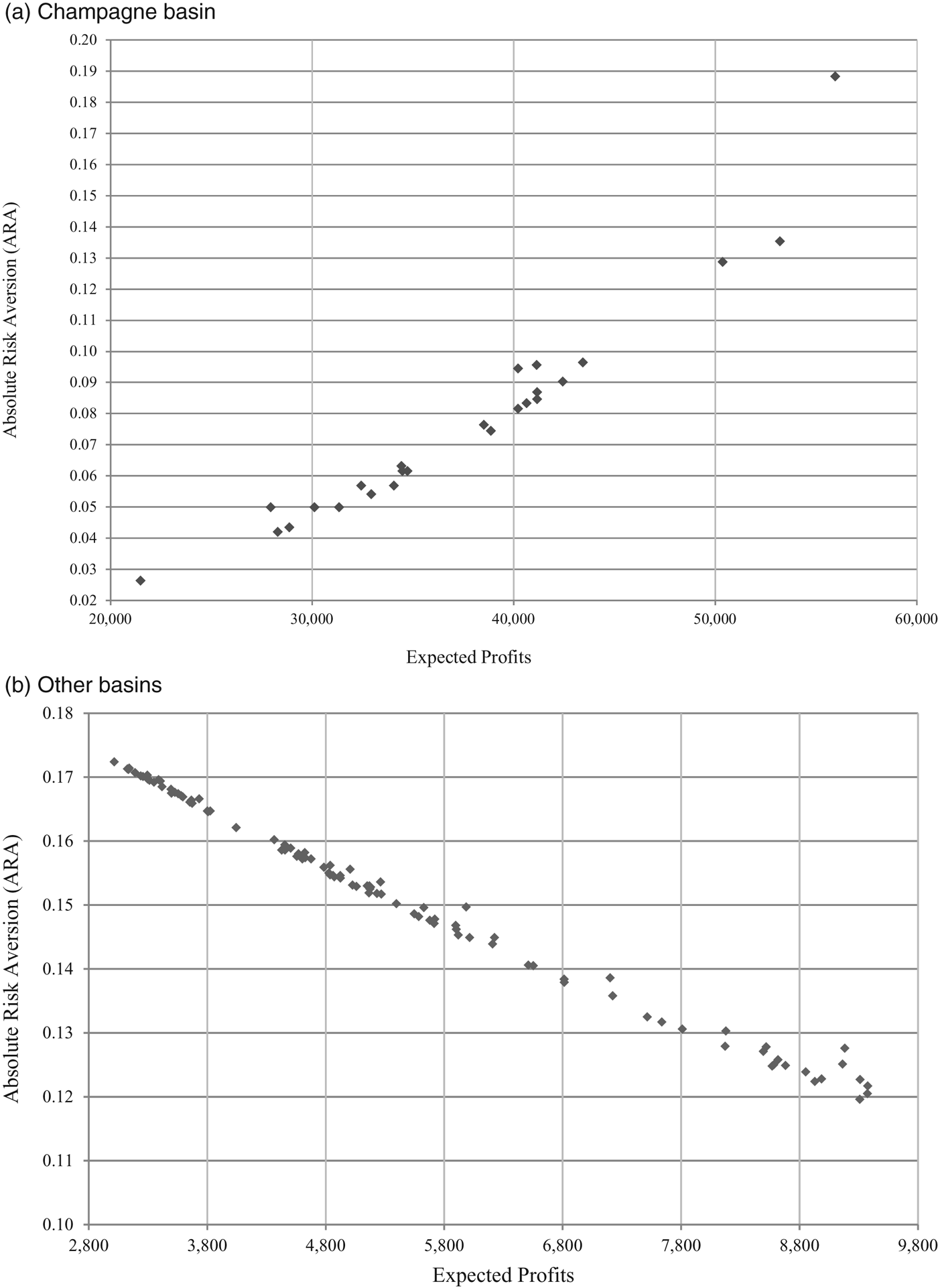
Figure 1 presents ARA points as a function of expected profits. We set out to test whether risk aversion is increasing or decreasing with expected profit. In our sample for other basins, we find that winegrowers display decreasing absolute risk aversion (ARA), or “DRA.” This finding is consistent with several empirical analyses on farmers’ risk attitudes (Koundouri et al., Reference Koundouri, Laukkanen, Myyra and Nauges2009; Foudi and Erdlenbruch, Reference Foudi and Erdlenbruch2012). Results for the Champagne region, however, are consistent with our initial intuition: when expected profits are very high, risk aversion increases with expected profit. The behavior of producers in Champagne is different from that in the other regions.

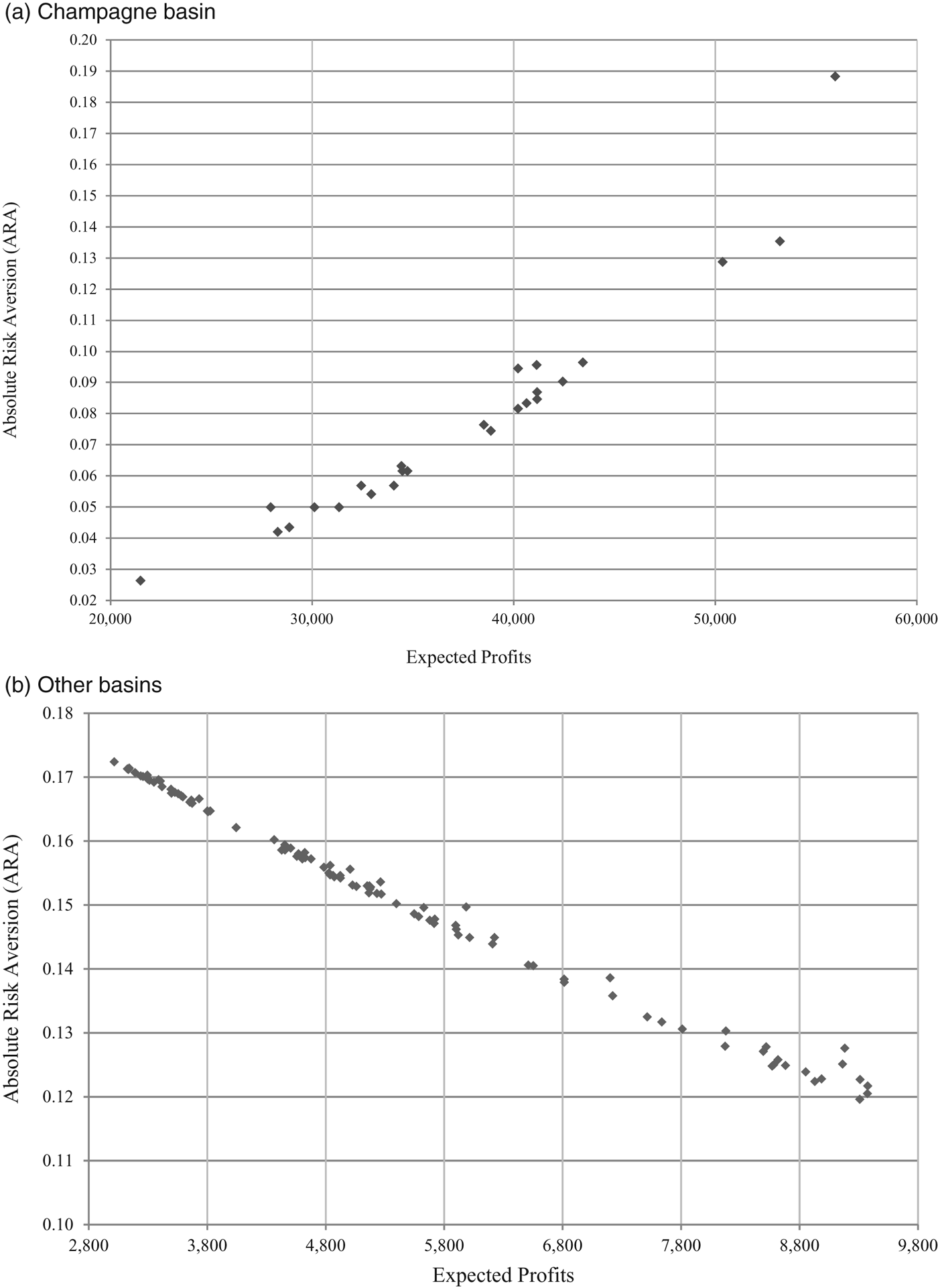
Figure 1 Arrow-Pratt Coefficients as a Function of Expected Profits

We now turn our attention to risk attitudes in the main wine basins. The ARA value in Alsace, Bourgogne, and Rhône is positive (0.14), but lower than in other basins, although the difference is small (0.15 or 0.16). Champagne stands out with an ARA coefficient of 0.08, indicating that Champagne winegrowers are less risk averse than winegrowers in other regions. RRPs in all basins range from 0.3 to 7%. RRP is highest in the Champagne basin. We find that risk aversion attitudes evolve differently in Champagne than in other regions: in Champagne, risk aversion increases with expected profit. This difference is due to Champagne's exceptionally high value of production. For this product, sometimes considered as a luxury good rather than a type of wine, the level of expected profit is such that the risk aversion of the producers is higher.