INTRODUCTION
Interactions among species are not randomly structured and numerous studies have shown that networks of species’ interactions show some recurrent patterns (Bascompte Reference BASCOMPTE2009). One such pattern is the presence of modules, i.e. subunits or compartments, with within-group prevalence of interactions (Olesen et al. Reference OLESEN, BASCOMPTE, DUPONT and JORDANO2007, Vázquez et al. Reference VÁZQUEZ, BLUTHGEN, CAGNOLO and CHACOFF2009a). Modules have been detected in distinct types of interaction networks, including plant-pollinator (Martín González et al. Reference MARTÍN GONZÁLEZ, ALLESINA, RODRIGO and BOSCH2012, Maruyama et al. Reference MARUYAMA, VIZENTIN-BUGONI, OLIVEIRA, OLIVEIRA and DALSGAARD2014, Olesen et al. Reference OLESEN, BASCOMPTE, DUPONT and JORDANO2007), prey-predator (Krause et al. Reference KRAUSE, FRANK, MASON, ULANOWICZ and TAYLOR2003), host-parasite (Krasnov et al. Reference KRASNOV, FORTUNA, MOUILLOT, KHOKHLOVA, SHENBROT and POULIN2012), plant-ant (Fonseca & Ganade Reference FONSECA and GANADE1996) and plant-frugivore networks (Donatti et al. Reference DONATTI, GUIMARÃES, GALETTI, PIZO, MARQUITTI and DIRZO2011, Mello et al. Reference MELLO, MARQUITTI, GUIMARÃES, KALKO, JORDANO and DE AGUIAR2011, Schleuning et al. Reference SCHLEUNING, INGMANN, STRAUS, FRITZ, DALSGAARD, MATTHIAS DEHLING, PLEIN, SAAVEDRA, SANDEL, SVENNING, BÖHNING-GAESE and DORMANN2014). Modular organization can also be found at different hierarchical levels; meaning that modules have been reported not only for communities, but also within population interactions performed by each individual of a species (Tur et al. Reference TUR, OLESEN and TRAVESET2015). Likewise, modules within modules are also expected in nature (Dormann & Strauss Reference DORMANN and STRAUSS2014). Organization of the interactions into distinct modules is theoretically expected to promote species coexistence and community stability as perturbations are unlikely to spread quickly across different modules in the network (Stouffer & Bascompte Reference STOUFFER and BASCOMPTE2011, Tylianakis et al. Reference TYLIANAKIS, LALIBERTÉ, NIELSEN and BASCOMPTE2010).
Once modules are identified, species in the network can also be classified according to distinct roles, whether they are important connectors of different modules and/or act as central components within a module (Olesen et al. Reference OLESEN, BASCOMPTE, DUPONT and JORDANO2007, Schleuning et al. Reference SCHLEUNING, INGMANN, STRAUS, FRITZ, DALSGAARD, MATTHIAS DEHLING, PLEIN, SAAVEDRA, SANDEL, SVENNING, BÖHNING-GAESE and DORMANN2014). Although modular structure is frequent in nature, this pattern might be less pronounced when analysing some subgroups within communities. For instance, plant-frugivore networks seem to be less modular than other types of interaction (Rezende et al. Reference REZENDE, ALBERT, FORTUNA and BASCOMPTE2009), but this trend might reflect the overrepresentation of plant-bird networks in the available datasets which in fact comprise only one taxonomic and presumably few functional groups of seed dispersers (Donatti et al. Reference DONATTI, GUIMARÃES, GALETTI, PIZO, MARQUITTI and DIRZO2011, Mello et al. Reference MELLO, MARQUITTI, GUIMARÃES, KALKO, JORDANO and DE AGUIAR2011). Furthermore, most of the studies conducted so far are based on binary interaction data which might overestimate the role of rare and singleton species and/or underestimate highly interactive species (Dormann & Strauss Reference DORMANN and STRAUSS2014).
Plant-frugivore interactions are marked by large overlaps and resource share (Silva & Melo Reference SILVA and MELO2013, Terborgh & Diamond Reference TERBORGH and DIAMOND1970), which ultimately lead to low levels of complementary specialization in relation to other types of interaction (Blüthgen et al. Reference BLÜTHGEN, MENZEL, HOVESTADT, FIALA and BLÜTHGEN2007). In spite of this, some assemblages of closely related animal-dispersed plants show apparent pattern of sequential fruiting, which might minimize the competition for seed dispersers and finally benefit the entire community of frugivores by providing constant supply of food resources (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999). In this sense, closely related plants which present similar fruits, thus impairing formation of morphology related modules, yet temporally segregating their fruiting phenology could be a good system to test whether temporal distribution of interactions drives formation of modules in small networks. By contrasting binary and weighted modularity algorithms, we can also demonstrate the importance of considering the strength of the interactions to detect subtle structural patterns in ecological networks (Dormann & Strauss Reference DORMANN and STRAUSS2014). Here we use data on interaction of four assemblages of Miconia (Melastomataceae) and their frugivorous birds from Neotropical habitats to test the following hypotheses: (1) networks centred on Miconia are modular and each module is composed of a Miconia species and their main partners; (2) modules in these networks can be efficiently detected by weighted algorithms and (3) dietary specialization is the bird trait that best explains species roles in the modular networks.
METHODS
Plant species
Miconia (Melastomataceae) with c. 1100 described species is one of the richest genera among Neotropical angiosperms. Miconia species can present many habits including shrubs, herbs, epiphytes, treelets and trees, and are usually associated with edges and natural gaps in the vegetation (Ellison et al. Reference ELLISON, DENSLOW, LOISELLE and BRENES1993). Plants from this group can be found in a range of environments, from open habitats as grasslands to savannas and extremely humid tropical rain forests (Romero & Martins Reference ROMERO and MARTINS2002). One important characteristic of Miconia is a tight association to frugivorous animals for seed dispersal. The small carbohydrate-rich fruits contain numerous tiny seeds and are eaten and dispersed by several species of bird, including many generalist species (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Snow Reference SNOW1981). Furthermore, species of Miconia are among the most important resources for fruit-eating birds in Neotropical environments (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Stiles & Rosselli Reference STILES and ROSSELLI1993). Commonly, assemblages of Miconia species show asynchronous and complementary fruiting period (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999) which is believed to reduce interspecific competition for dispersal agents (Wheelwright Reference WHEELWRIGHT1985) and might contribute to the high number of species of this genus occurring in sympatry.
Interaction data
Data on interaction of Miconia and frugivorous birds came from four distinct communities, three from the Neotropical savannas in Brazil and one from the rain forest of Panama. Savanna networks were collected at Caça e Pesca (18°55′S, 48°17′W, Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013), Panga (19°10′S, 48°23′W, Borges Reference BORGES2010, Appendix 1) and Duratex (18°50′S, 47°49′W, Paniago Reference PANIAGO2014, Appendix 2), all areas with remnants of native vegetation in the region. In each of these sites, interactions among species of Miconia and frugivore birds were recorded through focal observations, where the observers remained about 10 m distant from the focal tree and recorded the fruit-eating interactions. From these records, we constructed bipartite interaction matrices with each cell representing the number of interaction events, i.e. instances in which a bird visited a plant individual, of the corresponding plant-bird pair. For the Panamanian network, data were collected at Soberania National Park (09°10'N, 79°07'W, Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999) and instead of visits, interaction strength among a pair of species is represented by the number of fruit records in regurgitation or faecal samples collected from mist-netted birds (Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999). Although differences in the methods to record the interaction exist, this should not affect our overall interpretation of the results as we are characterizing the networks pattern within each of the communities. After constructing these matrices considering the frequency–strength of the interaction, we also constructed for each of the matrices a binary version, representing the presence or absence of interaction among a pair of plant and bird. Networks used in our study were the only ones in literature that are collected specifically for Miconia assemblages which ensured an equivalent sampling for each plant species. Hence, although some broader community-wide networks containing Miconia species are available in the literature, we did not include those here.
Network analysis
To measure the binary modularity in the networks, we used the software MODULAR (Marquitti et al. Reference MARQUITTI, GUIMARÃES, PIRES and BITTENCOURT2014), quantifying the modularity using the metric proposed by Barber (Reference BARBER2007) for bipartite networks:
 $$\begin{equation*}
{Q_B} = \mathop \sum \limits_{i = 1}^{{N_M}} \left[ {\frac{{{E_i}}}{E} - \left( {\frac{{k_i^C.{\rm{\ }}k_i^R}}{{{E^2}}}} \right)} \right],
\end{equation*}$$
$$\begin{equation*}
{Q_B} = \mathop \sum \limits_{i = 1}^{{N_M}} \left[ {\frac{{{E_i}}}{E} - \left( {\frac{{k_i^C.{\rm{\ }}k_i^R}}{{{E^2}}}} \right)} \right],
\end{equation*}$$
where NM is the number of modules, Ei is the number of links in module i, E is the number of links in the complete network, ki C is the sum of the degrees of the nodes within module i that belong to set C and ki R is the sum of the degrees of the nodes within module i that belong to set R. The significance of the bipartite modularity was compared against 1000 random networks, generated by two null models. The first one is the Erdős–Rényi model (Erdős & Rényi Reference ERDŐS and RÉNYI1959), where each pair of nodes has the same probability of being connected by a link and the second is null model 2 (Bascompte et al. Reference BASCOMPTE, JORDANO, MELIÁN and OLESEN2003), where the probability of a pair being connected by an edge is proportional to the number of edges that the nodes have.
To quantify the modularity in the weighted networks, we used the algorithm QuanBiMo (Dormann & Strauss Reference DORMANN and STRAUSS2014). This algorithm detects the presence of modules in weighted bipartite networks based on a hierarchical representation of species link weights and optimal allocation to modules (Dormann & Strauss Reference DORMANN and STRAUSS2014). The algorithm is a modification of the Newman's quantity of modularity Q (Barber Reference BARBER2007):
 $$\begin{equation*}
Q = \frac{1}{{2N}}\mathop \sum \limits_{ij}^{\rm{\ }} \left( {{A_{ij}} - {K_{ij}}} \right)\delta \left( {{m_i},{m_j}} \right),
\end{equation*}$$
$$\begin{equation*}
Q = \frac{1}{{2N}}\mathop \sum \limits_{ij}^{\rm{\ }} \left( {{A_{ij}} - {K_{ij}}} \right)\delta \left( {{m_i},{m_j}} \right),
\end{equation*}$$
where N is the total number of interactions in the network; Aij is the number of interactions between frugivorous species i and plant species j; Kij represents the random expected probability of interactions within a module; the function (mi , mj ) is 1 when species i and j are in the same module (mi = mj ) and 0 if they are in different modules (mi ≠ mj ). The modularity Q ranges from 0 (no support for division of modules) to 1 (maximum degree of modularity). The QuanBiMo algorithm was run with the function computeModules in R-package bipartite (Dormann et al. Reference DORMANN, FRÜND, BLÜTHGEN and GRUBER2009).
The absolute value of Q is dependent on network size and number of links (Dormann & Strauss Reference DORMANN and STRAUSS2014), so we tested the estimates of modularity Q with 1000 randomizations generated by two null models: Patefield null model (r2dtable) – which uses fixed marginal totals to distribute the interactions and produce a set of networks in which all species are randomly associated (Blüthgen et al. Reference BLÜTHGEN, FRÜND, VAZQUEZ and MENZEL2008); and the null model proposed by Vázquez et al. (Reference VÁZQUEZ, MELIÁN, WILLIAMS, BLÜTHGEN, KRASNOV and POULIN2007), which retain the number of interactions per species and the network connectance (vaznull).
To identify species roles in modular network we estimated for each species the within-module degree z and the among-module connectivity c-scores (Guimerà & Amaral Reference GUIMERÀ and AMARAL2005, Olesen et al. Reference OLESEN, BASCOMPTE, DUPONT and JORDANO2007):
 $$\begin{equation*}
c = 1 - \mathop \sum \limits_{t = 1}^{{N_M}} {\left( {\frac{{{k_{it}}}}{{{k_i}}}} \right)^2},{\rm{\ }}z = \frac{{{k_{is}} - {k_s}}}{{S{D_{ks}}}},
\end{equation*}$$
$$\begin{equation*}
c = 1 - \mathop \sum \limits_{t = 1}^{{N_M}} {\left( {\frac{{{k_{it}}}}{{{k_i}}}} \right)^2},{\rm{\ }}z = \frac{{{k_{is}} - {k_s}}}{{S{D_{ks}}}},
\end{equation*}$$
where, kis is number of links of i to other species in its own module s; ks and SDks are average and standard deviation of within module k of all species in s; ki is degree of species i; kit is number of links from i to species in module t. As binary networks did not show significant modularity, we only calculated the weighted version of these indices, which are computed based on species strength instead of number of links (Dormann & Strauss Reference DORMANN and STRAUSS2014). For calculations of weighted c and z-scores, we used the function czvalues in bipartite.
Bird traits
In order to relate network role of birds to their ecological traits, we gathered data on bird body mass, migration behaviour, dietary specialization and taxonomic family. As the morphology of the Miconia berries in this study is very similar (Maruyama et al. Reference MARUYAMA, ALVES-SILVA and MELO2007), bill gape width should not constrain the interaction, therefore, it was not considered here. The fruit-eating birds were classified into three dietary categories following Kissling et al. (Reference KISSLING, RAHBEK and BÖHNING-GAESE2007) as (1) obligate frugivores – species that have fruits as the major food items in their diet; (2) partial frugivores – species that include other major food items in diet; and (3) opportunistic fruit-eaters – species that only occasionally eat fruits as supplementary food resource. Data on the diet of birds were gathered from published studies, and for savanna areas also included personal observations in the areas of studies (del Hoyo et al. Reference DEL HOYO, ELLIOTT, SARGATAL, CHRISTIE and DE JUANA2015, Sick Reference SICK1997). Bird body mass influences food choices and the number of fruits consumed (Wotton & Kelly Reference WOTTON and KELLY2012), thus it might be related to the network role. For each bird species we obtained data on average body mass of adult specimens from the literature (Dunning Reference DUNNING2008). As temporal distribution of species in a community might constrain the partners to interact with (Vázquez et al. Reference VÁZQUEZ, CHACOFF and CAGNOLO2009b, Vizentin-Bugoni et al. Reference VIZENTIN-BUGONI, MARUYAMA and SAZIMA2014), we classified the migratory behaviour of the bird species as: (1) resident – sedentary species that remain year-round in the area; (2) nomad – a species that perform irregular moments in response to resource availability; and (3) migratory – species that make short or long and well-defined seasonal movements. Movement information was gathered from Loiselle & Blake (Reference LOISELLE and BLAKE1991), Nunes & Tomas (Reference NUNES and TOMAS2008), del Hoyo et al. (Reference DEL HOYO, ELLIOTT, SARGATAL, CHRISTIE and DE JUANA2015) and personal observations. Finally, as many traits in birds are phylogenetically conserved (Losos Reference LOSOS2008), we also included the family of birds as a category in our analysis to reflect species relatedness. Classification and nomenclature of birds followed the South American Classification Committee (Remsen et al. Reference REMSEN, ARETA, CADENA, JARAMILLO, NORES, PACHECO, PÉREZ-EMÁN, STILES, STOTZ and ZIMMER2015).
Statistical analysis
The relationship between network roles, as represented by c and z scores, and bird traits was evaluated with linear mixed-effects models (Bolker et al. Reference BOLKER, BROOKS, CLARK, GEANGE, POULSEN, STEVENS and WHITE2009). We used as fixed factors the body mass, dietary specialization, migratory behaviour and taxonomic family. Bird species identity was included as a random effect to account for non-independence within observations of the same species in different networks (Bolker et al. Reference BOLKER, BROOKS, CLARK, GEANGE, POULSEN, STEVENS and WHITE2009). For each of the response variables, c and z-scores, we ran the models separately. The full model including all factors and reduced models were fitted using the function dredge in R package MuMln and compared by their values of the Akaike information criterion corrected for small sample sizes (Bolker et al. Reference BOLKER, BROOKS, CLARK, GEANGE, POULSEN, STEVENS and WHITE2009). Models with ΔAICc ≤ 2 were considered as equivalent.
RESULTS
Considering all networks, 66 species of bird, 12 Miconia species and 953 interactions were recorded. Thraupidae were the best-represented family with 24 species (36.4%), followed by Tyrannidae with 11 (16.7%). Seventeen (25.8%) species were classified as obligate frugivores, while 23 (34.8%) and 26 (39.4%) were classified as partial frugivores and opportunistic fruit-eaters, respectively. For migratory behaviour, 43 species (65.1%) are resident, 10 (15.2%) are nomad and 13 (19.7%) are migrant. Considering the body mass, most birds are small with 87.9% of the bird species weighing less than 100 g.
When considering binary matrices, none of the networks had values of modularity different from random, irrespective of the null models used. All quantitative versions of the networks, in contrast, were modular with each presenting three modules (P < 0.01 for both null models; Table 1). Each module within these networks contained one or two Miconia species associated with their most common frugivores (Figure 1). Model selection showed that neither c nor z-scores can be associated to body mass, dietary specialization, migratory behaviour and bird family, as no model including fixed factors performed better than the model including only the intercept (Table 2).
Table 1. Values of modularity in binary and weighted versions of four Miconia-frugivore bird networks: Caça e Pesca (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013), Panga (Borges Reference BORGES2010), Duratex (Paniago Reference PANIAGO2014) and Panama (Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999); and the significance against the null models. Null 1 = Erdős and Rényi model (Erdős & Rényi Reference ERDŐS and RÉNYI1959); Null 2 = “null model 2” of Bascompte et al. (Reference BASCOMPTE, JORDANO, MELIÁN and OLESEN2003); r2dtable = Null model Patefield (Patefield Reference PATEFIELD1981); vaznull = Null model proposed by Vázquez et al. (Reference VÁZQUEZ, MELIÁN, WILLIAMS, BLÜTHGEN, KRASNOV and POULIN2007); Qobs = value of modularity Q observed in the networks; Qnull = value of mean modularity Q generated by 1000 null models.

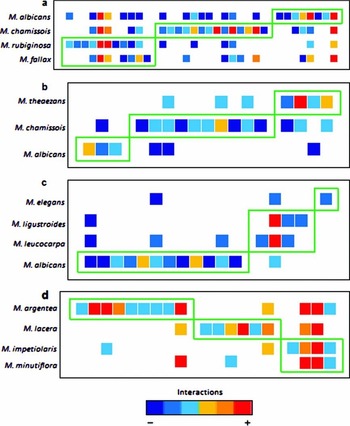
Figure 1. Modules identified by the QuanBiMo algorithm in four weighted Miconia-frugivore bird networks: Caça e Pesca (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013) (a), Panga (Borges Reference BORGES2010) (b), Duratex (Paniago Reference PANIAGO2014) (c) and Panama (Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999) (d). Warm tones represent a higher number of interactions and cool tones represent fewer interactions. The green boxes represent the modules identified and each row represents a Miconia species.
Table 2. Comparisons of statistical models containing combinations of bird traits that explaining the within- and among-module connectivity indices (c and z scores) in four Miconia-frugivore bird networks (Borges Reference BORGES2010, Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Paniago Reference PANIAGO2014, Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999). Models with ΔAICc < 2 were considered equivalent and include here in the table. None of the bird trait models has more explanatory power than the models containing only the intercept.

DISCUSSION
Modules could only be found by incorporating the strength of the interactions in Miconia-bird networks. The importance of using weighted information, such as interaction strength in network analyses has been recognized as an important step in understanding the architecture of ecological communities (Gilarranz et al. Reference GILARRANZ, PASTOR and GALEANO2012, Ings et al. Reference INGS, MONTOYA, BASCOMPTE, BLÜTHGEN, BROWN, DORMANN, EDWARDS, FIGUEROA, JACOB, JONES, LAURIDSEN, LEDGER, LEWIS, OLESEN, VAN VEEN, WARREN and WOODWARD2009). Schleuning et al. (Reference SCHLEUNING, INGMANN, STRAUS, FRITZ, DALSGAARD, MATTHIAS DEHLING, PLEIN, SAAVEDRA, SANDEL, SVENNING, BÖHNING-GAESE and DORMANN2014), in a study with 18 plant-frugivore networks, found that only one third presented significant modularity with binary data, while including information on the strength of interaction allowed the detection of modules in all but one of these networks. Similarly, although small binary pollination networks do not show distinct modular organization (Olesen et al. Reference OLESEN, BASCOMPTE, DUPONT and JORDANO2007), the inclusion of quantitative information led to the detection of modules even in species-poor hummingbird-plant pollination networks (Maruyama et al. Reference MARUYAMA, VIZENTIN-BUGONI, OLIVEIRA, OLIVEIRA and DALSGAARD2014, Reference MARUYAMA, VIZENTIN-BUGONI, DALSGAARD, SAZIMA and SAZIMA2015). Moreover, these modules are associated to the functional traits of the species (Maruyama et al. Reference MARUYAMA, VIZENTIN-BUGONI, OLIVEIRA, OLIVEIRA and DALSGAARD2014, Reference MARUYAMA, VIZENTIN-BUGONI, DALSGAARD, SAZIMA and SAZIMA2015). Overall, it seems that inclusion of quantitative information led to detection of finer partitioning in networks.
Interspecific competition among plants for dispersal agents is regarded as a force that can shape the structure of plant-frugivore interactions (Herrera Reference HERRERA1981, Howe & Estabrook Reference HOWE and ESTABROOK1977, Howe & Smallwood Reference HOWE and SMALLWOOD1982). As interaction pressures are expected to be stronger among closely related species due to similarity in niches (Webb et al. Reference WEBB, ACKERLY, MCPEEK and DONOGHUE2002), sympatric congeneric species tend to have mechanisms to ensure their co-existence (Beltrán et al. Reference BELTRÁN, VALIENTE-BANUET and VERDÚ2012). Berries of the 12 Miconia species analysed are very similar in morphology and nutritional values (Maruyama et al. Reference MARUYAMA, ALVES-SILVA and MELO2007), meaning that these traits play little role in selection of different dispersal agents, and hence in generating modules. However, the fruiting asynchrony observed, with no overlap in fruiting peak among the sympatric species (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999), potentially suffices to generate the modular structure and also facilitate the co-existence of species by promoting facilitation among plants (Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999).
The abundance of bird populations fluctuates year-round, especially in seasonal environments, due to several factors, such as total or partial migration and dispersal (Loiselle & Blake Reference LOISELLE and BLAKE1991). Moreover, more than one third of the species associated with the Miconia species perform seasonal movements. Frugivorous birds are subject to high resource fluctuations (Loiselle & Blake Reference LOISELLE and BLAKE1991), having greater tendency to seasonal movement compared with insectivorous species (Levey & Stiles Reference LEVEY and STILES1992). Nevertheless, bird migration behaviour did not strongly associate to species role in the networks. One important point that should be noticed, though, is that consumer species may seasonally switch their foraging behaviour according to resource variability (Carnicer et al. Reference CARNICER, JORDANO and MELIAN2009), e.g. insectivorous and omnivorous birds can change the proportion of fruits in their diet according to the availability of their main resources (Borghesio & Laiolo Reference BORGHESIO and LAIOLO2004) or with the life stage (Robbins Reference ROBBINS1981). Even within more specialized frugivorous birds, the availability of fruiting plants other than Miconia might change the relative attractiveness of these less-rewarding carbohydrate-rich fruits (Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013). In this sense, this potential diet variation in frugivorous birds would function as a seasonal pattern in fruit consumption, which coupled with possible abundance fluctuation and asynchronic fruiting period in Miconia could favour the formation of modules comprising birds (or their seasonal diet preferences) and plant species with stronger phenological overlap.
None of the bird morphological traits or taxonomic relatedness affected the within- and among-module connectivity. In general, body mass has been shown to be an important driver in structuring ecological networks (Arim et al. Reference ARIM, BERAZATEGUI, BARRENECHE, ZIEGLER, ZARUCKI and ABADES2011, Rezende et al. Reference REZENDE, ALBERT, FORTUNA and BASCOMPTE2009), although it has been shown to have little explanatory power in the variation of centrality metrics in plant-frugivore networks (Mello et al. Reference MELLO, RODRIGUES, COSTA, KISSLING, ŞEKERCIOĞLU, MARQUITTI and KALKO2015). This lack of association might be especially likely if the assemblage of animals considered shows little variation in the trait. Birds associated with Miconia are mostly passerines, a group composed by small- to medium-sized species. Fruit-eating bird assemblages dominated by small-bodied species tend to be less specialized (Menke et al. Reference MENKE, BÖHNING-GAESE and SCHLEUNING2012), resulting in modularity roles more evenly distributed among bird species. Furthermore, Saavedra et al. (Reference SAAVEDRA, HENSEN, BECK, BÖHNING-GAESE, LIPPOK, TÖPFER and SCHLEUNING2014) found little effect of morphological traits in interaction strength in the forest-edge frugivore networks, where Miconia species are widespread and small-bodied birds are predominant. Considering the dietary specialization, obligate and partial frugivorous had within- and among-module connectivity values higher than opportunistic ones in most community-wide plant-frugivorous bird networks (Schleuning et al. Reference SCHLEUNING, INGMANN, STRAUS, FRITZ, DALSGAARD, MATTHIAS DEHLING, PLEIN, SAAVEDRA, SANDEL, SVENNING, BÖHNING-GAESE and DORMANN2014). Once again, the fact that most birds associated with Miconia are generalist, small-bodied birds is probably related to the lack between diet and network roles, since even generalist frugivores have important roles in dispersing the seed of these species (Howe Reference HOWE1993, Maruyama et al. Reference MARUYAMA, BORGES, SILVA, BURNS and MELO2013, Poulin et al. Reference POULIN, WRIGHT, LEFEBVRE and CALDERÓN1999, Snow Reference SNOW1981). Nevertheless, this independence from specific groups of dispersal agents may ensure the seed dispersal services from a variety of species (Jordano et al. Reference JORDANO, GODOY, GARCIA and GARCÍA-CASTAÑO2007) which is especially important for high-fecundity pioneer species with small-seeded fruits (Howe Reference HOWE1993).
At what hierarchical level or with what kind of information, i.e. binary and weighted, modules can be detected in ecological systems is still only beginning to be addressed in the literature (Schleuning et al. Reference SCHLEUNING, INGMANN, STRAUS, FRITZ, DALSGAARD, MATTHIAS DEHLING, PLEIN, SAAVEDRA, SANDEL, SVENNING, BÖHNING-GAESE and DORMANN2014, Tur et al. Reference TUR, OLESEN and TRAVESET2015). We showed that modular structure can be detected within closely related sympatric species, but only when using weighted information incorporating the strength of the interactions. The use of quantitative information has been argued for in recent studies (Dormann & Strauss Reference DORMANN and STRAUSS2014, Schleuning et al. Reference SCHLEUNING, INGMANN, STRAUS, FRITZ, DALSGAARD, MATTHIAS DEHLING, PLEIN, SAAVEDRA, SANDEL, SVENNING, BÖHNING-GAESE and DORMANN2014) and we hope our study illustrated how finer partitioning of interactions can be detected by using it. Even when evaluating the role of species within networks, analysing quantitative data may deeply affect how we quantify the importance of each species in a network (Scotti et al. Reference SCOTTI, PODANI and JORDÁN2007). The next question to answer is at what hierarchical level the detection of modular organization has real impact on how we assess the stability and dynamics of ecological systems. Modules have been detected for a myriad of ecological systems, from entire assemblage/community to within species/populations individual-based networks (Donatti et al. Reference DONATTI, GUIMARÃES, GALETTI, PIZO, MARQUITTI and DIRZO2011, Tur et al. Reference TUR, OLESEN and TRAVESET2015). Closely related sympatric species also show a modular interaction pattern, possibly related to asynchronous fruiting period, but not with morphological and behavioural traits of birds such as body mass, diet and migratory behaviour. How each of these modular patterns, present at distinct layers of hierarchy, can promote co-existence of species and hence the functioning of ecological systems, deserve further investigation in the future.
ACKNOWLEDGEMENTS
We thank Jeferson Vizentin-Bugoni and Luís Paulo Pires for comments on a previous version of the manuscript. Funding was provided by CAPES through a PhD scholarship to AMS and CNPq through a PhD scholarship to PKM. We also thank Mariana Ribeiro Borges for sharing her data from Panga. Finally, we thank Duratex S.A. for financial support and permission to carry out data collection in their natural reserve area.
Appendix 1. Frugivory interaction matrix between three Miconia species and 17 bird species in a Neotropical savanna in Brazil (Panga; 19°10′S, 48°23′W). Frugivory interactions were recorded from April to November 2007 with 30–42 h of focal-plant observation per Miconia species. Source: Borges (Reference BORGES2010).

Appendix 2. Frugivory interaction matrix between four Miconia species and 17 bird species in a Neotropical savanna in Brazil (Duratex; 18°50′S, 47°49′W). Frugivory interactions were recorded from August 2012 to December 2013 with about 35 h of focal-plant observation per Miconia species. Source: Paniago (Reference PANIAGO2014).








