INTRODUCTION
Degradation rates in the lowland tropical rain forests of South-East Asia have increased significantly and secondary forests are rapidly becoming a common land-cover type in the area, especially in the last 50 y (Brown & Lugo Reference BROWN and LUGO1990, De Jong et al. Reference DE JONG, CHOKKALINGAN and SMITH2001, Hansen & DeFries Reference HANSEN and DEFRIES2004, Wright Reference WRIGHT2005). Consequently, secondary forests have the potential to assimilate and store relatively large fractions of carbon that are lost during deforestation and other land-use changes (Hughes et al. Reference HUGHES, KAUFFMAN and JARAMILLO1999, Jepsen Reference JEPSEN2006, Lawrence Reference LAWRENCE2005).
To accurately estimate biomass, it is preferable to develop allometric relationships for plant-part biomass components and tree diameter because disturbance is avoided and it is possible to investigate large study areas (Brown Reference BROWN1997, Chave et al. Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005, Cole & Ewel Reference COLE and EWEL2006, Lavigne & Krasowski Reference LAVIGNE and KRASOWSKI2007, Niklas Reference NIKLAS1994). Moreover, the reliability of estimation using the relationships is usually high, even when there are many tree species within the same forest stand (Kira & Shidei Reference KIRA and SHIDEI1967, Santantonio et al. Reference SANTANTONIO, HERMANN and OVERTON1977, Yamakura et al. Reference YAMAKURA, HAGIHARA, SUKARDJO and OGAWA1986).
Although several sets of allometric equations have been developed to estimate above-ground biomass in tropical secondary forests (Hashimoto et al. Reference HASHIMOTO, KOJIMA, TANGE and SASAKI2000, Ketterings et al. Reference KETTERINGS, COE, NOORDWIJK, AMBAGAU and PALM2001, Nelson et al. Reference NELSON, MESQUITA, PEREIRA, DE SOUZA, BATISTA and COUTO1999, Saldarriaga et al. Reference SALDARRIAGA, WEST, THARP and UHL1988, Uhl & Jordan Reference UHL and JORDAN1984), only a few studies have been conducted on root allometry in forests (Sierra et al. Reference SIERRA, DEL VALLE, ORREGO, MORENO, HARMON, ZAPATA, COLORADO, HERRERA, LARA, RESTREPO, BERROUET, LOAIZA and BENJUMEA2007). In particular, no studies have been done in South-East Asia due to the difficulty in directly measuring root biomass in the forest (Berish Reference BERISH1982, Cairns et al. Reference CAIRNS, BROWN, HELMER and BAUMGARDNER1997, Jackson et al. Reference JACKSON, CANADELL, EHLERINGER, MOONEY, SALA and SCHULZE1996, Vogt et al. Reference VOGT, VOGT, PALMIOTTO, BOON, O'HARA and ASBJORNSEN1996). Yet tree root systems must be considered because they are an important part of total forest biomass, representing 2–25% of the total biomass in various tropical rain forests (Andriesse & Schelhaas Reference ANDRIESSE and SCHELHAAS1987, Jackson et al. Reference JACKSON, MOONEY and SCHULZE1997, Lugo Reference LUGO1992, Sanford & Cuevas Reference SANFORD, CUEVAS, Mulkey, Chazdon and Smith1996, Santantonio et al. Reference SANTANTONIO, HERMANN and OVERTON1977), which have a larger amount of root biomass compared with other forest biomes (de Kroon & Visser Reference DE KROON and VISSER2003, Jackson et al. Reference JACKSON, CANADELL, EHLERINGER, MOONEY, SALA and SCHULZE1996).
Development of allometric relationships of both above- and below-ground biomass for tropical secondary-forest trees contributes to the accurate estimation of forest biomass in the tropical region. Presently, allometric equations derived from tropical primary forest trees are generally used to estimate the forest biomass of tropical regions including not only primary forest but also secondary forest (Brown Reference BROWN1997, Chave et al. Reference CHAVE, CONDIT, AGUILAR, HERNANDEZ, LAO and PEREZ2004, Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005; but see Jepsen Reference JEPSEN2006, Nelson et al. Reference NELSON, MESQUITA, PEREIRA, DE SOUZA, BATISTA and COUTO1999). However, tropical secondary forest consists of significantly different tree species with different structural traits such as lower wood density, tree height and rooting depth compared with the primary forest trees, and these traits generally relate to different coefficients of the allometric relationships (Chave et al. Reference CHAVE, CONDIT, AGUILAR, HERNANDEZ, LAO and PEREZ2004, Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005). Therefore, both above- and below-ground biomass of tropical secondary-forest trees may be overestimated compared with primary tropical rain-forest trees, and thus, development of allometric relationships of both above- and below-ground biomass for tropical secondary-forest trees is required for accurate estimation of biomass in the tropical area.
The objectives of this study were (1) to develop the allometric relationships between certain dimensional variables such as tree diameter and plant-part biomass, particularly in the roots, in tropical secondary forests in Sarawak, Malaysia and (2) to assess the variation and suitability of developed allometric relationships through comparison of relationships among previously reported equations developed for tropical primary and secondary forests and/or other forest biomes.
MATERIALS AND METHODS
Study sites
Our study was carried out in a post-fire secondary forest and a roadside secondary forest in the Niah Forest Reserve (3°39′N, 113°42′E) and the Sungai Liku area located in the Lambir Hills National Park (4°14′N, 114°04′E), respectively, in Sarawak, Malaysia. Both areas have a humid tropical climate. Annual rainfall and average temperature is about 2800 mm and 27 °C in Niah and 2400 mm and 26.3 °C in Sungai Liku, respectively (Kenzo et al. Reference KENZO, ICHIE, YONEDA, WATANABE, NINOMIYA and KOIKE2006, Reference KENZO, ICHIE, OZAWA, KASHIMURA, HATTORI, IRINO, KENDAWANG, SAKURAI and NINOMIYA2007). The soil at the Niah site is classified as Typic Kandihumult and is mainly composed of moderately soft grey mudstone and shale (Hattori et al. Reference HATTORI, SABANG, TANAKA, KENDAWANG, NINOMIYA and SAKURAI2005, Irino et al. Reference IRINO, KANG, KENZO, HATTORI, ISHIZUKA, NINOMIYA, IWASAKI, KENDAWANG and SAKURAI2005). The soil type at the Sungai Liku site is Ultisols. Soil chemical and physical properties at the A horizon were relatively similar between the two sites (Table 1).
Table 1. Mean total nitrogen (N), available phosphorus (P), exchangeable potassium (K), soil texture and elevation for the Niah site (Hattori et al. Reference HATTORI, SABANG, TANAKA, KENDAWANG, NINOMIYA and SAKURAI2005) and Sungai Liku site (Ishizuka et al. Reference ISHIZUKA, TANAKA, SAKURAI, HIRAI, HIROTANI, OGINO, LEE and KENDAWANG1998). Data on soil properties is at the A horizon (c. 0–10 cm from soil surface). Available phosphorus determined by the Bray II method and Truog method for Niah and Sungai Liku, respectively.

The original vegetation at both sites was lowland mixed dipterocarp forest. The forest at the Niah site underwent selective logging in the 1980s. At the end of the 1980s, after logging, shifting cultivation was started in the area. Shifting cultivation was conducted only once at the site. We mainly cut down the pioneer trees from 4–20-y-old forests after abandonment of shifting cultivation. We also conducted the study along a gravel road in the Sungai Liku area in Lambir. The road had been built around the 1980s and many pioneer trees, such as species of Macaranga and Ficus, covered the road side. The forests at Niah also mainly consist of pioneer trees such as species of Macaranga, Artocarpus and Ficus. Approximately 50% of the trees at both sites are Macaranga and Ficus species (Hattori et al. Reference HATTORI, KENZO, KENDAWANG, NINOMIYA, SAKURAI, Suzuki, Chong, Yoshifuji, Sakai, Kuraji and Nakashizuka2006). The other represented tree species were Glochidion spp., Callicarpa spp., Dillenia suffruticosa and Endospermum diadenum. Canopy height varied from 5 to 20 m with stand age. Relative light intensity measured by an illuminance meter (T-10, Konica Minolta, Japan) was approximately 8–10% (Kenzo et al. Reference KENZO, ICHIE, OZAWA, KASHIMURA, HATTORI, IRINO, KENDAWANG, SAKURAI and NINOMIYA2007). Such forests are widely distributed throughout tropical Asia, particularly on Borneo (Dennis et al. Reference DENNIS, HOFFMANN, APPLEGATE, VON GEMMINGEN and KARTAWINATA2001), and the species composition of the forests under study is typical of secondary tropical forests (Ewel et al. Reference EWEL, CHAI and LIM1983, Kendawang et al. Reference KENDAWANG, NINOMIYA, KENZO, OZAWA, HATTORI, TANAKA and SAKURAI2007, Mori Reference MORI, Guhardja, Fatawi, Sutisna, Mori and Ohta2000, Whitmore Reference WHITMORE1998).
Biomass measurements and allometric relationships
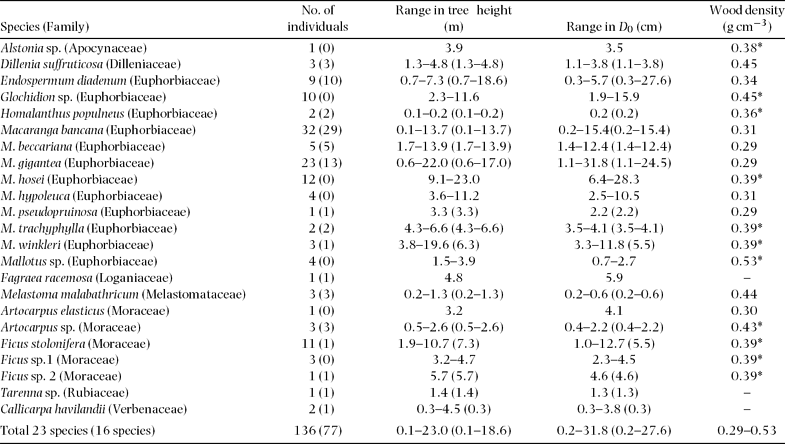
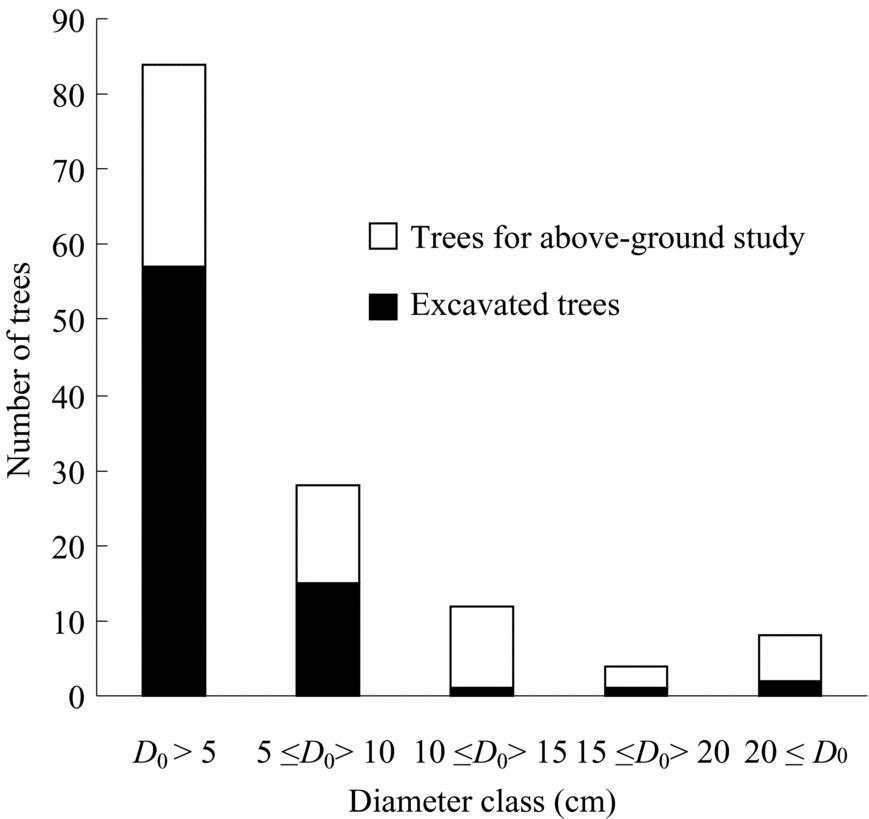
In total, 136 trees representing 23 species, 14 genera and eight families were harvested and measured for above-ground parts just before root excavation at the sites(Table 2, Figure 1, Appendix 1). Nomenclature follows Anderson (Reference ANDERSON1980), Nagamasu & Momose (Reference NAGAMASU, MOMOSE, Inoue and Hamid1997) and Soepadmo & Saw (Reference SOEPADMO and SAW2000). Individuals with damaged crowns or broken trunks were not considered. Harvested trees ranged from 0.1 to 23.0 m in height and from 0.2 to 31.8 cm in diameter at the ground surface (Table 2). All selected species were typical secondary-forest trees in the area. After harvesting, diameter at breast height (dbh, 1.3 m) and at ground surface (D 0), tree height (H), and leaf and stem fresh weight of all trees were measured.
Table 2. Sampled tree species, number of individuals, range of tree height, range of diameter at the ground surface, and wood density. Values in parentheses are from the below-ground survey. The asterisk (*) means average of generic values from Suzuki (Reference SUZUKI1999) and Burgess (1966).

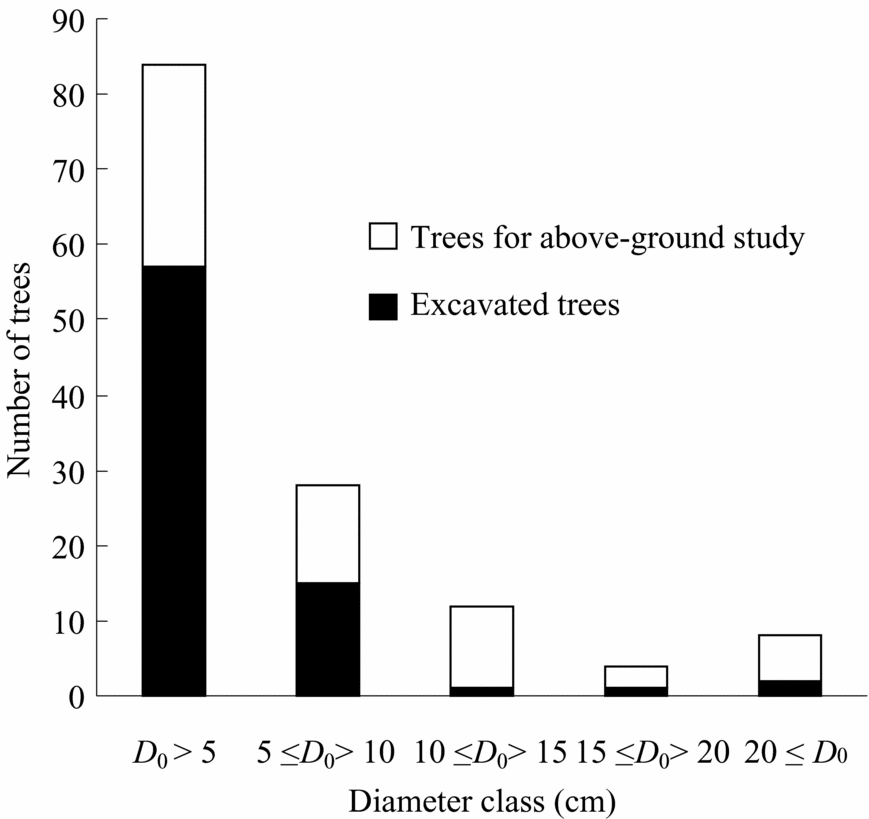
Figure 1. Number of excavated trees and trees for above-ground study with diameter class (diameter at ground surface).
Root excavation was carried out for 77 of the harvested trees, representing 16 species, 11 genera and seven families (Table 2, Figure 1). Excavated trees ranged from 0.1 to 18.6 m in height and from 0.2 to 27.6 cm in diameter at the ground surface (Table 2). Roots were carefully excavated, using hand tools, from the stump to less than 1–2 mm in diameter. Only live roots, noticeable by their healthy bark, were harvested. Roots were then washed by hand with water. We attempted to harvest all roots, but noted that not all fine roots could be harvested, especially ones less than 2 mm in diameter. Roots were then divided into small (diameter <5 mm) and coarse (diameter ≥5 mm) roots. Total fresh weight of each tree part was measured in the field and then representative samples were dried in the laboratory to determine moisture content. These samples were oven-dried at 60 °C for >72 h until they reached constant mass.
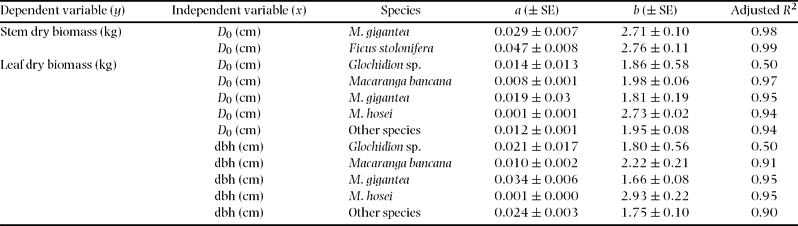
Diameters at breast height (dbh) and ground surface (D 0) were tested as independent variables. Preliminary analysis of alternative equations indicated that the allometric equation y = axb (where y is biomass (kg), x is dbh or D 0 (cm), and a and b are coefficients estimated by regression) fitted the data best. All regressions were carried out using SPSS ver. 11.5 for Windows (SPSS Japan Inc., Tokyo, Japan). We also tested interspecific differences in regression using several species, which included 10 of the above individuals for above-ground parts and five individuals for fine and total root biomass. Differences between species were tested by analysis of covariance (ANCOVA; SPSS v.11.5), with species as the main factor and dbh as a covariable (Sokal & Rohlf Reference SOKAL and ROHLF1995).
RESULTS
Allometric relationships
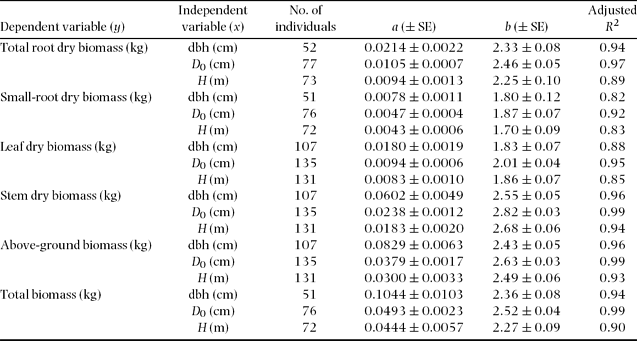
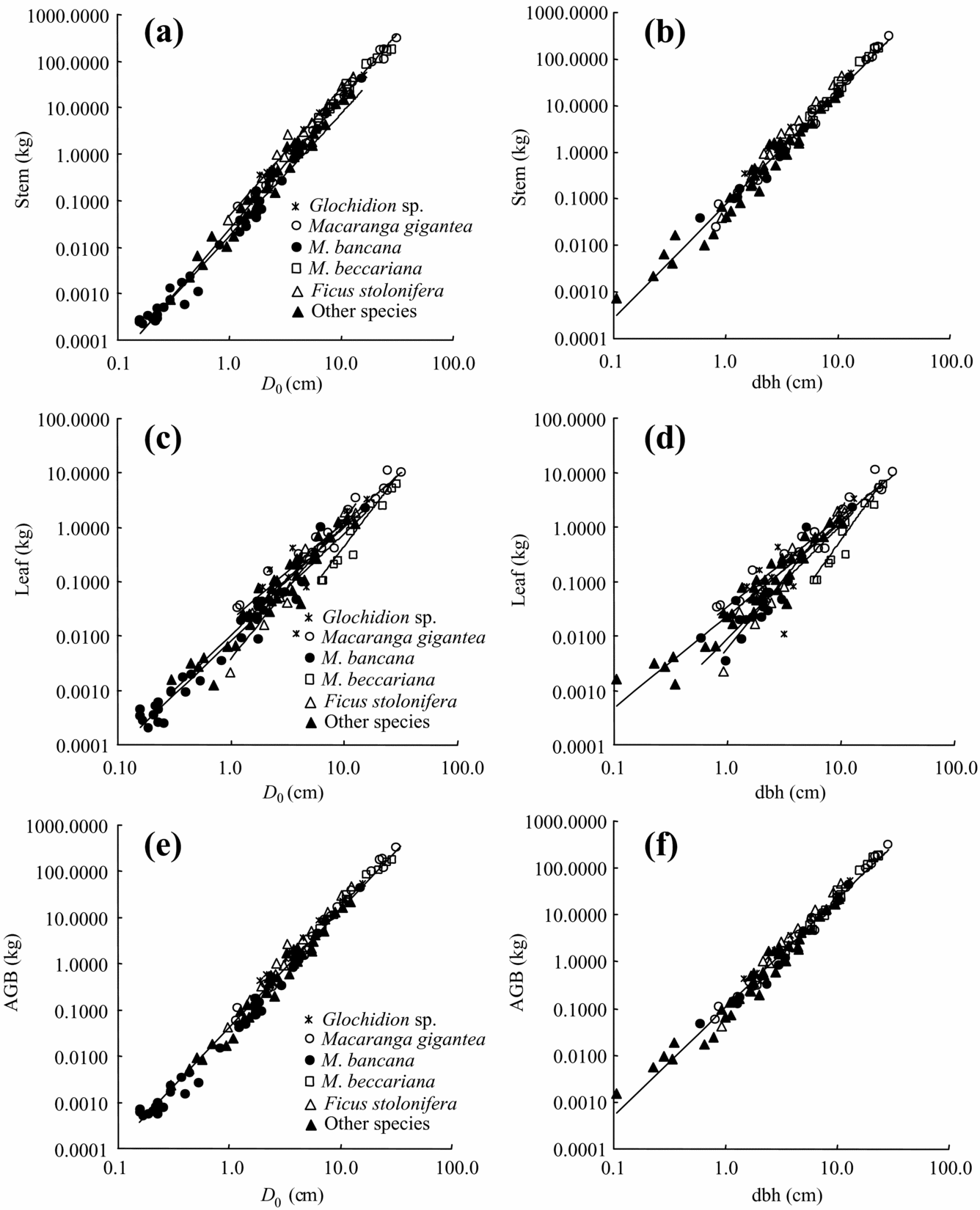
All allometric regressions such as total root biomass as a function of dbh or D 0 showed high correlation (Table 3, Figure 2, 3). A particularly high correlation (R 2 ≥ 0.94) was found with total root and stem biomass as a function of dbh or D 0. More accurate estimates of both total and small-root biomass were obtained by using D 0 instead of dbh (Table 3, Figure 3). We also found relatively high coefficients of allometric relationships between tree height and plant-part biomass ranging from 0.83 to 0.94 (Table 3).
Table 3. Results of regression analyses for predicting plant part biomass of subject trees from easily measured stem characteristics (y = axb) using data from all secondary-forest tree species.
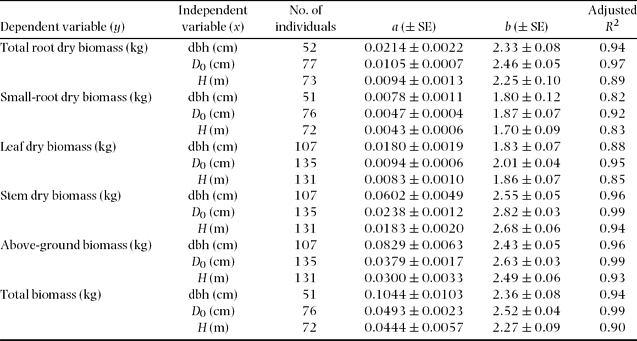

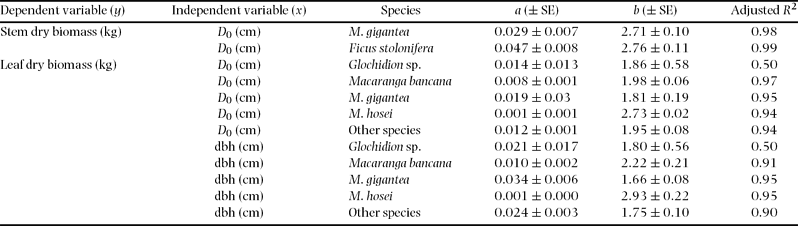
Figure 2. Allometric relationships between above-ground parts biomass and D 0 or dbh in tropical secondary forest trees. Stem biomass (a, b), leaf biomass (c, d), total above-ground biomass (AGB) (e, f) in relation to dbh and D 0, respectively. The regression coefficients appear in Table 3 and Appendix 2.
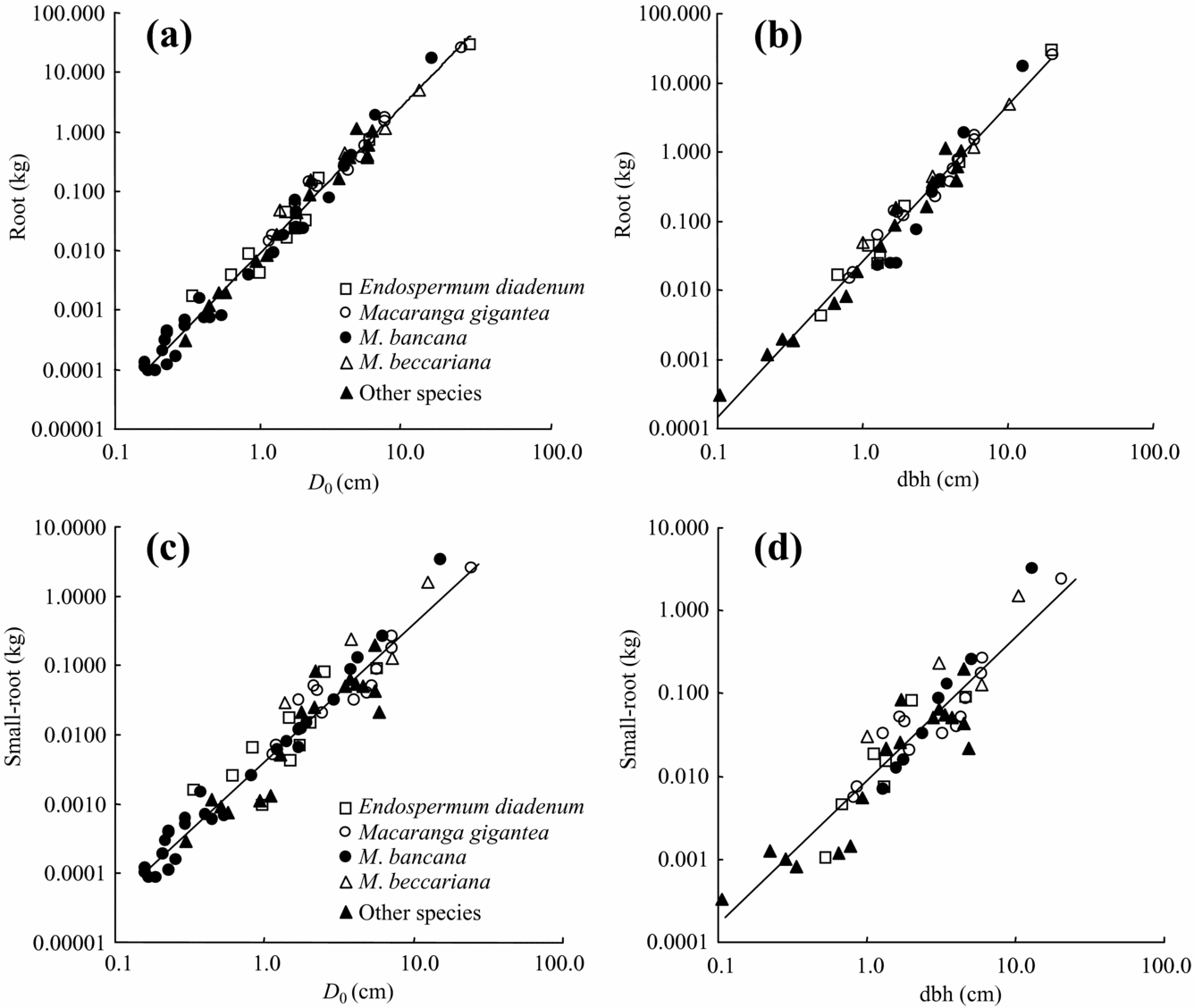
Figure 3. Allometric relationships between below-ground biomass and D 0 or dbh in tropical secondary forest trees. Total root biomass (a, b), small-root biomass (c, d) in relation to D 0 and dbh, respectively.
Analysis of covariance (ANCOVA) did not show any significant effect (P > 0.05) of tree species as a predictor variable for the stem, total and small-root biomass estimates, although interspecific differences in stems were found between Ficus stolonifera and Macaranga bancana when D 0 was used for the function (Figure 2, Appendix 2). On the other hand, significant interspecific differences were found among M. gigantea and M. hosei, M. hosei and other species groups, and M. bancana and Glochidion sp. in the regressions of leaf biomass using both dbh and D 0 (Figure 2, Appendix 2, P < 0.05, ANCOVA). However, interspecific differences were not significant when these regressions were explained by total above-ground biomass (sum of leaf and stem biomass) as a function of dbh or D 0 (Figure 2, P > 0.05, ANCOVA).
Effect of tree size on biomass partitioning ratios and root system
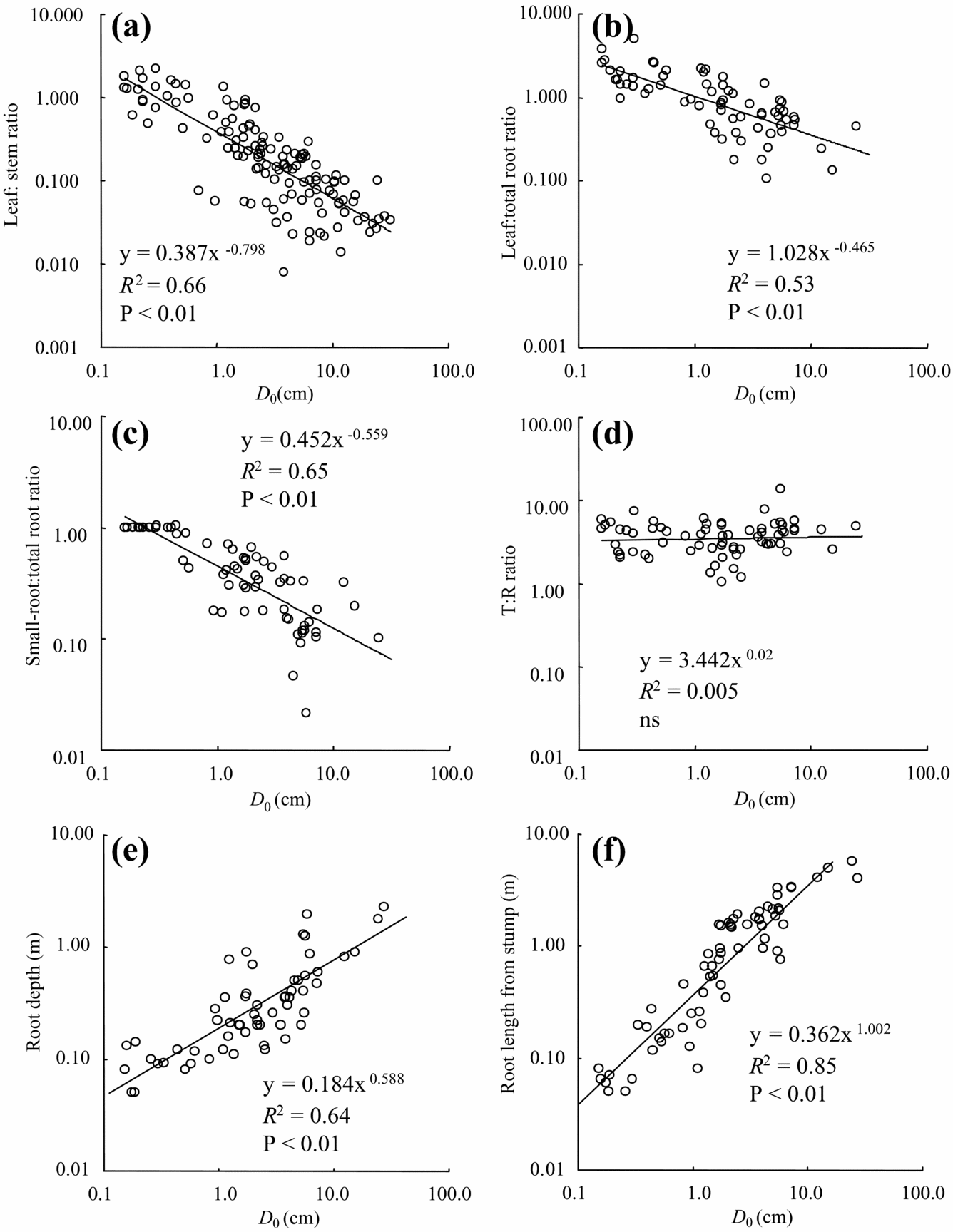
Tree-size-dependent biomass allocation was found in the leaf:total root ratio (leaf/root), leaf:stem ratio (leaf/stem) and small-root ratio (small-root/total root). Leaf biomass in both roots and stem biomass decreased significantly with tree diameter (Figure 4a, b). Small-root to total root biomass decreased significantly with diameter (Figure 4c). On the other hand, there was no significant relationship with tree diameter for either the above-ground biomass:root ratio T/R (Figure 4d) or the small-root:leaf ratio (data not shown).
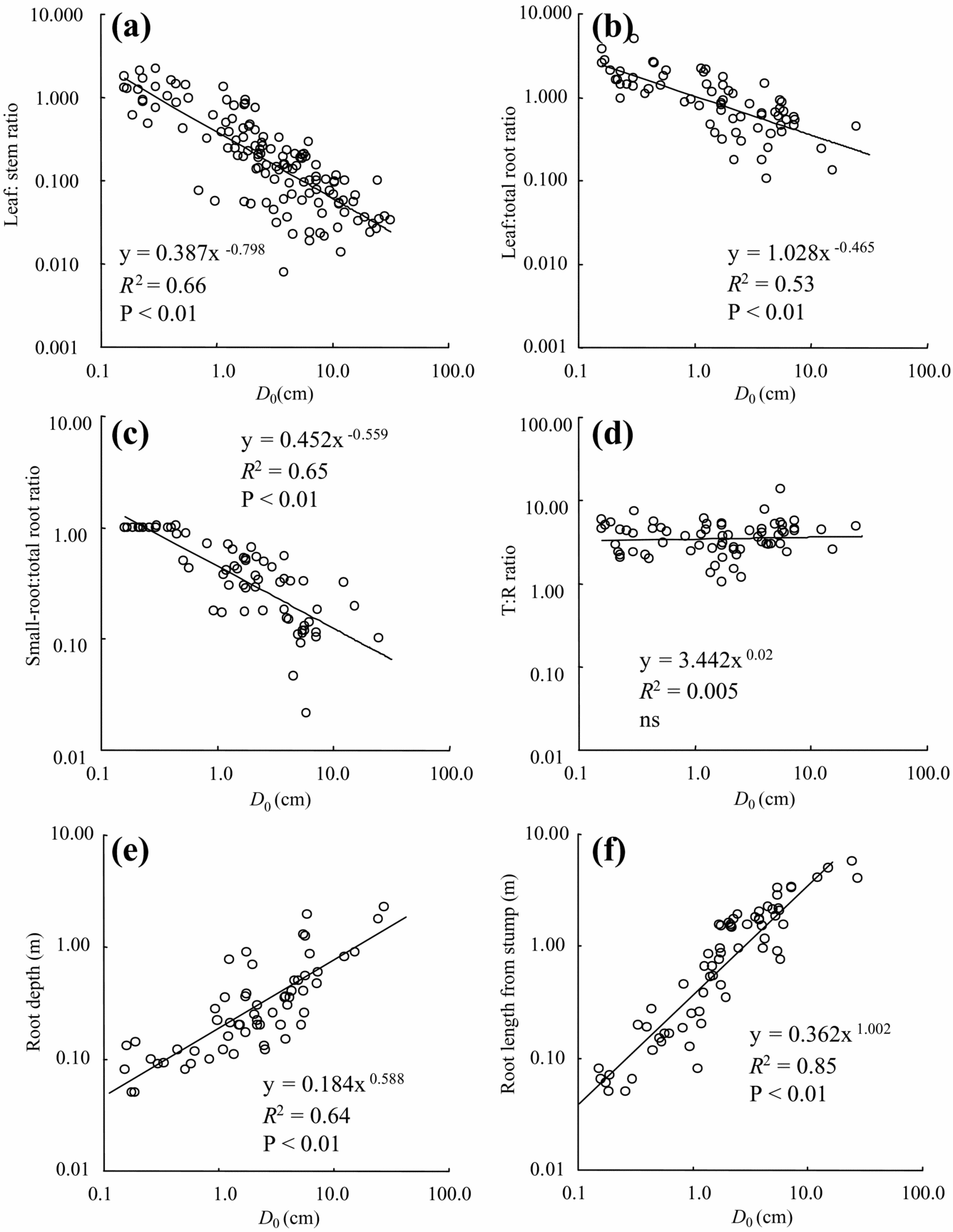
Figure 4. Biomass allocation and root characteristics with D 0. leaf:stem ratio (a), leaf:root ratio (b), small-root:total root ratio (c), total above-ground:total root biomass (d), root depth (e), and root length from stem (f).
Tree root depth increased with increased tree diameter, although rooting depth of most individuals was less than 1 m (Figure 4e). Only several species such as Fagraea racemosa and Endospermum diadenum showed relatively deep root systems over 1.2 m, even in small individuals (e.g. D 0 = 5.7 cm). Maximum depth in the largest individual of E. diadenum was 2.3 m (D 0 = 27.6 cm). In our observation, the majority of root systems existed in the shallow soil layer (approximately <20 cm), but we did not have a quantitative data set. Lateral root systems extended to relatively large areas and reached 5.5 m from the stump in the largest individuals of M. gigantea (Figure 4f, D 0 = 24.5 cm). Root grafting between secondary-forest trees was not frequent, although we did not have quantitative data. We also found self-grafted roots in some species such as F. stolonifera and Macaranga species.
Biomass model comparison both above and below ground
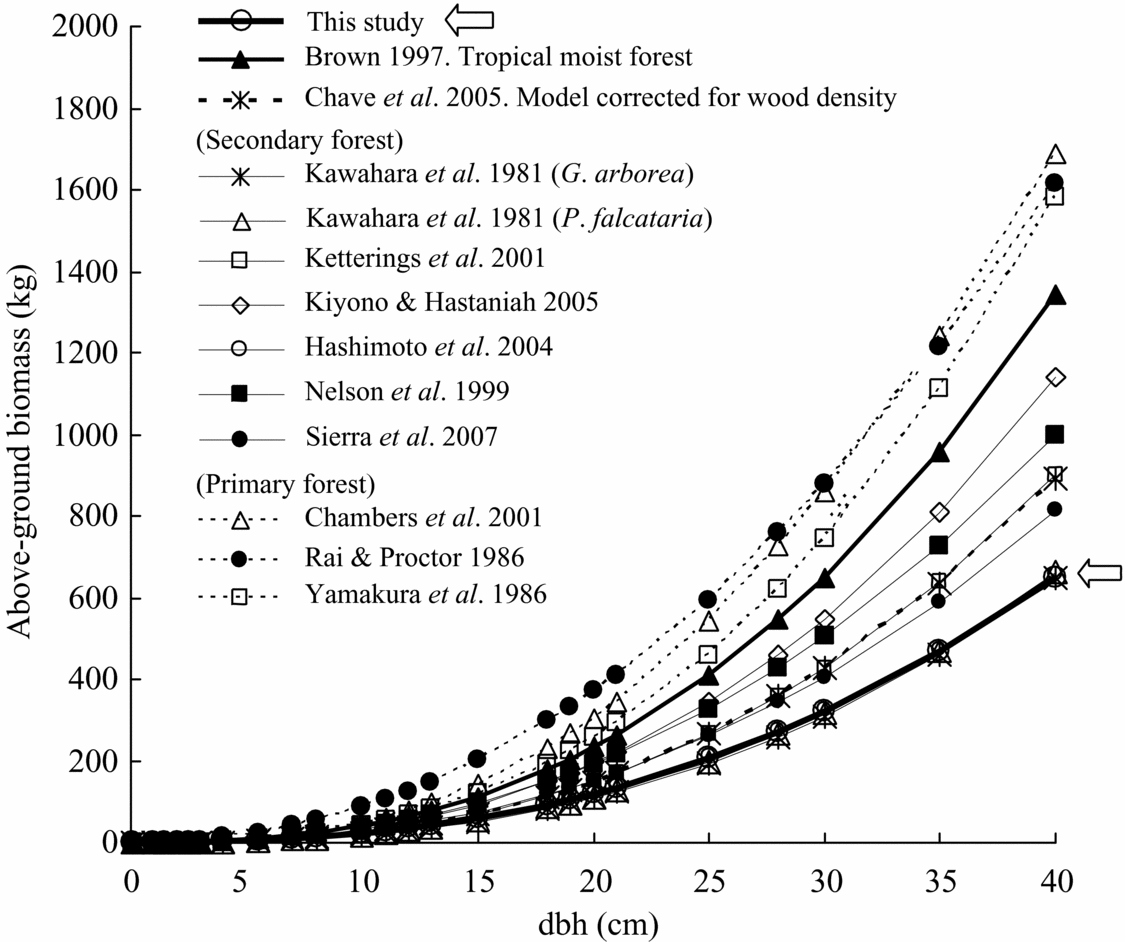
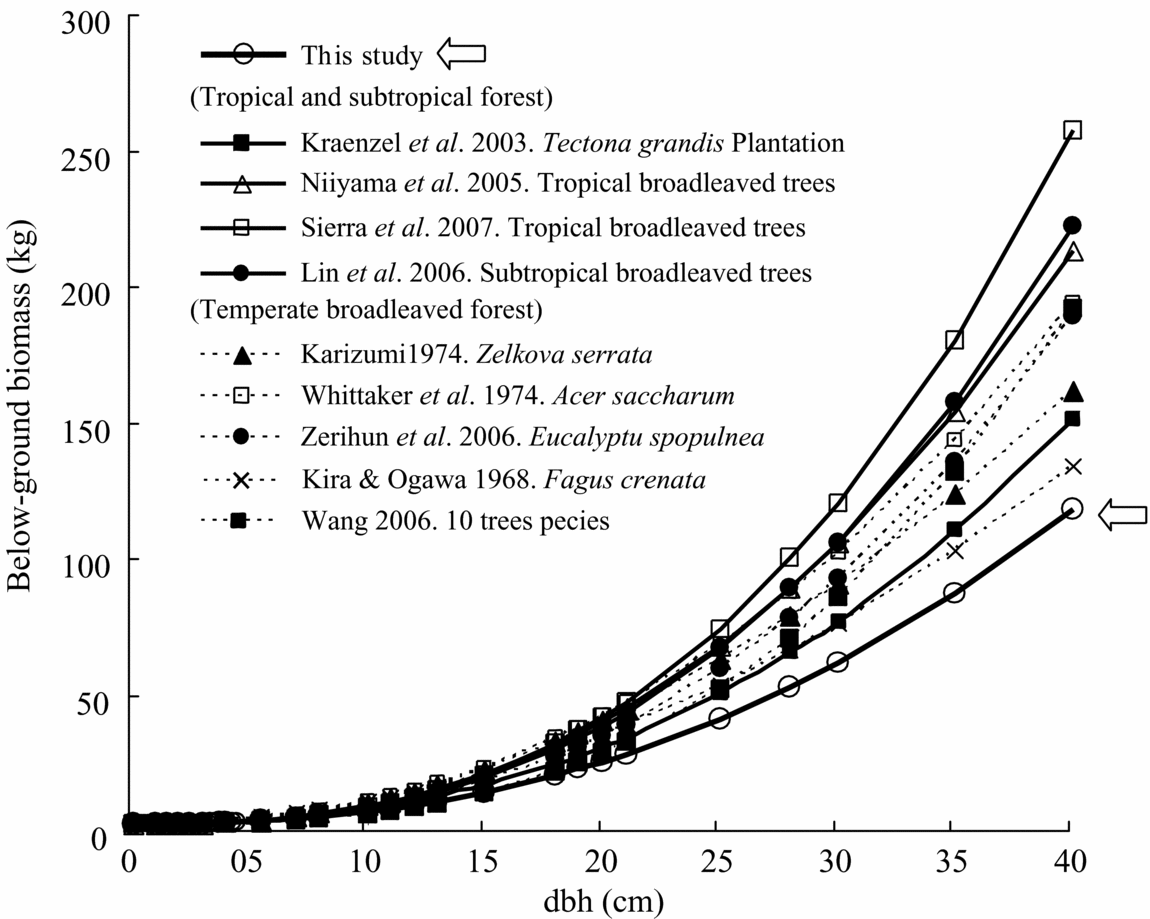
Comparison of total above-ground biomass equations for various tropical rain forests implies that there were significant differences between study forests, especially between secondary and primary forests (Table 4, Figure 5). Most previous equations for primary forest provided the highest estimate of biomass yield among the equations. In contrast, equations for secondary forest showed lower estimates of biomass. Especially, the equation for this study deviated least compared to almost all previous biomass equations, although equations reported by Hashimoto et al. (Reference HASHIMOTO, TANGE, MASUMORI, YAGI, SASAKI and KOJIMA2004) for young secondary-forest trees in Kalimantan and by Kawahara et al. (Reference KAWAHARA, KANAZAWA and SAKURAI1981) for fast-growing tropical secondary-forest trees of Paraserianthes falcataria and Gmelina arborea in the Philippines were similar (Figure 5). The equation by Brown (Reference BROWN1997), which is widely used for biomass estimation for tropical moist areas, estimated a much higher biomass than our equation. Even a biomass equation corrected by wood density (Model II.3 for moist forest stands, Chave et al. Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005) overestimated the biomass compared with our equation (wood density in our study is calculated as 0.354 g cm−3). For example, the equation by Chave et al. (Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005) overestimated by approximately 20% in above-ground biomass in the case of 20-cm dbh (Figure 5).
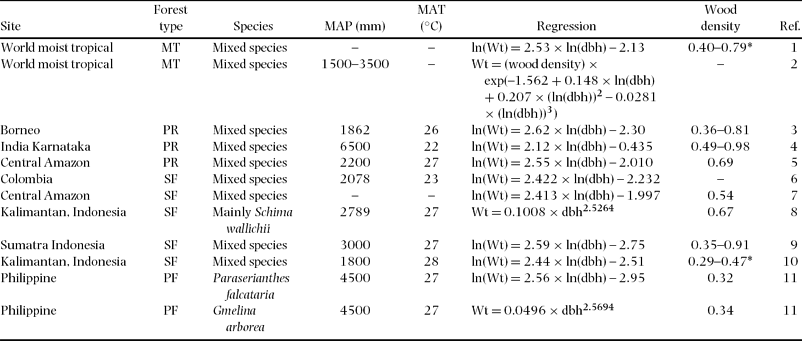
Table 4. Regression of above-ground biomass (Wt), species used for the regressions, mean annual precipitation (MAP) and temperature (MAT), and wood density (g cm−3) for different tropical moist areas and forest type. Units are kg for Wt and cm for dbh. Forest types: MT = moist tropical, PR = primary rain forest, SF = secondary forest, PF = plantation forest. References (Ref.): 1 = Brown Reference BROWN1997, 2 = Chave et al. Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005, 3 = Yamakura et al. Reference YAMAKURA, HAGIHARA, SUKARDJO and OGAWA1986, 4 = Rai & Proctor Reference RAI and PROCTOR1986, 5 = Chambers et al. Reference CHAMBERS, SANTOS, RIBEIRO and HIGUCHI2001, 6 = Sierra et al. Reference SIERRA, DEL VALLE, ORREGO, MORENO, HARMON, ZAPATA, COLORADO, HERRERA, LARA, RESTREPO, BERROUET, LOAIZA and BENJUMEA2007, 7 = Nelson et al. Reference NELSON, MESQUITA, PEREIRA, DE SOUZA, BATISTA and COUTO1999, 8 = Kiyono & Hastaniah Reference KIYONO and HASTANIAH2005, 9 = Ketterings et al. Reference KETTERINGS, COE, NOORDWIJK, AMBAGAU and PALM2001, 10 = Hashimoto et al. Reference HASHIMOTO, TANGE, MASUMORI, YAGI, SASAKI and KOJIMA2004, 11 = Kawahara et al. Reference KAWAHARA, KANAZAWA and SAKURAI1981.
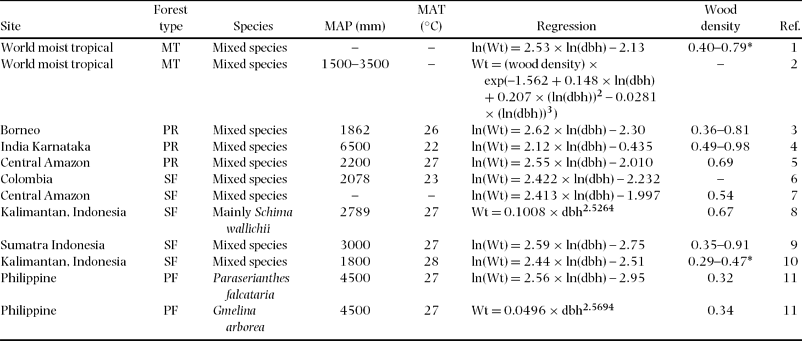

Figure 5. Comparison with previously reported relationships between above-ground biomass and dbh of tropical moist forest trees. Model parameters and site index appear in Table 4. The estimation line in this study overlaps the two lines of Kawahara et al. (Reference KAWAHARA, KANAZAWA and SAKURAI1981) and Hashimoto et al. (Reference HASHIMOTO, TANGE, MASUMORI, YAGI, SASAKI and KOJIMA2004).
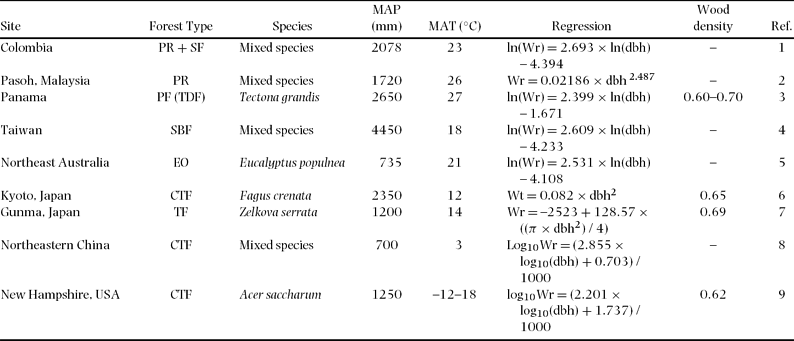
Comparison of the biomass equation for total below-ground biomass for our study with other equations developed for other tropical and temperate forest trees also showed highly varied results (Table 5, Figure 6). Compared with the root allometric equation obtained from other tropical rain-forest trees (Sierra et al. Reference SIERRA, DEL VALLE, ORREGO, MORENO, HARMON, ZAPATA, COLORADO, HERRERA, LARA, RESTREPO, BERROUET, LOAIZA and BENJUMEA2007), our equation provided a much lower estimate of root biomass for the same tree diameter, which was approximately 60% in the case of 20-cm dbh. Other equations for subtropical and temperate broadleaved forest trees also showed a higher estimation of root biomass compared with our tropical secondary-forest trees (Figure 6).
Table 5. Regression of below-ground biomass (Wr), species used for the regressions, mean annual precipitation (MAP) and temperature (MAT), and wood density (g cm−3) for different forest type. Units are kg for Wr and cm for dbh. Forest types: PR = primary rain forest, SF = secondary forest, PF = planted forest, TDF = tropical dry forest, SBF = subtropical broadleaved forest, EO = Eucalyptus open-woodland, CTF = cool temperate forest, TF = temperate forest. References (Ref.): 1 = Sierra et al. Reference SIERRA, DEL VALLE, ORREGO, MORENO, HARMON, ZAPATA, COLORADO, HERRERA, LARA, RESTREPO, BERROUET, LOAIZA and BENJUMEA2007, 2 = Niiyama et al. Reference NIIYAMA, KAJIMOTO, MATSUURA, YAMASHITA, KASSIM, RIPIN, NOOR, Okuda and Kondo2005, 3 = Kraenzel et al. Reference KRAENZEL, CASTILLO, MOORE and POTVIN2003, 4 = Lin et al. Reference LIN, DUH, HUANG and WANG2006, 5 = Zerihun et al. Reference ZERIHUN, MONTAGU, HOFFMANN and BRAY2006, 6 = Kira & Ogawa Reference KIRA, OGAWA, Ghilarov, Kovda, Novichkova-Ivanova, Robin and Sveshnikova1968, 7 = Karizumi Reference KARIZUMI1974, 8 = Wang Reference WANG2006, 9 = Whittaker et al. Reference WHITTAKER, BORMANN, LIKENS and SICCAMA1974.
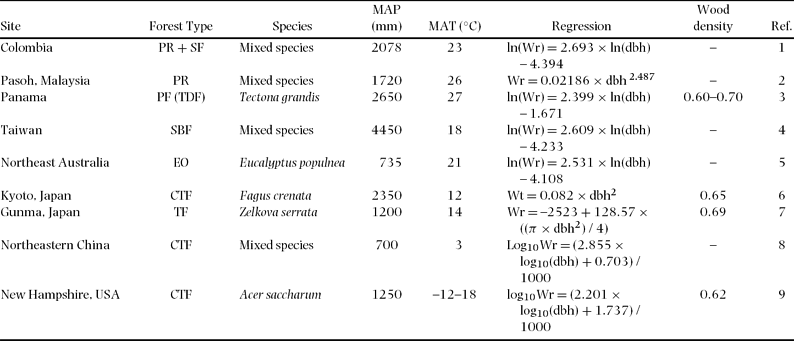
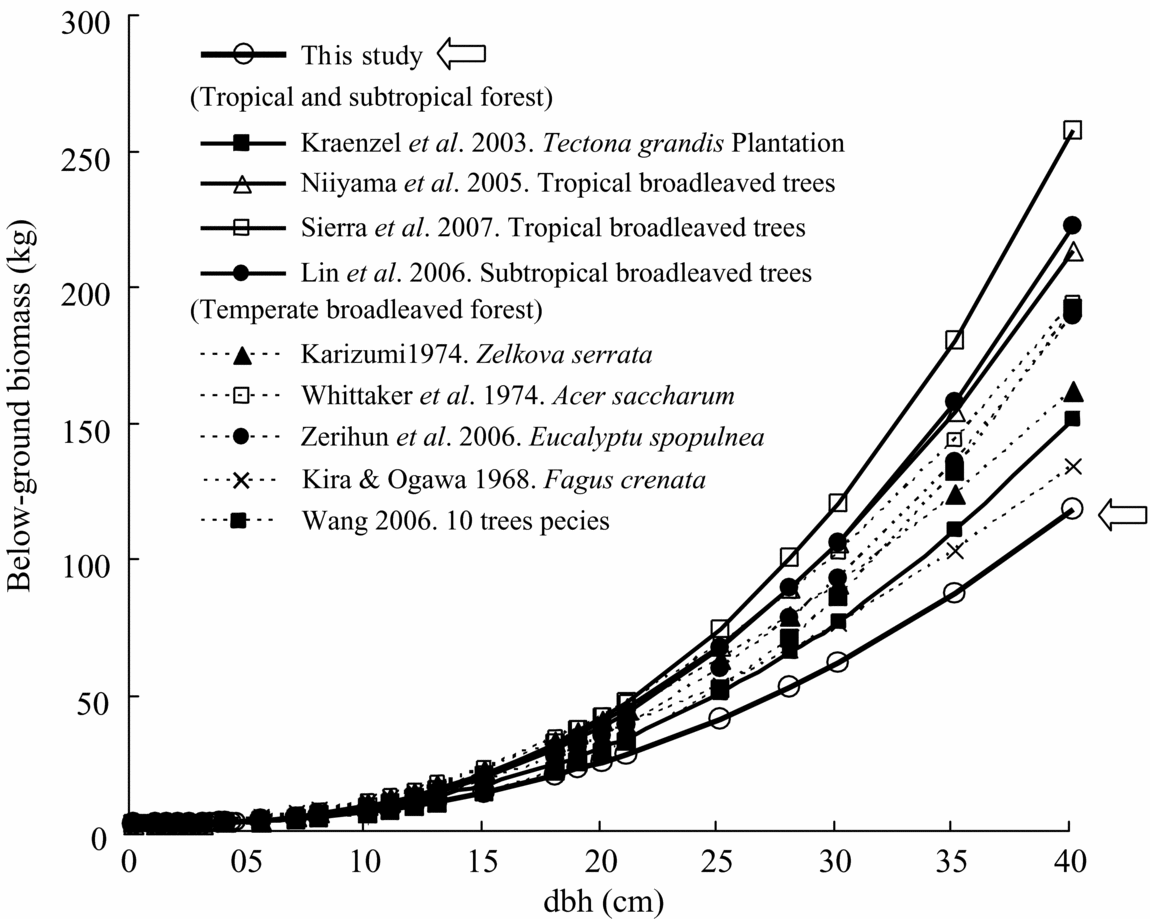
Figure 6. Comparison with previously reported relationships between below-ground biomass and dbh of broadleaved forest trees. Model parameters and site index appear in Table 5.
DISCUSSION
Allometric relationships and root characteristics of secondary-forest trees
All allometric relationships in this study showed a significantly high correlation coefficient with low interspecific differences, except for leaf biomass. This low interspecific variation in the allometric relationships of stem and total root biomass with dbh or D 0 may be derived from similar wood density among secondary-forest trees. In general, secondary-forest trees show lower wood density with lower variation among species from approximately 0.2–0.5 g cm−3 compared to late-successional tropical rain-forest trees, which range from 0.2–0.8 g cm−3 in the tropical rain forests of South-East Asia (Suzuki Reference SUZUKI1999, Whitmore Reference WHITMORE1998). In fact, the specific gravity of our studied tree species varied within a small range from 0.29 to 0.53 g cm−3. Hashimoto et al. (Reference HASHIMOTO, TANGE, MASUMORI, YAGI, SASAKI and KOJIMA2004) also reported that similar allometric relationships among their tropical secondary-forest trees, including species, were raised by Kawahara et al. (Reference KAWAHARA, KANAZAWA and SAKURAI1981), which also had similar wood density, in South-East Asia.
In contrast, allocation of leaf biomass with tree size shows greater fluctuation among species than that of root and stem biomass, because there are significant interspecific differences in leaf allometric equations. The allocation of leaf biomass in a plant body can vary greatly with its ontogeny and environmental conditions such as light, soil nutrients and water, even within the same tree species (Lambers et al. Reference LAMBERS, CHAPIN and PONS1998). This plasticity may appear in the interspecific differences in the leaf allometric relationships.
Tropical secondary-forest trees have relatively shallow root systems, although the maximum rooting depth of trees in evergreen tropical forests is generally deeper than most biomes except for tropical savanna (Canadell et al. Reference CANADELL, JACKSON, EHLERINGER, MOONEY, SALA and SCHULZE1996, de Kroon & Visser Reference DE KROON and VISSER2003). Maximum rooting depth in this study was only 2.3 m and this value is less than a third of the world average for tropical evergreen forests, which is 7.3 ± 2.8 m (Canadell et al. Reference CANADELL, JACKSON, EHLERINGER, MOONEY, SALA and SCHULZE1996). In addition, most trees in this study showed a depth of less than 1 m for the root system. Even young dipterocarp trees (c. 30-cm dbh), which are the dominant trees in the primary rain forests of South-East Asia, can have roots that reach down to 3.2 m (Baillie & Mamit Reference BAILLIE and MAMIT1983). In contrast, horizontal root length of secondary-forest trees shows a similar value to the root systems of young dipterocarp trees, as they can also reach 3–5 m from the stump (Baillie & Mamit Reference BAILLIE and MAMIT1983). This wide but shallow root system of secondary-forest trees implies a greater susceptibility to natural disturbance such as drought and strong wind, although it may also cause a high rate of nutrient uptake and above-ground growth (Becker & Castillo Reference BECKER and CASTILLO1990, Jaramillo et al. Reference JARAMILLO, AHEDO-HERNÁNDEZ and KAUFFMAN2003, Nicoll et al. Reference NICOLL, GARDINER, RAYNER and PEACE2006, Shukla & Ramakrishnan Reference SHUKLA and RAMAKRISHNAN1984). Several reports on tree mortality during severe drought events in El Niño obviously showed that species with low wood density had high mortality (van Nieuwstadt & Sheil Reference VAN NIEUWSTADT and SHEIL2005), especially pioneer Macaranga species, where the mortality rate reached 67% (Slik Reference SLIK2004). Cao (Reference CAO2000) also reported that tropical trees with a shallow root system (less than 20-cm depth), which include secondary-forest trees, showed higher mortality and lower predawn leaf water potential than primary forest trees with a deep root system (reaching 2-m depth) during severe drought events in El Niño in Borneo. On the other hand, trees with a shallow root system recovered faster from drought stress after first rains compared to deep tap-rooted species (Cao Reference CAO2000).
Biomass model comparisons for above-ground biomass among tropical moist forests
Comparison of above-ground biomass equations for various tropical rain forests implies that our allometric equation for tropical secondary-forest trees provided one of the lowest estimation equations for the biomass. Even the universal equation for tropical moist forest by Brown (Reference BROWN1997) overestimated by approximately twice the amount for our secondary-forest trees. This lower estimation may relate to their low wood density. The average wood density in our species was only 0.354 g cm−3 and this value was lower than the value in most other studies of primary and secondary tropical rain forest. However, biomass equations by Hashimoto et al. (Reference HASHIMOTO, TANGE, MASUMORI, YAGI, SASAKI and KOJIMA2004) and Kawahara et al. (Reference KAWAHARA, KANAZAWA and SAKURAI1981), which also had low wood density (0.32–0.49), showed almost similar biomass equations compared to our study. This indicates that a universal equation developed for above-ground biomass requires correction by wood density. In fact, corrected biomass equation for a tropical moist forest by wood density (Chave et al. Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005) could improve the biomass estimation for our secondary-forest trees, although it still overestimated the biomass by approximately 20% in the case of 20-cm dbh. This suggests that the model may require improvement for application to tropical secondary forests, especially for target trees with low wood density. When improving the biomass equation, it is also better to separate the secondary-forest trees from the primary-forest trees, because model parameters between forest types with similar diametric structure may vary considerably in canopy height (Chave et al. Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005). Chave et al. (Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005) also noted that if the model included a forest type, such as mangrove forest, as a predictive variable, the developed equations showed a poor fit with the data and poor estimation of above-ground biomass for over 50% of their study sites. In addition, more data sets may be needed for tropical secondary-forest trees in order to improve the corrected equation by wood density, because secondary-forest trees account for only 13% of the total tree data sets for their corrected models on tropical moist forests (Chave et al. Reference CHAVE, ANDALO, BROWN, CAIRNS, CHAMBERS, EAMUS, FÖLSTER, FROMARD, HIGUCHI, LESCURE, NELSON, OGAWA, PUIG, RIERA and YAMAKURA2005).
Biomass model comparisons for below-ground biomass among broadleaved forests
The allometric equations for total below-ground biomass for our tropical secondary-forest trees predicted the lowest yield of root biomass among the world's broadleaved forest trees, which include tropical, subtropical and temperate forests. For example, the root allometric equations obtained from tropical rain-forest trees (Sierra et al. Reference SIERRA, DEL VALLE, ORREGO, MORENO, HARMON, ZAPATA, COLORADO, HERRERA, LARA, RESTREPO, BERROUET, LOAIZA and BENJUMEA2007) provided a much higher estimate of root biomass for the same tree diameter, which was overestimated by approximately 60% in the case of 20-cm dbh. Thus, the allometric equations derived in this study may help provide a more accurate estimation of below-ground biomass in tropical secondary forests in South-East Asia. This lower-estimation equation may also be related to the lower wood density of studied trees similar to the equations for above-ground biomass and/or lower root depth compared with primary forest trees (Baillie & Mamit Reference BAILLIE and MAMIT1983). In addition, soil nutrient richness may also affect the root biomass differences between tropical forests (Cairns et al. Reference CAIRNS, BROWN, HELMER and BAUMGARDNER1997, Sanford & Cuevas Reference SANFORD, CUEVAS, Mulkey, Chazdon and Smith1996). To develop a universal equation for tropical root biomass, more data sets are needed from various tropical forest trees including both primary and secondary forest trees.
Conclusions
In this study, we accurately developed allometric relationships between dbh, D 0 and leaf, stem and total root biomass in various tropical secondary-forest trees with low interspecific differences. We also found relatively high correlation of allometric relationships between tree height and plant-part biomass. Comparison of above- and below-ground biomass equations for various tropical rain forests implies that our allometric equations differed largely from the equations for primary forests. Therefore, the developed allometric equations in this study may contribute to the accurate estimation of above- and below-ground biomass for the tropical secondary forests of South-East Asia.
ACKNOWLEDGEMENTS
The authors thank to the Sarawak Forestry Corporation, the Sarawak Forest Department, and to Prof. T. Nakashizuka, Dr K. Kamiya and Dr R. Yoneda for their kind support of this study. This research was partly supported by Grant-in-Aid for scientific research (No. 18780126 and No. 19255006) from the Ministry of Education, Culture, Sports, Science and Technology, Japan.
Appendix 1. All data sets on dry weight (g) of plant parts biomass, diameter at the ground surface (D 0), diameter at the breast height (dbh) and tree height (H).

Appendix 2. Results of interspecific regression analyses for predicting plant part biomass of subject trees from easily measured stem characteristics (y = axb).