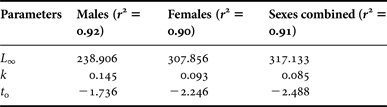INTRODUCTION
The evaluation of the status of fish stocks is often achieved by different stock assessment models. Nearly all the stock assessment models used in fisheries are based on population dynamic models, with varying levels of complexity depending on the available data for the species (Cooper, Reference Cooper2006). The basic population models assume that mortality, both natural and fishing-related, affects all fish equally. In reality, fish of different ages experience different rates of mortality. Thus, when length-age data are available for the species, age-structured models are usually preferred for assessment purposes. Such models increase the effectiveness of the models and management strategies due to the valuable information provided on the status of fish stocks (Hilborn & Walters, Reference Hilborn and Walters1992).
As with other large pelagic species, most billfish assessments have a high degree of uncertainty in their estimates, due mainly to the lack of biological information, particularly size-at-age (Kopf et al., Reference Kopf, Drew and Humphreys2009). Despite the difficulties to collect adequate sample sizes, growth models have been developed for various billfish species, particularly swordfish (Xiphias gladius L. 1758). Although growth models have been previously provided for a number of swordfish stocks, including the north-west Atlantic (Berkeley & Houde, Reference Berkeley and Houde1983; Ehrhardt, Reference Ehrhardt1992; Ehrhardt et al., Reference Ehrhardt, Robbins and Arocha1996; Castro-Longoria & Sosa-Nishizaki, Reference Castro-Longoria and Sosa-Nishizaki1998), central-north Atlantic (Esteves et al., Reference Esteves, Simões, Silva and Andrade1995), Mediterranean (Tsimenides & Tserpes, Reference Tsimenides and Tserpes1989; Tserpes & Tsimenides Reference Tserpes and Tsimenides1995) and the Pacific (Uchiyama et al., Reference Uchiyama, Skillman, Sampaga and DeMartini1998; Sun et al., Reference Sun, Wang and Yeh2002; DeMartini et al., Reference DeMartini, Uchiyama, Humphreys, Sampaga and Williams2007; Valeiras et al., Reference Valeiras, Mejuto and Ruiz2008; Cerna, Reference Cerna2009), the International Commission for the Conservation of Atlantic Tuna (ICCAT) has often highlighted the need for more information on age and growth for several areas (Anon, 2010), including from the South Atlantic. The South Atlantic swordfish is considered to be a unique stock, separated from the North Atlantic one at 5°N (Anon, 2009), and its growth model has not been validated so far. The provision of such parameters is currently of high importance, given the high commercial value of swordfish in European markets and the high degree of uncertainty particularly regarding the southern stock status, which has led to concerns about the ability of the fishery to sustain itself at current exploitation rates. The most recent ICCAT stock assessment (Anon, 2015) indicated that there was a greater than 90% probability that the northern swordfish stock has rebuilt to or above the biomass BMSY (Biomass corresponding to the Maximum Sustainable Yield), while southern Atlantic swordfish stock status is uncertain due to the unquantified uncertainties and the lack of signal in the available data.
Swordfish age determination studies have been conducted using different hard structures, such as otoliths (Castro-Longoria & Sosa-Nishizaki, Reference Castro-Longoria and Sosa-Nishizaki1998; Uchiyama et al., Reference Uchiyama, Skillman, Sampaga and DeMartini1998), vertebrae (Esteves et al., Reference Esteves, Simões, Silva and Andrade1995; Uchiyama et al., Reference Uchiyama, Skillman, Sampaga and DeMartini1998) and anal fin rays (Tsimenides & Tserpes, Reference Tsimenides and Tserpes1989; Ehrhardt, Reference Ehrhardt1992; Tserpes & Tsimenides, Reference Tserpes and Tsimenides1995; Ehrhardt et al., Reference Ehrhardt, Robbins and Arocha1996; Sun et al., Reference Sun, Wang and Yeh2002; DeMartini et al., Reference DeMartini, Uchiyama, Humphreys, Sampaga and Williams2007). Among the different structures used, there is currently a consensus that fin rays of billfish are of most use for ageing, mostly due to being easier to collect and process (Tsimenides & Tserpes, Reference Tsimenides and Tserpes1989; Uchiyama et al., Reference Uchiyama, Skillman, Sampaga and DeMartini1998). In fact, swordfish have small otoliths that are not amenable to traditional ageing techniques and difficult to collect (Ovchinnikov, Reference Ovchinnikov1971; Beckett, Reference Beckett1974), and the vertebrae collection is often difficult and/or impossible since it reduces the economic value of such a valuable fish species.
In many ageing studies the periodicity of the growth band increments has seldom been validated. The analysis of the growth area (opacity vs translucency) in the edge of the hard structures (edge analysis) and the variation of the increment of the last band over time (marginal increment analysis) are some of the most used techniques for validating age estimates (Tserpes & Tsimenides, Reference Tserpes and Tsimenides1995; Sun et al., Reference Sun, Wang and Yeh2002; DeMartini et al., Reference DeMartini, Uchiyama, Humphreys, Sampaga and Williams2007).
Given the worldwide importance of swordfish for commercial longline pelagic fisheries and the problems associated with the stock assessment, due to the current uncertainties regarding swordfish age validation and the lack of available information in certain areas, the main goals of the present study were to: (1) determine whether the growth increments in the anal fin spines of swordfish are formed annually, and (2) estimate for the first time the age and growth model for the South Atlantic swordfish.
MATERIALS AND METHODS
Sampling and spine preparation
Spine samples were collected from 502 (231 males and 271 females) swordfish caught in the equatorial and tropical waters of the south-east Atlantic (Figure 1). Sampling was undertaken onboard commercial longline vessels, in 2006 (March, April and September), 2007 (July, August and October) and 2009 (from July to October). For each specimen, the lower-jaw fork length (LJFL, to nearest centimetre) was taken, sex was determined and the anal fin was removed and frozen until assayed. In the laboratory, fins were thawed and sections of the second spine of the anal fin were prepared for reading, according to the method described by Tsimenides & Tserpes (Reference Tsimenides and Tserpes1989). Briefly, each anal fin was immersed in boiling water for a few minutes to remove the second spine and free it from skin and tissue. The spine was then cleaned with water and left to dry completely before being embedded in polyester resin. After drying (~12 h), a total of two cross-sections of c. 0.7 mm thickness were obtained from each spine, namely: two successive sections at the point where the spine flares (condyle). The cross-sections were cut using a low-speed precision saw and diamond wafering blade (BUEHLER® Isomet 1000).

Fig. 1. Study area. Black circles represent sampling locations.
Age estimation and precision
Spine sections were scanned using a previously calibrated scanner (HP® Scanjet 5530) and the digitalized images analysed with Image J 1.41 using dark background. Typically, broad translucent (slow growth) and narrow opaque bands (fast growth) could be seen in alternate positions from the core until the edge of the section. The total number of translucent bands (annulus) in spine sections was recorded and the distance from the focus to the edge of the section (spine radius) and to the anterior edge of each annulus was measured to the nearest 0.1 mm. The first section over the condyle was firstly observed and used, while the second section was only used in cases where the first section was not clear. The selected section of each spine was read twice by the same reader, about 2–3 months apart with no knowledge on fish length. Whenever there was disagreement between counts of translucent bands, spines were read for a third time. If an agreement could not be reached, those spines were excluded from further analysis.
Estimated age was assigned to each swordfish sample on the basis of the number of annuli and the characteristics of the bands as described by Tserpes & Tsimenides (Reference Tserpes and Tsimenides1995), namely the disappearance of the early growth rings and the existence of multiple bands in older fish. The spine nucleus is frequently reabsorbed and replaced by vascularized tissue that hides the first rings in older fish. Therefore, as suggested by Tserpes & Tsimenides (Reference Tserpes and Tsimenides1995), the mean radius of those annuli in spine sections of young fish were measured, allowing the estimation of their likely position in older fish. In such cases, if the total spine radius was greater than the mean radius estimated for the first three annuli (one, two or three years, respectively) were added to the assigned age. The appearance of multiple bands in older fish was described by Berkeley & Houde (Reference Berkeley and Houde1983) as those which form around the entire circumference of the spine, with lesser distance from the preceding and the following bands. In these cases, if the clearest band was possible to identify, it was considered an annulus and the others were ignored, otherwise the specimen was considered unreadable. Those spines where the opaque and translucent bands could not be identified were also considered unreadable.
To assess the reader precision, the average percentage of error (APE) was computed, as defined by Beamish & Fournier (Reference Beamish and Fournier1981):
 $$APE_j = 100\% {\displaystyle{1 \over R}\sum\limits_{i = 1}^R {\displaystyle{{\left( {x_{ij} - x_j} \right)} \over {x_j}}}}, $$
$$APE_j = 100\% {\displaystyle{1 \over R}\sum\limits_{i = 1}^R {\displaystyle{{\left( {x_{ij} - x_j} \right)} \over {x_j}}}}, $$
where x ij = ith age estimation of the jth fish;
x j = mean age estimated for the jth fish; and
R = number of occasions each fish was aged.
To improve the subsequent fit of growth curves to the age data, the ages of each fish were converted into absolute decimal age. The birth date was arbitrarily selected as 1 January, allowing for the minimization of the variability associated with a large sampling period (Coelho & Erzini, Reference Coelho and Erzini2002). Absolute decimal age was calculated as the number of annual bands plus the percentage of the year (from 1 January) that had passed since the date of capture.
Validation and growth
The marginal increment ratio (MIR) was estimated to determine the time of band formation, following Tserpes & Tsimenides (Reference Tserpes and Tsimenides1995):
where S = spine radius and r n = radius of the most recent annulus.
The mean MIR (±sd) was computed by month and age, for sexes combined, in order to locate periodic trends in band formation. Specimens estimated to be age 0+ were not included in MIR analysis because they lack formed bands. Likewise, fish younger than 2 years and older than 7 years were also excluded from this analysis due to the limited sample sizes. Monthly variations of MIR were analysed by means of Generalized Linear Modelling (GLM) techniques (McCullagh & Nelder, Reference McCullagh and Nelder1983). Apart from the variable ‘month’, the effect of ‘age’ was also included in the model to account for MIR differences among ages. Hence, the final model was expressed as:
MIR i,j ~ Intercept + Month i + Age j + error i,j
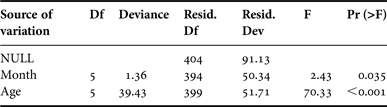
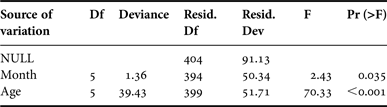
Interaction among ‘month’ and ‘age’ was not considered due to lack of sufficient data. Based on the deviance residuals plot, a model assuming a Gamma error structure with a ‘log’ link function was found to be the most appropriate. Model fitting was accomplished under the R language environment (R Development Core Team, 2010).
Preliminary analysis based on the AIC criterion showed that the power function modelled better the LJFL vs spine radius (S) relationship than a simple linear model. Thus, back calculations of length-at-age were estimated from the formula of Monastyrsky (Bagenal & Tesch, Reference Bagenal, Tesch and Bagenal1978) which assumes a power function for the above relationship. The back-calculation formula had the form:
where L n = LJFL when the annulus n was formed; L = LJFL at time of capture; b = the exponent of the regression of length (L) on spine radius (S) which is assumed to be a power function of the form L = aS b; S n = distance from spine focus to annulus n; and S = spine radius.
The parameter b of the power function was calculated for each sex separately using non-linear model (R Core Development Team, 2010). Differences among sexes were tested through the analysis of the residual sum of squares (ARSS) as suggested by Chen et al. (Reference Chen, Jackson and Harvey1992). This method is a modification of the ARSS, originally developed for the comparison of linear models (Zar, Reference Zar1984).
Estimates of theoretical growth in length were obtained by fitting mean monthly observed length-at-age data to the standard form of the von Bertalanffy growth equation described as:
where L t = mean length at age t; L ∞ = asymptotic length; k = growth coefficient; and t 0 = theoretical age at zero length.
The use of mean data instead of the raw data, although it may not be a statistically recommended procedure, was preferred since it assigns equal weight to all observations. Growth parameters for males, females and sexes combined were estimated iteratively using the ‘Gauss-Newton’ minimization algorithm under the R language environment (R Development Core Team, 2010). Confidence intervals were estimated through bootstrapping by means of the ‘nlsboot’ package (Huet et al., Reference Huet, Bouvier, Poursat and Jolivet2003). Sex differences were tested by means of ARSS. All statistical inference was based on the 95% confidence level.
RESULTS
Of the 502 anal fin spines sampled, 479 (95.2%) (224 males and 255 females) were aged successfully. The overall average percentage error (APE) was 3.35% (2.62% for males and 4.01% for females), indicating the goodness of the ageing procedure adopted. In 14 out of the 23 unreadable spines, annuli could not be identified due to lack of opaque-translucent area alternations. The remaining nine spines were considered unreadable due to the existence of multiple bands which made the identification of annuli difficult or resulted in ageing discrepancies between readings.
Lengths of the aged individuals ranged from 85 to 206 and 82 to 251 cm for males and females, respectively (Figure 2). For 139 spine sections, the total radius was greater than the mean value achieved for the first annulus measures, thus one year was added to the assigned age. For 79 sections, two years were added to each reading as the vascularized tissue area was greater than the mean achieved for the first and the second annuli. The vascularization of the third annulus was also observed for 46 spine sections, thus three years were added when the first measure was higher than the mean achieved for the first three annuli. The smallest estimated age was 0+ and the highest 12+ (sexes pooled). Age groups 3 and 4 predominated the whole sample, accounting for approximately 35%.

Fig. 2. Lower-jaw-fork-length frequency distribution for the aged swordfish specimens.
The estimated mean MIRs by age are illustrated in Figure 3. The applied GLM model explained about 45% of the total MIR variation and the analysis of deviance table indicated that both factors (‘month’ and ‘age’) were significant (Table 1). The plot of the month effect on MIR indicated that an annulus is formed in middle spring (Figure 4). This is generally in line with the observed monthly pattern of the mean MIRs by age estimates (Figure 3) but the relatively wide confidence intervals in the first months of the year do not allow for definitive conclusions. As was expected the age effect plot indicated that MIR decreases with age (Figure 5).

Fig. 3. Mean monthly marginal increment ratio for swordfish aged 2–7. Vertical bars represent standard deviation, and the numbers correspond to the sample size.

Fig. 4. Generalized linear model derived effect of month on marginal increment ratios. Dotted lines indicate two standard errors.

Fig. 5. Generalized linear model derived effect of age on marginal increment ratios. Dotted lines indicate two standard errors.
Table 1. Analysis of deviance for the generalized linear model fitted to the marginal increment ratio (MIR) data.
The spine radius ranged between 1.561 and 4.083 mm. The relationship between LJFL and S for males, females and sexes combined are as follows:
LJFL = 70.04 × S 0.55, r 2 = 0.83 for males;
LJFL = 67.57 × S 0.58, r 2 = 0.87 for females; and
LJFL = 67.65 × S 0.58, r 2 = 0.87 for sexes combined.
ARSS revealed that differences in the relationship between LJFL and S among sexes was marginally significant (F 2.472 = 3.02, P = 0.049). Mean back calculated length-at-age is shown on Table 2. Females grow faster than males after age 2. Back calculated length-at-age suggested slightly faster growth than that predicted by the von Bertalanffy growth model.
Table 2. Back-calculated and estimated lower-jaw-fork-length (LJFL, cm) at age for swordfish from south-east Atlantic waters.

Plots of the fitted von Bertalanffy growth function for males and females are shown in Figure 6 and the estimated parameters are provided in Table 3. Results of ARSS suggested that minor growth differences exist among sexes, although they are not significant at the 95% statistical level (F 3.82 = 2.38, P = 0.075).

Fig. 6. Standard von Bertalanffy (VB) growth curves for swordfish from south-east Atlantic waters. Continuous line and solid circles, males; Dotted line and empty circles, females.
Table 3. Parameter estimates for the standard von Bertalanffy growth model for swordfish from south-east Atlantic waters.
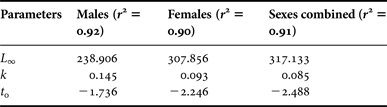
DISCUSSION
In the present study, reasonable reader precision was achieved for both males and females, which prove that anal fin spines are useful for swordfish ageing studies. According to Beamish & Fournier (Reference Beamish and Fournier1981) the average percentage error provides a good estimate of reading precision, as it describes the reproducibility of age estimates and not only the consistency among age determinations.
Marginal increment analysis demonstrated successfully for the first time the seasonality of band formation for South Atlantic swordfish, and partially validated the method used, for ages 2–7. In older fish, spine growth can be reduced considerably, thus an accurate validation of the method usually requires mark-recapture techniques and capture of fish of known age (Beamish & McFarlane, Reference Beamish and McFarlane1983). Predicted MIR variation by month and the deviance intervals obtained in the model suggested a good fit across the summer–early autumn months. The current analysis suggests that annulus formation occurs in mid spring. Since it has been suggested for Atlantic swordfish that spawning activity is observed more frequently in the western warm tropical and subtropical waters of the Atlantic, annulus formation may be related with drains on physiological condition, such as migration, as suggested by Berkeley & Houde (Reference Berkeley and Houde1983) for north-west Atlantic and by Tserpes & Tsimenides (Reference Tserpes and Tsimenides1995) for eastern Mediterranean swordfish stocks. The results of an event such as migration expose fish to different environments and place them under additional physiological stress (Campana, Reference Campana1999). The sampling location covered a wide area, including the transitional area between the known feeding and spawning grounds for the Atlantic. Moreover, the Gulf of Guinea was also covered, which according to Alvarado-Bremer et al. (Reference Alvarado-Bremer, Mejuto, Gómez-Márquez, Boán, Carpintero, Rodríguez, Viñas, Greig and Ely2005) is considered the main feeding area for the South Atlantic stock. Several other studies using swordfish anal fin spines revealed that spawning activity is the main mechanism regulating cyclic deposition of growth increments, as the fish spend more energy to produce gametes than for growth, resulting in a less calcified ring. In the north-west Atlantic one annulus is formed during the swordfish spawning season, in February and March (Ehrhardt et al., Reference Ehrhardt, Robbins and Arocha1996), in the North Pacific from July to September (Sun et al., Reference Sun, Wang and Yeh2002; DeMartini et al., Reference DeMartini, Uchiyama, Humphreys, Sampaga and Williams2007), while in the South Pacific it occurs from December to March (Cerna, Reference Cerna2009).
Similarly to the present study, several authors have indicated that the power function represents better than a linear model the relationship between spine radius and swordfish length (Ehrhardt, Reference Ehrhardt1992; Tserpes & Tsimenides, Reference Tserpes and Tsimenides1995; Sun et al., Reference Sun, Wang and Yeh2002; Chiang et al., Reference Chiang, Sun and Yeh2004). Hence a back calculation method based on such a function is preferable.
In the present study, the standard growth function for sexes combined provides a realistic description of age-size relationship of swordfish over the age ranges considered. Therefore, the estimation of a common growth equation for both sexes is valid and useful for management purposes. Ehrhardt (Reference Ehrhardt1992) also believed that the standard von Bertalanffy growth function represented swordfish growth adequately, and suggested that the generalized von Bertalanffy does not, as the parameters estimated were not biologically meaningful. The current study revealed inconsistencies between von Bertalanffy and back-calculated size-at-age estimates. Given that back-calculations are in principle based on an empirical formula, it is expected that the von Bertalanffy estimates, which derive from good fitting of a widely accepted growth model to the age readings, are representing better the growth pattern of the fish.
The estimated growth parameters from the present study seem to sufficiently describe the fish growth, as the predicted L ∞ is higher than the size of the largest fish sampled and the k indicated moderate low attainment of maximal size. The negative t 0 values obtained are frequent among fish species presenting rapid growth during the first year and slow growth in the following years (Craig et al., Reference Craig, Choat, Maxe and Saucerman1997). The estimated L ∞ obtained here was similar to those recorded for the north-west Atlantic swordfish (Berkeley & Houde, Reference Berkeley and Houde1983; Ehrhardt, Reference Ehrhardt1992), but higher than those for the Mediterranean (Tserpes & Tsimenides, Reference Tserpes and Tsimenides1995) and the north-west Pacific (Sun et al., Reference Sun, Wang and Yeh2002). In contrast, growth parameters achieved for swordfish caught in the south-east Pacific (Cerna, Reference Cerna2009), showed higher values than those observed in the present study. However, the swordfish caught in the north-west Atlantic grow in length faster than those caught in south-east Atlantic waters (Table 2; Table 4). For example, the mean length at age 1 of swordfish caught in the north-west Atlantic ranges from 89 cm (Ehrhardt, Reference Ehrhardt1992) to 98 cm LJFL (Berkeley & Houde, Reference Berkeley and Houde1983), whereas the mean length at age 1 in the south-east Atlantic is about 81 cm LJFL. Differences in mean size at age observed within the Atlantic (north-west vs south-east Atlantic) could be due to variations in growth patterns as the North and South Atlantic have been identified as different stocks (Anon, 2007). Almost all the samples used in this study coincide with the grade of differentiation between the two Atlantic swordfish populations, where the stock boundary is considered to be at 5°N for management purposes (Anon, 2009). Lower growth rates were also found for Pacific swordfish caught within an area where it is supposed to coincide with the grade of differentiation between populations (Cerna, Reference Cerna2009).
Table 4. Estimated lower-jaw-fork-length (LJFL, cm) at age for swordfish from north-west Atlantic waters.

The age determination and validation of growth increments for South Atlantic swordfish were presented for the first time in this paper. Combined sexes growth parameters can significantly support future stock assessment and management proposals for this stock. In fact, the last evaluation of South Atlantic swordfish stock status showed a high degree of uncertainty due to the conflicting signals of several indices used. Thus, for the sustainability of this commercially exploited fish stock, it has been of great urgency to conduct primary biological studies to obtain more accurate information on biological-related parameters.
ACKNOWLEDGEMENTS
The samples were obtained within the framework of the European Data Collection Regulation. The authors express their gratitude to Sérgio Amorim and the crew of F/V ‘Príncipe das Marés’, for collecting the fin rays.