INTRODUCTION
Cockles are ideal candidates for fisheries because of the fast growth rate, continuous reproduction throughout the year and high population abundance. Among cockles, Anadara granosa (Linnaeus 1758) of the family Arcidae is a commercially valuable species due to human consumption in Peninsular Malaysia (Vakily, Reference Vakily1992). Anadara granosa is exploited from both natural populations and as a farming resource. The commercial exploitation of this species in Malaysia began in 1948 in Perak, Malaysia. It has recently been extensively cultivated on several mudflats on the west coast of Malaysia such as Kedah (Merbok), Pulau Pinang (Juru), Perak (Kuala Gula, Kuala Sangga-Matang, Kuala Trong, Sg. Jarum), Selangor (Kuala Selangor) and Johor (Muar) (Izura & Hooi, Reference Izura and Hooi2008). Anadara granosa aquaculture is an important fishery in the inshore waters of Malaysia. Anadara granosa production contributed more than 50% to the national aquaculture production where Malaysia was ranked 5th in Asia Pacific with 78,712 tons in 2002 (Sugiyama et al., Reference Sugiyama, Staples and Funge-Smith2004). Cockle aquaculture in Penang makes the area the third largest producer of cockles in the west coast of peninsular Malaysia (Hassan, Reference Hassan2004).
Apart from the preliminary study of A. granosa by Broom (Reference Broom1983), there have been some basic studies on the ecology (Afiati, Reference Afiati1994; Brotohadikusomo, Reference Brotohadikusomo1994), reproductive cycle (Suwanjarat et al., Reference Suwanjarat, Pituksalee and Thongchai2009), gonad maturation (Afiati, Reference Afiati2007), growth rate (Din & Ahamad, Reference Din and Ahamad1995), mortality and the experimental populations (Broom, Reference Broom1983) of blood cockles in Malaysia.
Any study on the age and growth rate of A. granosa will lead to an understanding regarding the age class, structure of stock, population growth and longevity. Since growth rate in molluscs is described as an increase in total length and body weight, studying them could be the ideal method to estimate growth rate. An analysis of age and growth can be used to describe the effect of environmental factors on growth and the comparison of growth rates in different geographic areas (Ramesh et al., Reference Ramesh, Ravichandran and Rameshkumar2009). Although cockles are an important fishery in Malaysia, the population dynamics of this species are poorly known. Detailed information on growth rate and environmental parameters can be obtained from the length frequency of cockles over a period of time.
A number of methods have been used to estimate the age and growth rate of molluscs including the study of annual growth bands on the external surfaces of mollusc shells, determining microgrowth bands in the inner shell layer and mark–recapture experiments. In A. granosa, the bands may be missing or difficult to calculate, as in the case of the first-year growth bands and the closely packed bands produced later. Therefore, an alternative method, estimating the age at different sizes can be used to analyse the frequency distribution of molluscs over an extended time period (Fiori & Morsán, Reference Fiori and Morsán2004). Length-frequency data sets include a series of modes, each of which shows one particular age class. A growth model can be estimated with length at different age group using mean mode of each age class in the cockle population. The evolution of continuous data sets from the same population provides a more accurate analysis by using modes through the samples in a time series (Bjorndal et al., Reference Bjorndal, Bolten, Coan and Kleiber1995).
Information about a variety of population parameters such as asymptotic length (L ∞), growth coefficient (K), the mortality (natural and fishing) rate and exploitation level (E) are valuable for the evaluation and control of cockle resources (Malathi & Thippeswamy, Reference Malathi and Thippeswamy2013). Growth and mortality models are important for analytical fisheries management. The evaluation of the age of cockles is needed in order to complete the information about the abundance and fluctuations of any species (El-Haweet et al., Reference El-Haweet, Hegazy, Abu-Hatab and Sabry2005). There are several methods to determine the exploitation levels and population dynamics of cockles. FAO-ICLARM Stock Assessment Tools (FiSAT) is commonly used to assess the stock. This method requires length-frequency information (Amin et al., Reference Amin, Rahman, Haldar and Mazid2001; Vakily, Reference Vakily1992). The main advantage of this method is that during a 1 year study period, with enough available length-frequency information we are able to assess any bivalve stock (Al-Barwani et al., Reference Al-Barwani, Arshad, Amin, Japar, Siraj and Yap2007). A length-based stock assessment can be performed by plotting the variation of mean length or mean weight of individuals against age (Gosling, Reference Gosling2008). Although different equations are used to fit curves to the growth parameters, the ideal equation to study the growth rate is the von Bertalanffy growth function because it is used as a sub-model in more complex models which describe population dynamics (Rabaoui et al., Reference Rabaoui, Zouari, Katsanevakis and Hassine2007).
The main objectives of this study are (1) to determine the relationship between the length and weight of A. granosa cultured in Balik Pulau, Penang Island, Malaysia; (2) to confirm the application of length-frequency analysis to provide reliable growth parameters of A. granosa during growth, mortality and reproduction cycles in the cockle population; and (3) to ascertain the ageing and growth rate of A. granosa in Balik Pulau, Penang Island, Malaysia.
MATERIALS AND METHODS
Sample collection
Blood cockles A. granosa were collected from the intertidal areas (exposed during all low tides) of Balik Pulau (5°20′05.50″N 100°11′35.32″E), Penang Island, West Coast of Malaysia at monthly intervals from December 2011 to November 2012. A total of 548 individuals of A. granosa were collected during the study period and subjected to length measurements (Figure 1).

Fig. 1. Location of Anadara granosa study site, Penang Island, West Coast of Peninsular Malaysia.
Seawater temperature measurement
Daily seawater temperature was measured using a HOBO Pendant Temp/Light logger fixed in the study area. The logger was calibrated to record hourly seawater temperature in the study site for the period between December 2011 and November 2012.
Length-weight relationship
The length-weight relationship was calculated by measuring the shell length (anterior-posterior axis) to the nearest 0.1 mm by Vernier callipers, while the total weight was calculated for each individual by digital balance to the nearest 0.001 g.
The length-weight relationship was estimated by using the allometric equation W = aL b (Quinn II & Deriso, Reference Quinn and Deriso1999; Vieira et al., Reference Vieira, Neves, Sequeira, Paiva and Gordo2014), where W is the weight (g) and L is the total length (mm) of A. granosa, ‘a’ is the intercept (initial growth coefficient) and ‘b’ is the slope and relative growth rates of the variables. The ‘a’ and ‘b’ parameters were calculated using regression analysis of log-log transformed data:
The correlation (r 2), which is the level of relationship between the length and weight, was calculated from the linear analysis. The 95% confidence intervals for b (CI 95%) were calculated to determine differences of growth coefficient (b) from 3.0. If b = 3.0, growth is isometric, however if b > 3.0, growth is positive allometric. Growth is negative allometric when b < 3.0.
Estimation of growth parameters
The length-frequency records were arranged into 10 mm class intervals from December 2011 to November 2012. Length frequency data analysis was carried out by Electronic Length Frequency Analysis (ELEFAN I) following the FiSAT package. Growth parameters including asymptotic length (L ∞) and growth coefficient (K) were obtained by ELEFAN I.
The von Bertalanffy growth model
The von Bertalanffy Growth Function (VBGF) was used to obtain the size of the A. granosa at various ages. The von Bertalanffy equation was fitted to calculate the length-at-age curve by using the non-linear squares estimation method (Pauly et al., Reference Pauly, Soriano-Bartz, Moreau and Jarre-Teichmann1992). The von Bertalanffy function can be described by the following equation (Mohammadikia et al., Reference Mohammadikia, Kamrani, Reza Taherizadeh, Soleymani, Farokhi and Momeni2014):
L ∞ = Asymptotic length (L ∞), K = Growth coefficient, L t = Length at age ‘t’, t 0 = Hypothetical age at which the length is 0.
The ELEFAN method is unable to calculate the t 0 value through the length frequency records, an acceptable value of ‘t 0’ was predicted by Pauly (Reference Pauly1983) by replacing the L ∞ (mm) and K (year−1) in the following function (Kuganathan, Reference Kuganathan2006):
L ∞ and K selected from the compilation of length growth parameters so as to cover a wide diversity of taxa and size.
Growth performance index (Ø)
The growth performance index (Ø) was estimated using the Pauly & Munro (Reference Pauly and Munro1984) method with asymptotic length (L ∞) and growth coefficient (K).
Potential longevity
The potential longevity (t max) of A. granosa was obtained from the Pauly (Reference Pauly1983) equation:
t max: The approximate maximum age A. granosa in a given population will reach.
Mortality coefficients
Mortality coefficients such as total mortality (Z), natural mortality (M), fishing mortality (F) and exploitation rate (E) were calculated using FiSAT software and the steady-state sample method (Gayanilo, Reference Gayanilo1997; Cikes Kec & Zorica, Reference Cikes Kec and Zorica2013). Total mortality is comprised of two components: ‘natural’ mortality (M); mortality due to predation, disease, etc., and ‘fisheries’ mortality (F); mortality due to harvesting by humans, where
The Exploitataion rate was obtained using the following equation (Gulland & Rosenberg, Reference Gulland and Rosenberg1992):
RESULTS
Length-weight relationship
The length and weight of A. granosa ranged between 11.25 and 33.13 mm and 3.04 and 15.55 g, respectively. The length-weight relationship of A. granosa displayed as W = 0.002 L 2.328 (R 2 = 0.922) which was found by plotting the length values against weight (Figure 2). The growth coefficient (b) was 2.328 (±0.08). Therefore, the b values ranged from 2.248 to 2.408 at 95% confidence level (Table 1). From this graph, the exponential form was turned into a linear form to obtain the length-weight relationship equation. The calculated equation for the length-weight relationship is y = 2.328x − 2.537, R 2 = 0.922 (Figure 3).

Fig. 2. Length-weight relationship of Anadara granosa from Balik Pulau, Penang Island, Malaysia.

Fig. 3. The natural logarithms of length-weight relationship of Anadara granosa from Balik Pulau, Penang Island, Malaysia.
Table 1. Descriptive statistics and estimated parameters of length-weight relationships of Anadara granosa in Balik Pulau, Penang Island, Malaysia (December 2011–November 2012).

Size frequency
A total of 548 specimens of A. granosa were collected on the monthly basis during this study. The size frequency of the shell length and number of A. granosa from Balik Pulau, Penang Island are shown in Figure 4. This figure shows that the shells in the population ranged from 11.25 to 33.13 mm. The majority of A. granosa were between 23.5 and 24.5 mm (48 individuals), while the lowest numbers of individuals (five) were between 11.5 and 12.5 mm.

Fig. 4. Length-frequency distribution of samples of Anadara granosa collected from Balik Pulau, Penang Island, Malaysia.
The growth parameters
The growth parameters (L ∞, K, t 0) are useful in assessing the growth rates between and within individuals inhabiting various environments. The modified values for K and L ∞ for A. granosa were 1.1 year−1 and 35.40 mm, respectively (Table 2).
Table 2. Estimated growth parameters of Anadara granosa in Balik Pulau, Penang Island, Malaysia (December 2011–November 2012).

The ideal fit index (Rn) for asymptotic length (L ∞) and growth coefficient (K) was 0.371. Generally, the Rn value varies from 0 to 1 in the ELEFAN-FiSAT software. Since A. granosa is a tropical species, the oscillation parameter (C) and winter point should be 0. The estimated t 0 value was −0.140 for A. granosa in Balik Pulau, Penang Island. The computed growth curve using these parameters is shown over the restructured length distribution in Figure 5.

Fig. 5. Length-frequency distribution output from FiSAT with superimposed growth curves for Anadara granosa from Balik Pulau, Penang Island, Malaysia.
Von Bertalanffy growth model
The von Bertalanffy growth equation was L t = 35.40 [1−EXP−1.1 (t+0.140)]. It was found that the sizes attained by A. granosa were 10.13, 14.36, 17.89, 20.82, 23.65 and 25.29 mm at the end of 2, 4, 6, 8, 10 and 12 months of age, respectively (Figure 6).

Fig. 6. The von Bertalanffy growth curve (plot of age and growth) of Anadara granosa based on computed growth parameters.
Growth performance index
The growth performance (Ø′) was estimated at 3.13 using Pauly's method to compare growth patterns and evaluation of the reliability of the von Bertalanffy growth parameters.
Longevity
The longevity value for A. granosa was 2.72 years, which was obtained from Pauly's equation to identify the current state of fishery and manage cockle population exploitation. This value showed that A. granosa is a short-lived species.
Mortality and exploitation
Length-converted catch curve was used to estimate the total mortality (Z) (Figure 7). The estimated total mortality (Z) of A. granosa was 2.32 year−1. The natural mortality was estimated from the Pauly's equation. Therefore, the mean annual seawater temperature (28.8°C) was used in Pauly's equation to calculate the natural mortality in study site. Natural mortality (M) and fishing mortality (F) of A. granosa were 1.84 and 0.48 year−1, respectively. The exploitation level (E) of A. granosa was 0.20 in study area.

Fig. 7. Length-converted catch curve for Anadara granosa specimens collected from Balik Pulau, Penang Island from December 2011 to November 2012.
DISCUSSION
Size frequency
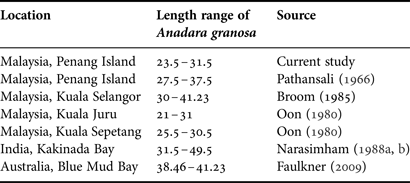
The size of blood cockles may be summarized by shell length-frequency distributions, which is the size structure of the underlying populations (single species) or assemblages (multiple species). Recognizing the size structure of cockle populations is essential in understanding growth, reproduction, and recruitment, with changes in size an early indicator of disturbance. The present study was designed to determine the length-frequency distribution of A. granosa in Balik Pulau, Penang Island. Based on the length-frequency data, which followed a direct method of growth study, the size of blood cockles varied from 11.25 to 33.13 mm and the majority of shell lengths ranged from 23.5 to 31.5 mm, when the average size of cockle was between 23.5 and 24 mm. The results obtained in this study corroborated the findings of previous work in this field (Table 3). Pathansali (Reference Pathansali1966) reported that the length of A. granosa ranged from 27.5 to 37.5 mm in Penang Island, Malaysia. Furthermore, Oon (Reference Oon1980) reported that the size frequency distribution of A. granosa ranged from 21 to 31 mm (Kuala Juru, Pulau Pinang) and 25.5 to 30.5 mm (Kuala Sepetang, Perak). The similarity ranges between the findings of current study and those described by researchers in Malaysia, might be due to the location of the study areas.
Table 3. The length range of blood cockles Anadara granosa derived by other authors in different study areas.

However, the size frequency estimated by the current study was lower compared with the findings of Broom (Reference Broom1985) in Kuala Selangor, Malaysia (30.00 to 41.23 mm), Narasimham (Reference Narasimham1988a) in Kakinada Bay, India (31.50 to 49.50 mm) and Faulkner (Reference Faulkner2009) in Blue Mud Bay, Australia (38.46 to 41.23 mm). The disparity observed in the size frequency distribution might be due to the influence of latitude-dependent environmental factors. The A. granosa in this study site were also reared in a higher density per metre squared compared with natural mud flat beds in other studies. A possible explanation for this is that at a higher population density food supply decreases for each individual. Another explanation is that growth decreased at high densities due to reduction in space; this may lead to raised physical contact between cockles in the study area. Alternatively, it may be a genetic characteristic of the population occurring in the above-mentioned study areas. It is of interest to note that Muthiah et al. (Reference Muthiah, Narasimham, Gopinathan and Sundararajan1992) mentioned that the length-frequency distribution of A. granosa was higher under field culture in India compared with the growth observed in the culture fields in Malaysia.
Length-weight relationship
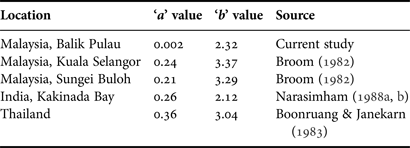
In the field of biology, there are few correlations that are exactly linear; most of the bivariate correlations studied are non-linear. For example, the increase in live organism population size with time is exponential if there are no environmental stresses. The regression linear model cannot be used directly for variables with non-linear correlation (Ward, Reference Ward2007). The direct usage of linear regression and the Pearson correlation was found to be inaccurate. Thus, one of the approaches used to solve this problem is to use data embodiment to obtain a linear correlation between these two variables. The growth coefficient ‘b’ may range from 2 to 4 (Koutrakis & Tsikliras, Reference Koutrakis and Tsikliras2003). As mentioned earlier, linear regression analysis on the logarithm-transformed data showed the ‘a’ (0.002) and ‘b’ (2.328) parameters in the length-weight relationship. The ‘b’ value (2.328) in the current study lay between the values mentioned by Koutrakis & Tsikliras (Reference Koutrakis and Tsikliras2003) and was significantly smaller than the isometric value (b = 3) at a 5% level. Therefore, the value of ‘b’ in the current study demonstrates that A. granosa grows negative allometrically instead of isometrically. However, the results of this study were similar to the general study trend shown by Narasimham (Reference Narasimham1988b) in Kakinada Bay, India (2.12). Nevertheless, the ‘b’ value of the current study had the smallest value compared with the findings of Broom (Reference Broom1982) in Kuala Selangor, Malaysia (3.37), Sungei Buloh, Malaysia (2.89) and Boonruang & Janekarn (Reference Boonruang and Janekarn1983) in Puket, Thailand (3.04) (Table 4). Several factors may influence the weight of soft tissue relative to shell length and can explain the differences in the current study. This might partly be explained through the influence of biological and ecological factors such as water temperature, density and shore level (Hickman, Reference Hickman1979). Furthermore, food availability can affect tissue growth, storage and utilization, which have the ability to change the ratio of total weight to shell length (Frechette et al., Reference Frechette, Aitken and Page1992; Nakaoka, Reference Nakaoka1992).
Table 4. Length–weight relationship parameters (regression coefficient b, regression constant a) of Anadara granosa derived by other authors from different areas.

In the current study, blood cockles of A. granosa were placed at an intertidal area in Balik Pulau, Penang Island. Therefore, differences of the growth rate of A. granosa compared with previous studies might be related to the time available for feeding and the available food supply during the immersion time in the intertidal area. The weight of soft tissue relative to shell length was lower at low elevation than high elevation. Differences in food density between the same species in different populations, or temporal variability in food availability may cause the different length-weight relationship (McKinney et al., Reference McKinney, Glatt and Williams2004). Furthermore, changes in shell morphology due to phenotypic variation are also able to affect the weight of soft tissue relative to shell length between locations (Trussell, Reference Trussell2000).
The age and growth parameters of Anadara granosa
The von Bertalanffy Growth Function (VBGF), a reliable explanation for growth rate of cockles (Caddy, Reference Caddy1989; Vakily, Reference Vakily1992), was examined in the present study for A. granosa and had a perfect fit for the length frequency data.
Yin et al. (Reference Yin, Goudriaan, Lantinga, Vos and Spiertz2003) found that the growth curve in bivalves was sigmoid in shape and the von Bertalanffy growth model was able to provide an ideal fit in relation to length frequency. Furthermore, the sigmoid growth curves were observed in bivalves by Tsoularis & Wallace (Reference Tsoularis and Wallace2002) and Lei & Zhang (Reference Lei and Zhang2004).
The growth parameters (L ∞, K, t 0) are helpful in comparing the growth rates between and within species inhabiting different habitats. In the current study, an estimation of the von Bertalanffy parameters including asymptotic length (L ∞) and growth coefficient (K) by ELEFAN I was 35.40 mm and 1.1 year−1, respectively.
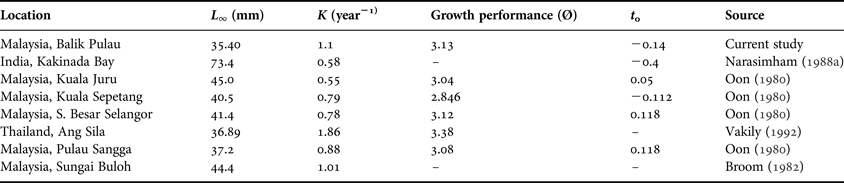
The growth parameters of A. granosa from this study showed differences from the results obtained in other studies (Table 5). The highest value of L ∞ was 73.4 mm from Kakinada Bay, India (Narasimham, Reference Narasimham1988Reference Narasimhamb). In Malaysia, Oon (Reference Oon1980) reported the value of L ∞ was 45.0 mm (Kuala Juru, Penang Island), 45.0 mm (Kuala Sepetang, Perak) and 41.4 mm (Sungai Besar Selangor). In addition, Broom (Reference Broom1982) showed the value of L ∞ was 44.4 (Sungai Buloh) which was also slightly higher than the value found in this study. Differences between ‘L ∞’ may be due to differences in ecological characteristics of the culture plots, different stock density or size distribution that is associated with water depth. Based on this observation, the L ∞ value of A. granosa from this study was similar to those results described by Vakily (Reference Vakily1992) in Ang Sila, Thailand (36.89) and Oon (Reference Oon1980) in Pulau Sangga, Perak, Malaysia (37.4).
Table 5. Estimated growth parameters of Anadara granosa derived by other authors in different areas

The K value, which determines how fast the blood cockle A. granosa approaches its L ∞ was a ‘curvature parameter’. The K value was very close to the findings of Broom (Reference Broom1982) in Malaysia, which showed the growth constant (K) was equal to 1.01 year−1. Nevertheless, the growth constant (K) in the current study was higher compared with other research performed in Malaysia.
As A. granosa does not grow according to the von Bertalanffy growth equation during its whole lifespan, particularly in the juvenile stage, the curve often starts from the negative side of the x-axis. Therefore, the theoretical age at zero length (t 0) often has a small negative value. The asymptotic age at zero length (t 0) of A. granosa for the current study was −0.14, which falls in the range of the initial condition parameters (t 0) of other studies. The value of this study was more than the value reported by Narasimham (Reference Narasimham1988a, Reference Narasimhamb) at Kakinada Bay, India (−0.4) and was very close to the values reported by Oon (Reference Oon1980) in Malaysia (Table 4).
The growth performance index (ϕ) is a length-based index of growth that shows the interaction of growth constant (K) and asymptotic length (L ∞). It was applied to give the potential growth rate of the blood cockle A. granosa. The ϕ was important for the evaluation of growth performance in similar species or between cockles of the same genus. There were similarities between the growth performance in this study (3.13) and those described by Oon (Reference Oon1980) at different areas in Malaysia and in the values of other studies. Therefore, it can be reasonably assumed that the growth constant (K) and asymptotic length (L ∞) were an accurate representation of the blood cockle, A. granosa population in Balik Pulau, Penang Island that the estimations in the present study using the length-frequency distribution method are reliable.
Based on an estimation of age frequency from length frequency with the von Bertalanffy growth equation, the results of the present study indicated that A. granosa was 25.00, 32.03 and 34.28 mm on completion of 1, 2 and 3 years, respectively. The present results showed that the blood cockle, A. granosa from Balik Pulau, Penang Island has a lower growth rate compared with other studies. However, it seems possible that the low growth rate was due to a high density of A. granosa in the sampling site. Another possible factor that may affect the growth rate was the difference between elevations. Samples of A. granosa were located in the intertidal zone and immersed on average twice a day. Therefore, tidal fluctuations in salinity and turbidity at this site might have reduced the time available for feeding and access to food supplies. It is still important to consider that the growth in cockles was significantly affected by geographic and environmental parameters. Moreover, it has been found that there may be big changes in growth between the same species in different populations (Vakily, Reference Vakily1992; Stern-Pirlot & Wolff, Reference Stern-Pirlot and Wolff2006). A variety of environmental factors such as the immersion period, turbidity, seawater temperature (Broom, Reference Broom1982), salinity (Ivanovici et al., Reference Ivanovici, Rainer and Wadley1981; Broom, Reference Broom1982) and water pollution (Din & Ahamad, Reference Din and Ahamad1995) have been confirmed to influence the growth rate of different Anadara spp. populations.
Longevity and mortality
The estimated longevity or maximum age value was 2.72 years for the blood cockle A. granosa in Balik Pulau, Penang Island, Malaysia. The present findings seem to be consistent with Narasimham (Reference Narasimham1969) in Kakinada Bay, India (3 years) which showed A. granosa is short-lived.
Mortality is an important parameter to understanding the dynamic population of cockles. The total mortality (Z), natural mortality (M) and fishing mortality (F) using the length-transformed catch curve was 2.32, 1.84 and 0.48 year−1, respectively (Table 6). Due to the experimental design in the preparatory step, the data for mortality study was obtained from individuals that were in an enclosure transplant area. As a result, mortality that occurred in the study site was considered to be from natural causes (M). There were little empty shells and dead samples in the study site, which could be the reason for the existence of natural mortality. In addition, the results of the theoretical calculation of total mortality in the current study showed that the fishing mortality level was very low and may be explained by the direct removal of animals (monthly sample collection) as fishing mortality in the study area.
Table 6. Estimated mortality parameters of Anadara granosa in Balik Pulau, Penang Island, Malaysia.
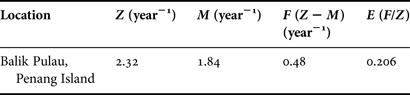
Based on Al-Barwani et al. (Reference Al-Barwani, Arshad, Amin, Japar, Siraj and Yap2007), total mortality included natural and fishing mortality (Z = M + F). The yield was ideal when F = M. Therefore, in the current study, higher natural mortality compared with fishing mortality indicated the unbalanced position of the cockle population.
The exploitation rate (E) was estimated with the value of fishing mortality divided by the value of total mortality (E = F/Z). When E was more than 0.5, the stock was over-fished (Gulland, Reference Gulland1965). However, the findings of this study confirmed the unbalanced condition in the stock and the lower value of E (0.20) indicated the ‘under-fishing’ condition (under-exploitation) of A. granosa which led to a decrease in biomass in the study area.
With this information, the management authorities can monitor the growth of the cockles and monitor the proper size for harvesting as well as for population growth. Further research regarding the stock assessment should take into account the marked differences in growth parameters of cockle populations. Furthermore, due to its economic importance, we recommend that future management should include better protection for A. granosa and a monitoring system should be initiated in order to collect size composition data for different fishing areas.
ACKNOWLEDGEMENT
The authors wish to acknowledge the financial support of the Universiti Sains Malaysia through Grant No. 1001/PB/844064.