Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T20:45:13.659Z Has data issue: false hasContentIssue false
  • English
  • Français

Our correct use of ANCOVA yields acceptable results

Published online by Cambridge University Press:  02 February 2007

KAARIN J. ANSTEY ,
AGUS SALIM ,
STEPHEN R. LORD ,
MICHAEL HENNESSY ,
PAUL MITCHELL ,
KATHERINE MILL  and
CHWEE VON SANDEN
KAARIN J. ANSTEY
Affiliation:
Centre for Mental Health Research, Australian National University, Canberra, Australia
AGUS SALIM
Affiliation:
Centre for Mental Health Research, Australian National University, Canberra, Australia
STEPHEN R. LORD
Affiliation:
Prince of Wales Medical Research Institute, Sydney, Australia
MICHAEL HENNESSY
Affiliation:
School of Ophthalmology, University of New South Wales, Sydney, Australia
PAUL MITCHELL
Affiliation:
School of Ophthalmology, University of Sydney, Sydney, Australia
KATHERINE MILL
Affiliation:
Prince of Wales Medical Research Institute, Sydney, Australia
CHWEE VON SANDEN
Affiliation:
Centre for Mental Health Research, Australian National University, Canberra, Australia
Rights & Permissions [Opens in a new window]

Extract

Gilmore (2007) argues that the use of ANCOVA in Anstey et al. (2006) is invalid. Based on quotes in Winer (1971), he claims that covariates cannot be used to adjust interaction terms involving within-subject variables. Because the within-subject variable in Anstey et al. (2006) is time, he concludes that the results involving Time × Group interaction coefficient are invalid and consequently all analyses need to be re-done.

Type
LETTERS TO THE EDITOR
Information
Journal of the International Neuropsychological Society , Volume 13 , Issue 2 , March 2007 , pp. 371
Copyright
© 2007 The International Neuropsychological Society

Gilmore (2007) argues that the use of ANCOVA in Anstey et al. (2006) is invalid. Based on quotes in Winer (1971), he claims that covariates cannot be used to adjust interaction terms involving within-subject variables. Because the within-subject variable in Anstey et al. (2006) is time, he concludes that the results involving Time × Group interaction coefficient are invalid and consequently all analyses need to be re-done.

However, our approach was more cautious than that proposed by Winer (1971) and we therefore argue that our analysis published in this journal is acceptable. We agree that with constant covariates, the classical ANCOVA of Winer (1971) can only be used to adjust the between-subjects (BS) effects. To see this, in a simplest case with time (T) as within-subject factor and treatment group (G) as between-subject factor and there are only two levels for T and G, we can represent Winer's ANCOVA model in notational form as

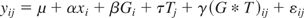
where yij refers to outcome for individual i measured at time Tj (0=pre-test,1=post-test), Gi is the treatment received by individual i (0= control, 1 = treatment), μ is the grand mean and xi is the covariate value of individual i and it is constant across time. We can see that since the G and x share the same subscript, the covariates only adjusts the group effects (BS effects) but not the other effects.

However, another class of ANCOVA can be created by having the covariates in the WS portion of the above model. This is achieved by adding interaction terms between the covariates and the WS variable (time). This is the default ANCOVA produced by SPSS (SPSS Resolution No. 22133). This model can now be written as

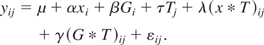
It can be seen now that the new interaction term (x * T) does not adjust the main within subject effect T (time) but nonetheless it adjusts the Time × Group interaction effect. A significant λ can be interpreted as the change of scores between pre- and post-test for an individual is affected also by his/her covariates value x, apart from the treatment group he/she is allocated to. More importantly, this model is better than Winer's model because a significant λ will indicate that the homogeneity of slopes (HOS) assumption implicit in Winer's ANCOVA in Eq. 1 is violated (see also SPSS Resolution No. 22133). On the other hand, if λ is not significant, our approach and Winer's approach will yield virtually the same numerical solutions.

Hence, we conclude that our approach is different from Winer's ANCOVA and is a more cautious one and hence no re-analysis is needed.

References

REFERENCES

Anstey, K.J., Lord, S.R., Hennessy, M., Mitchell, P., Mill, K., & von Sanden, C. (2006). The effect of cataract surgery on neuropsychological test performance: A randomized controlled trial. Journal of the International Neuropsychological Society, 12, 632–639.Google Scholar
Gilmore, G. (2007, this issue). Inappropriate use of covariate analysis renders meaningless results. Journal of the International Neuropsychological Society, 13, 370.Google Scholar
SPSS Knowledgebase (2001, December 10). Resolution 22133: Repeated measures with constant covariates in GLM. Message archived at http://support.spss.com/tech.
Winer, B.J. (1971). Statistical principles in experimental design (2nd ed.). New York: McGraw-Hill.