INTRODUCTION
The assessment of neuropsychological deficits in the individual case
normally involves comparing a patient's score on a
neuropsychological test (e.g., number of items correct) with the
distribution of scores obtained from an appropriate control or
normative sample. However, for some neuropsychological constructs and
their related measurement procedures, it is necessary, or at least
preferable, to quantify performance through the use of an
intra-individual measure of association (IIMA). These measures
of association can either be parametric or non-parametric correlation
coefficients, or the slopes of regression lines. Evaluation of an
individual patient's performance is made by comparing the
magnitude of the index of association observed for the patient with
those of a normative or control sample.
EXAMPLES OF NEUROPSYCHOLOGICAL MEASURES
WHERE PERFORMANCE IS EXPRESSED AS AN IIMA
The examination of memory for temporal order provides an obvious
example of the use of an IIMA. Typically, performance on a temporal
order memory task is quantified by computing the intra-individual (rank
order) correlation between the actual order in which items (e.g., words
or pictures) were presented, and the patient's memory for this
order (Shimamura et al., 1990). The
correlation computed from the patient's data can be compared with
the average correlation obtained from a control or normative sample (a
low correlation would suggest impairment); see Mayes et al. (2001) for a recent example.
As another example, in the area of motor control, there is a high
intra-individual correlation between maximum grip aperture when
reaching for objects and the size of the objects (Carey, 1996). An investigator may wish to determine
whether this relationship breaks down in an individual with
neurological disease. This could be examined by comparing the slopes of
the intra-individual regression lines (relating object size and
aperture size) obtained from healthy participants with the slope of the
regression line obtained from the patient. Relatedly, there is a
positive relationship between the peak velocity of manual reaching and
the distance from a target; the further away the target, the faster the
peak velocity (Jeannerod, 1984). Again, an
investigator may wish to examine whether this relationship breaks down
in cases with neurological disease; see Carey et al. (1998) for an example.
As a fourth example, in the area of object recognition, it has been
found that there is a robust intra-individual relationship between the
latency with which an object is named and the degree to which it is
rotated away from its prototypical orientation (Turnbull et al., 1997). Failure to find such an
association in a patient would suggest that mental rotation was not
being used to achieve object identification; see Turnbull et al. (2002) for a recent single-case study. Distance
estimation tasks provide yet another example from the area of visual
perception; here the issue would be whether a patient exhibits an
attenuation of the expected relationship between visually estimated
distance and actual distance (Carey et al.,
1998).
IIMAs have also been employed in the area of auditory perception. For
example, Steinke et al. (2001) used measures
of tonality to assess melody recognition in a patient with right
hemisphere damage. Performance on each of four tests of tonality (Steinke et al., 1997) was quantified by computing
the Spearman rank order correlation between a participant's
ratings of tonality and music-theoretic predicted levels of tonality.
Estimation of weight (Jones, 1986) provides
another example where IIMAs can be used (to compare estimated against
actual weight); estimation of weight has been found to be impaired in a
number of neurological conditions (see, e.g., Heindel et al., 1991; Lafargue
& Sirigu, 2002).
Finally, in the investigation of time estimation, accuracy can be
assessed by examining the strength of the intra-individual relationship
between the length of the actual time intervals and the estimated time
intervals. There is evidence that, particularly when the time intervals
exceed 20 s (Richards, 1973; Sherwin & Effron, 1980), amnesic patients
exhibit deficits in time estimation as indicated by a weakening of the
association between actual and estimated time (Nichelli et al., 1993; Venneri
et al., 1998). Indeed, in severe cases, the direction of the
relationship can be reversed (e.g., the correlation, or slope of the
regression line, has a negative sign), thereby indicating that shorter
intervals are estimated as longer.
In the foregoing examples the breakdown or weakening of an
intra-individual association found in healthy participants would
suggest impairment. However, in some circumstances an investigator may
seek evidence of impairment through demonstrating that there is a
strengthening of an intra-individual relationship in a
patient. For example, it might be found that a patient's
performance on a primary task is differentially sensitive to the degree
of working memory load (e.g., number of digits retained) imposed by a
secondary task. Were this the case, then one would expect to find a
higher (negative) correlation between working memory load and primary
task performance in the patient than in the healthy control
participants.
STATISTICAL METHODS FOR COMPARING AN
INDIVIDUAL WITH A CONTROL OR NORMATIVE SAMPLE
In all of the foregoing examples, correlation coefficients, or slopes
are treated as data. It is not uncommon for correlation
coefficients to be used in this way; see Howell (1997) for a brief commentary. A particularly
pertinent example is provided by the previously mentioned study by
Shimamura et al. (1990) on temporal order
memory. In this study, t tests and ANOVAs were used to compare
the mean intra-individual correlations (between the actual and reported
order of the stimulus items) obtained from healthy and amnesic samples.
Venneri et al. (1998), in their study of time
estimation in amnesic and control samples, used ANOVA to compare the
mean slopes (relating actual elapsed time to estimated elapsed time)
obtained from the amnesic and control participants.
In both these examples, inferential statistics were used to test
differences between two samples. In contrast, both academic
neuropsychologists who study single cases, and clinical
neuropsychologists, are concerned with comparing an individual
with a normative or control sample. However, just as the group
researcher is concerned with whether group differences are
statistically significant, so single case researchers or clinicians
would wish to determine whether the observed difference between their
patient and a normative or control sample was statistically
significant. More generally, neuropsychologists have an interest in
estimating the abnormality or rarity of a
patient's performance; that is, they wish to estimate the
proportion of the healthy population that would be more extreme than
their patient. The remainder of this paper is concerned with developing
statistical methods to address these needs.
The range of potential solutions to these problems is constrained by
the fact that the normative or control samples, against which an
individual is to be compared, will often be modest in size. Among the
reasons for this is the fact that theoretical advances in
neuropsychology continue to occur at a rapid rate, whereas the
collection of large-scale normative data is a time-consuming and often
arduous process (Crawford, 1996). Thus,
neuropsychologists may continue to have access only to provisional
normative data long after a new measure has been developed; these norms
may be no more than control sample data from an experimental study.
Second, when performance on a neuropsychological measure is best
expressed as an intra-individual measure of association, a specific
factor that may have discouraged collection of norms is the lack of
explicit, practical guidance on how to analyse and interpret an
individual's score when data are in this form. It is hoped that
the methods presented here will help remove this obstacle.
The need to develop methods that are suitable for use with small
control or normative samples is perhaps most apparent when one
considers single-case research. Within academic neuropsychology there
has been a resurgence of interest in single-case studies and this has
led to significant advances in our understanding of normal and
pathological cognitive function (Caramazza &
McCloskey, 1988; Code et al., 1996;
Ellis & Young, 1996; Humphreys, 1999; McCarthy &
Warrington, 1990; Shallice, 1988). In
many of these studies the theoretical questions posed cannot be
addressed using existing instruments and therefore novel instruments
are designed specifically for the study (Shallice,
1979). The sample size of the control or normative group
recruited for comparison purposes in such studies is typically below 10
and often less than 5. In passing, it may be noted that the control
group need not be healthy participants; for example, one can envisage
many hypotheses that state that a particular patient will exhibit a
breakdown in an association of interest in contrast to samples of
patients having other clinical features in common.
For the reasons outlined above it is clear that statistical methods
that treat the normative or control statistics as parameters (i.e.,
treat the normative sample as if it were a population rather than a
sample) would have limited applicability. In this respect, the need for
an appropriate method of dealing with intra-individual measures of
association, is directly analogous to the simpler case where the
researcher or clinician wishes to compare a conventional test score for
a patient (e.g., number of items passed on a memory test) with a
control or normative sample.
The ‘standard’ procedure for statistical inference in
this latter situation is well known. When it is reasonable to assume
that scores are normally distributed, the patient's score is
converted to a z score, based on the mean and standard
deviation in the normative sample, and evaluated using tables
of the area under the normal curve (Howell,
2002; Ley, 1972). Thus, if the
researcher or clinician has formed a directional hypothesis concerning
the patient's score prior to testing (e.g., that the score will be
below the mean), then a z score which fell below −1.64
would be considered statistically significant (using the conventional
5% level). More generally, the procedure provides the neuropsychologist
with information on the rarity or abnormality of the individual's
score. This method treats the normative sample statistics as if they
were parameters. When the N of the normative sample is large
this is not problematic. However, it is problematic when, for example,
the sample consists of only 10 persons.
Drawing on work by Sokal and Rohlf (1995),
Crawford and Howell (1998) presented a method
of comparing an individual's score with a normative sample in
which the sample statistics are used as sample statistics rather than
treated as population parameters. The method is a modified independent
samples t test in which the individual is treated as a sample
of N = 1 and, therefore, does not contribute to the estimate
of the within-group variance. The formula is
where X1 = the individual's score,
X2 = the mean score of
the normative sample,
= the standard deviation of the scores in the normative sample, and
N2 = the sample size. The degrees of freedom for
t are N2 + N1 −
2, which reduces to N2 − 1. This method can
be used to determine if an individual's score is significantly
different from that of the normative or control sample. More generally,
it provides an unbiased estimate of the abnormality of the
individual's score; i.e., if the p value (one-tailed) for
t was calculated to be 0.03 then it can be estimated that only
3% of the healthy population would exhibit a score lower than that
observed for the individual.
Crawford et al. (1998) extended this
approach to cover circumstances where the neuropsychologist wishes to
compare the difference between a pair of test scores (e.g., scores on
verbal versus spatial short-term memory tasks) observed for an
individual, with the distribution of differences observed in a control
or normative sample. Crawford and Garthwaite (2002) also extended it to permit comparison of the
differences between an individual's scores on each of k
tests and the individual's mean score on the k tests with
the differences between these quantities in a control or normative
sample.
In the present paper we further extend this general approach to cover
circumstances where the clinician or researcher wishes to compare an
intra-individual measure of association obtained from a patient with a
normative or control sample. Before presenting these methods it should
be noted that an additional consideration in developing them was that
they should only require summary statistics from the control or
normative sample and the patient, rather than the raw data. This was
motivated by three considerations. First, the summary statistics
required are easily obtained from any standard statistical package.
Second, working with the summary statistics is less time consuming for
the user. Third, by requiring only summary data, this should encourage
the development of norms for neuropsychological measures for which
performance is best expressed as an IIMA. That is, publication of the
summary statistics from a normative or control sample would be
sufficient for independent researchers or clinicians to use the norms
with their own patients.
The methods set out below can be used to compare an individual with a
normative sample when performance is expressed as a Pearson correlation
coefficient (i.e., a parametric coefficient) or a non-parametric
coefficient (Spearman Rank Order Correlation Coefficient or
Kendall's Tau). The only information required is N and
the correlation coefficients for each of the members of the control or
normative sample and the patient.
The original intention had been to also present methods for comparing
the slope of a patient's regression line with those of controls.
However, the procedures required in this latter case are more
complicated (partly because more information is available when working
with slopes). Prior to testing for a difference in slopes a sequence of
tests has to be run. These examine, (1) if the error variances of the
controls are homogenous, (2) if the error variance of the patient
differs significantly from controls, and, if so, whether (3) there
appears to be little variation between the controls in their slopes.
The results from these pre-tests determine which of three formulae
should be used to compare the patient's slope with controls. As
these methods are very different from the methods for correlation
coefficients, and require lengthy computations, we have prepared a
follow-up paper that deals with slopes (Crawford
& Garthwaite, 2003).
TESTING EQUALITY OF PEARSON CORRELATION
COEFFICIENTS
When performance on the task of interest is expressed as a Pearson
(i.e., parametric) correlation coefficient, we let
ρi denote the correlation coefficient for the
ith person and let ri denote its
sample estimate, based on k trials or items. The sampling
distribution of correlation coefficients is not normally distributed
and so we apply Fisher's transformation to the coefficients for
the individuals in the normative or control sample and the patient:
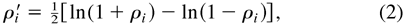
and,
then approximately,
We assume that ρ1′ …
ρn′ are values from a normal
distribution,
That is, we accept that the true values of the (transformed)
correlations differ between individuals. We denote their mean value in
the normative population by R and their variance by
λ2. Also, we assume these true values
(ρi′, i = 1… N)
follow a normal distribution. We want to test the null hypothesis that
ρn+1′ (the true correlation coefficient
for the patient) is from the same distribution. Assuming k is
sufficiently large (i.e., > 10) for the approximation in equation
(4) to hold, then
r1′…rn′
are a simple random sample from the normal distribution,
This last equation (6) shows that
ri′ varies from R both
because ri′ varies about
ρi′ (with variance 1/(k
− 3)), and because ρi′ varies about
R (with variance λ2). The variance of
ri′ is the sum of these components
of variance. If the null hypothesis holds, then
rn+1′ is also from the distribution
in (6). We calculate the mean and standard deviation of the transformed
correlations in the control sample, i.e.,
and
Then, if rn+1′ (the patient's
observed correlation) comes from the same normal distribution as
ri′…rn′,
has a t distribution on N − 1 degrees of
freedom. If the null hypothesis is rejected at the conventional .05
level, then the patient's correlation is significantly different
from that of the controls. Furthermore, if the precise one-tailed
probability for t is multiplied by 100 then we have an
estimate of the percentage of the population that would obtain a
correlation lower than the patient's.
It can readily be appreciated that formula (9) is directly equivalent
to the formula employed by Crawford and Howell (1998). In Equation (1)
the difference between a patient's score on a neuropsychological
test (e.g., number of items passed) and the mean score of the control
or normative sample is divided by the standard error of the mean of the
control sample. In the present case, where performance on the
neuropsychological task is represented not by a conventional score but
by a correlation coefficient, the difference between the patient's
transformed coefficient and the mean transformed coefficient of the
control sample is divided by the standard error of the mean
coefficient.
A potential alternative means of testing the difference between the
patient's transformed correlation and the mean correlation in the
controls would be simply to convert the patient's transformed
correlation to z, based on the mean and SD of the
controls, and refer this z to a table of the area under the
normal curve. (Such a method could also be used with the other forms of
correlation coefficients dealt with in the present paper.) However, as
when comparing a patient's performance on a conventionally scored
test with controls, this method is inappropriate, since it treats the
control sample statistics as if they were population parameters. The
practical effect of using this alternative method would be to
exaggerate the abnormality of the patient's performance and to
spuriously inflate the chance of finding statistically significant
effects. A comparison of the results from these methods is provided in
the worked example (see later section).
Obtaining Confidence Limits on the Abnormality of an
IIMA
The above method is designed to yield a point estimate of the rarity
or abnormality of a patient's IIMA when the IIMA employed is a
correlation coefficient. However, it would also be desirable to obtain
confidence limits on the abnormality of the patient's IIMA. That
is, using (9) we obtain a point estimate of the percentage of the
population that will perform more poorly than the patient but now we
wish to obtain confidence limits on this percentage. Such an aim is in
keeping with the contemporary emphasis in statistics, psychometrics,
and biometrics on the use of confidence limits (American Psychological Association, 2001; Daly et al., 1995; Gardner &
Altman, 1989; Zar, 1996). Gardner and
Altman (1989), for example, in discussing the
general issue of the error associated with sample estimates note that
“these quantities will be imprecise estimates of the values in
the overall population, but fortunately the imprecision itself can be
estimated and incorporated into the findings” (p. 3). Similarly
the American Psychological Association (2001)
take the view that confidence limits or intervals represent, “in
general the best reporting strategy. The use of confidence intervals is
therefore strongly recommended” (p. 22). The use of confidence
limits is particularly appropriate when results are obtained from small
samples.
To generate confidence limits on the abnormality of this form of IIMA
we use a result obtained by Crawford and Garthwaite (2002). Let P denote the percentage of the
population that will fall below a given individual's transformed
correlation (rn+1′), and suppose we
require a 100(1 − α)% confidence interval for P. As
in the formula for the point estimate, let
(rn+1′ −
r′) represent the difference
between the individual's score and the mean score of the normative
or control sample, let
be the standard deviation in the normative sample, and let N be
the size of the normative sample. We assume scores for the control
population are normally distributed. If we put
then c is an observation from a non-central t
distribution on N − 1 degrees of freedom. Non-central
t-distributions have a non-centrality parameter that affects
their shape and skewness. We find a value of this parameter,
δU, such that the resulting non-central
t-distribution has
as its 100α/2 percentile. Then we find the value
δL such that the resulting distribution has
as its 100(1 − α/2) percentile. From tables for a
standard normal distribution we obtain
These probabilities depend upon α, c and N and we
denote them by h(α/2;c; N) and
h(1 − α/2;c; N), respectively.
Then a 100(1 − α)% confidence interval for P may be
written as
From equation (3),
ri′ is a monotonically increasing
function of ri, so
(h(α/2;c; N), h(1 −
α/2;c; N)) is also a 100(1 − α)%
confidence interval for the percentage of the population that will fall
below a given individual's untransformed correlation,
rn+1. Details of the derivation of
h are given in Crawford and Garthwaite (2002) and a worked example of obtaining 95%
confidence limits on the rarity of an IIMA is provided in a later
section.
TESTING EQUALITY OF RANK CORRELATION
COEFFICIENTS
When performance on the task of interest is expressed as a
non-parametric correlation coefficient, i.e., Spearman Rank Order
Correlation Coefficient or Kendall's Tau, we suggest that, as was
done with Pearson correlations, Fisher's transformation is applied
to the coefficients of the control or normative sample and the
coefficient of the patient. Kraemer (1974),
in reviewing inferential methods for rank order coefficients notes that
Fisher's transformation “has proved successful as a
transformation which, when applied to several forms of correlation
coefficients, is approximately normally distributed with variance
independent of ρ” (p. 114). Fieller et al. (1957) and Fieller and Pearson (1961) showed that the approximation is good for
Spearman's Rank Order correlation coefficient and Kendall's
Tau for k > 10 and |ρ| < .9.
Therefore, if comparing the non-parametric coefficient obtained for a
patient with a control or normative sample, the procedure is identical
to that for parametric correlation coefficients. That is, the mean and
SD of the transformed coefficients are calculated and entered
into formula (9) along with the transformed coefficient for the
patient. Similarly, if confidence limits on the abnormality of the
patient's score are required, the procedure described for
parametric coefficients should be followed.
WORKED EXAMPLES
To illustrate the methods we use the example of the test of temporal
order memory developed by Shimamura et al. (1990). In this task participants are read a list of
15 words and are then given the words on individual cards and asked to
attempt to put them in the order in which they were originally
presented. A 34-year-old female patient with a left frontal lesion was
administered this test and the Spearman Rank Order correlation between
the actual order of the words and the order produced by the patient was
.210; the transformed correlation was .213. It will be noted that
k in this example (the number of items used to compute the
coefficient) is 15 and is thus sufficiently large for Fisher's
transformation to give approximately normal distributions.
In the course of studying the effects of ageing on memory and
executive functions, Crawford et al. (2000)
obtained data for this task from 111 healthy persons. Because we wish
to illustrate the use of this method when the control or normative
sample is modest in size, we selected 14 of these participants to match
the patient in terms of gender, age and years of education. Mean age in
the control sample was 34.2 (SD = 2.69) and mean years of
education was 12.0 (SD = 1.51); the patient had 13 years of
education. Table 1 presents the Rank Order
Correlation Coefficients and the transformed correlations for the
controls. The mean of the transformed correlations in the controls is
.637 with a SD of .180. Entering these data into formula (9)
yields the following result,
Correlation (r) and transformed (r′)
correlation between order and reported order on a temporal order memory
task in 14 control participants (the correlations are Spearman Rank
Order Correlation Coefficients); the final column presents raw scores
on a free recall task, used in the example of testing for
dissociations.
As the hypothesis tested by the researcher or clinician in this
example is directional, that is, that the patient's performance
will be significantly lower than matched controls, a one-tailed test is
appropriate. The one-tailed critical value for t at the 5%
level on 13 degrees of freedom is 1.77. The individual's score is,
therefore, significantly different from the controls at the 5% level.
The exact one-tailed probability for t in this example is
.0202 and so the expectation is that only 2.02% of individuals in the
population from which the normative sample was drawn would obtain a
score as low as that observed for the patient. To obtain 95% confidence
limits on this percentage we proceed as follows:
We want a non-central t distribution on N − 1
= 13 degrees of freedom that has −8.815 as its 0.975 quantile.
This determines the non-centrality parameter to be −12.652 so we
put δL = −12.652. We also want a
non-central t distribution on 13 df that has
−8.815 as its 0.025 quantile. This gives
δU = −4.892. Then,
Hence the 95% lower confidence limit for P is 0.04% and the
upper limit is 9.56%. To summarize the results for this case: the
patient's memory for temporal order was significantly poorer
(p < .05) than controls and it is estimated that only 2.02%
of the population would exhibit a score poorer than that observed; the
95% confidence interval on this percentage is .04% to 9.56%.
As noted in a previous section, a potential alternative means of
testing the difference between the patient and controls would be simply
to convert the patient's transformed correlation to z. It
is informative to compare this alternative with the proposed method for
the present example. The patient's correlation expressed as a
z score is −2.36. Referring this z to a table
of the normal curve reveals that the estimated percentage of the
population that would obtain a correlation lower than this is 0.9%.
This exaggeration of the abnormality of the patient's performance
would be even more pronounced with smaller control samples.
Furthermore, in the present example, the conclusion from application of
both the t test and z is that the patient is
significantly impaired (p < .05). However, obviously these
methods need not be in agreement. For example, if the patient's
transformed correlation had been .335, then z (−1.68)
would be significant (p < .05). However, this would be a
spurious result arising from treating the sample as a population; the
t-test would not be significant (t = 1.62, p
> .05).
As another example of the use of these methods, Steinke et al. (1997) conducted a single-case study of a patient,
C.N., who had suffered bilateral temporal lesions. Steinke et al.
administered a series of tests of music perception to C.N. and 6
matched controls. Performance on the tests of music perception was
quantified by the rank order correlation between an individual's
ratings of the stimulus items (e.g., of tonality) and music-theoretic
predicted levels. C.N. performed poorly on these tasks. No inferential
method was employed to test whether C.N. differed significantly from
controls but this can be readily achieved with the present method. For
example, on a test of novel melodies the correlation obtained for C.N.
was .46 (hence r′ is .497). The mean of the Fisher
transformed correlations (r′)
in the 6 controls was 1.29 with a SD of .305. Entering these
data into formula (9) yields a t of 2.406 and a one-tailed
probability of .031. Therefore, C.N.'s performance was
significantly poorer than controls. The confidence interval on the
percentage of the population that would obtain a lower score (i.e., a
lower correlation) than C.N. was from .008% to 20.3% (the point
estimate was 3.1%).
USE OF THESE METHODS WITH LARGE-SCALE
NORMATIVE DATA
The emphasis in the foregoing discussion of these methods has been on
their use with modest control or normative samples. However, it should
be stressed that these methods are applicable to comparison of an
individual with normative samples of any size. Indeed methods
such as these (i.e., methods that use the t distribution
rather than the standard normal distribution) are in fact technically
the correct way to make a comparison against any normative
sample because our normative samples are always just that, samples
rather than populations. Of course, if the normative sample is large,
then methods that use the t distribution and those that treat
the sample statistics as population parameters will converge; that is,
z can be used to provide an adequate approximation to
t with large Ns.
The amount of normative data on IIMA tasks is currently limited, at
least in part, because there has been little guidance on how to use
such data to draw inferences concerning an individual's
performance. It is to be hoped that the development of these methods
will help to remedy this situation. To illustrate, suppose a researcher
standardized a temporal order memory task on a large sample of the
general adult population. To make this available as normative data the
researcher would simply need to report the mean and SD of the
Fisher transformed correlations between actual and reported order
(separate means and SDs could be reported for different age
groups etc. if required). The end user would then enter these
statistics into formula (9) along with the transformed correlation for
their patient (most statistics texts provide a table for converting
between r and r′). In order to make this
process as convenient as possible, the program that accompanies this
paper (see later section) offers the option of entering the mean and
SD of the transformed correlations for the normative or
control sample and the raw (i.e., untransformed) correlation obtained
from the patient.
We hope that the availability of these methods will encourage the
development of normative data for tasks in which performance is
quantified using an IIMA. In the interim (i.e., prior to development of
large-scale normative data) the methods allow researchers and
clinicians to use IIMAs with the modest data that are already available
(including, in the case of single-case studies, data collected from a
control sample).
DETECTING DISSOCIATIONS WHEN PERFORMANCE ON
ONE OR BOTH OF THE TASKS IS EXPRESSED AS AN IIMA
Up to this point we have been concerned with methods of testing for a
significant deficit on a single task. Although the ability to identify
a deficit in the individual case is fundamental, the presence of a
deficit in a given cognitive function often only acquires theoretical
importance when it is accompanied by the absence of a deficit in other
related functions. That is, a central aim in many neuropsychological
case studies is to fractionate the cognitive system into its
constituent parts, and this aim is pursued by attempting to establish
the presence of dissociations of function. Typically, if a patient
obtains a score in the impaired range on a test of a particular
function and is within the normal range on a test of another function,
this is regarded as evidence of a dissociation. However, this evidence
in isolation may not be at all convincing (Crawford
& Garthwaite, 2002). For example, a patient's score on
the “impaired” task could lie just below the cut-point for
defining impairment and the performance on the other test lie just
above it. Therefore, a more stringent test for the presence of a
dissociation would also involve a comparison of the difference
between tests observed for the patient with the distribution of
differences between these same tests in the control sample (Crawford et al., 2003).
As previously noted, Crawford et al. (1998)
devised a method that can be used to test whether the difference
between an individual's score on two tasks is significantly
different from the differences observed in a control sample. This
method can, therefore, provide an additional test for the presence of a
dissociation. However, it is also useful in the converse situation
where a patient's scores are within the impaired range on
both tasks. When this pattern is observed, the researcher can
still test whether the magnitude of the difference between the two
tasks is abnormal; i.e., evidence can be sought for the presence of a
differential deficit on the test of one of the functions.
The method was developed for use with tasks in which performance is
quantified by conventional means (e.g., number of items correct). For
example, Crawford et al. (1998) use the
example of testing whether the difference between a patient's
performance on a verbal short-term memory task and a spatial short-term
memory was significantly larger than the differences in a control
sample. However, their method can be just as applicable when
performance on one or both of the tasks is expressed as an IIMA. The
formula for this test, which is essentially a modified paired samples
t test, is
where ZX and
ZY are the scores of an individual on Test
X and Test Y expressed as z scores formed
using the means and SDs of the control sample,
rxy is the correlation between Tests
X and Y in the control sample, and
N2 is the number of participants in the control
sample. The test statistic follows a t distribution on
N2 − 1 degrees of freedom. Multiplying the
one-tailed probability of t by 100 gives the point estimate of
the abnormality of the individual's score. A derivation for the
formula can be found in Appendix 1 of Crawford et al. (1998).
The use of this method is best illustrated with an example. Let us
suppose that the patient whose temporal order memory performance was
used to illustrate the method for correlations had also been
administered a conventional verbal free recall task involving recall of
15 words. Given the evidence that temporal order memory is
differentially impaired following frontal lesions in comparison with
free recall (e.g., Shimamura et al., 1991),
we could test the directional hypothesis that the patient's
temporal order memory will be significantly poorer than her performance
on free recall.
The healthy participants (N = 14) selected from Crawford et
al.'s (2000) sample to serve as controls
for this patient had in fact been administered the verbal free recall task
described above. Their mean score (i.e., number of words correctly recalled)
was 9.07 with a SD of 2.46 (range = 5–14). The raw scores of
the controls on this task are presented in the final column of Table 1 (thereby providing potential users of this
method with all the data required to work the example from scratch).
Suppose that the patient's score on the free recall task was 8. As
recorded earlier, the patient's score on the temporal order task
(i.e., the correlation between the actual and reported order of items)
was .213 after applying Fisher's transformation. Also as reported
earlier, the mean and SD of the transformed correlations in
the control sample was .637 with a SD of .180. The only
remaining statistic required to test for a dissociation between free
recall and temporal order memory is the correlation between performance
on the two tasks in the control sample; this (Pearson) correlation was
.51 (note that this correlation is computed from the free recall scores
and the transformed correlations of the controls).
Using the means and SDs of the controls, the patient's
score on the free recall task expressed as a z score is
−0.435 and the z score for temporal order is
−2.356. We will designate the free recall task as Test X
and the temporal order task as Test Y (the choice is arbitrary).
Entering these data into formula (12) we obtain t:
The one-tailed probability for a t of 1.87 on 13 degrees of
freedom is .042. We would conclude, therefore, that the patient's
performance on the temporal order task was significantly poorer than
performance on free recall; that is, there is evidence of a
dissociation between memory for temporal order and free recall of
equivalent stimuli. In addition, by multiplying this p value
by 100 we have an estimate of the percentage of the healthy population
that would exhibit a discrepancy in favor of recall larger than that
observed for the patient (4.2%); that is, discrepancies of this
magnitude are fairly rare. A confidence interval on this percentage can
be obtained using a method devised by Crawford and Garthwaite (2002). In the interests of brevity we do not
provide a worked example here but the 95% confidence interval for this
example is from 0.23% to 15.3%.
As another example, we return to Steinke et al.'s (1997) study of impaired music perception in case C.N. An
important aim of Steinke et al.'s case study was to test whether music
perception could be dissociated from non-musical cognitive abilities. To
examine this, C.N. and controls were also administered a series of other
tests, including subtests of the WAIS–R (Wechsler,
1981) and the Wisconsin Card Sorting Test (Heaton,
1981). Steinke et al. did not use an inferential method to test
whether C.N.'s performance on music perception was significantly
poorer than performance on these other tasks but this can readily be
achieved using the present method. For example, C.N.'s score on
the Wisconsin was 96 and the mean and SD in controls was 89.2
and 3.49, respectively (the correlation between performance on the
novel melodies task and the Wisconsin in the controls was 0.83).
Entering these data, together with the previously recorded data for the
novel melodies task, into formula (12), yields a t of 7.22 and
a one-tailed probability of .0004. Therefore, the discrepancy between
C.N.'s performance on the music perception and non-musical task
was highly significant and there is strong evidence for a
dissociation.
The foregoing examples involved comparing the difference between a
patient's performance on two tasks with the differences in
controls when performance on only one of the tasks was
expressed as an IIMA. However, as noted, Crawford et al.'s (1998) method is just as applicable when performance on
both tasks is expressed as an IIMA. Therefore, the method can be used
whenever there is a need to examine performance under different experimental
conditions (i.e., comparison of a patient's correlation obtained
under Condition A versus the correlation obtained under
Condition B).
For example, Carey et al. (1998) examined
the ability of a patient (D.F.) to visually estimate distance; they
reported the correlations between actual and estimated distance for
D.F. and controls under monocular and binocular conditions. Milner et
al. (1991) hypothesized that cases such as
D.F. should be markedly more impaired when distance is estimated using
monocular versus binocular vision. The present method could be used to
test this hypothesis by comparing the difference between the
correlations under monocular versus binocular conditions for a patient
against the differences between the correlations observed in controls.
The indications are that, in the case of D.F., application of such a
test would reveal a significant difference. Carey et al. (1998) found that the correlation between actual and
estimated distance for D.F. was markedly higher under binocular
conditions, whereas the correlations for two controls were very similar
under monocular and binocular conditions.
As another example, Venneri et al. (1998)
examined time estimation under single and secondary task conditions
(the secondary tasks imposed demands on either working memory or
attention). The method outlined could be used to examine whether a
patient's performance is more sensitive than controls to the
effects of these secondary tasks.
Furthermore, memory for temporal order can be tested with verbal and
non-verbal stimuli (Mayes et al., 2001); in
both cases performance is quantified by computing the correlation
between actual and reported order. The method described could be used
to test for a significant difference in performance on these two tasks
in the individual case. Finally, it was noted that Steinke et al.
(2001) have developed four tests of tonality
and that performance on each of these tasks is quantified by computing
the Spearman rank order correlation between a patient's ratings of
tonality and music-theoretic predicted levels of tonality. If a
researcher wished to test for possible dissociations between two of
these different aspects of tonality the method described above could be
used to test for their presence.
Before leaving this topic it should be noted that, in the
illustrative examples, the concern was with testing whether there was a
statistically significant dissociation between performance on the two
tasks. However, in the search for dissociations, the aim is to uncover
dissociations between functions, not the tests used as
(imperfect) indicators of these functions. Therefore, it can be of some
value to demonstrate that tests of a particular putative function
provide similar indications of impairment (i.e., that they do not
differ significantly). This is perilously close to attempting to prove
the null hypothesis and therefore such evidence can play only a
supporting role. That is, when there is evidence that was regarded as a
unitary function, which can be fractionated into two new putative
functions A and B (as indicated by the presence of significant
differences between measures of A and B), the lack of significant
differences among the tasks assessing each of these putative functions
lends support to the view that these new constructs possess internal
consistency.
ABNORMALITY AND RELIABILITY OF SCORES AND
SCORE DIFFERENCES AND THEIR CORRESPONDING CONFIDENCE INTERVALS
The present methods test whether a patient's score
(specifically, an IIMA) or score difference came from the same
population as a control or normative sample and are distinct from a
test on the reliability of differences. A reliable difference
between an individual's test scores is one unlikely to have arisen
from measurement error in the tests. However, many healthy individuals
will have reliable differences among their abilities in different
cognitive domains. Indeed, if the tests concerned have high
reliability, reliable differences will be very common and
therefore cannot be taken as indicating acquired impairment (see, e.g.,
Crawford, 2003; Crawford
& Allan, 1996). Therefore, methods that quantify the
probability that a patient's score difference was drawn from the
distribution of score differences in the healthy population are more
germane to the needs of clinicians and single-case researchers (Crawford & Garthwaite, 2002; Crawford et al., 1998).
Similarly, the confidence limits presented in the present paper are
confidence limits on the estimated rarity or abnormality of a given
score (specifically, an IIMA) or difference between scores. As noted,
they allow the user to quantify the effects of error arising from using
a sample in place of the population: they quantify the fallibility of
normative or control sample data. These confidence limits are therefore
distinct from confidence limits that quantify the effect of measurement
error in a test instrument (or instruments) on an individual's
score (or score differences). These latter limits are obtained by
multiplying a test's standard error of measurement (or the
standard error of measurement of the difference when concerned with
score differences) by a standard normal deviate (i.e., 1.96 for 95%
limits)
CAVEATS ON THE USE OF THE FOREGOING METHODS
The tests developed in the present paper involve assumptions about
the underlying distributions from which the normative data were
sampled. In the case of the simple comparison of a patient's IIMA
with a control mean, the assumption is that the control data were
sampled from a normal distribution. In the case of testing for a
dissociation, it is assumed that the differences between the two tasks
follow a normal distribution. This latter assumption holds if scores on
the two tasks follow a bivariate normal distribution but this condition
is not essential. These same assumptions apply to the corresponding
methods for obtaining confidence limits on the abnormality of an IIMA
or difference (i.e., potential dissociation) between an IIMA and
another task.
It follows that these procedures should be avoided when it is known
or suspected that the control or normative data are markedly skewed or
platykurtic–leptokurtic. It should be noted that the possible
alternative method discussed in a previous section (i.e., treating the
sample as a population and using z to evaluate a
patient's performance) makes exactly the same assumption of
normality and is equally compromised by nonnormality. When the control
or normative samples are small, the neuropsychologist should also be
alert to the presence of outliers. For example, in elderly control or
normative samples it is not uncommon to observe occasional cases who
perform very poorly despite the absence of any other evidence that
suggests the presence of a brain pathology (e.g., early stage
dementia).
When testing for differences between parametric (i.e., Pearson)
correlations, a crucial assumption is that relationships between the
variables involved are linear. A visual check of this assumption can be
made using scatterplots for each individual case. If non-linearity is
apparent, the neatest solution, if it works, is to transform the
variables; for example, by taking their logarithms, square roots or
reciprocals. Transformation of variables is discussed in all
comprehensive statistics textbooks; for example, see Tabachnick and
Fidell (1996) or Howell (2002). It must be emphasized that, if any of the
aforementioned transformations are employed, the same
transformation must be applied to the data from all cases
(i.e., all control cases and the patient). However, if the aim is to
detect dissociations between two tasks, where performance on one or
both of which are expressed as an IIMA, it is perfectly acceptable to
apply different transformations to the data from the two tasks
(provided that, within each task, the same transformation is applied to
all cases).
Finally, it will be appreciated that the statistical power of any
method of statistical inference will decline as sample size decreases.
Thus with the small Ns with which we are concerned it is
inevitable that power will be low. The most obvious way of increasing
power is to increase the size of the control or normative sample
against which the individual's score is to be compared. Power can
also be increased by adopting a more liberal significance level, e.g.,
15% rather than 5%, but although this more liberal strategy will
increase Type I errors (false positives), it will decrease Type II
errors (false negatives). The decision to depart from the conventional
5% level should be based on the relative risks the researcher or
clinician attaches to the occurrence of these two types of errors. The
reasons for departing from the 5% level must be strong, as the 5% level
has proved a good choice in general.
COMPUTER PROGRAM FOR EVALUATING IIMAS IN
THE SINGLE CASE
With the exception of the methods for finding confidence limits on
the abnormality of a patient's IIMA, the calculations involved in
the tests presented in the present paper are relatively
straightforward. Armed with a set of basic statistical tables,
they could be performed by hand or with the aid of a calculator or
spreadsheet. However, as we are aware of the time pressures under which
many neuropsychologists operate, we have written a computer program for
PCs to accompany this paper. Apart from saving time, use of the program
reduces the chance of arithmetic or clerical error. Furthermore, it
provides a precise probability value for the tests, whereas tabled
values of t only record the t value that must be
exceeded to achieve a given level of significance. An exact probability
is more useful in many situations as the emphasis will be on the rarity
or abnormality of the individual's level of performance. For
example, it is still of some value to have an estimate of the
percentage of healthy individuals expected to exhibit a coefficient as
extreme as the patient's when the t value for a given
test does not exceed the most liberal tabled value (e.g., .10 in many
tables). It also does away with the need for interpolation when
a value falls between two tabled critical values.
The program IIMA.EXE compares the parametric or
non-parametric correlation coefficient obtained for a patient with the
coefficients of a control or normative sample. The program prompts for
the number of cases in the control or normative sample (N),
the correlation coefficient for the patient
(rN+1) and the correlation coefficients
for each of the controls. The program then applies Fisher's
transformation to the coefficients. The output consists of the one and
two-tailed significance of the difference between the patient and
controls, the abnormality of the patient's coefficient (e.g., the
estimated percentage of the population that would obtain a coefficient
that was lower than the patient's) and 95% confidence limits on
the abnormality. The output can be viewed on the screen, printed, or
saved to a file.
As noted, the program incorporates an option of carrying out the test
using the mean and SD of the transformed coefficients for
controls rather than requiring that the user enters the untransformed
correlations individually. This is useful if a researcher or clinician
wishes to examine the performance of additional patients against the
same controls at a later point (the M and SD of the
transformed correlation is included in the output to enable users to
use the program in this way). This option also makes it easy for a
researcher to use normative data obtained from a third party.1
A compiled version of this program can be
downloaded from the following web site address:
www.psyc.abdn.ac.uk/homedir/jcrawford/iima.htm
If a researcher wishes to test for a dissociation between two tasks
when performance on one or both of the tasks is expressed as an IIMA,
then a program (DIFFLIMS.EXE) previously provided by Crawford
and Garthwaite (2002) can be used.2
This program can be downloaded from
http://www.psyc.abdn.ac.uk/homedir/jrawford/abnolims.htm
This program takes as input the mean and
SD of
controls on the measures of performance for the two tasks, the
correlation between the measures in the control sample, and
N
for the control sample. It then prompts for the patient's scores
on the two tasks. However, as noted, this method and the accompanying
program, was designed for use with conventionally scored tests.
Therefore, it is necessary to apply Fisher's transformation to the
correlation coefficients of the control sample before computing the
means and
SDs and correlation between these transformed
coefficients and the measure of performance on the other task. If the
other task was a conventionally scored test, then the measure of
performance would simply be the scores on the task; if performance on
the other task was also expressed as an IIMA, then this would also
consist of transformed correlations.
Computation of the mean and SDs and the correlation between
tasks in the controls could be carried out in a statistics or
spreadsheet package. If the package used does not offer Fisher's
transformation then the correlations could be entered into the
IIMA.EXE program as it provides the transformed correlations
for each of the controls and patient as output. (It is likely that
these data would be run through the IIMA.EXE program in any
case as the researcher would normally wish to test whether the
patient's IIMA was significantly different from controls before
testing if there is evidence of a dissociation between the IIMA and
performance on another task.) The transformed correlations could then
be entered into the statistics or spreadsheet package so that the
correlation between the IIMA scores and scores on the other task can be
computed for the controls. If any doubts remain over how to conduct
this test then the data from the worked example for dissociations could
be run through the DIFFLIMS.EXE program to verify that the
procedure is being followed correctly.
CONCLUSION
The single case approach in neuropsychology has made a significant
contribution to our understanding of the architecture of human
cognition (Caramazza & McCloskey, 1988;
Code et al., 1996; Ellis
& Young, 1996; Humphreys, 1999;
McCarthy & Warrington, 1990; Shallice, 1988). However, as Caramazza (1988) notes, if advances in theory are to be sustainable
they “must be based on unimpeachable methodological foundations”
(p. 619). The statistical analysis of single case data is an aspect of
methodology that has been relatively neglected. This is to be regretted.
Other methodological (and logical) considerations may have compelled many
researchers to abandon group-based research, but it is clear that the
statistical problems associated with drawing inferences from single
cases significantly exceed those of the former approach.
Very useful and elegant methods have been devised for drawing
inferences concerning an individual patient's performance on fully
standardized neuropsychological tests, that is, on tests that have been
normed on a large representative sample of the population (e.g., Capitani, 1997; Willmes,
1985). However, in neuropsychology, new tests are constantly
being devised to measure new theoretical constructs. Understandably,
these tests are not fully standardized when employed with single cases;
instead they are administered to a control sample that, typically, has
a very modest N. Therefore, methods that treat the control
sample statistics in such studies as population parameters are not
appropriate. Although there remains much to do, we believe that the
methods presented here make a useful contribution to the process of
developing valid, optimal, and practical statistical methods for
single-case research. To our knowledge the specific problems addressed
in the present paper are not covered in any existing textbooks or
papers in neuropsychology or psychological statistics. However, it is
clear from the list of examples provided (which is by no means
exhaustive) that intra-individual measures of association have a wide
range of applications in neuropsychological research and practice.
Finally, we reiterate our hope that these methods will encourage the
development of larger scale normative data for tasks in which
performance is best expressed as an IIMA.
ACKNOWLEDGMENTS
We are grateful to Dr. Sytse Knypstra of the Department of
Econometrics, University of Groningen, The Netherlands, for providing
an algorithm that finds the non-centrality parameter of a non-central
t distribution given a quantile, its associated probability,
and the degrees of freedom. The algorithm is incorporated into the
computer program IIMA.EXE that accompanies this paper. We are
grateful to Dr. Willi R. Steinke (Halton District School Board,
Toronto) and Professor Lola L. Cuddy (Queen's University, Ontario)
for providing the raw data for their case C.N. and controls. Thanks
also to Dr. David P. Carey (University of Aberdeen) for commenting on a
draft version of this paper.
