We study the complexities of isometry and isomorphism classes of separable Banach spaces in the Polish spaces of Banach spaces, recently introduced and investigated by the authors in [14]. We obtain sharp results concerning the most classical separable Banach spaces.
We prove that the infinite-dimensional separable Hilbert space is characterized as the unique separable infinite-dimensional Banach space whose isometry class is closed, and also as the unique separable infinite-dimensional Banach space whose isomorphism class is 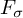 $F_\sigma $. For
$F_\sigma $. For 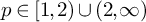 $p\in \left [1,2\right )\cup \left (2,\infty \right )$, we show that the isometry classes of
$p\in \left [1,2\right )\cup \left (2,\infty \right )$, we show that the isometry classes of 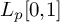 $L_p[0,1]$ and
$L_p[0,1]$ and  $\ell _p$ are
$\ell _p$ are  $G_\delta $-complete sets and
$G_\delta $-complete sets and 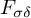 $F_{\sigma \delta }$-complete sets, respectively. Then we show that the isometry class of
$F_{\sigma \delta }$-complete sets, respectively. Then we show that the isometry class of 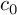 $c_0$ is an
$c_0$ is an 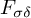 $F_{\sigma \delta }$-complete set.
$F_{\sigma \delta }$-complete set.
Additionally, we compute the complexities of many other natural classes of separable Banach spaces; for instance, the class of separable  $\mathcal {L}_{p,\lambda +}$-spaces, for
$\mathcal {L}_{p,\lambda +}$-spaces, for 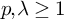 $p,\lambda \geq 1$, is shown to be a
$p,\lambda \geq 1$, is shown to be a 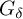 $G_\delta $-set, the class of superreflexive spaces is shown to be an
$G_\delta $-set, the class of superreflexive spaces is shown to be an 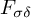 $F_{\sigma \delta }$-set, and the class of spaces with local
$F_{\sigma \delta }$-set, and the class of spaces with local  $\Pi $-basis structure is shown to be a
$\Pi $-basis structure is shown to be a  $\boldsymbol {\Sigma }^0_6$-set. The paper is concluded with many open problems and suggestions for a future research.
$\boldsymbol {\Sigma }^0_6$-set. The paper is concluded with many open problems and suggestions for a future research.
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
 $dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
$dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM