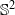Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T02:03:34.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Des points fixes communs pour des difféomorphismes de ${ \mathbb{S} }^{2} $ qui commutent et préservent une mesure de probabilité

Part of: Low-dimensional dynamical systems

Published online by Cambridge University Press:  08 February 2013

F. Béguin ,
P. Le Calvez ,
S. Firmo  and
T. Miernowski
F. Béguin
Affiliation:
Université Paris 13 Nord, France
P. Le Calvez
Affiliation:
Université Pierre-et-Marie-Curie, France
S. Firmo
Affiliation:
Universidade Federal Fluminense, Brésil
T. Miernowski
Affiliation:
Université de Aix-Marseille II, France
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Nous montrons des résultats d’existence de points fixes communs pour des homéomorphismes du plan ${ \mathbb{R} }^{2} $ ou la sphère ${ \mathbb{S} }^{2} $, qui commutent deux à deux et préservent une mesure de probabilité. Par exemple, nous montrons que des 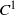${C}^{1} $-difféomorphismes 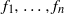${f}_{1} , \ldots , {f}_{n} $ de 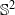${ \mathbb{S} }^{2} $ suffisamment proches de l’identité, qui commutent deux à deux, et qui préservent une mesure de probabilité dont le support n’est pas réduit à un point, ont au moins deux points fixes communs.

Abstract

We prove the existence of common fixed points for some homeomorphisms of the plane 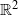${ \mathbb{R} }^{2} $ or the two-sphere ${ \mathbb{S} }^{2} $ which commute and preserve a probability measure. For example, if 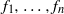${f}_{1} , \ldots , {f}_{n} $ are commuting 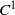${C}^{1} $-diffeomorphisms of 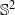${ \mathbb{S} }^{2} $ that are sufficiently close to the identity, and that preserve a probability measure whose support is not a single point, then they have at least two common fixed points.

Keywords

point fixemesure invariantehoméomorphisme conservatifrécurrencenombre de rotationfeuilletage topologiquenombre d’intersection

MSC classification

Secondary: 37E30: Homeomorphisms and diffeomorphisms of planes and surfaces 37E45: Rotation numbers and vectors
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 4 , October 2013 , pp. 821 - 851
Copyright
©Cambridge University Press 2013 

References

Bibliographie

Bonatti, Christian, Un point fixe commun pour des difféomorphismes commutants de ${S}^{2} $, Ann. of Math. (2) 129 (1) (1989), 61–69.CrossRefGoogle Scholar
Bonatti, Christian, Difféomorphismes commutants des surfaces et stabilité des fibrations en tores, Topology 29 (1) (1990), 101–126.Google Scholar
Brown, Morton et Kister, James M., Invariance of complementary domains of a fixed point set, Proc. Amer. Math. Soc. 91 (3) (1984), 503–504.Google Scholar
Brouwer, Luitzen E. J., Beweis des ebenen Translationssatzes, Math. Ann. 72 (1912), 37–54.CrossRefGoogle Scholar
Druck, Suely, Fang, Fuquan et Firmo, Sebastião, Fixed points of discrete nilpotent group actions on ${S}^{2} $, Ann. Inst. Fourier 52 (4) (2002), 1075–1091.Google Scholar
Firmo, Sebastião, A note on commuting diffeomorphisms on surfaces, Nonlinearity 18 (4) (2005), 1511–1526.Google Scholar
Franks, John, Generalizations of the Poincaré-Birkhoff theorem, Ann. of Math. (2) 128 (1) (1988), 139–151.Google Scholar
Franks, John, Handel, Michael et Parwani, Kamlesh, Fixed points of abelian actions on ${S}^{2} $, Ergodic Theory Dynam. Systems 27 (5) (2007), 1557–1581.Google Scholar
Franks, John, Handel, Michael et Parwani, Kamlesh, Fixed points of abelian actions, J. Mod. Dyn. 1 (3) (2007), 443–464.Google Scholar
Gambaudo, Jean-Marc et Ghys, Étienne, Commutators and diffeomorphisms of surfaces, Ergodic Theory Dynam. Systems 24 (5) (2004), 1591–1617.Google Scholar
Guillou, Lucien, Théorème de translation plane de Brouwer et généralisations du théorème de Poincaré-Birkhoff, Topology 33 (2) (1994), 331–351.Google Scholar
Handel, Michael, Commuting homeomorphisms of ${S}^{2} $, Topology 31 (2) (1992), 293–303.Google Scholar
Jaulent, Olivier, Existence d’un feuilletage positivement transverse à un homéomorphisme de surface (arXiv:1206.0213).Google Scholar
Kneser, Hellmuth, Die Deformationssätze der einfach zusammenhngenden Flächen, Math. Z. 25 (1) (1926), 362–372.Google Scholar
Le Calvez, Patrice, Une version feuilletée équivariante du théorème de translation de Brouwer, Publ. Math. Inst. Hautes études Sci. 102 (2005), 1–98.CrossRefGoogle Scholar
Le Roux, Frédéric, Étude topologique de l’espace des homéomorphismes de Brouwer. I, Topology 40 (5) (2001), 1051–1087.Google Scholar
Lima, Elon L., Commuting vector fields on ${S}^{2} $, Proc. Amer. Math. Soc. 15 (1964), 138–141.Google Scholar
Mann, Kathryn, Bounded orbits and global fixed points for groups acting on the plane (arXiv:1103.5060).Google Scholar
Plante, Joseph F., Fixed points of Lie group actions on surfaces, Ergodic Theory Dynam. Systems 6 (1) (1986), 149–161.Google Scholar
Viterbo, Claude, Symplectic topology as the geometry of generating functions, Math. Ann. 292 (4) (1992), 685–710.Google Scholar