Article contents
EXTENSIONS ENTRE SÉRIES PRINCIPALES 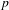 $p$-ADIQUES ET MODULO
$p$-ADIQUES ET MODULO  $p$ DE
$p$ DE 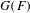 $G(F)$
$G(F)$
Published online by Cambridge University Press: 08 August 2014
Abstract
Soit  $G$ un groupe réductif connexe déployé sur une extension finie
$G$ un groupe réductif connexe déployé sur une extension finie  $F$ de
$F$ de 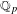 $\mathbb{Q}_{p}$. Nous déterminons les extensions entre séries principales continues unitaires
$\mathbb{Q}_{p}$. Nous déterminons les extensions entre séries principales continues unitaires 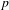 $p$-adiques et lisses modulo
$p$-adiques et lisses modulo  $p$ de
$p$ de  $G(F)$ dans le cas générique. Pour cela, nous calculons le delta-foncteur
$G(F)$ dans le cas générique. Pour cela, nous calculons le delta-foncteur  $\text{H}^{\bullet }\text{Ord}_{B(F)}$ des parties ordinaires dérivées d’Emerton relatif à un sous-groupe de Borel sur certaines représentations induites de
$\text{H}^{\bullet }\text{Ord}_{B(F)}$ des parties ordinaires dérivées d’Emerton relatif à un sous-groupe de Borel sur certaines représentations induites de 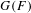 $G(F)$ en utilisant une filtration de Bruhat. Ces extensions interviennent dans le programme de Langlands
$G(F)$ en utilisant une filtration de Bruhat. Ces extensions interviennent dans le programme de Langlands 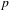 $p$-adique et modulo
$p$-adique et modulo 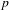 $p$.
$p$.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 2 , April 2016 , pp. 225 - 270
- Copyright
- © Cambridge University Press 2014
References
Bibliographie
- 10
- Cited by


