Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T17:14:22.617Z Has data issue: false hasContentIssue false
  • English
  • Français

THERMIC MINORANTS AND REDUCTIONS OF SUPERTEMPERATURES

Part of: Higher-dimensional theory Parabolic equations and systems

Published online by Cambridge University Press:  06 March 2015

NEIL A. WATSON
NEIL A. WATSON*
Affiliation:
School of Mathematics and Statistics, University of Canterbury, Private Bag, Christchurch, New Zealand email n.watson@math.canterbury.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

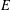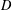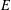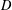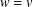Let $u$ be a supertemperature on an open set $E$, and let $v$ be a related temperature on an open subset $D$ of $E$. For example, $v$ could be the greatest thermic minorant of $u$ on $D$, if it exists. Putting $w=u$ on $E\setminus D$ and $w=v$ on 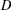$D$, we investigate whether 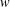$w$, or its lower semicontinuous smoothing, is a supertemperature on 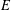$E$. We also give a representation of the greatest thermic minorant on 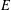$E$, if it exists, in terms of PWB solutions on an expanding sequence of open subsets of 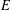$E$ with union 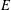$E$.  In addition, in the case of a nonnegative supertemperature, we prove inequalities that relate reductions to Dirichlet solutions. We also prove that the value of any reduction at a given time depends only on earlier times.

Keywords

thermic minorantsupertemperaturereductionPWB solution

MSC classification

Primary: 35K05: Heat equation
Secondary: 31B05: Harmonic, subharmonic, superharmonic functions 31B20: Boundary value and inverse problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 1 , August 2015 , pp. 128 - 144
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Armitage, D. H. and Gardiner, S. J., Classical Potential Theory (Springer, London, 2001).CrossRefGoogle Scholar
Bauer, H., Harmonische Räume und ihre Potentialtheorie, Lecture Notes in Mathematics, 22 (Springer, Berlin, 1966).CrossRefGoogle Scholar
Bauer, H., ‘Heat balls and Fulks measures’, Ann. Acad. Sci. Fenn. Ser. A I Math. 10 (1985), 67–82.CrossRefGoogle Scholar
Brelot, M., Éléments de la Théorie Classique du Potentiel, 4th edn (Centre de Documentation Universitaire, Paris, 1969).Google Scholar
Chow, B., Chu, S.-C., Glickenstein, D., Guenther, C., Isenberg, J., Ivey, T., Knoph, D., Lu, P., Luo, F. and Ni, L., The Ricci Flow: Techniques and Applications: Part III: Geometric–Analytic Aspects, Mathematical Surveys and Monographs, 163 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Doob, J. L., Classical Potential Theory and its Probabilistic Counterpart, Grundlehren der mathematischen Wissenschaften, 262 (Springer, New York, 1984).CrossRefGoogle Scholar
Ecker, K., Regularity Theory for Mean Curvature Flow, Progress in Nonlinear Differential Equations and their Applications, 57 (Birkhäuser, Basel, 2004).CrossRefGoogle Scholar
Evans, L. C., Partial Differential Equations, Graduate Studies in Mathematics, 19 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Frostman, O., ‘Potentiel d’équilibre et capacité des ensembles avec quelques applications à la théorie des fonctions’, Medd. Lunds Univ. Mat. Sem. 3 (1935), 1–118.Google Scholar
Fulks, W., ‘A mean value theorem for the heat equation’, Proc. Amer. Math. Soc. 17 (1966), 6–11.CrossRefGoogle Scholar
Pini, B., ‘Maggioranti e minoranti delle soluzione delle equazioni paraboliche’, Ann. Mat. Pura Appl. 37 (1954), 249–264.CrossRefGoogle Scholar
Watson, N. A., ‘Green functions, potentials, and the Dirichlet problem for the heat equation’, Proc. Lond. Math. Soc. 33 (1976), 251–298.CrossRefGoogle Scholar
Watson, N. A., Parabolic Equations on an Infinite Strip, Monographs and Textbooks in Pure and Applied Mathematics, 127 (Marcel Dekker, New York, 1989).Google Scholar
Watson, N. A., ‘A convexity theorem for local mean values of subtemperatures’, Bull. Lond. Math. Soc. 22 (1990), 245–252.CrossRefGoogle Scholar
Watson, N. A., ‘An extension theorem for supertemperatures’, Ann. Acad. Sci. Fenn. Math. 33 (2008), 131–141.Google Scholar
Watson, N. A., ‘A unifying definition of a subtemperature’, New Zealand J. Math. 38 (2008), 197–223.Google Scholar
Watson, N. A., Introduction to Heat Potential Theory, Mathematical Surveys and Monographs, 182 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Watson, N. A., ‘Caloric measure for arbitrary open sets’, J. Aust. Math. Soc. 92 (2012), 391–407.CrossRefGoogle Scholar
Widder, D. V., ‘Positive temperatures on an infinite rod’, Trans. Amer. Math. Soc. 55 (1944), 85–95.CrossRefGoogle Scholar