 $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
$\mathbf{n}$ TH CYCLOTOMIC POLYNOMIALPublished online by Cambridge University Press: 04 November 2015
Primitive prime divisors play an important role in group theory and number theory. We study a certain number-theoretic quantity, called 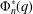 $\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)$ , which is closely related to the cyclotomic polynomial
$\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)$ , which is closely related to the cyclotomic polynomial 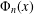 $\unicode[STIX]{x1D6F7}_{n}(x)$ and to primitive prime divisors of
$\unicode[STIX]{x1D6F7}_{n}(x)$ and to primitive prime divisors of 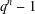 $q^{n}-1$ . Our definition of
$q^{n}-1$ . Our definition of  $\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)$ is novel, and we prove it is equivalent to the definition given by Hering. Given positive constants
$\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)$ is novel, and we prove it is equivalent to the definition given by Hering. Given positive constants  $c$ and
$c$ and 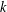 $k$ , we provide an algorithm for determining all pairs
$k$ , we provide an algorithm for determining all pairs 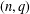 $(n,q)$ with
$(n,q)$ with 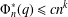 $\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)\leq cn^{k}$ . This algorithm is used to extend (and correct) a result of Hering and is useful for classifying certain families of subgroups of finite linear groups.
$\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)\leq cn^{k}$ . This algorithm is used to extend (and correct) a result of Hering and is useful for classifying certain families of subgroups of finite linear groups.