Published online by Cambridge University Press: 25 July 2014
Let 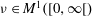 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\nu \in M^1([0,\infty [)$ be a fixed probability measure. For each dimension
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\nu \in M^1([0,\infty [)$ be a fixed probability measure. For each dimension  $p\in \mathbb{N}$, let
$p\in \mathbb{N}$, let 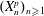 $(X_n^{p})_{n\geq 1}$ be independent and identically distributed
$(X_n^{p})_{n\geq 1}$ be independent and identically distributed 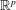 $\mathbb{R}^p$-valued random variables with radially symmetric distributions and radial distribution
$\mathbb{R}^p$-valued random variables with radially symmetric distributions and radial distribution  $\nu $. We investigate the distribution of the Euclidean length of
$\nu $. We investigate the distribution of the Euclidean length of  $S_n^{p}:=X_1^{p}+\cdots + X_n^{p}$ for large parameters
$S_n^{p}:=X_1^{p}+\cdots + X_n^{p}$ for large parameters  $n$ and
$n$ and 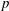 $p$. Depending on the growth of the dimension
$p$. Depending on the growth of the dimension  $p=p_n$ we derive by the method of moments two complementary central limit theorems (CLTs) for the functional
$p=p_n$ we derive by the method of moments two complementary central limit theorems (CLTs) for the functional 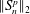 $\| S_n^{p}\| _2$ with normal limits, namely for
$\| S_n^{p}\| _2$ with normal limits, namely for  $n/p_n \to \infty $ and
$n/p_n \to \infty $ and 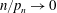 $n/p_n \to 0$. Moreover, we present a CLT for the case
$n/p_n \to 0$. Moreover, we present a CLT for the case 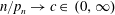 $n/p_n \to c\in \, (0,\infty )$. Thereby we derive explicit formulas and asymptotic results for moments of radial distributed random variables on
$n/p_n \to c\in \, (0,\infty )$. Thereby we derive explicit formulas and asymptotic results for moments of radial distributed random variables on 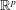 $\mathbb{R}^p$. All limit theorems are also considered for orthogonal invariant random walks on the space
$\mathbb{R}^p$. All limit theorems are also considered for orthogonal invariant random walks on the space 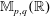 $\mathbb{M}_{p,q}(\mathbb{R})$ of
$\mathbb{M}_{p,q}(\mathbb{R})$ of 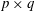 $p\times q$ matrices instead of
$p\times q$ matrices instead of 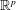 $\mathbb{R}^p$ for
$\mathbb{R}^p$ for 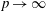 $p\to \infty $ and some fixed dimension
$p\to \infty $ and some fixed dimension 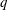 $q$.
$q$.