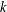 $k$
$k$Published online by Cambridge University Press: 22 January 2016
We provide a comprehensive study of the function 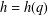 $h=h(q)$ defined by and show that it has many properties that are analogues of corresponding results for Ramanujan’s function
$h=h(q)$ defined by and show that it has many properties that are analogues of corresponding results for Ramanujan’s function 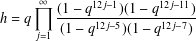 $$\begin{eqnarray}h=q\mathop{\prod }_{j=1}^{\infty }\frac{(1-q^{12j-1})(1-q^{12j-11})}{(1-q^{12j-5})(1-q^{12j-7})}\end{eqnarray}$$
$$\begin{eqnarray}h=q\mathop{\prod }_{j=1}^{\infty }\frac{(1-q^{12j-1})(1-q^{12j-11})}{(1-q^{12j-5})(1-q^{12j-7})}\end{eqnarray}$$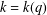 $k=k(q)$ defined by
$k=k(q)$ defined by 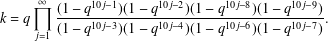 $$\begin{eqnarray}k=q\mathop{\prod }_{j=1}^{\infty }\frac{(1-q^{10j-1})(1-q^{10j-2})(1-q^{10j-8})(1-q^{10j-9})}{(1-q^{10j-3})(1-q^{10j-4})(1-q^{10j-6})(1-q^{10j-7})}.\end{eqnarray}$$
$$\begin{eqnarray}k=q\mathop{\prod }_{j=1}^{\infty }\frac{(1-q^{10j-1})(1-q^{10j-2})(1-q^{10j-8})(1-q^{10j-9})}{(1-q^{10j-3})(1-q^{10j-4})(1-q^{10j-6})(1-q^{10j-7})}.\end{eqnarray}$$