Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-14T20:47:57.596Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for the Asymptotic Growth Rate of an Age-Dependent Branching Process

Published online by Cambridge University Press:  09 April 2009

P. J. Brockwell
P. J. Brockwell
Affiliation:
Argonne National Laboratory Argonne, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M(t) denote the mean population size at time t (conditional on a single ancestor of age zero at time zero) of a branching process in which the distribution of the lifetime T of an individual is given by Pr {T≦t} =G(t), and in which each individual gives rise (at death) to an expected number A of offspring (1λ A λ ∞). expected number A of offspring (1 < A ∞). Then it is well-known (Harris [1], p. 143) that, provided G(O+)-G(O-) 0 and G is not a lattice distribution, M(t) is given asymptotically by 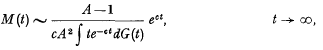where c is the unique positive value of p satisfying the equation .

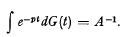Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 1-2 , August 1969 , pp. 231 - 235
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Harris, T. E., The theory of branching processes (Springer-Verlag, Berlin, 1963).CrossRefGoogle Scholar
[2]Heathcote, C. R. and Seneta, E., ‘Inequalities for branching processe’, J. Appl. Prob., 3, (1966), 261–67;CrossRefGoogle Scholar
Correction 4 (1967), 215.Google Scholar
[3]Seneta, E., ‘On the transient behaviour of a Poisson branching process’, J. Austral. Math. Soc. 7, (1967), 465–80.CrossRefGoogle Scholar
[4]Brook, D., ‘Bounds for moment generating functions and for extinction probabilities’, J. Appl. Prob., 3, (1966), 171–178.CrossRefGoogle Scholar