Hostname: page-component-6dbcb7884d-4kfsg Total loading time: 0 Render date: 2025-02-13T15:54:46.391Z Has data issue: false hasContentIssue false
  • English
  • Français

INFINITARY COMMUTATIVITY AND ABELIANIZATION IN FUNDAMENTAL GROUPS

Part of: Homotopy groups Low-dimensional topology Algebraic structures

Published online by Cambridge University Press:  23 November 2020

JEREMY BRAZAS Open the ORCID record for JEREMY BRAZAS [Opens in a new window]  and
PATRICK GILLESPIE
JEREMY BRAZAS
Affiliation:
West Chester University, Department of Mathematics, West Chester, PA19383, USA
PATRICK GILLESPIE
Affiliation:
West Chester University, Department of Mathematics, West Chester, PA19383, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Infinite product operations are at the forefront of the study of homotopy groups of Peano continua and other locally path-connected spaces. In this paper, we define what it means for a space X to have infinitely commutative 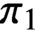$\pi _1$ -operations at a point 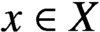$x\in X$ . Using a characterization in terms of the Specker group, we identify several natural situations in which this property arises. Maintaining a topological viewpoint, we define the transfinite abelianization of a fundamental group at any set of points 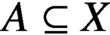$A\subseteq X$ in a way that refines and extends previous work on the subject.

Keywords

fundamental groupinfinitary operationtransfinite abelianizationtransfinite commutativity

MSC classification

Primary: 57M05: Fundamental group, presentations, free differential calculus
Secondary: 08A65: Infinitary algebras 55Q52: Homotopy groups of special spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 3 , June 2022 , pp. 289 - 311
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by George Willis

References

Bogopolski, O. and Zastrow, A., ‘An uncountable homology group, where each element is an infinite product of commutators’, Topology Appl. 197 (2016), 167–180.CrossRefGoogle Scholar
Brazas, J., ‘Transfinite product reduction in fundamental groupoids’, European J. Math., to appear. Published online (13 June 2020), https://doi.org/10.1007/s40879-020-00413-0.CrossRefGoogle Scholar
Brazas, J. and Fabel, P., ‘On fundamental groups with the quotient topology’, J. Homotopy Relat. Struct. 10 (2015), 71–91.CrossRefGoogle Scholar
Brazas, J. and Fischer, H., ‘Test map characterizations of local properties of fundamental groups’, J. Topol. Anal. 12 (2020), 37–85.CrossRefGoogle Scholar
Cannon, J. W. and Conner, G. R., ‘The combinatorial structure of the Hawaiian earring group’, Topology Appl. 106 (2000), 225–271.CrossRefGoogle Scholar
Conner, G. R. and Kent, C., ‘Fundamental groups of locally connected subsets of the plane’, Adv. Math. 347 (2019), 384–407.CrossRefGoogle Scholar
Conner, G. R., Meilstrup, M., Repovš, D., Zastrow, A. and Žljko, M., ‘On small homotopies of loops’, Topology Appl. 155 (2008), 1089–1097.CrossRefGoogle Scholar
Corson, S., ‘On subgroups of first homology’, Preprint, 2016, arXiv:1610.05422.Google Scholar
Eda, K., ‘Free $\sigma$ -products and noncommutatively slender groups’, J. Algebra 148 (1992), 243–263.CrossRefGoogle Scholar
Eda, K., ‘The fundamental groups of one-dimensional spaces and spatial homomorphisms’, Topology Appl. 123 (2002), 479–505.CrossRefGoogle Scholar
Eda, K., ‘Singular homology groups of one-dimensional Peano continua’, Fund. Math. 232 (2016), 99–115.CrossRefGoogle Scholar
Eda, K. and Fischer, H., ‘Cotorsion-free groups from a topological viewpoint’, Topology Appl. 214 (2016), 21–34.CrossRefGoogle Scholar
Eda, K. and Kawamura, K., ‘The fundamental groups of one-dimensional spaces’, Topology Appl. 87 (1998), 163–172.CrossRefGoogle Scholar
Eda, K. and Kawamura, K., ‘Homotopy and homology groups of the $n$ -dimensional Hawaiian earring’, Fund. Math. 165 (2000), 17–28.CrossRefGoogle Scholar
Eda, K. and Kawamura, K., ‘The singular homology of the Hawaiian earring’, J. Lond. Math. Soc. 62 (2000), 305–310.CrossRefGoogle Scholar
Fuchs, L., Infinite Abelian Groups I (Academic Press, New York, 1973).Google Scholar
Griffiths, H. B., ‘The fundamental group of two spaces with a point in common’, Q. J. Math. 5 (1954), 175–190.CrossRefGoogle Scholar
Herfort, W. and Hojka, W., ‘Cotorsion and wild homology’, Israel J. Math. 221 (2017), 275–290.CrossRefGoogle Scholar
Karimov, U. H., ‘An example of a space of trivial shape, all of whose fine coverings are cyclic’, Dokl. Akad. Nauk SSSR 286(3) (1986), 531–534 (in Russian); English translation in: Sov. Math. Dokl. 33(3) (1986), 113–117.Google Scholar
Karimov, U. H. and Repovš, D., ‘On the homology of the harmonic archipelago’, Cent. Eur. J. Math. 10(3) (2012), 863–872.CrossRefGoogle Scholar
Kawamura, K., ‘Low dimensional homotopy groups of suspensions of the Hawaiian earring’, Colloq. Math. 96(1) (2003), 27–39.CrossRefGoogle Scholar
Mardešić, S. and Segal, J., Shape Theory (North-Holland, Amsterdam, 1982).Google Scholar
Morgan, J. W. and Morrison, I. A., ‘A van Kampen theorem for weak joins’. Proc. Lond. Math. Soc. 53(3) (1986), 562–576.CrossRefGoogle Scholar