Methodology

The methodology required for investigating putatively significant numerical patterns in works of art is fraught with difficulties. With care, this methodology can be executed well; but it is also all too easy to pursue this kind of numerical pattern spotting badly. For this reason, it is instructive to reflect on the logical form of the reasoning that is involved, which can be compared to the protracted campaign Darwin prosecuted in support of his theory of biological inheritance subject to random minor variations and under natural selection.

To illustrate Darwin's methodological approach in The Origin of Species, consider the fact that both burrowing gophers and towering giraffes are observed to have the same number—seven—of vertebrae in their necks (Galis Reference Galis1999: 19). While it might sound like good news for Darwin's theory of evolution, this coincidence by itself, of course, is not enough to constitute a proof. (And for a Darwinist there is an acute danger of wishful thinking.) Nevertheless, it is immediately evident that Darwin's hypothesis of descent with gradual modification could surely provide at least one credible explanation for a numerical coincidence like this one. And The Origin of Species delivered a truckload of further nuggets of evidence of a similar kind.

Counting and comparing the numbers of vertebrae in the necks of gophers and giraffes is not the kind of thing that anyone would be especially likely to do in the absence of any prior reason to think that observations of that kind might be worth collecting. Furthermore, in gathering observations of this kind it is important to be patient—because, according to standard probability theory, a surprisingly large cohort of striking coincidences will often arise by chance alone. And there might be alternative theories that could have predicted the same numerical coincidences (as, for instance, the theory that the biological world was made by a mathematical God who particularly loves the number seven).

Darwin's methodology works by patient, incremental accumulation of evidence that lends numerous small boosts to the credibility of the theory. Each of these intuitive, incremental steps can be justified by the axioms of probability theory—using probabilistic inference guided especially by Bayes's theorem. There is a low prior rational expectation that gophers and giraffes would have the same number of vertebrae in their necks; but the probability would be higher under the supposition that they are descended from a common ancestor. Hence, when we count the seven vertebrae in the necks of each gopher and giraffe, the posterior probability that there was a common ancestor is ratcheted up a notch or two. With patience, in principle, this method can elevate rational credibility arbitrarily close to certainty—as it did, eventually, in the case of Darwin's theory of evolution.

In biology, chemical patterns in chromosomes are copied repeatedly and change gradually over time. In culture, mathematical patterns in works of art can also be copied and change over time. Richard Dawkins (Reference Dawkins1976) coined the term meme to signify any pattern that has a propensity to be replicated from one individual to others in whom it also possesses that same propensity to be replicated. The theory we explore in this essay concerns what might be thought of as the evolution of a Pythagorean and Platonic ‘memome’ that behaves analogously, in some respects, to a genome.

We start with the creation story found in Plato's Timaeus (all citations are to Plato Reference Cooper1997: 1224–91). In 34b–37a, Plato describes a mathematical pattern that guided an intelligent designer—the Artisan, or the Demiurge—who created the material world. In 43a–44c, he says that this same pattern is replicated in each human soul. But life in the material world inescapably creates internal discords, and at the close of the dialogue is the following advice: ‘We should redirect the revolutions in our heads that were thrown off course at our birth, by coming to learn the harmonies and revolutions of the universe’ (Timaeus 90d). Consonant with this worldview, an ambitious artist could well try to imitate the Demiurge's creative act, replicating the harmonious mathematical patterns of the macrocosm within the microcosm of a work of art, and thereby subliminally nudging souls toward a restoration of their original harmonies.

Numerous numerical details are visually embodied in Raphael's The School of Athens and the Disputa. Moreover, these details are aligned in symbolically significant ways with the mathematical patterns that are described in Plato's Timaeus. One such numerical detail is the frequent grouping of figures in multiples of seven. Like the seven vertebrae in the necks of both gophers and giraffes, the groupings of multiples of seven in these frescoes are not immediately apparent to casual inspection. They are noticed only if one spends a considerable amount of time counting. Nevertheless, this numerical detail (along with other related numerical details), once noticed, could be explained credibly and neatly under the supposition that Raphael—or whoever in the Vatican commissioned and directed his fresco program—was taking guidance from the implicit advice that is to be found in Plato's Timaeus.

There is a paucity of documentary evidence concerning Raphael's reading habits. It is not known if he read Plato's Timaeus. There is no known written record of the commission that he presumably received for his Vatican frescoes—either directly from Pope Julius II or from one or more of the pope's close advisors. But there is evidence linking the distinctive doctrines of the Timaeus with Platonists who were influential in Raphael's time, such as Marsilio Ficino (1433–1499). Platonic influences are also evident in others who are known to have influenced Raphael, such as his teacher in Urbino, Pietro Perugino, and Leonardo da Vinci. Ingrid Rowland (Reference Rowland and Hall1997: 137–38) also identifies possible Platonic influences in the Vatican that could have been transmitted to Raphael from Battista Casali (1473–1525), Egidio Antonini da Viterbo (1469–1523), and the pope's librarian, Tommaso Inghirami (1470–1516).

But, in addition to circumstantial documentary evidence of this kind, there is the directly observable visual evidence of numerical patterns that are incontestably observable in Raphael's frescoes. And that evidence, too, can carry epistemic weight.

Raphael's Epogdoôn

The largest of Raphael's four frescoes in the Stanza della Segnatura are the two on the interiors of the facing east and west walls. On the east wall is The School of Athens, which is populated by pagan ancient philosophers. On the west wall, facing The School of Athens, is the Disputa, which is populated by Christians and is so-called because these Christians are said to be engaged in a disputation concerning the sacraments. Because these frescoes are in the Vatican, which (along with Constantinople) has been one of the most salient seats of Christendom, the fact that the number of Christians on the west wall is noticeably greater than the number of pagans on the east wall might credibly have been of some iconographic significance.

Good reproductions of the frescoes can be found in Enrico Bruschini's Masterpieces of the Vatican (Reference Bruschini2004: 70–71, 72–73) and online. For the purposes of discussion, we use numbered diagrams of the frescoes. For The School of Athens, we use a diagram from Marcia Hall (Reference Hall1997: 2) (figure 1, hereafter referred to as Hall's diagram); the diagrams of the Disputa (figure 2), Parnassus (figure 5), and Jurisprudence (figure 6) are drawn by co-author John Bigelow.

Figure 1. Diagram of Raphael Sanzio, The School of Athens (fresco, c. 1508–1512, east wall of the Stanza della Segnatura, Vatican Museum, Vatican City), in Marcia Hall, introduction to Raphael's ‘School of Athens’, page 2 (Cambridge: Cambridge University Press, 1997). Reproduced by permission.

Figure 2. Diagram by John Bigelow of Raphael Sanzio, Disputa, fresco, c. 1509–1510, Vatican Museum, Vatican City.

Hall uses her diagram with numbered figures to facilitate discussion in the text of the various personages in the fresco. (For instance, the figure numbered 1 represents Plato and is also thought to resemble a drawing by Leonardo da Vinci; number 2 is Aristotle; number 29 resembles Michelangelo.) But Hall's diagram also conveys aesthetically relevant information, such as the evident near-symmetry in the fresco, with twenty-eight numbered philosophers on one side and another twenty-eight on the other side—in all, fifty-six numbered figures. The diagram of the Disputa (figure 2) numbers sixty-three figures. And while scholars do not always agree on the total numbers of figures in these two frescoes, there is a salient and observable ratio between the numbers of figures in the Disputa and The School of Athens: the ratio is at least approximately equal to 9:8.

Did this arithmetical ratio of 9:8 (or its inverse 8:9) have any significance for Raphael (or whoever was guiding his fresco program)? Relevant evidence can be found in the fact that this ratio is explicitly named within The School of Athens. A slate in the fresco (figure 3) bearing Greek words and Roman numerals in three sections presents the seminal Pythagorean frequency ratios for musical harmonies and discords as described in Plato's Timaeus 35a–36b.

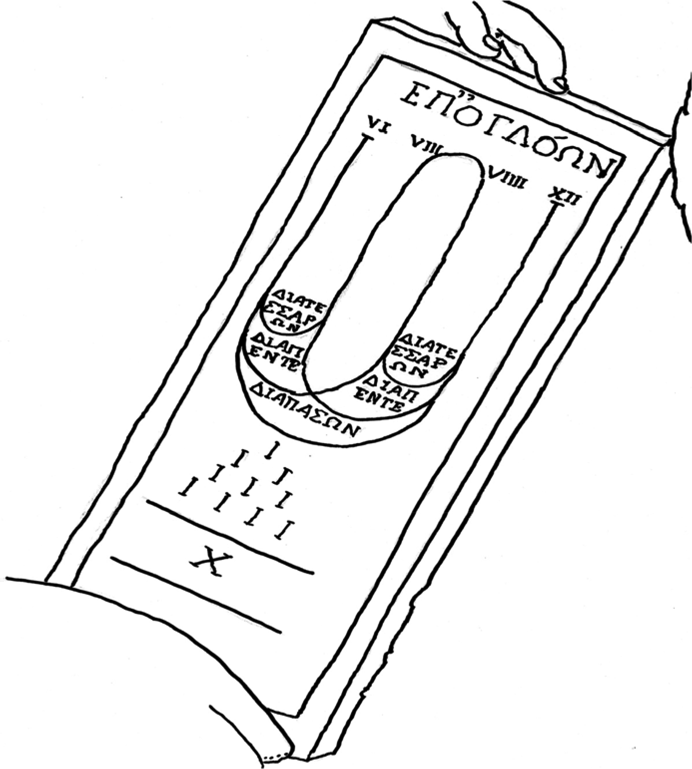
Figure 3. Drawing by John Bigelow of Raphael Sanzio, The School of Athens (detail), fresco, c. 1508–1512, Vatican Museum, Vatican City.

The title on the slate is ΕΠΟΓΔΟΩΝ, or epogdoôn, the Greek name of the ratio of 9:8. The etymology is roughly thus: ep– = epi- (as in epilogue) ≈ plus another; octo = eight; and the Greek ogdoôn (or ogdoôs) ≈ an eighth. Thus, epogdoôn means ‘plus an eighth’. It is a word that rarely occurs in classical literature, but it does make significant appearances both on the slate and in Plato's Timaeus 36a–36b, 43d–43e.

The imagery with which Raphael surrounds the slate strongly implies that, although the Greek mathematics it contains is difficult to master, it must surely be something important. The slate is positioned in the foreground of the entire scene, not far above a viewer's line of sight—just above and to the right of the door that is situated in the northeast corner of the room. It is held in place by an angelic form who is positioning it strategically in the line of sight of the figure numbered 33 in Hall's diagram. Some identify this figure as Saint Matthew (Vasari Reference Vasari and Bull1965: 292; Quinlan-McGrath Reference Quinlan-McGrath2016: 179–80). Nevertheless, he is looking at a slate inscribed with Pythagorean music theory, and so, following Hall (Reference Hall1997: 22–24) and others, it is useful to call him Pythagoras. Two scholars (numbered 34 and 35 in Hall's diagram) are eagerly leaning forward, peering intently over his shoulders, and one of them is copying or taking notes. Yet another prominent figure (numbered 30 in Hall's diagram) is looking obliquely down at Pythagoras and the slate while holding a large book open on his knee, and he is pointing to something that is written on one of the pages—as if in doubt or dispute over some point of detail. All these factors suggest that what is written on the slate, with its heading ΕΠΟΓΔΟΩΝ, must surely be important.

Hall (Reference Hall1997: 33–34) says it was Giovanni Bellori (Reference Bellori1695) who first called attention to the significance of the Greek words and the numbers on the slate. She cites André Chastel (Reference Chastel1959: 476–80) as suggesting that the inscription on the slate was closely influenced by Ficino and his Platonic cosmology, which is grounded in numbers and musical harmonies. The works of Ficino were readily available among Raphael's contemporaries in the Vatican, and the Pythagorean and Platonic cosmology behind the numbers on the slate can be pinpointed in Ficino ([1494] Reference Ficino and Farndell2010: 68–75, 185–87). Commentators seldom dwell on these numbers, but recognition of their symbolic importance has sometimes been registered, for instance by Emil Naumann (Reference Naumann1879) and Ann Moyer (Reference Moyer1992).

Plato's Timaeus

Unsurprisingly, given its technical meaning, the word epogdoôn rarely appears in ancient Greek literature. But the word does make several salient appearances in Plato's Timaeus. It appears twice in a passage describing the World Soul (Timaeus 36a–36b). And it is mentioned again in Timaeus 43d, in the context of discords within the human soul.

The World Soul is a mathematical pattern that guided the intelligent designer or Demiurge in crafting the Heavenly Spheres. In the Timaeus 35a–36b, the Demiurge mixed certain ingredients (‘the Same’, ‘the Different’, and ‘Being’) in a bowl. Then he separated from this mixture various individual portions, measuring them in quantities that embodied a handful of significant ratios—including the ratio of the epogdoôn, 9:8. These portions were then crafted into the heavenly spheres that carry the seven planets as they dance in cycles through the twelve fixed constellations of the signs of the zodiac.

After creating the heavens and the Earth, the Demiurge gathered together what remained of the original ingredients and, mixing them in the same bowl, he separated further portions ‘equal in number to the stars and assigned each soul to a star’ (Timaeus 41d–41e). Each of our souls received its first incarnation in a star, and our ultimate goal is to return to the star within which we received our first birth. Hence, the mathematical blueprint behind the planetary orbits is also said to have been closely (but not perfectly) mirrored in miniature within the microcosm of each individual human soul.

Musically, the epogdoôn, 9:8, is the Pythagorean frequency ratio for the musical whole tone interval. The familiar scale (ut, re, mi, fa, sol, la, ti) is called the diatonic division of the octave because it is built through (dia = through) a series of tonic intervals. But there is a hitch: six intervals of 9:8 would overshoot the perfect ratio of 2:1 for the octave. Consequently, the diatonic scale includes only five whole tones plus two so-called semitones, which the Timaeus describes as the ratio of 256:243, which is significantly less than half a whole tone of 9:8.

The perspective in The School of Athens draws the eye toward Plato and Aristotle, the two most salient figures in the fresco. There is an analogue in the Disputa, where the perspective is ‘strongly articulated in the pavement’ and the perspectival vanishing point ‘is placed in the Host’ (Hall Reference Hall1997: 15–16). The placement of the vanishing point appears to be of symbolic significance in both The School of Athens and the Disputa. And the Timaeus is placed at or very near the vanishing point in The School of Athens (Rowland Reference Rowland and Hall1997: 146; Quinlan-McGrath Reference Quinlan-McGrath2016: 166–67). The title TIMEO (Timaeus) is clearly visible on the book held by Plato (figure number 1 in Hall's diagram).

A third figure (number 49 in Hall's diagram) is commonly identified as Socrates: ‘Behind those listening to Plato there is Socrates . . . Socrates is bald and snub-nosed, as he is described and portrayed’ (Bellori Reference Bellori and Hall1997: 54). Socrates appears to be counting on his fingers as he addresses four other figures (numbers 45, 46, 47, 48 in Hall's diagram; number 48 is looking away, not paying attention). Considering the importance invested in Plato's Timaeus, it is reasonable to infer that those in the pope's inner circle would likely have known that the dialogue opens with four characters (Socrates, Timaeus, Critias, and Hermocrates) assembling for a prearranged meeting. The first words are those of Socrates: ‘One, two, three; but where, my dear Timaeus, is the fourth of those who were yesterday my guests and are to be my entertainers today?’ (Timaeus 17a). Thus, the image of Socrates relates closely to the Timaeus, further amplifying its importance.

It is thus reasonable to assume that Raphael (or whoever was directing the fresco program) anticipated that contemporary viewers would identify figures like Plato and Aristotle and Socrates—and the Timaeus—and that they would also recognize (either explicitly or at least subliminally) that the fresco represents all of these as being supremely significant protagonists in the legacy that Christianity has inherited from the ancient world.

Harmonious Ratios in Plato's Timaeus

As noted above, according to Plato's creation story in the Timaeus 35a–36b, when the cosmos was first being constructed seven initial portions of the initial mixture (Being, Sameness and Difference) were dished out, and they were measured out in ratios that can be specified by the numbers 1, 2, 3, 4, 9, 8, 27 (in that order).

Astronomically, in the Timaeus 38c–38e, these seven initial portions were molded into the seven heavenly spheres that guide the orbits of the Sun, Moon, Venus, Mercury, Mars, Jupiter, and Saturn. Musically, the double intervals 1, 2, 4, 8 correspond to the octaves that occur in the natural harmonics for any given note; and the triple intervals 1, 3, 9, 27 track the intervals of an octave plus a fifth, which also occur in the natural harmonics for any given note.

The Demiurge's second step was to place further portions of the mixture within the ‘double and triple intervals’ (Timaeus 36a); and these further portions establish the ratios of 3:2, 4:3, 9:8, and 256:243. The upshot is a division of the octave into the seven distinct notes of the diatonic scale in what is known as Pythagorean tuning.

Pythagorean tuning consists in a distinctive raft of precise relative frequencies for the seven notes ABCDEFG in the familiar diatonic division of the octave. In this scale, the sequence of five adjacent notes ABCDE is said to span the interval of a fifth. The distinctive feature of Pythagorean tuning is that all the octaves and the fifths aim for frequency ratios that are as close as possible to the mathematical ratios of 2:1 and 3:2, respectively. In experiential terms, these are the frequency ratios that will minimize audible interference beats in the overtones or natural harmonics that are generated when two notes are sounded simultaneously. Presumably for this reason, the frequency ratio of 3:2 is said to constitute a ‘perfect fifth’.

Under Pythagorean tuning, as an arithmetic consequence of setting the fifths at the ratio of 3:2, the frequency ratios between adjacent notes in the scale will all be either the whole tone frequency ratio of 9:8 (the epogdoôn) or else a so-called semitone (which will in fact be considerably less than half a whole tone).

Raphael's Multiple Multiples of Seven

In the Disputa, salient groupings of multiples of seven are especially evident. The image has three layers (see figure 2). At the top is God the Father with three angels on his right and three more on his left—seven altogether. Below God the Father is God the Son, with seven figures on his left and seven on his right. Below the Father and the Son is a dove representing the Holy Spirit. Counting the Trinity (Father, Son, and Holy Spirit) as one, there is thus a significant grouping of twenty-one figures hovering in the heavens—another multiple of seven.

Below the Heavens, there appear to be at least forty-two salient Christians on the Earth (not counting tiny figures in the distant background or the innumerable angelic or cherubic putti in the clouds or in the golden rays descending from above). The chances of its being a matter of some significance that this number is at least approximately forty-two are boosted by the fact that this number on Earth, forty-two, is double the twenty-one in the heavens above. There is a ratio of 1:2 (an octave) between the seven at the top and the fourteen Saints flanking Jesus. There is a ratio of 1:3 (an octave plus a fifth) between the Saints and those on the Earth. And (altogether) there is a ratio of 1:2 (an octave) between the Heavens and the Earth.

The chance that the presence of these multiples of seven is mere coincidence is further reduced by the significant multiples of seven in the opening words of Matthew, the book that opens the New Testament: ‘The book of the generation of Jesus Christ, the son of David, the son of Abraham. Abraham begat Isaac; and . . . And Jesse begat David the king . . . And Josias begat Jechonias and his brethren, about the time they were carried away to Babylon . . . So all the generations from Abraham to David are fourteen generations; and from David until the carrying away into Babylon are fourteen generations; and from the carrying away into Babylon unto Christ are fourteen generations’ (Matthew 1:1–17, King James translation). This biblical genealogy explicitly specifies three groups of fourteen—which total forty-two generations.

Moreover, this very passage from Matthew is, in fact, visibly and prominently on display in the Disputa. Just above the human forms on Earth, and flanking the dove of the Holy Ghost, four putti (or cherubs) are ostentatiously displaying the four Gospels. Clearly legible are the opening words of Matthew 1.1: ‘LIBER GENERATIONIS IESU CHRISTI’ (the book of the generations of Jesus Christ). This further boosts the credibility of the supposition that there is some significance behind the fact that the salient human figures in the Disputa located on the Earth number (at least approximately) forty-two.

Multiples of seven are also prominent in the fresco on the north wall, known as the Parnassus (figure 5). In this fresco, fourteen figures are arrayed in a chain that begins with Apollo at the visual center and then descends the right-hand side of the fresco. Then there are fourteen figures in another chain, which begins with Sappho at the bottom left, ascends on the left-hand side, and returns to Apollo.

The fresco on the south wall, known as Jurisprudence (figure 6), has three sections, a lunette above two panels flanking a window. These do not feature multiples of seven. But they do feature the epogdoôn. The right-hand panel, celebrating ecclesiastical law, features nine salient figures. The left-hand panel, celebrating secular law, has eight. Hence, the ratio between ecclesiastical law and secular law is 9:8, the epogdoôn. The ecclesiastical panel with nine salient human forms is adjacent to the (Christian) Disputa; and the secular panel with eight is adjacent to the (pagan) School of Athens. Thus, this numerical ratio of 9:8 on the south wall neatly echoes the numerical ratio between the Disputa and The School of Athens. Although the frescoes on the east, west, and north walls prominently feature multiples (or approximate multiples) of seven, the south wall does not. But this does not undermine the significance of the sevens on the other walls; it merely singles out the extra significance of the epogdoôn.

Further evidence reinforcing the significance of the numbers 8 and 9 in Jurisprudence can be found in the prominent lunette above the window on the south wall of the room. This lunette contains eight salient pagan divine forms—echoing the eight human forms in the panel below that lies nearest to The School of Athens.

Johann David Passavant (Reference Passavant1872: 224) counted eight human forms on the panel to the left of the window. But, inexplicably, he also counted eight in the panel to the right of the window. (Perhaps he was expecting symmetry?) We have not found any recent commentators who have corrected this error. Hence, we invite careful inspection of either the original or else a good reproduction, such as that in Richard Cocke's Raphael: Raffaello Sanzio (Reference Cocke2004: 75).

Pythagorean Tuning in Plato's Timaeus

On the slate in the School of Athens, immediately below ΕΠΟΓΔΟΩΝ are the numerals VI VIII VIIII XII (6, 8, 9, and 12). These numerals are linked by lines labeled with the Greek names of fundamental musical intervals:

From this division of the octave into two adjacent fourths, separated by a tone, is demonstrated the following:

In the third section is a pattern, called the tetraktys, which was a standard symbol for the Pythagorean brotherhoods:

The Roman numeral X is the sum of the lines above it: I + II + III + IIII = X (1 + 2 + 3 + 4 = 10). The tetraktys is echoed in the opening words of Timaeus 17a: ‘One, two, three . . . the fourth’. And it appears as the opening four numbers in the series of the seven portions (1, 2, 3, 4, 9, 8, 27) that make the backbone of the Platonic World Soul, according to the Timaeus 36a–b. The tetraktys neatly distils the fundamental musical ratios of 1:2, 2:3, and 3:4.

The Platonic significance of these numbers has been recognized by a long chain of commentators. There were several such sources that would have been available to Raphael (or whoever was directing the fresco program) at the time that he was working in the Vatican. Among these is a book on music theory by Franchino Gaffurio ([1496] Reference Gaffurio and Palisca1993), dedicated to Ludovico Sforza, the Duke of Milan (then a patron of Leonardo da Vinci, whom Raphael imitated and admired). A woodcut in the book not only vividly and explicitly displays the significant series of numbers 6, 8, 9, 12, but it also clearly links this series of four numbers both to music and to Pythagoras ([1496] Reference Gaffurio and Palisca1993: 48).

As noted, the Timaeus 35b–36a describes the measuring out of portions in ratios that can be given by the numbers 1, 2, 3, 4, 9, 8, 27. Plato then says that the Demiurge placed arithmetic and harmonic means in ‘the double and triple intervals’. Placing numbers that represent these means between the numbers 1 and 2 would require the use of fractions. It is possible, however, to avoid fractions by recalibrating the measurement of the first portion. If the quantity of mixture that is present in the first portion were to be measured by the number 6, then the other portions could still be measured (in the manner described in the Timaeus) as ratios of that first portion. Then the first of the ‘double intervals’ will be the interval between 6 and 12. And the arithmetic and harmonic means between 6 and 12 will be 9 and 8 (no fractions will be needed). This is the reason given by Ficino ([1494] Reference Ficino and Farndell2010: 75) for representing the first ‘double interval’ in the Timaeus as the interval between 6 and 12, thereby generating the series of numbers 6, 8, 9, 12. And that yields precisely the Pythagorean pattern on the slate in The School of Athens.

Ficino was enormously influential among Raphael's associates at the Vatican (Rowland Reference Rowland and Hall1997: 142). And Ficino, in turn, conveys information about a rich trail of influences that leads back through Proclus (Reference Baltzly2009) to Plato's Timaeus.

The Epogdoôn is Discordant

Given that both the Timaeus and a slate with Pythagorean references appear in The School of Athens and the word epogdoôn occurs in both, it is worth investigating even more closely the significance of the epogdoôn.

When two notes standing a whole tone apart (such as sol and fa) are sung simultaneously, there are audible interference beats between the two frequencies. These beats dissolve into the pure harmony of unison if the lower note is raised slightly or the higher note lowered. Presumably for these physical reasons, in the Renaissance, the musical interval of the epogdoôn, or whole tone, was experienced as a tension that strains to be resolved. Likewise, a seventh strains to be resolved into a pure octave.

Alternating tensions and their resolutions can be heard, for instance, in standard cadences in Gregorian chants. An archetype of this pattern can frequently be heard as these chants close with the word Amen. The syllable A– is characteristically sung to a note whose natural harmonics generate audible interference beats against those of the tonic or home note. And then that interference almost utterly disappears when the syllable –men is sung to notes either in unison with the tonic or else standing pure octaves or fifths from the tonic.

Thus, there is a musical significance to the numerical ratio between the (approximately) fifty-six pagans in The School of Athens and the (approximately) sixty-three Christians in the Disputa. If we take the Disputa to be characterized iconographically as the home note, then The School of Athens corresponds to a leading note that creates a temporary tension with the home note—but a tension that is destined very soon to be resolved into a perfect harmony with the home note. Corresponding to that musical iconography, the frescoes in the Stanza della Segnatura clearly depict Plato and Aristotle as walking toward the ultimate salvation that is depicted in the Disputa.

A natural implication carried by the iconography in the frescoes is surely that Christians can learn from the pagans. But they need to be wary. The word on the book in Plato's hand, TIMEO, is not only the Italian title of the Timaeus: it is also the first word in the famous line in Latin from the Aeneid 2.49, ‘Timeo Danaos et dona ferentes’ (I fear Greeks even bearing gifts). The symbolic presence of the epogdoôn in the frescoes aptly echoes this slightly uneasy relationship between the ancient Greeks and the Renaissance Christians.

Still more evidence of the symbolic significance of the epogdoôn can be found in Plato's Timaeus. In the preamble to the creation story, the epogdoôn, although not mentioned by name, is implicitly deployed in the account of Solon's visit to Egypt, where he learned of the lost civilization of Atlantis. The priests in Egypt tell Solon that their civilization was founded eight thousand years prior and that another civilization had been founded in Athens a thousand years before that (Timaeus 23d–23e). Neither the Bible nor archaeology can credit the existence of any civilization of the kind described (with written language and monumental architecture) as far back as eight or nine thousand years before Solon. However, there is ample reason to suspect that Plato used the numbers nine thousand and eight thousand at least in part because the ratio between these two numbers has an aptly corresponding musical significance. According to the Timaeus, Solon acquired precious knowledge in Egypt and brought it back to Greece. On his return he met with social discord, to which he responded by restoring harmony through the institution of wise laws. This historical sequence is analogous to the resolution of a dissonant epogdoôn into a perfect harmony. And a parallel symbolic narrative closely fits Raphael's fresco program.

Fine-Tuning Pythagorean Ratios

Plato's Timaeus describes musical ratios that are grounded in what is known as the cycle of fifths. It is possible to tune by ear all seven notes in the diatonic scale if one tunes successive notes upward in fifths: F, C, G, D, A, E, B (and as notes get too high, one may transpose downward in octaves). An equivalent way of achieving the same effect is by tuning upward in fourths instead of fifths, which is a method often used for stringed instruments like lutes and guitars.

A fifth is so-called because it is characteristically the interval spanned by five adjacent notes from the diatonic scale. But there is one anomaly: the interval B–F that is spanned by the five adjacent notes, BCDEF. The interval B–F is attended by extremely severe interference beats in the natural harmonics. This discord is like the serpent in the Garden of Eden. This interval B–F is an inescapably discordant consequence of the Pythagorean tuning of the sol–fa, diatonic, division of the octave. In the Renaissance, this interval was sometimes called the ‘wolf fifth’ (Smith Reference Smith2011: 50). There are several slightly different frequency ratios that arise in music theory, all lying in the same region between a fourth and a fifth. They are variously known as ‘an augmented fourth’, ‘a diminished fifth’, and ‘the tritone’ (sometimes called ‘the devil's interval’); and they all generate severe interference beats in the natural harmonics (precisely because they lie close to, but not on, both a fourth and a fifth).

Pythagorean tuning not only creates one wolf fifth that sounds painfully flat, but it also makes all the major thirds noticeably sharp and all the minor thirds noticeably flat. Anyone with a good ear can hear that interference beats in the natural harmonics will be noticeably reduced if a Pythagorean major third (two whole tones) is slightly narrowed or if a Pythagorean minor third (a whole tone plus a semitone) is slightly widened. Presumably Renaissance singers sometimes made these adjustments instinctively as they sang, as has been concluded by historians of music: ‘Thus singers needed to remain flexible in their tuning, slightly adjusting the pitch of specific notes within the musical context, while still remaining at the same level overall’ (Smith Reference Smith2011:51). For this reason, as a musical instrument, the voice cannot be relied upon to stick reliably to strict Pythagorean tuning.

However, some musical instruments can be tuned to strict Pythagorean tuning—and can be relied upon to hold the tuning. A church organ, for instance, is traditionally tuned only about once a year. Nor is it easy to alter the positions of frets on a lute or guitar. Hence, Johannes Kepler explains, ‘it may be possible for strings to be tuned in that way, seeing that as they are inanimate they do not interpose their own judgement but follow the hand of the foolish theorist without the least resistance’ ([1619] Reference Kepler, Aiton, Duncan and Field1997: 138).

Because it is possible to tune some instruments to whatever system one chooses, there is a way to restrain a singer's ever-present temptation to sweeten the thirds and thereby deviate from Pythagorean tuning. A strategy of this kind is enunciated in the prologue to Claudio Monteverdi's L'Orfeo ([1607] Reference Monteverdi2002), when Music aspires to ‘inspire souls with a longing / for the sonorous harmony of heaven's lyre’. Following this introduction by Music, a nymph sings,

Thus, in principle, singers could resist the temptation to deviate from Pythagorean tuning by singing in unison with ‘well-tuned strings’ (‘ben temprate corde’) (Monteverdi [1607] Reference Monteverdi2002: 294) that have been tuned precisely to whatever tuning system one prefers. Monteverdi might not have chosen Pythagorean tuning, but some of his prominent contemporaries—among them Giovanni Pierluigi da Palestrina—certainly did.

The dissonance in Pythagorean thirds arises because a Pythagorean major third is spanned by a double epogdoôn—two whole tone intervals of 9:8, yielding a ratio of (9/8) x (9/8) = 81/64. This ratio deviates just slightly from the ratio of 80/64 (5/4). And that frequency ratio does occur, along with octaves and fifths, in the natural harmonics of any given note. That is why Pythagorean major thirds generate interference beats in the natural harmonics. Thus, it is fundamentally the epogdoôn that lies behind the Pythagorean dissonance in major thirds.

As far back as 1511, organ builders described the problems in trying to remove dissonances by fine-tuning a series of notes and seeking local minimizations of interference beats. They called this ‘chasing the wolf’ (Schlick [1511] Reference Schlick and Barber1980: 75–76). Arnolt Schlick was writing his textbook on organ tuning at virtually the same time that Raphael was painting the School of Athens. As Schlick clearly explains, if one optimizes perceived harmonies in the fifths, the thirds will be perceived as ‘too high, horrid, and hard’ ([1511] Reference Schlick and Barber1980: 75). His remedy was to improve the thirds at the cost of inflicting slight damage on some of the fifths:

Manifestly, musicians do meet temptations to deviate from the pure Pythagorean frequency ratios. Nevertheless, there is a charm in music like that of Palestrina and Monteverdi, which is crafted in such a way as never to stray very far, for very long, from the perfect unison, octaves, and fifths that minimize interference beats in the natural harmonics. And that is precisely the kind of music that is described mathematically on the slate in The School of Athens.

The Necessity of Imperfection

Hall's diagram numbers fifty-six figures. However, close inspection of good reproductions of The School of Athens (such as that in Bruschini Reference Bruschini2004: 72–73) reveals two salient human forms visibly present in the fresco but unnumbered in Hall's diagram. One (just to the left of number 35) is included in the diagram but not numbered; the other (between numbers 7 and 8) is omitted from both the diagram and the count. These two unnumbered figures are also visible in the cartoon for the fresco (see Hall Reference Hall1997: 38, figure 19; Talvacchia Reference Talvacchia2007: 176–77). The number of salient human forms represented in The School of Athens is thus at least fifty-eight (as affirmed by Most Reference Most1996: 146).

If there had been fifty-six salient human forms in The School of Athens, it would have been a nice symmetry. And, since 56 = 7 x 8, these human forms could be aligned symbolically with musical notes spanning eight octaves, with seven distinct notes in each octave. These eight octaves could have been divided into four descending octaves on the right-hand side of the fresco, and four ascending octaves on the left-hand side. If the notes started with (say) G at the top (for Plato), then the descending four octaves would be as follows (using subscripts to signify downward transpositions in octaves):

$${\rm G} + {\rm F} + {\rm E} + {\rm D} + ... + {\rm C}_3 + {\rm B}_3 + {\rm A}_3$$

Hence, a total of fifty-six human forms in The School of Athens would be not only a symbolically apt number because it is a multiple of seven, but also a number that resonates well with a musical iconography.

However, when the seven notes of an octave are played in a scale, people often add an eighth note an octave from the one from which they began. When they play an upward and then a downward scale, sometimes the top note is repeated (‘la, ti, ut; ut, ti, la’), sometimes not (‘la, ti, ut, ti, la’). It would be consonant to the human ear to close twenty-eight notes covering four downward octaves with one further note five octaves below the initial note from which it began. Thus, for instance, a scale covering four octaves could be played as follows:

$${\rm G} + {\rm F} + {\rm E} + {\rm D} + .... + {\rm C}_3 + {\rm B}_3 + {\rm A}_3 + {\rm G}_4$$

If Raphael were to have mirrored that musical pattern in the philosophers on the right-hand side of his fresco, then we should expect the pattern down the right-hand side to contain the groupings: 7 + 7 + 7 + 7 + 1 = 29. Matching that pattern, the philosopher numbered 28 in Hall's diagram is placed strikingly apart from all the others. The philosopher numbered 29 also sits strikingly apart from all the other groupings. There is some evidence (Hall Reference Hall1997: 39–40) that this prominent figure might have been added very late (removing some of the original plaster and adding the figure on fresh plaster)—perhaps when an opportunity arose for Raphael to pay tribute to Michelangelo.

Thus, it would be possible to align musical scales with a total of either an ideal fifty-six or a deviant fifty-seven or fifty-eight human figures in The School of Athens. Raphael deviates slightly from the elsewhere ubiquitous multiples of seven, but he does so in a way that neatly fits the hypothesis that musical symbolism informs the fresco.

Are there truly sixty-three figures in the Disputa—twenty-one in the heavens plus forty-two below? Apparently not. For instance, Passavant (Reference Passavant1872: 221) describes the altar below, ‘round which are grouped forty-three figures’. The primary reference for the diagram of the Disputa (figure 2) was a reproduction in Enrico Bruschini's Masterpieces of the Vatican (Reference Bruschini2004: 70–71) and this did not facilitate a definitive verification of Passavant's count. Nevertheless, other reproductions and a colleague's personal observation of the fresco confirm that there is a shadowy figure in the group around the altar (see question mark between the figures numbered 40 and 41 in figure 5).

Consequently, the tallies of salient figures both in The School of Athens and in the Disputa evidently do not stand in the ideal Pythagorean whole tone ratio of exactly 9:8. There are minor deviations between Raphael's visual images and theoretically predicted Platonic ideals.

The existence of minor deviations from Platonic ideals does not undermine the theory that Raphael was taking (or receiving) guidance from the Platonic principles that are laid down in the Timaeus. Indeed, the deviations may further corroborate it. Taking guidance from the Timaeus, it would be reasonable for an artist to imitate the techniques that were used by the Demiurge, who is said to have succeeded in producing something that was supremely beautiful. What the Demiurge has created manifestly includes patterns that deviate slightly from simple numerical patterns. For instance, there is not a whole number of days in a month, or of days or months in a year. The inescapable imperfection of material embodiments of abstract ideals is a central theme in Plato's core philosophy, and especially in Plato's Timaeus 47e–48b: ‘if I'm to tell the story of how it really came to be in this way, I'd have to introduce the character of the Straying Cause—how it is its nature to set things adrift.’

This same theme of the unavoidability of imperfection recurs in many Greek myths. Both Plato's Timaeus and Raphael's frescoes allude to myths that warn artists against the hubris of thinking they can achieve the perfections that can be reached only by the gods. In one such myth, which is prominently depicted in the northwest corner of the Stanza della Segnatura in a spandrel that lies between the Parnassus and the Disputa, the musician Marsyas is skinned alive for his boast that he could play music better than could Apollo (Hall Reference Hall1997: 14). One message an artist might take from this myth is that deviations from perfection should be included in an artwork as a sign of humility before God, or the gods. In the craft traditions of many cultures it is considered good form to include at least one deliberate, minor imperfection in any work.

Stanisław Mossakowski (Reference Mossakowski1968: 13) offers another possible reason why Raphael included a depiction of the punishment of Marsyas, saying it shows the ‘victory of the divine music of Apollo's lyre, based on mathematic principles, over the uncontrollable sounds of Marsyas's flute.’ He says that Raphael is demonstrating the contrast between two kinds of music, the divine and the vulgar, where only the divine music fits the perfect mathematical patterns. He argues that in a later painting, Saint Cecilia (c. 1516–1517), Raphael conveys just the contrast we have identified between the perfect musical ratios that exist in heaven and in certain church music, and the deviations from these ratios that occur in the material realm and in popular music. In this painting, Saint Cecilia is depicted having a vision of six angels singing above her in heaven and, as Mossakowski says, they are arranged in such a way as to instantiate the ratios of an octave (2:1), a fifth (3:2), and a fourth (4:3). This spatial arrangement makes visible the Pythagorean musical harmonies that they are presumably singing. By contrast, she holds a broken portative organ, and at her feet lie discarded musical instruments, some of them broken, that are used in secular music; these instruments are generally tuned to play harmonies that deviate from these simple ratios.

An artist taking guidance (directly or indirectly) from the Timaeus should likewise respect the integrity of the materials upon which ideal forms are being imposed. There are ways in which artistic works are more beautiful—not less—when deviations from simple ideas are optimally motivated by the requirements of the context in which the artist is working. Thus, there are multiple independent reasons for Raphael to include deliberate deviations from the perfect Pythagorean ratio of 9:8.

Furthermore, the pattern of symbolic locations in the frescoes where these deviations from ideals occur is also significant. If the ratio of 9:8 were to be met, we would expect sixty-three (nine times seven) figures in the Disputa, but there are in fact sixty-four. This deviation from Platonic expectations arises because the human figures on earth number forty-three rather than forty-two, which would be precisely double the twenty-one figures in heaven. The number in heaven is a multiple of seven; the number below is not. There is displayed in heaven Matthew's gospel, which indicates the target number forty-two as the total number of generations in the genealogy of Jesus.

In The School of Athens, a similar structure of ideal pattern above and deviation below is even more clearly displayed. The ideal in this case is fifty-six: eight times seven. In this fresco Plato is pointing upward (see figure 4)—presumably toward the Platonic perfection of the mathematical Forms. Plato's gesture directs the eye to two monumental arches, each decorated with a pattern of eight adjacent rows of what may be called kissing hexagons (one hexagon touches the next just at one vertex). In each of these rows are seven hexagons. Hence, in each of these arches there are fifty-six hexagons. Thus, The School of Athens instantiates not only two Platonically perfect ornamental patterns of fifty-six in the world above Plato, but also a minor deviation from that pattern in the assemblage of fifty-eight philosophers below. The existence of that kind of complexity in the human realm is in perfect harmony with the central themes of Plato's Timaeus.

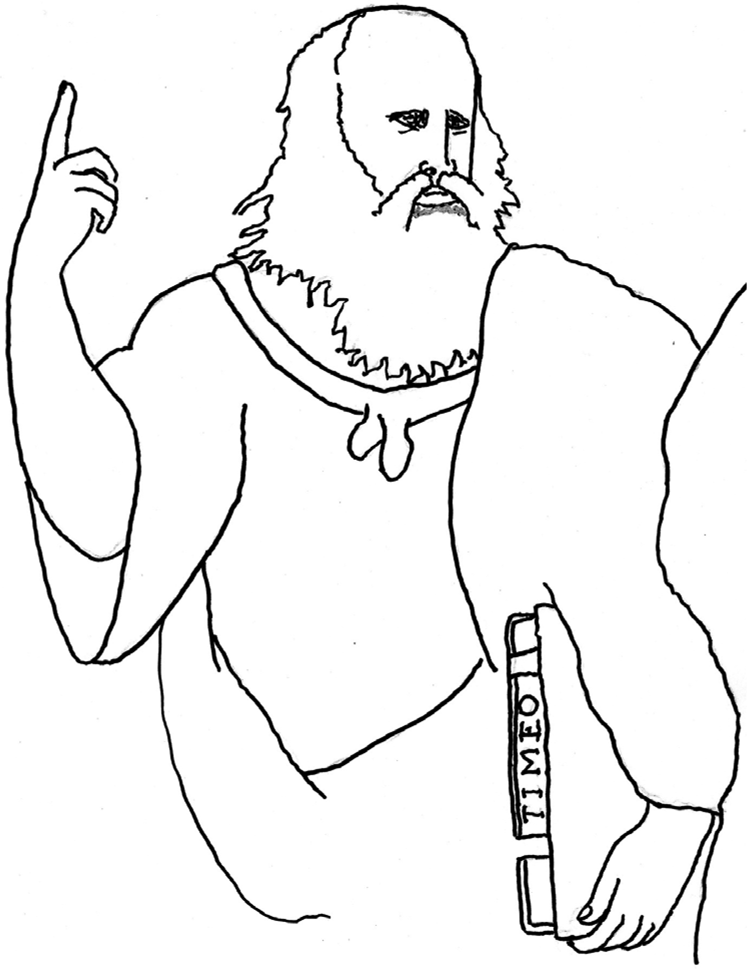
Figure 4. Drawing by John Bigelow of Raphael Sanzio, The School of Athens (detail), fresco, c. 1508–1512, Vatican Museum, Vatican City.

Figure 5. Diagram by John Bigelow of Raphael Sanzio, Parnassus, fresco, c. 1509–1511, Vatican Museum, Vatican City.

Figure 6. Diagram by John Bigelow of Raphael Sanzio, Jurisprudence, fresco, c. 1511, Vatican Museum, Vatican City.

Thus, the Stanza della Segnatura in the Vatican visibly embodies—approximately, and therefore even more convincingly—the epogdoôn and other musical ratios of ‘the music of the spheres’, as they are described in Plato's Timaeus. Approximate instantiations of the mathematical signature of the Pythagorean and Platonic World Soul are intricately incarnated within the microcosm of the Stanza della Segnatura. If ever a room had a soul of its own, then this one does.

Coda

If Raphael was deliberately weaving mathematical patterns into his frescoes, as we have argued, then what he was doing was analogous to a wide range of things that others have done at other times in history and in other places.

In Plato's Laws (819b–820b; all citations are to Plato Reference Cooper1997: 1318–1616), it is said that ‘gentlemen should study’ using the same methods that have for many centuries been taught to ‘very many children in Egypt’. The Laws is a dialogue, and the character who voices this opinion is ‘the Athenian’, who says that in Egypt teachers ‘make the uses of elementary arithmetic an integral part of their pupils’ play’. This, he says, ‘rescues them from the deep-rooted ignorance, at once comic and shocking, that all men display’. The Athenian ‘blushes’ to admit that Greeks are afflicted with an ignorance from which the Egyptians have been rescued by their superior education system.

The ancient Egyptians have not been alone in utilizing teaching techniques like those that Plato praised in the Laws. In his influential novel Waverley, Sir Walter Scott writes, ‘I am aware I may be here reminded of the necessity of rendering instruction agreeable to youth, and of Tasso's infusion of honey into the medicine prepared for a child’ and that the ‘history of England is now reduced to a game at cards,— the problems of mathematics to puzzles and riddles,—and the doctrines of arithmetic may, we are assured, be sufficiently acquired, by spending a few hours a-week at a new and complicated edition of the Royal Game of the Goose’ ([1814] Reference Scott1972: 46–47). The reference to Tasso is to book 1 of a poem from 1581, Jerusalem Liberated, and the ‘game at cards’ Scott refers to here is an old French game played with a pair of dice and a card divided into sixty-three spaces. Clearly, teaching methods of this kind have been practiced at many far distant times and in far-away places.

Like games, works of art can serve as both entertainment and education; and sometimes learning from it is one of the things we most enjoy about a work of art. In an episode of Sesame Street, Ernie talks earnestly and enthusiastically about how triangles have three sides and squares have four sides, and so on, and then begins to wonder how many sides a circle has. Two does not seem right. One does not seem right. None does not seem right. Perhaps a circle has very many incredibly tiny sides?

Sesame Street's writers could reasonably have expected that not all their viewers would find Ernie's mathematical musings of interest. But there were other things in the skit to appeal to other viewers. They could empathize with Bert, who becomes comically irritated by his loquacious roommate. Thus, Ernie's mathematical musings are generously overlaid with a narrative of a wider appeal, involving emotions and personal relations. In Sesame Street episodes featuring the Count (who ‘lo-o-o-ves to count’), lessons in mathematics are always overlaid with various nonmathematical things, such as thunder and lightning and allusions to stories about vampires and Count Dracula.

Part of the magic that music works on the soul is that it makes us count—but subliminally. Visual and other arts perform analogous magic in other ways. For instance, the special ratio of equality in number can sometimes be sensed, without counting, as symmetry. Like Plato's Egyptians and Tasso and Scott and the Sesame Street's writers, Raphael not only crafted lessons in mathematics but also overlaid them with abundant other layers that should be of interest to those who do not ‘love to count’.