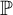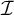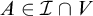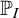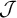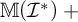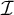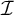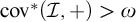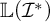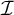1 Motivation
1.1 Ideals on
 $\omega $
and on Polish spaces
$\omega $
and on Polish spaces
If I is an ideal on an infinite set X, we will always assume that
![]() $[X]^{<\omega }=\{A\subseteq X:|A|<\omega \}\subseteq I$
and
$[X]^{<\omega }=\{A\subseteq X:|A|<\omega \}\subseteq I$
and
![]() $X\notin I$
. Let
$X\notin I$
. Let
![]() $I^+=\mathcal {P}(X)\setminus I$
be the family of I-positive sets and
$I^+=\mathcal {P}(X)\setminus I$
be the family of I-positive sets and
![]() $I^*=\{X\setminus A:A\in I\}$
be the dual filter of I. We will work with ideals on countable underlying sets, e.g.,
$I^*=\{X\setminus A:A\in I\}$
be the dual filter of I. We will work with ideals on countable underlying sets, e.g.,
 $$ \begin{align*} \mathcal{I}_{1/n} & =\Big\{A\subseteq\omega\setminus\{0\}:\sum_{n\in A}\frac{1}{n}<\infty\Big\},\\ \mathrm{Nwd} &=\big\{A\subseteq \mathbb{Q}:A\;\text{is nowhere dense (in }\mathbb{Q})\big\},\;\text{or}\\ \mathrm{Fin}\otimes\mathrm{Fin} & =\big\{A\subseteq\omega\times\omega:\forall^\infty\;n\;\,|(A)_n|<\omega\big\}, \end{align*} $$
$$ \begin{align*} \mathcal{I}_{1/n} & =\Big\{A\subseteq\omega\setminus\{0\}:\sum_{n\in A}\frac{1}{n}<\infty\Big\},\\ \mathrm{Nwd} &=\big\{A\subseteq \mathbb{Q}:A\;\text{is nowhere dense (in }\mathbb{Q})\big\},\;\text{or}\\ \mathrm{Fin}\otimes\mathrm{Fin} & =\big\{A\subseteq\omega\times\omega:\forall^\infty\;n\;\,|(A)_n|<\omega\big\}, \end{align*} $$
where
![]() $\forall ^\infty $
stands for “for all but finitely many,”
$\forall ^\infty $
stands for “for all but finitely many,”
![]() $ \exists ^\infty $
for
$ \exists ^\infty $
for
![]() $\neg \forall ^\infty \neg $
, that is, for “there is infinitely many,” and
$\neg \forall ^\infty \neg $
, that is, for “there is infinitely many,” and
![]() $(A)_n$
denotes
$(A)_n$
denotes
![]() $\{k:(n,k)\in A\}$
; also we will work with (
$\{k:(n,k)\in A\}$
; also we will work with (
![]() $\sigma $
-)ideals on uncountable Polish spaces, e.g.,
$\sigma $
-)ideals on uncountable Polish spaces, e.g.,
 $$ \begin{align*} \mathcal{M} &=\big\{B\subseteq\,\!^\omega 2:B\;\text{is meager (i.e., of first-category)}\big\},\\ \mathcal{N} &=\big\{B\subseteq\,\!^\omega 2:B\;\text{is of Lebesgue-measure null}\big\},\;\text{or}\\ \mathcal{K}_\sigma & =\big\{B\subseteq\,\!^\omega\omega:B\;\text{can be covered by a }\sigma\text{-compact set}\big\}, \end{align*} $$
$$ \begin{align*} \mathcal{M} &=\big\{B\subseteq\,\!^\omega 2:B\;\text{is meager (i.e., of first-category)}\big\},\\ \mathcal{N} &=\big\{B\subseteq\,\!^\omega 2:B\;\text{is of Lebesgue-measure null}\big\},\;\text{or}\\ \mathcal{K}_\sigma & =\big\{B\subseteq\,\!^\omega\omega:B\;\text{can be covered by a }\sigma\text{-compact set}\big\}, \end{align*} $$
where
![]() $\,\!^\omega 2$
and
$\,\!^\omega 2$
and
![]() $\,\!^\omega \omega $
are equipped with the usual Polish product topologies, that is, these topologies are generated by the clopen sets
$\,\!^\omega \omega $
are equipped with the usual Polish product topologies, that is, these topologies are generated by the clopen sets
![]() $\{f\in \,\!^\omega \ell :t\subseteq f\}$
where
$\{f\in \,\!^\omega \ell :t\subseteq f\}$
where
![]() $\ell =2$
or
$\ell =2$
or
![]() $\ell =\omega $
and
$\ell =\omega $
and
![]() $t\in \,\!^{<\omega }\ell =\{s:s$
is a function,
$t\in \,\!^{<\omega }\ell =\{s:s$
is a function,
![]() $\mathrm {dom}(s)\in \omega $
, and
$\mathrm {dom}(s)\in \omega $
, and
![]() $\mathrm {ran}(s)\subseteq \ell \}$
. The Cantor space
$\mathrm {ran}(s)\subseteq \ell \}$
. The Cantor space
![]() $\,\!^\omega 2$
is compact and the measure we referred to as the Lebesgue-measure above is the product probability measure (the power of the uniform distribution on
$\,\!^\omega 2$
is compact and the measure we referred to as the Lebesgue-measure above is the product probability measure (the power of the uniform distribution on
![]() $2$
).
$2$
).
By identifying
![]() $\mathcal {P}(\omega )$
and
$\mathcal {P}(\omega )$
and
![]() $\,\!^\omega 2$
, we can talk about measure, category, and complexity of subsets of
$\,\!^\omega 2$
, we can talk about measure, category, and complexity of subsets of
![]() $\mathcal {P}(\omega )$
, in particular, of ideals on
$\mathcal {P}(\omega )$
, in particular, of ideals on
![]() $\omega $
, and similarly on arbitrary countably infinite underlying sets (e.g.,
$\omega $
, and similarly on arbitrary countably infinite underlying sets (e.g.,
![]() $\mathcal {I}_{1/n}$
is
$\mathcal {I}_{1/n}$
is
![]() $F_\sigma $
,
$F_\sigma $
,
![]() $\mathrm {Nwd}$
is
$\mathrm {Nwd}$
is
![]() $F_{\sigma \delta }$
, and
$F_{\sigma \delta }$
, and
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
is
$\mathrm {Fin}\otimes \mathrm {Fin}$
is
![]() $F_{\sigma \delta \sigma }$
). In Section 2, we will present many classical examples of ideals on countable underlying sets.
$F_{\sigma \delta \sigma }$
). In Section 2, we will present many classical examples of ideals on countable underlying sets.
Concerning combinatorial properties and cardinal invariants of definable (typically Borel) ideals in forcing extensions, one of the most crucial points is to understand whether a forcing notion destroys an ideal, and if so, how “strongly.” We are interested in various notions of destroying ideals, in their possible characterisations, in their interactions with classical properties of forcing notions, and in the associated cardinal invariants.
We will mainly focus on classical forcing notions, and in general on forcing notions (which are equivalent to one) of the form
![]() $\mathbb {P}_I=(\mathcal {B}(X)\setminus I,\subseteq )$
where X is an uncountable Polish space,
$\mathbb {P}_I=(\mathcal {B}(X)\setminus I,\subseteq )$
where X is an uncountable Polish space,
![]() $\mathcal {B}(X)=\{$
Borel subsets of
$\mathcal {B}(X)=\{$
Borel subsets of
![]() $X\}$
, and I is a
$X\}$
, and I is a
![]() $\sigma $
-ideal on
$\sigma $
-ideal on
![]() $X\ \sigma $
-generated by a “definable” family of Borel sets (see later). For example,
$X\ \sigma $
-generated by a “definable” family of Borel sets (see later). For example,
![]() $\mathbb {C}=\mathbb {P}_{\mathcal {M}}$
is the Cohen forcing,
$\mathbb {C}=\mathbb {P}_{\mathcal {M}}$
is the Cohen forcing,
![]() $\mathbb {B}=\mathbb {P}_{\mathcal {N}}$
is the random forcing, and
$\mathbb {B}=\mathbb {P}_{\mathcal {N}}$
is the random forcing, and
![]() $\mathbb {P}_{\mathcal {K}_\sigma }$
is the Miller forcing. In general, we know (see [Reference Zapletal42, Proposition 2.1.2]) that
$\mathbb {P}_{\mathcal {K}_\sigma }$
is the Miller forcing. In general, we know (see [Reference Zapletal42, Proposition 2.1.2]) that
![]() $\mathbb {P}_I$
adds a “real”
$\mathbb {P}_I$
adds a “real”
![]() $r_I\in X$
(X can be seen as a
$r_I\in X$
(X can be seen as a
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $^\omega \,\![0,1]$
) determined by the following property: If V is a transitive model (of a large enough finite fragment) of
$^\omega \,\![0,1]$
) determined by the following property: If V is a transitive model (of a large enough finite fragment) of
![]() $\mathrm {ZFC}$
, I (more precisely, the family
$\mathrm {ZFC}$
, I (more precisely, the family
![]() $\sigma $
-generating I) is coded in V, G is
$\sigma $
-generating I) is coded in V, G is
![]() $\mathbb {P}_I$
-generic over V, and
$\mathbb {P}_I$
-generic over V, and
![]() $B\in \mathbb {P}_I$
is a Borel set coded in V, then
$B\in \mathbb {P}_I$
is a Borel set coded in V, then
![]() $r_I\in B$
iff
$r_I\in B$
iff
![]() $B\in G$
Footnote
1
(see [Reference Zapletal42] for a detailed study of these forcing notions).
$B\in G$
Footnote
1
(see [Reference Zapletal42] for a detailed study of these forcing notions).
1.2 Destroying ideals
Let us recall the classical notion of forcing (in)destructibility: We say that an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
is tall if every infinite
$\omega $
is tall if every infinite
![]() $X\subseteq \omega $
contains an infinite element of
$X\subseteq \omega $
contains an infinite element of
![]() $\mathcal {I}$
, e.g.,
$\mathcal {I}$
, e.g.,
![]() $\mathcal {I}_{1/n}$
,
$\mathcal {I}_{1/n}$
,
![]() $\mathrm {Nwd}$
, and
$\mathrm {Nwd}$
, and
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
are tall. A forcing notion
$\mathrm {Fin}\otimes \mathrm {Fin}$
are tall. A forcing notion
![]() $\mathbb {P}$
can destroy
$\mathbb {P}$
can destroy
![]() $\mathcal {I}$
if there is a condition
$\mathcal {I}$
if there is a condition
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
 $$ \begin{align*} & p\Vdash\text{"the ideal generated by }\mathcal{I}^V \text{ is not tall," i.e.,}\\ & p\Vdash\exists\;Y\in [\omega]^\omega\;\forall\;A\in\mathcal{I}^V\;|Y\cap A|<\omega, \end{align*} $$
$$ \begin{align*} & p\Vdash\text{"the ideal generated by }\mathcal{I}^V \text{ is not tall," i.e.,}\\ & p\Vdash\exists\;Y\in [\omega]^\omega\;\forall\;A\in\mathcal{I}^V\;|Y\cap A|<\omega, \end{align*} $$
where we write
![]() $\mathcal {I}^V$
to make it completely clear that even in the case of definable ideals, we refer to the ideal from (or interpreted in) the ground model.Footnote 2 We say that
$\mathcal {I}^V$
to make it completely clear that even in the case of definable ideals, we refer to the ideal from (or interpreted in) the ground model.Footnote 2 We say that
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {I}$
if
$\mathcal {I}$
if
![]() $p=1_{\mathbb {P}}$
, and that
$p=1_{\mathbb {P}}$
, and that
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\mathbb {P}$
-indestructible if
$\mathbb {P}$
-indestructible if
![]() $\mathbb {P}$
cannot destroy
$\mathbb {P}$
cannot destroy
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
We know that every ideal can be destroyed by a
![]() $\sigma $
-centered forcing notion: Let
$\sigma $
-centered forcing notion: Let
![]() $\mathcal {I}$
be arbitrary and define the associated Mathias–Prikry forcing
$\mathcal {I}$
be arbitrary and define the associated Mathias–Prikry forcing
![]() $\mathbb {M}(\mathcal {I}^*)$
as follows (see [Reference Canjar12, Reference Chodounský, Repovš and Zdomskyy13, Reference Hrušák27]):
$\mathbb {M}(\mathcal {I}^*)$
as follows (see [Reference Canjar12, Reference Chodounský, Repovš and Zdomskyy13, Reference Hrušák27]):
![]() $(s,F)\in \mathbb {M}(\mathcal {I}^*)$
if
$(s,F)\in \mathbb {M}(\mathcal {I}^*)$
if
![]() $s\in [\omega ]^{<\omega }$
and
$s\in [\omega ]^{<\omega }$
and
![]() $F\in \mathcal {I}^*$
;
$F\in \mathcal {I}^*$
;
![]() $(s_0,F_0)\leq (s_1,F_1)$
if
$(s_0,F_0)\leq (s_1,F_1)$
if
![]() $s_0$
end-extends
$s_0$
end-extends
![]() $s_1$
(with respect to a fixed enumeration of the underlying set of
$s_1$
(with respect to a fixed enumeration of the underlying set of
![]() $\mathcal {I}$
),
$\mathcal {I}$
),
![]() $F_0\subseteq F_1$
, and
$F_0\subseteq F_1$
, and
![]() $s_0\setminus s_1\subseteq F_1$
. We know that
$s_0\setminus s_1\subseteq F_1$
. We know that
![]() $\mathbb {M}(\mathcal {I}^*)$
is
$\mathbb {M}(\mathcal {I}^*)$
is
![]() $\sigma $
-centered (conditions with the same first coordinates are compatible), and it destroys
$\sigma $
-centered (conditions with the same first coordinates are compatible), and it destroys
![]() $\mathcal {I}$
: If G is
$\mathcal {I}$
: If G is
![]() $(V,\mathbb {M}(\mathcal {I}^*))$
-generic and
$(V,\mathbb {M}(\mathcal {I}^*))$
-generic and
![]() $Y_G=\bigcup \{s:(s,F)\in G$
for some
$Y_G=\bigcup \{s:(s,F)\in G$
for some
![]() $F\}$
, then
$F\}$
, then
![]() $Y_G\in [\omega ]^\omega \cap V[G]$
and
$Y_G\in [\omega ]^\omega \cap V[G]$
and
![]() $|Y_G\cap A|<\omega $
for every
$|Y_G\cap A|<\omega $
for every
![]() $A\in \mathcal {I}^V$
.
$A\in \mathcal {I}^V$
.
Sometimes
![]() $\mathbb {M}(\mathcal {I}^*)$
does more than just “simply” destroying
$\mathbb {M}(\mathcal {I}^*)$
does more than just “simply” destroying
![]() $\mathcal {I}$
: Trivial density arguments show that if
$\mathcal {I}$
: Trivial density arguments show that if
![]() $\mathcal {I}=\mathcal {I}_{1/n}$
or
$\mathcal {I}=\mathcal {I}_{1/n}$
or
![]() $\mathcal {I}=\mathrm {Nwd}$
then
$\mathcal {I}=\mathrm {Nwd}$
then
![]() $V^{\mathbb {M}(\mathcal {I}^*)}\models Y_{\mathring {G}}\in \mathcal {I}^+$
(where
$V^{\mathbb {M}(\mathcal {I}^*)}\models Y_{\mathring {G}}\in \mathcal {I}^+$
(where
![]() $\mathcal {I}^+$
is defined in the extension of course). In general,
$\mathcal {I}^+$
is defined in the extension of course). In general,
![]() $Y_{\mathring {G}}$
is not necessarily
$Y_{\mathring {G}}$
is not necessarily
![]() $\mathcal {I}$
-positive: If
$\mathcal {I}$
-positive: If
![]() $\mathcal {I}=\mathrm {Fin}\otimes \mathrm {Fin}$
and
$\mathcal {I}=\mathrm {Fin}\otimes \mathrm {Fin}$
and
![]() $Y\in \mathcal {I}^+\cap V^{\mathbb {P}}$
, then
$Y\in \mathcal {I}^+\cap V^{\mathbb {P}}$
, then
![]() $Y\cap (\{n\}\times \omega )$
is infinite for infinitely many n and
$Y\cap (\{n\}\times \omega )$
is infinite for infinitely many n and
![]() $\{n\}\times \omega \in \mathcal {I}^V$
for every n, in other words, no forcing notion can add an
$\{n\}\times \omega \in \mathcal {I}^V$
for every n, in other words, no forcing notion can add an
![]() $\mathcal {I}$
-positive set which is almost disjoint from all elements of
$\mathcal {I}$
-positive set which is almost disjoint from all elements of
![]() $\mathcal {I}^V$
. If
$\mathcal {I}^V$
. If
![]() $\mathcal {I}$
is analytic or coanalytic and
$\mathcal {I}$
is analytic or coanalytic and
![]() $\mathbb {P}$
adds a
$\mathbb {P}$
adds a
![]() $\mathring {Y}\in \mathcal {I}^+$
such that
$\mathring {Y}\in \mathcal {I}^+$
such that
![]() $|\mathring {Y}\cap A|<\omega $
for every
$|\mathring {Y}\cap A|<\omega $
for every
![]() $A\in \mathcal {I}^V$
, then we will say that
$A\in \mathcal {I}^V$
, then we will say that
![]() $\mathbb {P}\ +$
-destroys (or can
$\mathbb {P}\ +$
-destroys (or can
![]() $+$
-destroy)
$+$
-destroy)
![]() $\mathcal {I}$
. We will show (see Corollary 5.2) that if a Borel ideal
$\mathcal {I}$
. We will show (see Corollary 5.2) that if a Borel ideal
![]() $\mathcal {I}$
can be
$\mathcal {I}$
can be
![]() $+$
-destroyed, then
$+$
-destroyed, then
![]() $\mathbb {M}(\mathcal {I}^*)\ +$
-destroys it.
$\mathbb {M}(\mathcal {I}^*)\ +$
-destroys it.
We concentrate on analytic/coanalytic ideals because then the statements “
![]() $X\in \mathcal {I}$
” and “
$X\in \mathcal {I}$
” and “
![]() $\mathcal {I}$
is an ideal” are absolute between the ground model V and its forcing extensions (assuming of course that
$\mathcal {I}$
is an ideal” are absolute between the ground model V and its forcing extensions (assuming of course that
![]() $\mathcal {I}$
is coded in V and
$\mathcal {I}$
is coded in V and
![]() $X\in V$
).
$X\in V$
).
One may ask now if we can go even further and add a set
![]() $Z\in \mathcal {I}^*\cap V^{\mathbb {P}}$
which has finite intersection with every
$Z\in \mathcal {I}^*\cap V^{\mathbb {P}}$
which has finite intersection with every
![]() $A\in \mathcal {I}\cap V$
(where
$A\in \mathcal {I}\cap V$
(where
![]() $\mathcal {I}$
is analytic or coanalytic), if so, we say that
$\mathcal {I}$
is analytic or coanalytic), if so, we say that
![]() $\mathbb {P}$
$\mathbb {P}$
![]() $\ *$
-destroys (or can
$\ *$
-destroys (or can
![]() $*$
-destroy)
$*$
-destroy)
![]() $\mathcal {I}$
. Let us point out certain crucial observations concerning
$\mathcal {I}$
. Let us point out certain crucial observations concerning
![]() $*$
-destructibility:
$*$
-destructibility:
1) If we can add such a Z, then
![]() $A\subseteq ^* \omega \setminus Z\in \mathcal {I}$
(where
$A\subseteq ^* \omega \setminus Z\in \mathcal {I}$
(where
![]() $X\subseteq ^* Y$
iff
$X\subseteq ^* Y$
iff
![]() $|X\setminus Y|<\omega $
) for every
$|X\setminus Y|<\omega $
) for every
![]() $A\in \mathcal {I}^V$
. Therefore
$A\in \mathcal {I}^V$
. Therefore
![]() $\mathcal {I}$
must be a P-ideal, that is, for every countable
$\mathcal {I}$
must be a P-ideal, that is, for every countable
![]() $\mathcal {A}\subseteq \mathcal {I}$
there is a pseudounion
$\mathcal {A}\subseteq \mathcal {I}$
there is a pseudounion
![]() $B\in \mathcal {I}$
of
$B\in \mathcal {I}$
of
![]() $\mathcal {A}$
, that is,
$\mathcal {A}$
, that is,
![]() $A\subseteq ^* B$
for every
$A\subseteq ^* B$
for every
![]() $A\in \mathcal {A}$
(e.g.,
$A\in \mathcal {A}$
(e.g.,
![]() $\mathcal {I}_{1/n}$
is a P-ideal but
$\mathcal {I}_{1/n}$
is a P-ideal but
![]() $\mathrm {Nwd}$
and
$\mathrm {Nwd}$
and
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
are not). Why? The formula “
$\mathrm {Fin}\otimes \mathrm {Fin}$
are not). Why? The formula “
![]() $x=(x_n)_{n\in \omega }\in \,\!^\omega \mathcal {P}(\omega )$
is a sequence in
$x=(x_n)_{n\in \omega }\in \,\!^\omega \mathcal {P}(\omega )$
is a sequence in
![]() $\mathcal {I}$
without pseudounion in
$\mathcal {I}$
without pseudounion in
![]() $\mathcal {I}$
” is
$\mathcal {I}$
” is
![]() ${\underset{\sim}{\Pi}}{}^1_2$
and hence absolute between V and
${\underset{\sim}{\Pi}}{}^1_2$
and hence absolute between V and
![]() $V^{\mathbb {P}}$
.
$V^{\mathbb {P}}$
.
2) A
![]() $\sigma $
-centered forcing notion cannot
$\sigma $
-centered forcing notion cannot
![]() $*$
-destroy any tall analytic P-ideal
$*$
-destroy any tall analytic P-ideal
![]() $\mathcal {I}$
(see [Reference Farkas, Khomskii and Vidnyánszky18, Theorem 6.4]), in particular,
$\mathcal {I}$
(see [Reference Farkas, Khomskii and Vidnyánszky18, Theorem 6.4]), in particular,
![]() $\mathbb {M}(\mathcal {I}^*)$
cannot
$\mathbb {M}(\mathcal {I}^*)$
cannot
![]() $*$
-destroy
$*$
-destroy
![]() $\mathcal {I}$
. The same holds for somewhere tall analytic P-ideals, that is, when
$\mathcal {I}$
. The same holds for somewhere tall analytic P-ideals, that is, when
![]() $\mathcal {I}\!\upharpoonright \! X=\{A\subseteq X:A\in \mathcal {I}\}$
is tall for some
$\mathcal {I}\!\upharpoonright \! X=\{A\subseteq X:A\in \mathcal {I}\}$
is tall for some
![]() $X\in \mathcal {I}^+$
. What can we say about nowhere tall analytic P-ideals? Applying Solecki’s characterisation of analytic P-ideals, one can show (see later) that up to isomorphism (via a bijection between the underlying sets, in notation
$X\in \mathcal {I}^+$
. What can we say about nowhere tall analytic P-ideals? Applying Solecki’s characterisation of analytic P-ideals, one can show (see later) that up to isomorphism (via a bijection between the underlying sets, in notation
![]() $\mathcal {I}\simeq \mathcal {J}$
) there are only three nowhere tall analytic P-ideals: trivial modifications of
$\mathcal {I}\simeq \mathcal {J}$
) there are only three nowhere tall analytic P-ideals: trivial modifications of
![]() $\mathrm {Fin}=[\omega ]^{<\omega }$
, that is, ideals of the form
$\mathrm {Fin}=[\omega ]^{<\omega }$
, that is, ideals of the form
![]() $\{A\subseteq \omega :|A\cap X|<\omega \}$
for an infinite
$\{A\subseteq \omega :|A\cap X|<\omega \}$
for an infinite
![]() $X\subseteq \omega $
(clearly, there are two nonisomorphic ideals of this form); and the density ideal (see below for the definition of density ideals)
$X\subseteq \omega $
(clearly, there are two nonisomorphic ideals of this form); and the density ideal (see below for the definition of density ideals)
Clearly, every forcing notion
![]() $*$
-destroys trivial modifications of
$*$
-destroys trivial modifications of
![]() $\mathrm {Fin}$
, and
$\mathrm {Fin}$
, and
![]() $\mathbb {P}\ *$
-destroys
$\mathbb {P}\ *$
-destroys
![]() $\{\varnothing \}\otimes \mathrm {Fin}$
iff
$\{\varnothing \}\otimes \mathrm {Fin}$
iff
![]() $\mathbb {P}$
adds a dominating real (and hence in these three special cases,
$\mathbb {P}$
adds a dominating real (and hence in these three special cases,
![]() $*$
-destruction is possible by
$*$
-destruction is possible by
![]() $\sigma $
-centered forcing notions).
$\sigma $
-centered forcing notions).
3) And finally, we know that every analytic P-ideal
![]() $\mathcal {I}$
can be
$\mathcal {I}$
can be
![]() $*$
-destroyed: We either use Solecki’s characterisation and an ad hoc construction for a fixed analytic P-ideal, or consider the localization forcing (see below or [Reference Brendle and Yatabe6, Lemma 3.1]).
$*$
-destroyed: We either use Solecki’s characterisation and an ad hoc construction for a fixed analytic P-ideal, or consider the localization forcing (see below or [Reference Brendle and Yatabe6, Lemma 3.1]).
1.3 The role of the Katětov(–Blass) preorder
Probably the most well-known characterisation of (classical) forcing destructibility of ideals is via Katětov-reductions to trace ideals (see [Reference Brendle, Farkas and Verner9, Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui28]). If
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
are ideals on
$\mathcal {J}$
are ideals on
![]() $\omega $
, then
$\omega $
, then
![]() $\mathcal {I}$
is Katětov-below
$\mathcal {I}$
is Katětov-below
![]() $\mathcal {J}$
,
$\mathcal {J}$
,
If we restrict f to be finite-to-one in this definition, we obtain the Katětov–Blass-preorder,
![]() $\leq _{\mathrm {KB}}$
. These preorders play a fundamental role in characterising combinatorial properties of ideals (see, e.g., [Reference Hrušák and Zapletal22–Reference Hrušák and Minami26, Reference Kanovei and Reeken29, Reference Solecki39, Reference Zapletal43]). Let us point out here that if
$\leq _{\mathrm {KB}}$
. These preorders play a fundamental role in characterising combinatorial properties of ideals (see, e.g., [Reference Hrušák and Zapletal22–Reference Hrušák and Minami26, Reference Kanovei and Reeken29, Reference Solecki39, Reference Zapletal43]). Let us point out here that if
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
are Borel ideals, then the statement “
$\mathcal {J}$
are Borel ideals, then the statement “
![]() $\mathcal {I}\leq _{\mathrm {K(B)}}\mathcal {J}$
” is
$\mathcal {I}\leq _{\mathrm {K(B)}}\mathcal {J}$
” is
![]() ${\underset{\sim}{\Sigma}}{}^1_2$
and hence absolute between V and
${\underset{\sim}{\Sigma}}{}^1_2$
and hence absolute between V and
![]() $V^{\mathbb {P}}$
.
$V^{\mathbb {P}}$
.
Observation 1.1. If
![]() $\mathcal {I}\ne \mathrm {Fin}$
,
$\mathcal {I}\ne \mathrm {Fin}$
,
![]() $\mathcal {J}$
is a P-ideal, and
$\mathcal {J}$
is a P-ideal, and
![]() $\mathcal {I}\leq _{\mathrm {K}}\mathcal {J}$
, then
$\mathcal {I}\leq _{\mathrm {K}}\mathcal {J}$
, then
![]() $\mathcal {I}\leq _{\mathrm {KB}}\mathcal {J}$
holds as well.
$\mathcal {I}\leq _{\mathrm {KB}}\mathcal {J}$
holds as well.
Proof. Fix a K-reduction
![]() $f:\omega \to \omega $
(that is,
$f:\omega \to \omega $
(that is,
![]() $f^{-1}[A]\in \mathcal {J}$
for every
$f^{-1}[A]\in \mathcal {J}$
for every
![]() $A\in \mathcal {I}$
) which is not finite-to-one and a
$A\in \mathcal {I}$
) which is not finite-to-one and a
![]() $B\in \mathcal {J}$
such that
$B\in \mathcal {J}$
such that
![]() $f^{-1}[\{n\}]\subseteq ^* B$
for every n (in particular, B is infinite). Let
$f^{-1}[\{n\}]\subseteq ^* B$
for every n (in particular, B is infinite). Let
![]() $F_n=f^{-1}[\{n\}]\setminus B$
and fix an infinite element
$F_n=f^{-1}[\{n\}]\setminus B$
and fix an infinite element
![]() $A\in \mathcal {I}$
. Define
$A\in \mathcal {I}$
. Define
![]() $g:\omega \to \omega $
such that
$g:\omega \to \omega $
such that
![]() $g\!\upharpoonright \! F_n\equiv n$
for every n and
$g\!\upharpoonright \! F_n\equiv n$
for every n and
![]() $g\!\upharpoonright \! B$
is a bijection between B and A. Then g is a KB-reduction.⊣
$g\!\upharpoonright \! B$
is a bijection between B and A. Then g is a KB-reduction.⊣
For
![]() $A\subseteq \,\!^{<\omega }\ell $
where
$A\subseteq \,\!^{<\omega }\ell $
where
![]() $\ell =2$
or
$\ell =2$
or
![]() $\ell =\omega $
, define the
$\ell =\omega $
, define the
![]() $G_\delta $
-closure of A as
$G_\delta $
-closure of A as
and for any ideal I on
![]() $\,\!^\omega \ell $
define the trace of I, an ideal on
$\,\!^\omega \ell $
define the trace of I, an ideal on
![]() $\,\!^{<\omega }\ell $
, as follows:
$\,\!^{<\omega }\ell $
, as follows:
For example if
![]() $\mathrm {NWD}$
is the ideal of nowhere dense subsets of
$\mathrm {NWD}$
is the ideal of nowhere dense subsets of
![]() $\,\!^\omega 2$
, then
$\,\!^\omega 2$
, then
![]() $\mathrm {tr}(\mathrm {NWD})=\mathrm {tr}(\mathcal {M})=$
$\mathrm {tr}(\mathrm {NWD})=\mathrm {tr}(\mathcal {M})=$
where
![]() $t^\uparrow =\{t'\in \,\!^{<\omega } 2:t\subseteq t'\}$
. It is trivial to see that
$t^\uparrow =\{t'\in \,\!^{<\omega } 2:t\subseteq t'\}$
. It is trivial to see that
![]() $\mathbb {P}_I$
destroys
$\mathbb {P}_I$
destroys
![]() $\mathrm {tr}(I)$
: If
$\mathrm {tr}(I)$
: If
![]() $\mathring {r}_I\in \,\!^\omega \ell \cap V^{\mathbb {P}_I}$
is the
$\mathring {r}_I\in \,\!^\omega \ell \cap V^{\mathbb {P}_I}$
is the
![]() $\mathbb {P}_I$
-generic real over V,
$\mathbb {P}_I$
-generic real over V,
![]() $\mathring {R}=\{\mathring {r}_I\!\upharpoonright \! n:n\in \omega \}\in [\,\!^{<\omega }\ell ]^\omega \cap V^{\mathbb {P}_I}$
,
$\mathring {R}=\{\mathring {r}_I\!\upharpoonright \! n:n\in \omega \}\in [\,\!^{<\omega }\ell ]^\omega \cap V^{\mathbb {P}_I}$
,
![]() $B\in \mathbb {P}_I$
, and
$B\in \mathbb {P}_I$
, and
![]() $A\in \mathrm {tr}(I)$
, then
$A\in \mathrm {tr}(I)$
, then
![]() $B'=B\setminus [A]_\delta \in \mathbb {P}_I$
,
$B'=B\setminus [A]_\delta \in \mathbb {P}_I$
,
![]() $B'\leq B$
, and
$B'\leq B$
, and
![]() $B'\Vdash |A\cap \mathring {R}|<\omega $
.
$B'\Vdash |A\cap \mathring {R}|<\omega $
.
Theorem 1.2 (see [Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui28, Theorem 1.6]).
Let I be a
![]() $\sigma $
-ideal on
$\sigma $
-ideal on
![]() $\,\!^\omega \ell $
such that
$\,\!^\omega \ell $
such that
![]() $\mathbb {P}_I$
is proper and I satisfies the continuous readings of names (CRN, see below), and let
$\mathbb {P}_I$
is proper and I satisfies the continuous readings of names (CRN, see below), and let
![]() $\mathcal {J}$
be an ideal on
$\mathcal {J}$
be an ideal on
![]() $\omega $
. Then
$\omega $
. Then
![]() $\mathbb {P}_I$
can destroy
$\mathbb {P}_I$
can destroy
![]() $\mathcal {J}$
if, and only if,
$\mathcal {J}$
if, and only if,
![]() $\mathcal {J}\leq _{\mathrm {K}}\mathrm {tr}(I)\!\upharpoonright \! X$
for some
$\mathcal {J}\leq _{\mathrm {K}}\mathrm {tr}(I)\!\upharpoonright \! X$
for some
![]() $X\in \mathrm {tr}(I)^+$
.
$X\in \mathrm {tr}(I)^+$
.
The paper is organised as follows: In Section 2, we present many classical Borel ideals, as well as the characterisations of
![]() $F_\sigma $
ideals and of analytic P-ideals (due to Mazur and Solecki). In Section 3, we give a detailed introduction to the notions of destructibility of ideals and to the associated cardinal invariants, and also we present a combinatorial characterisation of forcing (in)destructibility by proper real forcing notions. In Section 4, we discuss our examples of non P-ideals from Section 2 in the context of
$F_\sigma $
ideals and of analytic P-ideals (due to Mazur and Solecki). In Section 3, we give a detailed introduction to the notions of destructibility of ideals and to the associated cardinal invariants, and also we present a combinatorial characterisation of forcing (in)destructibility by proper real forcing notions. In Section 4, we discuss our examples of non P-ideals from Section 2 in the context of
![]() $+$
-destructibility and the new cardinal invariants. In Section 5, applying Laflamme’s filter games and his results, we characterise when the Mathias–Prikry and Laver–Prikry generic reals, and in the case of the first one, the forcing notion in general,
$+$
-destructibility and the new cardinal invariants. In Section 5, applying Laflamme’s filter games and his results, we characterise when the Mathias–Prikry and Laver–Prikry generic reals, and in the case of the first one, the forcing notion in general,
![]() $+$
-destroy the defining ideal. In Section 6, we characterise when exactly the Laver–Prikry forcing
$+$
-destroy the defining ideal. In Section 6, we characterise when exactly the Laver–Prikry forcing
![]() $+$
-destroys the defining P-ideal. In Section 7, we present a survey on
$+$
-destroys the defining P-ideal. In Section 7, we present a survey on
![]() $*$
-destructibility and its connection to the null ideal. Finally, in Section 8, we list all our remaining open questions.
$*$
-destructibility and its connection to the null ideal. Finally, in Section 8, we list all our remaining open questions.
2 Borel ideals
We present some additional classical examples of Borel ideals (for their specific roles in characterisation results see, e.g., [Reference Hrušák and Zapletal22] or [Reference Hrušák, Meza-Alcántara and Minami23], and also find more citations below). We already defined
![]() $\mathcal {I}_{1/n}$
,
$\mathcal {I}_{1/n}$
,
![]() $\mathrm {Nwd}$
,
$\mathrm {Nwd}$
,
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
, and
$\mathrm {Fin}\otimes \mathrm {Fin}$
, and
![]() $\{\varnothing \}\otimes \mathrm {Fin}$
.
$\{\varnothing \}\otimes \mathrm {Fin}$
.
Summable ideals (a.k.a. generalisations of
![]() $\mathcal {I}_{1/n}$
): Let
$\mathcal {I}_{1/n}$
): Let
![]() $h:\omega \to [0,\infty )$
such that
$h:\omega \to [0,\infty )$
such that
![]() $\sum _{n\in \omega } h(n)=\infty $
. Then the summable ideal generated by h is
$\sum _{n\in \omega } h(n)=\infty $
. Then the summable ideal generated by h is
 $$ \begin{align*} \mathcal{I}_h=\bigg\{A\subseteq\omega:\sum_{n\in A} h(n)<\infty\bigg\}.\end{align*} $$
$$ \begin{align*} \mathcal{I}_h=\bigg\{A\subseteq\omega:\sum_{n\in A} h(n)<\infty\bigg\}.\end{align*} $$
![]() $\mathcal {I}_h$
is an
$\mathcal {I}_h$
is an
![]() $F_\sigma $
P-ideal, and it is tall iff
$F_\sigma $
P-ideal, and it is tall iff
![]() $\lim _{n\to \infty }h(n)=0$
.
$\lim _{n\to \infty }h(n)=0$
.
Eventually different ideals: Let
![]() $\Delta =\{(n,k)\in \omega \times \omega :k\leq n\}$
, and
$\Delta =\{(n,k)\in \omega \times \omega :k\leq n\}$
, and
![]() $\mathcal {ED}_{\mathrm {fin}}=\mathcal {ED}\!\upharpoonright \! \Delta $
. Then
$\mathcal {ED}_{\mathrm {fin}}=\mathcal {ED}\!\upharpoonright \! \Delta $
. Then
![]() $\mathcal {ED}$
and
$\mathcal {ED}$
and
![]() $\mathcal {ED}_{\mathrm {fin}}$
are tall
$\mathcal {ED}_{\mathrm {fin}}$
are tall
![]() $F_\sigma $
non P-ideals.
$F_\sigma $
non P-ideals.
The random graph ideal: Let
where the random graph
![]() $(\omega ,E)$
,
$(\omega ,E)$
,
![]() $E\subseteq [\omega ]^2$
is up to isomorphism uniquely determined by the following property: For every pair
$E\subseteq [\omega ]^2$
is up to isomorphism uniquely determined by the following property: For every pair
![]() $A,B\subseteq \omega $
of nonempty, finite, disjoint sets, there is an
$A,B\subseteq \omega $
of nonempty, finite, disjoint sets, there is an
![]() $n\in \omega \setminus (A\cup B)$
such that
$n\in \omega \setminus (A\cup B)$
such that
![]() $\{\{n,a\}:a\in A\}\subseteq E$
and
$\{\{n,a\}:a\in A\}\subseteq E$
and
![]() $\{\{n,b\}:b\in B\}\cap E=\varnothing $
. A set
$\{\{n,b\}:b\in B\}\cap E=\varnothing $
. A set
![]() $H\subseteq \omega $
is (E-)homogeneous iff
$H\subseteq \omega $
is (E-)homogeneous iff
![]() $[H]^2\subseteq E$
or
$[H]^2\subseteq E$
or
![]() $[H]^2\cap E=\varnothing $
; and
$[H]^2\cap E=\varnothing $
; and
![]() $\mathrm {id}(\mathcal {H})$
stands for the ideal generated by
$\mathrm {id}(\mathcal {H})$
stands for the ideal generated by
![]() $\mathcal {H}$
(that is, the collection of all subsets of
$\mathcal {H}$
(that is, the collection of all subsets of
![]() $\bigcup \mathcal {H}$
which can be covered by finitely many elements of
$\bigcup \mathcal {H}$
which can be covered by finitely many elements of
![]() $\mathcal {H}$
, and of course in general
$\mathcal {H}$
, and of course in general
![]() $\mathrm {id}(\mathcal {H})$
is not necessarily proper).
$\mathrm {id}(\mathcal {H})$
is not necessarily proper).
![]() $\mathrm {Ran}$
is a tall
$\mathrm {Ran}$
is a tall
![]() $F_\sigma $
non P-ideal.
$F_\sigma $
non P-ideal.
Solecki’s ideal (see [Reference Hrušák24, Reference Kanovei and Reeken29, Reference Solecki39]): Let
![]() $\mathrm {CO}(\,\!^\omega 2)$
be the family of clopen subsets of
$\mathrm {CO}(\,\!^\omega 2)$
be the family of clopen subsets of
![]() $\,\!^\omega 2$
and
$\,\!^\omega 2$
and
![]() $\Omega =\{C\in \mathrm {CO}(\,\!^\omega 2):\lambda (C)=1/2\}$
where
$\Omega =\{C\in \mathrm {CO}(\,\!^\omega 2):\lambda (C)=1/2\}$
where
![]() $\lambda $
is the Lebesgue-measure on
$\lambda $
is the Lebesgue-measure on
![]() $\,\!^\omega 2$
(clearly, C is clopen iff C is a union of finitely many basic clopen sets, and hence
$\,\!^\omega 2$
(clearly, C is clopen iff C is a union of finitely many basic clopen sets, and hence
![]() $|\mathrm {CO}(\,\!^\omega 2)|=|\Omega |=\omega $
). The ideal
$|\mathrm {CO}(\,\!^\omega 2)|=|\Omega |=\omega $
). The ideal
![]() $\mathcal {S}$
on
$\mathcal {S}$
on
![]() $\Omega $
is generated by
$\Omega $
is generated by
![]() $\{\mathcal {C}_x:x\in \,\!^\omega 2\}$
where
$\{\mathcal {C}_x:x\in \,\!^\omega 2\}$
where
![]() $\mathcal {C}_x=\{C\in \Omega :x\in C\}$
.
$\mathcal {C}_x=\{C\in \Omega :x\in C\}$
.
![]() $\mathcal {S}$
is a tall
$\mathcal {S}$
is a tall
![]() $F_\sigma $
non P-ideal.
$F_\sigma $
non P-ideal.
Density and generalised density ideals. Let
![]() $(P_n)_{n\in \omega }$
be a partition of
$(P_n)_{n\in \omega }$
be a partition of
![]() $\omega $
into nonempty finite sets and let
$\omega $
into nonempty finite sets and let
![]() $\vec {\vartheta }=(\vartheta _n)_{n\in \omega }$
be a sequences of measures or submeasures (in the generalised case, see the definition below),
$\vec {\vartheta }=(\vartheta _n)_{n\in \omega }$
be a sequences of measures or submeasures (in the generalised case, see the definition below),
![]() $\vartheta _n:\mathcal {P}(P_n)\to [0,\infty )$
such that
$\vartheta _n:\mathcal {P}(P_n)\to [0,\infty )$
such that
![]() $\limsup _{n\to \infty }\vartheta _n(P_n)>0$
. The (generalised) density ideal generated by
$\limsup _{n\to \infty }\vartheta _n(P_n)>0$
. The (generalised) density ideal generated by
![]() $\vec {\vartheta }$
is
$\vec {\vartheta }$
is
Ideals of this form are
![]() $F_{\sigma \delta }$
P-ideals, and the ideal
$F_{\sigma \delta }$
P-ideals, and the ideal
![]() $\mathcal {Z}_{\vec {\vartheta }}$
is tall iff
$\mathcal {Z}_{\vec {\vartheta }}$
is tall iff
![]() $\max \{\vartheta _n(\{k\}):k\in P_n\}\xrightarrow {n\to \infty }0$
. The density zero ideal
$\max \{\vartheta _n(\{k\}):k\in P_n\}\xrightarrow {n\to \infty }0$
. The density zero ideal
 $$ \begin{align*} \mathcal{Z}=\big\{A\subseteq\omega\setminus\{0\}:|A\cap n|/n\to 0\big\}=\bigg\{A\subseteq\omega\setminus\{0\}:\frac{|A\cap [2^n,2^{n+1})|}{2^n}\to 0\bigg\}\end{align*} $$
$$ \begin{align*} \mathcal{Z}=\big\{A\subseteq\omega\setminus\{0\}:|A\cap n|/n\to 0\big\}=\bigg\{A\subseteq\omega\setminus\{0\}:\frac{|A\cap [2^n,2^{n+1})|}{2^n}\to 0\bigg\}\end{align*} $$
is a tall density ideal. It is easy to see that
![]() $\mathcal {I}_{1/n}\subsetneq \mathcal {Z}$
. Also, it is straightforward to check that
$\mathcal {I}_{1/n}\subsetneq \mathcal {Z}$
. Also, it is straightforward to check that
![]() $\{\varnothing \}\otimes \mathrm {Fin}$
is a density ideal.
$\{\varnothing \}\otimes \mathrm {Fin}$
is a density ideal.
The trace ideal of the null ideal:
is a tall
![]() $F_{\sigma \delta }$
P-ideal (but in general, trace ideals can be very complex, see [Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui28, Proposition 5.1]).
$F_{\sigma \delta }$
P-ideal (but in general, trace ideals can be very complex, see [Reference Hrušák, Meza-Alcántara, Thümmel and Uzcátegui28, Proposition 5.1]).
The ideal
![]() $\mathrm {Conv}$
is generated by those infinite subsets of
$\mathrm {Conv}$
is generated by those infinite subsets of
![]() $\mathbb {Q}\cap [0,1]$
which are convergent in
$\mathbb {Q}\cap [0,1]$
which are convergent in
![]() $[0,1]$
, in other words
$[0,1]$
, in other words
This ideal is a tall,
![]() $F_{\sigma \delta \sigma }$
, non P-ideal.
$F_{\sigma \delta \sigma }$
, non P-ideal.
It is easy to see that there are no
![]() $G_\delta $
(i.e.,
$G_\delta $
(i.e.,
![]() ${\underset{\sim}{\Pi}}{}^0_2$
) ideals, and we know that there are many
${\underset{\sim}{\Pi}}{}^0_2$
) ideals, and we know that there are many
![]() $F_\sigma $
(i.e.,
$F_\sigma $
(i.e.,
![]() ${\underset{\sim}{\Sigma}}{}^0_2$
) ideals. In general, we know (see [Reference Calbrix10, Reference Calbrix11]) that there are
${\underset{\sim}{\Sigma}}{}^0_2$
) ideals. In general, we know (see [Reference Calbrix10, Reference Calbrix11]) that there are
![]() ${\underset{\sim}{\Sigma}}{}^0_\alpha $
- and
${\underset{\sim}{\Sigma}}{}^0_\alpha $
- and
![]() ${\underset{\sim}{\Pi}}{}^0_\alpha $
-complete ideals for every
${\underset{\sim}{\Pi}}{}^0_\alpha $
-complete ideals for every
![]() $\alpha \geq 3$
. About ideals on the ambiguous levels of the Borel hierarchy see [Reference van Engelen16]. For projective examples, see [Reference Farkas and Soukup17].
$\alpha \geq 3$
. About ideals on the ambiguous levels of the Borel hierarchy see [Reference van Engelen16]. For projective examples, see [Reference Farkas and Soukup17].
Katětov and Katětov–Blass reducibilities between our main examples have been extensively studied (see, e.g., [Reference Brendle and Yatabe6, Reference Brendle and Hrušák7, Reference Hrušák, Meza-Alcántara and Minami23]), and apart from the very few unknown reducibilities (e.g., the still open
![]() $\mathrm {Ran}\leq _{\mathrm {K(B)}}\mathcal {S}$
), we are provided with a quite satisfying “map” of Katětov-reducibilities between our main examples. Moreover, all these reductions can be chosen as finite-to-one (i.e., as KB-reductions), and in almost all cases, if we know that there is no KB-reduction then there is no K-reduction either between these examples.
$\mathrm {Ran}\leq _{\mathrm {K(B)}}\mathcal {S}$
), we are provided with a quite satisfying “map” of Katětov-reducibilities between our main examples. Moreover, all these reductions can be chosen as finite-to-one (i.e., as KB-reductions), and in almost all cases, if we know that there is no KB-reduction then there is no K-reduction either between these examples.
2.1
 $F_{\sigma} $
ideals and analytic
$F_{\sigma} $
ideals and analytic
 $\mathrm{P} $
-ideals
$\mathrm{P} $
-ideals
There is a natural way of defining nice ideals on
![]() $\omega $
from submeasures. A function
$\omega $
from submeasures. A function
![]() $\varphi :\mathcal {P}({\omega })\to [0,\infty ]$
is a submeasure on
$\varphi :\mathcal {P}({\omega })\to [0,\infty ]$
is a submeasure on
![]() $\omega $
if
$\omega $
if
![]() $\varphi (\varnothing )=0$
;
$\varphi (\varnothing )=0$
;
![]() ${\varphi }(X)\le \varphi (X\cup Y)\le \varphi (X)+\varphi (Y)$
for every
${\varphi }(X)\le \varphi (X\cup Y)\le \varphi (X)+\varphi (Y)$
for every
![]() $X,Y\subseteq \omega $
; and
$X,Y\subseteq \omega $
; and
![]() $\varphi (\{n\})<\infty $
for every
$\varphi (\{n\})<\infty $
for every
![]() $n\in {\omega }$
.
$n\in {\omega }$
.
![]() $\varphi $
is lower semicontinuous (lsc, for short) if
$\varphi $
is lower semicontinuous (lsc, for short) if
![]() $\varphi (X)=\sup \{\varphi (X\cap n):n\in \omega \}$
for each
$\varphi (X)=\sup \{\varphi (X\cap n):n\in \omega \}$
for each
![]() $X\subseteq \omega $
.
$X\subseteq \omega $
.
If
![]() $\varphi $
is an lsc submeasure on
$\varphi $
is an lsc submeasure on
![]() $\omega $
then for
$\omega $
then for
![]() $X\subseteq \omega $
let
$X\subseteq \omega $
let
![]() $\|X\|_\varphi =\lim _{n\to \infty }\varphi (X\setminus n)$
. We assign two ideals to a submeasure
$\|X\|_\varphi =\lim _{n\to \infty }\varphi (X\setminus n)$
. We assign two ideals to a submeasure
![]() $\varphi $
as follows:
$\varphi $
as follows:
 $$ \begin{align*} \mathrm{Fin}(\varphi) & = \big\{X\subseteq\omega:\varphi(X)<\infty\big\},\\ \mathrm{Exh}(\varphi) & = \big\{X\subseteq {\omega}:\|X\|_\varphi=0\big\}. \end{align*} $$
$$ \begin{align*} \mathrm{Fin}(\varphi) & = \big\{X\subseteq\omega:\varphi(X)<\infty\big\},\\ \mathrm{Exh}(\varphi) & = \big\{X\subseteq {\omega}:\|X\|_\varphi=0\big\}. \end{align*} $$
It is easy to see that if
![]() $\mathrm {Fin}(\varphi )\ne \mathcal {P}(\omega )$
, then it is an
$\mathrm {Fin}(\varphi )\ne \mathcal {P}(\omega )$
, then it is an
![]() $F_\sigma $
ideal; and similarly if
$F_\sigma $
ideal; and similarly if
![]() $\mathrm {Exh}(\varphi )\ne \mathcal {P}(\omega )$
, then it is an
$\mathrm {Exh}(\varphi )\ne \mathcal {P}(\omega )$
, then it is an
![]() $F_{\sigma \delta }$
P-ideal. Clearly,
$F_{\sigma \delta }$
P-ideal. Clearly,
![]() $\mathcal {I}_{\varphi (\{\cdot \})}\subseteq \mathrm {Exh}(\varphi )\subseteq \mathrm {Fin}(\varphi )$
always holds where
$\mathcal {I}_{\varphi (\{\cdot \})}\subseteq \mathrm {Exh}(\varphi )\subseteq \mathrm {Fin}(\varphi )$
always holds where
![]() $\mathcal {I}_{\varphi (\{\cdot \})}$
stands for the summable ideal generated by the sequence
$\mathcal {I}_{\varphi (\{\cdot \})}$
stands for the summable ideal generated by the sequence
![]() $(\varphi (\{n\}))_{n\in \omega }$
. From now on, when working with
$(\varphi (\{n\}))_{n\in \omega }$
. From now on, when working with
![]() $\mathrm {Fin}(\varphi )$
or
$\mathrm {Fin}(\varphi )$
or
![]() $\mathrm {Exh}(\varphi )$
, we will always assume that they are proper ideals. It is straightforward to see that if
$\mathrm {Exh}(\varphi )$
, we will always assume that they are proper ideals. It is straightforward to see that if
![]() $\varphi $
is an lsc submeasure on
$\varphi $
is an lsc submeasure on
![]() $\omega $
then
$\omega $
then
![]() $\mathrm {Exh}(\varphi )$
is tall iff
$\mathrm {Exh}(\varphi )$
is tall iff
![]() $\lim _{n\to \infty }\varphi (\{n\})=0$
.
$\lim _{n\to \infty }\varphi (\{n\})=0$
.
Example 2.1. If
![]() $\mathcal {I}_h$
is a summable ideal then
$\mathcal {I}_h$
is a summable ideal then
![]() $\mathcal {I}_h=\mathrm {Fin}(\varphi _h)=\mathrm {Exh}(\varphi _h)$
where
$\mathcal {I}_h=\mathrm {Fin}(\varphi _h)=\mathrm {Exh}(\varphi _h)$
where
![]() $\varphi _h(A)=\sum _{n\in A}h(n)$
; if
$\varphi _h(A)=\sum _{n\in A}h(n)$
; if
![]() $\mathcal {Z}_{\vec \vartheta }$
is a generalised density ideal, then
$\mathcal {Z}_{\vec \vartheta }$
is a generalised density ideal, then
![]() $\mathcal {Z}_{\vec \vartheta }=\mathrm {Exh}(\varphi _{\vec \vartheta })$
where
$\mathcal {Z}_{\vec \vartheta }=\mathrm {Exh}(\varphi _{\vec \vartheta })$
where
![]() $\varphi _{\vec \vartheta }(A)=\sup \{\vartheta _n(A\cap P_n):n\in \omega \}$
; and finally
$\varphi _{\vec \vartheta }(A)=\sup \{\vartheta _n(A\cap P_n):n\in \omega \}$
; and finally
![]() $\mathrm {tr}(\mathcal {N})=\mathrm {Exh}(\psi )$
where
$\mathrm {tr}(\mathcal {N})=\mathrm {Exh}(\psi )$
where
![]() $\psi (A)=\sum \{2^{-|s|}:s\in A$
is
$\psi (A)=\sum \{2^{-|s|}:s\in A$
is
![]() $\subseteq $
-minimal in
$\subseteq $
-minimal in
![]() $A\}$
(and of course,
$A\}$
(and of course,
![]() $\varphi _h$
,
$\varphi _h$
,
![]() $\varphi _{\vec \vartheta }$
, and
$\varphi _{\vec \vartheta }$
, and
![]() $\psi $
are lsc submeasures).
$\psi $
are lsc submeasures).
The following characterisation theorem gives us the most important tool when working on combinatorics of
![]() $F_\sigma $
ideals and analytic P-ideals.
$F_\sigma $
ideals and analytic P-ideals.
Theorem 2.2 [Reference Mazur36, Reference Solecki38].
Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
.
$\omega $
.
-
•
 $\mathcal {I}$
is an
$\mathcal {I}$
is an
 $F_\sigma $
ideal iff
$F_\sigma $
ideal iff
 $\mathcal {I}=\mathrm {Fin}(\varphi )$
for some lsc submeasure
$\mathcal {I}=\mathrm {Fin}(\varphi )$
for some lsc submeasure
 $\varphi $
.
$\varphi $
. -
•
 $\mathcal {I}$
is an analytic P-ideal iff
$\mathcal {I}$
is an analytic P-ideal iff
 $\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lsc submeasure
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lsc submeasure
 $\varphi $
.
$\varphi $
. -
•
 $\mathcal {I}$
is an
$\mathcal {I}$
is an
 $F_\sigma $
P-ideal iff
$F_\sigma $
P-ideal iff
 $\mathcal {I}=\mathrm {Fin}(\varphi )=\mathrm {Exh}(\varphi )$
for some lsc submeasure
$\mathcal {I}=\mathrm {Fin}(\varphi )=\mathrm {Exh}(\varphi )$
for some lsc submeasure
 $\varphi $
.
$\varphi $
.
In particular, analytic P-ideals are
![]() $F_{\sigma \delta }$
. When working with
$F_{\sigma \delta }$
. When working with
![]() $\mathrm {Exh}(\varphi )$
, we can always assume that
$\mathrm {Exh}(\varphi )$
, we can always assume that
![]() $\varphi (\{n\})>0$
for every n, and that
$\varphi (\{n\})>0$
for every n, and that
![]() $\varphi (\omega )=\|\omega \|_\varphi =1$
: Let
$\varphi (\omega )=\|\omega \|_\varphi =1$
: Let
![]() $\varphi _0(A)=\varphi (A)+\sum _{n\in A}2^{-n}$
,
$\varphi _0(A)=\varphi (A)+\sum _{n\in A}2^{-n}$
,
![]() $\varphi _1(A)=\min (\varphi _0(A),1)$
,
$\varphi _1(A)=\min (\varphi _0(A),1)$
,
![]() $\varphi _2(A)=\varphi _1(A)/\|\omega \|_{\varphi _1}$
, and
$\varphi _2(A)=\varphi _1(A)/\|\omega \|_{\varphi _1}$
, and
![]() $\varphi _3(A)=\min (\varphi _2(A),1)$
, then
$\varphi _3(A)=\min (\varphi _2(A),1)$
, then
![]() $\mathrm {Exh}(\varphi _i)=\mathrm {Exh}(\varphi )$
for
$\mathrm {Exh}(\varphi _i)=\mathrm {Exh}(\varphi )$
for
![]() $i=0,1,2,3$
and
$i=0,1,2,3$
and
![]() $\varphi _3(\omega )=\|\omega \|_{\varphi _3}=1$
.
$\varphi _3(\omega )=\|\omega \|_{\varphi _3}=1$
.
As promised, we give an easy characterisation of nowhere tall analytic P-ideals:
Fact 2.3. Assume that
![]() $\mathcal {I}$
is a nowhere tall analytic P-ideal. Then
$\mathcal {I}$
is a nowhere tall analytic P-ideal. Then
![]() $\mathcal {I}$
is a trivial modification of
$\mathcal {I}$
is a trivial modification of
![]() $\mathrm {Fin}$
or
$\mathrm {Fin}$
or
![]() $\mathcal {I}\simeq \{\varnothing \}\otimes \mathrm {Fin}$
.
$\mathcal {I}\simeq \{\varnothing \}\otimes \mathrm {Fin}$
.
Proof. Let
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lsc submeasure
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lsc submeasure
![]() $\varphi $
. First we show that
$\varphi $
. First we show that
![]() $\mathcal {I}$
is nowhere tall iff
$\mathcal {I}$
is nowhere tall iff
![]() $\mathcal {I}=\mathcal {I}':=\{A\subseteq \omega :A$
is finite or
$\mathcal {I}=\mathcal {I}':=\{A\subseteq \omega :A$
is finite or
![]() $\lim _{n\in A}\varphi (\{n\})=0\}$
.
$\lim _{n\in A}\varphi (\{n\})=0\}$
.
First assume that
![]() $\mathcal {I}$
is nowhere tall. As
$\mathcal {I}$
is nowhere tall. As
![]() $\mathcal {I}\subseteq \mathcal {I}'$
always holds, we show that if
$\mathcal {I}\subseteq \mathcal {I}'$
always holds, we show that if
![]() $A\in \mathcal {I}'$
then
$A\in \mathcal {I}'$
then
![]() $A\in \mathcal {I}$
. Assume on the contrary that
$A\in \mathcal {I}$
. Assume on the contrary that
![]() $A\notin \mathcal {I}$
. Then there is an infinite
$A\notin \mathcal {I}$
. Then there is an infinite
![]() $A'\subseteq A$
such that
$A'\subseteq A$
such that
![]() $\mathcal {I}\!\upharpoonright \! A'=[A']^{<\omega }$
. If
$\mathcal {I}\!\upharpoonright \! A'=[A']^{<\omega }$
. If
![]() $B=\{b_0<b_1<b_2<\cdots \}\subseteq A'$
such that
$B=\{b_0<b_1<b_2<\cdots \}\subseteq A'$
such that
![]() $\varphi (\{b_n\})<2^{-n}$
for every n, then
$\varphi (\{b_n\})<2^{-n}$
for every n, then
![]() $B\in \mathcal {I}$
, a contradiction. Conversely, assume now that
$B\in \mathcal {I}$
, a contradiction. Conversely, assume now that
![]() $\mathcal {I}=\mathcal {I}'$
, and let
$\mathcal {I}=\mathcal {I}'$
, and let
![]() $X\in \mathcal {I}^+$
. If
$X\in \mathcal {I}^+$
. If
![]() $Y\subseteq X$
is infinite and
$Y\subseteq X$
is infinite and
![]() $\inf \{\varphi (\{k\}):k\in Y\}>0$
then
$\inf \{\varphi (\{k\}):k\in Y\}>0$
then
![]() $\mathcal {I}\!\upharpoonright \! Y=[Y]^{<\omega }$
and hence
$\mathcal {I}\!\upharpoonright \! Y=[Y]^{<\omega }$
and hence
![]() $\mathcal {I}\!\upharpoonright \! X$
is not tall.
$\mathcal {I}\!\upharpoonright \! X$
is not tall.
Therefore, if
![]() $\mathcal {I}$
is a nowhere tall analytic P-ideal, then there is a sequence
$\mathcal {I}$
is a nowhere tall analytic P-ideal, then there is a sequence
![]() $x_n>0$
such that
$x_n>0$
such that
![]() $\mathcal {I}=\{A\subseteq \omega :A$
is finite or
$\mathcal {I}=\{A\subseteq \omega :A$
is finite or
![]() $\lim _{n\in A}x_n=0\}$
. By slightly perturbing
$\lim _{n\in A}x_n=0\}$
. By slightly perturbing
![]() $x_n$
, we can assume that
$x_n$
, we can assume that
![]() $x_n\ne x_m$
for every
$x_n\ne x_m$
for every
![]() $n\ne m$
. Let
$n\ne m$
. Let
![]() $X=\{x_n:n\in \omega \}$
,
$X=\{x_n:n\in \omega \}$
,
![]() $X'$
be set of accumulation points of X, and
$X'$
be set of accumulation points of X, and
![]() $X"=(X')'$
; we know that
$X"=(X')'$
; we know that
![]() $X'\supseteq X"$
are closed. We have the following three cases: (1)
$X'\supseteq X"$
are closed. We have the following three cases: (1)
![]() $0\notin X'$
. Then
$0\notin X'$
. Then
![]() $\mathcal {I}=\mathrm {Fin}$
. (2)
$\mathcal {I}=\mathrm {Fin}$
. (2)
![]() $0\in X'\setminus X"$
. Let
$0\in X'\setminus X"$
. Let
![]() $y=\min (X'\setminus \{0\})>0$
. Now
$y=\min (X'\setminus \{0\})>0$
. Now
![]() $A\subseteq \omega $
belongs to
$A\subseteq \omega $
belongs to
![]() $\mathcal {I}$
iff
$\mathcal {I}$
iff
![]() $|A\cap \{n:x_n\geq y\}|<\omega $
, hence
$|A\cap \{n:x_n\geq y\}|<\omega $
, hence
![]() $\mathcal {I}$
is a trivial modification of
$\mathcal {I}$
is a trivial modification of
![]() $\mathrm {Fin}$
. (3)
$\mathrm {Fin}$
. (3)
![]() $0\in X"$
. Fix a sequence
$0\in X"$
. Fix a sequence
![]() $y_0=\infty>y_1>y_2\dots $
tending to
$y_0=\infty>y_1>y_2\dots $
tending to
![]() $0$
such that each
$0$
such that each
![]() $[y_{k+1},y_k)$
contains infinitely many
$[y_{k+1},y_k)$
contains infinitely many
![]() $x_n$
, and let
$x_n$
, and let
![]() $P_k=\{n:x_n\in [y_{k+1},y_k)\}$
. Then
$P_k=\{n:x_n\in [y_{k+1},y_k)\}$
. Then
![]() $A\in \mathcal {I}$
iff
$A\in \mathcal {I}$
iff
![]() $A\cap P_k$
is finite for every k, and hence
$A\cap P_k$
is finite for every k, and hence
![]() $\mathcal {I}\simeq \{\varnothing \}\otimes \mathrm {Fin}$
.⊣
$\mathcal {I}\simeq \{\varnothing \}\otimes \mathrm {Fin}$
.⊣
3 Degrees of destruction
Starting with the usual forcing destructibility of ideals, we define three notions of destroying ideals in forcing extensions:
Definition 3.1. Let
![]() $\mathcal {I}$
be an analytic or coanalytic ideal on
$\mathcal {I}$
be an analytic or coanalytic ideal on
![]() $\omega $
,
$\omega $
,
![]() $\mathcal {D}=[\omega ]^\omega ,\mathcal {I}^+$
, or
$\mathcal {D}=[\omega ]^\omega ,\mathcal {I}^+$
, or
![]() $\mathcal {I}^*$
, and let
$\mathcal {I}^*$
, and let
![]() $\mathbb {P}$
be a forcing notion. We say that
$\mathbb {P}$
be a forcing notion. We say that
![]() $\mathbb {P}$
can
$\mathbb {P}$
can
![]() $\mathcal {D}$
-destroy
$\mathcal {D}$
-destroy
![]() $\mathcal {I}$
if there is a
$\mathcal {I}$
if there is a
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\exists\ Y\in \mathcal {D}\ \forall\ A\in \mathcal {I}^V |X\cap A|<\omega $
.” Mostly we will write (
$\exists\ Y\in \mathcal {D}\ \forall\ A\in \mathcal {I}^V |X\cap A|<\omega $
.” Mostly we will write (
![]() $\infty $
-)destroy,
$\infty $
-)destroy,
![]() $+$
-destroy, and
$+$
-destroy, and
![]() $*$
-destroy instead of
$*$
-destroy instead of
![]() $[\omega ]^\omega /\mathcal {I}^+/\mathcal {I}^*$
-destroy.
$[\omega ]^\omega /\mathcal {I}^+/\mathcal {I}^*$
-destroy.
Clearly,
![]() $*$
-destruction implies
$*$
-destruction implies
![]() $+$
-destruction which implies
$+$
-destruction which implies
![]() $\infty $
-destruction. All these notions can be reformulated with pseudounions:
$\infty $
-destruction. All these notions can be reformulated with pseudounions:
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {I}$
if it adds a pseudounion of
$\mathcal {I}$
if it adds a pseudounion of
![]() $\mathcal {I}\cap V$
with infinite complement, it
$\mathcal {I}\cap V$
with infinite complement, it
![]() $+$
-destroys
$+$
-destroys
![]() $\mathcal {I}$
if it adds a pseudounion of
$\mathcal {I}$
if it adds a pseudounion of
![]() $\mathcal {I}\cap V$
with
$\mathcal {I}\cap V$
with
![]() $\mathcal {I}$
-positive complement, and
$\mathcal {I}$
-positive complement, and
![]() $\mathbb {P}\ *$
-destroys
$\mathbb {P}\ *$
-destroys
![]() $\mathcal {I}$
if it adds a pseudounion of
$\mathcal {I}$
if it adds a pseudounion of
![]() $\mathcal {I}\cap V$
with complement in
$\mathcal {I}\cap V$
with complement in
![]() $\mathcal {I}^*$
, i.e., a pseudounion which belongs to
$\mathcal {I}^*$
, i.e., a pseudounion which belongs to
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Our main goals is to deepen our understanding of
![]() $\infty /+/*$
-destructibility of Borel ideals, in particular, to characterise which ideals a fixed “nice” forcing notion
$\infty /+/*$
-destructibility of Borel ideals, in particular, to characterise which ideals a fixed “nice” forcing notion
![]() $\mathbb {P}$
can
$\mathbb {P}$
can
![]() $\infty /+/*$
-destroy and to study the associated cardinal invariants of these ideals.
$\infty /+/*$
-destroy and to study the associated cardinal invariants of these ideals.
Let us take a look at forcing (in)destructibility in the context of cardinal invariants.
Definition 3.2. Let I be an ideal on X, then its additivity, cofinality, uniformity, and covering numbers are the following cardinals:
 $$ \begin{align*} \mathrm{add}(I) & = \min\big\{|J|:J\subseteq I\;\text{and}\;\bigcup J\notin I\big\},\\ \mathrm{cof}(I) & = \min\big\{|D|:D\;\text{is cofinal in}\;(I,\subseteq)\big\},\\ \mathrm{non}(I) & = \min\big\{|Y|:Y\subseteq X\;\text{and}\;Y\notin I\big\}, \text{and}\\ \mathrm{cov}(I) & = \min\big\{|C|:C\subseteq I\;\text{and}\;\bigcup C=X\big\}. \end{align*} $$
$$ \begin{align*} \mathrm{add}(I) & = \min\big\{|J|:J\subseteq I\;\text{and}\;\bigcup J\notin I\big\},\\ \mathrm{cof}(I) & = \min\big\{|D|:D\;\text{is cofinal in}\;(I,\subseteq)\big\},\\ \mathrm{non}(I) & = \min\big\{|Y|:Y\subseteq X\;\text{and}\;Y\notin I\big\}, \text{and}\\ \mathrm{cov}(I) & = \min\big\{|C|:C\subseteq I\;\text{and}\;\bigcup C=X\big\}. \end{align*} $$
In the case of ideals on countable underlying sets, most of these invariants equal
![]() $\omega $
. In [Reference Hernández-Hernández and Hrušák21], for tall ideals on
$\omega $
. In [Reference Hernández-Hernández and Hrušák21], for tall ideals on
![]() $\omega $
the following cardinal invariants were introduced:
$\omega $
the following cardinal invariants were introduced:
 $$ \begin{align*} \mathrm{add}^*(\mathcal{I})&= \min\big\{|\mathcal{U}|:\mathcal{U}\;\text{is unbounded in}\;(\mathcal{I},\subseteq^*)\big\},\\ \mathrm{cof}^*(\mathcal{I}) & = \min\big\{|\mathcal{D}|:\mathcal{D}\;\text{is cofinal in}\;(\mathcal{I},\subseteq^*)\big\},\\ \mathrm{non}^*(\mathcal{I}) & = \min\big\{|\mathcal{Y}|:Y\subseteq [\omega]^\omega\;\text{and}\;\forall\;A\in\mathcal{I}\;\exists\;Y\in \mathcal{Y}\;|A\cap Y|<\omega\big\}, \text{ and}\\ \mathrm{cov}^*(\mathcal{I}) & = \min\big\{|\mathcal{C}|:\mathcal{C}\subseteq \mathcal{I}\;\text{and}\;\forall\;Y\in [\omega]^\omega\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\}. \end{align*} $$
$$ \begin{align*} \mathrm{add}^*(\mathcal{I})&= \min\big\{|\mathcal{U}|:\mathcal{U}\;\text{is unbounded in}\;(\mathcal{I},\subseteq^*)\big\},\\ \mathrm{cof}^*(\mathcal{I}) & = \min\big\{|\mathcal{D}|:\mathcal{D}\;\text{is cofinal in}\;(\mathcal{I},\subseteq^*)\big\},\\ \mathrm{non}^*(\mathcal{I}) & = \min\big\{|\mathcal{Y}|:Y\subseteq [\omega]^\omega\;\text{and}\;\forall\;A\in\mathcal{I}\;\exists\;Y\in \mathcal{Y}\;|A\cap Y|<\omega\big\}, \text{ and}\\ \mathrm{cov}^*(\mathcal{I}) & = \min\big\{|\mathcal{C}|:\mathcal{C}\subseteq \mathcal{I}\;\text{and}\;\forall\;Y\in [\omega]^\omega\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\}. \end{align*} $$
Notice that in this context, destroying a Borel
![]() $\mathcal {I}$
is associated with increasing
$\mathcal {I}$
is associated with increasing
![]() $\mathrm {cov}^*(\mathcal {I})$
, and similarly,
$\mathrm {cov}^*(\mathcal {I})$
, and similarly,
![]() $*$
-destroying
$*$
-destroying
![]() $\mathcal {I}$
is associated with increasing
$\mathcal {I}$
is associated with increasing
![]() $\mathrm {add}^*(\mathcal {I})$
. Strictly speaking, these invariants are not new; they can be seen as usual additivity, cofinality, uniformity, and covering numbers (see [Reference Hernández-Hernández and Hrušák21]): If
$\mathrm {add}^*(\mathcal {I})$
. Strictly speaking, these invariants are not new; they can be seen as usual additivity, cofinality, uniformity, and covering numbers (see [Reference Hernández-Hernández and Hrušák21]): If
![]() $\mathcal {I}$
is a tall ideal on
$\mathcal {I}$
is a tall ideal on
![]() $\omega $
, then let
$\omega $
, then let
![]() $\widehat {\mathcal {I}}$
be the ideal on
$\widehat {\mathcal {I}}$
be the ideal on
![]() $[\omega ]^\omega $
generated by all sets of the form
$[\omega ]^\omega $
generated by all sets of the form
![]() $\widehat {A}=\{X\in [\omega ]^\omega :|A\cap X|=\omega \}$
,
$\widehat {A}=\{X\in [\omega ]^\omega :|A\cap X|=\omega \}$
,
![]() $A\in \mathcal {I}$
.
$A\in \mathcal {I}$
.
Fact 3.3.
![]() $\mathrm {inv}^*(\mathcal {I})=\mathrm {inv}(\widehat {\mathcal {I}})$
for all four invariants above.
$\mathrm {inv}^*(\mathcal {I})=\mathrm {inv}(\widehat {\mathcal {I}})$
for all four invariants above.
To put
![]() $+$
-destructibility into the context of cardinal invariants, we can easily generalise these cardinals by replacing
$+$
-destructibility into the context of cardinal invariants, we can easily generalise these cardinals by replacing
![]() $[\omega ]^\omega $
with
$[\omega ]^\omega $
with
![]() $\mathcal {I}^+$
in their definitions. In general, if
$\mathcal {I}^+$
in their definitions. In general, if
![]() $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
![]() $\omega $
then we define
$\omega $
then we define
in particular,
![]() $\mathrm {inv}^*(\mathcal {I})=\mathrm {inv}^*(\mathcal {I},[\omega ]^\omega )$
. To avoid tedious notations, especially if the notation for an ideal or for its underlying set is too long (e.g.,
$\mathrm {inv}^*(\mathcal {I})=\mathrm {inv}^*(\mathcal {I},[\omega ]^\omega )$
. To avoid tedious notations, especially if the notation for an ideal or for its underlying set is too long (e.g.,
![]() $\mathrm {Conv}$
or
$\mathrm {Conv}$
or
![]() $\omega \times \omega $
), we will write
$\omega \times \omega $
), we will write
![]() $\mathrm {inv}^*(\mathcal {I},\infty )=\mathrm {inv}^*(\mathcal {I},[\omega ]^\omega )$
,
$\mathrm {inv}^*(\mathcal {I},\infty )=\mathrm {inv}^*(\mathcal {I},[\omega ]^\omega )$
,
![]() $\mathrm {inv}^*(\mathcal {I},+)=\mathrm {inv}^*(\mathcal {I},\mathcal {I}^+)$
, and
$\mathrm {inv}^*(\mathcal {I},+)=\mathrm {inv}^*(\mathcal {I},\mathcal {I}^+)$
, and
![]() $\mathrm {inv}^*(\mathcal {I},*)=\mathrm {inv}^*(\mathcal {I},\mathcal {I}^*)$
.
$\mathrm {inv}^*(\mathcal {I},*)=\mathrm {inv}^*(\mathcal {I},\mathcal {I}^*)$
.
When exactly are these cardinals defined? The invariants
![]() $\mathrm {add},\mathrm {cof},\mathrm {non},$
and
$\mathrm {add},\mathrm {cof},\mathrm {non},$
and
![]() $\mathrm {cov}$
are defined for proper ideals containing all finite subsets of their underlying sets. Properness is not an issue because if
$\mathrm {cov}$
are defined for proper ideals containing all finite subsets of their underlying sets. Properness is not an issue because if
![]() $\mathcal {I}$
is proper, then
$\mathcal {I}$
is proper, then
![]() $\mathcal {I}^*\notin \widehat {\mathcal {I}}$
. Considering finite subsets of the underlying set,
$\mathcal {I}^*\notin \widehat {\mathcal {I}}$
. Considering finite subsets of the underlying set,
![]() $[\omega ]^\omega =\bigcup \widehat {\mathcal {I}}$
iff
$[\omega ]^\omega =\bigcup \widehat {\mathcal {I}}$
iff
![]() $\mathcal {I}^+=\bigcup (\widehat {\mathcal {I}}\!\upharpoonright \! \mathcal {I}^+)$
iff
$\mathcal {I}^+=\bigcup (\widehat {\mathcal {I}}\!\upharpoonright \! \mathcal {I}^+)$
iff
![]() $\mathcal {I}$
is tall; and
$\mathcal {I}$
is tall; and
![]() $\mathcal {I}^*=\bigcup (\widehat {\mathcal {I}}\!\upharpoonright \!\mathcal {I}^*)$
iff
$\mathcal {I}^*=\bigcup (\widehat {\mathcal {I}}\!\upharpoonright \!\mathcal {I}^*)$
iff
![]() $\mathcal {I}$
is not a trivial modification of
$\mathcal {I}$
is not a trivial modification of
![]() $\mathrm {Fin}$
. To simplify our list of conditions in the forthcoming statements, whenever we work with cardinal invariants of the form
$\mathrm {Fin}$
. To simplify our list of conditions in the forthcoming statements, whenever we work with cardinal invariants of the form
![]() $\mathrm {inv}^*(\mathcal {I},\infty )$
or
$\mathrm {inv}^*(\mathcal {I},\infty )$
or
![]() $\mathrm {inv}^*(\mathcal {I},+)$
, we will always assume that
$\mathrm {inv}^*(\mathcal {I},+)$
, we will always assume that
![]() $\mathcal {I}$
is tall. Similarly, when
$\mathcal {I}$
is tall. Similarly, when
![]() $\mathrm {inv}^*(\mathcal {I},*)$
is involved, we will assume that
$\mathrm {inv}^*(\mathcal {I},*)$
is involved, we will assume that
![]() $\mathcal {I}$
is not a trivial modification of
$\mathcal {I}$
is not a trivial modification of
![]() $\mathrm {Fin}$
.
$\mathrm {Fin}$
.
The cardinal invariants
![]() $\mathrm {inv}^*(\mathcal {I},\infty )$
have been extensively studied (see, e.g., [1, Reference Hernández-Hernández and Hrušák21, Reference Hrušák and Meza-Alcántara25, Reference Meza-Alcántara37]) but we know much less about, e.g.,
$\mathrm {inv}^*(\mathcal {I},\infty )$
have been extensively studied (see, e.g., [1, Reference Hernández-Hernández and Hrušák21, Reference Hrušák and Meza-Alcántara25, Reference Meza-Alcántara37]) but we know much less about, e.g.,
![]() $\mathrm {inv}^*(\mathcal {I},+)$
(it was introduced in [Reference Brendle and Hrušák7]). As we will mainly focus on uniformity and covering, let us reformulate these coefficients without referring to
$\mathrm {inv}^*(\mathcal {I},+)$
(it was introduced in [Reference Brendle and Hrušák7]). As we will mainly focus on uniformity and covering, let us reformulate these coefficients without referring to
![]() $\widehat {\mathcal {I}}$
:
$\widehat {\mathcal {I}}$
:
Fact 3.4. The following equalities hold:
 $$ \begin{align*} \mathrm{non}^*(\mathcal{I},\infty) &=\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq[\omega]^\omega,\;\forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\}, \\ \mathrm{cov}^*(\mathcal{I},\infty) &=\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\;\forall\;Y\in[\omega]^\omega\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\},\\ \mathrm{non}^*(\mathcal{I},+)&=\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^+,\;\forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\},\\ \mathrm{cov}^*(\mathcal{I},+) &=\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\;\forall\;Y\in\mathcal{I}^+\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\},\\ \mathrm{non}^*(\mathcal{I},*)&=\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^*,\;\forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\}, \text{ and}\\ \mathrm{cov}^*(\mathcal{I},*) &=\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\;\forall\;Y\in\mathcal{I}^*\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\}. \end{align*} $$
$$ \begin{align*} \mathrm{non}^*(\mathcal{I},\infty) &=\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq[\omega]^\omega,\;\forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\}, \\ \mathrm{cov}^*(\mathcal{I},\infty) &=\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\;\forall\;Y\in[\omega]^\omega\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\},\\ \mathrm{non}^*(\mathcal{I},+)&=\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^+,\;\forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\},\\ \mathrm{cov}^*(\mathcal{I},+) &=\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\;\forall\;Y\in\mathcal{I}^+\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\},\\ \mathrm{non}^*(\mathcal{I},*)&=\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^*,\;\forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\}, \text{ and}\\ \mathrm{cov}^*(\mathcal{I},*) &=\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\;\forall\;Y\in\mathcal{I}^*\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\}. \end{align*} $$
-
(1) Let
 $\mathcal {I}$
be an arbitrary tall ideal on
$\mathcal {I}$
be an arbitrary tall ideal on
 $\omega $
and
$\omega $
and
 $A,B\in \mathcal {I}$
. Then the following are equivalent: (i)
$A,B\in \mathcal {I}$
. Then the following are equivalent: (i)
 $A\subseteq ^* B$
, (ii)
$A\subseteq ^* B$
, (ii)
 $\widehat {A}\subseteq \widehat {B}$
, (iii)
$\widehat {A}\subseteq \widehat {B}$
, (iii)
 $\widehat {A}\cap \mathcal {I}^+\subseteq \widehat {B}\cap \mathcal {I}^+$
, and (iv)
$\widehat {A}\cap \mathcal {I}^+\subseteq \widehat {B}\cap \mathcal {I}^+$
, and (iv)
 $\widehat {A}\cap \mathcal {I}^*\subseteq \widehat {B}\cap \mathcal {I}^*$
.
$\widehat {A}\cap \mathcal {I}^*\subseteq \widehat {B}\cap \mathcal {I}^*$
. -
(2) Some of these new coefficients are actually equal:
 $$ \begin{align*} \mathrm{cof}^*(\mathcal{I},\infty) & =\mathrm{cof}^*(\mathcal{I},+)=\mathrm{cof}^*(\mathcal{I},*)=\mathrm{non}^*(\mathcal{I},*), \text{ and} \\ \mathrm{add}^*(\mathcal{I},\infty) & =\mathrm{add}^*(\mathcal{I},+)=\mathrm{add}^*(\mathcal{I},*)=\mathrm{cov}^*(\mathcal{I},*). \end{align*} $$
$$ \begin{align*} \mathrm{cof}^*(\mathcal{I},\infty) & =\mathrm{cof}^*(\mathcal{I},+)=\mathrm{cof}^*(\mathcal{I},*)=\mathrm{non}^*(\mathcal{I},*), \text{ and} \\ \mathrm{add}^*(\mathcal{I},\infty) & =\mathrm{add}^*(\mathcal{I},+)=\mathrm{add}^*(\mathcal{I},*)=\mathrm{cov}^*(\mathcal{I},*). \end{align*} $$
-
(3) The remaining cardinal coefficients form the following diagram (where
 $a\to b$
stands for
$a\to b$
stands for
 $a\leq b$
, and
$a\leq b$
, and
 $\mathcal {D}$
stands for
$\mathcal {D}$
stands for
 $[\omega ]^\omega ,\mathcal {I}^+$
, or
$[\omega ]^\omega ,\mathcal {I}^+$
, or
 $\mathcal {I}^*$
):
$\mathcal {I}^*$
):
-
(4) If
 $\mathcal {I}$
is tall then
$\mathcal {I}$
is tall then
 $\mathrm {cov}^*(\mathcal {I},\infty )>\omega $
. If
$\mathrm {cov}^*(\mathcal {I},\infty )>\omega $
. If
 $\mathcal {I}$
is Borel and
$\mathcal {I}$
is Borel and
 $\mathrm {cov}^*(\mathcal {I},+)=\omega $
, then no forcing notion can
$\mathrm {cov}^*(\mathcal {I},+)=\omega $
, then no forcing notion can
 $+$
-destroy
$+$
-destroy
 $\mathcal {I}$
. If
$\mathcal {I}$
. If
 $\mathcal {I}$
is Borel and
$\mathcal {I}$
is Borel and
 $\mathrm {cov}^*(\mathcal {I},*)=\omega $
(i.e.,
$\mathrm {cov}^*(\mathcal {I},*)=\omega $
(i.e.,
 $\mathcal {I}$
is not a P-ideal), then no forcing notion can
$\mathcal {I}$
is not a P-ideal), then no forcing notion can
 $*$
-destroy
$*$
-destroy
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(5) If
 $\mathcal {I}\leq _{\mathrm {KB}}\mathcal {J}$
are Borel, then
$\mathcal {I}\leq _{\mathrm {KB}}\mathcal {J}$
are Borel, then-
(5a-i)
 $\mathrm {cov}^*(\mathcal {I},\infty )\geq \mathrm {cov}^*(\mathcal {J},\infty )$
,
$\mathrm {cov}^*(\mathcal {I},\infty )\geq \mathrm {cov}^*(\mathcal {J},\infty )$
, -
(5a-ii)
 $\mathrm {non}^*(\mathcal {I},\infty )\leq \mathrm {non}^*(\mathcal {J},\infty )$
,
$\mathrm {non}^*(\mathcal {I},\infty )\leq \mathrm {non}^*(\mathcal {J},\infty )$
, -
(5b-i) if
 $\mathbb {P}$
cannot destroy
$\mathbb {P}$
cannot destroy
 $\mathcal {I}$
then
$\mathcal {I}$
then
 $\mathbb {P}$
cannot destroy
$\mathbb {P}$
cannot destroy
 $\mathcal {J}$
either, and
$\mathcal {J}$
either, and -
(5b-ii) if
 $\Vdash _{\mathbb {P}}[\omega ]^\omega \cap V\in \widehat {\mathcal {I}}$
then
$\Vdash _{\mathbb {P}}[\omega ]^\omega \cap V\in \widehat {\mathcal {I}}$
then
 $\Vdash _{\mathbb {P}}[\omega ]^\omega \cap V\in \widehat {\mathcal {J}}$
.
$\Vdash _{\mathbb {P}}[\omega ]^\omega \cap V\in \widehat {\mathcal {J}}$
.
-
-
(6) If
 $\mathcal {I}\leq _{\mathrm {K}}\mathcal {J}$
are Borel, then (5a-i) and (5b-i) hold; furthermore
$\mathcal {I}\leq _{\mathrm {K}}\mathcal {J}$
are Borel, then (5a-i) and (5b-i) hold; furthermore-
(6a)
 $\mathrm {cov}^*(\mathcal {I},+)\geq \mathrm {cov}^*(\mathcal {J},+)$
and
$\mathrm {cov}^*(\mathcal {I},+)\geq \mathrm {cov}^*(\mathcal {J},+)$
and
 $\mathrm {non}^*(\mathcal {I},+)\leq \mathrm {non}^*(\mathcal {J},+)$
, and
$\mathrm {non}^*(\mathcal {I},+)\leq \mathrm {non}^*(\mathcal {J},+)$
, and -
(6b) if
 $\mathbb {P}$
cannot
$\mathbb {P}$
cannot
 $+$
-destroy
$+$
-destroy
 $\mathcal {I}$
then
$\mathcal {I}$
then
 $\mathbb {P}$
cannot
$\mathbb {P}$
cannot
 $+$
-destroy
$+$
-destroy
 $\mathcal {J}$
either, and dually, if
$\mathcal {J}$
either, and dually, if
 $\Vdash _{\mathbb {P}}\mathcal {I}^+\cap V\in \widehat {\mathcal {I}}$
then
$\Vdash _{\mathbb {P}}\mathcal {I}^+\cap V\in \widehat {\mathcal {I}}$
then
 $\Vdash _{\mathbb {P}}\mathcal {J}^+\cap V\in \widehat {\mathcal {J}}$
.
$\Vdash _{\mathbb {P}}\mathcal {J}^+\cap V\in \widehat {\mathcal {J}}$
.
-
Proof. (1): (i)
![]() $\to $
(ii)
$\to $
(ii)
![]() $\to $
(iii)
$\to $
(iii)
![]() $\to $
(iv) are trivial, and (iv) implies (i) because if
$\to $
(iv) are trivial, and (iv) implies (i) because if
![]() $|A\setminus B|=\omega $
then
$|A\setminus B|=\omega $
then
![]() $\omega \setminus B\in (\widehat {A}\cap \mathcal {I}^*) \setminus \widehat {B}$
.
$\omega \setminus B\in (\widehat {A}\cap \mathcal {I}^*) \setminus \widehat {B}$
.
(2):
![]() $\mathrm {add}^*(\mathcal {I},\infty ) \leq \mathrm {add}^*(\mathcal {I},+)\leq \mathrm {add}^*(\mathcal {I},*)\leq \mathrm {cov}^*(\mathcal {I},*)$
are trivial (actually, (1) implies that the three additivities are equal), and
$\mathrm {add}^*(\mathcal {I},\infty ) \leq \mathrm {add}^*(\mathcal {I},+)\leq \mathrm {add}^*(\mathcal {I},*)\leq \mathrm {cov}^*(\mathcal {I},*)$
are trivial (actually, (1) implies that the three additivities are equal), and
![]() $\mathrm {cov}^*(\mathcal {I},*)=\mathrm {add}^*(\mathcal {I},\infty )$
because an
$\mathrm {cov}^*(\mathcal {I},*)=\mathrm {add}^*(\mathcal {I},\infty )$
because an
![]() $\mathcal {A}\subseteq \mathcal {I}$
is
$\mathcal {A}\subseteq \mathcal {I}$
is
![]() $\subseteq ^*$
-unbounded in
$\subseteq ^*$
-unbounded in
![]() $\mathcal {I}$
iff
$\mathcal {I}$
iff
![]() $\forall F\in \mathcal {I}^* \,\exists A\in \mathcal {A}\, |F\cap A\ |=\omega $
. This argument can be “dualised,” and we obtain the equalities
$\forall F\in \mathcal {I}^* \,\exists A\in \mathcal {A}\, |F\cap A\ |=\omega $
. This argument can be “dualised,” and we obtain the equalities
![]() $\mathrm {cof}^*(\mathcal {I},\infty ) =\mathrm {cof}^*(\mathcal {I},+)=\mathrm {cof}^*(\mathcal {I},*)=\mathrm {non}^*(\mathcal {I},*)$
.
$\mathrm {cof}^*(\mathcal {I},\infty ) =\mathrm {cof}^*(\mathcal {I},+)=\mathrm {cof}^*(\mathcal {I},*)=\mathrm {non}^*(\mathcal {I},*)$
.
(3) follows from the definitions and from (2).
(4): The first statement is trivial. To show the second and the third, notice that if
![]() $\mathcal {I}$
is Borel, then “
$\mathcal {I}$
is Borel, then “
![]() $(A_n)_{n\in \omega }$
witnesses
$(A_n)_{n\in \omega }$
witnesses
![]() $\mathrm {cov}^*(\mathcal {I},+/*)=\omega $
” is a
$\mathrm {cov}^*(\mathcal {I},+/*)=\omega $
” is a
![]() ${\underset{\sim}{\Pi}}{}^1_1$
property.
${\underset{\sim}{\Pi}}{}^1_1$
property.
(5) and (6) follow from the definitions.⊣
Point (6) above, more precisely the fact that K-reducibility is enough to obtain “half” of the consequences of KB-reducibility from point (5) is not so surprising after our remark on Katětov and Katětov–Blass reductions between our main examples (see the comments following the definitions of these examples).
One may have noticed that
![]() $*$
-destructibility, more precisely, the effect of reducibility between ideals on
$*$
-destructibility, more precisely, the effect of reducibility between ideals on
![]() $*$
-destructibility, is missing from the list of our basic observations above. We will need a more general notion of reduction between ideals, see Section 7 for details.
$*$
-destructibility, is missing from the list of our basic observations above. We will need a more general notion of reduction between ideals, see Section 7 for details.
We give a combinatorial characterisation of
![]() $\infty /{+}/*$
-destructibility of Borel ideals by forcing notions of the form
$\infty /{+}/*$
-destructibility of Borel ideals by forcing notions of the form
![]() $\mathbb {P}_I$
. Unlike in the case of the original Theorem 1.2, we can work with arbitrary Polish spaces, do not have to understand trace ideals, and do not need continuous reading of names. Of course, this does not make this characterisation “better” (and it is certainly not “deeper”) but it provides a new approach to forcing indestructibility of ideals.
$\mathbb {P}_I$
. Unlike in the case of the original Theorem 1.2, we can work with arbitrary Polish spaces, do not have to understand trace ideals, and do not need continuous reading of names. Of course, this does not make this characterisation “better” (and it is certainly not “deeper”) but it provides a new approach to forcing indestructibility of ideals.
In [Reference Balcerzak, Farkas and Głab2], based on a result from [Reference Elekes15], the authors introduced and studied the following notion: Let X be an uncountable Polish space, I be a
![]() $\sigma $
-ideal on X, and
$\sigma $
-ideal on X, and
![]() $\mathcal {J}$
be an ideal on
$\mathcal {J}$
be an ideal on
![]() $\omega $
. Assuming that X is clear from the context, we say that I has the
$\omega $
. Assuming that X is clear from the context, we say that I has the
![]() $\mathcal {J}$
-covering property,
$\mathcal {J}$
-covering property,
![]() $\mathcal {J}$
-c.p. if for every I-almost everywhere infinite-fold cover
$\mathcal {J}$
-c.p. if for every I-almost everywhere infinite-fold cover
![]() $(B_n)_{n\in \omega }$
of X by Borel set, that is,
$(B_n)_{n\in \omega }$
of X by Borel set, that is,
![]() $\{x\in X:\{n\in \omega :x\in B_n\}$
is finite
$\{x\in X:\{n\in \omega :x\in B_n\}$
is finite
![]() $\}\in I$
, there is an
$\}\in I$
, there is an
![]() $S\in \mathcal {J}$
(a “small” index set) such that
$S\in \mathcal {J}$
(a “small” index set) such that
![]() $(B_n)_{n\in S}$
is still an I-a.e. infinite fold cover of X. It turned out that this property is a strong variant of forcing indestructibility: If
$(B_n)_{n\in S}$
is still an I-a.e. infinite fold cover of X. It turned out that this property is a strong variant of forcing indestructibility: If
![]() $\mathbb {P}_I$
is proper and I has the
$\mathbb {P}_I$
is proper and I has the
![]() $\mathcal {J}$
-c.p., then
$\mathcal {J}$
-c.p., then
![]() $\mathbb {P}_I$
cannot destroy
$\mathbb {P}_I$
cannot destroy
![]() $\mathcal {J}$
. In general, the covering property is stronger:
$\mathcal {J}$
. In general, the covering property is stronger:
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
is Cohen-indestructible but
$\mathrm {Fin}\otimes \mathrm {Fin}$
is Cohen-indestructible but
![]() $\mathcal {M}$
does not have the
$\mathcal {M}$
does not have the
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
-c.p. See [Reference Balcerzak, Farkas and Głab2] for more results about this property.
$\mathrm {Fin}\otimes \mathrm {Fin}$
-c.p. See [Reference Balcerzak, Farkas and Głab2] for more results about this property.
We show that a natural weak variant of the covering property is equivalent to forcing indestructibility, and, moreover, that the appropriate modifications work for
![]() $+$
- and
$+$
- and
![]() $*$
-indestructibility as well.
$*$
-indestructibility as well.
Theorem 3.6. Let
![]() $\mathcal {J}$
be a Borel ideal on
$\mathcal {J}$
be a Borel ideal on
![]() $\omega $
,
$\omega $
,
![]() $\mathcal {D}=[\omega ]^\omega ,\mathcal {J}^+$
, or
$\mathcal {D}=[\omega ]^\omega ,\mathcal {J}^+$
, or
![]() $\mathcal {J}^*$
, and let I be a
$\mathcal {J}^*$
, and let I be a
![]() $\sigma $
-ideal on a Polish space X such that
$\sigma $
-ideal on a Polish space X such that
![]() $\mathbb {P}_I$
is proper. Then
$\mathbb {P}_I$
is proper. Then
![]() $\mathbb {P}_I$
cannot
$\mathbb {P}_I$
cannot
![]() $\mathcal {D}$
-destroy
$\mathcal {D}$
-destroy
![]() $\mathcal {J}$
if, and only if, for every sequence
$\mathcal {J}$
if, and only if, for every sequence
![]() $(B_n)_{n\in \omega }$
of Borel subsets of X
$(B_n)_{n\in \omega }$
of Borel subsets of X
 $$ \begin{align*} \textit{IF} &\;\;\;\big\{x:\big\{n\in\omega:x\in B_n\}\in\mathcal{D}\big\}\in I^+, and\\ \textit{THEN} &\;\;\;\big\{x:\big|\big\{n\in S:x\in B_n\big\}\big|=\omega\big\}\in I^+\;\;\text{for some}\;S\in\mathcal{J}. \end{align*} $$
$$ \begin{align*} \textit{IF} &\;\;\;\big\{x:\big\{n\in\omega:x\in B_n\}\in\mathcal{D}\big\}\in I^+, and\\ \textit{THEN} &\;\;\;\big\{x:\big|\big\{n\in S:x\in B_n\big\}\big|=\omega\big\}\in I^+\;\;\text{for some}\;S\in\mathcal{J}. \end{align*} $$
Proof. Let
![]() $\mathcal {D}=[\omega ]^\omega $
or
$\mathcal {D}=[\omega ]^\omega $
or
![]() $\mathcal {J}^+$
or
$\mathcal {J}^+$
or
![]() $\mathcal {J}^*$
accordingly.
$\mathcal {J}^*$
accordingly.
The “if” direction: Assume on the contrary that
![]() $\Vdash _{\mathbb {P}_I}\mathring {Y}\in \mathcal {D}$
and
$\Vdash _{\mathbb {P}_I}\mathring {Y}\in \mathcal {D}$
and
![]() $C\Vdash \forall A\in \mathcal J^V |\mathring {Y}\cap A|<\omega $
for some
$C\Vdash \forall A\in \mathcal J^V |\mathring {Y}\cap A|<\omega $
for some
![]() $C\in \mathbb {P}_I$
. Applying the Borel reading of names (see [Reference Zapletal42, Proposition 2.3.1]), there are a
$C\in \mathbb {P}_I$
. Applying the Borel reading of names (see [Reference Zapletal42, Proposition 2.3.1]), there are a
![]() $C'\in \mathbb {P}_I$
,
$C'\in \mathbb {P}_I$
,
![]() $C'\leq C$
, and a Borel function
$C'\leq C$
, and a Borel function
![]() $f:C'\to \mathcal {D}$
(coded in the ground model) such that
$f:C'\to \mathcal {D}$
(coded in the ground model) such that
![]() $C'\Vdash _{\mathbb {P}_I}f(\mathring {r}_I)=\mathring {Y}$
where
$C'\Vdash _{\mathbb {P}_I}f(\mathring {r}_I)=\mathring {Y}$
where
![]() $\mathring {r}_I$
is the generic real. For
$\mathring {r}_I$
is the generic real. For
![]() $n\in \omega $
define
$n\in \omega $
define
![]() $B_n=\{x\in C':n\in f(x)\}$
. Then
$B_n=\{x\in C':n\in f(x)\}$
. Then
![]() $B_n=f^{-1}[\{A\subseteq \omega :n\in A\}]$
is Borel and
$B_n=f^{-1}[\{A\subseteq \omega :n\in A\}]$
is Borel and
![]() $C'=\{x\in X:\{n\in \omega :x\in B_n\}\in \mathcal {D}\}\in I^+$
. Applying our assumption, there is an
$C'=\{x\in X:\{n\in \omega :x\in B_n\}\in \mathcal {D}\}\in I^+$
. Applying our assumption, there is an
![]() $S\in \mathcal {J}$
such that
$S\in \mathcal {J}$
such that
![]() $C"=\{x\in C':|\{n\in S:x\in B_n\}|=\omega \}\in I^+$
. Notice that
$C"=\{x\in C':|\{n\in S:x\in B_n\}|=\omega \}\in I^+$
. Notice that
![]() $C"=\{x\in C':|f(x)\cap S|=\omega \}=f^{-1}[\{A\subseteq \omega :|A\cap S|=\omega \}]$
is also Borel and hence it is a condition below
$C"=\{x\in C':|f(x)\cap S|=\omega \}=f^{-1}[\{A\subseteq \omega :|A\cap S|=\omega \}]$
is also Borel and hence it is a condition below
![]() $C'$
, and of course
$C'$
, and of course
![]() $C"\Vdash _{\mathbb {P}_I}|f(\mathring {r}_I)\cap S|=\omega $
, a contradiction.
$C"\Vdash _{\mathbb {P}_I}|f(\mathring {r}_I)\cap S|=\omega $
, a contradiction.
The “only if” direction: Let
![]() $(B_n)_{n\in \omega }$
be a sequence of Borel subsets of X such that
$(B_n)_{n\in \omega }$
be a sequence of Borel subsets of X such that
![]() $\{x:\{n\in \omega :x\in B_n\}\in \mathcal {D}\}=C\in I^+$
. Notice that C is Borel because
$\{x:\{n\in \omega :x\in B_n\}\in \mathcal {D}\}=C\in I^+$
. Notice that C is Borel because
![]() $g:X\to \mathcal {P}(\omega )$
,
$g:X\to \mathcal {P}(\omega )$
,
![]() $g(x)=\{n\in \omega :x\in B_n\}$
is a Borel function, and
$g(x)=\{n\in \omega :x\in B_n\}$
is a Borel function, and
![]() $C=g^{-1}[\mathcal {D}]$
. In particular,
$C=g^{-1}[\mathcal {D}]$
. In particular,
![]() $C\in \mathbb {P}_I$
,
$C\in \mathbb {P}_I$
,
![]() $C\Vdash \mathring {Y}:=\{n\in \omega :\mathring {r}_I\in B_n\}\in \mathcal {D}$
, and hence (as
$C\Vdash \mathring {Y}:=\{n\in \omega :\mathring {r}_I\in B_n\}\in \mathcal {D}$
, and hence (as
![]() $\mathbb {P}_I$
cannot
$\mathbb {P}_I$
cannot
![]() $\mathcal {D}$
-destroy
$\mathcal {D}$
-destroy
![]() $\mathcal {J}$
) there are a
$\mathcal {J}$
) there are a
![]() $C'\leq C$
and an
$C'\leq C$
and an
![]() $S\in \mathcal {J}$
such that
$S\in \mathcal {J}$
such that
![]() $C'\Vdash \mathring {Y}\cap S=|\{n\in S:\mathring {r}_I\in B_n\}|=\omega $
, equivalently,
$C'\Vdash \mathring {Y}\cap S=|\{n\in S:\mathring {r}_I\in B_n\}|=\omega $
, equivalently,
![]() $\{x\in C':|\{n\in S:x\in B_n\}|<\omega \}\in I$
, and hence
$\{x\in C':|\{n\in S:x\in B_n\}|<\omega \}\in I$
, and hence
![]() $\{x:|\{n\in S:x\in B_n\}|=\omega \}\in I^+$
.⊣
$\{x:|\{n\in S:x\in B_n\}|=\omega \}\in I^+$
.⊣
One may wonder what the exact role of CRN was in the original characterisation of forcing indestructibility of ideals (see Theorem 1.2). The ideal I satisfies the continuous reading of names, if for every Polish space Y,
![]() $B\in \mathbb {P}_I$
, and Borel
$B\in \mathbb {P}_I$
, and Borel
![]() $g:B\to \,\!^\omega 2$
, there is a
$g:B\to \,\!^\omega 2$
, there is a
![]() $C\in \mathbb {P}_I$
,
$C\in \mathbb {P}_I$
,
![]() $C\subseteq B$
such that
$C\subseteq B$
such that
![]() $g\!\upharpoonright \! C$
is continuous (in particular, the function f in the application of Borel reading of names above can be chosen as continuous). We know that if I satisfies the CRN and
$g\!\upharpoonright \! C$
is continuous (in particular, the function f in the application of Borel reading of names above can be chosen as continuous). We know that if I satisfies the CRN and
![]() $\mathcal {J}$
is an ideal on
$\mathcal {J}$
is an ideal on
![]() $\omega $
, then
$\omega $
, then
![]() $\mathbb {P}_I$
cannot destroy
$\mathbb {P}_I$
cannot destroy
![]() $\mathcal {J}$
iff
$\mathcal {J}$
iff
![]() $\mathcal {J}\nleq _{\mathrm {K}}\mathrm {tr}(I)\!\upharpoonright \! X$
for every
$\mathcal {J}\nleq _{\mathrm {K}}\mathrm {tr}(I)\!\upharpoonright \! X$
for every
![]() $X\in \mathrm {tr}(I)^+$
. We show that one implication still holds without assuming CRN:
$X\in \mathrm {tr}(I)^+$
. We show that one implication still holds without assuming CRN:
Fact 3.7. If
![]() $\mathbb {P}_I$
cannot destroy
$\mathbb {P}_I$
cannot destroy
![]() $\mathcal {J}$
then
$\mathcal {J}$
then
![]() $\mathcal {J}\nleq _{\mathrm {K}}\mathrm {tr}(I)\!\upharpoonright \! X$
for every
$\mathcal {J}\nleq _{\mathrm {K}}\mathrm {tr}(I)\!\upharpoonright \! X$
for every
![]() $X\in \mathrm {tr}(I)^+$
.
$X\in \mathrm {tr}(I)^+$
.
Proof. Assume on the contrary that
![]() $f:X\to \omega $
witnesses
$f:X\to \omega $
witnesses
![]() $\mathcal {J}\leq _{\mathrm {K}} \mathrm {tr}(I)\!\upharpoonright \! X$
for some
$\mathcal {J}\leq _{\mathrm {K}} \mathrm {tr}(I)\!\upharpoonright \! X$
for some
![]() $X\in \mathrm {tr}(I)^+$
. Then
$X\in \mathrm {tr}(I)^+$
. Then
![]() $[X]_\delta $
is an I-positive
$[X]_\delta $
is an I-positive
![]() $G_\delta $
set. Define the Borel sets
$G_\delta $
set. Define the Borel sets
![]() $B_n=\{x\in [X]_\delta : \exists\ k (x\!\upharpoonright \! k\in X$
and
$B_n=\{x\in [X]_\delta : \exists\ k (x\!\upharpoonright \! k\in X$
and
![]() $f(x\!\upharpoonright \! k)=n)\}$
. Now if
$f(x\!\upharpoonright \! k)=n)\}$
. Now if
![]() $x\in [X]_\delta $
, then
$x\in [X]_\delta $
, then
![]() $|\{n\in \omega :x\in B_n\}|<\omega $
iff
$|\{n\in \omega :x\in B_n\}|<\omega $
iff
![]() $f[\{x\!\upharpoonright \! k:k\in \omega \}\cap X]\subseteq m$
for some m, in particular,
$f[\{x\!\upharpoonright \! k:k\in \omega \}\cap X]\subseteq m$
for some m, in particular,
![]() $x\in \bigcup _{m\in \omega } [f^{-1}[m]]_\delta \in I$
, and hence
$x\in \bigcup _{m\in \omega } [f^{-1}[m]]_\delta \in I$
, and hence
![]() $\{x\in [X]_\delta :|\{n\in \omega :x\in B_n\}|=\omega \}\in I^+$
. Applying Theorem 3.6, there is an
$\{x\in [X]_\delta :|\{n\in \omega :x\in B_n\}|=\omega \}\in I^+$
. Applying Theorem 3.6, there is an
![]() $S\in \mathcal {J}$
such that
$S\in \mathcal {J}$
such that
![]() $\{x\in [X]_\delta :|\{n\in S:x\in B_n\}|=\omega \}\in I^+$
but
$\{x\in [X]_\delta :|\{n\in S:x\in B_n\}|=\omega \}\in I^+$
but
![]() $\{x\in [X]_\delta :|\{n\in S:x\in B_n\}|=\omega \}=[f^{-1}[S]]_\delta \in I$
, a contradiction.⊣
$\{x\in [X]_\delta :|\{n\in S:x\in B_n\}|=\omega \}=[f^{-1}[S]]_\delta \in I$
, a contradiction.⊣
4 Examples
In this section, we discuss some of our main examples
![]() $\mathcal {I}$
, their cardinal invariants
$\mathcal {I}$
, their cardinal invariants
![]() $\mathrm {non}^*(\mathcal {I},+)$
and
$\mathrm {non}^*(\mathcal {I},+)$
and
![]() $\mathrm {cov}^*(\mathcal {I},+)$
, and their (
$\mathrm {cov}^*(\mathcal {I},+)$
, and their (
![]() $+$
-)destructibility. For a survey on the invariants
$+$
-)destructibility. For a survey on the invariants
![]() $\mathrm {inv}^*(\mathcal {I},\infty )$
, see, e.g., [Reference Hrušák and Meza-Alcántara25, Reference Meza-Alcántara37] (for
$\mathrm {inv}^*(\mathcal {I},\infty )$
, see, e.g., [Reference Hrušák and Meza-Alcántara25, Reference Meza-Alcántara37] (for
![]() $\mathcal {ED}$
and
$\mathcal {ED}$
and
![]() $\mathcal {ED}_{\mathrm {fin}}$
) and [Reference Balcar, Hernández-Hernández and Hrušák1] (for
$\mathcal {ED}_{\mathrm {fin}}$
) and [Reference Balcar, Hernández-Hernández and Hrušák1] (for
![]() $\mathrm {Nwd}$
).
$\mathrm {Nwd}$
).
4.1 Easy examples:
 $\mathrm {Fin}\otimes \mathrm {Fin}$
,
$\mathrm {Fin}\otimes \mathrm {Fin}$
,
 $\mathrm {Conv}$
, and
$\mathrm {Conv}$
, and
 $\mathrm {Ran}$
$\mathrm {Ran}$
Example 4.1. When working with cardinal invariants of
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
we will write
$\mathrm {Fin}\otimes \mathrm {Fin}$
we will write
![]() $\mathrm {Fin}^2=\mathrm {Fin}\otimes \mathrm {Fin}$
. We know that
$\mathrm {Fin}^2=\mathrm {Fin}\otimes \mathrm {Fin}$
. We know that
![]() $\mathrm {non}^*(\mathrm {Fin}^2,\infty )=\omega $
,
$\mathrm {non}^*(\mathrm {Fin}^2,\infty )=\omega $
,
![]() $\mathrm {cov}^*(\mathrm {Fin}^2,\infty )=\mathfrak {b}$
, and
$\mathrm {cov}^*(\mathrm {Fin}^2,\infty )=\mathfrak {b}$
, and
![]() $\mathrm {cof}^*(\mathrm {Fin}^2,\infty )=\mathfrak {d}$
; and it is easy to show the following:
$\mathrm {cof}^*(\mathrm {Fin}^2,\infty )=\mathfrak {d}$
; and it is easy to show the following:
-
(1)
 $\mathrm {non}^*(\mathrm {Fin}^2,+)=\mathfrak {d}$
and
$\mathrm {non}^*(\mathrm {Fin}^2,+)=\mathfrak {d}$
and
 $\mathrm {cov}^*(\mathrm {Fin}^2,+)=\omega $
.
$\mathrm {cov}^*(\mathrm {Fin}^2,+)=\omega $
. -
(2a)
 $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
 $\mathrm {Fin}\otimes \mathrm {Fin}$
iff
$\mathrm {Fin}\otimes \mathrm {Fin}$
iff
 $\mathbb {P}$
adds dominating reals.
$\mathbb {P}$
adds dominating reals. -
(2b) No forcing notion can
 $+$
-destroy
$+$
-destroy
 $\mathrm {Fin}\otimes \mathrm {Fin}$
.
$\mathrm {Fin}\otimes \mathrm {Fin}$
.
Example 4.2. We know that
![]() $\mathrm {non}^*(\mathrm {Conv},\infty )=\omega $
and
$\mathrm {non}^*(\mathrm {Conv},\infty )=\omega $
and
![]() $\mathrm {cov}^*(\mathrm {Conv},\infty )=\mathfrak {c}$
. We show the following:
$\mathrm {cov}^*(\mathrm {Conv},\infty )=\mathfrak {c}$
. We show the following:
-
(1)
 $\mathrm {non}^*(\mathrm {Conv},+)=\omega $
and
$\mathrm {non}^*(\mathrm {Conv},+)=\omega $
and
 $\mathrm {cov}^*(\mathrm {Conv},+)=\mathfrak {c}$
.
$\mathrm {cov}^*(\mathrm {Conv},+)=\mathfrak {c}$
. -
(2) If a forcing notion adds new reals then it
 $+$
-destroys
$+$
-destroys
 $\mathrm {Conv}$
.
$\mathrm {Conv}$
.
(1): A countable base of the topology of
![]() $\mathbb {Q}$
witnesses the uniformity. Now if
$\mathbb {Q}$
witnesses the uniformity. Now if
![]() $x^\alpha _n\to y_\alpha $
are convergent sequences,
$x^\alpha _n\to y_\alpha $
are convergent sequences,
![]() $x^\alpha _n\in \mathbb {Q}$
and
$x^\alpha _n\in \mathbb {Q}$
and
![]() $\alpha <\kappa <\mathfrak {c}$
, then there is a (nontrivial) convergent sequence
$\alpha <\kappa <\mathfrak {c}$
, then there is a (nontrivial) convergent sequence
![]() $z_n\to z$
,
$z_n\to z$
,
![]() $z_n,z\in [0,1]\setminus \{y_\alpha :\alpha <\kappa \}$
, and if
$z_n,z\in [0,1]\setminus \{y_\alpha :\alpha <\kappa \}$
, and if
![]() $\mathbb {Q}\ni r^n_k\xrightarrow {k\to \infty }z_n$
such that
$\mathbb {Q}\ni r^n_k\xrightarrow {k\to \infty }z_n$
such that
![]() $R=\{r^n_k:n,k\in \omega \}$
has no accumulation points apart from the
$R=\{r^n_k:n,k\in \omega \}$
has no accumulation points apart from the
![]() $z_n$
’s and z, then
$z_n$
’s and z, then
![]() $R\in \mathrm {Conv}^+$
witnesses that
$R\in \mathrm {Conv}^+$
witnesses that
![]() $\{\{x^\alpha _n:n\in \omega \}:\alpha <\omega \}$
cannot be a covering family.
$\{\{x^\alpha _n:n\in \omega \}:\alpha <\omega \}$
cannot be a covering family.
(2): Notice that if
![]() $\mathbb {P}$
adds a new real then it adds a (nontrivial) sequence
$\mathbb {P}$
adds a new real then it adds a (nontrivial) sequence
![]() $(z_n)_{n\in \omega }$
of new reals converging to a new real z, and hence the argument above shows that
$(z_n)_{n\in \omega }$
of new reals converging to a new real z, and hence the argument above shows that
![]() $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
![]() $\mathrm {Conv}$
.
$\mathrm {Conv}$
.
Example 4.3. We know that
![]() $\mathrm {non}^*(\mathrm {Ran},\infty )=\omega $
and
$\mathrm {non}^*(\mathrm {Ran},\infty )=\omega $
and
![]() $\mathrm {cov}^*(\mathrm {Ran},\infty )=\mathfrak {c}$
; and applying
$\mathrm {cov}^*(\mathrm {Ran},\infty )=\mathfrak {c}$
; and applying
![]() $\mathrm {Ran}\leq _{\mathrm {KB}}\mathrm {Conv}$
(see, e.g., [Reference Hrušák, Meza-Alcántara and Minami23]), the last example, and Observations 3.5(5) and (6), we get that
$\mathrm {Ran}\leq _{\mathrm {KB}}\mathrm {Conv}$
(see, e.g., [Reference Hrušák, Meza-Alcántara and Minami23]), the last example, and Observations 3.5(5) and (6), we get that
-
(1)
 $\mathrm {non}^*(\mathrm {Ran},+)=\omega $
and
$\mathrm {non}^*(\mathrm {Ran},+)=\omega $
and
 $\mathrm {cov}^*(\mathrm {Ran},+)=\mathfrak {c}$
, and
$\mathrm {cov}^*(\mathrm {Ran},+)=\mathfrak {c}$
, and -
(2) if a forcing notion adds new reals then it
 $+$
-destroys
$+$
-destroys
 $\mathrm {Ran}$
.
$\mathrm {Ran}$
.
Problem 4.4. Can we characterise those Borel ideals which are (
![]() $+$
-)destroyed by every forcing notion introducing a new real? (Loosely speaking, we would like to characterise those Borel ideals
$+$
-)destroyed by every forcing notion introducing a new real? (Loosely speaking, we would like to characterise those Borel ideals
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
![]() $\mathrm {ZFC}$
proves
$\mathrm {ZFC}$
proves
![]() $\mathrm {cov}^*(\mathcal {I},\infty /+)=\mathfrak {c}$
.) Does there exist a tall Borel ideal
$\mathrm {cov}^*(\mathcal {I},\infty /+)=\mathfrak {c}$
.) Does there exist a tall Borel ideal
![]() $\mathcal {I}$
which is destroyed by every forcing notion introducing a new real but
$\mathcal {I}$
which is destroyed by every forcing notion introducing a new real but
![]() $\mathcal {I}$
is not
$\mathcal {I}$
is not
![]() $+$
-destroyed by all these forcing notions?
$+$
-destroyed by all these forcing notions?
4.2 Around
 $\mathcal {ED}$
and
$\mathcal {ED}$
and
 $\mathcal {ED}_{\mathrm {fin}}$
$\mathcal {ED}_{\mathrm {fin}}$
We know (see [Reference Hrušák and Meza-Alcántara25]) that
![]() $\mathrm {non}^*(\mathcal {ED},\infty )=\omega $
,
$\mathrm {non}^*(\mathcal {ED},\infty )=\omega $
,
![]() $\mathrm {cov}^*(\mathcal {ED},\infty )=\mathrm {non}(\mathcal {M})$
, and
$\mathrm {cov}^*(\mathcal {ED},\infty )=\mathrm {non}(\mathcal {M})$
, and
![]() $\mathrm {cof}^*(\mathcal {ED},\infty )=\mathfrak {c}$
.
$\mathrm {cof}^*(\mathcal {ED},\infty )=\mathfrak {c}$
.
-
(1a)
 $\ \ \mathrm {non}^*(\mathcal {ED},+)=\mathrm {cov}(\mathcal {M})$
.
$\ \ \mathrm {non}^*(\mathcal {ED},+)=\mathrm {cov}(\mathcal {M})$
. -
(1b)
 $\ \ \mathrm {cov}^*(\mathcal {ED},+)=\mathrm {non}(\mathcal {M})$
.
$\ \ \mathrm {cov}^*(\mathcal {ED},+)=\mathrm {non}(\mathcal {M})$
. -
(2)
 $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
 $\mathcal {ED}$
iff
$\mathcal {ED}$
iff
 $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
 $\mathcal {ED}$
iff
$\mathcal {ED}$
iff
 $\mathbb {P}$
adds an eventually different real (that is, an
$\mathbb {P}$
adds an eventually different real (that is, an
 $f\in \,\!^\omega \omega $
such that
$f\in \,\!^\omega \omega $
such that
 $|f\cap g|<\omega $
for every
$|f\cap g|<\omega $
for every
 $g\in \,\!^\omega \omega \cap V$
).
$g\in \,\!^\omega \omega \cap V$
).
Proof. (1a): Let us recall the following characterisations of
![]() $\mathrm {cov}(\mathcal {M})$
(see [Reference Bartoszyński and Judah3, Lemma 2.4.2 and Theorem 2.4.5]): Let
$\mathrm {cov}(\mathcal {M})$
(see [Reference Bartoszyński and Judah3, Lemma 2.4.2 and Theorem 2.4.5]): Let
![]() $\mathcal {C}=\{S\in \,\!^\omega ([\omega ]^{<\omega }):\sum _{n\in \omega }|S(n)|/n^2<\infty \}$
(for now let
$\mathcal {C}=\{S\in \,\!^\omega ([\omega ]^{<\omega }):\sum _{n\in \omega }|S(n)|/n^2<\infty \}$
(for now let
![]() $1/0=1$
). Then
$1/0=1$
). Then
To show
![]() $\mathrm {non}^*(\mathcal {ED},+)\leq \mathrm {cov}(\mathcal {M})$
, fix an
$\mathrm {non}^*(\mathcal {ED},+)\leq \mathrm {cov}(\mathcal {M})$
, fix an
![]() $F\subseteq \,\!^\omega \omega $
witnessing the above characterisation. For every
$F\subseteq \,\!^\omega \omega $
witnessing the above characterisation. For every
![]() $f\in F$
define
$f\in F$
define
![]() $X_f\in \mathcal {ED}^+$
as follows:
$X_f\in \mathcal {ED}^+$
as follows:
Let
![]() $A\in \mathcal {ED}$
, we show that there is an
$A\in \mathcal {ED}$
, we show that there is an
![]() $f\in F$
such that
$f\in F$
such that
![]() $|A\cap X_f|<\omega $
, and hence
$|A\cap X_f|<\omega $
, and hence
![]() $\mathrm {non}^*(\mathcal {ED},+)\leq |F|=\mathrm {cov}(\mathcal {M})$
. As columns have finite intersection with every
$\mathrm {non}^*(\mathcal {ED},+)\leq |F|=\mathrm {cov}(\mathcal {M})$
. As columns have finite intersection with every
![]() $X_f$
, we can assume that A is of the form
$X_f$
, we can assume that A is of the form
![]() $\bigcup \{\{n\}\times F_n:n\in \omega \}$
where
$\bigcup \{\{n\}\times F_n:n\in \omega \}$
where
![]() $F_n\in [\omega ]^m$
for some fixed
$F_n\in [\omega ]^m$
for some fixed
![]() $m\in \omega $
. Let
$m\in \omega $
. Let
![]() $S_A:\omega \to [\omega ]^{<\omega }$
,
$S_A:\omega \to [\omega ]^{<\omega }$
,
Then
![]() $S_A\in \mathcal {C}$
and hence there is an
$S_A\in \mathcal {C}$
and hence there is an
![]() $f\in F$
such that
$f\in F$
such that
![]() $f(n)\notin S_A(n)$
for almost all n, and so
$f(n)\notin S_A(n)$
for almost all n, and so
![]() $(\{n\}\times F_n)\cap X_f=\varnothing $
for almost all n, i.e.,
$(\{n\}\times F_n)\cap X_f=\varnothing $
for almost all n, i.e.,
![]() $|A\cap X_f|<\omega $
.
$|A\cap X_f|<\omega $
.
Conversely, we show that if a family
![]() $\{X_\alpha :\alpha <\kappa \}$
witnesses
$\{X_\alpha :\alpha <\kappa \}$
witnesses
![]() $\mathrm {non}^*(\mathcal {ED},+)$
then there is a family
$\mathrm {non}^*(\mathcal {ED},+)$
then there is a family
![]() $\mathcal {D}$
of dense subsets of
$\mathcal {D}$
of dense subsets of
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $|\mathcal {D}|=\kappa $
such that no filter on
$|\mathcal {D}|=\kappa $
such that no filter on
![]() $\mathbb {C}$
is
$\mathbb {C}$
is
![]() $\mathcal {D}$
-generic. We know that for every
$\mathcal {D}$
-generic. We know that for every
![]() $\alpha $
there are infinitely k such that
$\alpha $
there are infinitely k such that
![]() $(X_\alpha )_k\ne \varnothing $
. Interpret
$(X_\alpha )_k\ne \varnothing $
. Interpret
![]() $\mathbb {C}$
now as
$\mathbb {C}$
now as
![]() $(\,\!^{<\omega }\omega ,\supseteq )$
and for every
$(\,\!^{<\omega }\omega ,\supseteq )$
and for every
![]() $\alpha $
and n let
$\alpha $
and n let
![]() $D_{\alpha ,n}=\{s\in \mathbb {C}:\exists\ k\geq n\ s(k)\in (X_\alpha )_k\}$
. Then
$D_{\alpha ,n}=\{s\in \mathbb {C}:\exists\ k\geq n\ s(k)\in (X_\alpha )_k\}$
. Then
![]() $D_{\alpha ,n}$
is dense in
$D_{\alpha ,n}$
is dense in
![]() $\mathbb {C}$
, and if
$\mathbb {C}$
, and if
![]() $G\subseteq \mathbb {C}$
is a
$G\subseteq \mathbb {C}$
is a
![]() $\{D_{\alpha ,n}:\alpha <\kappa ,n\in \omega \}$
-generic filter, then
$\{D_{\alpha ,n}:\alpha <\kappa ,n\in \omega \}$
-generic filter, then
![]() $g=\bigcup G:\omega \to \omega $
(in particular,
$g=\bigcup G:\omega \to \omega $
(in particular,
![]() $g\in \mathcal {ED}$
) and
$g\in \mathcal {ED}$
) and
![]() $|g\cap X_\alpha |=\omega $
for every
$|g\cap X_\alpha |=\omega $
for every
![]() $\alpha $
, a contradiction.
$\alpha $
, a contradiction.
(1b): We already know that
![]() $\mathrm {cov}^*(\mathcal {ED},+)\leq \mathrm {cov}^*(\mathcal {ED},\infty )=\mathrm {non}(\mathcal {M})$
. To show the reverse inequality, we will need the following characterisation (see [Reference Bartoszyński and Judah3, Lemma 2.4.8]):
$\mathrm {cov}^*(\mathcal {ED},+)\leq \mathrm {cov}^*(\mathcal {ED},\infty )=\mathrm {non}(\mathcal {M})$
. To show the reverse inequality, we will need the following characterisation (see [Reference Bartoszyński and Judah3, Lemma 2.4.8]):
Notice that there is a family witnessing
![]() $\mathrm {cov}^*(\mathcal {ED},+)$
of the form
$\mathrm {cov}^*(\mathcal {ED},+)$
of the form
![]() $\{\{n\}\times \omega :n\in \omega \}\cup \{f_\alpha :\alpha <\kappa \}$
where
$\{\{n\}\times \omega :n\in \omega \}\cup \{f_\alpha :\alpha <\kappa \}$
where
![]() $f_\alpha :\omega \to \omega $
. For every
$f_\alpha :\omega \to \omega $
. For every
![]() $\alpha $
define
$\alpha $
define
![]() $S_\alpha \in \mathcal {C}$
,
$S_\alpha \in \mathcal {C}$
,
![]() $S_\alpha (n)=(X_{f_\alpha })_n=\big [f_\alpha (n)-\lfloor \sqrt {n}\rfloor , f_\alpha (n)+\lfloor \sqrt {n}\rfloor \big ]\cap \omega $
. Using the same argument we used in (1a), one can easily show that
$S_\alpha (n)=(X_{f_\alpha })_n=\big [f_\alpha (n)-\lfloor \sqrt {n}\rfloor , f_\alpha (n)+\lfloor \sqrt {n}\rfloor \big ]\cap \omega $
. Using the same argument we used in (1a), one can easily show that
![]() $\{S_\alpha :\alpha <\kappa \}$
satisfies the conditions in the above characterisation of
$\{S_\alpha :\alpha <\kappa \}$
satisfies the conditions in the above characterisation of
![]() $\mathrm {non}(\mathcal {M})$
, and hence
$\mathrm {non}(\mathcal {M})$
, and hence
![]() $\mathrm {non}(\mathcal {M})\leq \kappa $
.
$\mathrm {non}(\mathcal {M})\leq \kappa $
.
(2): The first “left to right” implication is trivial. The second one is basically [Reference Bartoszyński and Judah3, Lemma 2.4.8, (2)
![]() $\to$
(3)]. We show the third. Assume that in an extension
$\to$
(3)]. We show the third. Assume that in an extension
![]() $W\supseteq V$
there is an
$W\supseteq V$
there is an
![]() $A\in [\omega \times \omega ]^\omega $
such that
$A\in [\omega \times \omega ]^\omega $
such that
![]() $|A\cap B|<\omega $
for every
$|A\cap B|<\omega $
for every
![]() $B\in \mathcal {ED}\cap V$
. By shrinking A can assume that
$B\in \mathcal {ED}\cap V$
. By shrinking A can assume that
![]() $A=\{(n,k_n):n\in E\}$
,
$A=\{(n,k_n):n\in E\}$
,
![]() $E\in [\omega ]^\omega $
is an infinite partial function. Let
$E\in [\omega ]^\omega $
is an infinite partial function. Let
![]() $E=\{n_0<n_1<\cdots \}$
,
$E=\{n_0<n_1<\cdots \}$
,
![]() $\mathrm {FP}=\{$
finite partial functions
$\mathrm {FP}=\{$
finite partial functions
![]() $\omega \to \omega \}$
, and let
$\omega \to \omega \}$
, and let
![]() $f\in \,\!^\omega \mathrm {FP}\cap W$
,
$f\in \,\!^\omega \mathrm {FP}\cap W$
,
![]() $f(m)=\{(n_i,k_{n_i}):i\leq m\}$
. We show that f is an eventually different real over
$f(m)=\{(n_i,k_{n_i}):i\leq m\}$
. We show that f is an eventually different real over
![]() $\,\!^\omega \mathrm {FP}\cap V$
. Let
$\,\!^\omega \mathrm {FP}\cap V$
. Let
![]() $g\in \,\!^\omega \mathrm {FP}\cap V$
and assume on the contrary that
$g\in \,\!^\omega \mathrm {FP}\cap V$
and assume on the contrary that
![]() $f(m)=g(m)$
for infinitely many m. We can assume that
$f(m)=g(m)$
for infinitely many m. We can assume that
![]() $|\mathrm {dom}(g(m))|=m+1$
for every m. Define the infinite partial function
$|\mathrm {dom}(g(m))|=m+1$
for every m. Define the infinite partial function
![]() $g'\in V$
by recursion as follows: Let
$g'\in V$
by recursion as follows: Let
![]() $\mathrm {dom}(g(0))=\{m_0\}$
and
$\mathrm {dom}(g(0))=\{m_0\}$
and
![]() $g'(m_0)=g(0)(m_0)$
. If we already have
$g'(m_0)=g(0)(m_0)$
. If we already have
![]() $m_0,m_1,\dots ,m_{n-1}$
and
$m_0,m_1,\dots ,m_{n-1}$
and
![]() $g'$
is defined on these entries, then pick an
$g'$
is defined on these entries, then pick an
![]() $m_n\in \mathrm {dom}(g(n))\setminus \{m_0,m_1,\dots ,m_{n-1}\}$
and define
$m_n\in \mathrm {dom}(g(n))\setminus \{m_0,m_1,\dots ,m_{n-1}\}$
and define
![]() $g'(m_n)=g(n)(m_n)$
. It is trivial to show that
$g'(m_n)=g(n)(m_n)$
. It is trivial to show that
![]() $|A\cap g'|=\omega $
, a contradiction.
$|A\cap g'|=\omega $
, a contradiction.
Finally we show that if
![]() $f\in \,\!^\omega \omega \cap W$
is an eventually different real over V then
$f\in \,\!^\omega \omega \cap W$
is an eventually different real over V then
![]() $\mathcal {ED}\cap V$
is
$\mathcal {ED}\cap V$
is
![]() $+$
-destroyed in W. Fix an interval partition
$+$
-destroyed in W. Fix an interval partition
![]() $(P_n)_{n\in \omega }$
in V such that
$(P_n)_{n\in \omega }$
in V such that
![]() $|P_n|=n+1$
, and fix enumerations
$|P_n|=n+1$
, and fix enumerations
![]() $\{(a^n_i,b^n_i):i\in \omega \}=P_n\times \omega $
. Define
$\{(a^n_i,b^n_i):i\in \omega \}=P_n\times \omega $
. Define
![]() $X=\{(n,i):f(a^n_i)=b^n_i\}\in \mathcal {ED}^+\cap W$
(because
$X=\{(n,i):f(a^n_i)=b^n_i\}\in \mathcal {ED}^+\cap W$
(because
![]() $|(X)_n|=n+1$
). We claim that
$|(X)_n|=n+1$
). We claim that
![]() $X\ +$
-destroys
$X\ +$
-destroys
![]() $\mathcal {ED}\cap V$
. Let
$\mathcal {ED}\cap V$
. Let
![]() $g\in \,\!^\omega \omega \cap V$
and assume on the contrary that
$g\in \,\!^\omega \omega \cap V$
and assume on the contrary that
![]() $|X\cap g|=\omega $
. Define
$|X\cap g|=\omega $
. Define
![]() $g'\in \,\!^\omega \omega \cap V$
as follows: If
$g'\in \,\!^\omega \omega \cap V$
as follows: If
![]() $g(n)=i$
then let
$g(n)=i$
then let
![]() $g' \!\upharpoonright \! P_n\equiv b^n_i$
. It follows that
$g' \!\upharpoonright \! P_n\equiv b^n_i$
. It follows that
![]() $f(a)=g'(a)$
for infinitely many a, a contradiction.⊣
$f(a)=g'(a)$
for infinitely many a, a contradiction.⊣
Cardinal invariants of
![]() $\mathcal {ED}_{\mathrm {fin}}$
are more intriguing (see [Reference Hrušák and Meza-Alcántara25]):
$\mathcal {ED}_{\mathrm {fin}}$
are more intriguing (see [Reference Hrušák and Meza-Alcántara25]):
![]() $\mathrm {add}^*(\mathcal {ED}_{\mathrm {fin}},\infty )=\omega $
,
$\mathrm {add}^*(\mathcal {ED}_{\mathrm {fin}},\infty )=\omega $
,
![]() $\mathrm {cof}^*(\mathcal {ED}_{\mathrm {fin}},\infty )=\mathfrak {c}$
,
$\mathrm {cof}^*(\mathcal {ED}_{\mathrm {fin}},\infty )=\mathfrak {c}$
,
![]() $\mathfrak {s}\leq \mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
,
$\mathfrak {s}\leq \mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
,
![]() $\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )\leq \mathfrak {r}$
(where
$\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )\leq \mathfrak {r}$
(where
![]() $\mathfrak {s}$
and
$\mathfrak {s}$
and
![]() $\mathfrak {r}$
are the slitting and reaping numbers), furthermore,
$\mathfrak {r}$
are the slitting and reaping numbers), furthermore,
![]() $\mathrm {cov}(\mathcal {M})=\min \{\mathfrak {d},\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )\}$
, and
$\mathrm {cov}(\mathcal {M})=\min \{\mathfrak {d},\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )\}$
, and
![]() $\mathrm {non}(\mathcal {M})=\max \{\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty ),\mathfrak {b}\}$
.
$\mathrm {non}(\mathcal {M})=\max \{\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty ),\mathfrak {b}\}$
.
Proposition 4.6.
-
(1)
 $\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},+)=\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
and
$\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},+)=\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
and
 $\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},+)=\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
.
$\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},+)=\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
. -
(2)
 $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
 $\mathcal {ED}_{\mathrm {fin}}$
iff
$\mathcal {ED}_{\mathrm {fin}}$
iff
 $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
 $\mathcal {ED}_{\mathrm {fin}}$
iff
$\mathcal {ED}_{\mathrm {fin}}$
iff
 $\mathbb {P}$
adds an eventually different infinite partial function
$\mathbb {P}$
adds an eventually different infinite partial function
 $f\subseteq \Delta $
iff
$f\subseteq \Delta $
iff
 $\mathbb {P}$
adds an eventually different infinite partial function bounded by a ground model real.
$\mathbb {P}$
adds an eventually different infinite partial function bounded by a ground model real.
Proof. (1): For every
![]() $n\in \omega $
fix a partition
$n\in \omega $
fix a partition
![]() $\{P^n_k:k\leq n\}$
of
$\{P^n_k:k\leq n\}$
of
![]() $(\Delta )_{(n+1)^2-1}=\{((n+1)^2-1,i):i< (n+1)^2\}$
such that
$(\Delta )_{(n+1)^2-1}=\{((n+1)^2-1,i):i< (n+1)^2\}$
such that
![]() $|P^n_k|=n+1$
for every k, and define the following functions:
$|P^n_k|=n+1$
for every k, and define the following functions:
-
(i)
 $f:\Delta \to [\Delta ]^{<\omega }$
,
$f:\Delta \to [\Delta ]^{<\omega }$
,
 $f(n,k)=P^n_k$
;
$f(n,k)=P^n_k$
; -
(ii)
 $\alpha :[\Delta ]^\omega \to \mathcal {ED}_{\mathrm {fin}}^+$
,
$\alpha :[\Delta ]^\omega \to \mathcal {ED}_{\mathrm {fin}}^+$
,
 $\alpha (X)=\bigcup \{f(n,k):(n,k)\in X\}$
; and
$\alpha (X)=\bigcup \{f(n,k):(n,k)\in X\}$
; and -
(iii)
 $\beta :\mathcal {ED}_{\mathrm {fin}}\to \mathcal {ED}_{\mathrm {fin}}$
,
$\beta :\mathcal {ED}_{\mathrm {fin}}\to \mathcal {ED}_{\mathrm {fin}}$
,
 $\beta (A)=\{(n,k):f(n,k)\cap A\ne \varnothing \}$
.
$\beta (A)=\{(n,k):f(n,k)\cap A\ne \varnothing \}$
.
We know that
![]() $\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},+)\geq \mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
and
$\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},+)\geq \mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
and
![]() $\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},+)\leq \mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
. Now, if
$\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},+)\leq \mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
. Now, if
![]() $\mathcal {X}\subseteq [\Delta ]^\omega $
witnesses
$\mathcal {X}\subseteq [\Delta ]^\omega $
witnesses
![]() $\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
then
$\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
then
![]() $\alpha [\mathcal {X}]=\{\alpha (X):X\in \mathcal {X}\}$
witnesses
$\alpha [\mathcal {X}]=\{\alpha (X):X\in \mathcal {X}\}$
witnesses
![]() $\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},+)$
: Otherwise, if
$\mathrm {non}^*(\mathcal {ED}_{\mathrm {fin}},+)$
: Otherwise, if
![]() $A\in \mathcal {ED}_{\mathrm {fin}}$
and
$A\in \mathcal {ED}_{\mathrm {fin}}$
and
![]() $|A\cap \alpha (X)|=\omega $
for every
$|A\cap \alpha (X)|=\omega $
for every
![]() $X\in \mathcal {X}$
, then
$X\in \mathcal {X}$
, then
![]() $|\beta (A)\cap X|=\omega $
for every
$|\beta (A)\cap X|=\omega $
for every
![]() $X\in \mathcal {X}$
, a contradiction. Similarly, if
$X\in \mathcal {X}$
, a contradiction. Similarly, if
![]() $\mathcal {A}\subseteq \mathcal {ED}_{\mathrm {fin}}$
witnesses
$\mathcal {A}\subseteq \mathcal {ED}_{\mathrm {fin}}$
witnesses
![]() $\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},+)$
then
$\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},+)$
then
![]() $\beta [\mathcal {A}]$
witnesses
$\beta [\mathcal {A}]$
witnesses
![]() $\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
: Otherwise, if
$\mathrm {cov}^*(\mathcal {ED}_{\mathrm {fin}},\infty )$
: Otherwise, if
![]() $Y\in [\Delta ]^\omega $
has finite intersection with all
$Y\in [\Delta ]^\omega $
has finite intersection with all
![]() $\beta (A)$
, then
$\beta (A)$
, then
![]() $\alpha (Y)\in \mathcal {ED}_{\mathrm {fin}}^+$
has finite intersection with all
$\alpha (Y)\in \mathcal {ED}_{\mathrm {fin}}^+$
has finite intersection with all
![]() $Y\in \mathcal {A}$
, a contradiction.
$Y\in \mathcal {A}$
, a contradiction.
(2): All “left to right” implications are trivial. Assume now that
![]() $V\subseteq W$
is an extension and
$V\subseteq W$
is an extension and
![]() $g\in W$
is an eventually different infinite partial function over V,
$g\in W$
is an eventually different infinite partial function over V,
![]() $g\leq h\in \omega ^\omega \cap V$
. We can assume that h is strictly increasing. It is straightforward to show that
$g\leq h\in \omega ^\omega \cap V$
. We can assume that h is strictly increasing. It is straightforward to show that
![]() $X=\{(h(n),g(n)):n\in \omega \}\subseteq \Delta $
is also an eventually different infinite partial function over V, and hence
$X=\{(h(n),g(n)):n\in \omega \}\subseteq \Delta $
is also an eventually different infinite partial function over V, and hence
![]() $\alpha (X)\ +$
-destroys
$\alpha (X)\ +$
-destroys
![]() $\mathcal {ED}_{\mathrm {fin}}\cap V$
.⊣
$\mathcal {ED}_{\mathrm {fin}}\cap V$
.⊣
4.3 Around
 $\mathcal {S}$
$\mathcal {S}$
We know (see [Reference Meza-Alcántara37, Theorem 1.6.2]) that
![]() $\mathrm {non}^*(\mathcal {S},\infty )=\omega $
,
$\mathrm {non}^*(\mathcal {S},\infty )=\omega $
,
![]() $\mathrm {cov}^*(\mathcal {S},\infty )=\mathrm {non}(\mathcal {N})$
, and
$\mathrm {cov}^*(\mathcal {S},\infty )=\mathrm {non}(\mathcal {N})$
, and
![]() $\mathrm {cof}^*(\mathcal {S},\infty )=\mathfrak {c}$
.
$\mathrm {cof}^*(\mathcal {S},\infty )=\mathfrak {c}$
.
Proposition 4.7. (basically [Reference Meza-Alcántara37, Theorem 1.6.2])
-
(1a)
 $\ \ \mathrm {non}^*(\mathcal {S},+)=\omega $
.
$\ \ \mathrm {non}^*(\mathcal {S},+)=\omega $
. -
(1b)
 $\ \ \mathrm {cov}^*(\mathcal {S},+)=\mathrm {non}(\mathcal {N})$
.
$\ \ \mathrm {cov}^*(\mathcal {S},+)=\mathrm {non}(\mathcal {N})$
. -
(2)
 $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
 $\mathcal {S}$
iff
$\mathcal {S}$
iff
 $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
 $\mathcal {S}$
iff
$\mathcal {S}$
iff
 $\Vdash _{\mathbb {P}} \,\!^\omega 2\cap V\in \mathcal {N}$
.
$\Vdash _{\mathbb {P}} \,\!^\omega 2\cap V\in \mathcal {N}$
.
Proof. (1a): Let
![]() $\mathcal {F}=\{F\in [\,\!^{<\omega }2]^{<\omega }\setminus \{\varnothing \}:\sum _{t\in F} 2^{-|t|}\leq 1/4\}$
and for every
$\mathcal {F}=\{F\in [\,\!^{<\omega }2]^{<\omega }\setminus \{\varnothing \}:\sum _{t\in F} 2^{-|t|}\leq 1/4\}$
and for every
![]() $F\in \mathcal {F}$
define the clopen set
$F\in \mathcal {F}$
define the clopen set
![]() $U_F=\bigcup _{t\in F}\{x\in \,\!^\omega 2:t\subseteq x\}$
and the family
$U_F=\bigcup _{t\in F}\{x\in \,\!^\omega 2:t\subseteq x\}$
and the family
![]() $\mathcal {U}_F=\{C\in \Omega :C\cap U_F=\varnothing \}$
. Notice that
$\mathcal {U}_F=\{C\in \Omega :C\cap U_F=\varnothing \}$
. Notice that
![]() $\mathcal {U}_F\in \mathcal {S}^+$
because if
$\mathcal {U}_F\in \mathcal {S}^+$
because if
![]() $X\subseteq \,\!^\omega 2$
is finite then
$X\subseteq \,\!^\omega 2$
is finite then
![]() $U_F\cup X$
is a closed set of measure
$U_F\cup X$
is a closed set of measure
![]() $\leq 1/4<1/2$
and hence there is a clopen set C of measure
$\leq 1/4<1/2$
and hence there is a clopen set C of measure
![]() $1/2$
inside its complement; therefore,
$1/2$
inside its complement; therefore,
![]() $\mathcal {U}_F\nsubseteq \bigcup _{x\in X}\mathcal {C}_x$
. We show that for every
$\mathcal {U}_F\nsubseteq \bigcup _{x\in X}\mathcal {C}_x$
. We show that for every
![]() $\mathcal {A}\in \mathcal {S}$
there is an
$\mathcal {A}\in \mathcal {S}$
there is an
![]() $F\in \mathcal {F}$
such that
$F\in \mathcal {F}$
such that
![]() $\mathcal {A}\cap \mathcal {U}_F=\varnothing $
, i.e., that
$\mathcal {A}\cap \mathcal {U}_F=\varnothing $
, i.e., that
![]() $\{\mathcal {U}_F:F\in \mathcal {F}\}$
witnesses
$\{\mathcal {U}_F:F\in \mathcal {F}\}$
witnesses
![]() $\mathrm {non}^*(\mathcal {S},+)=\omega $
. Let
$\mathrm {non}^*(\mathcal {S},+)=\omega $
. Let
![]() $\{x_i:i<k\}\subseteq \,\!^\omega 2$
be finite. Pick finite initials
$\{x_i:i<k\}\subseteq \,\!^\omega 2$
be finite. Pick finite initials
![]() $t_i\subseteq x_i$
such that
$t_i\subseteq x_i$
such that
![]() $\sum _{i<k}2^{-|t_i|}\leq 1/4$
and let
$\sum _{i<k}2^{-|t_i|}\leq 1/4$
and let
![]() $F=\{t_i:i<k\}\in \mathcal {F}$
, then
$F=\{t_i:i<k\}\in \mathcal {F}$
, then
![]() $\mathcal {U}_F\cap \bigcup _{i<k}\mathcal {C}_{x_i}=\varnothing $
(because
$\mathcal {U}_F\cap \bigcup _{i<k}\mathcal {C}_{x_i}=\varnothing $
(because
![]() $x_i\in U_F$
for every i, and
$x_i\in U_F$
for every i, and
![]() $C\cap U_F=\varnothing $
for every
$C\cap U_F=\varnothing $
for every
![]() $C\in \mathcal {U}_F$
).
$C\in \mathcal {U}_F$
).
(1b): Let
![]() $\lambda ^*$
be the Lebesgue outer measure on
$\lambda ^*$
be the Lebesgue outer measure on
![]() $\,\!^\omega 2$
. We show that if
$\,\!^\omega 2$
. We show that if
![]() $\lambda ^*(Y)<1/2$
then there is an
$\lambda ^*(Y)<1/2$
then there is an
![]() $\mathcal {S}$
-positive
$\mathcal {S}$
-positive
![]() $\mathcal {D}\subseteq \Omega $
such that
$\mathcal {D}\subseteq \Omega $
such that
![]() $|\mathcal {C}_y\cap \mathcal {D}|<\omega $
for every
$|\mathcal {C}_y\cap \mathcal {D}|<\omega $
for every
![]() $y\in Y$
. This implies that
$y\in Y$
. This implies that
![]() $\mathrm {non}(\mathcal {N})\leq \mathrm {cov}^*(\mathcal {S},+)$
, and the reverse inequality follows from
$\mathrm {non}(\mathcal {N})\leq \mathrm {cov}^*(\mathcal {S},+)$
, and the reverse inequality follows from
![]() $\mathrm {cov}^*(\mathcal {S},+)\leq \mathrm {cov}^*(\mathcal {S},\infty )=\mathrm {non}(\mathcal {N})$
.
$\mathrm {cov}^*(\mathcal {S},+)\leq \mathrm {cov}^*(\mathcal {S},\infty )=\mathrm {non}(\mathcal {N})$
.
Fix an increasing sequence of clopen sets
![]() $U_n$
such that
$U_n$
such that
![]() $Y\subseteq \bigcup _{n\in \omega }U_n$
and the measure of this union is less than
$Y\subseteq \bigcup _{n\in \omega }U_n$
and the measure of this union is less than
![]() $1/2-\varepsilon $
for some
$1/2-\varepsilon $
for some
![]() $\varepsilon>0$
. Enumerate
$\varepsilon>0$
. Enumerate
![]() $\{V_n:n\in \omega \}$
all clopen sets of measure
$\{V_n:n\in \omega \}$
all clopen sets of measure
![]() $<\varepsilon $
and for each n pick a
$<\varepsilon $
and for each n pick a
![]() $C_n\in \Omega $
such that
$C_n\in \Omega $
such that
![]() $C_n\cap (U_n\cup V_n)=\varnothing $
(this is possible because
$C_n\cap (U_n\cup V_n)=\varnothing $
(this is possible because
![]() $U_n\cup V_n$
is a closed set of measure
$U_n\cup V_n$
is a closed set of measure
![]() $<1/2$
). The set
$<1/2$
). The set
![]() $\mathcal {D}=\{C_n:n\in \omega \}$
is
$\mathcal {D}=\{C_n:n\in \omega \}$
is
![]() $\mathcal {S}$
-positive because if
$\mathcal {S}$
-positive because if
![]() $X\subseteq \,\!^\omega 2$
is finite, then
$X\subseteq \,\!^\omega 2$
is finite, then
![]() $X\subseteq V_n$
for some n, hence
$X\subseteq V_n$
for some n, hence
![]() $C_n\notin \bigcup _{x\in X} \mathcal {C}_x$
(and so
$C_n\notin \bigcup _{x\in X} \mathcal {C}_x$
(and so
![]() $\mathcal {D}\nsubseteq \bigcup _{x\in X} \mathcal {C}_x$
). Also, if
$\mathcal {D}\nsubseteq \bigcup _{x\in X} \mathcal {C}_x$
). Also, if
![]() $y\in Y$
, then
$y\in Y$
, then
![]() $y\in U_n$
in particular
$y\in U_n$
in particular
![]() $y\notin C_n$
for every large enough n, and hence
$y\notin C_n$
for every large enough n, and hence
![]() $|\mathcal {D}\cap \mathcal {C}_y|<\omega $
.
$|\mathcal {D}\cap \mathcal {C}_y|<\omega $
.
(2): The first “only if” implication is trivial.
Now assume that
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {S}$
. We will need the following result (see [Reference Meza-Alcántara37, Lemma 1.6.3(b)]): If
$\mathcal {S}$
. We will need the following result (see [Reference Meza-Alcántara37, Lemma 1.6.3(b)]): If
![]() $\lambda ^*(Y)>1/2$
then for every infinite
$\lambda ^*(Y)>1/2$
then for every infinite
![]() $\mathcal {D}\subseteq \Omega $
there is a
$\mathcal {D}\subseteq \Omega $
there is a
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $|\mathcal {D}\cap \mathcal {C}_y|=\omega $
. This implies that
$|\mathcal {D}\cap \mathcal {C}_y|=\omega $
. This implies that
![]() $\Vdash _{\mathbb {P}}\lambda ^*(\,\!^\omega 2\cap V)\leq 1/2$
. Notice that
$\Vdash _{\mathbb {P}}\lambda ^*(\,\!^\omega 2\cap V)\leq 1/2$
. Notice that
![]() $\Vdash _{\mathbb {P}}$
“
$\Vdash _{\mathbb {P}}$
“
![]() $\lambda ^*(\,\!^\omega 2\cap V)=0$
or
$\lambda ^*(\,\!^\omega 2\cap V)=0$
or
![]() $1$
” holds for every
$1$
” holds for every
![]() $\mathbb {P}$
: If
$\mathbb {P}$
: If
![]() $V[G]\models \lambda ^*(\,\!^\omega 2\cap V)<1$
then there is a compact set
$V[G]\models \lambda ^*(\,\!^\omega 2\cap V)<1$
then there is a compact set
![]() $C\in V[G]$
of positive measure which is disjoint from V, and hence, applying the
$C\in V[G]$
of positive measure which is disjoint from V, and hence, applying the
![]() $0$
–
$0$
–
![]() $1$
law, the
$1$
law, the
![]() $F_\sigma $
tail-set
$F_\sigma $
tail-set
![]() $\{x\in \,\!^\omega 2:\exists\ y\in C |x\vartriangle y|<\omega \}$
generated by C is of measure
$\{x\in \,\!^\omega 2:\exists\ y\in C |x\vartriangle y|<\omega \}$
generated by C is of measure
![]() $1$
, and of course, this set is also disjoint from V. We conclude that
$1$
, and of course, this set is also disjoint from V. We conclude that
![]() $\Vdash _{\mathbb {P}} \,\!^\omega 2\cap V\in \mathcal {N}$
.
$\Vdash _{\mathbb {P}} \,\!^\omega 2\cap V\in \mathcal {N}$
.
Finally, the result we proved and applied in (1b) implies that if
![]() $\Vdash _{\mathbb {P}} \,\!^\omega 2\cap V\in \mathcal {N}$
then
$\Vdash _{\mathbb {P}} \,\!^\omega 2\cap V\in \mathcal {N}$
then
![]() $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
![]() $\mathcal {S}$
.⊣
$\mathcal {S}$
.⊣
4.4 Around
 $\mathrm {Nwd}$
$\mathrm {Nwd}$
We know (see [Reference Balcar, Hernández-Hernández and Hrušák1]) that
![]() $\mathrm {non}^*(\mathrm {Nwd},\infty )=\omega $
,
$\mathrm {non}^*(\mathrm {Nwd},\infty )=\omega $
,
![]() $\mathrm {cov}^*(\mathrm {Nwd},\infty )=\mathrm {cov}(\mathcal {M})$
, and
$\mathrm {cov}^*(\mathrm {Nwd},\infty )=\mathrm {cov}(\mathcal {M})$
, and
![]() $\mathrm {cof}^*(\mathrm {Nwd},\infty )=\mathrm {cof}(\mathcal {M})$
.
$\mathrm {cof}^*(\mathrm {Nwd},\infty )=\mathrm {cof}(\mathcal {M})$
.
Proposition 4.8.
-
(1) (see [Reference Balcar, Hernández-Hernández and Hrušák1, Reference Keremedis30])
 $\mathrm {non}^*(\mathrm {Nwd},+)=\omega $
and
$\mathrm {non}^*(\mathrm {Nwd},+)=\omega $
and
 $\mathrm {cov}^*(\mathrm {Nwd},+)=\mathrm {add}(\mathcal {M})$
.
$\mathrm {cov}^*(\mathrm {Nwd},+)=\mathrm {add}(\mathcal {M})$
. -
(2) If
 $\mathbb {P}$
adds Cohen reals then it destroys
$\mathbb {P}$
adds Cohen reals then it destroys
 $\mathrm {Nwd}$
. If
$\mathrm {Nwd}$
. If
 $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
 $\mathrm {Nwd}$
then it adds both dominating and Cohen reals.
$\mathrm {Nwd}$
then it adds both dominating and Cohen reals. -
(2-cd) (see [Reference Balcar, Hernández-Hernández and Hrušák1]) If
 $\mathbb {P}$
adds a Cohen real and
$\mathbb {P}$
adds a Cohen real and
 $\Vdash _{\mathbb {P}}$
“
$\Vdash _{\mathbb {P}}$
“
 $\mathring {\mathbb {Q}}$
adds a dominating real,” then
$\mathring {\mathbb {Q}}$
adds a dominating real,” then
 $\mathbb {P}\ast \mathring {\mathbb {Q}}\ +$
-destroys
$\mathbb {P}\ast \mathring {\mathbb {Q}}\ +$
-destroys
 $\mathrm {Nwd}$
.
$\mathrm {Nwd}$
. -
(2-dc) Adding first a dominating then a Cohen real does not necessarily
 $+$
-destroy
$+$
-destroy
 $\mathrm {Nwd}$
: If
$\mathrm {Nwd}$
: If
 $\mathbb {P}$
has the Laver property then
$\mathbb {P}$
has the Laver property then
 $\mathbb {P}$
cannot destroy
$\mathbb {P}$
cannot destroy
 $\mathrm {Nwd}$
and
$\mathrm {Nwd}$
and
 $\mathbb {P}\ast \mathbb {C}$
cannot
$\mathbb {P}\ast \mathbb {C}$
cannot
 $+$
-destroy
$+$
-destroy
 $\mathrm {Nwd}$
.
$\mathrm {Nwd}$
.
Proof. (1): A countable base of the topology witnesses
![]() $\mathrm {non}^*(\mathrm {Nwd},+)=\omega $
, and reformulating a result from [Reference Keremedis30] (see also in [Reference Balcar, Hernández-Hernández and Hrušák1]) shows that
$\mathrm {non}^*(\mathrm {Nwd},+)=\omega $
, and reformulating a result from [Reference Keremedis30] (see also in [Reference Balcar, Hernández-Hernández and Hrušák1]) shows that
![]() $\mathrm {cov}^*(\mathrm {Nwd},+)=\mathrm {add}(\mathcal {M})$
.
$\mathrm {cov}^*(\mathrm {Nwd},+)=\mathrm {add}(\mathcal {M})$
.
(2): We already know that
![]() $\mathbb {C}=\mathbb {P}_{\mathcal {M}}$
destroys
$\mathbb {C}=\mathbb {P}_{\mathcal {M}}$
destroys
![]() $\mathrm {tr}(\mathcal {M})\simeq \mathrm {Nwd}$
, and hence adding a Cohen real destroys
$\mathrm {tr}(\mathcal {M})\simeq \mathrm {Nwd}$
, and hence adding a Cohen real destroys
![]() $\mathrm {Nwd}$
.
$\mathrm {Nwd}$
.
First we show that if
![]() $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
![]() $\mathrm {Nwd}$
, then
$\mathrm {Nwd}$
, then
![]() $\mathbb {P}$
adds a dominating real. For now let
$\mathbb {P}$
adds a dominating real. For now let
![]() $\mathrm {Nwd}=\{A\subseteq \,\!^{<\omega } 2:\forall \ s\ \exists \ t\ (s\subseteq t$
and
$\mathrm {Nwd}=\{A\subseteq \,\!^{<\omega } 2:\forall \ s\ \exists \ t\ (s\subseteq t$
and
![]() $A\cap t^\uparrow =\varnothing )\}$
, and let
$A\cap t^\uparrow =\varnothing )\}$
, and let
![]() $\mathring {X}$
be a
$\mathring {X}$
be a
![]() $\mathbb {P}$
-name such that
$\mathbb {P}$
-name such that
![]() $\Vdash _{\mathbb {P}}\mathring {X}\in \mathrm {Nwd}^+$
and
$\Vdash _{\mathbb {P}}\mathring {X}\in \mathrm {Nwd}^+$
and
![]() $\Vdash _{\mathbb {P}}|\mathring {X}\cap A|<\omega $
for every
$\Vdash _{\mathbb {P}}|\mathring {X}\cap A|<\omega $
for every
![]() $A\in \mathrm {Nwd}\cap V$
. We can assume that
$A\in \mathrm {Nwd}\cap V$
. We can assume that
![]() $\mathring {X}$
is dense in
$\mathring {X}$
is dense in
![]() $\,\!^{<\omega } 2$
, that is,
$\,\!^{<\omega } 2$
, that is,
![]() $\Vdash _{\mathbb {P}}\forall \ s\ \exists \ t\in \mathring {X} s\subseteq t$
(because there is a
$\Vdash _{\mathbb {P}}\forall \ s\ \exists \ t\in \mathring {X} s\subseteq t$
(because there is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\mathring {t}$
for a node in
$\mathring {t}$
for a node in
![]() $\,\!^{<\omega } 2$
such that
$\,\!^{<\omega } 2$
such that
![]() $\Vdash _{\mathbb {P}}$
“
$\Vdash _{\mathbb {P}}$
“
![]() $\mathring {X}$
is dense in
$\mathring {X}$
is dense in
![]() $\mathring {t}^\uparrow $
” and the proof below can be easily relativized to
$\mathring {t}^\uparrow $
” and the proof below can be easily relativized to
![]() $\mathring {t}^\uparrow \simeq \,\!^{<\omega } 2$
). Let
$\mathring {t}^\uparrow \simeq \,\!^{<\omega } 2$
). Let
![]() $\mathring {f}$
be a
$\mathring {f}$
be a
![]() $\mathbb {P}$
-name for an element of
$\mathbb {P}$
-name for an element of
![]() $\,\!^\omega \omega $
such that
$\,\!^\omega \omega $
such that
We claim that
![]() $\mathring {f}$
is dominating over
$\mathring {f}$
is dominating over
![]() $\,\!^\omega \omega \cap V$
: Let
$\,\!^\omega \omega \cap V$
: Let
![]() $g\in \,\!^\omega \omega \cap V$
be strictly increasing and satisfying
$g\in \,\!^\omega \omega \cap V$
be strictly increasing and satisfying
![]() $g(0)>1$
. Fix an infinite maximal antichain
$g(0)>1$
. Fix an infinite maximal antichain
![]() $\{a_n:n\in \omega \}\subseteq \,\!^{<\omega } 2$
such that
$\{a_n:n\in \omega \}\subseteq \,\!^{<\omega } 2$
such that
![]() $|a_n|=g(n)$
, and let
$|a_n|=g(n)$
, and let
![]() $A=\,\!^{<\omega } 2\setminus \bigcup \{a_n^\uparrow :n\in \omega \}\in \mathrm {Nwd}$
. It is easy to see that
$A=\,\!^{<\omega } 2\setminus \bigcup \{a_n^\uparrow :n\in \omega \}\in \mathrm {Nwd}$
. It is easy to see that
![]() $|A\cap \,\!^n 2|\geq 2^{n-1}$
for every n. We know that in the extension
$|A\cap \,\!^n 2|\geq 2^{n-1}$
for every n. We know that in the extension
![]() $A\cap \mathring {X}\subseteq \,\!^{\leq N} 2$
for an
$A\cap \mathring {X}\subseteq \,\!^{\leq N} 2$
for an
![]() $N\in \omega $
. Now if
$N\in \omega $
. Now if
![]() $n>N$
then we can pick a point
$n>N$
then we can pick a point
![]() $s\in A\cap \,\!^n 2$
such that
$s\in A\cap \,\!^n 2$
such that
![]() $s\nsubseteq a_k$
for
$s\nsubseteq a_k$
for
![]() $k<n$
. As there can be no
$k<n$
. As there can be no
![]() $a_k$
below s,
$a_k$
below s,
![]() $K=\min \{k:s\subseteq a_k\}<\omega $
, and
$K=\min \{k:s\subseteq a_k\}<\omega $
, and
![]() $|a_K|>K\geq n$
. In particular,
$|a_K|>K\geq n$
. In particular,
![]() $s^\uparrow \cap \,\!^{<|a_K|}2\subseteq A$
, and hence
$s^\uparrow \cap \,\!^{<|a_K|}2\subseteq A$
, and hence
![]() $\mathring {f}(n)\geq \min \{|t|:s\subseteq t\in \mathring {X}\}\geq |a_K|=g(K)\geq g(n)$
.
$\mathring {f}(n)\geq \min \{|t|:s\subseteq t\in \mathring {X}\}\geq |a_K|=g(K)\geq g(n)$
.
Now we show that if
![]() $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
![]() $\mathrm {Nwd}$
, then it adds Cohen reals. Let
$\mathrm {Nwd}$
, then it adds Cohen reals. Let
![]() $\mathring {X}$
be as above, then in the extension
$\mathring {X}$
be as above, then in the extension
![]() $[\mathring {X}]_\delta \ne \varnothing $
. We show that every element y of this set is Cohen over V: If
$[\mathring {X}]_\delta \ne \varnothing $
. We show that every element y of this set is Cohen over V: If
![]() $C\subseteq \,\!^\omega 2$
is a closed and nowhere dense set coded in V, then there is a tree
$C\subseteq \,\!^\omega 2$
is a closed and nowhere dense set coded in V, then there is a tree
![]() $T\subseteq \,\!^{<\omega }2$
,
$T\subseteq \,\!^{<\omega }2$
,
![]() $T\in \mathrm {Nwd}$
such that
$T\in \mathrm {Nwd}$
such that
![]() $C=[T]_\delta =[T]:=\{x\in \,\!^\omega 2:\forall \ n\ x\!\upharpoonright \! n\in T\}$
, in particular
$C=[T]_\delta =[T]:=\{x\in \,\!^\omega 2:\forall \ n\ x\!\upharpoonright \! n\in T\}$
, in particular
![]() $|\mathring {X}\cap T|<\omega $
and hence
$|\mathring {X}\cap T|<\omega $
and hence
![]() $y\notin [T]$
.
$y\notin [T]$
.
(2-cd): This is basically [Reference Balcar, Hernández-Hernández and Hrušák1, Theorem 1.4(ii)]. Let G be
![]() $(V,\mathbb {P})$
-generic,
$(V,\mathbb {P})$
-generic,
![]() $c\in \,\!^\omega 2\cap V[G]$
be Cohen over V, H be
$c\in \,\!^\omega 2\cap V[G]$
be Cohen over V, H be
![]() $(V[G],\mathring {\mathbb {Q}}[G])$
-generic, and
$(V[G],\mathring {\mathbb {Q}}[G])$
-generic, and
![]() $d\in \,\!^\omega \omega \cap V[G,H]$
be dominating over
$d\in \,\!^\omega \omega \cap V[G,H]$
be dominating over
![]() $V[G]$
. Enumerate
$V[G]$
. Enumerate
![]() $\,\!^{<\omega } 2=\{t_n:n\in \omega \}$
in V and for every n define
$\,\!^{<\omega } 2=\{t_n:n\in \omega \}$
in V and for every n define
![]() $c_n\in \,\!^\omega 2\cap V[G]$
as
$c_n\in \,\!^\omega 2\cap V[G]$
as
![]() $c_n=t_n^\frown (c(k):k\geq |t_n|)$
, then
$c_n=t_n^\frown (c(k):k\geq |t_n|)$
, then
![]() $c_n$
is also Cohen over V, and let
$c_n$
is also Cohen over V, and let
![]() $X=\{c_n\!\upharpoonright \! m:n\in \omega ,m\geq d(n)\}\in V[G,H]$
. Notice that X is dense in
$X=\{c_n\!\upharpoonright \! m:n\in \omega ,m\geq d(n)\}\in V[G,H]$
. Notice that X is dense in
![]() $\,\!^{<\omega } 2$
. Now if
$\,\!^{<\omega } 2$
. Now if
![]() $A\in \mathrm {Nwd}\cap V$
then
$A\in \mathrm {Nwd}\cap V$
then
![]() $|A\cap \{c_n\!\upharpoonright \! m:m\in \omega \}|<\omega $
, in particular
$|A\cap \{c_n\!\upharpoonright \! m:m\in \omega \}|<\omega $
, in particular
is well defined, and
![]() $f_A\in \,\!^\omega \omega \cap V[G]$
. We know that
$f_A\in \,\!^\omega \omega \cap V[G]$
. We know that
![]() $f_A(n)\leq d(n)$
for every
$f_A(n)\leq d(n)$
for every
![]() $n\geq N_A$
for some
$n\geq N_A$
for some
![]() $N_A\in \omega $
, and hence
$N_A\in \omega $
, and hence
![]() $X\cap A\subseteq \{c_n\!\upharpoonright \! m:n<N_A,m<f_A(n)\}$
.
$X\cap A\subseteq \{c_n\!\upharpoonright \! m:n<N_A,m<f_A(n)\}$
.
(2-dc): If
![]() $\mathring {X}$
is a
$\mathring {X}$
is a
![]() $\mathbb {P}$
-name,
$\mathbb {P}$
-name,
![]() $p\in \mathbb {P}$
, and
$p\in \mathbb {P}$
, and
![]() $p\Vdash \mathring {X}\in [\,\!^{<\omega } 2]^\omega $
, then we can assume that
$p\Vdash \mathring {X}\in [\,\!^{<\omega } 2]^\omega $
, then we can assume that
![]() $\mathring {X}$
is either (i) an infinite chain, that is,
$\mathring {X}$
is either (i) an infinite chain, that is,
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\mathring {X}=\{\mathring {s}_0\subsetneq \mathring {s}_1\subsetneq \dots \}$
and
$\mathring {X}=\{\mathring {s}_0\subsetneq \mathring {s}_1\subsetneq \dots \}$
and
![]() $\mathring {s}_k\subseteq \mathring {x}\in \,\!^\omega 2$
for every k,” or (ii) a converging antichain, that is, there is a
$\mathring {s}_k\subseteq \mathring {x}\in \,\!^\omega 2$
for every k,” or (ii) a converging antichain, that is, there is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\mathring {y}$
such that
$\mathring {y}$
such that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\mathring {y}\in \,\!^\omega 2$
and
$\mathring {y}\in \,\!^\omega 2$
and
![]() $\forall \ n\ \forall ^\infty \ s\in \mathring {X}\ \mathring {y}\!\upharpoonright \! n\subseteq s$
.”
$\forall \ n\ \forall ^\infty \ s\in \mathring {X}\ \mathring {y}\!\upharpoonright \! n\subseteq s$
.”
In the first case, as
![]() $\mathbb {P}$
satisfies the Laver-property,
$\mathbb {P}$
satisfies the Laver-property,
![]() $\mathring {x}$
cannot be a Cohen real over V, and hence a
$\mathring {x}$
cannot be a Cohen real over V, and hence a
![]() $q\leq p$
forces that
$q\leq p$
forces that
![]() $\mathring {x}\in C$
for some nowhere dense closed set
$\mathring {x}\in C$
for some nowhere dense closed set
![]() $C=[T]\in V$
,
$C=[T]\in V$
,
![]() $T\in \mathrm {Nwd}\cap V$
, and so
$T\in \mathrm {Nwd}\cap V$
, and so
![]() $q\Vdash |\mathring {X}\cap T|=\omega $
.
$q\Vdash |\mathring {X}\cap T|=\omega $
.
In the second case, we can shrink
![]() $\mathring {X}$
and assume that it has an enumeration
$\mathring {X}$
and assume that it has an enumeration
![]() $\mathring {X}=\{\mathring {s}_k:k\in \omega \}$
and there is a sequence
$\mathring {X}=\{\mathring {s}_k:k\in \omega \}$
and there is a sequence
![]() $(\mathring {n}_k)_{k\in \omega }$
of
$(\mathring {n}_k)_{k\in \omega }$
of
![]() $\mathbb {P}$
-names for an increasing sequence in
$\mathbb {P}$
-names for an increasing sequence in
![]() $\omega $
such that p forces the following:
$\omega $
such that p forces the following:
Now define the
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\mathring {E}_m$
as follows: p forces that if
$\mathring {E}_m$
as follows: p forces that if
![]() $m\in [\mathring {n}_k,\mathring {n}_{k+1})$
and
$m\in [\mathring {n}_k,\mathring {n}_{k+1})$
and
![]() $m>|\mathring {s}_k|$
then
$m>|\mathring {s}_k|$
then
![]() $\mathring {E}_m=\{\mathring {y}\!\upharpoonright \! m\}$
, and if
$\mathring {E}_m=\{\mathring {y}\!\upharpoonright \! m\}$
, and if
![]() $m\in [\mathring {n}_k,\mathring {n}_{k+1})$
and
$m\in [\mathring {n}_k,\mathring {n}_{k+1})$
and
![]() $m\leq |\mathring {s}_k|$
then
$m\leq |\mathring {s}_k|$
then
![]() $\mathring {E}_m=\{\mathring {y}\!\upharpoonright \! m,\mathring {s}_k\!\upharpoonright \! m\}$
. Now
$\mathring {E}_m=\{\mathring {y}\!\upharpoonright \! m,\mathring {s}_k\!\upharpoonright \! m\}$
. Now
![]() $\mathring {E}_m\subseteq \,\!^m 2$
is of size
$\mathring {E}_m\subseteq \,\!^m 2$
is of size
![]() $\leq 2$
, hence applying the Laver property, there are a
$\leq 2$
, hence applying the Laver property, there are a
![]() $q\leq p$
and a sequence
$q\leq p$
and a sequence
![]() $F_m\subseteq [\,\!^m 2]^{\leq 2}$
in V such that
$F_m\subseteq [\,\!^m 2]^{\leq 2}$
in V such that
![]() $|F_m|= m+1$
and
$|F_m|= m+1$
and
![]() $q\Vdash \mathring {E}_m\in F_m$
for every m, in particular, if
$q\Vdash \mathring {E}_m\in F_m$
for every m, in particular, if
![]() $F^{\prime }_m=\bigcup F_m\in [\,\!^m 2]^{\leq 2m+2}$
then
$F^{\prime }_m=\bigcup F_m\in [\,\!^m 2]^{\leq 2m+2}$
then
![]() $q\Vdash \mathring {E}_m\subseteq F^{\prime }_m$
for every m. Let
$q\Vdash \mathring {E}_m\subseteq F^{\prime }_m$
for every m. Let
![]() $A=\{t\in \,\!^{<\omega } 2:\forall \ m\leq |t|\ t\!\upharpoonright \! m\in F^{\prime }_m\}$
. Then
$A=\{t\in \,\!^{<\omega } 2:\forall \ m\leq |t|\ t\!\upharpoonright \! m\in F^{\prime }_m\}$
. Then
![]() $A\in \mathrm {Nwd}$
because for every
$A\in \mathrm {Nwd}$
because for every
![]() $t\in \,\!^{<\omega } 2$
there is a
$t\in \,\!^{<\omega } 2$
there is a
![]() $t'\supseteq t$
such that
$t'\supseteq t$
such that
![]() $t'\notin F^{\prime }_{|t'|}$
and hence no extension of
$t'\notin F^{\prime }_{|t'|}$
and hence no extension of
![]() $t'$
belongs to A, and of course
$t'$
belongs to A, and of course
![]() $q\Vdash \mathring {X}\subseteq A$
.
$q\Vdash \mathring {X}\subseteq A$
.
We show that
![]() $\mathbb {P}\ast \mathbb {C}$
cannot
$\mathbb {P}\ast \mathbb {C}$
cannot
![]() $+$
-destroy
$+$
-destroy
![]() $\mathrm {Nwd}$
. First notice that if
$\mathrm {Nwd}$
. First notice that if
![]() $\mathring {X}$
is a
$\mathring {X}$
is a
![]() $\mathbb {C}$
-name for a dense subset of
$\mathbb {C}$
-name for a dense subset of
![]() $\,\!^{<\omega } 2$
, then there is a countable family
$\,\!^{<\omega } 2$
, then there is a countable family
![]() $\{Y_n:n\in \omega \}$
of dense subsets of
$\{Y_n:n\in \omega \}$
of dense subsets of
![]() $\,\!^{<\omega }2$
such that if an
$\,\!^{<\omega }2$
such that if an
![]() $A\in \mathrm {Nwd}$
has infinite intersection with all
$A\in \mathrm {Nwd}$
has infinite intersection with all
![]() $Y_n$
(there is always such an A because each
$Y_n$
(there is always such an A because each
![]() $Y_n$
is dense) then
$Y_n$
is dense) then
![]() $\Vdash _{\mathbb {C}}|A\cap \mathring {X}|=\omega $
. Why? Enumerate
$\Vdash _{\mathbb {C}}|A\cap \mathring {X}|=\omega $
. Why? Enumerate
![]() $\mathbb {C}=\{q_n:n\in \omega \}$
and define
$\mathbb {C}=\{q_n:n\in \omega \}$
and define
![]() $Y_n=\{s\in \,\!^{<\omega }2:\exists\ q'\leq \ q_n\ q'\Vdash s\in \mathring {X}\}$
. It is easy to see that this family satisfies our requirements. Now if
$Y_n=\{s\in \,\!^{<\omega }2:\exists\ q'\leq \ q_n\ q'\Vdash s\in \mathring {X}\}$
. It is easy to see that this family satisfies our requirements. Now if
![]() $\mathring {X}$
is a
$\mathring {X}$
is a
![]() $\mathbb {P}\ast \mathbb {C}$
-name and
$\mathbb {P}\ast \mathbb {C}$
-name and
![]() $(p,q)\Vdash \mathring {X}\in \mathrm {Nwd}^+$
then we can assume that
$(p,q)\Vdash \mathring {X}\in \mathrm {Nwd}^+$
then we can assume that
![]() $(p,q)$
forces that
$(p,q)$
forces that
![]() $\mathring {X}$
is dense (because a condition below
$\mathring {X}$
is dense (because a condition below
![]() $(p,q)$
decides where
$(p,q)$
decides where
![]() $\mathring {X}$
is dense and we can work inside that cone in
$\mathring {X}$
is dense and we can work inside that cone in
![]() $\,\!^{<\omega }2$
). Therefore there are
$\,\!^{<\omega }2$
). Therefore there are
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\mathring {Y}_n$
for dense subsets of
$\mathring {Y}_n$
for dense subsets of
![]() $\,\!^{<\omega }2$
such that p forces the following: “If
$\,\!^{<\omega }2$
such that p forces the following: “If
![]() $A\in \mathrm {Nwd}$
and
$A\in \mathrm {Nwd}$
and
![]() $|A\cap \mathring {Y}_n|=\omega $
for every n, then
$|A\cap \mathring {Y}_n|=\omega $
for every n, then
![]() $q\Vdash _{\mathbb {C}}|A\cap \mathring {X}|=\omega $
.” Working in
$q\Vdash _{\mathbb {C}}|A\cap \mathring {X}|=\omega $
.” Working in
![]() $V^{\mathbb {P}}$
, it is trivial to construct an antichain
$V^{\mathbb {P}}$
, it is trivial to construct an antichain
![]() $\mathring {Z}\subseteq \,\!^{<\omega }2$
satisfying
$\mathring {Z}\subseteq \,\!^{<\omega }2$
satisfying
![]() $(\sharp )$
which has infinite intersection with all
$(\sharp )$
which has infinite intersection with all
![]() $\mathring {Y}_n$
, and hence there is an
$\mathring {Y}_n$
, and hence there is an
![]() $A\in \mathrm {Nwd}\cap V$
covering
$A\in \mathrm {Nwd}\cap V$
covering
![]() $\mathring {Z}$
. It follows that
$\mathring {Z}$
. It follows that
![]() $(p,q)\Vdash |A\cap \mathring {X}|=\omega $
.⊣
$(p,q)\Vdash |A\cap \mathring {X}|=\omega $
.⊣
Remark 4.9. Notice that the proof of part (2) of the last Proposition “almost” shows that destroying
![]() $\mathrm {Nwd}$
requires Cohen reals: Assume that there is an
$\mathrm {Nwd}$
requires Cohen reals: Assume that there is an
![]() $X\in [\,\!^{<\omega } 2]^\omega \cap V^{\mathbb {P}}$
such that
$X\in [\,\!^{<\omega } 2]^\omega \cap V^{\mathbb {P}}$
such that
![]() $|X\cap A|<\omega $
for every
$|X\cap A|<\omega $
for every
![]() $A\in \mathrm {Nwd}\cap V$
. Then either
$A\in \mathrm {Nwd}\cap V$
. Then either
![]() $[X]_\delta \ne \varnothing $
, i.e., X contains an infinite chain Y defining a real
$[X]_\delta \ne \varnothing $
, i.e., X contains an infinite chain Y defining a real
![]() $y=\bigcup Y\in \,\!^\omega 2$
or X contains an infinite “convergent” antichain Z defining
$y=\bigcup Y\in \,\!^\omega 2$
or X contains an infinite “convergent” antichain Z defining
![]() $z\in \,\!^\omega 2$
as the unique real such that
$z\in \,\!^\omega 2$
as the unique real such that
![]() $\forall \ n\ \forall ^\infty \ t\in Z\ z\!\upharpoonright \! n\subseteq t$
. In the first case we can use the same argument as above but the second case is unclear.
$\forall \ n\ \forall ^\infty \ t\in Z\ z\!\upharpoonright \! n\subseteq t$
. In the first case we can use the same argument as above but the second case is unclear.
Problem 4.10. Does there exist a forcing notion
![]() $\mathbb {P}$
which destroys
$\mathbb {P}$
which destroys
![]() $\mathrm {Nwd}$
but does not add Cohen reals? (This problem might be quite difficult because we know that
$\mathrm {Nwd}$
but does not add Cohen reals? (This problem might be quite difficult because we know that
![]() $\mathrm {cov}^*(\mathrm {Nwd},\infty )=\mathrm {cov}(\mathcal {M})$
and hence iterated destruction of
$\mathrm {cov}^*(\mathrm {Nwd},\infty )=\mathrm {cov}(\mathcal {M})$
and hence iterated destruction of
![]() $\mathrm {Nwd}$
implies adding Cohen reals. In other words, this problem resembles to the well-known “half-a-Cohen-real” problem, see [Reference Zapletal44].)
$\mathrm {Nwd}$
implies adding Cohen reals. In other words, this problem resembles to the well-known “half-a-Cohen-real” problem, see [Reference Zapletal44].)
Problem 4.11. Is there any reasonable characterisation of those tall Borel ideals
![]() $\mathcal {I}$
such that destruction of
$\mathcal {I}$
such that destruction of
![]() $\mathcal {I}$
implies
$\mathcal {I}$
implies
![]() $+$
-destruction of it? (We will show later that there are
$+$
-destruction of it? (We will show later that there are
![]() $F_\sigma $
counterexamples too, e.g.,
$F_\sigma $
counterexamples too, e.g.,
![]() $\mathcal {I}_{1/n}$
.)
$\mathcal {I}_{1/n}$
.)
We will discuss analytic P-ideals later.
5 The
 $\mathbb {M}(\mathcal {I}^*)$
- and
$\mathbb {M}(\mathcal {I}^*)$
- and
 $\mathbb {L}(\mathcal {I}^*)$
-generic reals
$\mathbb {L}(\mathcal {I}^*)$
-generic reals
In this section, applying Laflamme’s filter games and his characterisations of the existence of winning strategies in these games, we will characterise when the generic reals added by the Mathias–Prikry forcing
![]() $\mathbb {M}(\mathcal {I}^*)$
and the Laver–Prikry forcing
$\mathbb {M}(\mathcal {I}^*)$
and the Laver–Prikry forcing
![]() $\mathbb {L}(\mathcal {I}^*)$
(see below)
$\mathbb {L}(\mathcal {I}^*)$
(see below)
![]() $+$
-destroy
$+$
-destroy
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Fix an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
. Then we can talk about infinite games of the following form (see [Reference Laflamme32, Reference Laflamme and Leary33])
$\omega $
. Then we can talk about infinite games of the following form (see [Reference Laflamme32, Reference Laflamme and Leary33])
![]() $G(\mathcal {X},Y,\mathcal {O})$
where
$G(\mathcal {X},Y,\mathcal {O})$
where
![]() $\mathcal {X}=\mathcal {I}^*$
or
$\mathcal {X}=\mathcal {I}^*$
or
![]() $\mathcal {I}^+$
,
$\mathcal {I}^+$
,
![]() $Y=\omega $
or
$Y=\omega $
or
![]() $[\omega ]^{<\omega }$
, and
$[\omega ]^{<\omega }$
, and
![]() $\mathcal {O}=\mathcal {I}^*$
,
$\mathcal {O}=\mathcal {I}^*$
,
![]() $\mathcal {I}^+$
, or
$\mathcal {I}^+$
, or
![]() $\mathcal {P}(\omega )\setminus \mathcal {I}^*$
. In the nth round Player I chooses an
$\mathcal {P}(\omega )\setminus \mathcal {I}^*$
. In the nth round Player I chooses an
![]() $X_n\in \mathcal {X}$
and Player II responds with a
$X_n\in \mathcal {X}$
and Player II responds with a
![]() $k_n\in X_n$
(if
$k_n\in X_n$
(if
![]() $Y=\omega $
) or with an
$Y=\omega $
) or with an
![]() $F_n\in [X_n]^{<\omega }$
(if
$F_n\in [X_n]^{<\omega }$
(if
![]() $Y=[\omega ]^{<\omega }$
, respectively). Player II wins if
$Y=[\omega ]^{<\omega }$
, respectively). Player II wins if
![]() $\{k_n:n\in \omega \}\in \mathcal {O}$
(if
$\{k_n:n\in \omega \}\in \mathcal {O}$
(if
![]() $Y=\omega $
) or
$Y=\omega $
) or
![]() $\bigcup \{F_n:n\in \omega \}\in \mathcal {O}$
(if
$\bigcup \{F_n:n\in \omega \}\in \mathcal {O}$
(if
![]() $Y=[\omega ]^{<\omega }$
).
$Y=[\omega ]^{<\omega }$
).
It is straightforward to show that Borel Determinacy (see [Reference Martin35]) implies that all these games are determined if
![]() $\mathcal {I}$
is Borel.
$\mathcal {I}$
is Borel.
We say that a tall ideal
![]() $\mathcal {I}$
is a weak P-ideal, if every sequence
$\mathcal {I}$
is a weak P-ideal, if every sequence
![]() $X_n\in \mathcal {I}^*$
(
$X_n\in \mathcal {I}^*$
(
![]() $n\in \omega $
) has an
$n\in \omega $
) has an
![]() $\mathcal {I}$
-positive pseudointersection, i.e.,
$\mathcal {I}$
-positive pseudointersection, i.e.,
![]() $\mathrm {cov}^*(\mathcal {I},+)>\omega $
. To define the next property, we need the following construction: For a fixed tall
$\mathrm {cov}^*(\mathcal {I},+)>\omega $
. To define the next property, we need the following construction: For a fixed tall
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
, we define
$\omega $
, we define
![]() $\mathcal {I}^{<\omega }$
on
$\mathcal {I}^{<\omega }$
on
![]() $[\omega ]^{<\omega }\setminus \{\varnothing \}$
(see [Reference Hrušák27]) as the ideal generated by all sets of the form
$[\omega ]^{<\omega }\setminus \{\varnothing \}$
(see [Reference Hrušák27]) as the ideal generated by all sets of the form
![]() $A^{<\omega }=\{x\in [\omega ]^{<\omega }:A\cap x\ne \varnothing \}$
for
$A^{<\omega }=\{x\in [\omega ]^{<\omega }:A\cap x\ne \varnothing \}$
for
![]() $A\in \mathcal {I}$
(notice that this family is closed under taking finite unions). We say that
$A\in \mathcal {I}$
(notice that this family is closed under taking finite unions). We say that
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\omega $
-diagonalisable by
$\omega $
-diagonalisable by
![]() $\mathcal {I}$
-universal sets if there is a countable family
$\mathcal {I}$
-universal sets if there is a countable family
![]() $\{X_n:n\in \omega \}\subseteq (\mathcal {I}^{<\omega })^+$
(i.e.,
$\{X_n:n\in \omega \}\subseteq (\mathcal {I}^{<\omega })^+$
(i.e.,
![]() $\forall \ n\ \forall \ A\in \mathcal {I}\ \exists \ x\in X_n\ A\cap x=\varnothing $
) such that
$\forall \ n\ \forall \ A\in \mathcal {I}\ \exists \ x\in X_n\ A\cap x=\varnothing $
) such that
Theorem 5.1 (see [Reference Laflamme32]).
In
![]() $G(\mathcal {I}^*,[\omega ]^{<\omega },\mathcal {I}^+)$
,
I
has a winning strategy iff
$G(\mathcal {I}^*,[\omega ]^{<\omega },\mathcal {I}^+)$
,
I
has a winning strategy iff
![]() $\mathcal {I}$
is not a weak P-ideal, and
II
has a winning strategy iff
$\mathcal {I}$
is not a weak P-ideal, and
II
has a winning strategy iff
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\omega $
-diagonalisable by
$\omega $
-diagonalisable by
![]() $\mathcal {I}$
-universal sets.
$\mathcal {I}$
-universal sets.
Corollary 5.2. Let
![]() $\mathcal {I}$
be a tall Borel ideal on
$\mathcal {I}$
be a tall Borel ideal on
![]() $\omega $
. Then the following are equivalent:
$\omega $
. Then the following are equivalent:
-
(a) The
 $\mathbb {M}(\mathcal {I}^*)$
-generic
$\mathbb {M}(\mathcal {I}^*)$
-generic
 $+$
-destroys
$+$
-destroys
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(b)
 $\mathbb {M}(\mathcal {I}^*)\ +$
-destroys
$\mathbb {M}(\mathcal {I}^*)\ +$
-destroys
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(c) There is a forcing notion which
 $+$
-destroys
$+$
-destroys
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(d)
 $\mathrm {cov}^*(\mathcal {I},+)>\omega $
.
$\mathrm {cov}^*(\mathcal {I},+)>\omega $
.
Proof. (a)
![]() $\rightarrow $
(b)
$\rightarrow $
(b)
![]() $\rightarrow $
(c) is trivial and (c)
$\rightarrow $
(c) is trivial and (c)
![]() $\rightarrow $
(d) follows from Observation 3.5(4). To show (d)
$\rightarrow $
(d) follows from Observation 3.5(4). To show (d)
![]() $\to $
(a), assume that
$\to $
(a), assume that
![]() $\mathrm {cov}^*(\mathcal {I},+)>\omega $
, i.e., that
$\mathrm {cov}^*(\mathcal {I},+)>\omega $
, i.e., that
![]() $\mathcal {I}$
is a weak P-ideal. As
$\mathcal {I}$
is a weak P-ideal. As
![]() $G(\mathcal {I}^*,[\omega ]^{<\omega },\mathcal {I}^+)$
is determined, II has winning strategy in this game, i.e.,
$G(\mathcal {I}^*,[\omega ]^{<\omega },\mathcal {I}^+)$
is determined, II has winning strategy in this game, i.e.,
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\omega $
-diagonalisable by
$\omega $
-diagonalisable by
![]() $\mathcal {I}$
-universal sets. Fix a witnessing family
$\mathcal {I}$
-universal sets. Fix a witnessing family
![]() $\{X_n:n\in \omega \}\subseteq (\mathcal {I}^{<\omega })^+$
. Notice that property (
$\{X_n:n\in \omega \}\subseteq (\mathcal {I}^{<\omega })^+$
. Notice that property (
![]() $\ast $
) of this family is
$\ast $
) of this family is
![]() ${\underset{\sim}{\Pi}}{}^1_1$
and hence holds in
${\underset{\sim}{\Pi}}{}^1_1$
and hence holds in
![]() $V^{\mathbb {M}(\mathcal {I}^*)}$
as well. It is straightforward to check that the sets
$V^{\mathbb {M}(\mathcal {I}^*)}$
as well. It is straightforward to check that the sets
are dense in
![]() $\mathbb {M}(\mathcal {I}^*)$
and hence the generic
$\mathbb {M}(\mathcal {I}^*)$
and hence the generic
![]() $R\subseteq \omega $
does not satisfy (
$R\subseteq \omega $
does not satisfy (
![]() $\ast $
) (that is,
$\ast $
) (that is,
![]() $\forall \ n\ \exists ^\infty \ x\in X_n\ x\subseteq R$
), in particular,
$\forall \ n\ \exists ^\infty \ x\in X_n\ x\subseteq R$
), in particular,
![]() $V^{\mathbb {M}(\mathcal {I}^*)}\models R\in \mathcal {I}^+$
.⊣
$V^{\mathbb {M}(\mathcal {I}^*)}\models R\in \mathcal {I}^+$
.⊣
If
![]() $\mathcal {I}$
is an ideal on
$\mathcal {I}$
is an ideal on
![]() $\omega $
, then the associated Laver–Prikry forcing
$\omega $
, then the associated Laver–Prikry forcing
![]() $\mathbb {L}(\mathcal {I}^*)$
is defined as follows (see [Reference Brendle and Flašková8, Reference Hrušák27]):
$\mathbb {L}(\mathcal {I}^*)$
is defined as follows (see [Reference Brendle and Flašková8, Reference Hrušák27]):
![]() $T\in \mathbb {L}(\mathcal {I}^*)$
if
$T\in \mathbb {L}(\mathcal {I}^*)$
if
![]() $T\subseteq \,\!^{<\omega }\omega $
is a tree containing a (unique)
$T\subseteq \,\!^{<\omega }\omega $
is a tree containing a (unique)
![]() $\mathrm {stem}(T)\in T$
such that (i)
$\mathrm {stem}(T)\in T$
such that (i)
![]() $\forall t\in T (t\subseteq \mathrm {stem}(T)$
or
$\forall t\in T (t\subseteq \mathrm {stem}(T)$
or
![]() $\mathrm {stem}(T)\subseteq t)$
, and (ii)
$\mathrm {stem}(T)\subseteq t)$
, and (ii)
![]() $\mathrm {ext}_T(t)=\{n:t^\frown (n)\in T\}\in \mathcal {I}^*$
for every
$\mathrm {ext}_T(t)=\{n:t^\frown (n)\in T\}\in \mathcal {I}^*$
for every
![]() $t\in T$
,
$t\in T$
,
![]() $\mathrm {stem}(T)\subseteq t$
; and
$\mathrm {stem}(T)\subseteq t$
; and
![]() $T_0\leq T_1$
if
$T_0\leq T_1$
if
![]() $T_0\subseteq T_1$
.
$T_0\subseteq T_1$
.
![]() $\mathbb {L}(\mathcal {I}^*)$
is
$\mathbb {L}(\mathcal {I}^*)$
is
![]() $\sigma $
-centered (if
$\sigma $
-centered (if
![]() $\mathrm {stem}(T_0)=\mathrm {stem}(T_1)$
then
$\mathrm {stem}(T_0)=\mathrm {stem}(T_1)$
then
![]() $T_0\| T_1$
) and destroys
$T_0\| T_1$
) and destroys
![]() $\mathcal {I}$
: If G is
$\mathcal {I}$
: If G is
![]() $\mathbb {L}(\mathcal {I}^*)$
-generic over V,
$\mathbb {L}(\mathcal {I}^*)$
-generic over V,
![]() $r_G=\bigcup \{\mathrm {stem}(T):T\in G\}\in \,\!^\omega \omega $
, and
$r_G=\bigcup \{\mathrm {stem}(T):T\in G\}\in \,\!^\omega \omega $
, and
![]() $Y_G=\mathrm {ran}(r_G)$
, then
$Y_G=\mathrm {ran}(r_G)$
, then
![]() $Y_G\in [\omega ]^\omega $
and
$Y_G\in [\omega ]^\omega $
and
![]() $|Y_G\cap A|<\omega $
for every
$|Y_G\cap A|<\omega $
for every
![]() $A\in \mathcal {I}^V$
.
$A\in \mathcal {I}^V$
.
Perhaps the most important difference between
![]() $\mathbb {M}(\mathcal {I}^*)$
and
$\mathbb {M}(\mathcal {I}^*)$
and
![]() $\mathbb {L}(\mathcal {I}^*)$
is that
$\mathbb {L}(\mathcal {I}^*)$
is that
![]() $\mathbb {L}(\mathcal {I}^*)$
always adds dominating reals, and we know (see [Reference Chodounský, Repovš and Zdomskyy13]) that for a Borel
$\mathbb {L}(\mathcal {I}^*)$
always adds dominating reals, and we know (see [Reference Chodounský, Repovš and Zdomskyy13]) that for a Borel
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathbb {M}(\mathcal {I}^*)$
adds dominating reals iff
$\mathbb {M}(\mathcal {I}^*)$
adds dominating reals iff
![]() $\mathcal {I}$
is not
$\mathcal {I}$
is not
![]() $F_\sigma $
. Another important, and for us relevant, difference between the two forcing notions is that while (see above) the
$F_\sigma $
. Another important, and for us relevant, difference between the two forcing notions is that while (see above) the
![]() $\mathbb {M}(\mathcal {I}^*)$
-generic object is
$\mathbb {M}(\mathcal {I}^*)$
-generic object is
![]() $\mathcal {I}$
-positive for every tall Borel
$\mathcal {I}$
-positive for every tall Borel
![]() $\mathcal {I}$
satisfying
$\mathcal {I}$
satisfying
![]() $\mathrm {cov}^*(\mathcal {I},+)>\omega $
, the
$\mathrm {cov}^*(\mathcal {I},+)>\omega $
, the
![]() $\mathbb {L}(\mathcal {I}^*)$
-generic object
$\mathbb {L}(\mathcal {I}^*)$
-generic object
![]() $Y_G$
need not be, e.g., it is easy to see that
$Y_G$
need not be, e.g., it is easy to see that
![]() $V^{\mathbb {L}(\mathcal {ED}^*)}\models Y_{\mathring {G}}\in \mathcal {ED}$
. Of course, this does not mean that
$V^{\mathbb {L}(\mathcal {ED}^*)}\models Y_{\mathring {G}}\in \mathcal {ED}$
. Of course, this does not mean that
![]() $\mathbb {L}(\mathcal {ED}^*)$
cannot
$\mathbb {L}(\mathcal {ED}^*)$
cannot
![]() $+$
-destroy
$+$
-destroy
![]() $\mathcal {ED}$
, and indeed, we already know that if
$\mathcal {ED}$
, and indeed, we already know that if
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {ED}$
then it
$\mathcal {ED}$
then it
![]() $+$
-destroys
$+$
-destroys
![]() $\mathcal {ED}$
. We will see later that, e.g.,
$\mathcal {ED}$
. We will see later that, e.g.,
![]() $\mathbb {L}(\mathcal {Z}^*)$
cannot
$\mathbb {L}(\mathcal {Z}^*)$
cannot
![]() $+$
-destroy
$+$
-destroy
![]() $\mathcal {Z}$
.
$\mathcal {Z}$
.
We say that an ideal
![]() $\mathcal {I}$
is weakly Ramsey if every
$\mathcal {I}$
is weakly Ramsey if every
![]() $T\in \mathbb {L}(\mathcal {I}^*)$
has a branch
$T\in \mathbb {L}(\mathcal {I}^*)$
has a branch
![]() $x\in [T]$
such that
$x\in [T]$
such that
![]() $\mathrm {ran}(x)\in \mathcal {I}^+$
.
$\mathrm {ran}(x)\in \mathcal {I}^+$
.
Theorem 5.3 (see [Reference Laflamme32]).
In
![]() $G(\mathcal {I}^*,\omega ,\mathcal {I}^+)$
,
I
has a winning strategy iff
$G(\mathcal {I}^*,\omega ,\mathcal {I}^+)$
,
I
has a winning strategy iff
![]() $\mathcal {I}$
is not weakly Ramsey, and
II
has a winning strategy iff
$\mathcal {I}$
is not weakly Ramsey, and
II
has a winning strategy iff
![]() $\mathrm {non}^*(\mathcal {I},+)=\omega $
.
$\mathrm {non}^*(\mathcal {I},+)=\omega $
.
Corollary 5.4. Let
![]() $\mathcal {I}$
be a tall Borel ideal on
$\mathcal {I}$
be a tall Borel ideal on
![]() $\omega $
. Then the following are equivalent:
$\omega $
. Then the following are equivalent:
![]() $(a)$
The
$(a)$
The
![]() $\mathbb {L}(\mathcal {I}^*)$
-generic
$\mathbb {L}(\mathcal {I}^*)$
-generic
![]() $+$
-destroys
$+$
-destroys
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
![]() $(b)\ \mathrm {non}^*(\mathcal {I},+)=\omega $
.
$(b)\ \mathrm {non}^*(\mathcal {I},+)=\omega $
.
Proof. (a)
![]() $\to $
(b): First of all, (a) implies that
$\to $
(b): First of all, (a) implies that
![]() $\mathcal {I}$
must be weakly Ramsey. If
$\mathcal {I}$
must be weakly Ramsey. If
![]() $T\in \mathbb {L}(\mathcal {I}^*)$
does not have
$T\in \mathbb {L}(\mathcal {I}^*)$
does not have
![]() $\mathcal {I}$
-positive branches, then this holds in
$\mathcal {I}$
-positive branches, then this holds in
![]() $V^{\mathbb {L}(\mathcal {I}^*)}$
as well because this property of T is
$V^{\mathbb {L}(\mathcal {I}^*)}$
as well because this property of T is
![]() ${\underset{\sim}{\Pi}}{}^1_1$
, in particular,
${\underset{\sim}{\Pi}}{}^1_1$
, in particular,
![]() $T\Vdash Y_{\mathring {G}}\in \mathcal {I}$
. As
$T\Vdash Y_{\mathring {G}}\in \mathcal {I}$
. As
![]() $G(\mathcal {I}^*,\omega ,\mathcal {I}^+)$
is determined,
$G(\mathcal {I}^*,\omega ,\mathcal {I}^+)$
is determined,
![]() $\mathrm {non}^*(\mathcal {I},+)=\omega $
.
$\mathrm {non}^*(\mathcal {I},+)=\omega $
.
(b)
![]() $\to $
(a): If
$\to $
(a): If
![]() $\{X_n:n\in \omega \}\subseteq \mathcal {I}^+$
witnesses
$\{X_n:n\in \omega \}\subseteq \mathcal {I}^+$
witnesses
![]() $\mathrm {non}^*(\mathcal {I},+)=\omega $
, then this property of this family is
$\mathrm {non}^*(\mathcal {I},+)=\omega $
, then this property of this family is
![]() ${\underset{\sim}{\Pi}}{}^1_1$
hence it is still a witness of
${\underset{\sim}{\Pi}}{}^1_1$
hence it is still a witness of
![]() $\mathrm {non}^*(\mathcal {I},+)=\omega $
in the extension as well. It is easy to show that the sets
$\mathrm {non}^*(\mathcal {I},+)=\omega $
in the extension as well. It is easy to show that the sets
are dense in
![]() $\mathbb {L}(\mathcal {I}^*)$
, in particular, in the extension
$\mathbb {L}(\mathcal {I}^*)$
, in particular, in the extension
![]() $|Y_G\cap X_n|=\omega $
for every n, and hence
$|Y_G\cap X_n|=\omega $
for every n, and hence
![]() $Y_G\notin \mathcal {I}$
.⊣
$Y_G\notin \mathcal {I}$
.⊣
Notice that unlike in the case of
![]() $\mathbb {M}(\mathcal {I}^*)$
, the characterisation above says much less about
$\mathbb {M}(\mathcal {I}^*)$
, the characterisation above says much less about
![]() $\mathbb {L}(\mathcal {I}^*)$
. In the next section, we will characterise when exactly
$\mathbb {L}(\mathcal {I}^*)$
. In the next section, we will characterise when exactly
![]() $\mathbb {L}(\mathcal {I}^*)\ +$
-destroys an analytic P-ideal
$\mathbb {L}(\mathcal {I}^*)\ +$
-destroys an analytic P-ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
6 Fragile ideals
Definition 6.1. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
. We say that
$\omega $
. We say that
![]() $\mathcal {I}$
is fragile if there are a
$\mathcal {I}$
is fragile if there are a
![]() $Y\in \mathcal {I}^+$
and an
$Y\in \mathcal {I}^+$
and an
![]() $f:Y\to [\omega ]^{<\omega }$
such that the following holds:
$f:Y\to [\omega ]^{<\omega }$
such that the following holds:
-
(a) f witnesses
 $\mathcal {I}^{<\omega }\leq _{\mathrm {K}}\mathcal {I}\!\upharpoonright \! Y$
, i.e.,
$\mathcal {I}^{<\omega }\leq _{\mathrm {K}}\mathcal {I}\!\upharpoonright \! Y$
, i.e.,
 $f^{-1}[A^{<\omega }]\in \mathcal {I}$
for every
$f^{-1}[A^{<\omega }]\in \mathcal {I}$
for every
 $A\in \mathcal {I}$
; and
$A\in \mathcal {I}$
; and -
(b)
 $\bigcup _{n\in H}f(n)\in \mathcal {I}^+$
for every infinite
$\bigcup _{n\in H}f(n)\in \mathcal {I}^+$
for every infinite
 $H\subseteq Y$
.
$H\subseteq Y$
.
It is trivial to see that
![]() $\mathcal {I}^{<\omega }\leq _{\mathrm {K}} \mathcal {I}\upharpoonright Y$
for every
$\mathcal {I}^{<\omega }\leq _{\mathrm {K}} \mathcal {I}\upharpoonright Y$
for every
![]() $Y\in \mathcal {I}^+$
; simply consider the map
$Y\in \mathcal {I}^+$
; simply consider the map
![]() $n\mapsto \{n\}$
. Loosely speaking, an ideal
$n\mapsto \{n\}$
. Loosely speaking, an ideal
![]() $\mathcal {I}$
is fragile if there is a very nontrivial reduction
$\mathcal {I}$
is fragile if there is a very nontrivial reduction
![]() $\mathcal {I}^{<\omega }\leq _{\mathrm {K}} \mathcal {I}\upharpoonright Y$
for some
$\mathcal {I}^{<\omega }\leq _{\mathrm {K}} \mathcal {I}\upharpoonright Y$
for some
![]() $Y\in \mathcal {I}^+$
. Notice that for Borel ideals, being fragile is a
$Y\in \mathcal {I}^+$
. Notice that for Borel ideals, being fragile is a
![]() ${\underset{\sim}{\Sigma}}{}^1_2$
property and hence absolute between V and
${\underset{\sim}{\Sigma}}{}^1_2$
property and hence absolute between V and
![]() $V^{\mathbb {P}}$
.
$V^{\mathbb {P}}$
.
Fact 6.2. Let
![]() $\mathcal {I}$
be a fragile Borel ideal witnessed by
$\mathcal {I}$
be a fragile Borel ideal witnessed by
![]() $f:Y\to [\omega ]^{<\omega }$
. If a forcing notion
$f:Y\to [\omega ]^{<\omega }$
. If a forcing notion
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {I}\!\upharpoonright \! Y$
, then it
$\mathcal {I}\!\upharpoonright \! Y$
, then it
![]() $+$
-destroys
$+$
-destroys
![]() $\mathcal {I}$
. In particular, if
$\mathcal {I}$
. In particular, if
![]() $\mathcal {I}\!\upharpoonright \! Y\leq _{\mathrm {K}}\mathcal {I}$
(e.g.,
$\mathcal {I}\!\upharpoonright \! Y\leq _{\mathrm {K}}\mathcal {I}$
(e.g.,
![]() $Y=\omega $
or
$Y=\omega $
or
![]() $\mathcal {I}$
is K-uniform, that is,
$\mathcal {I}$
is K-uniform, that is,
![]() $\mathcal {I}\!\upharpoonright \! Y\leq _{\mathrm {K}}\mathcal {I}$
for every
$\mathcal {I}\!\upharpoonright \! Y\leq _{\mathrm {K}}\mathcal {I}$
for every
![]() $Y\in \mathcal {I}^+$
), then destroying
$Y\in \mathcal {I}^+$
), then destroying
![]() $\mathcal {I}$
implies
$\mathcal {I}$
implies
![]() $+$
-destroying it.
$+$
-destroying it.
Proof. Let
![]() $\mathring {H}$
be a
$\mathring {H}$
be a
![]() $\mathbb {P}$
-name such that
$\mathbb {P}$
-name such that
![]() $\Vdash _{\mathbb {P}}$
“
$\Vdash _{\mathbb {P}}$
“
![]() $\mathring {H}\in [Y]^\omega $
and
$\mathring {H}\in [Y]^\omega $
and
![]() $|\mathring {H}\cap A|< \omega $
for every
$|\mathring {H}\cap A|< \omega $
for every
![]() $A\in \mathcal {I}\cap V$
.” In the extension,
$A\in \mathcal {I}\cap V$
.” In the extension,
![]() $\mathring {X}=\bigcup _{n\in \mathring {H}}f(n)\in \mathcal {I}^+$
because (b) is a
$\mathring {X}=\bigcup _{n\in \mathring {H}}f(n)\in \mathcal {I}^+$
because (b) is a
![]() ${\underset{\sim}{\Pi}}{}^1_1$
property of
${\underset{\sim}{\Pi}}{}^1_1$
property of
![]() $(f(n))_{n\in Y}\in \,\!^Y\mathrm {Fin}$
; and
$(f(n))_{n\in Y}\in \,\!^Y\mathrm {Fin}$
; and
![]() $|\mathring {X}\cap A|<\omega $
for every
$|\mathring {X}\cap A|<\omega $
for every
![]() $A\in \mathcal {I}\cap V$
because for such an A,
$A\in \mathcal {I}\cap V$
because for such an A,
![]() $f^{-1}[A^{<\omega }]\in \mathcal {I}\cap V$
, therefore
$f^{-1}[A^{<\omega }]\in \mathcal {I}\cap V$
, therefore
![]() $\mathring {H}\cap f^{-1}[A^{<\omega }]=\{n\in \mathring {H}:f(n)\cap A\ne \varnothing \}$
is finite.⊣
$\mathring {H}\cap f^{-1}[A^{<\omega }]=\{n\in \mathring {H}:f(n)\cap A\ne \varnothing \}$
is finite.⊣
One can easily show that
![]() $\mathcal {ED}$
and
$\mathcal {ED}$
and
![]() $\mathrm {Conv}$
are not fragile. Also, it is easy to see that
$\mathrm {Conv}$
are not fragile. Also, it is easy to see that
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
and
$\mathrm {Fin}\otimes \mathrm {Fin}$
and
![]() $\mathrm {Nwd}$
are K-uniform, and we know that
$\mathrm {Nwd}$
are K-uniform, and we know that
![]() $\mathrm {Fin}\otimes \mathrm {Fin}$
cannot be
$\mathrm {Fin}\otimes \mathrm {Fin}$
cannot be
![]() $+$
-destroyed, and that
$+$
-destroyed, and that
![]() $\mathrm {Nwd}$
can be destroyed without being
$\mathrm {Nwd}$
can be destroyed without being
![]() $+$
-destroyed, hence they are not fragile either. Our flagship example of a fragile K-uniform ideal is
$+$
-destroyed, hence they are not fragile either. Our flagship example of a fragile K-uniform ideal is
![]() $\mathcal {ED}_{\mathrm {fin}}$
(see the proof of Proposition 4.6(1)). Let us present “very” fragile summable and density ideals as well:
$\mathcal {ED}_{\mathrm {fin}}$
(see the proof of Proposition 4.6(1)). Let us present “very” fragile summable and density ideals as well:
Example 6.3. There are a tall summable ideal
![]() $\mathcal {I}_h$
and a tall density ideal
$\mathcal {I}_h$
and a tall density ideal
![]() $\mathcal {Z}_{\vec \mu }$
which are fragile with
$\mathcal {Z}_{\vec \mu }$
which are fragile with
![]() $Y=\omega $
in the definition (and hence destruction of these ideals implies
$Y=\omega $
in the definition (and hence destruction of these ideals implies
![]() $+$
-destruction of them): Fix an interval partition
$+$
-destruction of them): Fix an interval partition
![]() $(P_n)$
such that
$(P_n)$
such that
![]() $|P_{n+1}|=2^{n+1}|P_n|$
, let
$|P_{n+1}|=2^{n+1}|P_n|$
, let
![]() $h(k)=\mu _n(\{k\})=2^{-n}$
if
$h(k)=\mu _n(\{k\})=2^{-n}$
if
![]() $k\in P_n=\mathrm {supp}(\mu _n)$
, fix partitions
$k\in P_n=\mathrm {supp}(\mu _n)$
, fix partitions
![]() $P_{n+1}=\bigcup _{k\in P_n}P^{n+1}_k$
such that
$P_{n+1}=\bigcup _{k\in P_n}P^{n+1}_k$
such that
![]() $|P^{n+1}_k|=2^{n+1}$
for every
$|P^{n+1}_k|=2^{n+1}$
for every
![]() $k\in P_n$
and
$k\in P_n$
and
![]() $n\in \omega $
, and define
$n\in \omega $
, and define
![]() $f(k)=P^{n+1}_k$
if
$f(k)=P^{n+1}_k$
if
![]() $k\in P_n$
.
$k\in P_n$
.
We will show that fragility plays a fundamental role when discussing whether an analytic P-ideal
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $+$
-destroyed by
$+$
-destroyed by
![]() $\mathbb {L}(\mathcal {I}^*)$
or not, but first let us show some less trivial examples of non-fragile ideals.
$\mathbb {L}(\mathcal {I}^*)$
or not, but first let us show some less trivial examples of non-fragile ideals.
Observation 6.4. If an analytic P-ideal
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
is fragile as witnessed by
$\mathcal {I}=\mathrm {Exh}(\varphi )$
is fragile as witnessed by
![]() $f:Y\to [\omega ]^{<\omega }$
, then there are a
$f:Y\to [\omega ]^{<\omega }$
, then there are a
![]() $Z\subseteq Y$
,
$Z\subseteq Y$
,
![]() $Z\in \mathcal {I}^+$
, and an
$Z\in \mathcal {I}^+$
, and an
![]() $\varepsilon>0$
such that with
$\varepsilon>0$
such that with
![]() $g=f\!\upharpoonright \! Z$
(clearly, g also witnesses fragility of
$g=f\!\upharpoonright \! Z$
(clearly, g also witnesses fragility of
![]() $\mathcal {I}$
) the following holds: (i)
$\mathcal {I}$
) the following holds: (i)
![]() $g^{-1}[k^{<\omega }]$
is finite for every
$g^{-1}[k^{<\omega }]$
is finite for every
![]() $k\in \omega $
, and (ii)
$k\in \omega $
, and (ii)
![]() $\varphi (g(z))>\varepsilon $
for every z.
$\varphi (g(z))>\varepsilon $
for every z.
Proof. Fix a
![]() $C\in \mathcal {I}$
such that
$C\in \mathcal {I}$
such that
![]() $g^{-1}[k^{<\omega }]\subseteq ^* C$
for every k, and define
$g^{-1}[k^{<\omega }]\subseteq ^* C$
for every k, and define
![]() $Z=Y\setminus C$
. Then (i) holds. To show that (ii) also holds, assume on the contrary that there is a sequence
$Z=Y\setminus C$
. Then (i) holds. To show that (ii) also holds, assume on the contrary that there is a sequence
![]() $z_0<z_1<\cdots $
in Z such that
$z_0<z_1<\cdots $
in Z such that
![]() $\varphi (g(z_i))\xrightarrow {i\to \infty } 0$
. Then there is an infinite
$\varphi (g(z_i))\xrightarrow {i\to \infty } 0$
. Then there is an infinite
![]() $H=\{i_0<i_1<\cdots \}\subseteq \omega $
such that
$H=\{i_0<i_1<\cdots \}\subseteq \omega $
such that
![]() $g(z_{i_0})<g(z_{i_1})<\cdots $
(because of (i)) and
$g(z_{i_0})<g(z_{i_1})<\cdots $
(because of (i)) and
![]() $\varphi (g(z_{i_m}))<2^{-m}$
. Now
$\varphi (g(z_{i_m}))<2^{-m}$
. Now
![]() $\bigcup _{i\in H} g(z_i)\in \mathcal {I}$
(because
$\bigcup _{i\in H} g(z_i)\in \mathcal {I}$
(because
![]() $\varphi $
is
$\varphi $
is
![]() $\sigma $
-subadditive) but this contradicts (b) in the definition of fragility.⊣
$\sigma $
-subadditive) but this contradicts (b) in the definition of fragility.⊣
Proposition 6.5.
![]() $\mathcal {I}_{1/n}$
is not fragile.
$\mathcal {I}_{1/n}$
is not fragile.
Proof. We will work with the canonical isomorphic copy
![]() $\mathcal {I}=\{A\subseteq \,\!^{<\omega }2:h(A):=\sum _{s\in A}2^{-|s|}<\infty \}$
of
$\mathcal {I}=\{A\subseteq \,\!^{<\omega }2:h(A):=\sum _{s\in A}2^{-|s|}<\infty \}$
of
![]() $\mathcal {I}_{1/n}$
, and assume on the contrary that
$\mathcal {I}_{1/n}$
, and assume on the contrary that
![]() $\mathcal {I}$
is fragile. Applying the last observation, we can assume that there are a
$\mathcal {I}$
is fragile. Applying the last observation, we can assume that there are a
![]() $Y\in \mathcal {I}^+$
, an
$Y\in \mathcal {I}^+$
, an
![]() $f:Y\to [\,\!^{<\omega }2]^{<\omega }$
, and an
$f:Y\to [\,\!^{<\omega }2]^{<\omega }$
, and an
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $f^{-1}[A^{<\omega }]\in \mathcal {I}$
for every
$f^{-1}[A^{<\omega }]\in \mathcal {I}$
for every
![]() $A\in \mathcal {I}$
,
$A\in \mathcal {I}$
,
![]() $f^{-1}[(\,\!^{<n}2)^{<\omega }]$
is finite for every n, and
$f^{-1}[(\,\!^{<n}2)^{<\omega }]$
is finite for every n, and
![]() $h(f(y))>\varepsilon $
for every
$h(f(y))>\varepsilon $
for every
![]() $y\in Y$
.
$y\in Y$
.
Further restricting f, we can assume that there is a sequence
![]() $m_0=0<m_1<\cdots $
such that if
$m_0=0<m_1<\cdots $
such that if
![]() $I_n:=[m_n,m_{n+1})$
,
$I_n:=[m_n,m_{n+1})$
,
![]() $B_n:=\bigcup _{k\in I_n}\,\!^k 2$
, and
$B_n:=\bigcup _{k\in I_n}\,\!^k 2$
, and
![]() $Y_n=Y\cap B_n$
, then
$Y_n=Y\cap B_n$
, then
![]() $h(Y_n)=1$
and
$h(Y_n)=1$
and
![]() $\cup f[Y_n]\subseteq B_n$
(here we use that
$\cup f[Y_n]\subseteq B_n$
(here we use that
![]() $f^{-1}[(\,\!^{<n}2)^{<\omega }]$
is finite for every n).
$f^{-1}[(\,\!^{<n}2)^{<\omega }]$
is finite for every n).
Now, let
![]() $Z_n=\,\!^{m_{n+1}}2$
,
$Z_n=\,\!^{m_{n+1}}2$
,
![]() $Z=\bigcup _{n\in \omega }Z_n\in \mathcal {I}^+$
, fix a partition
$Z=\bigcup _{n\in \omega }Z_n\in \mathcal {I}^+$
, fix a partition
![]() $Z_n=\bigcup _{y\in Y_n}Z^n_y$
such that
$Z_n=\bigcup _{y\in Y_n}Z^n_y$
such that
![]() $h(Z^n_y)=h(y)$
, and define
$h(Z^n_y)=h(y)$
, and define
![]() $g:Z\to [\,\!^{<\omega }2]^{<\omega }$
by
$g:Z\to [\,\!^{<\omega }2]^{<\omega }$
by
![]() $g(z)=f(y)$
if
$g(z)=f(y)$
if
![]() $z\in Z^n_y$
. It is trivial to show that g still witnesses fragility of
$z\in Z^n_y$
. It is trivial to show that g still witnesses fragility of
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
There is an N such that
![]() $2^{-m_N}<\varepsilon $
, and hence, by shrinking values of g, we can assume that
$2^{-m_N}<\varepsilon $
, and hence, by shrinking values of g, we can assume that
![]() $\varepsilon <h(g(z))<2\varepsilon $
for every
$\varepsilon <h(g(z))<2\varepsilon $
for every
![]() $z\in \bigcup _{n\geq N}Z_n$
. Fix an
$z\in \bigcup _{n\geq N}Z_n$
. Fix an
![]() $n\geq N$
. We claim that we can pick single points at each level in
$n\geq N$
. We claim that we can pick single points at each level in
![]() $B_n$
, that is, we can construct an
$B_n$
, that is, we can construct an
![]() $F_n=\{t_k:k\in I_n\}$
where
$F_n=\{t_k:k\in I_n\}$
where
![]() $t_k\in \,\!^k2$
such that
$t_k\in \,\!^k2$
such that
![]() $h(g^{-1}[F_n^{<\omega }])\geq \varepsilon /(1+2\varepsilon )$
. Then we are done, because
$h(g^{-1}[F_n^{<\omega }])\geq \varepsilon /(1+2\varepsilon )$
. Then we are done, because
![]() $h(F_n)<2^{-m_n+1}$
and hence
$h(F_n)<2^{-m_n+1}$
and hence
![]() $A=\bigcup _{n\geq N}F_n\in \mathcal {I}$
but
$A=\bigcup _{n\geq N}F_n\in \mathcal {I}$
but
![]() $h(g^{-1}[A^{<\omega }])=\infty $
, a contradiction.
$h(g^{-1}[A^{<\omega }])=\infty $
, a contradiction.
For every
![]() $z\in Z_n$
define the “vector”
$z\in Z_n$
define the “vector”
![]() $v_z\in \,\!^{I_n}[0,\infty )$
,
$v_z\in \,\!^{I_n}[0,\infty )$
,
![]() $v_z(k)=h(g(z)\cap \,\!^k2)=|g(z)\cap \,\!^k 2|\cdot 2^{-k}$
. Now
$v_z(k)=h(g(z)\cap \,\!^k2)=|g(z)\cap \,\!^k 2|\cdot 2^{-k}$
. Now
![]() $\varepsilon <\sum v_z=h(g(z))< 2\varepsilon $
for every
$\varepsilon <\sum v_z=h(g(z))< 2\varepsilon $
for every
![]() $z\in Z_n$
. Picture these vectors as columns next to each other in a
$z\in Z_n$
. Picture these vectors as columns next to each other in a
![]() $I_n\times Z_n$
matrix. The next diagram may help following the construction of
$I_n\times Z_n$
matrix. The next diagram may help following the construction of
![]() $F_n$
below:
$F_n$
below:

We will construct
![]() $t_k$
by recursion on
$t_k$
by recursion on
![]() $k\in I_n$
as follows: Let
$k\in I_n$
as follows: Let
![]() $a_{m_n}=\lceil \sum _{z\in Z_n}v_z(m_n)\rceil $
. A trivial version of Fubini’s theorem shows that there is a point
$a_{m_n}=\lceil \sum _{z\in Z_n}v_z(m_n)\rceil $
. A trivial version of Fubini’s theorem shows that there is a point
![]() $t_{m_n}\in \,\!^{m_n}2$
such that
$t_{m_n}\in \,\!^{m_n}2$
such that
![]() $|\{z\in Z_n:t_{m_n}\in g(z)\}|=|g^{-1}[\{t_{m_n}\}^{<\omega }]|\geq a_{m_n}$
, we fix a
$|\{z\in Z_n:t_{m_n}\in g(z)\}|=|g^{-1}[\{t_{m_n}\}^{<\omega }]|\geq a_{m_n}$
, we fix a
![]() $Z_{n,m_n}\in [Z_n]^{a_{m_n}}$
such that
$Z_{n,m_n}\in [Z_n]^{a_{m_n}}$
such that
![]() $t_{m_n}\in g(z)$
for every
$t_{m_n}\in g(z)$
for every
![]() $z\in Z_{n,m_n}$
. If we are done below k, define
$z\in Z_{n,m_n}$
. If we are done below k, define
and fix a
![]() $t_k\in \,\!^k2$
such that
$t_k\in \,\!^k2$
such that
![]() $|g^{-1}[\{t_k\}^{<\omega }]|\geq a_k$
and a
$|g^{-1}[\{t_k\}^{<\omega }]|\geq a_k$
and a
![]() $Z_{n,k}\in [Z_n\setminus (Z_{n,m_n}\cup \cdots \cup Z_{n,k-1})]^{a_k}$
such that
$Z_{n,k}\in [Z_n\setminus (Z_{n,m_n}\cup \cdots \cup Z_{n,k-1})]^{a_k}$
such that
![]() $t_k\in g(z)$
for every
$t_k\in g(z)$
for every
![]() $z\in Z_{n,k}$
.
$z\in Z_{n,k}$
.
Of course, it is possible that
![]() $Z_n\setminus (Z_{n,m_n}\cup \cdots \cup Z_{n,k-1})= \varnothing $
. Then declare the empty sum to be
$Z_n\setminus (Z_{n,m_n}\cup \cdots \cup Z_{n,k-1})= \varnothing $
. Then declare the empty sum to be
![]() $0$
, and let
$0$
, and let
![]() $t_k\in \,\!^k 2$
be arbitrary and
$t_k\in \,\!^k 2$
be arbitrary and
![]() $Z_{n,k}=\varnothing $
. Now the sum of all elements in this matrix is
$Z_{n,k}=\varnothing $
. Now the sum of all elements in this matrix is
![]() $S=\sum _{k\in I_n}\sum _{z\in Z_n}v_z(k)>|Z_n|\varepsilon =2^{m_{n+1}}\varepsilon $
, also
$S=\sum _{k\in I_n}\sum _{z\in Z_n}v_z(k)>|Z_n|\varepsilon =2^{m_{n+1}}\varepsilon $
, also
![]() $S\leq \sum _{k\in I_n}a_k+\sum $
“grey section,” and, by extending the grey section with all elements above it, we obtain that
$S\leq \sum _{k\in I_n}a_k+\sum $
“grey section,” and, by extending the grey section with all elements above it, we obtain that
 $$ \begin{align*} \sum\text{"grey section"}\leq \sum_{k\in I_n}\sum_{z\in Z_{n,k}}\sum_{\ell\in I_n} v_z(\ell)<\sum_{k\in I_n}a_k 2\varepsilon.\end{align*} $$
$$ \begin{align*} \sum\text{"grey section"}\leq \sum_{k\in I_n}\sum_{z\in Z_{n,k}}\sum_{\ell\in I_n} v_z(\ell)<\sum_{k\in I_n}a_k 2\varepsilon.\end{align*} $$
Therefore,
![]() $2^{m_{n+1}}\varepsilon <(1+2\varepsilon )\sum _{k\in I_n}a_k$
, and so
$2^{m_{n+1}}\varepsilon <(1+2\varepsilon )\sum _{k\in I_n}a_k$
, and so
![]() $h(g^{-1}[F_n^{<\omega }])\geq 2^{-m_{n+1}}\sum _{k\in I_n}a_k>\varepsilon /(1+2\varepsilon )$
.⊣
$h(g^{-1}[F_n^{<\omega }])\geq 2^{-m_{n+1}}\sum _{k\in I_n}a_k>\varepsilon /(1+2\varepsilon )$
.⊣
Proposition 6.6.
![]() $\mathcal {Z}$
is not fragile.
$\mathcal {Z}$
is not fragile.
Proof. Let
![]() $P_n=[2^n,2^{n+1})$
and
$P_n=[2^n,2^{n+1})$
and
![]() $\varphi (A)=\sup _{n\to \infty }|A\cap P_n|/2^n$
. Then clearly
$\varphi (A)=\sup _{n\to \infty }|A\cap P_n|/2^n$
. Then clearly
![]() $\|A\|_\varphi =\limsup _{n\to \infty }|A\cap P_n|/2^n$
and
$\|A\|_\varphi =\limsup _{n\to \infty }|A\cap P_n|/2^n$
and
![]() $\mathcal {Z}=\mathrm {Exh}(\varphi )$
. Assume on the contrary that
$\mathcal {Z}=\mathrm {Exh}(\varphi )$
. Assume on the contrary that
![]() $\mathcal {Z}$
is fragile. By applying Observation 6.4, there are a
$\mathcal {Z}$
is fragile. By applying Observation 6.4, there are a
![]() $Y\in \mathcal {Z}^+$
, an
$Y\in \mathcal {Z}^+$
, an
![]() $f:Y\to [\omega ]^{<\omega }$
, and an
$f:Y\to [\omega ]^{<\omega }$
, and an
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $f^{-1}[A^{<\omega }]\in \mathcal {Z}$
for every
$f^{-1}[A^{<\omega }]\in \mathcal {Z}$
for every
![]() $A\in \mathcal {Z}$
,
$A\in \mathcal {Z}$
,
![]() $f^{-1}[n^{<\omega }]$
is finite for every n, and
$f^{-1}[n^{<\omega }]$
is finite for every n, and
![]() $\varphi (f(y))>\varepsilon $
for every
$\varphi (f(y))>\varepsilon $
for every
![]() $y\in Y$
. Furthermore, we can assume the following:
$y\in Y$
. Furthermore, we can assume the following:
-
(i)
 $f(y)\subseteq P_{k(y)}$
for some
$f(y)\subseteq P_{k(y)}$
for some
 $k(y)\in \omega $
for every
$k(y)\in \omega $
for every
 $y\in Y$
(because
$y\in Y$
(because
 $\varphi (f(y))>\varepsilon $
is witnessed by a
$\varphi (f(y))>\varepsilon $
is witnessed by a
 $P_{k(y)}$
and we can work with
$P_{k(y)}$
and we can work with
 $f'(y)=f(y)\cap P_{k(y)}$
);
$f'(y)=f(y)\cap P_{k(y)}$
); -
(ii) there is a sequence
 $m(0)<m(1)<m(2)<\cdots $
such that
$m(0)<m(1)<m(2)<\cdots $
such that
 $Y=\bigcup _{n\in \omega } Y_n$
where
$Y=\bigcup _{n\in \omega } Y_n$
where
 $Y_n\subseteq P_{m(n)}$
and
$Y_n\subseteq P_{m(n)}$
and
 $\varphi (Y_n)=|Y_n|/2^{m(n)}>\|Y\|_\varphi -2^{-n}$
for every n; and
$\varphi (Y_n)=|Y_n|/2^{m(n)}>\|Y\|_\varphi -2^{-n}$
for every n; and -
(iii)
 $\max \{k(y):y\in Y_n\}<\min \{k(y):y\in Y_{n+1}\}$
for every n.
$\max \{k(y):y\in Y_n\}<\min \{k(y):y\in Y_{n+1}\}$
for every n.
We will define a sequence
![]() $A_0<A_1<\cdots $
of finite sets such that
$A_0<A_1<\cdots $
of finite sets such that
![]() $A_n\subseteq \bigcup _{y\in Y_n}P_{k(y)}$
,
$A_n\subseteq \bigcup _{y\in Y_n}P_{k(y)}$
,
![]() $|A_n\cap P_k|\leq 1$
for every k, and
$|A_n\cap P_k|\leq 1$
for every k, and
![]() $\varphi (f^{-1}[A_n^{<\omega }])=|f^{-1}[A_n^{<\omega }]|/2^{m(n)}\geq \varepsilon \varphi (Y_n)$
. In particular, if
$\varphi (f^{-1}[A_n^{<\omega }])=|f^{-1}[A_n^{<\omega }]|/2^{m(n)}\geq \varepsilon \varphi (Y_n)$
. In particular, if
![]() $A=\bigcup _{n\in \omega }A_n$
then
$A=\bigcup _{n\in \omega }A_n$
then
![]() $A\in \mathcal {Z}$
and
$A\in \mathcal {Z}$
and
![]() $\|f_n^{-1}[A^{<\omega }]\|_\varphi \geq \varepsilon \|Y\|_\varphi $
, a contradiction.
$\|f_n^{-1}[A^{<\omega }]\|_\varphi \geq \varepsilon \|Y\|_\varphi $
, a contradiction.
Fix an n, let
![]() $\{k_i:i<d\}=\{k(y):y\in Y_n\}$
be an enumeration, and partition
$\{k_i:i<d\}=\{k(y):y\in Y_n\}$
be an enumeration, and partition
![]() $Y_n$
accordingly, that is,
$Y_n$
accordingly, that is,
![]() $Y_n=\bigcup _{i<d} Q_i$
where
$Y_n=\bigcup _{i<d} Q_i$
where
![]() $y\in Q_i$
iff
$y\in Q_i$
iff
![]() $k(y)=k_i$
. Now in
$k(y)=k_i$
. Now in
![]() $P_{k_i}$
we have
$P_{k_i}$
we have
![]() $|Q_i|$
many sets
$|Q_i|$
many sets
![]() $f(y)\in [P_{k_i}]^{>\varepsilon |P_{k_i}|}$
. Counting with multiplicity, at least
$f(y)\in [P_{k_i}]^{>\varepsilon |P_{k_i}|}$
. Counting with multiplicity, at least
![]() $|Q_i|\varepsilon |P_{k_i}|$
many points are covered by these sets in
$|Q_i|\varepsilon |P_{k_i}|$
many points are covered by these sets in
![]() $P_{k_i}$
, and hence there must be an
$P_{k_i}$
, and hence there must be an
![]() $a_{n,i}\in P_{k_i}$
which is contained at least in
$a_{n,i}\in P_{k_i}$
which is contained at least in
![]() $\varepsilon |Q_i|$
many of these sets. Now if
$\varepsilon |Q_i|$
many of these sets. Now if
![]() $A_n=\{a_{n,i}:i<d\}$
then
$A_n=\{a_{n,i}:i<d\}$
then
and so
![]() $\varphi (f^{-1}[A_n^{<\omega }])\geq \varepsilon \varphi (Y_n)$
.⊣
$\varphi (f^{-1}[A_n^{<\omega }])\geq \varepsilon \varphi (Y_n)$
.⊣
In the case of
![]() $\mathrm {tr}(\mathcal {N})$
, we know more. As one can show that
$\mathrm {tr}(\mathcal {N})$
, we know more. As one can show that
![]() $\mathrm {tr}(\mathcal {N})$
is K-uniform (or see, e.g., [Reference Meza-Alcántara37, Theorem 2.1.17]), Fact 6.2 and the following easy one imply that
$\mathrm {tr}(\mathcal {N})$
is K-uniform (or see, e.g., [Reference Meza-Alcántara37, Theorem 2.1.17]), Fact 6.2 and the following easy one imply that
![]() $\mathrm {tr}(\mathcal {N})$
is not fragile either.
$\mathrm {tr}(\mathcal {N})$
is not fragile either.
Fact 6.7. The random forcing cannot
![]() $+$
-destroy
$+$
-destroy
![]() $\mathrm {tr}(\mathcal {N})$
, in particular,
$\mathrm {tr}(\mathcal {N})$
, in particular,
![]() $\mathrm {cov}^*(\mathrm {tr}(\mathcal {N}),+)<\mathrm {cov}^*(\mathrm {tr}(\mathcal {N}),\infty )$
in the random model.
$\mathrm {cov}^*(\mathrm {tr}(\mathcal {N}),+)<\mathrm {cov}^*(\mathrm {tr}(\mathcal {N}),\infty )$
in the random model.
Proof. We know (see, e.g., [Reference Bartoszyński and Judah3, Lemma 6.3.12]) that
![]() $V^{\mathbb {B}}\models \lambda ^*(\,\!^\omega 2\cap V)>0$
and hence
$V^{\mathbb {B}}\models \lambda ^*(\,\!^\omega 2\cap V)>0$
and hence
![]() $V^{\mathbb {B}}\models \lambda ^*(\,\!^\omega 2\cap V)=1$
, i.e., every positive Borel set coded in
$V^{\mathbb {B}}\models \lambda ^*(\,\!^\omega 2\cap V)=1$
, i.e., every positive Borel set coded in
![]() $V^{\mathbb {B}}$
, e.g.,
$V^{\mathbb {B}}$
, e.g.,
![]() $[X]_\delta $
for
$[X]_\delta $
for
![]() $X\in \mathrm {tr}(\mathcal {N})^+\cap V^{\mathbb {B}}$
, contains ground model reals. In the case of
$X\in \mathrm {tr}(\mathcal {N})^+\cap V^{\mathbb {B}}$
, contains ground model reals. In the case of
![]() $[X]_\delta $
, the branch associated with such a ground model real has infinite intersection with X.⊣
$[X]_\delta $
, the branch associated with such a ground model real has infinite intersection with X.⊣
In the proof of the main result of this section, we will need the following technical lemma:
Lemma 6.8. An analytic P-ideal
![]() $\mathcal {I}$
is not fragile if, and only if, the following holds for an (equivalently, for every) lsc submeasure
$\mathcal {I}$
is not fragile if, and only if, the following holds for an (equivalently, for every) lsc submeasure
![]() $\varphi $
generating
$\varphi $
generating
![]() $\mathcal {I}$
:
$\mathcal {I}$
:
![]() $\textit {IF}$
$\textit {IF}$
![]() $\varepsilon \in (0,\|\omega \|_\varphi )$
,
$\varepsilon \in (0,\|\omega \|_\varphi )$
,
![]() $Y_n\in \mathcal {I}^+$
, and
$Y_n\in \mathcal {I}^+$
, and
![]() $f_n:Y_n\to \mathcal {H}_{\varphi ,\varepsilon }:=\{F\in [\omega ]^{<\omega }:\varphi (F)>\varepsilon \}$
such that
$f_n:Y_n\to \mathcal {H}_{\varphi ,\varepsilon }:=\{F\in [\omega ]^{<\omega }:\varphi (F)>\varepsilon \}$
such that
![]() $f_n^{-1}[\{H\}]\in \mathcal {I}$
for every
$f_n^{-1}[\{H\}]\in \mathcal {I}$
for every
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $H\in [\omega ]^{<\omega }$
,
$H\in [\omega ]^{<\omega }$
,
![]() $\textit {THEN}$
there is an
$\textit {THEN}$
there is an
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $f_n^{-1}[A^{<\omega }]\in \mathcal {I}^+$
for every n.
$f_n^{-1}[A^{<\omega }]\in \mathcal {I}^+$
for every n.
Proof. Assume first that
![]() $\mathcal {I}$
is fragile witnessed by an
$\mathcal {I}$
is fragile witnessed by an
![]() $f:Y\to [\omega ]^{<\omega }$
. By Observation 6.4, we can assume that
$f:Y\to [\omega ]^{<\omega }$
. By Observation 6.4, we can assume that
![]() $\mathrm {ran}(f)\subseteq \mathcal {H}_{\varphi ,\varepsilon }$
for some
$\mathrm {ran}(f)\subseteq \mathcal {H}_{\varphi ,\varepsilon }$
for some
![]() $\varepsilon>0$
; therefore, the trivial sequence
$\varepsilon>0$
; therefore, the trivial sequence
![]() $f_n=f$
witnesses that the second statement fails.
$f_n=f$
witnesses that the second statement fails.
Conversely, assume that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
and that the second statement does not hold, that is, there are
$\mathcal {I}=\mathrm {Exh}(\varphi )$
and that the second statement does not hold, that is, there are
![]() $Y_n\in \mathcal {I}^+$
and
$Y_n\in \mathcal {I}^+$
and
![]() $f_n:Y_n\to \mathcal {H}_{\varphi ,\varepsilon }$
for some
$f_n:Y_n\to \mathcal {H}_{\varphi ,\varepsilon }$
for some
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $f^{-1}_n[\{H\}]\in \mathcal {I}$
for every n and H, and
$f^{-1}_n[\{H\}]\in \mathcal {I}$
for every n and H, and
![]() $\forall A\in \mathcal {I}\ \exists\ n_A\in \omega\ f^{-1}_{n_A}[A^{<\omega }]\in \mathcal {I}$
. We can assume that
$\forall A\in \mathcal {I}\ \exists\ n_A\in \omega\ f^{-1}_{n_A}[A^{<\omega }]\in \mathcal {I}$
. We can assume that
![]() $\mathcal {I}$
is tall; otherwise, it is trivially fragile. By shrinking the values of these functions, we can assume that
$\mathcal {I}$
is tall; otherwise, it is trivially fragile. By shrinking the values of these functions, we can assume that
![]() $\varphi (f_n(y))\geq \varepsilon $
for every n and
$\varphi (f_n(y))\geq \varepsilon $
for every n and
![]() $y\in Y_n$
but
$y\in Y_n$
but
![]() $\varphi (F)<\varepsilon $
for every
$\varphi (F)<\varepsilon $
for every
![]() $F\subsetneq f_n(y)$
. Let
$F\subsetneq f_n(y)$
. Let
![]() $\mathcal {A}_n=\{A\in \mathcal {I}:n_A=n\}$
. Then
$\mathcal {A}_n=\{A\in \mathcal {I}:n_A=n\}$
. Then
![]() $\mathcal {I}=\bigcup _{n\in \omega }\mathcal {A}_n$
and hence there is an N such that
$\mathcal {I}=\bigcup _{n\in \omega }\mathcal {A}_n$
and hence there is an N such that
![]() $\mathcal {A}_N$
is
$\mathcal {A}_N$
is
![]() $\subseteq ^*$
-cofinal in
$\subseteq ^*$
-cofinal in
![]() $\mathcal {I}$
. Then
$\mathcal {I}$
. Then
holds, in particular, the set
![]() $\mathrm {Bad}=\{k\in \omega :f^{-1}_N[\{k\}^{<\omega }]\in \mathcal {I}^+\}$
is finite (otherwise there was an infinite
$\mathrm {Bad}=\{k\in \omega :f^{-1}_N[\{k\}^{<\omega }]\in \mathcal {I}^+\}$
is finite (otherwise there was an infinite
![]() $B\in \mathcal {I}$
such that
$B\in \mathcal {I}$
such that
![]() $f_N^{-1}[\{k\}^{<\omega }]\in \mathcal {I}^+$
for every
$f_N^{-1}[\{k\}^{<\omega }]\in \mathcal {I}^+$
for every
![]() $k\in B$
).
$k\in B$
).
Now, fix a
![]() $C\in \mathcal {I}$
which almost contains
$C\in \mathcal {I}$
which almost contains
![]() $f_N^{-1}[\{k\}^{<\omega }]$
for every
$f_N^{-1}[\{k\}^{<\omega }]$
for every
![]() $k\in \omega \setminus \mathrm {Bad}$
, and define
$k\in \omega \setminus \mathrm {Bad}$
, and define
![]() $Y=Y_N\setminus (C\cup f_N^{-1}[\mathcal {P}(\mathrm {Bad})])\in \mathcal {I}^+$
and
$Y=Y_N\setminus (C\cup f_N^{-1}[\mathcal {P}(\mathrm {Bad})])\in \mathcal {I}^+$
and
![]() $f:Y\to [\omega ]^{<\omega }$
,
$f:Y\to [\omega ]^{<\omega }$
,
![]() $f(y)=f_N(y)\setminus \mathrm {Bad}$
. Then f witnesses
$f(y)=f_N(y)\setminus \mathrm {Bad}$
. Then f witnesses
![]() $\mathcal {I}^{<\omega }\leq _{\mathrm {K}}\mathcal {I}\!\upharpoonright \! Y$
because if
$\mathcal {I}^{<\omega }\leq _{\mathrm {K}}\mathcal {I}\!\upharpoonright \! Y$
because if
![]() $B\in \mathcal {I}$
and m is as in (
$B\in \mathcal {I}$
and m is as in (
![]() $\star $
) then
$\star $
) then
![]() $f^{-1}[B^{<\omega }]\subseteq f^{-1}[m^{<\omega }]\cup f^{-1}[(B\setminus m)^{<\omega }]$
where
$f^{-1}[B^{<\omega }]\subseteq f^{-1}[m^{<\omega }]\cup f^{-1}[(B\setminus m)^{<\omega }]$
where
![]() $f^{-1}[m^{<\omega }]\in \mathcal {I}$
because
$f^{-1}[m^{<\omega }]\in \mathcal {I}$
because
![]() $f(y)\cap \mathrm {Bad}=\varnothing $
for every
$f(y)\cap \mathrm {Bad}=\varnothing $
for every
![]() $y\in Y$
, and
$y\in Y$
, and
![]() $f^{-1}[(B\setminus m)^{<\omega }]\in \mathcal {I}$
because of (
$f^{-1}[(B\setminus m)^{<\omega }]\in \mathcal {I}$
because of (
![]() $\star $
).
$\star $
).
It is left to show that
![]() $\bigcup _{n\in H}f(n)\in \mathcal {I}^+$
for every
$\bigcup _{n\in H}f(n)\in \mathcal {I}^+$
for every
![]() $H\in [Y]^\omega $
(then f witnesses that
$H\in [Y]^\omega $
(then f witnesses that
![]() $\mathcal {I}$
is fragile). By removing C from
$\mathcal {I}$
is fragile). By removing C from
![]() $Y_N$
, we ensured that
$Y_N$
, we ensured that
![]() $f^{-1}[\{k\}^{<\omega }]$
and hence
$f^{-1}[\{k\}^{<\omega }]$
and hence
![]() $f^{-1}[k^{<\omega }]$
is finite for every k. In particular, if
$f^{-1}[k^{<\omega }]$
is finite for every k. In particular, if
![]() $H=\{a_0<a_1<\cdots \}\subseteq Y$
is infinite, then we can assume that
$H=\{a_0<a_1<\cdots \}\subseteq Y$
is infinite, then we can assume that
![]() $f(a_0)<f(a_1)<\cdots $
. To finish the proof we show that there is an
$f(a_0)<f(a_1)<\cdots $
. To finish the proof we show that there is an
![]() $\varepsilon '>0$
such that
$\varepsilon '>0$
such that
![]() $\varphi (f(y))\geq \varepsilon '$
for every
$\varphi (f(y))\geq \varepsilon '$
for every
![]() $y\in Y$
(and hence
$y\in Y$
(and hence
![]() $\|\bigcup _{i\in \omega }f(a_i)\|_\varphi \geq \varepsilon '$
). We know that
$\|\bigcup _{i\in \omega }f(a_i)\|_\varphi \geq \varepsilon '$
). We know that
![]() $f_N(y)\nsubseteq \mathrm {Bad}$
for any
$f_N(y)\nsubseteq \mathrm {Bad}$
for any
![]() $y\in Y$
, and hence
$y\in Y$
, and hence
![]() $\varphi (f_N(y)\cap \mathrm {Bad})<\varepsilon $
. This implies that
$\varphi (f_N(y)\cap \mathrm {Bad})<\varepsilon $
. This implies that
![]() $\varepsilon '=\varepsilon -\max \{\varphi (F):F\subseteq \mathrm {Bad},\varphi (F)<\varepsilon \}$
is as desired.⊣
$\varepsilon '=\varepsilon -\max \{\varphi (F):F\subseteq \mathrm {Bad},\varphi (F)<\varepsilon \}$
is as desired.⊣
Theorem 6.9. Let
![]() $\mathcal {I}$
be an analytic P-ideal. Then
$\mathcal {I}$
be an analytic P-ideal. Then
![]() $\mathbb {L}(\mathcal {I}^*)$
can
$\mathbb {L}(\mathcal {I}^*)$
can
![]() $+$
-destroy
$+$
-destroy
![]() $\mathcal {I}$
iff
$\mathcal {I}$
iff
![]() $\mathcal {I}$
is fragile.
$\mathcal {I}$
is fragile.
Proof. A trivial density argument shows that
![]() $\mathbb {L}(\mathcal {I}^*)$
destroys
$\mathbb {L}(\mathcal {I}^*)$
destroys
![]() $\mathcal {I}\!\upharpoonright \! Y$
for every
$\mathcal {I}\!\upharpoonright \! Y$
for every
![]() $Y\in \mathcal {I}^+\cap V$
, and hence applying Fact 6.2, if
$Y\in \mathcal {I}^+\cap V$
, and hence applying Fact 6.2, if
![]() $\mathcal {I}$
is fragile, then
$\mathcal {I}$
is fragile, then
![]() $\mathbb {L}(\mathcal {I}^*)\ +$
-destroys
$\mathbb {L}(\mathcal {I}^*)\ +$
-destroys
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Conversely, assume that
![]() $\mathcal {I}$
is not fragile. Let
$\mathcal {I}$
is not fragile. Let
![]() $\varphi $
be an lsc submeasure such that
$\varphi $
be an lsc submeasure such that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
, let
$\mathcal {I}=\mathrm {Exh}(\varphi )$
, let
![]() $\mathring {X}$
be an
$\mathring {X}$
be an
![]() $\mathbb {L}(\mathcal {I}^*)$
-name for an
$\mathbb {L}(\mathcal {I}^*)$
-name for an
![]() $\mathcal {I}$
-positive set, and fix a
$\mathcal {I}$
-positive set, and fix a
![]() $T_0\in \mathbb {L}(\mathcal {I}^*)$
and an
$T_0\in \mathbb {L}(\mathcal {I}^*)$
and an
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $T_0\Vdash \|\mathring {X}\|_\varphi>\varepsilon $
. We show that there is an
$T_0\Vdash \|\mathring {X}\|_\varphi>\varepsilon $
. We show that there is an
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $T_0\Vdash |\mathring {X}\cap A|=\omega $
.
$T_0\Vdash |\mathring {X}\cap A|=\omega $
.
Fix a bijection
![]() $e:[\omega ]^{<\omega }\to \omega $
and a sequence
$e:[\omega ]^{<\omega }\to \omega $
and a sequence
![]() $(\mathring {H}_m)_{m\in \omega }$
of
$(\mathring {H}_m)_{m\in \omega }$
of
![]() $\mathbb {L}(\mathcal {I}^*)$
-names such that
$\mathbb {L}(\mathcal {I}^*)$
-names such that
![]() $T_0$
forces the following for every m: (i)
$T_0$
forces the following for every m: (i)
![]() $\mathring {H}_m\subseteq \mathring {X}$
and
$\mathring {H}_m\subseteq \mathring {X}$
and
![]() $\varphi (\mathring {H}_m)>\varepsilon $
, (ii)
$\varphi (\mathring {H}_m)>\varepsilon $
, (ii)
![]() $\max (\mathring {H}_m)<\min (\mathring {H}_{m+1})$
, and (iii)
$\max (\mathring {H}_m)<\min (\mathring {H}_{m+1})$
, and (iii)
![]() $e(\mathring {H}_m)>\mathring {\ell }(m)$
where
$e(\mathring {H}_m)>\mathring {\ell }(m)$
where
![]() $\mathring {\ell }$
is an
$\mathring {\ell }$
is an
![]() $\mathbb {L}(\mathcal {I}^*)$
-name for the generic
$\mathbb {L}(\mathcal {I}^*)$
-name for the generic
![]() $\omega \to \omega $
function.
$\omega \to \omega $
function.
We will use a rank argument on
![]() $Q=T_0\cap \mathrm {stem}(T_0)^\uparrow $
. We say that an
$Q=T_0\cap \mathrm {stem}(T_0)^\uparrow $
. We say that an
![]() $s\in Q$
favors “
$s\in Q$
favors “
![]() $\mathring {H}_m=E$
” (for some
$\mathring {H}_m=E$
” (for some
![]() $E\in \mathcal {H}_{\varphi ,\varepsilon }$
) if
$E\in \mathcal {H}_{\varphi ,\varepsilon }$
) if
Now define the rank functions
![]() $\varrho _m$
on Q for every
$\varrho _m$
on Q for every
![]() $m\in \omega $
by recursion as follows:
$m\in \omega $
by recursion as follows:
![]() $\varrho _m(s)=0$
if there is an
$\varrho _m(s)=0$
if there is an
![]() $E^s_m\in \mathcal {H}_{\varphi ,\varepsilon }$
such that s favors “
$E^s_m\in \mathcal {H}_{\varphi ,\varepsilon }$
such that s favors “
![]() $\mathring {H}_m=E^s_m$
”; and
$\mathring {H}_m=E^s_m$
”; and
![]() $\varrho _m(s)=\alpha>0$
if
$\varrho _m(s)=\alpha>0$
if
![]() $\varrho _m(s)\not <\alpha $
and
$\varrho _m(s)\not <\alpha $
and
![]() $\{n:\varrho _m(s^\frown (n))<\alpha \}\in \mathcal {I}^+$
. It is trivial to show that
$\{n:\varrho _m(s^\frown (n))<\alpha \}\in \mathcal {I}^+$
. It is trivial to show that
![]() $\mathrm {dom}(\varrho _m)=Q$
.
$\mathrm {dom}(\varrho _m)=Q$
.
We claim that
![]() $\varrho _m(s)>0$
whenever
$\varrho _m(s)>0$
whenever
![]() $m\geq |s|$
. Fix conditions
$m\geq |s|$
. Fix conditions
![]() $S_k\leq T_0$
for every k such that
$S_k\leq T_0$
for every k such that
![]() $\mathrm {stem}(S_k)=s$
and
$\mathrm {stem}(S_k)=s$
and
![]() $\mathrm {ext}_{S_k}(t)\subseteq \omega \setminus k$
for every
$\mathrm {ext}_{S_k}(t)\subseteq \omega \setminus k$
for every
![]() $t\in S_k\cap s^\uparrow $
. Now if
$t\in S_k\cap s^\uparrow $
. Now if
![]() $m\geq |s|$
then
$m\geq |s|$
then
![]() $S_k\Vdash k\leq \mathring {\ell }(m)< e(\mathring {H}_m)$
, and hence s cannot favor
$S_k\Vdash k\leq \mathring {\ell }(m)< e(\mathring {H}_m)$
, and hence s cannot favor
![]() $\mathring {H}_m=E$
for any E because
$\mathring {H}_m=E$
for any E because
![]() $e(E)=k$
for some k.
$e(E)=k$
for some k.
If
![]() $\varrho _m(s)=1$
then
$\varrho _m(s)=1$
then
![]() $Y_{m,s}=\{n:\varrho _m(s^\frown (n))=0\}\in \mathcal {I}^+$
, and
$Y_{m,s}=\{n:\varrho _m(s^\frown (n))=0\}\in \mathcal {I}^+$
, and
![]() $s^\frown (n)$
favors
$s^\frown (n)$
favors
![]() $\mathring {H}_m=E^{s^\frown (n)}_m$
for every
$\mathring {H}_m=E^{s^\frown (n)}_m$
for every
![]() $n\in Y_{m,s}$
. Define
$n\in Y_{m,s}$
. Define
![]() $f_{m,s}:Y_{m,s}\to \mathcal {H}_{\varphi ,\varepsilon }$
as
$f_{m,s}:Y_{m,s}\to \mathcal {H}_{\varphi ,\varepsilon }$
as
![]() $f_{m,s}(n)=E^{s^\frown (n)}_m$
. Notice that
$f_{m,s}(n)=E^{s^\frown (n)}_m$
. Notice that
![]() $f_{m,s}^{-1}[\{E\}]\in \mathcal {I}$
for every E because otherwise s would favor
$f_{m,s}^{-1}[\{E\}]\in \mathcal {I}$
for every E because otherwise s would favor
![]() $\mathring {H}_m=E$
, and hence
$\mathring {H}_m=E$
, and hence
![]() $\varrho _m(s)$
would be
$\varrho _m(s)$
would be
![]() $0$
.
$0$
.
Applying Lemma 6.8, there is an
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $f_{m,s}^{-1}[A^{<\omega }]\in \mathcal {I}^+$
whenever
$f_{m,s}^{-1}[A^{<\omega }]\in \mathcal {I}^+$
whenever
![]() $\varrho _m(s)=1$
. We claim that
$\varrho _m(s)=1$
. We claim that
![]() $T_0\Vdash |\mathring {X}\cap A|=\omega $
. Otherwise, there is a
$T_0\Vdash |\mathring {X}\cap A|=\omega $
. Otherwise, there is a
![]() $T\leq T_0$
with stem s forcing
$T\leq T_0$
with stem s forcing
![]() $\mathring {X}\cap A\subseteq M$
for some
$\mathring {X}\cap A\subseteq M$
for some
![]() $M\in \omega $
. Fix an
$M\in \omega $
. Fix an
![]() $m\geq M,|s|$
, then
$m\geq M,|s|$
, then
![]() $\varrho _m(s)>0$
and hence there is a
$\varrho _m(s)>0$
and hence there is a
![]() $t\in T$
above its stem of m-rank
$t\in T$
above its stem of m-rank
![]() $1$
(this can be shown by induction on
$1$
(this can be shown by induction on
![]() $\varrho _m(s)$
). As
$\varrho _m(s)$
). As
![]() $f^{-1}_{m,t}[A^{<\omega }]\in \mathcal {I}^+$
, we know that there is an
$f^{-1}_{m,t}[A^{<\omega }]\in \mathcal {I}^+$
, we know that there is an
![]() $n\in \mathrm {ext}_T(t)\cap f^{-1}_{m,t}[A^{<\omega }]$
, in particular,
$n\in \mathrm {ext}_T(t)\cap f^{-1}_{m,t}[A^{<\omega }]$
, in particular,
![]() $t^\frown (n)$
favors
$t^\frown (n)$
favors
![]() $\mathring {H}_m=f_{m,t}(n)=E^{t^\frown (n)}_m\subseteq \omega \setminus m\subseteq \omega \setminus M$
and this set has nonempty intersection with A. If
$\mathring {H}_m=f_{m,t}(n)=E^{t^\frown (n)}_m\subseteq \omega \setminus m\subseteq \omega \setminus M$
and this set has nonempty intersection with A. If
![]() $T'\leq T\!\upharpoonright \! (t^\frown (n))$
forces
$T'\leq T\!\upharpoonright \! (t^\frown (n))$
forces
![]() $\mathring {H}_m=E^{t^\frown (n)}_m$
then
$\mathring {H}_m=E^{t^\frown (n)}_m$
then
![]() $T'\Vdash \mathring {X}\cap A\nsubseteq M$
, a contradiction.⊣
$T'\Vdash \mathring {X}\cap A\nsubseteq M$
, a contradiction.⊣
Unfortunately, it is still unclear what happens under iterations:
Problem 6.10. Let
![]() $\mathcal {I}$
be an analytic P-ideal which is not fragile. Is it true that finite support iterations of
$\mathcal {I}$
be an analytic P-ideal which is not fragile. Is it true that finite support iterations of
![]() $\mathbb {L}(\mathcal {I}^*)$
cannot
$\mathbb {L}(\mathcal {I}^*)$
cannot
![]() $+$
-destroy
$+$
-destroy
![]() $\mathcal {I}$
? Or at least, is
$\mathcal {I}$
? Or at least, is
![]() $\mathrm {cov}^*(\mathcal {I},+)<\mathrm {cov}^*(\mathcal {I},\infty )$
consistent? (We have seen that for
$\mathrm {cov}^*(\mathcal {I},+)<\mathrm {cov}^*(\mathcal {I},\infty )$
consistent? (We have seen that for
![]() $\mathcal {I}=\mathrm {tr}(\mathcal {N})$
, this strict inequality holds in the random model.) Similarly, one can ask about possible separations of the uniformity numbers.
$\mathcal {I}=\mathrm {tr}(\mathcal {N})$
, this strict inequality holds in the random model.) Similarly, one can ask about possible separations of the uniformity numbers.
7 Remarks on
 $*$
-destruction
$*$
-destruction
Let us begin with a short introduction to (Borel) Tukey connections using Fremlin’s notation (for more details, see [Reference Fremlin20] or [Reference Blass4]): A triple
![]() $\mathcal {R}=(A,R,B)$
is a (supported) relation if
$\mathcal {R}=(A,R,B)$
is a (supported) relation if
![]() $R\subseteq A\times B$
,
$R\subseteq A\times B$
,
![]() $A=\mathrm {dom}(R)$
,
$A=\mathrm {dom}(R)$
,
![]() $B=\mathrm {ran}(R)$
, and
$B=\mathrm {ran}(R)$
, and
![]() $\nexists \ b\in B\ \forall \ a\in A\ aRb$
(where
$\nexists \ b\in B\ \forall \ a\in A\ aRb$
(where
![]() $aRb$
stands for
$aRb$
stands for
![]() $(a,b)\in R$
). The relation
$(a,b)\in R$
). The relation
![]() $\mathcal {R}$
is Borel if
$\mathcal {R}$
is Borel if
![]() $A,B\subseteq \,\!^\omega \omega $
and R are Borel sets. For a given
$A,B\subseteq \,\!^\omega \omega $
and R are Borel sets. For a given
![]() $\mathcal {R}=(A,R,B)$
, a set
$\mathcal {R}=(A,R,B)$
, a set
![]() $X\subseteq A$
is
$X\subseteq A$
is
![]() $\mathcal {R}$
-unbounded if there is no
$\mathcal {R}$
-unbounded if there is no
![]() $b\in B R$
-above every
$b\in B R$
-above every
![]() $a\in X$
, and a
$a\in X$
, and a
![]() $Y\subseteq B$
is
$Y\subseteq B$
is
![]() $\mathcal {R}$
-cofinal if for every
$\mathcal {R}$
-cofinal if for every
![]() $a\in A$
there is a
$a\in A$
there is a
![]() $b\in Y$
such that
$b\in Y$
such that
![]() $aRb$
. We define the unbounding and dominating numbers of
$aRb$
. We define the unbounding and dominating numbers of
![]() $\mathcal {R}$
as follows:
$\mathcal {R}$
as follows:
 $$ \begin{align*} \mathfrak{b}(\mathcal{R})&=\min\big\{|X|:X\subseteq A\;\text{is}\;\mathcal{R}\text{-unbounded}\big\},\\ \mathfrak{d}(\mathcal{R}) &=\min\big\{|Y|:Y\subseteq B\;\text{is}\;\mathcal{R}\text{-cofinal}\big\}. \end{align*} $$
$$ \begin{align*} \mathfrak{b}(\mathcal{R})&=\min\big\{|X|:X\subseteq A\;\text{is}\;\mathcal{R}\text{-unbounded}\big\},\\ \mathfrak{d}(\mathcal{R}) &=\min\big\{|Y|:Y\subseteq B\;\text{is}\;\mathcal{R}\text{-cofinal}\big\}. \end{align*} $$
Every cardinal invariant from Cichoń’s diagram (see [Reference Blass4]) and from above can easily be written in this form, for example,
![]() $\mathrm {cov}(\mathcal {M})=\mathfrak {d}(\,\!^\omega 2,\in ,\mathcal {M})$
,
$\mathrm {cov}(\mathcal {M})=\mathfrak {d}(\,\!^\omega 2,\in ,\mathcal {M})$
,
![]() $\mathfrak {d}=\mathfrak {d}(\,\!^\omega \omega ,\leq ^*,\,\!^\omega \omega )$
,
$\mathfrak {d}=\mathfrak {d}(\,\!^\omega \omega ,\leq ^*,\,\!^\omega \omega )$
,
![]() $\mathrm {add}(\mathcal {N})=\mathfrak {b}(\mathcal {N},\subseteq ,\mathcal {N})$
,
$\mathrm {add}(\mathcal {N})=\mathfrak {b}(\mathcal {N},\subseteq ,\mathcal {N})$
,
![]() $\mathrm {non}^*(\mathcal {I},\infty )=\mathfrak {b}([\omega ]^\omega ,\in ,\widehat {\mathcal {I}})=\mathfrak {b}([\omega ]^\omega ,R_{\mathrm {ii}},\mathcal {I})$
, and
$\mathrm {non}^*(\mathcal {I},\infty )=\mathfrak {b}([\omega ]^\omega ,\in ,\widehat {\mathcal {I}})=\mathfrak {b}([\omega ]^\omega ,R_{\mathrm {ii}},\mathcal {I})$
, and
![]() $\mathrm {cov}^*(\mathcal {I},+)=\mathfrak {d}(\mathcal {I}^+,\in ,\widehat {\mathcal {I}})=\mathfrak {d}(\mathcal {I}^+,R_{\mathrm {ii}},\mathcal {I})$
where
$\mathrm {cov}^*(\mathcal {I},+)=\mathfrak {d}(\mathcal {I}^+,\in ,\widehat {\mathcal {I}})=\mathfrak {d}(\mathcal {I}^+,R_{\mathrm {ii}},\mathcal {I})$
where
![]() $XR_{\mathrm {ii}} A$
iff
$XR_{\mathrm {ii}} A$
iff
![]() $|X\cap A|=\omega $
, etc. Notice that each unbounding number is actually a dominating number and vice versa: If
$|X\cap A|=\omega $
, etc. Notice that each unbounding number is actually a dominating number and vice versa: If
![]() $\mathcal {R}^\perp =(B,\neg R^{-1},A)$
then
$\mathcal {R}^\perp =(B,\neg R^{-1},A)$
then
![]() $\mathfrak {b}(\mathcal {R}^\perp )=\mathfrak {d}(\mathcal {R})$
and
$\mathfrak {b}(\mathcal {R}^\perp )=\mathfrak {d}(\mathcal {R})$
and
![]() $\mathfrak {d}(\mathcal {R}^\perp )=\mathfrak {b}(\mathcal {R})$
. Furthermore, all these underlying relations can be seen as Borel (in the cases of
$\mathfrak {d}(\mathcal {R}^\perp )=\mathfrak {b}(\mathcal {R})$
. Furthermore, all these underlying relations can be seen as Borel (in the cases of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
, and
$\mathcal {N}$
, and
![]() $\widehat {\mathcal {I}}$
we can use natural codings of nice bases of these ideals).
$\widehat {\mathcal {I}}$
we can use natural codings of nice bases of these ideals).
Fremlin and Vojtáš isolated a method of comparing cardinal invariants of these forms (see [Reference Fremlin19, Reference Vojtáš41]), it turned out that most of the known inequalities can be proved by this method, and most importantly, applying this approach we immediately obtain more than “just” inequalities between cardinal invariants. For given (Borel)
![]() $\mathcal {R}_0=(A_0,R_0,B_0)$
and
$\mathcal {R}_0=(A_0,R_0,B_0)$
and
![]() $\mathcal {R}_1=(A_1,R_1,B_1)$
, we say that
$\mathcal {R}_1=(A_1,R_1,B_1)$
, we say that
![]() $\mathcal {R}_0$
is (Borel) Tukey-reducible to
$\mathcal {R}_0$
is (Borel) Tukey-reducible to
![]() $\mathcal {R}_1$
,
$\mathcal {R}_1$
,
![]() $\mathcal {R}_0\leq _{\mathrm {(B)T}} \mathcal {R}_1$
,Footnote 4 if there are (Borel) maps
$\mathcal {R}_0\leq _{\mathrm {(B)T}} \mathcal {R}_1$
,Footnote 4 if there are (Borel) maps
![]() $\alpha :A_0\to A_1$
and
$\alpha :A_0\to A_1$
and
![]() $\beta :B_1\to B_0$
such that
$\beta :B_1\to B_0$
such that
![]() $aR_0\beta (b)$
whenever
$aR_0\beta (b)$
whenever
![]() $\alpha (a)R_1 b$
, in a diagram:
$\alpha (a)R_1 b$
, in a diagram:

We write
![]() $\mathcal {R}_0\equiv _{\mathrm {(B)T}}\mathcal {R}_1$
if both
$\mathcal {R}_0\equiv _{\mathrm {(B)T}}\mathcal {R}_1$
if both
![]() $\mathcal {R}_0\leq _{\mathrm {(B)T}}\mathcal {R}_1$
and
$\mathcal {R}_0\leq _{\mathrm {(B)T}}\mathcal {R}_1$
and
![]() $\mathcal {R}_1\leq _{\mathrm {(B)T}}\mathcal {R}_0$
hold.
$\mathcal {R}_1\leq _{\mathrm {(B)T}}\mathcal {R}_0$
hold.
It is trivial to check the following:
Fact 7.1. If
![]() $\mathcal {R}_0\leq _{\mathrm {T}}\mathcal {R}_1$
then
$\mathcal {R}_0\leq _{\mathrm {T}}\mathcal {R}_1$
then
-
(Ia)
 $\mathfrak {b}(\mathcal {R}_0)\geq \mathfrak {b}(\mathcal {R}_1)$
.
$\mathfrak {b}(\mathcal {R}_0)\geq \mathfrak {b}(\mathcal {R}_1)$
. -
(Ib)
 $\mathfrak {d}(\mathcal {R}_0)\leq \mathfrak {d}(\mathcal {R}_1)$
.
$\mathfrak {d}(\mathcal {R}_0)\leq \mathfrak {d}(\mathcal {R}_1)$
.
If
![]() $\mathcal {R}_0\leq _{\mathrm {BT}}\mathcal {R}_1$
then we know more but first we need the following definitions: Let
$\mathcal {R}_0\leq _{\mathrm {BT}}\mathcal {R}_1$
then we know more but first we need the following definitions: Let
![]() $\mathbb {P}$
be a forcing notion and
$\mathbb {P}$
be a forcing notion and
![]() $\mathcal {R}=(A,R,B)$
be a Borel relation. We say that
$\mathcal {R}=(A,R,B)$
be a Borel relation. We say that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathcal {R}$
-bounding if
$\mathcal {R}$
-bounding if
![]() $\Vdash _{\mathbb {P}}\forall a\in A\cap V[\mathring {G}]\ \exists\ b\in B\cap V\ aRb$
, i.e.,
$\Vdash _{\mathbb {P}}\forall a\in A\cap V[\mathring {G}]\ \exists\ b\in B\cap V\ aRb$
, i.e.,
![]() $B\cap V$
remains
$B\cap V$
remains
![]() $\mathcal {R}$
-cofinal in
$\mathcal {R}$
-cofinal in
![]() $V^{\mathbb {P}}$
; and we say that
$V^{\mathbb {P}}$
; and we say that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathcal {R}$
-dominating if
$\mathcal {R}$
-dominating if
![]() $\Vdash _{\mathbb {P}}\exists\ b\in B\cap V[\mathring {G}]\ \forall \ a\in A\cap V\ aRb$
, i.e.,
$\Vdash _{\mathbb {P}}\exists\ b\in B\cap V[\mathring {G}]\ \forall \ a\in A\cap V\ aRb$
, i.e.,
![]() $A\cap V$
is
$A\cap V$
is
![]() $\mathcal {R}$
-bounded in
$\mathcal {R}$
-bounded in
![]() $V^{\mathbb {P}}$
. For example,
$V^{\mathbb {P}}$
. For example,
![]() $\mathbb {P}$
adds Cohen reals iff it is
$\mathbb {P}$
adds Cohen reals iff it is
![]() $(\mathcal {M},\not \ni ,\,\!^\omega 2)$
-dominating,
$(\mathcal {M},\not \ni ,\,\!^\omega 2)$
-dominating,
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\,\!^\omega \omega $
-bounding iff it is
$\,\!^\omega \omega $
-bounding iff it is
![]() $(\,\!^\omega \omega ,\leq ^*,\,\!^\omega \omega )$
-bounding,
$(\,\!^\omega \omega ,\leq ^*,\,\!^\omega \omega )$
-bounding,
![]() $\Vdash _{\mathbb {P}}\,\!^\omega 2\cap V\notin \mathcal {N}$
iff
$\Vdash _{\mathbb {P}}\,\!^\omega 2\cap V\notin \mathcal {N}$
iff
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $(\mathcal {N},\not \ni ,\,\!^\omega 2)$
-bounding,Footnote
5
$(\mathcal {N},\not \ni ,\,\!^\omega 2)$
-bounding,Footnote
5
![]() $\mathbb {P}\ +$
-destroys
$\mathbb {P}\ +$
-destroys
![]() $\mathcal {I}$
iff it is
$\mathcal {I}$
iff it is
![]() $(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^+)$
-dominating, and
$(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^+)$
-dominating, and
![]() $\mathbb {P}\ *$
-destroys
$\mathbb {P}\ *$
-destroys
![]() $\mathcal {I}$
iff it is
$\mathcal {I}$
iff it is
![]() $(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^*)$
-dominating iff it is
$(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^*)$
-dominating iff it is
![]() $(\mathcal {I}\subseteq ^*,\mathcal {I})$
-dominating, etc.
$(\mathcal {I}\subseteq ^*,\mathcal {I})$
-dominating, etc.
Now it is straightforward to show the following:
Fact 7.2. If
![]() $\mathcal {R}_0\leq _{\mathrm {BT}}\mathcal {R}_1$
and
$\mathcal {R}_0\leq _{\mathrm {BT}}\mathcal {R}_1$
and
![]() $\mathbb {P}$
is a forcing notion then the following holds:
$\mathbb {P}$
is a forcing notion then the following holds:
-
(IIa) if
 $\mathbb {P}$
is
$\mathbb {P}$
is
 $\mathcal {R}_1$
-bounding then
$\mathcal {R}_1$
-bounding then
 $\mathbb {P}$
is
$\mathbb {P}$
is
 $\mathcal {R}_0$
-bounding
$\mathcal {R}_0$
-bounding
 $;$
and
$;$
and -
(IIb) if
 $\mathbb {P}$
is
$\mathbb {P}$
is
 $\mathcal {R}_1$
-dominating then
$\mathcal {R}_1$
-dominating then
 $\mathbb {P}$
is
$\mathbb {P}$
is
 $\mathcal {R}_0$
-dominating.
$\mathcal {R}_0$
-dominating.
For example, now we can add the “missing” last point to Observation 3.5:
Observation 7.3. Let
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
be Borel ideals and assume that
$\mathcal {J}$
be Borel ideals and assume that
![]() $(\mathcal {I},\subseteq ^*,\mathcal {I})\leq _{\mathrm {BT}}(\mathcal {J},\subseteq ^*,\mathcal {J})$
, that is, there are Borel functions
$(\mathcal {I},\subseteq ^*,\mathcal {I})\leq _{\mathrm {BT}}(\mathcal {J},\subseteq ^*,\mathcal {J})$
, that is, there are Borel functions
![]() $\alpha :\mathcal {I}\to \mathcal {J}$
and
$\alpha :\mathcal {I}\to \mathcal {J}$
and
![]() $\beta :\mathcal {J}\to \mathcal {I}$
such that for every
$\beta :\mathcal {J}\to \mathcal {I}$
such that for every
![]() $A\in \mathcal {I}$
and
$A\in \mathcal {I}$
and
![]() $B\in \mathcal {J}$
,
$B\in \mathcal {J}$
,
![]() $\alpha (A)\subseteq ^* B$
implies
$\alpha (A)\subseteq ^* B$
implies
![]() $A\subseteq ^* \beta (B)$
. Then
$A\subseteq ^* \beta (B)$
. Then
![]() $\mathrm {cof}^*(\mathcal {I},\infty )=\mathrm {non}^*(\mathcal {I},*)\leq \mathrm {non}^*(\mathcal {J},*)=\mathrm {cof}^*(\mathcal {J},\infty )$
and
$\mathrm {cof}^*(\mathcal {I},\infty )=\mathrm {non}^*(\mathcal {I},*)\leq \mathrm {non}^*(\mathcal {J},*)=\mathrm {cof}^*(\mathcal {J},\infty )$
and
![]() $\mathrm {add}^*(\mathcal {I},\infty )=\mathrm {cov}^*(\mathcal {I},*)\geq \mathrm {cov}^*(\mathcal {J},*)=\mathrm {add}^*(\mathcal {J},\infty )$
; and if
$\mathrm {add}^*(\mathcal {I},\infty )=\mathrm {cov}^*(\mathcal {I},*)\geq \mathrm {cov}^*(\mathcal {J},*)=\mathrm {add}^*(\mathcal {J},\infty )$
; and if
![]() $\mathbb {P}$
cannot
$\mathbb {P}$
cannot
![]() $*$
-destroy
$*$
-destroy
![]() $\mathcal {I}$
then
$\mathcal {I}$
then
![]() $\mathbb {P}$
cannot
$\mathbb {P}$
cannot
![]() $*$
-destroy
$*$
-destroy
![]() $\mathcal {J}$
either, and dually, if
$\mathcal {J}$
either, and dually, if
![]() $\Vdash _{\mathbb {P}}\mathcal {I}^*\cap V\in \widehat {\mathcal {I}}$
then
$\Vdash _{\mathbb {P}}\mathcal {I}^*\cap V\in \widehat {\mathcal {I}}$
then
![]() $\Vdash _{\mathbb {P}}\mathcal {J}^*\cap V\in \widehat {\mathcal {J}}$
.
$\Vdash _{\mathbb {P}}\mathcal {J}^*\cap V\in \widehat {\mathcal {J}}$
.
Example 7.4. Let
![]() $\mathcal {I}$
be a Borel ideal. The identity maps show that
$\mathcal {I}$
be a Borel ideal. The identity maps show that
![]() $(\mathcal {I},\neg R_{\mathrm {ii}},[\omega ]^\omega )\leq _{\mathrm {BT}}(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^+)$
holds. Conversely, if
$(\mathcal {I},\neg R_{\mathrm {ii}},[\omega ]^\omega )\leq _{\mathrm {BT}}(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^+)$
holds. Conversely, if
![]() $\mathcal {I}$
is fragile with
$\mathcal {I}$
is fragile with
![]() $Y=\omega $
is the definition, then a trivial modification of the proof of Proposition 4.6 shows that
$Y=\omega $
is the definition, then a trivial modification of the proof of Proposition 4.6 shows that
![]() $(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^+)\leq _{\mathrm {BT}}(\mathcal {I},\neg R_{\mathrm {ii}},[\omega ]^\omega )$
also holds, and so
$(\mathcal {I},\neg R_{\mathrm {ii}},\mathcal {I}^+)\leq _{\mathrm {BT}}(\mathcal {I},\neg R_{\mathrm {ii}},[\omega ]^\omega )$
also holds, and so
![]() $\mathrm {non}^*(\mathcal {I},+)=\mathrm {non}^*(\mathcal {I},\infty )$
,
$\mathrm {non}^*(\mathcal {I},+)=\mathrm {non}^*(\mathcal {I},\infty )$
,
![]() $\mathrm {cov}^*(\mathcal {I},+)=\mathrm {cov}^*(\mathcal {I},\infty )$
, if
$\mathrm {cov}^*(\mathcal {I},+)=\mathrm {cov}^*(\mathcal {I},\infty )$
, if
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {I}$
then it
$\mathcal {I}$
then it
![]() $+$
-destroys
$+$
-destroys
![]() $\mathcal {I}$
, and if
$\mathcal {I}$
, and if
![]() $\Vdash _{\mathbb {P}} [\omega ]^\omega \cap V\notin \widehat {\mathcal {I}}$
then
$\Vdash _{\mathbb {P}} [\omega ]^\omega \cap V\notin \widehat {\mathcal {I}}$
then
![]() $\Vdash _{\mathbb {P}} \mathcal {I}^+\cap V\notin \widehat {\mathcal {I}}$
.
$\Vdash _{\mathbb {P}} \mathcal {I}^+\cap V\notin \widehat {\mathcal {I}}$
.
Concerning analytic P-ideals and their
![]() $*$
-destructibility, we know (basically [Reference Brendle and Yatabe6, Lemma 3.1]) that
$*$
-destructibility, we know (basically [Reference Brendle and Yatabe6, Lemma 3.1]) that
![]() $(\mathcal {I},\subseteq ^*,\mathcal {I})\leq _{\mathrm {BT}}(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})$
for every such ideal where
$(\mathcal {I},\subseteq ^*,\mathcal {I})\leq _{\mathrm {BT}}(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})$
for every such ideal where
![]() $\mathrm {Slm}=\prod _{n\in \omega }[\omega ]^{\leq n}$
is the family of slaloms on
$\mathrm {Slm}=\prod _{n\in \omega }[\omega ]^{\leq n}$
is the family of slaloms on
![]() $\omega $
(equipped with the product topology where
$\omega $
(equipped with the product topology where
![]() $[\omega ]^{\leq n}$
is discrete) and
$[\omega ]^{\leq n}$
is discrete) and
![]() $f\in ^* S$
iff
$f\in ^* S$
iff
![]() $f(n)\in S(n)$
for almost every n; and (see [Reference Fremlin20, Corollary 524H]) that
$f(n)\in S(n)$
for almost every n; and (see [Reference Fremlin20, Corollary 524H]) that
![]() $(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})\equiv _{\mathrm {BT}}(\mathcal {N}\subseteq ,\mathcal {N})$
. In particular, if
$(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})\equiv _{\mathrm {BT}}(\mathcal {N}\subseteq ,\mathcal {N})$
. In particular, if
![]() $\mathcal {I}$
is tall, then
$\mathcal {I}$
is tall, then
The question whether these inequalities and implications are actually equalities and equivalences for every tall analytic P-ideal is still open, but there are some partial results (see also the paragraph after Corollary 7.6). An lsc submeasure
![]() $\varphi $
is summable-like if there is an
$\varphi $
is summable-like if there is an
![]() $\varepsilon>0$
such that for every
$\varepsilon>0$
such that for every
![]() $\delta>0$
we can pick a sequence
$\delta>0$
we can pick a sequence
![]() $(F_k)$
of pairwise disjoint finite sets and an
$(F_k)$
of pairwise disjoint finite sets and an
![]() $m\in \omega $
such that (i)
$m\in \omega $
such that (i)
![]() $\varphi (F_k)<\delta $
for every k and (ii)
$\varphi (F_k)<\delta $
for every k and (ii)
![]() $\varphi (\bigcup _{k\in H}F_k)\geq \varepsilon $
for every
$\varphi (\bigcup _{k\in H}F_k)\geq \varepsilon $
for every
![]() $H\in [\omega ]^m$
. We say that an analytic P-ideal
$H\in [\omega ]^m$
. We say that an analytic P-ideal
![]() $\mathcal {I}$
is summable-like if
$\mathcal {I}$
is summable-like if
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
for some summable-like submeasure
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for some summable-like submeasure
![]() $\varphi $
(which implies that if
$\varphi $
(which implies that if
![]() $\mathcal {I}=\mathrm {Exh}(\psi )$
then
$\mathcal {I}=\mathrm {Exh}(\psi )$
then
![]() $\psi $
is also summable-like, and this follows from [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Remark 3.3]). For example, summable ideals which are not trivial modifications of
$\psi $
is also summable-like, and this follows from [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Remark 3.3]). For example, summable ideals which are not trivial modifications of
![]() $\mathrm {Fin}$
and
$\mathrm {Fin}$
and
![]() $\mathrm {tr}(\mathcal {N})$
(see [Reference Borodulin-Nadzieja, Farkas and Plebanek5]) are summable-like. Also, if
$\mathrm {tr}(\mathcal {N})$
(see [Reference Borodulin-Nadzieja, Farkas and Plebanek5]) are summable-like. Also, if
![]() $\mathcal {I}\!\upharpoonright \! X$
is summable-like for some
$\mathcal {I}\!\upharpoonright \! X$
is summable-like for some
![]() $X\in \mathcal {I}^+$
, then
$X\in \mathcal {I}^+$
, then
![]() $\mathcal {I}$
is summable-like too. The next result is a special case of [Reference Solecki and Todorčević40, Theorem 3.7(ii)].
$\mathcal {I}$
is summable-like too. The next result is a special case of [Reference Solecki and Todorčević40, Theorem 3.7(ii)].
Proposition 7.5.
![]() $(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})\leq _{\mathrm {BT}}(\mathcal {I},\subseteq ^*,\mathcal {I})$
for every summable-like ideal
$(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})\leq _{\mathrm {BT}}(\mathcal {I},\subseteq ^*,\mathcal {I})$
for every summable-like ideal
![]() $\mathcal {I}$
, and hence these relations are BT-equivalent.
$\mathcal {I}$
, and hence these relations are BT-equivalent.
Corollary 7.6. If
![]() $\mathcal {I}$
is tall and summable-like then in (Ia,Ib) the inequalities are actually equalities, and in (IIa,IIb) the implications are actually equivalences.
$\mathcal {I}$
is tall and summable-like then in (Ia,Ib) the inequalities are actually equalities, and in (IIa,IIb) the implications are actually equivalences.
Concerning
![]() $*$
-destructibility and combinatorics of analytic P-ideals, one of the most fundamental questions is if the above proposition, or at least the reverse inequalities in (Ia,Ib) and reverse implications in (IIa,IIb) hold for every tall analytic P-ideal.
$*$
-destructibility and combinatorics of analytic P-ideals, one of the most fundamental questions is if the above proposition, or at least the reverse inequalities in (Ia,Ib) and reverse implications in (IIa,IIb) hold for every tall analytic P-ideal.
Concerning non summable-like ideals, e.g., density ideals, in [Reference Hernández-Hernández and Hrušák21] (applying results due to Fremlin and Farah), the authors proved that
![]() $\mathrm {add}^*(\mathcal {Z}_{\vec {\mu }},\infty )=\mathrm {add}(\mathcal {N})$
and
$\mathrm {add}^*(\mathcal {Z}_{\vec {\mu }},\infty )=\mathrm {add}(\mathcal {N})$
and
![]() $\mathrm {cof}^*(\mathcal {Z}_{\vec {\mu }},\infty )=\mathrm {cof}(\mathcal {N})$
hold for every tall density ideal
$\mathrm {cof}^*(\mathcal {Z}_{\vec {\mu }},\infty )=\mathrm {cof}(\mathcal {N})$
hold for every tall density ideal
![]() $\mathcal {Z}_{\vec {\mu }}$
. Their proof is of a purely combinatorial nature—it does not go via Borel Tukey connections.
$\mathcal {Z}_{\vec {\mu }}$
. Their proof is of a purely combinatorial nature—it does not go via Borel Tukey connections.
Concerning
![]() $\mathcal {Z}$
, there are strong indications that
$\mathcal {Z}$
, there are strong indications that
![]() $(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})\leq _{\mathrm {BT}}(\mathcal {Z},\subseteq ^*,\mathcal {Z})$
does not hold (see, e.g., [Reference Fremlin20, Corollary 524H], [Reference Louveau and Veličković34, Theorem 7]). At the same time, we already know that
$(\,\!^\omega \omega ,\in ^*,\mathrm {Slm})\leq _{\mathrm {BT}}(\mathcal {Z},\subseteq ^*,\mathcal {Z})$
does not hold (see, e.g., [Reference Fremlin20, Corollary 524H], [Reference Louveau and Veličković34, Theorem 7]). At the same time, we already know that
![]() $\mathrm {add}^*(\mathcal {Z},\infty )=\mathrm {add}(\mathcal {N})$
and
$\mathrm {add}^*(\mathcal {Z},\infty )=\mathrm {add}(\mathcal {N})$
and
![]() $\mathrm {cof}^*(\mathcal {Z},\infty )=\mathrm {cof}(\mathcal {N})$
, and also (see [Reference Farkas, Khomskii and Vidnyánszky18, Theorem 6.16], based on Fremlin’s proof of these last equalities) that the “reverse” (IIa) holds for
$\mathrm {cof}^*(\mathcal {Z},\infty )=\mathrm {cof}(\mathcal {N})$
, and also (see [Reference Farkas, Khomskii and Vidnyánszky18, Theorem 6.16], based on Fremlin’s proof of these last equalities) that the “reverse” (IIa) holds for
![]() $\mathcal {Z}$
, that is, if
$\mathcal {Z}$
, that is, if
![]() $\mathcal {Z}\cap V$
is cofinal in
$\mathcal {Z}\cap V$
is cofinal in
![]() $\mathcal {Z}\cap V^{\mathbb {P}}$
, then
$\mathcal {Z}\cap V^{\mathbb {P}}$
, then
![]() $\mathbb {P}$
has the Sacks-property. The last missing implication, (IIb) for
$\mathbb {P}$
has the Sacks-property. The last missing implication, (IIb) for
![]() $\mathcal {Z}$
is still an open problem:
$\mathcal {Z}$
is still an open problem:
Problem 7.7. Does there exist a
![]() $\mathbb {P}$
which
$\mathbb {P}$
which
![]() $*$
-destroys
$*$
-destroys
![]() $\mathcal {Z}$
but does not add a slalom capturing all ground model reals?
$\mathcal {Z}$
but does not add a slalom capturing all ground model reals?
8 Further questions
In addition to the problems from the previous sections, here we list a couple of further questions we found interesting.
8.1 Destruction without collateral damage
Fix two Borel ideals
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
and assume that there is no “obvious” reason why
$\mathcal {J}$
and assume that there is no “obvious” reason why
![]() $\infty /+$
-destruction of
$\infty /+$
-destruction of
![]() $\mathcal {J}$
would imply
$\mathcal {J}$
would imply
![]() $\infty /+$
-destruction of
$\infty /+$
-destruction of
![]() $\mathcal {I}$
, e.g.,
$\mathcal {I}$
, e.g.,
![]() $\mathcal {I}\nleq _{\mathrm {K}}\mathcal {J}\!\upharpoonright \! X$
for any
$\mathcal {I}\nleq _{\mathrm {K}}\mathcal {J}\!\upharpoonright \! X$
for any
![]() $X\in \mathcal {J}^+$
. One may ask if we can find a forcing notion
$X\in \mathcal {J}^+$
. One may ask if we can find a forcing notion
![]() $\mathbb {P}$
which
$\mathbb {P}$
which
![]() $\infty /+$
-destroys
$\infty /+$
-destroys
![]() $\mathcal {J}$
but does not
$\mathcal {J}$
but does not
![]() $\infty /+$
-destroy
$\infty /+$
-destroy
![]() $\mathcal {I}$
, or even
$\mathcal {I}$
, or even
![]() $+$
-destroys
$+$
-destroys
![]() $\mathcal {J}$
without destroying
$\mathcal {J}$
without destroying
![]() $\mathcal {I}$
, etc.
$\mathcal {I}$
, etc.
8.2 Destruction without adding unbounded reals
Applying results from [Reference Laflamme31], it is not hard to see that every
![]() $F_\sigma $
ideal can be
$F_\sigma $
ideal can be
![]() $+$
-destroyed by an
$+$
-destroyed by an
![]() $\,\!^\omega \omega $
-bounding proper forcing notion.
$\,\!^\omega \omega $
-bounding proper forcing notion.
Problem 8.1. Which Borel ideals can be
![]() $+$
-destroyed by
$+$
-destroyed by
![]() $\,\!^\omega \omega $
-bounding proper forcing notions?
$\,\!^\omega \omega $
-bounding proper forcing notions?
8.3 More general degrees of destruction
We can define an even more general notion of destroying ideals as follows: Fix a Borel ideal
![]() $\mathcal {I}$
and a Borel
$\mathcal {I}$
and a Borel
![]() $\mathcal {D}\subseteq \bigcup \widehat {\mathcal {I}}$
. We say that
$\mathcal {D}\subseteq \bigcup \widehat {\mathcal {I}}$
. We say that
![]() $\mathbb {P}$
can
$\mathbb {P}$
can
![]() $\mathcal {D}$
-destroy
$\mathcal {D}$
-destroy
![]() $\mathcal {I}$
if there is a
$\mathcal {I}$
if there is a
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $p\Vdash \exists\ D\in \mathcal {D}\ \forall \ A\in \mathcal {I}^V\ |D\cap A|<\omega $
, and of course, we can define the cardinal invariants
$p\Vdash \exists\ D\in \mathcal {D}\ \forall \ A\in \mathcal {I}^V\ |D\cap A|<\omega $
, and of course, we can define the cardinal invariants
![]() $\mathrm {inv}^*(\mathcal {I},\mathcal {D})$
as well. This notion raises a plethora of questions, for example: We know that
$\mathrm {inv}^*(\mathcal {I},\mathcal {D})$
as well. This notion raises a plethora of questions, for example: We know that
![]() $\mathcal {I}_{1/n}\subseteq \mathcal {Z}$
, and hence
$\mathcal {I}_{1/n}\subseteq \mathcal {Z}$
, and hence
![]() $\mathcal {I}^+_{1/n}\supseteq \mathcal {Z}^+$
. In particular,
$\mathcal {I}^+_{1/n}\supseteq \mathcal {Z}^+$
. In particular,
![]() $\mathbb {M}(\mathcal {Z}^*)\ \mathcal {I}^+_{1/n}$
-destroys
$\mathbb {M}(\mathcal {Z}^*)\ \mathcal {I}^+_{1/n}$
-destroys
![]() $\mathcal {Z}$
. Does there exist a forcing notion
$\mathcal {Z}$
. Does there exist a forcing notion
![]() $\mathbb {P}$
which
$\mathbb {P}$
which
![]() $\mathcal {I}^+_{1/n}$
-destroys
$\mathcal {I}^+_{1/n}$
-destroys
![]() $\mathcal {Z}$
but cannot
$\mathcal {Z}$
but cannot
![]() $\mathcal {Z}^+$
-destroy
$\mathcal {Z}^+$
-destroy
![]() $\mathcal {Z}$
?
$\mathcal {Z}$
?
8.4 Forcing with
 $\mathbb {P}_{\widehat {\mathcal {I}}}$
$\mathbb {P}_{\widehat {\mathcal {I}}}$
Let
![]() $\mathcal {I}$
be a tall analytic P-ideal. What can we say about the forcing notion
$\mathcal {I}$
be a tall analytic P-ideal. What can we say about the forcing notion
![]() $\mathbb {P}_{\widehat {\mathcal {I}}}=\mathcal {B}([\omega ]^\omega )\setminus \widehat {\mathcal {I}}$
? We know that it is proper (see [Reference Zapletal42, Section 4.6]) and it clearly destroys
$\mathbb {P}_{\widehat {\mathcal {I}}}=\mathcal {B}([\omega ]^\omega )\setminus \widehat {\mathcal {I}}$
? We know that it is proper (see [Reference Zapletal42, Section 4.6]) and it clearly destroys
![]() $\mathcal {I}$
. Also, notice that
$\mathcal {I}$
. Also, notice that
![]() $\mathcal {I}^+\in \mathbb {P}_{\widehat {\mathcal {I}}}$
is a condition and forces that
$\mathcal {I}^+\in \mathbb {P}_{\widehat {\mathcal {I}}}$
is a condition and forces that
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $+$
-destroyed, similarly,
$+$
-destroyed, similarly,
![]() $\mathcal {I}^*$
forces that
$\mathcal {I}^*$
forces that
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $*$
-destroyed. In other words, it seems reasonable to decompose
$*$
-destroyed. In other words, it seems reasonable to decompose
![]() $\mathbb {P}_{\widehat {\mathcal {I}}}$
into three forcing notions
$\mathbb {P}_{\widehat {\mathcal {I}}}$
into three forcing notions
![]() $\mathbb {P}(\mathcal {I},\infty )=\mathbb {P}_{\widehat {\mathcal {I}}\upharpoonright (\mathcal {I}\cap [\omega ]^\omega )}$
,
$\mathbb {P}(\mathcal {I},\infty )=\mathbb {P}_{\widehat {\mathcal {I}}\upharpoonright (\mathcal {I}\cap [\omega ]^\omega )}$
,
![]() $\mathbb {P}(\mathcal {I},+)=\mathbb {P}_{\widehat {\mathcal {I}}\upharpoonright (\mathcal {I}^+\setminus \mathcal {I}^*)}$
, and
$\mathbb {P}(\mathcal {I},+)=\mathbb {P}_{\widehat {\mathcal {I}}\upharpoonright (\mathcal {I}^+\setminus \mathcal {I}^*)}$
, and
![]() $\mathbb {P}(\mathcal {I},*)=\mathbb {P}_{\widehat {\mathcal {I}}\upharpoonright \mathcal {I}^*}$
.
$\mathbb {P}(\mathcal {I},*)=\mathbb {P}_{\widehat {\mathcal {I}}\upharpoonright \mathcal {I}^*}$
.
Problem 8.2. Can
![]() $\mathbb {P}(\mathcal {I},\infty )\ +$
-destroy or
$\mathbb {P}(\mathcal {I},\infty )\ +$
-destroy or
![]() $\mathbb {P}(\mathcal {I},+)\ *$
-destroy
$\mathbb {P}(\mathcal {I},+)\ *$
-destroy
![]() $\mathcal {I}$
? If not, what can we say about their countable support iterations? Do they add dominating etc reals?
$\mathcal {I}$
? If not, what can we say about their countable support iterations? Do they add dominating etc reals?
If
![]() $\mathcal {I}$
is not a P-ideal but
$\mathcal {I}$
is not a P-ideal but
![]() $\mathrm {cov}^*(\mathcal {I},\infty )>\omega $
, then we can talk about the
$\mathrm {cov}^*(\mathcal {I},\infty )>\omega $
, then we can talk about the
![]() $\sigma $
-ideal
$\sigma $
-ideal
![]() $\widehat {\mathcal {I}}^\sigma \not \ni [\omega ]^\omega $
generated by
$\widehat {\mathcal {I}}^\sigma \not \ni [\omega ]^\omega $
generated by
![]() $\widehat {\mathcal {I}}$
and the forcing notion
$\widehat {\mathcal {I}}$
and the forcing notion
![]() $\mathbb {P}(\mathcal {I},\infty )=\mathbb {P}_{\widehat {\mathcal {I}}^\sigma \upharpoonright (\mathcal {I}\cap [\omega ]^\omega )}$
. Similarly, if even
$\mathbb {P}(\mathcal {I},\infty )=\mathbb {P}_{\widehat {\mathcal {I}}^\sigma \upharpoonright (\mathcal {I}\cap [\omega ]^\omega )}$
. Similarly, if even
![]() $\mathrm {cov}^*(\mathcal {I},+)>\omega $
, then we can talk about
$\mathrm {cov}^*(\mathcal {I},+)>\omega $
, then we can talk about
![]() $\mathbb {P}(\mathcal {I},+)=\mathbb {P}_{\widehat {\mathcal {I}}^\sigma \upharpoonright (\mathcal {I}^+\setminus \mathcal {I}^*)}$
too. In particular, one can ask the questions above about these forcing notions as well.
$\mathbb {P}(\mathcal {I},+)=\mathbb {P}_{\widehat {\mathcal {I}}^\sigma \upharpoonright (\mathcal {I}^+\setminus \mathcal {I}^*)}$
too. In particular, one can ask the questions above about these forcing notions as well.
Acknowledgments
The first author was supported by the Austrian Science Fund (FWF) project P29907. The second author was supported by the Austrian Science Fund (FWF) project I2374-N35.