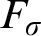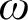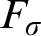1. Introduction
The present paper is a contribution to the study of the structure of the Tukey order on definable directed sets; for background, see [Reference Fremlin2, Reference Fremlin4, Reference Hrušák, Babinkostova, Caicedo, Geschke and Scheepers5, Reference Isbell7, Reference Louveau and Veličković10, Reference Mátrai13, Reference Schmidt16, Reference Solecki18, Reference Solecki and Todorcevic19, Reference Todorčević21, Reference Tukey22]. For two directed orders P and Q, we write
![]() $P\leq _T Q$
if there is a function
$P\leq _T Q$
if there is a function
![]() $h: P \to Q$
sending unbounded sets to unbounded sets.Footnote
1
Such an h is called a Tukey map and P is said to be Tukey reducible to Q. We write
$h: P \to Q$
sending unbounded sets to unbounded sets.Footnote
1
Such an h is called a Tukey map and P is said to be Tukey reducible to Q. We write
![]() $P\equiv _T Q$
if both
$P\equiv _T Q$
if both
![]() $P\leq _T Q$
and
$P\leq _T Q$
and
![]() $Q\leq _T P$
. Tukey order was introduced in [Reference Tukey22] to study convergence of nets and was recast by Schmidt [Reference Schmidt16] and Isbell [Reference Isbell7] to compare cofinal types of directed orders. The main class of directed orders considered by us are
$Q\leq _T P$
. Tukey order was introduced in [Reference Tukey22] to study convergence of nets and was recast by Schmidt [Reference Schmidt16] and Isbell [Reference Isbell7] to compare cofinal types of directed orders. The main class of directed orders considered by us are
![]() $F_{\sigma }$
ideals of subsets of
$F_{\sigma }$
ideals of subsets of
![]() $\omega $
taken with inclusion as the order relation.
$\omega $
taken with inclusion as the order relation.
Recall that a subset of a metric space is
![]() $F_{\sigma }$
if it is the union of a countable family of closed sets; it is
$F_{\sigma }$
if it is the union of a countable family of closed sets; it is
![]() $G_{\delta }$
if it is the intersection of a countable family of open sets. To be
$G_{\delta }$
if it is the intersection of a countable family of open sets. To be
![]() $F_{\sigma }$
for an ideal of subsets of
$F_{\sigma }$
for an ideal of subsets of
![]() $\omega $
means
$\omega $
means
![]() $F_{\sigma }$
with respect to the product topology on
$F_{\sigma }$
with respect to the product topology on
![]() ${\mathcal P}(\omega )= \{ 0,1\}^{\omega }$
, with
${\mathcal P}(\omega )= \{ 0,1\}^{\omega }$
, with
![]() $\{ 0,1\}$
given the discrete topology. To be
$\{ 0,1\}$
given the discrete topology. To be
![]() $G_{\delta }$
for an ideal of compact subsets of a Polish space X means
$G_{\delta }$
for an ideal of compact subsets of a Polish space X means
![]() $G_{\delta }$
with respect to the Vietoris topology on the space of all compact subsets of X.
$G_{\delta }$
with respect to the Vietoris topology on the space of all compact subsets of X.
An important role in the study of ideals of subsets of
![]() $\omega $
is played by lower semicontinuous submeasures. A function
$\omega $
is played by lower semicontinuous submeasures. A function
![]() $\varphi \colon {\mathcal P}(\omega )\to [0,\infty ]$
is a submeasure if
$\varphi \colon {\mathcal P}(\omega )\to [0,\infty ]$
is a submeasure if
-
–
 $\varphi (\emptyset )=0$
,
$\varphi (\emptyset )=0$
, -
–
 $\varphi (a)\leq \varphi (b)$
, for
$\varphi (a)\leq \varphi (b)$
, for
 $a\subseteq b$
,
$a\subseteq b$
, -
–
 $\varphi (a\cup b)\leq \varphi (a) +\varphi (b)$
, for all
$\varphi (a\cup b)\leq \varphi (a) +\varphi (b)$
, for all
 $a,b\subseteq \omega $
.
$a,b\subseteq \omega $
.
A submeasure
![]() $\varphi $
is lower semicontinuous (lsc) if
$\varphi $
is lower semicontinuous (lsc) if
-
–
 $\varphi (a)=\lim _{n\to \infty } \varphi (a\cap [0,n])$
, for all
$\varphi (a)=\lim _{n\to \infty } \varphi (a\cap [0,n])$
, for all
 $a\subseteq \omega $
.
$a\subseteq \omega $
.
By a theorem of Mazur [Reference Mazur14], an ideal
![]() $\mathcal {I}$
of subsets of
$\mathcal {I}$
of subsets of
![]() $\omega $
is
$\omega $
is
![]() $F_{\sigma }$
precisely when there is a lower semicontinuous submeasure
$F_{\sigma }$
precisely when there is a lower semicontinuous submeasure
![]() $\varphi $
such that
$\varphi $
such that
We study the place
![]() $F_{\sigma }$
ideals of subsets of
$F_{\sigma }$
ideals of subsets of
![]() $\omega $
occupy in the Tukey order. As a point of reference we use the following, now standard, diagram which summarizes the known Tukey reductions among the well-studied directed sets; see [Reference Bartoszyński1, Reference Fremlin2, Reference Fremlin4, Reference Isbell7, Reference Louveau and Veličković10, Reference Mátrai12, Reference Moore and Solecki15, Reference Solecki17–Reference Solecki and Todorcevic19, Reference Solecki and Todorcevic20]. As usual, in the diagram, an arrow denotes reduction and the absence of arrows non-reduction. The partial orders in the diagram are defined below it.
$\omega $
occupy in the Tukey order. As a point of reference we use the following, now standard, diagram which summarizes the known Tukey reductions among the well-studied directed sets; see [Reference Bartoszyński1, Reference Fremlin2, Reference Fremlin4, Reference Isbell7, Reference Louveau and Veličković10, Reference Mátrai12, Reference Moore and Solecki15, Reference Solecki17–Reference Solecki and Todorcevic19, Reference Solecki and Todorcevic20]. As usual, in the diagram, an arrow denotes reduction and the absence of arrows non-reduction. The partial orders in the diagram are defined below it.

The partial orders in the diagram are Tukey equivalent to ideals of subsets of
![]() $\omega $
or to ideals of compact subsets of compact metric spaces. The order
$\omega $
or to ideals of compact subsets of compact metric spaces. The order
![]() $[\mathfrak c]^{<\omega }$
of finite subsets of
$[\mathfrak c]^{<\omega }$
of finite subsets of
![]() $2^{\omega }$
taken with inclusion as the order relation is Tukey equivalent to an
$2^{\omega }$
taken with inclusion as the order relation is Tukey equivalent to an
![]() $F_{\sigma }$
ideal of subsets of
$F_{\sigma }$
ideal of subsets of
![]() $\omega $
, see [Reference Louveau and Veličković10, Section 5, Proposition 3]. The summable ideal and the density zero ideal are defined, respectively, as
$\omega $
, see [Reference Louveau and Veličković10, Section 5, Proposition 3]. The summable ideal and the density zero ideal are defined, respectively, as
 $$ \begin{align*} l_1=\left\{A\subseteq \omega: \sum_{n\in A}\frac1{n+1}<\infty\right\}\;\text{ and }\;\mathcal{Z}_0=\left\{A\subseteq\omega: \lim_n \frac{|A\cap n|}{n}=0\right\}. \end{align*} $$
$$ \begin{align*} l_1=\left\{A\subseteq \omega: \sum_{n\in A}\frac1{n+1}<\infty\right\}\;\text{ and }\;\mathcal{Z}_0=\left\{A\subseteq\omega: \lim_n \frac{|A\cap n|}{n}=0\right\}. \end{align*} $$
The ideal
![]() $\mathrm {Fin}$
of finite subsets of
$\mathrm {Fin}$
of finite subsets of
![]() $\omega $
is Tukey equivalent to
$\omega $
is Tukey equivalent to
![]() $\omega $
, and
$\omega $
, and
The ideal
![]() $\mathrm {NWD}$
is the ideal of closed nowhere dense subsets of
$\mathrm {NWD}$
is the ideal of closed nowhere dense subsets of
![]() $2^{\omega }$
, and
$2^{\omega }$
, and
![]() $\mathcal E_{\mu }$
is the ideal of closed measure zero subsets of
$\mathcal E_{\mu }$
is the ideal of closed measure zero subsets of
![]() $2^{\omega }$
. To define
$2^{\omega }$
. To define
![]() $\mathcal I_0$
, denote by
$\mathcal I_0$
, denote by
![]() $\mathcal S$
the collection of all block sequences of finite partial functions from
$\mathcal S$
the collection of all block sequences of finite partial functions from
![]() $\omega $
into
$\omega $
into
![]() $2$
of even or infinite length, and for
$2$
of even or infinite length, and for
![]() $\overline s\in \mathcal S$
let
$\overline s\in \mathcal S$
let
and
The only
![]() $F_{\sigma }$
ideals appearing in the diagram are
$F_{\sigma }$
ideals appearing in the diagram are
![]() $\omega $
,
$\omega $
,
![]() $[\mathfrak c]^{<\omega }$
, and
$[\mathfrak c]^{<\omega }$
, and
![]() $l_1$
.
$l_1$
.
The left column of the above diagram, or more accurately the class of all
![]() $G_{\delta }$
ideals of compact subsets of Polish spaces, is often referred to as the category leaf. The right column, or more precisely the class of all analytic P-ideals of subsets of
$G_{\delta }$
ideals of compact subsets of Polish spaces, is often referred to as the category leaf. The right column, or more precisely the class of all analytic P-ideals of subsets of
![]() $\omega $
, is called the measure leaf.
$\omega $
, is called the measure leaf.
In the present paper, we study a third leaf, one could call the
![]() $F_{\sigma }$
leaf, consisting of
$F_{\sigma }$
leaf, consisting of
![]() $F_{\sigma }$
ideals of subsets of
$F_{\sigma }$
ideals of subsets of
![]() $\omega $
. First, we look into the relationship between
$\omega $
. First, we look into the relationship between
![]() $F_{\sigma }$
ideals and the category leaf. We show in Theorem 2.1 that, except for trivial situations,
$F_{\sigma }$
ideals and the category leaf. We show in Theorem 2.1 that, except for trivial situations,
![]() $F_{\sigma }$
ideals are not reducible to
$F_{\sigma }$
ideals are not reducible to
![]() $G_{\delta }$
ideals of compact subsets of Polish spaces. Next, we restrict our attention to a class of
$G_{\delta }$
ideals of compact subsets of Polish spaces. Next, we restrict our attention to a class of
![]() $F_{\sigma }$
ideals that we call flat. We prove that flat ideals are not basic, except, again, for trivial situations. This and the previous result indicate distinctness of the leaf studied in this paper from the other two leaves. Within the class of flat ideals, we show a dichotomy, Theorem 4.2, saying that a flat ideal is Tukey equivalent to the top order in the diagram, namely
$F_{\sigma }$
ideals that we call flat. We prove that flat ideals are not basic, except, again, for trivial situations. This and the previous result indicate distinctness of the leaf studied in this paper from the other two leaves. Within the class of flat ideals, we show a dichotomy, Theorem 4.2, saying that a flat ideal is Tukey equivalent to the top order in the diagram, namely
![]() $[\mathfrak c]^{<\omega }$
, or it has a structural property, which we call gradual flatness. Then, in Theorem 5.1, we compare gradual flatness with the measure leaf by showing that such ideals are reducible to the density zero ideal
$[\mathfrak c]^{<\omega }$
, or it has a structural property, which we call gradual flatness. Then, in Theorem 5.1, we compare gradual flatness with the measure leaf by showing that such ideals are reducible to the density zero ideal
![]() ${\mathcal Z}_0$
. In fact, Theorem 5.1 shows that gradual flatness is a robust property, as it turns out to be equivalent to a number of diverse conditions. In the remarks following Theorem 5.1, we point out the high complexity of the structure of the Tukey reduction among gradually flat ideals.
${\mathcal Z}_0$
. In fact, Theorem 5.1 shows that gradual flatness is a robust property, as it turns out to be equivalent to a number of diverse conditions. In the remarks following Theorem 5.1, we point out the high complexity of the structure of the Tukey reduction among gradually flat ideals.
2.
 $F_{\sigma\ }$
ideals of subsets of
$F_{\sigma\ }$
ideals of subsets of
 ${\ \omega\ }$
and
${\ \omega\ }$
and
 $\ G_{\delta\ }$
ideals of compact sets
$\ G_{\delta\ }$
ideals of compact sets
We prove a theorem that is an indication of “orthogonality” between
![]() $F_{\sigma }$
ideals of subsets of
$F_{\sigma }$
ideals of subsets of
![]() $\omega $
and
$\omega $
and
![]() $G_{\delta }$
ideals of compact subsets of Polish spaces. By [Reference Solecki and Todorcevic19, Corollary 6.4], a similar relation holds between analytic P-ideals of subsets of
$G_{\delta }$
ideals of compact subsets of Polish spaces. By [Reference Solecki and Todorcevic19, Corollary 6.4], a similar relation holds between analytic P-ideals of subsets of
![]() $\omega $
and
$\omega $
and
![]() $G_{\delta }$
ideals of compact subsets of Polish spaces.
$G_{\delta }$
ideals of compact subsets of Polish spaces.
Theorem 2.1. If
![]() $\mathcal J$
is a
$\mathcal J$
is a
![]() $G_{\delta }$
ideal of compact subsets of a Polish space and
$G_{\delta }$
ideal of compact subsets of a Polish space and
![]() $\mathcal I$
is an uncountably generated
$\mathcal I$
is an uncountably generated
![]() $F_{\sigma }$
ideal on
$F_{\sigma }$
ideal on
![]() $\omega $
, then
$\omega $
, then
![]() $\mathcal I\not \leq _T \mathcal J$
.
$\mathcal I\not \leq _T \mathcal J$
.
For the proof of this theorem, we use the second of Fremlin’s games introduced in [Reference Fremlin3]. Let
![]() $P\not =\emptyset $
be a partially ordered set. The Game
$P\not =\emptyset $
be a partially ordered set. The Game
![]() $\Gamma _2(P)$
is the two-player game where, setting
$\Gamma _2(P)$
is the two-player game where, setting
![]() $U_{-1}=P$
, the nth move of the game is described for both players as follows. Given
$U_{-1}=P$
, the nth move of the game is described for both players as follows. Given
![]() $U_{n-1}\subseteq P$
, Player I plays a countable cover
$U_{n-1}\subseteq P$
, Player I plays a countable cover
![]() $\mathcal {U}_n$
of
$\mathcal {U}_n$
of
![]() $U_{n-1}$
, and Player II responds with
$U_{n-1}$
, and Player II responds with
![]() $U_n\in \mathcal {U}_n$
and a finite set
$U_n\in \mathcal {U}_n$
and a finite set
![]() $I_n\subseteq U_n$
. (By countable cover here we mean that
$I_n\subseteq U_n$
. (By countable cover here we mean that
![]() $\mathcal {U}_n$
is a countable family of sets and
$\mathcal {U}_n$
is a countable family of sets and
![]() $\bigcup \mathcal {U}_n =U_{n-1}$
.) The following diagram gives a pictorial representation of the nth move.
$\bigcup \mathcal {U}_n =U_{n-1}$
.) The following diagram gives a pictorial representation of the nth move.

Player I wins the game if the set
![]() $\bigcup _{n\in \omega }I_n$
is bounded in P, otherwise Player II wins.
$\bigcup _{n\in \omega }I_n$
is bounded in P, otherwise Player II wins.
The theorem follows directly from the following three lemmas. The first one is easy to prove and is contained in [Reference Fremlin3].
Lemma 2.2 [Reference Fremlin3]
Let P and Q be partially ordered sets such that
![]() $P\leq _T Q$
.
$P\leq _T Q$
.
-
(1) If Player I has a winning strategy in
 $\Gamma _2(Q)$
, then Player I also has a winning strategy in
$\Gamma _2(Q)$
, then Player I also has a winning strategy in
 $\Gamma _2(P)$
.
$\Gamma _2(P)$
. -
(2) If Player II has a winning strategy in
 $\Gamma _2(P)$
, then Player II also has a winning strategy in
$\Gamma _2(P)$
, then Player II also has a winning strategy in
 $\Gamma _2(Q)$
.
$\Gamma _2(Q)$
.
Lemma 2.3. Player II has a winning strategy in
![]() $\Gamma _2(\mathcal {I})$
for every uncountably generated
$\Gamma _2(\mathcal {I})$
for every uncountably generated
![]() $F_{\sigma }$
ideal
$F_{\sigma }$
ideal
![]() $\mathcal I$
on
$\mathcal I$
on
![]() $\omega $
.
$\omega $
.
Proof Let
![]() $\varphi $
be an lsc submeasure such that
$\varphi $
be an lsc submeasure such that
![]() $\mathcal I=\mathrm {Fin}(\varphi )$
. A winning strategy for Player II can be described as follows. Start with
$\mathcal I=\mathrm {Fin}(\varphi )$
. A winning strategy for Player II can be described as follows. Start with
![]() $U_0=\mathcal I$
. Once
$U_0=\mathcal I$
. Once
![]() $\mathcal {U}_{n-1}$
has been played, as
$\mathcal {U}_{n-1}$
has been played, as
![]() $\mathcal {I}$
is not countably generated, choose
$\mathcal {I}$
is not countably generated, choose
![]() $U_n\in \mathcal {U}_{n-1}$
which is not countably generated, and
$U_n\in \mathcal {U}_{n-1}$
which is not countably generated, and
![]() $I_n\in [U_n]^{<\omega }$
such that
$I_n\in [U_n]^{<\omega }$
such that
![]() $\varphi (\bigcup I_n)>n$
.⊣
$\varphi (\bigcup I_n)>n$
.⊣
Lemma 2.4. Player I has a winning strategy in
![]() $\Gamma _2(\mathcal J)$
for every
$\Gamma _2(\mathcal J)$
for every
![]() $G_{\delta }$
ideal
$G_{\delta }$
ideal
![]() $\mathcal J$
of compact sets of some Polish space X.
$\mathcal J$
of compact sets of some Polish space X.
Proof Let
![]() $\delta $
be the Hausdorff metric on
$\delta $
be the Hausdorff metric on
![]() $\mathcal K(X)$
. Since
$\mathcal K(X)$
. Since
![]() $\mathcal J$
is
$\mathcal J$
is
![]() $G_{\delta }$
, let
$G_{\delta }$
, let
![]() $\{ F_n: n\in \omega \}$
be a sequences of closed subset of
$\{ F_n: n\in \omega \}$
be a sequences of closed subset of
![]() $\mathcal K(X)$
such that
$\mathcal K(X)$
such that
 $\mathcal K(X)\setminus \mathcal J=\bigcup _{n\in \omega } F_n$
.
$\mathcal K(X)\setminus \mathcal J=\bigcup _{n\in \omega } F_n$
.
We can describe a winning strategy for Player I as follows. At Step
![]() $0$
, for each
$0$
, for each
![]() $A\in \mathcal J$
, choose
$A\in \mathcal J$
, choose
![]() $\epsilon _A>0$
such that
$\epsilon _A>0$
such that
![]() $B_{ \delta }( A,\epsilon _A)\cap F_0=\emptyset $
. Since
$B_{ \delta }( A,\epsilon _A)\cap F_0=\emptyset $
. Since
![]() $(\mathcal K(X),\delta )$
is Lindelöf, there exists a countable subcover
$(\mathcal K(X),\delta )$
is Lindelöf, there exists a countable subcover
 $\{ B_{\delta }(A^1_i, \epsilon _{A^1_i}): i\in \omega \}$
of
$\{ B_{\delta }(A^1_i, \epsilon _{A^1_i}): i\in \omega \}$
of
![]() $\mathcal J$
. Player I plays
$\mathcal J$
. Player I plays
 $\mathcal U_0=\{ B_{\delta }(A^1_i, \epsilon _{A^1_i}): i\in \omega \}$
. At Step
$\mathcal U_0=\{ B_{\delta }(A^1_i, \epsilon _{A^1_i}): i\in \omega \}$
. At Step
![]() $n+1$
, suppose Player II plays
$n+1$
, suppose Player II plays
 $B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})$
and a finite subset
$B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})$
and a finite subset
 $I_n\subseteq B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})\cap \mathcal J $
. As in Step
$I_n\subseteq B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})\cap \mathcal J $
. As in Step
![]() $1$
, for each
$1$
, for each
 $A\in B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})\cap \mathcal J$
, there is an
$A\in B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})\cap \mathcal J$
, there is an
 $\epsilon _A\in (0, \frac {1}{n+1})$
such that
$\epsilon _A\in (0, \frac {1}{n+1})$
such that
![]() $B_{ \delta }( A,\epsilon _A)\cap F_n=\emptyset $
. Player I plays a countable subcover
$B_{ \delta }( A,\epsilon _A)\cap F_n=\emptyset $
. Player I plays a countable subcover
 $\mathcal U_{n+1}=\{ B_{\delta }(A^{n+1}_i, \epsilon _{A^{n+1}_i}): i\in \omega \}$
of
$\mathcal U_{n+1}=\{ B_{\delta }(A^{n+1}_i, \epsilon _{A^{n+1}_i}): i\in \omega \}$
of
 $B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})\cap \mathcal J$
.
$B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})\cap \mathcal J$
.
To see that the strategy is winning, note that the sequence
![]() $\{ A^n_{i_n}: n\in \omega \}$
is a Cauchy sequence in
$\{ A^n_{i_n}: n\in \omega \}$
is a Cauchy sequence in
![]() $\mathcal K(X)$
and hence converges to some
$\mathcal K(X)$
and hence converges to some
![]() $A\in \mathcal K(X)$
. By the construction,
$A\in \mathcal K(X)$
. By the construction,
![]() $A\not \in \bigcup _{n\in \omega } F_n$
, so
$A\not \in \bigcup _{n\in \omega } F_n$
, so
![]() $A\in \mathcal J$
. As each
$A\in \mathcal J$
. As each
![]() $I_n$
is a finite subset of
$I_n$
is a finite subset of
 $B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})$
, the sequence
$B_{\delta }(A^n_{i_n},\epsilon _{A^n_{i_n}})$
, the sequence
![]() $\bigcup _{n\in \omega } I_n$
also converges to A, and as, by [Reference Kechris8, Theorem 3],
$\bigcup _{n\in \omega } I_n$
also converges to A, and as, by [Reference Kechris8, Theorem 3],
![]() $\mathcal J$
is a
$\mathcal J$
is a
![]() $\sigma $
-ideal of compact sets, we get
$\sigma $
-ideal of compact sets, we get
![]() $A\cup \bigcup _{n\in \omega } \bigcup I_n \in \mathcal J$
. (Theorem 3 in [Reference Kechris8] is stated only for
$A\cup \bigcup _{n\in \omega } \bigcup I_n \in \mathcal J$
. (Theorem 3 in [Reference Kechris8] is stated only for
![]() $G_{\delta }$
ideals of compact subsets of compact metric spaces, but its proof works for
$G_{\delta }$
ideals of compact subsets of compact metric spaces, but its proof works for
![]() $G_{\delta }$
ideals of compact subsets of arbitrary Polish spaces.)⊣
$G_{\delta }$
ideals of compact subsets of arbitrary Polish spaces.)⊣
For more information on ideals of compact sets, the reader may consult [Reference Kechris, Louveau and Woodin9, Reference Matheron and Zelený11, Reference Mátrai12, Reference Moore and Solecki15, Reference Solecki and Todorcevic19].
3. Flat ideals
In this and subsequent sections, we restrict our attention to a broad subclass of
![]() $F_{\sigma }$
ideals that is defined in terms of submeasures. An lsc submeasure
$F_{\sigma }$
ideals that is defined in terms of submeasures. An lsc submeasure
![]() $\varphi $
is flat if, for each
$\varphi $
is flat if, for each
![]() $M>0$
, there exists
$M>0$
, there exists
![]() $N>0$
such that, for each finite set
$N>0$
such that, for each finite set
![]() $a\in {\mathcal P}(\omega )$
with
$a\in {\mathcal P}(\omega )$
with
![]() $\varphi (a)<N$
, we have
$\varphi (a)<N$
, we have
 $$ \begin{align*} \exists j \ \forall b\in {\mathcal P}(\omega\setminus j) \ \Big(\varphi(b)< M\Rightarrow \varphi(a\cup b)< N\Big). \end{align*} $$
$$ \begin{align*} \exists j \ \forall b\in {\mathcal P}(\omega\setminus j) \ \Big(\varphi(b)< M\Rightarrow \varphi(a\cup b)< N\Big). \end{align*} $$
We will sometimes say that N witnesses flatness of
![]() $\varphi $
for M. An ideal is called flat if it is of the form
$\varphi $
for M. An ideal is called flat if it is of the form
![]() $\mathrm {Fin}(\varphi )$
for a flat submeasure
$\mathrm {Fin}(\varphi )$
for a flat submeasure
![]() $\varphi $
. We point out that fragmented ideals,Footnote
2
as introduced in [Reference Hrušák, Rojas-Rebolledo and Zapletal6], are clearly flat. Note that if
$\varphi $
. We point out that fragmented ideals,Footnote
2
as introduced in [Reference Hrušák, Rojas-Rebolledo and Zapletal6], are clearly flat. Note that if
![]() $\mathcal {I}=\mathrm {Fin}(\varphi )= \mathrm {Fin}(\psi )$
and
$\mathcal {I}=\mathrm {Fin}(\varphi )= \mathrm {Fin}(\psi )$
and
![]() $\varphi $
is flat, it does not follow that
$\varphi $
is flat, it does not follow that
![]() $\psi $
is flat. For example,
$\psi $
is flat. For example,
Both
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are lsc submeasures,
$\psi $
are lsc submeasures,
![]() $\varphi $
is flat, while
$\varphi $
is flat, while
![]() $\psi $
is not.
$\psi $
is not.
It was proved in [Reference Solecki and Todorcevic19] that both the measure leaf and the category leaf, that is, all analytic P-ideals of subsets of
![]() $\omega $
and all
$\omega $
and all
![]() $G_{\delta }$
ideals of compact subsets of Polish spaces, are included in a general class of partial orders, called basic partial orders. (This notion is defined below.) As shown in [Reference Solecki and Todorcevic19], a number of arguments related to Tukey reductions can be run for general basic orders. Here, however, we prove that, unless a flat ideal is countably generated (so very simple) it is not basic. This result, along with Theorem 2.1, highlights “orthogonality” of the partial orders considered in this paper with the previously studied classes of analytic P-ideals and
$G_{\delta }$
ideals of compact subsets of Polish spaces, are included in a general class of partial orders, called basic partial orders. (This notion is defined below.) As shown in [Reference Solecki and Todorcevic19], a number of arguments related to Tukey reductions can be run for general basic orders. Here, however, we prove that, unless a flat ideal is countably generated (so very simple) it is not basic. This result, along with Theorem 2.1, highlights “orthogonality” of the partial orders considered in this paper with the previously studied classes of analytic P-ideals and
![]() $G_{\delta }$
ideals of compact sets.
$G_{\delta }$
ideals of compact sets.
In order to state our result, we recall the definition of basic orders from [Reference Solecki and Todorcevic19, Section 3]. This definition involves a topology on a partial order; in the two cases mentioned above, of analytic P-ideals of subsets of
![]() $\omega $
and
$\omega $
and
![]() $G_{\delta }$
ideals of compact subsets of Polish spaces, the topologies making the orders into basic orders are the submeasure topology and the Vietoris topology, respectively; see [Reference Solecki and Todorcevic19, Section 3] for details. A partial order
$G_{\delta }$
ideals of compact subsets of Polish spaces, the topologies making the orders into basic orders are the submeasure topology and the Vietoris topology, respectively; see [Reference Solecki and Todorcevic19, Section 3] for details. A partial order
![]() $(P, \leq )$
with a metric separable topology on P is basic provided that
$(P, \leq )$
with a metric separable topology on P is basic provided that
-
– any pair of elements of P has the least upper bound with respect to
 $\leq $
and the binary operation of taking the least upper bound is continuous;
$\leq $
and the binary operation of taking the least upper bound is continuous; -
– each bounded sequence has a convergent subsequence;
-
– each convergent sequence has a bounded subsequence.
A result analogous to Theorem 3.1 below was proved by Mátrai in [Reference Mátrai13, Proposition 5.28] for a specific family of ideals. Our theorem generalizes Mátrai’s result; our proof expands on his approach. On the other hand, Theorem 3.1 strengthens, within the class of flat ideals, the general result [Reference Solecki and Todorcevic19, Corollary 4.2].
Theorem 3.1. Let
![]() $\mathcal {I}$
be a flat ideal. Then either
$\mathcal {I}$
be a flat ideal. Then either
![]() $\mathcal {I}$
is countably generated or
$\mathcal {I}$
is countably generated or
![]() $\mathcal {I}$
is not basic with any topology on
$\mathcal {I}$
is not basic with any topology on
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Proof Let
![]() $\varphi $
be a flat submeasure with
$\varphi $
be a flat submeasure with
![]() $\mathcal {I} = \mathrm {Fin}(\phi )$
. If
$\mathcal {I} = \mathrm {Fin}(\phi )$
. If
 $$ \begin{align} \forall x\in {\mathcal P}(\omega)\ \big(\sup_{n\in x} \phi(\{ n\}) <\infty \Rightarrow \phi(x)<\infty\big), \end{align} $$
$$ \begin{align} \forall x\in {\mathcal P}(\omega)\ \big(\sup_{n\in x} \phi(\{ n\}) <\infty \Rightarrow \phi(x)<\infty\big), \end{align} $$
then
![]() $\mathcal {I}$
is generated by the sets
$\mathcal {I}$
is generated by the sets
with
![]() $M\in \omega $
. Thus,
$M\in \omega $
. Thus,
![]() $\mathcal {I}$
is countably generated.
$\mathcal {I}$
is countably generated.
Assume, therefore, that (1) fails, which allows us to fix
![]() $x_0\in {\mathcal P}(\omega )$
such that
$x_0\in {\mathcal P}(\omega )$
such that
 $$ \begin{align} \sup_{n\in x_0}\varphi(\{ n\}) <\infty \;\text{ and }\; \varphi(x_0)=\infty. \end{align} $$
$$ \begin{align} \sup_{n\in x_0}\varphi(\{ n\}) <\infty \;\text{ and }\; \varphi(x_0)=\infty. \end{align} $$
Set
 $$ \begin{align} M_0=\sup_{n\in x_0}\varphi(\{ n\}). \end{align} $$
$$ \begin{align} M_0=\sup_{n\in x_0}\varphi(\{ n\}). \end{align} $$
Using (2), the definition (3), and the semicontinuity of
![]() $\varphi $
, we can find, for each
$\varphi $
, we can find, for each
![]() $M>2M_0$
, a sequence
$M>2M_0$
, a sequence
![]() $(a^M_i)_{i\in \omega }$
of finite subsets of
$(a^M_i)_{i\in \omega }$
of finite subsets of
![]() $x_0$
such that, for all i,
$x_0$
such that, for all i,
 $$ \begin{align} \max a^M_i < \min a^M_{i+1}\;\text{ and }\; M-M_0\leq \varphi(a^M_i)<M. \end{align} $$
$$ \begin{align} \max a^M_i < \min a^M_{i+1}\;\text{ and }\; M-M_0\leq \varphi(a^M_i)<M. \end{align} $$
By flatness of
![]() $\varphi $
, we can find
$\varphi $
, we can find
![]() $N_M>0$
and a subsequence
$N_M>0$
and a subsequence
 $(a^M_{i_j})$
of
$(a^M_{i_j})$
of
![]() $(a^M_i)$
such that, for each
$(a^M_i)$
such that, for each
![]() $t\in \omega $
,
$t\in \omega $
,
 $\varphi \big (\bigcup _{j\leq t} a^M_{i_j}\big ) < N_M$
, from which, by semicontinuity of
$\varphi \big (\bigcup _{j\leq t} a^M_{i_j}\big ) < N_M$
, from which, by semicontinuity of
![]() $\varphi $
, we get
$\varphi $
, we get
 $$ \begin{align} \varphi\big(\bigcup_j a^M_{i_j}\big) \leq N_M. \end{align} $$
$$ \begin{align} \varphi\big(\bigcup_j a^M_{i_j}\big) \leq N_M. \end{align} $$
For ease of notation, we assume that the whole sequence
![]() $(a^M_i)$
has property (5).
$(a^M_i)$
has property (5).
Towards a contradiction, suppose that there is a topology
![]() $\tau $
on
$\tau $
on
![]() $\mathcal {I}$
that makes
$\mathcal {I}$
that makes
![]() $\mathcal {I}$
into a basic partial order. For
$\mathcal {I}$
into a basic partial order. For
![]() $k\in \omega $
, let
$k\in \omega $
, let
 $$ \begin{align*} x^M_k= \bigcup_{i\geq k} a^M_{i}. \end{align*} $$
$$ \begin{align*} x^M_k= \bigcup_{i\geq k} a^M_{i}. \end{align*} $$
Note that, by (5), we have that
![]() $x^M_k\in \mathcal {I}$
; moreover, the sequence
$x^M_k\in \mathcal {I}$
; moreover, the sequence
![]() $(x^M_k)$
is bounded in
$(x^M_k)$
is bounded in
![]() $\mathcal {I}$
by
$\mathcal {I}$
by
![]() $x^M_0$
. Thus, it has a subsequence
$x^M_0$
. Thus, it has a subsequence
 $(x^M_{k_n})_n$
that is convergent with respect to
$(x^M_{k_n})_n$
that is convergent with respect to
![]() $\tau $
. By the fact that
$\tau $
. By the fact that
![]() $\tau $
is basic, for each k, the set
$\tau $
is basic, for each k, the set
![]() ${\mathcal P}(x_k^M)$
is a
${\mathcal P}(x_k^M)$
is a
![]() $\tau $
-compact subset of
$\tau $
-compact subset of
![]() $\mathcal {I}$
. It follows that the limit of
$\mathcal {I}$
. It follows that the limit of
 $(x^M_{k_n})_n$
is an element of
$(x^M_{k_n})_n$
is an element of
![]() ${\mathcal P}(x_k^M)$
for each k; thus,
${\mathcal P}(x_k^M)$
for each k; thus,
 $$ \begin{align*} x_{k_n}^M \to \emptyset\text{ with respect to }\tau, \text{ as }n\to\infty, \end{align*} $$
$$ \begin{align*} x_{k_n}^M \to \emptyset\text{ with respect to }\tau, \text{ as }n\to\infty, \end{align*} $$
since
![]() $\bigcap _k {\mathcal P}(x_k^M) =\{\emptyset \}$
. Since
$\bigcap _k {\mathcal P}(x_k^M) =\{\emptyset \}$
. Since
![]() $\tau $
is a metric topology, we can find a diagonal sequence
$\tau $
is a metric topology, we can find a diagonal sequence
![]() $(y_M)_{M\in \omega }$
convergent to
$(y_M)_{M\in \omega }$
convergent to
![]() $\emptyset $
, that is, for each M, there exists n with
$\emptyset $
, that is, for each M, there exists n with
 $y_M= x_{k_n}^M$
and
$y_M= x_{k_n}^M$
and
![]() $y_M\to \emptyset $
with respect to
$y_M\to \emptyset $
with respect to
![]() $\tau $
as
$\tau $
as
![]() $M\to \infty $
. Again, by using the fact that
$M\to \infty $
. Again, by using the fact that
![]() $\mathcal {I}$
is basic with
$\mathcal {I}$
is basic with
![]() $\tau $
, the convergent sequence
$\tau $
, the convergent sequence
![]() $(y_M)_M$
has a bounded subsequence. But this is impossible, since by the second part of (4) and the definitions of
$(y_M)_M$
has a bounded subsequence. But this is impossible, since by the second part of (4) and the definitions of
![]() $x^M_k$
and
$x^M_k$
and
![]() $y_M$
, we have
$y_M$
, we have
![]() $\phi (y_M)\geq M-M_0$
for each M.⊣
$\phi (y_M)\geq M-M_0$
for each M.⊣
4. A dichotomy for flat ideals
We prove a dichotomy theorem that is the starting point of our investigation of flat ideals. A result of this form was proved in [Reference Hrušák, Rojas-Rebolledo and Zapletal6] for fragmented ideals. Here we extend it to flat ideals building on the proof from [Reference Hrušák, Rojas-Rebolledo and Zapletal6]. The theorem asserts that flat ideals that are not gradually flat are of the highest possible cofinal type. Note that the ideal of subsets of
![]() $\omega $
from [Reference Louveau and Veličković10, Section 5, Proposition 3] that is Tukey equivalent to
$\omega $
from [Reference Louveau and Veličković10, Section 5, Proposition 3] that is Tukey equivalent to
![]() $[\mathfrak c]^{<\omega }$
is easily seen to be flat. In the next section, in Theorem 5.1, we illuminate the second half of this dichotomy by giving several conditions on flat ideals equivalent to gradual flatness.
$[\mathfrak c]^{<\omega }$
is easily seen to be flat. In the next section, in Theorem 5.1, we illuminate the second half of this dichotomy by giving several conditions on flat ideals equivalent to gradual flatness.
An lsc submeasure
![]() $\varphi $
is said to be gradual if, for each
$\varphi $
is said to be gradual if, for each
![]() $M>0$
, there exists
$M>0$
, there exists
![]() $N>0$
such that, for each l, we have
$N>0$
such that, for each l, we have
 $$ \begin{align*} \exists j \ \forall B\in [\mathcal P(\omega\setminus j)]^{\leq l}\, \Big( \max_{b\in B}\varphi(b)< M\Rightarrow \varphi(\bigcup B)< N\Big). \end{align*} $$
$$ \begin{align*} \exists j \ \forall B\in [\mathcal P(\omega\setminus j)]^{\leq l}\, \Big( \max_{b\in B}\varphi(b)< M\Rightarrow \varphi(\bigcup B)< N\Big). \end{align*} $$
We call an lsc submeasure
![]() $\varphi $
gradually flat if it is both flat and gradual, and we say that an ideal
$\varphi $
gradually flat if it is both flat and gradual, and we say that an ideal
![]() $\mathcal I$
is gradually flat if
$\mathcal I$
is gradually flat if
![]() $\mathcal I=\mathrm {Fin}(\varphi )$
for some gradually flat lsc submeasure
$\mathcal I=\mathrm {Fin}(\varphi )$
for some gradually flat lsc submeasure
![]() $\varphi $
.
$\varphi $
.
Lemma 4.1. If
![]() $\varphi ,\psi $
are flat and
$\varphi ,\psi $
are flat and
![]() $\mathcal {I}=\mathrm {Fin}(\varphi )=\mathrm {Fin}(\psi )$
, then
$\mathcal {I}=\mathrm {Fin}(\varphi )=\mathrm {Fin}(\psi )$
, then
![]() $\varphi $
is gradually flat if and only if
$\varphi $
is gradually flat if and only if
![]() $\psi $
is gradually flat.
$\psi $
is gradually flat.
Proof First, we prove that, for each
![]() $K_1>0$
, there exists
$K_1>0$
, there exists
![]() $K_2>0$
such that, for each
$K_2>0$
such that, for each
![]() $b\in {\mathcal P}(\omega )$
,
$b\in {\mathcal P}(\omega )$
,
Otherwise, there exists
![]() $K>0$
such that, for each
$K>0$
such that, for each
![]() $n\in \omega $
, there exists a set
$n\in \omega $
, there exists a set
![]() $b_n\in {\mathcal P}(\omega )$
with either
$b_n\in {\mathcal P}(\omega )$
with either
![]() $\varphi (b_n)\leq K $
and
$\varphi (b_n)\leq K $
and
![]() $\psi (b_n)> n$
, or
$\psi (b_n)> n$
, or
![]() $\psi (b_n)\leq K $
and
$\psi (b_n)\leq K $
and
![]() $\varphi (b_n)> n$
. By pigeonhole principle and compactness of
$\varphi (b_n)> n$
. By pigeonhole principle and compactness of
![]() ${\mathcal P}(\omega )$
, we can assume that
${\mathcal P}(\omega )$
, we can assume that
Since
![]() $\psi (b_n)\leq K$
, for all n, by lower semicontinuous of
$\psi (b_n)\leq K$
, for all n, by lower semicontinuous of
![]() $\psi $
, we have
$\psi $
, we have
![]() $\psi (b)\leq K$
, from which, by
$\psi (b)\leq K$
, from which, by
![]() ${\mathcal I} =\mathrm {Fin}(\varphi )=\mathrm {Fin}(\psi )$
, we get
${\mathcal I} =\mathrm {Fin}(\varphi )=\mathrm {Fin}(\psi )$
, we get
Let N witness flatness of
![]() $\psi $
for
$\psi $
for
![]() $K+1$
. Using (7), (8), and lower semicontinuity of
$K+1$
. Using (7), (8), and lower semicontinuity of
![]() $\varphi $
, one recursively constructs finite sets
$\varphi $
, one recursively constructs finite sets
![]() $c_n\in \mathcal P(b_{j_n}\setminus b)$
,
$c_n\in \mathcal P(b_{j_n}\setminus b)$
,
![]() $n\in \omega $
, for some increasing sequence
$n\in \omega $
, for some increasing sequence
![]() $(j_n)_n$
, so that
$(j_n)_n$
, so that
 $$ \begin{align*} \psi(\bigcup_{i\leq n}c_i)< N\text{ and }\varphi(c_n)> n,\text{ for all }n\in \omega. \end{align*} $$
$$ \begin{align*} \psi(\bigcup_{i\leq n}c_i)< N\text{ and }\varphi(c_n)> n,\text{ for all }n\in \omega. \end{align*} $$
The above inequalities give
 $\psi (\bigcup _{n\in \omega } c_n )\leq N$
and
$\psi (\bigcup _{n\in \omega } c_n )\leq N$
and
 $\varphi (\bigcup _{n\in \omega }c_n)=\infty $
, contradicting
$\varphi (\bigcup _{n\in \omega }c_n)=\infty $
, contradicting
![]() $\mathrm {Fin}(\varphi )=\mathrm {Fin}(\psi )$
, and therefore proving (6).
$\mathrm {Fin}(\varphi )=\mathrm {Fin}(\psi )$
, and therefore proving (6).
Assume
![]() $\psi $
is not gradual. This assumption allows us to fix
$\psi $
is not gradual. This assumption allows us to fix
![]() $M>0$
, for which the following condition holds. For each
$M>0$
, for which the following condition holds. For each
![]() $N>0$
, we can find
$N>0$
, we can find
![]() $l_N$
and a sequence
$l_N$
and a sequence
![]() $(B^N_n)_n$
of finite families of subsets of
$(B^N_n)_n$
of finite families of subsets of
![]() $\omega $
so that:
$\omega $
so that:
![]() $|B^N_n|\leq l_N$
,
$|B^N_n|\leq l_N$
,
![]() $\min \{ \min b\colon b\in B^N_n\} \to \infty $
as
$\min \{ \min b\colon b\in B^N_n\} \to \infty $
as
![]() $n\to \infty $
,
$n\to \infty $
,
 $\max _{b\in B^N_n}\psi (b)< M$
, and
$\max _{b\in B^N_n}\psi (b)< M$
, and
![]() $\psi (\bigcup B^N_n)\geq N$
. It follows now from the second part of (6) that there exists
$\psi (\bigcup B^N_n)\geq N$
. It follows now from the second part of (6) that there exists
![]() $M'>0$
such that
$M'>0$
such that
 $\max _{b\in B^N_n}\varphi (b)< M'$
for all
$\max _{b\in B^N_n}\varphi (b)< M'$
for all
![]() $n, N$
. From the first part of (6), it follows that there exists a function g with
$n, N$
. From the first part of (6), it follows that there exists a function g with
![]() $g(N)\to \infty $
as
$g(N)\to \infty $
as
![]() $N\to \infty $
such that
$N\to \infty $
such that
![]() $\varphi (\bigcup B^N_n)> g(N)$
, for all
$\varphi (\bigcup B^N_n)> g(N)$
, for all
![]() $n, N$
. Thus,
$n, N$
. Thus,
![]() $\varphi $
is not gradual, and the lemma is proved.⊣
$\varphi $
is not gradual, and the lemma is proved.⊣
The following result is the promised dichotomy theorem. Recall that if a directed partial order contains a strongly unbounded set of size
![]() $\mathfrak c$
, then it is Tukey equivalent to
$\mathfrak c$
, then it is Tukey equivalent to
![]() $[\mathfrak c]^{<\omega }$
. Here, a subset X of a partial order is strongly unbounded if every infinite subset of X is unbounded.
$[\mathfrak c]^{<\omega }$
. Here, a subset X of a partial order is strongly unbounded if every infinite subset of X is unbounded.
Theorem 4.2. Let
![]() $\mathcal {I}$
be a flat ideal. Then either
$\mathcal {I}$
be a flat ideal. Then either
![]() $\mathcal {I} \equiv _T [\mathfrak c]^{<\omega }$
or
$\mathcal {I} \equiv _T [\mathfrak c]^{<\omega }$
or
![]() $\mathcal {I}$
is gradually flat.
$\mathcal {I}$
is gradually flat.
Proof Let
![]() $\mathcal {I} = \mathrm {Fin}(\varphi )$
for a flat submeasure
$\mathcal {I} = \mathrm {Fin}(\varphi )$
for a flat submeasure
![]() $\varphi $
, and assume that
$\varphi $
, and assume that
![]() $\varphi $
is not gradual. This assumption allows us to fix
$\varphi $
is not gradual. This assumption allows us to fix
![]() $M>0$
such that for each N there exists
$M>0$
such that for each N there exists
![]() $\ell _N$
and a sequence
$\ell _N$
and a sequence
![]() $(B^N_n)$
of families of subsets of
$(B^N_n)$
of families of subsets of
![]() $\omega $
such that, for all
$\omega $
such that, for all
![]() $n, N\in \omega $
,
$n, N\in \omega $
,
 $$ \begin{align} |B^N_n| \leq \ell_N,\; n\leq \min_{b\in B^N_n} b,\; \max_{b\in B^N_n}\varphi(b)<M,\text{ and } \varphi(\bigcup B^N_n)\geq N. \end{align} $$
$$ \begin{align} |B^N_n| \leq \ell_N,\; n\leq \min_{b\in B^N_n} b,\; \max_{b\in B^N_n}\varphi(b)<M,\text{ and } \varphi(\bigcup B^N_n)\geq N. \end{align} $$
By semicontinuity of
![]() $\varphi $
, we can assume that the sets in
$\varphi $
, we can assume that the sets in
![]() $B^N_n$
are finite for each
$B^N_n$
are finite for each
![]() $n, N$
. By going to subsequences of
$n, N$
. By going to subsequences of
![]() $(B^N_n)$
, we can assume that, for each n,
$(B^N_n)$
, we can assume that, for each n,
and
 $$ \begin{align*} (n,N)\not= (n', N')\Rightarrow \left(\max \bigcup B^N_n<\min \bigcup B^{N'}_{n'}\,\text{ or }\,\max \bigcup B^{N'}_{n'}<\min \bigcup B^N_n\right). \end{align*} $$
$$ \begin{align*} (n,N)\not= (n', N')\Rightarrow \left(\max \bigcup B^N_n<\min \bigcup B^{N'}_{n'}\,\text{ or }\,\max \bigcup B^{N'}_{n'}<\min \bigcup B^N_n\right). \end{align*} $$
Let
![]() $K_M$
witness flatness of
$K_M$
witness flatness of
![]() $\varphi $
for M. By the choice of
$\varphi $
for M. By the choice of
![]() $K_M$
and by (9), we see that, for each
$K_M$
and by (9), we see that, for each
![]() $p\in \omega $
, the following statement holds: for each N, for large enough n, if
$p\in \omega $
, the following statement holds: for each N, for large enough n, if
![]() $a\subseteq p$
is such that
$a\subseteq p$
is such that
![]() $\varphi (a)<K_M$
and
$\varphi (a)<K_M$
and
![]() $b\in B^N_n$
, then
$b\in B^N_n$
, then
![]() $ \varphi (a\cup b) <K_M$
. Using this observation and the inequality
$ \varphi (a\cup b) <K_M$
. Using this observation and the inequality
![]() $\varphi (\emptyset )=0<K_M$
, a recursive construction allows us to pick, for each N, an infinite subset
$\varphi (\emptyset )=0<K_M$
, a recursive construction allows us to pick, for each N, an infinite subset
![]() $D^N$
of
$D^N$
of
![]() $\omega $
with the following property: for each finite sequence
$\omega $
with the following property: for each finite sequence
![]() $(b_i)_{i<t}$
, with
$(b_i)_{i<t}$
, with
![]() $t\in \omega $
, of sets picked from distinct
$t\in \omega $
, of sets picked from distinct
![]() $B^N_n$
with
$B^N_n$
with
![]() $N\in \omega $
and
$N\in \omega $
and
![]() $n\in D^N$
, we have
$n\in D^N$
, we have
 $$ \begin{align*} \varphi( \bigcup_{i<t} b_i)<K_M. \end{align*} $$
$$ \begin{align*} \varphi( \bigcup_{i<t} b_i)<K_M. \end{align*} $$
Thus, by going to subsequences, we can assume that the above inequality holds for all finite sequences
![]() $(b_i)_{i<t}$
of sets picked from distinct
$(b_i)_{i<t}$
of sets picked from distinct
![]() $B^N_n$
with
$B^N_n$
with
![]() $n, N\in \omega $
. Now, lower semicontinuity of
$n, N\in \omega $
. Now, lower semicontinuity of
![]() $\varphi $
gives that, for each infinite sequence
$\varphi $
gives that, for each infinite sequence
![]() $(b_i)_i$
of sets picked from distinct
$(b_i)_i$
of sets picked from distinct
![]() $B^N_n$
with
$B^N_n$
with
![]() $n, N\in \omega $
, we have
$n, N\in \omega $
, we have
 $$ \begin{align} \varphi( \bigcup_i b_i)\leq K_M. \end{align} $$
$$ \begin{align} \varphi( \bigcup_i b_i)\leq K_M. \end{align} $$
From this point on, we follow the lines of the proof of [Reference Hrušák, Rojas-Rebolledo and Zapletal6, Theorem 2.4] with appropriate modifications. Let
![]() $C^k$
,
$C^k$
,
![]() $k\in \omega $
, be a partition of
$k\in \omega $
, be a partition of
![]() $\omega $
into infinite sets. For each N, let
$\omega $
into infinite sets. For each N, let
 $(f_p^N)_p$
be a sequence of functions
$(f_p^N)_p$
be a sequence of functions
 $$ \begin{align*} f_p^{k,N}\colon C^k\to \bigcup_{n\in C^k} B^N_n \end{align*} $$
$$ \begin{align*} f_p^{k,N}\colon C^k\to \bigcup_{n\in C^k} B^N_n \end{align*} $$
such that
 $f_p^{k,N}(n)\in B^N_n$
for all
$f_p^{k,N}(n)\in B^N_n$
for all
![]() $n\in C^k$
and, for all k and
$n\in C^k$
and, for all k and
![]() $a\in [\omega ]^{l_N}$
,
$a\in [\omega ]^{l_N}$
,
 $$ \begin{align} \{ f^{k,N}_p(n)\colon p\in a\} = B^N_n,\text{ for some }n\in C^k. \end{align} $$
$$ \begin{align} \{ f^{k,N}_p(n)\colon p\in a\} = B^N_n,\text{ for some }n\in C^k. \end{align} $$
Such sequences can be found by [Reference Hrušák, Rojas-Rebolledo and Zapletal6, Claim 2.5, p. 33]. Now, for each p, we let
 $$ \begin{align*} J^k_p= \bigcup_N \bigcup_{n\in C^k} f^{k,N}_p(n). \end{align*} $$
$$ \begin{align*} J^k_p= \bigcup_N \bigcup_{n\in C^k} f^{k,N}_p(n). \end{align*} $$
From the definition of
![]() $J^k_p$
, by (11) and (9), we get that, for each N,
$J^k_p$
, by (11) and (9), we get that, for each N,
 $$ \begin{align} \varphi(\bigcup_{p\in a} J^k_p)\geq N, \text{ for all }k\text{ and }a\in [\omega]^{l_N}. \end{align} $$
$$ \begin{align} \varphi(\bigcup_{p\in a} J^k_p)\geq N, \text{ for all }k\text{ and }a\in [\omega]^{l_N}. \end{align} $$
On the other hand, observe that, for each
![]() $g\in \omega ^{\omega }$
, the set
$g\in \omega ^{\omega }$
, the set
 $\bigcup _k J^k_{g(k)}$
is the union of a sequence
$\bigcup _k J^k_{g(k)}$
is the union of a sequence
![]() $(b_i)$
, where sets
$(b_i)$
, where sets
![]() $b_i$
are chosen from distinct
$b_i$
are chosen from distinct
![]() $B^N_n$
with
$B^N_n$
with
![]() $n, N\in \omega $
. Thus, (10) implies that
$n, N\in \omega $
. Thus, (10) implies that
 $$ \begin{align} \varphi(\bigcup_k J^k_{g(k)} ) \leq N_M, \text{ for each }g\in \omega^{\omega}. \end{align} $$
$$ \begin{align} \varphi(\bigcup_k J^k_{g(k)} ) \leq N_M, \text{ for each }g\in \omega^{\omega}. \end{align} $$
Let
![]() ${\mathcal A}\subseteq \omega ^{\omega }$
be a perfect family of eventually different elements of
${\mathcal A}\subseteq \omega ^{\omega }$
be a perfect family of eventually different elements of
![]() $\omega ^{\omega }$
. For
$\omega ^{\omega }$
. For
![]() $g\in {\mathcal A}$
, define
$g\in {\mathcal A}$
, define
 $$ \begin{align*} G(g)= \bigcup_k J^k_{g(k)}. \end{align*} $$
$$ \begin{align*} G(g)= \bigcup_k J^k_{g(k)}. \end{align*} $$
It is clear that
![]() $G\colon {\mathcal A}\to 2^{\omega }$
is a continuous injection and (13) implies that
$G\colon {\mathcal A}\to 2^{\omega }$
is a continuous injection and (13) implies that
![]() $G(g)\in \mathcal {I}$
for each
$G(g)\in \mathcal {I}$
for each
![]() $g\in {\mathcal A}$
.
$g\in {\mathcal A}$
.
We check that the family
![]() $\{ G(g)\colon g\in {\mathcal A}\}$
is strongly unbounded in
$\{ G(g)\colon g\in {\mathcal A}\}$
is strongly unbounded in
![]() $\mathcal {I}$
. Let
$\mathcal {I}$
. Let
![]() $g_i$
,
$g_i$
,
![]() $i<l_N$
, be distinct elements of
$i<l_N$
, be distinct elements of
![]() $\mathcal A$
. Then, there exists
$\mathcal A$
. Then, there exists
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $g_i(k)$
are all distinct for
$g_i(k)$
are all distinct for
![]() $i<l_N$
. Therefore, by (12), we get
$i<l_N$
. Therefore, by (12), we get
 $$ \begin{align*} \varphi\left(\bigcup_{i<l_N} G(g_i)\right)\geq \varphi(\bigcup_{i<l_N} J^k_{g_i(k)})\geq N. \end{align*} $$
$$ \begin{align*} \varphi\left(\bigcup_{i<l_N} G(g_i)\right)\geq \varphi(\bigcup_{i<l_N} J^k_{g_i(k)})\geq N. \end{align*} $$
Thus, if
![]() $g_i\in {\mathcal A}$
,
$g_i\in {\mathcal A}$
,
![]() $i\in \omega $
, are all distinct, then
$i\in \omega $
, are all distinct, then
 $$ \begin{align*} \bigcup_i G(g_i)\not\in \mathcal{I}, \end{align*} $$
$$ \begin{align*} \bigcup_i G(g_i)\not\in \mathcal{I}, \end{align*} $$
and the conclusion follows.⊣
5. Characterizations of gradually flat ideals
In this section we give various characterizations of gradually flat ideals. To formulate our theorem, we need to introduce some notions.
Recall that a subset X of a partial order P is called weakly bounded if every infinite subset of X contains an infinite bounded subset. (Note that this condition is equivalent to X not containing an infinite strongly unbounded subset, where strong unboundedness is defined in Section 4.) Following [Reference Louveau and Veličković10], we say that a partial order P is
![]() $\sigma $
-weakly bounded if P is the union of a countable family of weakly bounded sets.
$\sigma $
-weakly bounded if P is the union of a countable family of weakly bounded sets.
Let
![]() $\mathcal {I}$
be an ideal of subsets of
$\mathcal {I}$
be an ideal of subsets of
![]() $\omega $
. We will use another game introduced by Fremlin in [Reference Fremlin3]. Given an ideal
$\omega $
. We will use another game introduced by Fremlin in [Reference Fremlin3]. Given an ideal
![]() $\mathcal {I}$
, the game
$\mathcal {I}$
, the game
![]() $\Gamma _1(\mathcal {I})$
is a two-player game, where the nth move for each player is described as follows.
$\Gamma _1(\mathcal {I})$
is a two-player game, where the nth move for each player is described as follows.
-
By convention,
 $U_{-1} =\mathcal {I}$
. Given
$U_{-1} =\mathcal {I}$
. Given
 $U_{n-1}\subseteq \mathcal {I}$
,
$U_{n-1}\subseteq \mathcal {I}$
, -
Player I plays a countable cover
 $\mathcal {U}_n$
of
$\mathcal {U}_n$
of
 $U_{n-1}$
,
$U_{n-1}$
, -
Player II responds with
 $U_n\in \mathcal {U}_n$
and a sequence
$U_n\in \mathcal {U}_n$
and a sequence
 $\langle x^n_i\rangle _i$
in
$\langle x^n_i\rangle _i$
in
 $U_n$
,
$U_n$
, -
Player I then chooses a subsequence by playing
 $A_n\in [\omega ]^{\omega }$
,
$A_n\in [\omega ]^{\omega }$
, -
Player II plays the last bit by choosing
 $m_n\in \omega $
.
$m_n\in \omega $
.
More graphically, the nth move is represented as follows.

After the nth move has been made, we define
 $$ \begin{align} b_n=\bigcup\{x^n_i:i\in A_n\cap m_n\}\in\mathcal I. \end{align} $$
$$ \begin{align} b_n=\bigcup\{x^n_i:i\in A_n\cap m_n\}\in\mathcal I. \end{align} $$
We declare that Player I wins if the sequence
![]() $\langle b_n\rangle _n$
is bounded in
$\langle b_n\rangle _n$
is bounded in
![]() $\mathcal {I}$
, that is, if
$\mathcal {I}$
, that is, if
![]() $\bigcup _n b_n\in \mathcal {I}$
; otherwise Player II wins.
$\bigcup _n b_n\in \mathcal {I}$
; otherwise Player II wins.
We say that an ideal
![]() $\mathcal {I}$
is Fremlin if Player I has a winning strategy in the game
$\mathcal {I}$
is Fremlin if Player I has a winning strategy in the game
![]() $\Gamma _1(\mathcal {I})$
.
$\Gamma _1(\mathcal {I})$
.
Two results from [Reference Fremlin3] concerning Fremlin ideals relevant to us are:
-
– being Fremlin is a property that is downward closed under Tukey reduction;
-
– the density zero ideal
 ${\mathcal Z}_0$
is Fremlin; hence, if
${\mathcal Z}_0$
is Fremlin; hence, if
 $\mathcal {I}$
is Tukey below
$\mathcal {I}$
is Tukey below
 $\mathcal {Z}_0$
, then
$\mathcal {Z}_0$
, then
 $\mathcal {I}$
is Fremlin.
$\mathcal {I}$
is Fremlin.
We can now state our characterization theorem.
Theorem 5.1. If
![]() $\mathcal I$
is a flat ideal, then the following conditions are equivalent.
$\mathcal I$
is a flat ideal, then the following conditions are equivalent.
-
(i)
 $\mathcal I$
is gradually flat.
$\mathcal I$
is gradually flat. -
(ii)
 $\mathcal I\leq _T \mathcal Z_0$
.
$\mathcal I\leq _T \mathcal Z_0$
. -
(iii)
 $\mathcal I\leq _T l_1$
.
$\mathcal I\leq _T l_1$
. -
(iv)
 $\mathcal I \not \equiv _T [\mathfrak c]^{<\omega }$
.
$\mathcal I \not \equiv _T [\mathfrak c]^{<\omega }$
. -
(v)
 $\mathcal I$
is Fremlin.
$\mathcal I$
is Fremlin. -
(vi)
 $\mathcal I$
is
$\mathcal I$
is
 $\sigma $
-weakly bounded.
$\sigma $
-weakly bounded. -
(vii)
 $\omega ^{\omega }\not \leq _T \mathcal I$
.
$\omega ^{\omega }\not \leq _T \mathcal I$
.
In relation to considering gradually flat ideals with the Tukey order, we point out that it follows from [Reference Mátrai13, Proposition 5.28] that the class of gradually flat ideals equipped with
![]() $\leq _T$
is rich; namely, the quasi-order
$\leq _T$
is rich; namely, the quasi-order
![]() $({\mathcal P}(\omega ), \subseteq ^*)$
, where
$({\mathcal P}(\omega ), \subseteq ^*)$
, where
![]() $\subseteq ^*$
is inclusion modulo finite sets, embeds into it. To see this, it suffices to notice that the ideals considered in [Reference Mátrai13, Proposition 5.28] are flat by their definitions, and they are gradually flat by [Reference Mátrai13, formula (5.4)].
$\subseteq ^*$
is inclusion modulo finite sets, embeds into it. To see this, it suffices to notice that the ideals considered in [Reference Mátrai13, Proposition 5.28] are flat by their definitions, and they are gradually flat by [Reference Mátrai13, formula (5.4)].
Theorem 5.1 above raises some natural questions.
Question 5.2. Let
![]() $\mathcal I$
be an
$\mathcal I$
be an
![]() $F_{\sigma }$
ideal of subsets of
$F_{\sigma }$
ideal of subsets of
![]() $\omega $
.
$\omega $
.
-
(1) Is
 $\mathcal {I}\equiv _T [\mathfrak c]^{<\omega }$
or
$\mathcal {I}\equiv _T [\mathfrak c]^{<\omega }$
or
 $\mathcal {I}\leq _T l_1$
?
$\mathcal {I}\leq _T l_1$
? -
(2) Assume
 $\omega ^{\omega }\leq _T \mathcal {I}$
. Is
$\omega ^{\omega }\leq _T \mathcal {I}$
. Is
 $l_1\leq _T\mathcal {I}$
?
$l_1\leq _T\mathcal {I}$
? -
(3) [Reference Louveau and Veličković10] Assume
 $\omega ^{\omega }\not \leq _T \mathcal {I}$
. Is
$\omega ^{\omega }\not \leq _T \mathcal {I}$
. Is
 $\mathcal {I}\ \sigma $
-weakly bounded?
$\mathcal {I}\ \sigma $
-weakly bounded?
It may be worth mentioning in the context of the question above that, by [Reference Louveau and Veličković10], if
![]() $\mathcal {I}$
is an analytic ideal of subsets of
$\mathcal {I}$
is an analytic ideal of subsets of
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{\omega }\not \leq _T \mathcal {I}$
, then
$\omega ^{\omega }\not \leq _T \mathcal {I}$
, then
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $F_{\sigma }$
.
$F_{\sigma }$
.
In our proof of Theorem 5.1, we start with a lemma connecting Fremliness and
![]() $\sigma $
-weak boundedness. The lemma is somewhat more general than needed in order to prove Theorem 5.1, and may be of some independent interest.
$\sigma $
-weak boundedness. The lemma is somewhat more general than needed in order to prove Theorem 5.1, and may be of some independent interest.
Lemma 5.3. If
![]() $\mathcal {I}$
is a Fremlin
$\mathcal {I}$
is a Fremlin
![]() $F_{\sigma }$
ideal, then
$F_{\sigma }$
ideal, then
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\sigma $
-weakly bounded.
$\sigma $
-weakly bounded.
Proof Let
![]() $\varphi $
be a lower semicontinuous submeasure such that
$\varphi $
be a lower semicontinuous submeasure such that
![]() $\mathcal {I}=\text {Fin}(\varphi )$
, and let
$\mathcal {I}=\text {Fin}(\varphi )$
, and let
![]() $\tau $
be a winning strategy for Player I in
$\tau $
be a winning strategy for Player I in
![]() $\Gamma _1(\mathcal {I})$
. Assume, in order to reach a contradiction, that
$\Gamma _1(\mathcal {I})$
. Assume, in order to reach a contradiction, that
![]() $\mathcal {I}$
is not
$\mathcal {I}$
is not
![]() $\sigma $
-weakly bounded. We will play against
$\sigma $
-weakly bounded. We will play against
![]() $\tau $
and produce a play in which Player II wins:
$\tau $
and produce a play in which Player II wins:
![]() $\mathcal {I}=U_0$
is by assumption not
$\mathcal {I}=U_0$
is by assumption not
![]() $\sigma $
-weakly bounded. After Move
$\sigma $
-weakly bounded. After Move
![]() $n-1$
has been made, assume that
$n-1$
has been made, assume that
![]() $U_{n-1}$
is chosen so that the restriction of I to
$U_{n-1}$
is chosen so that the restriction of I to
![]() $U_{n-1}$
is not
$U_{n-1}$
is not
![]() $\sigma $
-weakly bounded. Now, in the nth move, if
$\sigma $
-weakly bounded. Now, in the nth move, if
![]() $\mathcal {U}_n=\tau (U_{n-1})$
is a covering for
$\mathcal {U}_n=\tau (U_{n-1})$
is a covering for
![]() $U_{n-1}$
, there must be
$U_{n-1}$
, there must be
![]() $U_n\in \mathcal {U}_n$
that is not
$U_n\in \mathcal {U}_n$
that is not
![]() $\sigma $
-weakly bounded, we play such
$\sigma $
-weakly bounded, we play such
![]() $U_n$
together with a strongly unbounded sequence
$U_n$
together with a strongly unbounded sequence
![]() $(x^n_i)_i$
in
$(x^n_i)_i$
in
![]() $U_n$
. Once
$U_n$
. Once
![]() $\tau $
has chosen
$\tau $
has chosen
![]() $A_n\in [\omega ]^{\omega }$
, as any subsequence of
$A_n\in [\omega ]^{\omega }$
, as any subsequence of
![]() $(x^n_i)_i$
is strongly unbounded, we can find
$(x^n_i)_i$
is strongly unbounded, we can find
![]() $m_n$
large enough so that
$m_n$
large enough so that
![]() $\varphi (b_n)>n$
, where
$\varphi (b_n)>n$
, where
![]() $b_n$
is as in (14). At the end, this play against
$b_n$
is as in (14). At the end, this play against
![]() $\tau $
would have produced the sequence
$\tau $
would have produced the sequence
![]() $(b_n)_n$
which is unbounded in
$(b_n)_n$
which is unbounded in
![]() $\mathcal {I}$
.⊣
$\mathcal {I}$
.⊣
Now, we prove a lemma on gradually flat ideals that will be our main technical tool when dealing with such ideals in the proof of Theorem 5.1.
Lemma 5.4. Let
![]() $\mathcal {I}$
be gradually flat. There are sequences
$\mathcal {I}$
be gradually flat. There are sequences
![]() $\mathcal {X}_k, {\mathcal Y}_k$
,
$\mathcal {X}_k, {\mathcal Y}_k$
,
![]() $k\in \omega $
, of downward closed subsets of
$k\in \omega $
, of downward closed subsets of
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
-
(i)
 $\bigcup _k {\mathcal X}_k =\mathcal {I};$
$\bigcup _k {\mathcal X}_k =\mathcal {I};$
-
(ii)
 $\overline {{\mathcal Y}_k} \subseteq \mathcal {I}$
, for each
$\overline {{\mathcal Y}_k} \subseteq \mathcal {I}$
, for each
 $k;$
$k;$
-
(iii) for each
 $k, l$
, there exists
$k, l$
, there exists
 $g_{k,l}\in \omega ^{\omega }$
with
$g_{k,l}\in \omega ^{\omega }$
with  $$ \begin{align*} \forall n \ \big(\forall a\in \mathcal{Y}_{k}\cap \mathcal{P}(n)\big)\ \big(\forall B\in [\mathcal{X}_k\cap {\mathcal P}\big(\omega\setminus g_{k,l}(n)\big)]^{\leq l}\big)\left(a\cup\bigcup B\in\mathcal{Y}_{k}\right). \end{align*} $$
$$ \begin{align*} \forall n \ \big(\forall a\in \mathcal{Y}_{k}\cap \mathcal{P}(n)\big)\ \big(\forall B\in [\mathcal{X}_k\cap {\mathcal P}\big(\omega\setminus g_{k,l}(n)\big)]^{\leq l}\big)\left(a\cup\bigcup B\in\mathcal{Y}_{k}\right). \end{align*} $$
Proof Fix a gradually flat submeasure
![]() $\varphi $
such that
$\varphi $
such that
![]() $\mathcal {I}=\mathrm {Fin}(\varphi )$
. Given
$\mathcal {I}=\mathrm {Fin}(\varphi )$
. Given
![]() $k\in \omega $
, there exists
$k\in \omega $
, there exists
![]() $M_k>0$
as in the definition of gradual submeasure (with
$M_k>0$
as in the definition of gradual submeasure (with
![]() $k+1$
playing the role of M and
$k+1$
playing the role of M and
![]() $M_k$
playing the role of N), for which there is a function
$M_k$
playing the role of N), for which there is a function
![]() $h_k\in \omega ^{\omega }$
such that
$h_k\in \omega ^{\omega }$
such that
 $$ \begin{align*} \forall l\ \forall B\in [{\mathcal P}(\omega\setminus h_k(l))]^{\leq l} \big( \max_{b\in B}\varphi(b)< k+1\Rightarrow \varphi(\bigcup B)<M_k\big). \end{align*} $$
$$ \begin{align*} \forall l\ \forall B\in [{\mathcal P}(\omega\setminus h_k(l))]^{\leq l} \big( \max_{b\in B}\varphi(b)< k+1\Rightarrow \varphi(\bigcup B)<M_k\big). \end{align*} $$
Given this
![]() $M_k$
, we find
$M_k$
, we find
![]() $N_k>0$
as in the definition of a flat submeasure, for which there is a function
$N_k>0$
as in the definition of a flat submeasure, for which there is a function
![]() $h_k'\in \omega ^{\omega }$
such that for each n and each
$h_k'\in \omega ^{\omega }$
such that for each n and each
![]() $a\in {\mathcal P}(n)$
with
$a\in {\mathcal P}(n)$
with
![]() $\varphi (a)<N_k$
, we have
$\varphi (a)<N_k$
, we have
 $$ \begin{align*} \forall b\in {\mathcal P}(\omega\setminus h_k'(n)) \big(\varphi(b)<M_k\Rightarrow \varphi(a\cup b)<N_k\big). \end{align*} $$
$$ \begin{align*} \forall b\in {\mathcal P}(\omega\setminus h_k'(n)) \big(\varphi(b)<M_k\Rightarrow \varphi(a\cup b)<N_k\big). \end{align*} $$
For
![]() $k\in \omega $
, set
$k\in \omega $
, set
Point (i) is obvious from the definition of
![]() ${\mathcal X}_k$
. Point (ii) follows from the set
${\mathcal X}_k$
. Point (ii) follows from the set
![]() $\{ x\in {\mathcal P}(\omega )\colon \varphi (x)\leq N_k\}$
being a closed subset of
$\{ x\in {\mathcal P}(\omega )\colon \varphi (x)\leq N_k\}$
being a closed subset of
![]() ${\mathcal P}(\omega )$
, by semicontinuity of
${\mathcal P}(\omega )$
, by semicontinuity of
![]() $\varphi $
, and from
$\varphi $
, and from
Let
Observe that
![]() $g_{k,l}$
has the following property:
$g_{k,l}$
has the following property:
 $$ \begin{align} \begin{array}{ll} \forall n &\!\!\!\!\!\! \forall a\in {\mathcal P}(n) \Big( \phi(a)<N_k \Rightarrow\\ &\forall B\in [{\mathcal P}(\omega\setminus g_{k,l}(n))]^{\leq l} \big( \max_{b\in B}\phi(b)< k+1\Rightarrow \varphi(a\cup \bigcup B)<N_k\big)\Big). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \forall n &\!\!\!\!\!\! \forall a\in {\mathcal P}(n) \Big( \phi(a)<N_k \Rightarrow\\ &\forall B\in [{\mathcal P}(\omega\setminus g_{k,l}(n))]^{\leq l} \big( \max_{b\in B}\phi(b)< k+1\Rightarrow \varphi(a\cup \bigcup B)<N_k\big)\Big). \end{array} \end{align} $$
Property (15) implies (iii). The lemma follows.⊣
Proof of Theorem 5.1
![]() $\textrm{(i)}\Rightarrow \textrm{(ii)}\;$
We will use the following ideal introduced in [Reference Louveau and Veličković10]. Let
$\textrm{(i)}\Rightarrow \textrm{(ii)}\;$
We will use the following ideal introduced in [Reference Louveau and Veličković10]. Let
![]() $\alpha \in \omega ^{\omega }$
, and define
$\alpha \in \omega ^{\omega }$
, and define
where
![]() $A(n) = \{ m\in \omega \colon (n,m)\in A\}$
. (Such an ideal is called
$A(n) = \{ m\in \omega \colon (n,m)\in A\}$
. (Such an ideal is called
![]() ${\mathcal J}^{\alpha , (2^n)}( c_0)$
in [Reference Louveau and Veličković10]. For convenience, we shortened this piece of notation.) It was proved in [Reference Louveau and Veličković10, Proposition 4(b) and the Remark that follows pp. 186–187] that
${\mathcal J}^{\alpha , (2^n)}( c_0)$
in [Reference Louveau and Veličković10]. For convenience, we shortened this piece of notation.) It was proved in [Reference Louveau and Veličković10, Proposition 4(b) and the Remark that follows pp. 186–187] that
Now, given a sequence
![]() $\alpha _k\in \omega ^{\omega }$
,
$\alpha _k\in \omega ^{\omega }$
,
![]() $k\in \omega $
, we consider the ideal
$k\in \omega $
, we consider the ideal
 $$ \begin{align*} \bigoplus_k {\mathcal J}^{\alpha_k} = \{ A\subseteq \omega\times\omega\times\omega \colon \big( \forall k \ A(k) \in {\mathcal J}^{\alpha_k}\big) \text{ and } \big(\exists k_0\forall k\geq k_0 \ A(k)=\emptyset\big) \}, \end{align*} $$
$$ \begin{align*} \bigoplus_k {\mathcal J}^{\alpha_k} = \{ A\subseteq \omega\times\omega\times\omega \colon \big( \forall k \ A(k) \in {\mathcal J}^{\alpha_k}\big) \text{ and } \big(\exists k_0\forall k\geq k_0 \ A(k)=\emptyset\big) \}, \end{align*} $$
where
![]() $A(k) = \{ (n,m)\in \omega \colon (k, n,m)\in A\}$
. We argue that
$A(k) = \{ (n,m)\in \omega \colon (k, n,m)\in A\}$
. We argue that
 $$ \begin{align} \bigoplus_k {\mathcal J}^{\alpha_k}\leq_T{\mathcal Z}_0. \end{align} $$
$$ \begin{align} \bigoplus_k {\mathcal J}^{\alpha_k}\leq_T{\mathcal Z}_0. \end{align} $$
Indeed, for each k, fix a Tukey map
![]() $f_k\colon {\mathcal J}^{\alpha _k} \to {\mathcal Z}_0$
that exists by (16). For
$f_k\colon {\mathcal J}^{\alpha _k} \to {\mathcal Z}_0$
that exists by (16). For
![]() $A\in \bigoplus _k {\mathcal J}^{\alpha _k}$
, let
$A\in \bigoplus _k {\mathcal J}^{\alpha _k}$
, let
![]() $k_A$
be the smallest element of
$k_A$
be the smallest element of
![]() $\omega $
such that
$\omega $
such that
![]() $A(k)=\emptyset $
for all
$A(k)=\emptyset $
for all
![]() $k\geq k_A$
. Define
$k\geq k_A$
. Define
 $$ \begin{align*} F(A)= k_A\cup \bigcup_{k< k_A} f_k\big(A(k)\big). \end{align*} $$
$$ \begin{align*} F(A)= k_A\cup \bigcup_{k< k_A} f_k\big(A(k)\big). \end{align*} $$
Obviously,
![]() $F\colon \bigoplus _k {\mathcal J}^{\alpha _k}\to {\mathcal Z}_0$
, and it is easy to check that it is a Tukey map.
$F\colon \bigoplus _k {\mathcal J}^{\alpha _k}\to {\mathcal Z}_0$
, and it is easy to check that it is a Tukey map.
By (17), it suffices to show that, for appropriately chosen
![]() $\alpha _k$
,
$\alpha _k$
,
![]() $k\in \omega $
, we have
$k\in \omega $
, we have
 $$ \begin{align} \mathcal{I}\leq_T \bigoplus_k {\mathcal J}^{\alpha_k}. \end{align} $$
$$ \begin{align} \mathcal{I}\leq_T \bigoplus_k {\mathcal J}^{\alpha_k}. \end{align} $$
We define
![]() $\alpha _k\in \omega ^{\omega }$
, for
$\alpha _k\in \omega ^{\omega }$
, for
![]() $k\in \omega $
. Let
$k\in \omega $
. Let
![]() $g_{k,l}$
,
$g_{k,l}$
,
![]() ${\mathcal X}_k$
, and
${\mathcal X}_k$
, and
![]() ${\mathcal Y}_k$
,
${\mathcal Y}_k$
,
![]() $k,l\in \omega $
, be as in the conclusion of Lemma 5.4. Set
$k,l\in \omega $
, be as in the conclusion of Lemma 5.4. Set
 $$ \begin{align*} m^k_0=0 \;\text{ and }\; m^k_{l} = g_{k, 2^{l+1}}(m^k_{l-1}), \text{ for }l>0. \end{align*} $$
$$ \begin{align*} m^k_0=0 \;\text{ and }\; m^k_{l} = g_{k, 2^{l+1}}(m^k_{l-1}), \text{ for }l>0. \end{align*} $$
Then, by Lemma 5.4(iii), the sequence
 $(m^k_l)$
has the following property for each
$(m^k_l)$
has the following property for each
![]() $l>0$
:
$l>0$
:
 $$ \begin{align} \begin{array}{ll} \forall a\in {\mathcal P}(m^k_{l-1}) \ \forall B\in [{\mathcal P}(\omega\setminus m^k_{l})]^{\leq 2^{l+1}} \big( ( a\in {\mathcal Y}_k\; &\!\!\!\!\!\! \text{and }B\subseteq {\mathcal X}_k)\\ &\Rightarrow a\cup \bigcup B \in {\mathcal Y}_k\big). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \forall a\in {\mathcal P}(m^k_{l-1}) \ \forall B\in [{\mathcal P}(\omega\setminus m^k_{l})]^{\leq 2^{l+1}} \big( ( a\in {\mathcal Y}_k\; &\!\!\!\!\!\! \text{and }B\subseteq {\mathcal X}_k)\\ &\Rightarrow a\cup \bigcup B \in {\mathcal Y}_k\big). \end{array} \end{align} $$
Let
![]() $B_l$
, for
$B_l$
, for
![]() $l\in \omega $
, and
$l\in \omega $
, and
![]() $l_0$
be such that
$l_0$
be such that
 $$ \begin{align} B_l\subseteq {\mathcal X}_k\cap {\mathcal P}\big([m^k_l, m^k_{l+1})\big)\text{ and } |B_l|\leq 2^{l+1}, \text{ for all }l\geq l_0. \end{align} $$
$$ \begin{align} B_l\subseteq {\mathcal X}_k\cap {\mathcal P}\big([m^k_l, m^k_{l+1})\big)\text{ and } |B_l|\leq 2^{l+1}, \text{ for all }l\geq l_0. \end{align} $$
By using (19) recursively and then taking the union, we get that
 $$ \begin{align} \bigcup_{l>l_0/2} \bigcup B_{2l} \in \overline{{\mathcal Y}_k}\;\text{ and }\; \bigcup_{l\geq l_0/2} \bigcup B_{2l+1} \in \overline{{\mathcal Y}_k}. \end{align} $$
$$ \begin{align} \bigcup_{l>l_0/2} \bigcup B_{2l} \in \overline{{\mathcal Y}_k}\;\text{ and }\; \bigcup_{l\geq l_0/2} \bigcup B_{2l+1} \in \overline{{\mathcal Y}_k}. \end{align} $$
Since the closure of
![]() $\mathcal Y_k$
is contained in
$\mathcal Y_k$
is contained in
![]() $\mathcal I$
, we have
$\mathcal I$
, we have
![]() $\bigcup _{l} \bigcup B_{l} \in \mathcal {I}$
, from which we draw the following immediate conclusion:
$\bigcup _{l} \bigcup B_{l} \in \mathcal {I}$
, from which we draw the following immediate conclusion:
 $$ \begin{align} \{ x\in {\mathcal P}(\omega)\colon \forall l \ \big( x\cap [m^k_l, m^k_{l+1}) \in B_l\big)\} \text{ is bounded in }\mathcal{I}. \end{align} $$
$$ \begin{align} \{ x\in {\mathcal P}(\omega)\colon \forall l \ \big( x\cap [m^k_l, m^k_{l+1}) \in B_l\big)\} \text{ is bounded in }\mathcal{I}. \end{align} $$
For
![]() $l\in \omega $
, let
$l\in \omega $
, let
 $$ \begin{align*} I^k_l= [m^k_l, m^k_{l+1}). \end{align*} $$
$$ \begin{align*} I^k_l= [m^k_l, m^k_{l+1}). \end{align*} $$
Fix a one-to-one function
 $\pi _k:\bigcup _l\mathcal {P}(I^k_l)\to \omega $
, and define
$\pi _k:\bigcup _l\mathcal {P}(I^k_l)\to \omega $
, and define
![]() $\alpha _k\in \omega ^{\omega }$
by letting
$\alpha _k\in \omega ^{\omega }$
by letting
 $$ \begin{align*} \alpha_k(l)=1+\max \pi_k\big(\mathcal{P}(I^k_l)\big). \end{align*} $$
$$ \begin{align*} \alpha_k(l)=1+\max \pi_k\big(\mathcal{P}(I^k_l)\big). \end{align*} $$
Now we produce a function
![]() $\Psi \colon \mathcal {I} \to \bigoplus _k {\mathcal J}^{\alpha _k}$
. For
$\Psi \colon \mathcal {I} \to \bigoplus _k {\mathcal J}^{\alpha _k}$
. For
![]() $x\in \mathcal {I}$
, we have
$x\in \mathcal {I}$
, we have
![]() $\varphi (x)<\infty $
, which allows us to define
$\varphi (x)<\infty $
, which allows us to define
![]() $k_x\in \omega $
to be the smallest k with
$k_x\in \omega $
to be the smallest k with
![]() $x\in {\mathcal X}_k$
. Let
$x\in {\mathcal X}_k$
. Let
![]() $A_x\subseteq \omega \times \omega $
be defined by
$A_x\subseteq \omega \times \omega $
be defined by
 $$ \begin{align*} (l,m)\in A_x\Leftrightarrow x\cap I^{k_x}_l\not=\emptyset\text{ and }m=\pi(x\cap I^{k_x}_l). \end{align*} $$
$$ \begin{align*} (l,m)\in A_x\Leftrightarrow x\cap I^{k_x}_l\not=\emptyset\text{ and }m=\pi(x\cap I^{k_x}_l). \end{align*} $$
Observe that for every x,
![]() $A_x\in \mathcal {J}^{\alpha _{k_x}}$
. Define
$A_x\in \mathcal {J}^{\alpha _{k_x}}$
. Define
![]() $\Psi $
by
$\Psi $
by
![]() $\Psi (x)= \{ k_x\}\times A_x$
. It is clear that
$\Psi (x)= \{ k_x\}\times A_x$
. It is clear that
![]() $\Psi \colon \mathcal {I}\to \bigoplus _k {\mathcal J}^{\alpha _k}$
.
$\Psi \colon \mathcal {I}\to \bigoplus _k {\mathcal J}^{\alpha _k}$
.
We claim that
![]() $\Psi $
is Tukey. Let
$\Psi $
is Tukey. Let
![]() $A\in \bigoplus _k\mathcal {J}^{\alpha _k}$
and
$A\in \bigoplus _k\mathcal {J}^{\alpha _k}$
and
We need to see that
![]() $\bigcup {\mathcal A}\in \mathcal {I}$
. As
$\bigcup {\mathcal A}\in \mathcal {I}$
. As
![]() $A\in \bigoplus _k\mathcal {J}^{\alpha _k}$
, we have that
$A\in \bigoplus _k\mathcal {J}^{\alpha _k}$
, we have that
![]() $A(k)=\emptyset $
for all but finitely many k. Thus, it suffices to see that for a fixed k
$A(k)=\emptyset $
for all but finitely many k. Thus, it suffices to see that for a fixed k
 $$ \begin{align*} \bigcup \{ x\in {\mathcal X}_k \colon A_x\subseteq A(k)\}\in \mathcal{I}. \end{align*} $$
$$ \begin{align*} \bigcup \{ x\in {\mathcal X}_k \colon A_x\subseteq A(k)\}\in \mathcal{I}. \end{align*} $$
Fix k, and set
![]() $B=A(k)$
,
$B=A(k)$
,
 $I_l = I^k_l$
, and
$I_l = I^k_l$
, and
![]() ${\mathcal B}= \{ x\in {\mathcal X}_k\colon A_x\subseteq B\}$
. We need to see that
${\mathcal B}= \{ x\in {\mathcal X}_k\colon A_x\subseteq B\}$
. We need to see that
Since
![]() $B\in {\mathcal J}^{\alpha _k}$
, there is
$B\in {\mathcal J}^{\alpha _k}$
, there is
![]() $l_0$
such that for all
$l_0$
such that for all
![]() $l\geq l_0$
,
$l\geq l_0$
,
![]() $|B(l)|<2^l$
. So, for each
$|B(l)|<2^l$
. So, for each
![]() $l\geq l_0$
,
$l\geq l_0$
,
 $$ \begin{align*} |\{x\cap I_l: x\in {\mathcal B}\}|=|\{m: \exists x\in {\mathcal B}\ \pi(x\cap I_l)=m \}|\leq|B(l)|<2^l. \end{align*} $$
$$ \begin{align*} |\{x\cap I_l: x\in {\mathcal B}\}|=|\{m: \exists x\in {\mathcal B}\ \pi(x\cap I_l)=m \}|\leq|B(l)|<2^l. \end{align*} $$
Hence, for each
![]() $l\geq l_0$
, if
$l\geq l_0$
, if
![]() $|\{x\cap I_l: x\in {\mathcal B}\}|<2^l$
, and, therefore, by (22), we get (23), as required.
$|\{x\cap I_l: x\in {\mathcal B}\}|<2^l$
, and, therefore, by (22), we get (23), as required.
![]() $\textrm{(ii)}\Rightarrow \textrm{(iii)}\;$
follows from
$\textrm{(ii)}\Rightarrow \textrm{(iii)}\;$
follows from
![]() $\mathcal Z_0\leq _T l_1$
, see [Reference Louveau and Veličković10].
$\mathcal Z_0\leq _T l_1$
, see [Reference Louveau and Veličković10].
![]() $\textrm{(iii)}\Rightarrow \textrm{(iv)}\;$
follows from
$\textrm{(iii)}\Rightarrow \textrm{(iv)}\;$
follows from
![]() $l_1<_T [\mathfrak c]^{<\omega }$
, see [Reference Louveau and Veličković10].
$l_1<_T [\mathfrak c]^{<\omega }$
, see [Reference Louveau and Veličković10].
![]() $\textrm{(iv)}\Rightarrow \textrm{(i)}\; $
Since
$\textrm{(iv)}\Rightarrow \textrm{(i)}\; $
Since
![]() $\mathcal {I}$
is flat, by Theorem 4.2,
$\mathcal {I}$
is flat, by Theorem 4.2,
![]() $\mathcal {I}$
is gradually flat.
$\mathcal {I}$
is gradually flat.
![]() $\textrm{(i)}\Rightarrow \textrm{(v)}\;$
We describe a winning strategy for Player I in
$\textrm{(i)}\Rightarrow \textrm{(v)}\;$
We describe a winning strategy for Player I in
![]() $\Gamma _1(\mathcal I)$
. Let the sets
$\Gamma _1(\mathcal I)$
. Let the sets
![]() $\mathcal {X}_k$
and
$\mathcal {X}_k$
and
![]() ${\mathcal Y}_k$
,
${\mathcal Y}_k$
,
![]() $k\in \omega $
, be as in the conclusion of Lemma 5.4. By Lemma 5.4(i), the family
$k\in \omega $
, be as in the conclusion of Lemma 5.4. By Lemma 5.4(i), the family
![]() $\{ {\mathcal X}_k\colon k\in \omega \}$
forms a covering of
$\{ {\mathcal X}_k\colon k\in \omega \}$
forms a covering of
![]() $\mathcal {I}$
. In Move
$\mathcal {I}$
. In Move
![]() $0$
, Player I plays this covering. Player II responds by picking a set
$0$
, Player I plays this covering. Player II responds by picking a set
![]() ${\mathcal X}_k$
and a sequence
${\mathcal X}_k$
and a sequence
![]() $(x_i)$
of elements of
$(x_i)$
of elements of
![]() ${\mathcal X}_k$
. So k is fixed by Player II. For the fixed k, we perform the following analysis. Let
${\mathcal X}_k$
. So k is fixed by Player II. For the fixed k, we perform the following analysis. Let
![]() $g_{k,l}$
,
$g_{k,l}$
,
![]() $k,l\in \omega $
, be as in the conclusion of Lemma 5.4. Since k is fixed, we set
$k,l\in \omega $
, be as in the conclusion of Lemma 5.4. Since k is fixed, we set
![]() $g_l=g_{k,l}$
. Define
$g_l=g_{k,l}$
. Define
 $$ \begin{align*} m_0=0 \;\text{ and }\; m_{l} = g_{(l+1)^2+1}(m_{l-1}), \text{ for }l>0. \end{align*} $$
$$ \begin{align*} m_0=0 \;\text{ and }\; m_{l} = g_{(l+1)^2+1}(m_{l-1}), \text{ for }l>0. \end{align*} $$
Then, by Lemma 5.4(iii), the sequence
![]() $(m_l)$
has the following property for each
$(m_l)$
has the following property for each
![]() $l>0$
:
$l>0$
:
 $$ \begin{align} \begin{array}{ll} \forall a\in {\mathcal P}(m_{l-1}) \ \forall B\in [{\mathcal P}(\omega\setminus m_{l})]^{\leq (l+1)^2+1} \big( ( a\in {\mathcal Y}_k\; &\!\!\!\!\!\! \text{and }B\subseteq {\mathcal X}_k)\\ &\Rightarrow a\cup \bigcup B \in {\mathcal Y}_k\big). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \forall a\in {\mathcal P}(m_{l-1}) \ \forall B\in [{\mathcal P}(\omega\setminus m_{l})]^{\leq (l+1)^2+1} \big( ( a\in {\mathcal Y}_k\; &\!\!\!\!\!\! \text{and }B\subseteq {\mathcal X}_k)\\ &\Rightarrow a\cup \bigcup B \in {\mathcal Y}_k\big). \end{array} \end{align} $$
Let
![]() $B_l$
, for
$B_l$
, for
![]() $l\in \omega $
, be such that
$l\in \omega $
, be such that
 $$ \begin{align} B_l\subseteq {\mathcal X}_k\cap {\mathcal P}\left([m_l, m_{l+1})\right)\text{ and } |B_l|\leq (l+1)^2+1. \end{align} $$
$$ \begin{align} B_l\subseteq {\mathcal X}_k\cap {\mathcal P}\left([m_l, m_{l+1})\right)\text{ and } |B_l|\leq (l+1)^2+1. \end{align} $$
By an argument similar to the one justifying (21), it follows from (24) that
 $$ \begin{align*} \bigcup_{l>0} \bigcup B_{2l} \in \overline{{\mathcal Y}_k}\;\text{ and }\; \bigcup_{l} \bigcup B_{2l+1} \in \overline{{\mathcal Y}_k}. \end{align*} $$
$$ \begin{align*} \bigcup_{l>0} \bigcup B_{2l} \in \overline{{\mathcal Y}_k}\;\text{ and }\; \bigcup_{l} \bigcup B_{2l+1} \in \overline{{\mathcal Y}_k}. \end{align*} $$
Thus, by Lemma 5.4(ii), we have
![]() $\bigcup _{l} \bigcup B_{l} \in \mathcal {I}$
, from which we get
$\bigcup _{l} \bigcup B_{l} \in \mathcal {I}$
, from which we get
 $$ \begin{align} \{ x\in {\mathcal P}(\omega)\colon \forall l \ \big( x\cap [m_l, m_{l+1}) \in B_l\big)\} \text{ is bounded in }\mathcal{I}. \end{align} $$
$$ \begin{align} \{ x\in {\mathcal P}(\omega)\colon \forall l \ \big( x\cap [m_l, m_{l+1}) \in B_l\big)\} \text{ is bounded in }\mathcal{I}. \end{align} $$
Now Player I plays a convergent subsequence
![]() $(y^0_i)_{i<\omega }$
of
$(y^0_i)_{i<\omega }$
of
![]() $(x_i)_{i<\omega }$
so that
$(x_i)_{i<\omega }$
so that
 $$ \begin{align} \forall l\ |\{ y^0_i\colon i\in \omega\} \cap [m_l, m_{l+1})| \leq l+1. \end{align} $$
$$ \begin{align} \forall l\ |\{ y^0_i\colon i\in \omega\} \cap [m_l, m_{l+1})| \leq l+1. \end{align} $$
Assume Players I and II are about to make Move
![]() $n+1$
. Assume we have a sequence of sets
$n+1$
. Assume we have a sequence of sets
![]() $a_l\subseteq [m_l, m_{l+1})$
,
$a_l\subseteq [m_l, m_{l+1})$
,
![]() $l<n$
, such that the set played by Player II in Move p with
$l<n$
, such that the set played by Player II in Move p with
![]() $1\leq p\leq n$
is
$1\leq p\leq n$
is
Now, in Move
![]() $n+1$
, Player I plays the family of sets
$n+1$
, Player I plays the family of sets
Then, still in Move
![]() $n+1$
, Player II picks one of these sets, which amounts to picking
$n+1$
, Player II picks one of these sets, which amounts to picking
![]() $a_{n+1} \subseteq [m_n, m_{n+1})$
. We let
$a_{n+1} \subseteq [m_n, m_{n+1})$
. We let
![]() $U_{n+1}= V_{a_{n+1}}$
. Further, Player II plays an arbitrary sequence
$U_{n+1}= V_{a_{n+1}}$
. Further, Player II plays an arbitrary sequence
![]() $(x_i)$
in
$(x_i)$
in
![]() $U_{n+1}$
. Then Player I picks a convergent subsequence
$U_{n+1}$
. Then Player I picks a convergent subsequence
 $(y^{n+1}_i)_{i<\omega }$
of
$(y^{n+1}_i)_{i<\omega }$
of
![]() $(x_i)_{i<\omega }$
so that
$(x_i)_{i<\omega }$
so that
 $$ \begin{align} \forall l\geq n+1 \ |\{ y^{n+1}_i\colon i\in \omega\} \cap [m_l, m_{l+1})| \leq l+1. \end{align} $$
$$ \begin{align} \forall l\geq n+1 \ |\{ y^{n+1}_i\colon i\in \omega\} \cap [m_l, m_{l+1})| \leq l+1. \end{align} $$
This concludes our description of a strategy for Player I. We claim this is a winning strategy.
Indeed, after a run of the game is finished, we set
Clearly,
![]() $B_l\subseteq {\mathcal X}_k$
. It follows from (27) and (28) that
$B_l\subseteq {\mathcal X}_k$
. It follows from (27) and (28) that
![]() $|B_l|\leq l^2+1$
. Thus, condition (25) is fulfilled. Therefore, the set
$|B_l|\leq l^2+1$
. Thus, condition (25) is fulfilled. Therefore, the set
is bounded in
![]() $\mathcal {I}$
as it is included in
$\mathcal {I}$
as it is included in
 $$ \begin{align*} \{ x\in {\mathcal P}(\omega)\colon \forall l \ \big( x\cap [m_l, m_{l+1}) \in B_l\big)\}, \end{align*} $$
$$ \begin{align*} \{ x\in {\mathcal P}(\omega)\colon \forall l \ \big( x\cap [m_l, m_{l+1}) \in B_l\big)\}, \end{align*} $$
which is bounded in
![]() $\mathcal {I}$
by (26). It follows that Player I wins.
$\mathcal {I}$
by (26). It follows that Player I wins.
![]() $\textrm{(v)}\Rightarrow \textrm{(vi)}$
follows from Lemma 5.3.
$\textrm{(v)}\Rightarrow \textrm{(vi)}$
follows from Lemma 5.3.
![]() $\textrm{(vi)}\Rightarrow \textrm{(vii)}$
follows directly from [Reference Louveau and Veličković10, Theorem 1].
$\textrm{(vi)}\Rightarrow \textrm{(vii)}$
follows directly from [Reference Louveau and Veličković10, Theorem 1].
![]() $\textrm{(vii)}\Rightarrow \textrm{(i)}$
follows from Theorem 4.2.⊣
$\textrm{(vii)}\Rightarrow \textrm{(i)}$
follows from Theorem 4.2.⊣
Acknowledgments
The first author was partially supported by NSF of China grants 11801386 and 11771311. The second author was partially supported by PAPIIT grants IN 100317 and IN 104220, and a CONACyT grant A1-S-16164. The fourth author was partially supported by NSF grant DMS-1954069.