Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-14T09:15:06.199Z Has data issue: false hasContentIssue false
  • English
  • Français

STRUCTURE OF SUMMABLE TALL IDEALS UNDER KATĚTOV ORDER

Part of: Set theory

Published online by Cambridge University Press:  20 April 2023

JIALIANG HE ,
ZUOHENG LI  and
SHUGUO ZHANG
JIALIANG HE
Affiliation:
COLLEGE OF MATHEMATICS SICHUAN UNIVERSITY NO. 24 SOUTH SECTION 1, YIHUAN ROAD CHENGDU 610065, SICHUAN, CHINA E-mail: jialianghe@scu.edu.cn E-mail: zhangsg@scu.edu.cn
ZUOHENG LI*
Affiliation:
COLLEGE OF MATHEMATICS SICHUAN UNIVERSITY NO. 24 SOUTH SECTION 1, YIHUAN ROAD CHENGDU 610065, SICHUAN, CHINA E-mail: jialianghe@scu.edu.cn E-mail: zhangsg@scu.edu.cn
SHUGUO ZHANG
Affiliation:
COLLEGE OF MATHEMATICS SICHUAN UNIVERSITY NO. 24 SOUTH SECTION 1, YIHUAN ROAD CHENGDU 610065, SICHUAN, CHINA E-mail: jialianghe@scu.edu.cn E-mail: zhangsg@scu.edu.cn
*
E-mail: 18653730429@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that Katětov and Rudin–Blass orders on summable tall ideals coincide. We prove that Katětov order on summable tall ideals is Galois–Tukey equivalent to 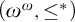$(\omega ^\omega ,\le ^*)$. It follows that Katětov order on summable tall ideals is upwards directed which answers a question of Minami and Sakai. In addition, we prove that 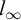${l_\infty }$ is Borel bireducible to an equivalence relation induced by Katětov order on summable tall ideals.

Keywords

summable idealKatětov orderGalois–Tukey connection

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E15: Descriptive set theory 03E04: Ordered sets and their cofinalities; pcf theory
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blass, A., Combinatorial cardinal characteristics of the continumm, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Berlin, 2010, pp. 395–489.CrossRefGoogle Scholar
Farah, I., Analytic ideals and their quotients, Ph.D. thesis, University of Toronto, 1997.Google Scholar
Hrušák, M., Combinatorics of filters and ideals, Set Theory and Its Applications (L. Babinkostova, A. E. Caicedo, S. Geschke, and M. Scheepers, editors), Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 29–69.CrossRefGoogle Scholar
Mazur, K., ${F}_{\sigma }$ -ideals and ${\omega}_1{\omega}_1^{\ast }$ -gaps in the Boolean algebras $\mathbf{\mathcal{P}}\left(\omega \right) / \mathbf{\mathcal{I}}$ $.$ Fundamenta Mathematicae, vol. 138 (1991), no. 2, pp. 103–111.CrossRefGoogle Scholar
Minami, H. and Sakai, H., Katětov and Katětov-Blass orders on ${F}_{\sigma }$ -ideals. Archive for Mathematical Logic, vol. 55 (2016), pp. 883–898.CrossRefGoogle Scholar
Rosendal, C., Cofinal families of Borel equivalence relations and quasiorders, this Journal, vol. 70 (2005), no. 4, pp. 1325–1340.Google Scholar
Vojtáš, P., Generalized Galois-Tukey connections between explicit relations on classical objects of real analysis, Set Theory of the Reals (Judah, H., editor), Israel Mathematical Conference Proceedings, vol. 6, American Mathematical Society, Providence, RI, 1993, pp. 619–643.Google Scholar