Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-14T10:42:40.375Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONG COMPLETENESS OF PROVABILITY LOGIC FOR ORDINAL SPACES

Published online by Cambridge University Press:  19 June 2017

JUAN P. AGUILERA  and
DAVID FERNÁNDEZ-DUQUE
JUAN P. AGUILERA
Affiliation:
INSTITUT FÜR ALGEBRA UND DISKRETE MATHEMATIK TECHNISCHE UNIVERSITÄT WIEN VIENNA, AUSTRIA E-mail: aguilera@logic.at
DAVID FERNÁNDEZ-DUQUE
Affiliation:
CENTRE INTERNATIONAL DE MATHÉMATIQUES ET D’INFORMATIQUE UNIVERSITY OF TOULOUSE, TOULOUSE, FRANCE and DEPARTMENT OF MATHEMATICS INSTITUTO TECNOLÓGICO AUTÓNOMO DE MÉXICO MEXICO CITY, MEXICO E-mail: david.fernandez@irit.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a scattered space 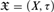$\mathfrak{X} = \left( {X,\tau } \right)$ and an ordinal λ, we define a topology 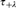$\tau _{ + \lambda } $ in such a way that τ +0 = τ and, when 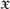$\mathfrak{X}$ is an ordinal with the initial segment topology, the resulting sequence {τ +λ}λ∈Ord coincides with the family of topologies 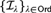$\left\{ {\mathcal{I}_\lambda } \right\}_{\lambda \in Ord} $ used by Icard, Joosten, and the second author to provide semantics for polymodal provability logics.

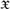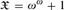We prove that given any scattered space $\mathfrak{X}$ of large-enough rank and any ordinal λ > 0, GL is strongly complete for τ + λ. The special case where $\mathfrak{X} = \omega ^\omega + 1$ and λ = 1 yields a strengthening of a theorem of Abashidze and Blass.

Keywords

Primary 03F45Secondary 03E1003F1554G12provability logictopological semanticsscattered space
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 608 - 628
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abashidze, M., Ordinal completeness of the Gödel-Löb modal system . Intensional Logics and the Logical Structure of Theories, Metsniereba, Tbilisi, 1985, pp. 49–73 (In Russian).Google Scholar
Beklemishev, L., Bezhanishvili, G., and Icard, T., On topological models of GLF, Ways of Proof Theory (Schindler, R., editor), Ontos Mathematical Logic, vol. 2, De Gruyter, Berlin, 2010, pp. 133–153.Google Scholar
Beklemishev, L. D., Veblen hierarchy in the context of provability algebras , Logic, Methodology and Philosophy of Science, Proceedings of the Twelfth International Congress (Hájek, P., Valdés-Villanueva, L., and Westerståhl, D., editors), Kings College Publications, London, 2005, pp. 65–78.Google Scholar
Beklemishev, L. D. and Gabelaia, D., Topological completeness of the provability logic GLP . Annals of Pure and Applied Logic, vol. 164 (2013), no. 12, pp. 1201–1223.CrossRefGoogle Scholar
Beklemishev, L. D. and Gabelaia, D., Topological Interpretations of Provability Logic . Leo Esakia on Duality in Modal and Intuitionistic Logics (Bezhanishvili, G., editor), Springer, 2014, pp. 259–290.Google Scholar
Bezhanishvili, G., Mines, R., and Morandi, P. J., Scattered, Hausdorff-reducible, and hereditarily irresolvable spaces . Topology and its Applications, vol.132 (2003), no. 3, pp. 291–306.Google Scholar
Bezhanishvili, G. and Morandi, P. J., Scattered and hereditarily irresolvable spaces in modal logic . Archive for Mathematical Logic, vol. 49 (2010), pp. 343–365.Google Scholar
Blass, A., Infinitary combinatorics and modal logic, this Journal, vol. 55 (1990), no. 2, pp. 761–778.Google Scholar
Esakia, L., Diagonal constructions, löb’s formula and cantor’s scattered space (in russian) . Studies in Logic and Semantics, vol. 132 (1981), no. 3, pp. 128–143.Google Scholar
Fernández-Duque, D., The polytopologies of transfinite provability logic . Archive for Mathematical Logic, vol. 53 (2014), no. 3–4, pp. 385–431.Google Scholar
Fernández-Duque, D. and Joosten, J. J., Models of transfinite provability logic, this Journal, vol. 78 (2011), no. 2, pp. 543–561.Google Scholar
Fernández-Duque, D. and Joosten, J. J., Hyperations, Veblen progressions, and transfinite iteration of ordinal functions . Annals of Pure and Applied Logic, vol. 164 (2013), no. 7–8, pp. 785–801.Google Scholar
Gödel, K., Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I . Monatshefte für Mathematik Physik, vol. 38 (1931), pp. 173–198.CrossRefGoogle Scholar
Icard, T. F., A topological study of the closed fragment of GLP. Journal of Logic and Computation, vol. 21 (2011), no. 4, pp. 683–696.Google Scholar
Japaridze, G., The polymodal provability logic , Intensional Logics and the Logical Structure of Theories: Material from the Fourth Soviet-Finnish Symposium on Logic, Metsniereba, Tbilisi, 1988, pp. 16–48.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, Heidelberg, 2006.Google Scholar
Segerberg, K., An Essay in Classical Modal Logic, Filosofiska Fóreningen och Filosofiska Institutionen vid Uppsala Universitet, Uppsala, 1971.Google Scholar
Shehtman, V., On Strong Neighbourhood Completeness of Modal And Intermediate Propositional Logics (Part II) , JFAK. Essays Dedicated to Johan van Benthem on the Occasion of his 50th Birthday, University of Amsterdam, Amsterdam, 1999, pp. 1–11.Google Scholar
van Benthem, J and Bezhanishvili, G., Modal Logics of Space, Institute for Logic, Language and Computation, Springer, Netherlands, 2006.Google Scholar