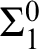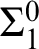1 Introduction
In this article, we classify computability-theoretic preservation properties studied in reverse mathematics, namely cone avoidance, preservation of hyperimmunities, preservation of non-
$\Sigma ^{0}_{1}$
definitions, among others. Many of these preservation properties have already been separated using natural problems in reverse mathematics—that is, there is a natural problem which is known to admit preservation of one property but not preservation of the other. The observation that emerges from our work is that those properties which have not already been separated in fact coincide.Footnote
1
Reverse mathematics is a foundational program whose goal is to determine the optimal axioms for proving ordinary theorems. It uses subsystems of second-order arithmetics, with a base theory,
$\operatorname {\mathsf{RCA}}_0$
, capturing computable mathematics. See Simpson’s book [Reference Simpson31] for a reference in reverse mathematics. A structure in this language is a tuple
$(N, {\mathcal {S}}, +_N, *_N, <_N, 0_N, 1_N)$
, where N stands for the first-order part, and
${\mathcal {S}}$
for the set of reals. We are in particular interested in structures in which the first-order part consists of the standard integers
$\omega $
, equipped with the natural operations. These structures are called
$\omega $
-structures, and are fully specified by their second-order part
${\mathcal {S}}$
. The choice of the axioms of
$ \operatorname {\mathsf{RCA}}_0$
yields a nice characterization of the second-order part of
$\omega $
-models of
$ \operatorname {\mathsf{RCA}}_0$
in terms of Turing ideals.
Definition 1.1. A Turing ideal is a collection of reals
${\mathcal {S}} \subseteq 2^{\omega }$
which is closed under the effective join and downward-closed under the Turing reduction. In other words
-
(a)
$\forall X, Y \in {\mathcal {S}}, X \oplus Y = \{2n : n \in X\} \cup \{2n+1 : n \in Y\} \in {\mathcal {S}},$
-
(b)
$\forall X \in {\mathcal {S}}, \forall Y \leqslant _T X, Y \in {\mathcal {S}}.$
Many statements studied in reverse mathematics can be formulated as mathematical problems, with instances and solutions. For example, weak König’s lemma (
$ \operatorname {\mathsf{WKL}}$
) asserts that every infinite, finitely branching subtree of
$2^{<\omega }$
has an infinite path. Here, an instance is such a tree T, and a solution to T is an infinite path through it. An
$\omega $
-structure
${\mathcal {M}}$
with second-order part
${\mathcal {S}}$
is a model of a problem
${\mathsf {P}}$
(written
${\mathcal {M}} \models {\mathsf {P}}$
) if every instance in
${\mathcal {S}}$
has a solution in it. In this case we also say that
${\mathsf {P}}$
holds in
${\mathcal {S}}$
. In order to separate a problem
${\mathsf {P}}$
from another problem
${\mathsf {Q}}$
in reverse mathematics, one usually constructs a Turing ideal
${\mathcal {S}}$
in which
${\mathsf {P}}$
holds, but not
${\mathsf {Q}}$
. However, when closing the Turing ideal with solution to instances of
${\mathsf {P}}$
, one must be careful not to make it a model of
${\mathsf {Q}}$
. This motivates the use of preservation properties.
Definition 1.2. Fix a collection of sets
${\mathcal {W}} \subseteq 2^{\omega }$
downward-closed under Turing reduction. A problem
${\mathsf {P}}$
admits preservation of
${\mathcal {W}}$
if for every set
$Z \in {\mathcal {W}}$
and every Z-computable instance X of
${\mathsf {P}}$
, there is a solution Y to X such that
$Z \oplus Y \in {\mathcal {W}}$
.
The following basic lemma is at the core of separations in reverse mathematics.
Lemma 1.3. Suppose a problem
${\mathsf {P}}$
admits preservation of some collection
${\mathcal {W}}$
, but another problem
${\mathsf {Q}}$
does not. Then there is a Turing ideal
${\mathcal {S}} \subseteq {\mathcal {W}}$
in which
${\mathsf {P}}$
holds, but not
${\mathsf {Q}}$
.
Proof. Since
${\mathsf {Q}}$
does not admit preservation of
${\mathcal {W}}$
, there is some
$Z \in {\mathcal {W}}$
, and a
${\mathsf {Q}}$
-instance
$X_{{\mathsf {Q}}} \leqslant _T Z$
such that for every solution Y to
$X_{{\mathsf {Q}}}$
,
$Z \oplus Y \not \in {\mathcal {W}}$
. We will build a Turing ideal
${\mathcal {S}} \subseteq {\mathcal {W}}$
containing Z and in which
${\mathsf {P}}$
holds. In particular,
${\mathsf {Q}}$
cannot hold in any such Turing ideal. We build a countable sequence of sets
$Z_0, Z_1, \dots $
such that for every
$n \in \omega $
,
$\bigoplus _{s < n} Z_s \in {\mathcal {W}}$
, and for every
${\mathsf {P}}$
-instance
$X \leqslant _T \bigoplus _{s < n} Z_s$
, there is some
$m \in \omega $
such that
$Z_m$
is a
${\mathsf {P}}$
-solution to X. Start with
$Z_0 = Z$
. Having defined
$Z_0, \dots , Z_{n-1}$
, pick the next
${\mathsf {P}}$
-instance
$X \leqslant _T \bigoplus _{s < n} Z_s$
by ensuring that each instance will receive attention at a finite stage. Since
${\mathsf {P}}$
admits preservation of
${\mathcal {W}}$
, there is a
${\mathsf {P}}$
-solution
$Z_n$
to X such that
$\bigoplus _{s \leqslant n} Z_s \in {\mathcal {W}}_n$
. Then go to the next stage. The collection
${\mathcal {S}} = \{ X : (\exists s) X \leqslant _T \bigoplus _{s < n} Z_s \}$
is a Turing ideal included in
${\mathcal {W}}$
in which
${\mathsf {P}}$
holds but not
${\mathsf {Q}}$
. ⊣
Many statements in reverse mathematics, mostly coming from Ramsey theory, have been separated by looking at the appropriate computability-theoretic notion of preservation. We now detail some outstanding ones, which will serve as a basis for our classification study.
1.1 Cone avoidance
Perhaps the most important property of preservation in reverse mathematics is the notion of cone avoidance, both for its intrinsic significance, namely, the inability to code sets into the solutions of a computable instance of a problem, and as a tool to separate statements from the Arithmetic Comprehension Axiom (
$ \operatorname {\mathsf{ACA}}$
).
Definition 1.4. Fix
$n \leqslant \omega $
. A problem
${\mathsf {P}}$
admits avoidance of n cones if for every set Z and every collection
$\{ B_s : s < n \}$
of non-Z-computable sets, every
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
has a solution Y such that for every
$s < n$
,
$B_s \not \leqslant _T Z \oplus Y$
.
This definition can be understood in terms of Definition 1.2 by defining
$$ \begin{align*} {\mathcal{W}}(B_s : s < n) = \{ Y : (\forall s < n)\, B_s \not \le_T Y\}. \end{align*} $$
Then
${\mathsf {P}}$
admits avoidance of n cones precisely if it admits preservation of
${\mathcal {W}}(B_s : s < n)$
for every collection
$\{B_s : s < n\}$
. A similar analysis applies to all of the avoidance properties we will study, although for the rest we will not take the time to make it explicit.
Jockusch and Soare [Reference Jockusch and Robert13, Theorem 2.5] proved that weak König’s lemma (
$ \operatorname {\mathsf{WKL}}$
) admits avoidance of
$\omega $
cones.Footnote
2
Seetapun’s celebrated theorem (see [Reference Seetapun and Slaman29]) states that Ramsey’s theorem for pairs (
$ \operatorname {\mathsf {RT}}^2_2$
) admits avoidance of
$\omega $
cones, answering a long-standing open question. On the other hand, Jockusch [Reference Jockusch12] proved that Ramsey’s theorem for triples (
$ \operatorname {\mathsf {RT}}^3_2$
) does not. Later, Wang [Reference Wang34] proved the surprising result that for every
$n \geqslant 2$
, there is some
$k \in \omega $
such that
$ \operatorname {\mathsf {RT}}^n_{k+1,k}$
admits avoidance of
$\omega $
cones, where
$ \operatorname {\mathsf{RT}}^n_{k+1,k}$
asserts that for every coloring
$f : [\omega ]^n \to k+1$
, there is an infinite set
$H \subseteq \omega $
such that
$|f[H]^n| \leqslant k$
. By looking at the literature, one can observe that all the proofs of cone avoidance hold for
$\omega $
cones simultaneously. In this paper, we justify this observation by proving that avoidance of 1 cone and of
$\omega $
cones coincide.
1.2 Preservation of non-
$\Sigma ^{0}_{1}$
definitions
Wang [Reference Wang33] dramatically simplified separation proofs of the Erdős–Moser (
$ \operatorname {\mathsf{EM}}$
) from the Ascending Descending Sequence (
$ \operatorname {\mathsf{ADS}}$
) of Lerman, Solomon and Towsner [Reference Lerman, Solomon and Towsner18] by proving that some problems “preserve” the arithmetical hierarchy, in the sense that given a fixed strictly non-
$\Sigma ^0_n$
set A and given a
${\mathsf {P}}$
-instance, there is a solution Y such that A is not
$\Sigma ^0_n(Y)$
. We consider the case of non-
$\Sigma ^{0}_{1}$
sets.
Definition 1.5. Fix
$n \leqslant \omega $
. A problem
${\mathsf {P}}$
admits preservation of n non-
$\Sigma ^{0}_{1}$
definitions if for every set Z and every collection
$\{ B_s : s < n \}$
of non-Z-c.e. sets, every
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
has a solution Y such that for every
$s < n$
,
$B_s$
is not
$Z \oplus Y$
-c.e.
This framework was very successful in proving separation results between Ramsey-like statements over
$\omega $
-models. Wang [Reference Wang33] proved that
$ \operatorname {\mathsf{WKL}}$
and the
$ \operatorname {\mathsf{EM}} $
theorem admits preservation of
$\omega $
non-
$\Sigma ^{0}_{1}$
definitions, while the thin set theorem for pairs (
$ \operatorname {\mathrm {{\mbox {TS}}}}^2_{\omega }$
) does not. Patey [Reference Patey24] proved that for every
$k \geqslant 1$
,
$ \operatorname {\mathsf{RT}}^2_{k+1,k}$
admits preservation of k but not
$k+1$
non-
$\Sigma ^{0}_{1}$
definitions. In particular, Ramsey’s theorem for pairs and two colors admits preservation of one but not two non-
$\Sigma ^{0}_{1}$
definitions.
1.3 Preservation of hyperimmunities
The proof that Ramsey’s theorem for triples does not admit cone avoidance consists of constructing a computable coloring
$f : [\omega ]^3 \to 2$
such that every f-homogeneous set
$H = \{x_0 < x_1 < \cdots \}$
is so sparse that its principal function
$p_H : \omega \to \omega $
defined by
$p_H(n) = x_n$
grows faster than the settling time of the halting set. Actually, all the proofs that a Ramsey-like statement does not admit cone avoidance exploit the existence of instances whose solutions are all sufficiently sparse to compute fast-growing functions dominating moduli of computation [Reference Patey26]. It is therefore natural to consider which problems have the ability to compute fast-growing functions.
A function
$f : \omega \to \omega $
is hyperimmune if it is not dominated by any computable function. An infinite set
$A = \{x_0 < x_1 < \dotsb \}$
is hyperimmune if its principal function
$p_A$
is hyperimmune. Equivalently, a set A is hyperimmune if for every computable sequence of pairwise disjoint non-empty finite coded sets
$F_0, F_1, \dots $
, there is some
$n \in \omega $
such that
$A \cap F_n = \emptyset $
.
Definition 1.6. Fix
$n \leqslant \omega $
. A problem
${\mathsf {P}}$
admits preservation of n hyperimmunities if for every set Z and every collection
$\{ f_s : s < n \}$
of Z-hyperimmune functions, every
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
has a solution Y such that for every
$s < n$
,
$f_s$
is
$Z \oplus Y$
-hyperimmune.
Jockusch and Soare [Reference Jockusch and Robert13, Theorem 2.4] proved that
$ \operatorname {\mathsf{WKL}}$
admits preservation of
$\omega $
hyperimmunities (in fact, every computable instance of
$ \operatorname {\mathsf{WKL}}$
has a solution of hyperimmune-free degree). Patey [Reference Patey25] proved that the
$ \operatorname {\mathsf{EM}}$
theorem admits preservation of
$\omega $
hyperimmunities and that for every
$k \geqslant 1$
,
$ \operatorname {\mathsf{RT}}^2_{k+1,k}$
admits preservation of k, but not
$k+1$
, hyperimmunities. He also proved that the thin set theorem for pairs admits preservation of k hyperimmunities for every
$k \in \omega $
, but not of
$\omega $
hyperimmunities.
As it happens, all the separations over
$\omega $
-models and over computable reduction which have been proven by notions of preservation of non-
$\Sigma ^{0}_{1}$
definitions can also be proved by preservation of hyperimmunities, and vice versa. We prove in this paper that this is not a coincidence, and that the two notions of preservation are indeed equivalent.
1.4 Constant-bound trace avoidance
Both the original proof of cone avoidance of Ramsey’s theorem for pairs by Seetapun [Reference Seetapun and Slaman29] and the proof by Cholak, Jockusch and Slaman [Reference Cholak, Jockusch and Slaman4] involve Mathias-like notions of forcing within models of weak König’s lemma. Their proofs seem to make an essential use of compactness, and the community naturally wondered whether this use was necessary. Liu [Reference Liu19] recently negatively answered the long-standing open question of whether Ramsey’s theorem for pairs implies weak König’s lemma in reverse mathematics. He later [Reference Liu20] refined his argument and proved that
$ \operatorname {\mathsf{RT}}^2_2$
does not even imply the existence of Martin–Löf randoms, using the notion of constant-bound trace avoidance for closed sets.Footnote
3
Given a closed set
${\mathcal {C}} \subseteq 2^{\omega }$
, a trace is a collection of finite coded sets of strings
$F_0, F_1, \dots $
such that for every
$n \in \omega $
,
$F_n$
contains only strings of length exactly n, and
${\mathcal {C}} \cap [F_n] \neq \emptyset $
where
$[F_n]$
is the clopen set generated by
$F_n$
. In other words, for every
$n \in \omega $
, there is a string
$\sigma \in F_n$
with
$|\sigma | = n$
such that
$\sigma \prec P$
for some
$P \in {\mathcal {C}}$
. A k-trace of
${\mathcal {C}}$
is a trace such that
$|F_n| = k$
for every
$n \in \omega $
. A constant-bound trace of
${\mathcal {C}}$
is a k-trace for some
$k \in \omega $
.
Definition 1.7. Fix
$n \leqslant \omega $
. A problem
${\mathsf {P}}$
admits avoidance of constant-bound traces for n closed sets if for every set Z and every collection of closed sets
$\{ {\mathcal {C}}_s \subseteq 2^{\omega } : s < n \}$
with no Z-computable constant-bound trace, every
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
has a solution Y such that for every
$s < n$
,
${\mathcal {C}}_s$
has no
$Z \oplus Y$
-computable constant-bound trace.
This notion of avoidance, which at first sight seems slightly more artificial, happens to be a very powerful tool to prove that Ramsey-like statements do not imply notions of compactness.
Liu [Reference Liu20] proved that Ramsey’s theorem for pairs and two colors (
$ \operatorname {\mathsf{RT}}^2_2$
) admits avoidance of constant-bound traces for one closed set, while
$ \operatorname {\mathsf{WKL}}$
does not. Patey [Reference Patey22] proved that the
$ \operatorname {\mathsf{EM}}$
theorem admits avoidance of constant-bound traces for
$\omega $
closed sets, and that for every
$k \geqslant 1$
,
$ \operatorname {\mathsf{RT}}^2_{k+1,k}$
admits avoidance of constant-bound traces for k but not
$k+1$
closed sets, and that
$ \operatorname {\mathsf{TS}}^2_{\omega }$
admits avoidance of constant-bound traces for k closed sets for every
$k \in \omega $
, but not for
$\omega $
closed sets.
1.5 Other preservation notions
As explained, the notion of hyperimmunity can be expressed both in terms of fast-growing functions, and as sets which cannot be traced by computable strong arrays. Hyperimmunity strengthens another property of sets called immunity, which refers to the impossibility of computing an infinite subset of the set. Immunity is a natural notion to look at when considering Ramsey-like theorems, since their sets of solutions are closed under infinite subsets. Although hyperimmunity is a strengthening of immunity, preservation of hyperimmunity is actually strictly weaker than preservation of immunity.
Definition 1.8. Fix
$n \leqslant \omega $
. A problem
${\mathsf {P}}$
admits preservation of n immunities if for every set Z and every collection
$\{ B_s : s < n \}$
of Z-immune sets, every
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
has a solution Y such that for every
$s < n$
,
$B_s$
is
$Z \oplus Y$
-immune.
Very few statements in reverse mathematics admit preservation of
$\omega $
immunities. The most notable is the cohesiveness principle (
$ \operatorname {\mathsf{COH}}$
). All the statements which are known to admit preservation of
$\omega $
immunities actually also preserve the following seemingly stronger notion.
Definition 1.9. Fix
$n \leqslant \omega $
. A problem
${\mathsf {P}}$
admits avoidance of n closed sets in the Baire space if for every set Z and every collection
$\{ {\mathcal {C}}_s : s < n \}$
of closed sets in the Baire space with no Z-computable member, every
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
has a solution Y such that for every
$s < n$
,
${\mathcal {C}}_s$
has no
$Z \oplus Y$
-computable member.
A similar notion can be defined for closed sets in the Cantor space. We will prove that avoiding closed sets in the Cantor space or in the Baire space are equivalent. We leave open the question whether every problem admitting preservation of
$\omega $
immunities also admits avoidance of
$\omega $
closed sets.
1.6 Summary of the relations between properties of preservation
Figure 1 Diagram of relations between properties of preservation. A double arrow denotes a strict implication, a dotted double arrows express a strict hierarchy, while a bidirectional arrow is an equivalence. The only unknown arrow is the reversal from preservation of
$\omega $
immunities to avoidance of
$\omega $
closed sets.
The notions of preservation admit a combinatorial counterpart, in which no effectiveness restriction is imposed on the instance of the problem. This is the notion of strong preservation.
Definition 1.10. Fix a collection of sets
${\mathcal {W}} \subseteq 2^{\omega }$
downward-closed under the Turing reduction. A problem
${\mathsf {P}}$
admits strong preservation of
${\mathcal {W}}$
if for every set
$Z \in {\mathcal {W}}$
and every (not-necessarily Z-computable) instance X of
${\mathsf {P}}$
, there is a solution Y to X such that
$Z \oplus Y \in {\mathcal {W}}$
.
Considering strong preservation has two main justifications. First, its reflects the combinatorial weakness of problems, as opposed to the computational weakness of standard notions of preservation. Indeed, by proving that the infinite pigeonhole principle admits strong avoidance of
$\omega $
cones, Dzhafarov and Jockusch [Reference Dzhafarov and Jockusch8] show that there is an intrinsic combinatorial weakness in the pigeonhole principle which prevents the coding of arbitrary sets in the collection of solutions. On the other hand, the proof of Seetapun [Reference Seetapun and Slaman29] that Ramsey’s theorem for pairs admits avoidance of
$\omega $
cones strongly relies on the effectiveness of the colorings of pairs. When removing the effectiveness restriction, one can code any hyperarithmetical set, and therefore
$ \operatorname {\mathsf{RT}}^2_2$
does not admit strong avoidance of
$\omega $
cones. These results can be considered as interesting per se.
The second reason is more technical, and specific to Ramsey-like statements. Many such statements are about colorings over
$[\omega ]^n$
and are parametrized by the size n of the tuples. See for example Ramsey’s theorem [Reference Jockusch12], the thin set [Reference Cholak3], free set [Reference Cholak3], and rainbow Ramsey [Reference Wang34] theorems. Such theorems admit inductive proofs based on n. Proofs that such a statement
${\mathsf {P}}^{n+1}$
admits some preservation are usually obtained by proving that
${\mathsf {P}}^n$
admits strong preservation of the property, and then deducing the non-strong version for
${\mathsf {P}}^{n+1}$
. One can even obtain reversals for the notions of avoidance mentioned in this article. See for example Theorem 1.5. of [Reference Cholak and Patey5].
One can directly deduce implications between strong notions of preservation from their corresponding weak notions of preservation.
Theorem 1.11. Suppose preservation of
${\mathcal {W}}_1$
implies preservation of
${\mathcal {W}}_2$
. Then strong preservation of
${\mathcal {W}}_1$
implies strong preservation of
${\mathcal {W}}_2$
.
Proof. Let
${\mathsf {P}}$
be a problem which admits strong preservation of
${\mathcal {W}}_1$
. We prove that
${\mathsf {P}}$
admits strong preservation of
${\mathcal {W}}_2$
. Fix a set
$Z \in {\mathcal {W}}_2$
and an instance X of
${\mathsf {P}}$
. Let
$\tilde {{\mathsf {P}}}$
be the problem whose unique instance is
$\emptyset $
, and whose solutions are the
${\mathsf {P}}$
-solutions of X. In particular,
$\tilde {{\mathsf {P}}}$
admits preservation of
${\mathcal {W}}_1$
, so it admits preservation of
${\mathcal {W}}_2$
. Let Y be a
$\tilde {{\mathsf {P}}}$
-solution to the
$\tilde {{\mathsf {P}}}$
-instance
$\emptyset $
such that
$Z \oplus Y \in {\mathcal {W}}_2$
. In particular, Y is a
${\mathsf {P}}$
-solution to the
${\mathsf {P}}$
-instance X. ⊣
The remainder of this article is devoted to proving the equivalences and nonequivalences of the notions of preservation presented above.
2 Avoiding cones
The goal of this section is to prove the following theorem. The variety of notions of preservation which happen to be equivalent can be taken as an argument in favor of the naturality of the notion.
Theorem 2.1. Let
${\mathsf {P}}$
be a problem. Then the following are equivalent:
-
1.
${\mathsf {P}}$
admits avoidance of 1 cone. -
2.
${\mathsf {P}}$
admits avoidance of
$\omega $
cones. -
3.
${\mathsf {P}}$
admits preservation of 1 non-
$\Sigma ^{0}_{1}$
definition. -
4.
${\mathsf {P}}$
admits preservation of 1 hyperimmunity.
The proof of Theorem 2.1 breaks into several parts, corresponding to subsections. In the first part, we prove the equivalence between avoiding one cone and avoiding
$\omega $
cones. Then, we prove the equivalence between avoiding one cone and preserving one non-
$\Sigma ^{0}_{1}$
definition. Last, we prove the equivalence between avoiding one cone and preserving 1 hyperimmunity.
2.1 Avoiding
$\omega $
cones
We start by proving that the notions of avoidance of 1 cone and of
$\omega $
cones coincide. For this, we need to prove two lemmas which say that given a collection of nonzero Turing degrees
$\boldsymbol {d}_0, \boldsymbol {d}_1, \dots $
, one can always find a degree
$\boldsymbol {e}$
relative to which these degrees collapse into a single nonzero degree.
Lemma 2.2. Fix Z and
$B,A_0,A_1,\ldots \nleq _T Z$
. Then there is G such that
$A_0,A_1,\ldots \nleq _T Z \oplus G$
but
$A_0,A_1,\ldots \leqslant _T Z \oplus G \oplus B$
.
Proof. We may assume that B is not
$\Sigma ^{0}_{1}(Z)$
(otherwise we replace it by its complement). We build G by finite extensions as the union of a sequence
$\sigma _{-1} \subseteq \tau _{0} \subseteq \sigma _0 \subseteq \tau _1 \subseteq \sigma _1 \subseteq \tau _1 \subseteq \cdots $
.
Begin
$\sigma _{-1} = \varnothing $
. In general, let
$\sigma _{{\langle } j,k {\rangle }} = \tau _{{\langle } j,k {\rangle }} {\text {^}} {\langle } A_j(k) {\rangle }$
. Given
$\sigma _i$
, define
$\tau _i$
as follows. Let
$i = {\langle } j,k {\rangle }$
. Define a
$\Sigma ^{0}_{1}(Z)$
set D such that
$n \in D$
if and only if there are
$\rho _0, \rho _1 \succeq \sigma _i {\text {^}} 0^n {\text {^}} 1$
and
$\ell $
with
$$ \begin{align*} \Phi_j^{Z \oplus \rho_0}(\ell) \neq \Phi_j^{Z \oplus \rho_1}(\ell). \end{align*} $$
Now as B is not
$\Sigma ^{0}_{1}(Z)$
there is
$n \in B \triangle D$
. If
$n \in B - D$
, then let
$\tau _i = \sigma _i {\text {^}} 0^n {\text {^}} 1$
. If
$n \in D - B$
, find the first witness
$(\rho _0,\rho _1,\ell )$
and choose
$\tau _i$
to be whichever
$\rho $
has
$$ \begin{align*} \Phi_j^{Z \oplus \rho}(\ell) \neq A_k(\ell).\end{align*} $$
This completes the construction of G.
First we claim that
$A_k \nleq _T Z \oplus G$
. Indeed, suppose that
$\Phi _j^{Z \oplus G} = A_k$
. Let
$i = {\langle } j,k {\rangle }$
. Then, when defining
$\tau _i$
, we must have had
$n \in B - D$
, or we would have chosen
$\tau _i$
such that for some
$\ell $
$$ \begin{align*} \Phi_j^{Z \oplus \tau_i}(\ell) \neq A_k(\ell).\end{align*} $$
So we set
$\tau _i = \sigma _i {\text {^}} 0^n {\text {^}} 1$
and for all
$\rho _0,\rho _1 \succeq \tau _i$
and
$\ell $
,
$$ \begin{align*} \Phi_j^{Z \oplus \rho_0}(\ell)\downarrow \text{ and } \Phi_j^{Z \oplus \rho_1}(\ell) \downarrow \qquad \Longrightarrow \qquad \Phi_j^{Z \oplus \rho_0}(\ell) = \Phi_j^{Z \oplus \rho_1}(\ell).\end{align*} $$
Thus
$Z \geqslant _T A_k$
, a contradiction.
Finally, we argue that for each j,
$A_j \leqslant _T Z \oplus G \oplus B$
. This is because
$Z \oplus G \oplus B$
can reconstruct the sequence
$\sigma _{-1} \subseteq \tau _0 \subseteq \sigma _0 \subseteq \tau _1 \subseteq \cdots $
, and
$\sigma _{{\langle } j,k {\rangle }} = \tau _{{\langle } j,k {\rangle }} {\text {^}} {\langle } A_j(k) {\rangle }$
. Indeed, given
$\tau _i$
, G can determine
$\sigma _{i+1}$
. Given
$\sigma _i$
, using G we can find n such that
$\sigma _i {\text {^}} 0^n {\text {^}} 1 \prec G$
. If
$n \in B$
, then
$\tau _i = \sigma _i {\text {^}} 0^n {\text {^}} 1$
. If
$n \notin B$
, let
$i = {\langle } j,k {\rangle }$
and search for the first
$\rho _0,\rho _1 \succeq \sigma _i$
and
$\ell $
with
$$ \begin{align*} \Phi_j^{Z \oplus \rho_0}(\ell) \neq \Phi_j^{Z \oplus \rho_1}(\ell). \end{align*} $$
Then
$\tau _i$
is whichever
$\rho $
has
$\rho \prec G$
.⊣
Lemma 2.3. Fix Z and
$B, A_0,A_1,A_2,\ldots \nleq _T Z$
. Then there is G such that
$B \nleq _T Z \oplus G$
but, for each i,
$B \leqslant _T Z \oplus G \oplus A_i$
.
Proof. Using Lemma 2.2 we can inductively choose
$G_0,G_1,G_2,\ldots $
such that for each n,
$B,A_{n+1},A_{n+2},\ldots \nleq _T Z \oplus G_0 \oplus \cdots \oplus G_n$
but
$B \leqslant _T Z \oplus G_0 \oplus \cdots \oplus G_n \oplus A_n$
.
We will define
$H = \bigoplus H_n$
where
$H_n =^* G_n$
. We want to have that
$B \nleq _T Z \oplus H$
; since
$H_n =^* G_n$
, it will be automatic that for each i,
$B \leqslant _T Z \oplus H \oplus A_i$
. We define H by forcing; our conditions are of the form
$H_0 \oplus \cdots \oplus H_{\ell }$
where
$H_n =^* G_n$
. We argue that given a Turing reduction
$\Phi $
and a condition
$H_0 \oplus \cdots \oplus H_{\ell }$
, there is an extension
$H_0 \oplus \cdots \oplus H_k$
such that we either force that
$\Phi ^{Z \oplus H}$
is partial or that
$\Phi ^{Z \oplus H} \neq B$
. If there are x, k,
$\sigma _{\ell +1},\ldots ,\sigma _k$
such that
$$ \begin{align*} \Phi^{Z \oplus H_0 \oplus \cdots \oplus H_{\ell} \oplus \sigma_{\ell+1} \oplus \cdots \oplus \sigma_k}(x) \downarrow \neq B(x) \end{align*} $$
then we can find a condition extending
$H_0 \oplus \cdots \oplus H_{\ell }$
which forces that
$\Phi ^{Z \oplus H} \neq B$
. Otherwise, suppose that for each x there are
$\sigma _{\ell +1},\ldots ,\sigma _k$
such that
$$ \begin{align*} \Phi^{Z \oplus H_0 \oplus \cdots \oplus H_{\ell} \oplus \sigma_{\ell+1} \oplus \cdots \oplus \sigma_k}(x) \downarrow. \end{align*} $$
Then
$B \leqslant _T Z \oplus H_0 \oplus \cdots \oplus H_{\ell }$
, a contradiction. So there must be some x such that for all
$\sigma _{\ell +1},\ldots ,\sigma _k$
,
$$ \begin{align*} \Phi^{Z \oplus H_0 \oplus \cdots \oplus H_{\ell} \oplus \sigma_{\ell+1} \oplus \cdots \oplus \sigma_k}(x) \uparrow. \end{align*} $$
Then
$H_0 \oplus \cdots \oplus H_{\ell }$
already forces that
$\Phi ^{Z \oplus H}(x)$
does not converge. ⊣
Corollary 2.4. Avoidance of 1 cone implies avoidance of
$\omega $
cones.
Proof. Let
${\mathsf {P}}$
be a problem admitting avoidance of 1 cone. Fix some set Z, non-Z-computable sets
$A_0, A_1, \dots $
and a Z-computable instance X of
${\mathsf {P}}$
. By Lemma 2.3, letting
$B = A_0$
, there is a set G such that
$B \nleq _T Z \oplus G$
but, for each i,
$B \leqslant _T Z \oplus G \oplus A_i$
. Since
${\mathsf {P}}$
admits avoidance of 1 cone, there is a
${\mathsf {P}}$
-solution Y to X such that
$B \nleq _T Z \oplus G \oplus Y$
. We claim that for every
$i \in \omega $
,
$A_i \nleq _T Z \oplus Y$
. Indeed, otherwise,
$B \leqslant _T Z \oplus G \oplus A_i$
, but then
$B \leqslant _T Z \oplus G \oplus Y$
, contradiction. ⊣
However, when considering nonrelativized versions of cone avoidance, avoiding two cones is strictly stronger than avoiding one cone. We call unrelativized a notion for which the ground set Z is
$\emptyset $
. A pair of Turing degrees
$\boldsymbol {a}, \boldsymbol {b}$
is minimal if they are both nonzero,
$\boldsymbol {0}$
is the only degree below both of them.
Theorem 2.5. There is a problem which admits nonrelativized avoidance of one cone, but not of two cones.
Proof. Fix two sets A and B whose Turing degrees form a minimal pair. Let
${\mathsf {P}}$
be the problem with unique instance
$\emptyset $
. A solution is either of A or B.
${\mathsf {P}}$
does not admit nonrelativized avoidance of two cones, as witnessed by taking the cones A and B. On the other hand,
${\mathsf {P}}$
admits nonrelativized avoidance of one cone. Indeed, let C be a noncomputable set, and consider the unique instance
$\emptyset $
of
${\mathsf {P}}$
. By minimality of the pair of degrees of A and B, either
$A \not \geqslant _T C$
or
$B \not \geqslant _T C$
. In either case, there is a
${\mathsf {P}}$
-solution
$Y \in \{A,B\}$
to
$\emptyset $
such that
$C \not \leqslant _T Y$
. ⊣
The equivalence between the two relativized notions show in particular that there is no pair of Turing degrees which is minimal relative to every degree which lies above neither of them. Indeed, if there were such a pair
$A, B$
, one could define the problem
${\mathsf {P}}$
whose unique instance is
$\emptyset $
and whose solutions are either A or B. The problem
${\mathsf {P}}$
would not admit avoidance of two cones as witnessed by the cones above A and B. However, by relativizing the argument of Theorem 2.5, one could prove that
${\mathsf {P}}$
admits avoidance of 1 cone, contradicting Corollary 2.4.
2.2 Preserving 1 hyperimmunity
We now prove that preserving one cone is equivalent to preserving one hyperimmunity. The forward implication is relatively simple.
Lemma 2.6. Fix a set Z and a nondecreasing Z-hyperimmune function
$f : \omega \to \omega $
. There is a set G and a
$\Delta ^{0}_{2}(G)$
set
$A \not \leqslant _T Z \oplus G$
such that f is a G-modulus for A.
Proof. We construct G which will be a
$\Delta ^{0}_{2}$
-approximation of A, with f a G-modulus for A. More precisely,
$$ \begin{align*} (\forall x)(\forall y> f(x))\, G(x, y) = G(x, f(x)) = A(x) \end{align*} $$
It is now clear that for any h dominating f,
$A \leqslant _T G \oplus h$
. It remains only to show that
$A \not \leqslant _T Z\oplus G$
. We will construct our set G by forcing. A condition is a partial function
$\sigma : \omega ^2 \to 2$
with finite domain. The function
$\sigma $
is a stem for the
$\Delta ^{0}_{2}$
approximation
$G : \omega ^2 \to 2$
. We moreover require that there can only be
$(x, y), (x, z) \in \operatorname {\mathrm {dom}}(\sigma )$
with
$\sigma (x, z) \neq \sigma (x, y)$
if
$f(x) \geqslant \min (y, z)$
. This ensures that f is a modulus for the convergence of G.
A condition
$\tau $
extends
$\sigma $
(written
$\tau \leqslant \sigma $
) if
$\tau \supseteq \sigma $
. Every sufficiently generic filter yields G such that G is a stable function whose limit is
$A := \lim _s G(\cdot , s)$
. We now prove that the set of conditions forcing
$\Phi ^{G \oplus Z}_e \neq A$
is dense.
Fix a condition
$\sigma $
. For each
$x \le n$
, let
$s_x$
be largest with
$(x, s_x) \in \operatorname {\mathrm {dom}}(\sigma )$
, if this exists, and
$s_x = 0$
otherwise. For every n, we define
$h(n)$
by a Z-computable search. We search for
$\tau \supseteq \sigma $
such that:
-
• For all
$x \le n$
and all
$t, r \geqslant s_x$
with
$(x,t), (x,r) \in \operatorname {\mathrm {dom}}(\tau )$
,
$\tau (x,t) = \tau (x,r)$
; and -
•
$\Phi ^{\tau \oplus Z}(n)\downarrow $
.
We define
$h(n) = |\tau |$
for the first such
$\tau $
found, and
$h(n)\uparrow $
if there is no such
$\tau $
. Note that we are not restricting our search to conditions, as that would not be a Z-computable search. We have two cases.
Case 1:
$h(n)\uparrow $
for some
$n \in \omega $
. Then let
$\mu \prec \sigma $
be a condition such that for all
$x \le n$
and all t with
$s_x < t \le f(x)$
,
$(x,t) \in \operatorname {\mathrm {dom}}(\mu )$
and
$\mu (x,t) = \sigma (x,s_x)$
if
$(x,s_x) \in \operatorname {\mathrm {dom}}(\sigma )$
, and
$\mu (x,t) = 0$
otherwise. This condition forces
$\Phi ^{G\oplus Z}_e(n)\uparrow $
.
Case 2: the function h is total Z-computable. Since f is Z-hyperimmune, there is some
$n> |\sigma |$
such that
$f(n)> h(n)$
. Let
$\tau $
witness that
$h(n)\downarrow = |\tau |$
. Let
$\hat {\tau } \supset \tau $
be obtained by defining
$\hat {\tau }(n, s) = 1-\Phi ^{\tau \oplus Z}(n)$
for all s with
$h(n) < s \le f(n)$
. Note that
$\tau $
has no alternations in the columns
$x < n$
that weren’t present in
$\sigma $
, and any alternations in a column
$x \geqslant n$
occur before
$|\tau | = h(n) < f(n) \le f(x)$
. There is possibly one more alteration in
$\hat {\tau }$
, in column n, but by construction this occurs before
$f(n)$
. So
$\hat {\tau }$
is a valid condition extending
$\sigma $
. Moreover,
$\hat {\tau }$
forces
$\Phi ^{G \oplus Z}_e(n)\downarrow \neq A$
⊣
Corollary 2.7. Avoidance of 1 cone implies preservation of 1 hyperimmunity.
Proof. Suppose a problem
${\mathsf {P}}$
admits avoidance of one cone. Fix a set Z, a Z-hyperimmune function
$f : \omega \to \omega $
and a
${\mathsf {P}}$
-instance
$X \leqslant _T Z$
. By Lemma 2.6, there is a set G and a
$\Delta ^{0}_{2}(G)$
set
$A \not \leqslant _T Z \oplus G$
such that f is a modulus for A. Since
${\mathsf {P}}$
admits avoidance of 1 cone, then there is a
${\mathsf {P}}$
-solution Y to X such that
$A \not \leqslant _T Z \oplus G \oplus Y$
. If f is not
$Z \oplus Y$
-hyperimmune, then
$Z \oplus Y$
computes a function h dominating f, and since f is a
$Z \oplus G$
-modulus for A,
$Z \oplus G \oplus Y$
computes A, contradiction. ⊣
Lemma 2.8. (Patey [Reference Patey22])
For every set Z, every closed set
${\mathcal {C}} \subseteq \omega ^{\omega }$
with no Z-computable member, and every set A, there is a set G such that
${\mathcal {C}}$
has no
$Z \oplus G$
-computable member and A is
$\Delta ^{0}_{2}(G)$
.
Proof. Consider the notion of forcing whose conditions are pairs
$(\sigma , n)$
, where
$\sigma $
is a partial function
$\subseteq \omega ^2 \to 2$
with finite support, and
$n \in \omega $
. Informally,
$\sigma $
is a stem of the
$\Delta ^{0}_{2}$
approximations
$G : \omega ^2 \to 2$
of A, and n specifies that the n first columns of
$\sigma $
are already locked to
$A {\upharpoonright } n$
. Accordingly, a condition
$(\tau , m)$
extends
$(\sigma , n)$
(written
$(\tau , m) \leqslant (\sigma , n)$
) if
$\tau \supseteq \sigma $
,
$m \geqslant n$
, and for every
$x < n$
and t with
$(x, t) \in \operatorname {\mathrm {dom}} \tau {\smallsetminus } \operatorname {\mathrm {dom}}(\sigma )$
,
$\tau (x,t) = A(x)$
. Any sufficiently generic filter yields a stable function whose limit we denote A.
We now prove that the set of conditions forcing
$\Phi _e^{G \oplus Z}$
not to be a member of
${\mathcal {C}}$
is dense. Given a condition
$(\sigma , n)$
, define a Z-computable decreasing sequence of conditions
$(\sigma , n) \geqslant (\tau _0, n) \geqslant (\tau _1, n) \geqslant \cdots $
such that for every i,
$\Phi _e^{\tau _i \oplus Z}(i)\downarrow $
. We have two cases. In the first case, this sequence is finite, with some maximal element
$(\tau _k, n)$
. Then the condition
$(\tau _k, n)$
is an extension of
$(\sigma , n)$
forcing
$\Phi ^{G \oplus Z}_e(k+1)\uparrow $
. In the second case, the sequence is infinite. Since
${\mathcal {C}}$
has no computable member, and by closure of
${\mathcal {C}}$
, there must be some
$k \in \omega $
such that
$\Phi ^{\tau _k \oplus Z}_e {\upharpoonright } k \downarrow = \rho $
for some
$\rho \in \omega ^{<\omega }$
such that
${\mathcal {C}} \cap [\rho ] = \emptyset $
. Again, the condition
$(\tau _k, n)$
is an extension of
$(\sigma , n)$
forcing
$\Phi ^{G \oplus Z}_e$
not to be a member of
${\mathcal {C}}$
. This completes the proof of the lemma. ⊣
Lemma 2.9. Fix a set Z and
$C \nleq _T Z$
. There is a set G and a function
$f \colon \omega \to \omega $
such that f is
$G \oplus Z$
-hyperimmune, but
$Z \oplus G \oplus C$
computes a function dominating f.
Proof. By Lemma 2.8 applies to Z and the closed set
$\{C\}$
, there is G such that C is
$\Delta ^{0}_{2}(Z \oplus G)$
but
$C \nleq _T Z \oplus G$
. Fix a
$\Delta ^{0}_{2}$
approximation
$C(x,s)$
for C relative to
$Z \oplus G$
. Let
$f \colon \omega \to \omega $
be the modulus for C with respect to this approximation, i.e.,
$f(n)$
is the least
$s \geqslant n$
such that for all
$m \leqslant n$
,
$C(m,s) = C(m)$
. Note that
$Z \oplus G \oplus C \geqslant _T f$
, and any function dominating f, together with
$Z \oplus G$
, computes C: given g dominating f, compute
$C(n)$
by finding
$s^* \geqslant n$
such that for all s with
$s^* \leqslant s \leqslant g(s^*)$
,
$C(m,s) = C(m,s^*)$
; then
$C(n) = C(n,s^*)$
(see [Reference Groszek and Slaman10]).
Then f is
$G \oplus Z$
-hyperimmune, as any function dominating f would together with
$Z \oplus G$
compute C, and
$C \nleq _T Z \oplus G$
. But
$Z \oplus G \oplus C$
computes a function dominating f, namely f itself. ⊣
Corollary 2.10. Preservation of 1 hyperimmunity implies avoidance of 1 cone.
Proof. Suppose that
${\mathsf {P}}$
admits preservation of one hyperimmunity. Fix a set Z, a
$C \nleq _T Z$
, and a Z-computable instance X of
${\mathsf {P}}$
. By Lemma 2.9, there is a set G and a function
$f \colon \omega \to \omega $
such that f is
$G \oplus Z$
-hyperimmune but
$Z \oplus G \oplus C$
computes a function dominating f. Since
${\mathsf {P}}$
admits preservation of one hyperimmunity, there is a solution Y to X such that f is
$Z \oplus G \oplus Y$
-hyperimmune. Then
$C \nleq _T Z \oplus Y$
. ⊣
Here again, we can consider unrelativized versions of these notions of preservation, and prove that they do not coincide.
Theorem 2.11. There is a problem which admits nonrelativized avoidance of one cone, but not non-relativized preservation of one hyperimmunity.
Proof. Fix a
$\Delta ^1_1$
-random set
$A = \{x_0 < x_1 < \cdots \}$
, and let
$p_A$
denote its principal function, that is, the function defined by
$p_A(n) = x_n$
. Let
${\mathsf {P}}$
be the problem with unique instance
$\emptyset $
. A solution is any function dominating
$p_A$
. Since A is
$\Delta ^1_1$
-random, it is in particular hyperimmune [Reference Kautz16], so
${\mathsf {P}}$
does not admit unrelativized preservation of one hyperimmunity. We now prove that
${\mathsf {P}}$
admits nonrelativized avoidance of one cone. Fix a noncomputable set C, and the unique instance
$\emptyset $
of
${\mathsf {P}}$
. If C is hyperarithmetical, then since any
$\Delta ^1_1$
-random forms a minimal pair with any nonzero hyperarithmetical set [Reference Downey, Nies, Weber and Yu7],
$C \not \leqslant _T A$
, and therefore
$p_A$
is a
${\mathsf {P}}$
-solution to
$\emptyset $
such that
$C \not \leqslant _T p_A$
. If C is nonhyperarithmetical, then it does not admit a modulus [Reference Groszek and Slaman10], and therefore there is a function
$f : \omega \to \omega $
dominating
$p_A$
such that
$C \not \leqslant _T f$
. In either case, there is a
${\mathsf {P}}$
-solution f to
$\emptyset $
such that
$C \not \leqslant _T f$
. ⊣
The other direction does not hold either. A Turing degree
$\boldsymbol {d}$
is hyperimmune-free if it does not bound a hyperimmune function. There exists nonzero hyperimmune-free degrees.
Theorem 2.12. There is a problem which admits nonrelativized preservation of one hyperimmunity, but not nonrelativized avoidance of one cone.
Proof. Fix a set A of nonzero hyperimmune-free degree. Let
${\mathsf {P}}$
be the problem with unique instance
$\emptyset $
. The unique solution is the set A. Clearly,
${\mathsf {P}}$
does not admit nonrelativized avoidance of one cone. On the other hand,
${\mathsf {P}}$
admits nonrelativized preservation of one hyperimmunity. Indeed, fix a hyperimmune function f and the unique
${\mathsf {P}}$
-instance
$\emptyset $
. Since every A-computable function is dominated by a computable function, f is hyperimmune relative to A. ⊣
Again, the fact that the relativized version of these notions coincide shows that every hyperimmune function behaves, relative to some degree, like a modulus for a noncomputable set. On the other hand, no nonzero hyperimmune-free degree remains hyperimmune-free relative to every degree not above it. Indeed, the failure of the former property could be used to relativize the proof of Theorem 2.11, and the failure of the latter would enable us to relativize Theorem 2.12.
2.3 Preserving 1 non-
$\Sigma ^{0}_{1}$
definition
We now prove our last equivalence of Theorem 2.1, namely, preserving 1 non-
$\Sigma ^{0}_{1}$
definition is equivalent to avoiding one cone. The first direction is immediate, given the fact that if a set is noncomputable, then either it or its complement is not
$\Sigma ^{0}_{1}$
.
Lemma 2.13. Preservation of one non-
$\Sigma ^{0}_{1}$
definition implies avoidance of one cone.
Proof. Suppose that
${\mathsf {P}}$
admits preservation of one non-
$\Sigma ^{0}_{1}$
definition. Fix A and Z such that
$A \nleq _T Z$
, and let X be a Z-computable instance of
${\mathsf {P}}$
. We may assume that A is not
$\Sigma ^{0}_{1}(Z)$
, otherwise we take the complement of A. Then there is a solution Y to X such that A is not
$\Sigma ^{0}_{1}(Z \oplus Y)$
, and so
$A \nleq _T Z \oplus Y$
. ⊣
The reversal requires several lemmas which will also be useful in a latter section, when studying the hierarchy of preservation of k non-
$\Sigma ^{0}_{1}$
definitions. In particular, these lemmas imply the non-existence of some particular enumeration degrees, namely, totally cototal degrees.
We review some basic facts about the enumeration degrees. Enumeration reducibility was introduced by Friedberg and Rogers in 1959 [Reference Friedberg and Rogers9]. This reducibility mimics Turing reducibility, except that only positive information about sets is used or required. Formally, for
$A,B\subseteq \omega $
, we say that A is enumeration reducible to B (and write
$A\le _e B$
) if there is a uniform way to compute an enumeration of A from an enumeration of B; equivalently, if there is a c.e. set
$\Phi $
of pairs of finite sets (called an enumeration functional, or operator) such that
$A = \Phi (B) = \bigcup \big \{ a \,:\, (\exists b\subseteq B) \,\, (a,b)\in \Phi \big \}$
. There is a natural embedding of the Turing degrees into the enumeration degrees, by mapping
$\deg _T(A)$
to
$\deg _e (A\oplus \overline A)$
. The latter is called the total degree of A, and the degrees thus obtained are called total degrees (the terminology originates in viewing the enumeration degrees as the degrees of partial functions, by identifying a partial function with its graph. The total degrees are then the degrees containing total functions).
For our purposes, enumeration reducibility is useful since a set A is c.e. relative to B if and only if
$A\le _e B\oplus \overline B$
, that is, if the enumeration degree of A lies below the total degree of B. Thus, avoiding making A c.e. is the same as avoiding the upper cone above A in the enumeration degrees (but considering the degree doing the avoiding as total). Relevant here is Selman’s theorem [Reference Selman30], that states that every enumeration degree is determined by the total degrees above it; indeed, every enumeration degree is the infimum of two total degrees. It follows that enumeration reducibility is equivalent to its non-uniform version:
$A\le _e B$
if and only if every enumeration of B computes an enumeration of A.
Now, the plan for showing the converse of Lemma 2.13 is as follows. We suppose that a problem
${\mathsf {P}}$
avoids upper cones in the Turing degrees. Ignoring the parameter Z for notational simplicity for the moment, let X be a computable instance of
${\mathsf {P}}$
and let A be a set which is not c.e. We would like to “change the basis” to a parameter G which makes enumerating A equivalent to computing it; that is, some G such that A is co-c.e. in G, but not c.e. in G (so that it is not G-computable). We cannot always do this; but we can show that there is some
$B\le _e A$
, still not c.e., such that
$B\in \Pi ^{0}_{1}(G){\smallsetminus } \Sigma ^{0}_{1}(G)$
. This suffices, because avoiding the enumeration cone above B will clearly imply avoiding the cone above A.
Now it turns out that the existence of such G is equivelnt to B being not cototal. A set B is cototal if
$B\le _e \overline B$
. The reason for this terminology is a characterisation of the total degrees as those enumeration degrees containing sets C satisfying
$\overline C \le _e C$
. Every total degree is cototal (contains a cototal set) but not vice-versa. The cototal degrees were investigated extensively by Miller, Soskova and their co-authors [Reference Andrews1, Reference Miller and Soskova21]. Now, the existence of some G making a set B co-c.e. but not c.e. is equivalent to the existence of some total degree above
$\deg _e \overline B$
which is not above
$\deg _e B$
. By Selman’s theorem mentioned above, this is equivalent to
$B\nleq _e \overline B$
, i.e., to B not being cototal. Thus, our main technical result required for the proof is that every nonzero enumeration degree bounds a set which is not cototal. We say that A is totally cototal if every
$B\le _e A$
is a cototal set. We show:
Proposition 2.14. There is no totally cototal degree above
$\boldsymbol {0}_e$
.
To show Proposition 2.14, we use th notion of semi-computable sets. A set X is semi-computable if there is a total computable function
$g : [\omega ]^2 \to \omega $
such that for every
$\{x,y\} \in [\omega ]^2$
, if
$\{x,y\} \cap X \neq \emptyset $
then
$g(\{x,y\}) \in \{x,y\} \cap X$
. This notion was introduced by Jockusch in his Ph.D. thesis [Reference Jockusch15]; he studied them in relation to Dekker’s retraceable sets [Reference Dekker and Myhill6]. In [Reference Jockusch14], Jockusch showed that a set X is semi-computable if and only if it is an initial segment of some computable linear ordering. The relevance of semi-computable sets to our proof is the following:
Lemma 2.15. (Arslanov, Cooper, Kalimullin [Reference Arslanov, Kalimullin and Kuper2])
Let A be a semi-computable set. Then:
-
1. A and
$\overline {A}$
form a minimal pair in the enumeration degrees. -
2. A is not cototal unless A is c.e.
Proof. For (1), suppose that
$B \leqslant _e A$
and
$B \leqslant _e \overline {A}$
via enumeration operators
$\Phi $
and
$\Psi $
respectively. Let f be the function that witnesses that A is semi-computable. Then to see that B is c.e., note that
$$ \begin{align*} B &= \{x : \exists \text{ finite sets } F,G \text{ such that } x \in \Phi^F, x \in \Psi^G, \\ & \qquad \text{ and for all } a \in F \text{ and } b \in G, f(a,b) = a\}. \end{align*} $$
For (2), suppose that A is cototal. Then
$\overline {A} \geqslant _e A$
, and so since A and
$\overline {A}$
form a minimal pair in the enumeration degrees,
$A \equiv _e \varnothing $
.⊣
Thus, it suffices to show that if A is non-c.e., then there is some
$C\le _e A$
which is semi-computable. This was independently proved by Kihara, Ng and Pauly [Reference Kihara, Ng and Pauly17, Lemma 7.12]. As we will shortly see, the main case is when A is
$\Delta ^{0}_{2}$
. We prove:
Lemma 2.16. For every
$A \in \Delta ^{0}_{2} - \Sigma ^{0}_{1}$
, there is
$B \le _e A$
such that:
-
1.
$B \in \Delta ^{0}_{2}$
; and -
2. B is neither left c.e. nor right c.e.
Here we identify the set B with the real with binary representation
$0.B$
.
Given this lemma, we proceed as follows.
Corollary 2.17. For any set
$A \in \Delta ^{0}_{2} - \Sigma ^{0}_{1}$
, there is
$C \le _e A$
which is semi-computable and immune.
Proof. The argument is due to Jockusch [Reference Jockusch14]. Fix
$B \le _e A$
as from Lemma 2.16. Since B is
$\Delta ^{0}_{2}$
, fix a computable sequence of rationals
$(q_e)_{e \in \omega }$
converging to B. Let
$C = \{ i : q_i < B\} = \{ i : q_i \le B\}$
(since B is noncomputable). Then
$C \le _e B$
, and C is semi-computable via the induced ordering from
${\mathbb {Q}}$
. C is infinite because B is not right c.e., and it is immune because B is not left c.e. ⊣
We remark that for our purposes now, we do not need the immunity of C; this will be used in a later section.
Proof of Theorem 2.14. The argument is due to Mariya Soskova (private communication).
Suppose A is a totally cototal set of non-zero degree. First we argue that A is
$\Delta ^{0}_{2}$
. Let
$L_{A}$
be the set of all finite binary strings lexicographically to the left of or along A. Then
$L_{A} \leqslant _e A$
. Moreover,
$L_{A}$
is semi-computable: let
$f(x,y)$
be the left-most of x and y. Since
$L_{A} \leqslant _e A$
, it is cototal, but by Lemma 2.15
$L_{A}$
cannot be cototal unless it is c.e. We also have that
$L_A \geqslant _T A$
so A is
$\Delta ^{0}_{2}$
.
Since A is
$\Delta ^{0}_{2}$
and not
$\Sigma ^{0}_{1}$
, by Corollary 2.17 there is
$C \leqslant _e A$
which is semi-computable and immune, hence not
$\Sigma ^{0}_{1}$
. By assumption, C must be cototal, and so
$C \leqslant _e \overline {C}$
. But as mentioned above, each semi-computable set forms a minimal pair in the enumeration degrees with its complement. This gives a contradiction. ⊣
Corollary 2.18. Avoidance of one cone implies preservation of one non-
$\Sigma ^{0}_{1}$
definition.
Proof. Suppose a problem
${\mathsf {P}}$
admits avoidance of one cone. Fix a set Z, a non-
$\Sigma ^{0}_{1}(Z)$
set A and a Z-computable instance X of
${\mathsf {P}}$
. By Proposition 2.14 relativized to Z, there is a non-
$\Sigma ^{0}_{1}(Z)$
set
$C \leqslant _e A \oplus Z \oplus \overline {Z}$
which is not Z-cototal. In other words, there is an enumeration G of
$\overline {C}$
such that C is not
$\Sigma ^{0}_{1}(Z \oplus G)$
. Since
${\mathsf {P}}$
admits avoidance of one cone, there is a
${\mathsf {P}}$
-solution Y to X such that
$C \not \leqslant _T Z \oplus G \oplus Y$
. We claim that A is not
$\Sigma ^{0}_{1}(Z \oplus Y)$
. Indeed, otherwise C would be
$\Sigma ^{0}_{1}(Z \oplus Y)$
, and therefore
$C \leqslant _T Z \oplus G \oplus Y$
, contradiction. ⊣
It remains to prove Lemma 2.16.
Proof of Theorem 2.16. Fix a computable sequence
$(A_s)_{s \in \omega }$
converging to A. We simultaneously construct B and an enumeration functional
$\Phi $
with
$B = \Phi (A)$
. Our functional
$\Phi $
will have the property that for any x, there will be at most one axiom
$(x, F) \in \Phi $
with
$F \neq \emptyset $
; from this it follows that
$B \in \Delta ^{0}_{2}$
(using
$A \in \Delta ^{0}_{2}$
).
We interpret c.e. sets as subsets of the rationals. We have the following requirements to meet, for all
$e \in \omega $
:
-
R e :
$B \neq \sup (W_e)$
; -
Q e :
$B \neq \inf (W_e)$
.
Our construction will be a finite injury construction, and so a strategy for a given requirement will act under the assumption that no higher priority strategy will ever act.
Strategy for requirement
$Q_e$
:
-
1. Choose a large x, and keep both x and
$x+1$
out of B (no axioms for x or
$x+1$
are to be enumerated into
$\Phi $
). -
2. Wait for a stage s and a
$y \in W_{e,s}$
with
$y - B_s < 2^{-(x+2)}$
. -
3. Declare
$x \in B$
and enumerate the axiom
$(x, \emptyset )$
into
$\Phi $
.
Strategy for requirement
$R_e$
:
We construct a c.e. set
$D_e$
as we work. This set is reset whenever the strategy is initialized.
Our strategy will have modules for each
$k \in \omega $
. We will begin by running the
$0$
-module. For each k, the k-module may run the
$(k+1)$
-module, but we will argue that this iteration will eventually terminate.
Here is the k-module:
-
1. Choose a large
$x_k$
. Let the current stage be
$s_k$
. Declare
$x, x+1 \in B$
, enumerating the axioms
$(x, F_k)$
and
$(x+1, F_k)$
into
$\Phi $
, where
$F_k$
is the positive information from
$A_{s_k}{\! \upharpoonright _{k}}$
. -
2. Wait for a stage s at which one of the following happens:
-
(a)
$A_s{\! \upharpoonright _{k}} \neq A_{s_k}{\! \upharpoonright _{k}}$
. In this case, enumerate axioms
$(x, \emptyset )$
and
$(x+1, \emptyset )$
into
$\Phi $
, declaring
$x, x+1 \in B$
. Return to Step (1). -
(b) There is a
$y \in W_{e,s}$
with
$B_s - y < 2^{-(x+2)}$
. In this case, enumerate all of
$F_k$
into
$D_e$
and proceed to Step (3).
-
-
3. Wait for a stage s with
$F_k \not \subseteq A_s$
. While waiting, run the
$(k+1)$
-module. -
4. Freeze the action of any running j-modules for
$j> k$
. -
5. Wait for a stage s with
$F_k \subseteq A_s$
. When found, return to Step (3), resuming the action of any frozen j-modules.
Full construction: Whenever a strategy moves between steps, we initialize all lower priority strategies. When a
$Q_e$
-strategy is initialized, we enumerate
$(x, \emptyset )$
and
$(x+1, \emptyset )$
into
$\Phi $
for the strategy’s chosen x, declaring them both to be in B. Similarly, when an
$R_e$
-strategy is initialized, we enumerate
$(x_j, \emptyset )$
and
$(x_j+1, \emptyset )$
into
$\Phi $
for all appropriate j.
Verification:
Claim 1. For each e:
-
(a) The
$Q_e$
-strategy eventually waits forever at Step (2) or Step (3). -
(b) There is some k such that for all
$j < k$
, the j-module of the
$R_e$
-strategy eventually waits forever at Step (3), and the k-module eventually waits forever at Step (2) or Step (5).⊣
Proof. By simultaneous induction. (a)
$_e$
is immediate.
For (b)
$_e$
, by induction there is a final time when the
$R_e$
-strategy is intialized. Let
$s_k$
be the stage at which
$x_k$
is chosen after this final initialization, and suppose towards contradiction that
$s_k$
is defined for all
$k < \omega $
. Since
$(A_s)_{s \in \omega }$
converges to A, the k-module cannot move between Steps (3) and (5) infinitely often, so it must be that each k-module eventually waits forever at Step (3).
But then each
$F_k \subseteq A$
, and
$D_e = \bigcup _k F_k$
. Further, for any
$z \in A$
, there is a sufficiently large k such that
$z \in A_{s_k} = F_k$
, so
$D = A$
, contrary to A not being c.e. ⊣
It follows that each strategy is initialized only finitely many times.
Claim 2. Each
$Q_e$
-strategy meets its requirement.
Proof. Let t be the final stage at which the
$Q_e$
-strategy is initialized, so no higher priority strategy acts at any stage
$s> t$
. Consider the x chosen by this strategy. Since lower priority strategies choose their elements large,
$B_s{\! \upharpoonright _{x}} = B_t{\! \upharpoonright _{x}}$
for all
$s> t$
. Observe that by construction,
$x+1 \not \in B$
.
If the strategy waits forever at Step (2), then certainly
$B \neq \inf (W_e)$
.
Suppose the strategy moves from Step (2) to Step (3) at stage
$t_1> t$
. Since
$x, x+1 \not \in B_{t_1}$
, but
$x \in B$
, we have
$$ \begin{align*} \inf(W_e) &< B_{t_1} + 2^{-(x+2)}\\ &\leqslant (B{\! \upharpoonright_{x}}){\widehat{\phantom{\alpha}}} 0^{\infty} + 2^{-(x+2)} + 2^{-(x+2)}\\ &= (B{\! \upharpoonright_{x}}){\widehat{\phantom{\alpha}}} 1{\widehat{\phantom{\alpha}}} 0^{\infty} - 2^{-(x+1)} + 2^{-(x+2)} + 2^{-(x+2)}\\ &= (B{\! \upharpoonright_{x}}){\widehat{\phantom{\alpha}}}1{\widehat{\phantom{\alpha}}}0^{\infty}\\ &\leqslant B. \end{align*} $$
Thus
$B \neq \inf (W_e)$
.⊣
Claim 3. Each
$R_e$
-strategy meets its requirement.
Proof. Let k be such that the k-module of the strategy eventually waits forever at Step (2) or Step (5), and let
$s_j$
for
$j \le k$
be the stages at which the
$x_j$
is chosen after the strategy’s final initialization. If it is defined, let
$s_{k+1}$
be the same for
$x_{k+1}$
. Note that for
$j < k$
,
$s_{j+1}$
is also the stage at which the j-module first reaches Step (3). Similarly,
$s_{k+1}$
is defined precisely if the k-module reaches Step (3), in which case
$s_{k+1}$
is the first stage at which this happens.
By construction, for any
$y \in (x_{j}+1, x_{j+1})$
, one of the following must occur:
-
(i)
$(y, \emptyset )$
has been enumerated into
$\Phi $
by stage
$s_{j+1}$
; or -
(ii) For all finite sets F,
$(y, F) \not \in \Phi $
.
To see this: since
$x_j$
is chosen large and no higher priority strategy acts after stage
$s_0$
, no such y can be chosen by a higher priority strategy. Also, no such y can be chosen by a lower priority strategy after stage
$s_{j+1}$
, since elements are always chosen large. If y is chosen by a lower priority strategy before stage
$s_{j+1}$
, then at stage
$s_{j+1}$
we initialize that strategy and enumerate
$(y,\emptyset )$
into
$\Phi $
, if we have not already done so. If y is chosen by no strategy, then no axioms for y are ever enumerated into
$\Phi $
.
Note also that for all
$j < k$
,
$x_j \in B$
, and indeed
$x_j \in B_s$
for any stage at which the k-module is running (not frozen). So
$B_{s_k}{\! {\upharpoonright }_{{x}_{k}}}= B_s{\! {\upharpoonright }_{{x}_{k}}}$
for any
$s> s_k$
at which the k-module is not frozen. The argument is now identical to the argument for the
$Q_e$
-strategy.⊣
This completes the proof.
Note that the implication from preservation of one non-
$\Sigma ^{0}_{1}$
definition to avoidance of one cone is natural enough to hold again when considering their nonrelativized counterparts. However, these notions are not equivalent.
Lemma 2.19. (Folklore) Let A be a semi-computable set. The following are equivalent:
-
(a) A is immune.
-
(b) A is hyperimmune.
Either implies (c) that A is not c.e.
Proof.
$(\mathrm{b}) \rightarrow (\mathrm{a})$
is immediate as every hyperimmune set is immune.
$(\mathrm{a}) \rightarrow (\mathrm{c})$
is also immediate as every infinite c.e. set contains an infinite computable subset. Last, we prove
$(\mathrm{a}) \rightarrow (\mathrm{b})$
. Suppose A is not hyperimmune. Then there is a computable strong array
$F_0, F_1, \dots $
such that for every
$n \in \omega $
,
$F_n \cap A \neq \emptyset $
. By [Reference Jockusch14, Theorem 4.1], any semi-computable set A is the initial segment of a computable linear order
${\mathcal {L}}$
. Then
$\{ \min _{{\mathcal {L}}} F_n : n \in \omega \}$
is an infinite c.e. subset of A and contains an infinite computable subset. ⊣
Theorem 2.20. There is a problem which admits nonrelativized avoidance of one cone, but not nonrelativized preservation of one non-
$\Sigma ^{0}_{1}$
definition.
Proof. Fix a computable linear ordering
${\mathcal {L}}$
of order type
$\omega +\omega ^{*}$
with no infinite computable ascending or descending sequence. Such a linear order exists by Tennenbaum (see [Reference Rosenstein28]). Let A be the
$\omega $
part of this linear order. In particular, A and
$\overline {A}$
are both
$\Delta ^{0}_{2}$
, semi-computable and immune. By Lemma 2.19, A and
$\overline {A}$
are both non-
$\Sigma ^{0}_{1}$
and hyperimmune. Let
${\mathsf {P}}$
be the problem with unique instance
$\emptyset $
. A solution is an infinite subset of A.
For any solution
$Y \subseteq A$
,
$A = \{ x : \exists y \in Y\, x \le _{{\mathcal {L}}} y\}$
, so
$A \in \Sigma ^{0}_{1}(Y)$
, and thus
${\mathsf {P}}$
does not admit nonrelativized preservation of 1 non-
$\Sigma ^{0}_{1}$
definition. We claim that
${\mathsf {P}}$
admits nonrelativized avoidance of 1 cone. Fix a noncomputable set C and the unique
${\mathsf {P}}$
-instance
$\emptyset $
. If C is not
$\Delta ^{0}_{2}$
, then A is a
${\mathsf {P}}$
-solution to
$\emptyset $
such that
$C \not \leqslant _T A$
. If C is
$\Delta ^{0}_{2}$
, then since
$\overline {A}$
is hyperimmune and
$\Delta ^{0}_{2}$
, by Proposition 4.4 of [Reference Hirschfeldt11], there is an infinite subset
$H \subseteq A$
such that
$C \not \leqslant _T H$
. In both cases, there is a
${\mathsf {Q}}$
-solution Y to
$\emptyset $
such that
$C \not \leqslant _T Y$
. ⊣
3 The hierarchy of preservations
Given a coloring
$f : [\omega ]^n \to k$
, an infinite set
$H \subseteq \omega $
is f-homogeneous if f uses only one color on
$[H]^n$
. Ramsey’s theorem asserts the existence of homogeneous sets for every k-coloring of
$[\omega ]^n$
. Jockusch [Reference Jockusch12] proved that whenever
$n \geqslant 3$
, there is a computable coloring
$f : [\omega ]^n \to 2$
such that every f-homogeneous set computes
$\emptyset '$
. However, Wang [Reference Wang34] proved the surprising result that this is no longer the case when we relax the f-homogeneity condition to allow more colors.
Definition 3.1. For every
$n, \ell \geqslant 2$
, let
$ \operatorname {\mathsf{RT}}^n_{<\infty , \ell }$
be the problem whose instances are functions
$f : [\omega ]^n \to k$
for some
$k \in \omega $
. An
$ \operatorname {\mathsf{RT}}^n_{<\infty , \ell }$
-solution to f is an infinite set
$H \subseteq \omega $
such that
$|f[H]^n| \leqslant \ell $
.
Wang [Reference Wang34] proved that for every
$n \geqslant 1$
, there is some
$\ell $
such that
$ \operatorname {\mathsf{RT}}^n_{<\infty , \ell }$
admits cone avoidance. Patey [Reference Patey24, Reference Patey25] proved the following theorem, which shows in particular that the hierarchies of preservation of
$\ell $
hyperimmunities and
$\ell $
non-
$\Sigma ^{0}_{1}$
definitions is strictly increasing.
Theorem 3.2. For every
$\ell \geqslant 1$
,
$ \operatorname {\mathsf{RT}}^2_{<\infty , \ell }$
admits preservation of
$\ell $
but not
$\ell +1$
non-
$\Sigma ^{0}_{1}$
definitions, and of
$\ell $
but not
$\ell +1$
hyperimmunities.
Let us sketch the proof that
$ \operatorname {\mathsf{RT}}^n_{<\infty , \ell }$
does not admit preservation of
$\ell +1$
hyperimmunities. Given
$\ell \geqslant 1$
, build a
$\Delta ^{0}_{2} (\ell +1)$
-partition
$A_0 \sqcup \dots \sqcup A_{\ell } = \omega $
such that for every
$i \le \ell $
,
$\overline {A}_i$
is hyperimmune. By Schoenfield’s limit lemma, there is a computable coloring
$f : [\omega ]^2 \to \ell +1$
such that for every
$x \in \omega $
,
$\lim _y f(x, y)$
exists, and
$x \in A_{\lim _y f(x, y)}$
. We claim that for every
$ \operatorname {\mathsf{RT}}^2_{<\infty , \ell }$
-solution H to f, there is some
$i \leqslant \ell $
such that
$\overline {A}_i$
is not H-hyperimmune. Since
$|f[H]^2| \leqslant \ell $
, there is some
$i \leqslant \ell $
such that
$i \not \in f[H]^2$
. In particular,
$H \subseteq \overline {A}_i$
, so the principal function of H dominates the principal function of
$\overline {A}_i$
, which proves that
$\overline {A}_i$
is not H-hyperimmune.
3.1 The hyperimmunities and non-
$\Sigma ^{0}_{1}$
definitions hierarchies
We now prove that the two hierarchies of preservation of hyperimmunities and of non-
$\Sigma ^{0}_{1}$
definitions coincide.
Lemma 3.3. For every
$k \leqslant \omega $
and every Z, for any nondecreasing functions
$(f_i)_{i < k}$
which are not Z-computably dominated, there is a G and sets
$(A_i)_{i < k}$
such that none of the
$A_i$
is c.e. relative to
$Z\oplus G$
, but for any i and any function h dominating
$f_i$
,
$A_i$
is c.e. relative to
$Z\oplus G \oplus h$
.
Proof. We construct
$(G_i)_{i < k}$
which will be
$\Pi ^{0}_{2}$
-approximations to the
$A_i$
, with each
$f_i$
a
$\Sigma ^{0}_{1}$
-modulus for
$G_i$
. That is,
$$ \begin{align*} x \in A_i \iff \exists^{\infty} s\, [(x,s) \in G_i] \iff \exists s> f_i(x)\, [(x,s) \in G_i]. \end{align*} $$
Then
$G = \bigoplus _{i < k} G_i$
. It is now clear that for any h dominating
$f_i$
,
$A_i$
is c.e. relative to
$Z\oplus G \oplus h$
. It remains only to show that none of the
$A_i$
is c.e. relative to
$Z\oplus G$
.
We will construct our
$G_i$
generically. Conditions in our notion of forcing are pairs of sequences
$( (\sigma _i)_{i < k}, (N_i)_{i < k})$
, with:
-
•
$\sigma _i \in 2^{<\omega \times \omega }$
; -
•
$N_i \in [\omega ]^{<\omega }$
; -
• If
$x \in N_i$
,
$s> f_i(x)$
and
$(x, s) \in \operatorname {\mathrm {dom}}(\sigma _i)$
, then
$\sigma _i(x,s) = 0$
; and -
• All but finitely many of the
$\sigma _i$
and
$N_i$
are empty.
Of course the last requirement only matters when
$k = \omega $
. Extension is defined elementwise.
Note that for a sufficiently generic filter F,
$x \in A_i^F \iff x \not \in N_i^F$
.
Note also that for any
$s> f_j(x)$
and any condition
$\rho = ( (\sigma _i)_{i < k}, (N_i)_{i < k})$
, if
$\sigma _j(x,s) = 1$
then
$\rho \Vdash [x \not \in N_i]$
. So for a sufficiently generic filter F, each
$A_i^F$
is infinite.
For a c.e. operator W and a
$j < k$
, we must show that for a sufficiently generic G,
$A_j \neq W^{Z\oplus G}$
. Given a condition
$\rho = ((\sigma _i)_{i < k}, (N_i)_{i < k})$
, we define a function g. For each n, search Z-effectively for a
$(\tau _i)_{i< k}$
and a
$y \in \omega $
such that:
-
•
$y> n$
; -
• For each
$i < k$
,
$\tau _i$
extends
$\sigma _i$
; -
• For all
$i < k$
,
$x \in N_i$
and
$s> f_i(x)$
, we have
$\tau _i(x,s) \neq 1$
; and -
•
$y \in W^{Z\oplus (\tau _i)_{i < k}}$
.
Note that this search is Z-effective, albeit nonuniformly in the information
$\{(i, x, f_i(x)) : x \in N_i\}$
. For the first y and
$(\tau _i)_{i < k}$
found, define
$g(n)$
to be the largest s with
$\tau _j(y,s) = 1$
, or
$g(n) = 0$
if no such s exists.
If some
$g(n)$
is undefined, then no extension of
$\rho $
forces any
$y> n$
into
$W^{Z\oplus G}$
, and so
$W^{Z\oplus G}$
is finite. But we already said that
$A_j$
is infinite, and so
$\rho \Vdash [A_j \neq W_j^{Z\oplus G}]$
.
If g is total, then since g is Z-computable, there must be an n with
$g(n) < f_j(n)$
. Let
$(\tau _i)_{i < k}$
and y be the witnesses to the definition of
$g(n)$
. Define
$M_i = N_i$
for
$i \neq j$
, and define
$M_j = N_j \cup \{ y \}$
. Since
$f_j(n) \le f_j(y)$
, there is no
$s> f_j(y)$
with
$\tau _j(y, s) = 1$
, so
$\hat {\rho } = ( (\tau _i)_{i < k}, (M_i)_{i < k})$
is a condition extending
$\rho $
, and
$\hat {\rho } \Vdash [y \in W^{Z\oplus G} - A_j]$
.⊣
Corollary 3.4. For any
$k \le \omega $
, preservation of k non-
$\Sigma ^{0}_{1}$
definitions implies preservation of k hyperimmunities.
Proof. Suppose a problem
${\mathsf {P}}$
admits preservation of k non-
$\Sigma ^{0}_{1}$
definitions. Fix a set Z,
$k Z$
-hyperimmune functions
$f_0, f_1, \dots , f_{k-1}$
and a Z-computable
${\mathsf {P}}$
-instance X. By Lemma 3.3, there is a G and sets
$(A_i)_{i < k}$
such that none of the
$A_i$
is
$\Sigma ^{0}_{1}(Z\oplus G)$
, but for any i and any function h dominating
$f_i$
,
$A_i$
is
$\Sigma ^{0}_{1}(Z\oplus G \oplus h)$
. Since
${\mathsf {P}}$
admits preservation of k non-
$\Sigma ^{0}_{1}$
definitions, there is a
${\mathsf {P}}$
-solution Y to X such that for every
$i < k$
,
$A_i$
is not
$\Sigma ^{0}_{1}(Z \oplus G \oplus Y)$
. In particular, for every
$i < k$
,
$f_i$
is
$Z \oplus G \oplus Y$
-hyperimmune. ⊣
Lemma 3.5. For every set Z, every countable sequence of non-Z-c.e. sets
$B_0, B_1, \dots $
, and every set A, there is a set G such that
$B_i$
is not
$Z \oplus G$
-c.e. for every
$i \in \omega $
and A is
$\Delta ^{0}_{2}(G)$
.
Proof. Consider again the notion of forcing whose conditions are pairs
$(\sigma , n)$
, where
$\sigma $
is a partial function
$\subseteq \omega ^2 \to 2$
with finite support, and
$n \in \omega $
. A condition
$(\tau , m)$
extends
$(\sigma , n)$
if
$\tau \supseteq \sigma $
,
$m \geqslant n$
, and for every
$(x, y) \in \operatorname {\mathrm {dom}} \tau {\smallsetminus } \operatorname {\mathrm {dom}} \sigma $
such that
$x < n$
,
$\tau (x, y) = A(x)$
. Any sufficiently generic filter yields a stable function whose limit is A.
We now prove that the set of conditions forcing
$W_e^{G \oplus Z} \neq B_i$
is dense. Given a condition
$(\sigma , n)$
, let
$U = \{ x : \exists (\tau , n) \leqslant (\sigma , n)\, x \in W_e^{\tau \oplus Z}\}$
. The set U is
$\Sigma ^{0}_{1}(Z)$
, so
$B_i \Delta U \neq \emptyset $
. If there is some
$x \in B_i {\smallsetminus } U$
then the condition
$(\sigma , n)$
already forces
$x \not \in W_e^{G \oplus Z}$
are we are done. If there is some
$x \in U {\smallsetminus } B_i$
, then then condition
$(\tau , n) \leqslant (\sigma , n)$
such that
$x \in W_e^{\tau \oplus Z}$
is an extension forcing
$x \in W_e^{G \oplus Z}$
. In both cases, there is an extension forcing
$W_e^{G \oplus Z} \neq B_i$
. This completes the proof of the lemma. ⊣
Corollary 3.6. For any
$k \leqslant \omega $
, preservation of k hyperimmunities implies preservation of k non-
$\Sigma ^{0}_{1}$
definitions.
Proof. Suppose some problem
${\mathsf {P}}$
admits preservation of k hyperimmunites. Fix a set Z and k non-
$\Sigma ^{0}_{1}(Z)$
sets
$\langle A_i : i < k \rangle $
. By Lemma 3.5, there is a set G such that for every
$i < k$
,
$A_i$
is not
$\Sigma ^{0}_{1}(Z \oplus G)$
, but
$\bigoplus _{i < k} A_i$
is
$\Delta ^{0}_{2}(G)$
. By Corollary 2.17, there are semi-
$Z \oplus G$
-computable sets
$\langle B_i : i < k \rangle $
such that for every
$i < k$
,
$B_i \leqslant _e A_i \oplus Z \oplus G \oplus \overline {Z} \oplus \overline {G}$
and
$B_i$
is
$Z \oplus G$
-immune. By Lemma 2.19,
$B_i$
is
$Z \oplus G$
-hyperimmune. Since
${\mathsf {P}}$
admits preservation of k hyperimmunites, there is a
${\mathsf {P}}$
-solution Y to X such that
$B_i$
is
$Z \oplus G \oplus Y$
-hyperimmune for every
$i < k$
. We claim that
$A_i$
is not
$\Sigma ^{0}_{1}(Z \oplus G \oplus Y)$
. Indeed, otherwise,
$B_i$
would be
$\Sigma ^{0}_{1}(Z \oplus G \oplus Y)$
, and by Lemma 2.19,
$B_i$
would not be
$Z \oplus G \oplus Y$
-hyperimmune. ⊣
3.2 The hierarchy of constant-bound traces of closed sets
One can define a similar hierarchy for avoidance of constant-bound traces of closed sets. By the hyperimmune-free basis theorem,
$ \operatorname {\mathsf{WKL}}$
admits preservation of
$\omega $
hyperimmunities (hence of
$\omega $
non-
$\Sigma ^{0}_{1}$
definitions as well). On the other hand,
$ \operatorname {\mathsf{WKL}}$
does not admit avoidance of constant-bound traces of even one closed set. Indeed, letting
${\mathcal {C}}$
be the effectively closed set of all the completions of Peano arithmetics, every constant-bound trace of
${\mathcal {C}}$
computes a member of
${\mathcal {C}}$
. This separates the hierarchies of preservation of hyperimmunities and non-
$\Sigma ^{0}_{1}$
definitions from the hierarchy of constant-bound traces of closed sets.
On the other direction, avoidance of constant-bound traces for closed sets does not imply the preservation of more hyperimmunities than closed sets, as shows the following theorem.
Theorem 3.7. For every
$\ell \geqslant 1$
, there is a problem which admits avoidance of constant-bound traces for
$\ell $
closed sets, but not preservation of
$\ell +1$
hyperimmunities.
Proof. Patey [Reference Patey22] proved that
$ \operatorname {\mathsf{RT}}^2_{<\infty , \ell }$
admits avoidance of constant-bound traces of
$\ell $
closed sets. On the other hand, we already argued that
$ \operatorname {\mathsf{RT}}^2_{<\infty , \ell }$
does not admit preservation of
$\ell +1$
hyperimmunities. ⊣
We finish this section by proving that avoidance of constant-bound traces for k closed sets implies preservation of k hyperimmunities.
Lemma 3.8. For any
$k \le \omega $
, for any
$Z \in 2^{\omega }$
and
$(f_i)_{i < k}$
such that each
$f_i$
is Z-hyperimmune, there is a
$G \in 2^{\omega }$
and closed sets
$(C_i)_{i < k}$
in Cantor space such that each
$C_i$
has no constant-bound
$(Z\oplus G)$
-trace, but for any function h dominating
$f_i$
, there is a
$(Z\oplus G\oplus h)$
-computable element of
$C_i$
.
Proof. We construct sets
$(E_i)_{i < k}$
and
$(F_i)_{i < k}$
, which will be
$\Sigma ^{0}_{2}$
approximations to sets
$A_i$
and
$B_i$
, respectively, and such that each
$f_i$
is a
$\Pi ^{0}_{1}$
-modulus for
$A_i$
and
$B_i$
. That is,
$$ \begin{align*} x \in A_i \iff \exists s\, \forall t> s\, [(x, t) \in E_i] \iff \forall t > f_i(x)\, [(x,t) \in E_i] \end{align*} $$
and
$$ \begin{align*} x \in B_i \iff \exists s\, \forall t> s\, [(x, t) \in F_i] \iff \forall t > f_i(x)\, [(x,t) \in F_i]. \end{align*} $$
Then
$G = \bigoplus _{i < k} E_i \oplus \bigoplus _{i < k} F_i$
.
Our sets will have the property that
$A_i \cap B_i = \emptyset $
. Each
$C_i$
will then be the set of separators of
$A_i$
and
$B_i$
. That is,
$C_i = \{ X \in 2^{\omega } : A_i \subseteq X \wedge B_i \subseteq \overline {X}\}$
. Observe that if h dominates
$f_i$
, then
$A_i$
and
$B_i$
are
$\Pi ^{0}_{1}(h\oplus G)$
, and so
$h\oplus G$
computes an element of
$C_i$
. It remains only to show that none of the
$C_i$
has a constant-bound trace relative to
$Z\oplus G$
.
We will construct our
$E_i$
and
$F_i$
simultaneously generically. Conditions in our notion of forcing are tuples of sequences
$( (\sigma _i)_{i < k}, (N_i)_{i < k}, (\tau _i)_{i < k}, (M_i)_{i < k})$
with:
-
•
$\sigma _i, \tau _i \in 2^{<\omega \times \omega }$
; -
•
$N_i, M_i \in [\omega ]^{<\omega }$
; -
• If
$x \in N_i$
,
$s> f_i(x)$
and
$(x,s) \in \operatorname {\mathrm {dom}}(\sigma _i)$
, then
$\sigma _i(x,s) = 1$
; -
• If
$x \in M_i$
,
$s> f_i(x)$
and
$(x,s) \in \operatorname {\mathrm {dom}}(\tau _i)$
, then
$\tau _i(x,s) = 1$
; -
•
$N_i \cap M_i = \emptyset $
; and -
• All but finitely many of the
$\sigma _i, \tau _i, N_i$
and
$M_i$
are empty.
Extension is defined elementwise.
Note that for a sufficiently generic filter,
$A_i = N_i$
and
$B_i = M_i$
.
For a
$b \in \omega $
, a
$j < k$
and a Turing functional
$\Phi $
, we must show that for a sufficiently generically chosen G,
$\Phi ^{Z\oplus G}$
is not a b-bounded trace of
$C_j$
. We may assume that for all oracles X and all
$n \in \omega $
,
$\Phi ^X(n)$
is a subset of
$2^n$
of size at most b. Given a condition
$\rho = ( (\sigma _i)_{i \,<\, k}, (N_i)_{i \,<\, k}, (\tau _i)_{i \,<\, k}, (M_i)_{i \,<\, k})$
, we define a function g. On input n, we search for
$(\hat {\sigma }_i)_{i \,<\, k}$
and
$(\hat {\tau }_i)_{i \,<\, k}$
such that:
-
• For each i,
$\hat {\sigma }_i$
extends
$\sigma _i$
, and
$\hat {\tau }_i$
extends
$\tau _i$
; -
• For all
$i < k$
,
$x \in N_i$
and
$s> f_i(x)$
with
$(x,s) \in \operatorname {\mathrm {dom}}(\hat {\sigma }_i)$
, we have
$\hat {\sigma }_i(x,s) = 1$
; -
• For all
$i < k$
,
$x \in M_i$
and
$s> f_i(x)$
with
$(x,s) \in \operatorname {\mathrm {dom}}(\hat {\tau }_i)$
, we have
$\hat {\tau }_i(x,s) = 1$
; and -
•
$\Phi ^{Z\oplus (\hat {\sigma }_i)_{i \,<\, k} \oplus (\hat {\tau }_i)_{i \,<\, k}}(n+b){\downarrow }$
.
Note that this search is Z-effective, albeit nonuniformly in the information
$\{(i, x, f_i(x)) : x \in N_i \cup M_i\}$
. For the first
$(\hat {\sigma }_i)_{i \,<\, k}$
and
$(\hat {\tau }_i)_{i \,<\, k}$
found, define
$g(n)$
to be the largest s with
$\hat {\sigma }_j(n+a, s) = 0$
or
$\hat {\tau }_j(n+a,s) = 0$
for some
$a < b$
, or
$g(n) = 0$
if no such s exists.
If some
$g(n)$
is undefined, then no extension of
$\rho $
forces
$\Phi ^{Z\oplus G}(n+b){\downarrow }$
, and so
$\rho $
forces that
$\Phi ^{Z\oplus G}$
is partial, and thus not a b-bounded trace.
If g is total, then since it is Z-computable, there must be an n with
$g(n) < f_j(n)$
. Let
$(\hat {\sigma }_i)_{i \,<\, k}$
and
$(\hat {\tau }_i)_{i \,<\, k}$
be the witnesses to the definition of
$g(n)$
. Let
$\Phi ^{Z\oplus (\hat {\sigma }_i)_{i \,<\, k} \oplus (\hat {\tau }_i)_{i \,<\, k}}(n+b) = \{ \pi _0, \dots , \pi _{b-1}\}$
. Define
$\hat {N}_i = N_i$
and
$\hat {M}_i = M_i$
for
$i \neq j$
. Define
$\hat {N}_j = N_j \cup \{ a < b : \pi _a(n+a) = 0 \}$
and
$\hat {M}_j = M_j \cup \{ a < b : \pi _a(n+a) = 1\}$
. Since
$f_j(n)> g(n)$
, there is no
$s> f_j$
and
$a < b$
with
$\hat {\sigma }_j(n+a,s) = 0$
or
$\hat {\tau }_j(n+a,s) = 0$
, so
$\hat {\rho } = ( (\hat {\sigma }_i)_{i \,<\, k}, (\hat {N}_i)_{i \,<\, k}, (\hat {\tau }_i)_{i \,<\, k}, (\hat {M}_i)_{i \,<\, k})$
is a condition extending
$\rho $
, and
$\hat {\rho }$
forces that no element of
$\Phi ^{Z\oplus G}(n)$
is extendible to an element of
$C_j$
.⊣
Corollary 3.9. For all
$k \le \omega $
, avoidance of constant-bound traces for k closed sets implies preserving k hyperimmunities.
Proof. Suppose a problem
${\mathsf {P}}$
admits avoidance of constant-bound traces for k closed sets. Fix a set Z, a collection of Z-hyperimmune functions
$(f_i)_{i \,<\, k}$
and a Z-computable
${\mathsf {P}}$
-instance X. By Lemma 3.8, there is a G and closed sets
$({\mathcal {C}}_i)_{i \,<\, k}$
in the Cantor space such that none of the
${\mathcal {C}}_i$
has a constant-bound
$Z \oplus G$
-trace, but for any function h dominating
$f_i$
, there is a
$Z \oplus G \oplus h$
-computable element of
${\mathcal {C}}_i$
. Since
${\mathsf {P}}$
admits avoidance of constant-bound traces for k closed sets, there is a
${\mathsf {P}}$
-solution Y to X such that for every
$i < k$
,
${\mathcal {C}}_i$
has no constant-bound
$Z \oplus G \oplus Y$
-trace. In particular, for every
$i < k$
,
$f_i$
is
$Z \oplus G \oplus Y$
-hyperimmune. ⊣
4 Immunity and closed sets
This last section is devoted to the study of two notions of preservation whose hierarchies collapse, namely, preservation of immunities and avoidance of closed sets. These notions are strictly stronger than the notions of preservation we considered so far, and are not known to be distinct.
Lemma 4.1. Fix a set Z and
$A_0,A_1,\ldots $
all Z-immune. There is a set G which is Z-immune and such that for every n,
$G[n] =^* A_n$
.
Proof. Write
$\omega ^{[n]} = \{{\langle } n,x {\rangle } : x \in \omega \}$
. We will define
$G = \bigoplus _{n \in \omega } G_n$
where
$G_n =^* A_n$
. We want G to be Z-immune, so that no Z-computable set is a subset of G. Since each
$A_n$
is immune, no Z-computable infinite set which is a subset of
$\omega ^{[0]} \cup \cdots \cup \omega ^{[n]}$
can be a subset of G.
Let
$B_0,B_1,\ldots $
be a list of the infinite Z-computable sets which intersect infinitely many of the
$\omega ^{[n]}$
. Suppose that we have defined
$a_0 < a_1 < \cdots < a_k$
and
$G_0,\ldots ,G_k$
such that for each
$i \leqslant k$
,
$B_i \cap \omega ^{[a_k]} \nsubseteq {\langle } k , G_k {\rangle }$
. Then for some
$a_{k+1}> a_k$
,
$B_{k+1}$
intersects
$\omega ^{[a_{k+1}]}$
, say
${\langle } a_{k+1},n {\rangle } \in B_{k+1}$
. Set
$G_{i} = A_{i}$
for
$a_k < i < a_{k+1}$
, and
$G_{a_{k+1}} = A_{a_{k+1}} - \{n\}$
. So no
$B_i$
is a subset of G, and hence
$G = \bigoplus _{n \in \omega } G_n$
is Z-immune. ⊣
Theorem 4.2. Let
${\mathsf {P}}$
be a problem. Then the following are equivalent:
-
1.
${\mathsf {P}}$
admits preservation of one immunity. -
2.
${\mathsf {P}}$
admits preservation of
$\omega $
immunities.
Proof. (2)
$\Rightarrow $
(1) is obvious. For (1)
$\Rightarrow $
(2): Let Z be a set and X a Z-computable instance of
${\mathsf {P}}$
. Suppose that
$A_1,A_2,\ldots $
are Z-immune. Let G be as in Lemma 4.1: G is Z-immune, and
$G[i] =^* A_i$
for all i. Then there is a solution Y to X such that G is
$Z \oplus Y$
-immune. If, for some i,
$A_i$
was not
$Z \oplus Y$
-immune, then
$Z \oplus Y$
would compute an infinite subset of
$A_i$
, and hence of G (since
$G[i] =^* A_i$
). This cannot happen as G is
$Z \oplus Y$
-immune. ⊣
Lemma 4.3. Preservation of
$\omega $
immunities implies avoidance of constant-bound traces for
$\omega $
closed sets.
Proof. Suppose a problem
${\mathsf {P}}$
admits preservation of
$\omega $
immunities. Fix a set Z and a countable collection of closed sets
${\mathcal {C}}_0, {\mathcal {C}}_1, \dots \subseteq 2^{\omega }$
with no Z-computable constant-bound trace. For every
$n, k \in \omega $
, let
$A_{n,k}$
be the set of all finite coded k-sets F of binary strings such that every string in F has the same length, and such that
$[F] \cap {\mathcal {C}}_n \neq \emptyset $
. Every infinite subset of
$A_{n,k}$
computes a k-trace of
${\mathcal {C}}_n$
, so
$A_{n,k}$
is Z-immune. Conversely, every k-trace of
${\mathcal {C}}_n$
computes an infinite subset of
$A_{n,k}$
. Since
${\mathsf {P}}$
admits preservation of
$\omega $
immunities, there is a
${\mathsf {P}}$
-solution Y to X such that for every
$n, k$
,
$A_{n,k}$
is
$Z \oplus Y$
-immune. In particular, for every
$n \in \omega $
,
${\mathcal {C}}_n$
has no
$Z \oplus Y$
-computable constant-bound trace. ⊣
Lemma 4.4. Fix a set Z and a closed set
${\mathcal {C}} \subseteq \omega ^{\omega }$
in the Baire space with no Z-computable member. There exists a closed set
${\mathcal {D}} \subseteq 3^{\omega }$
with no Z-computable member, and such that every member of
${\mathcal {C}}$
computes a member of
${\mathcal {D}}$
.
Proof. Fix Z and
${\mathcal {C}}$
. Let
$T \subseteq 2^{<\omega }$
be a Z-computable infinite tree with no Z-computable infinite path. Given some
$P \in {\mathcal {C}}$
, let
$\hat {P} \in 3^{\omega }$
be defined by
$\sigma _02\sigma _12\sigma _22\sigma _32\dots $
, where for every
$n \in \omega $
,
$\sigma _n$
is the left-most string in T of length
$P(n)$
. Let
${\mathcal {D}}$
be the closure of
$\{ \hat {P} : P \in {\mathcal {C}} \}$
. Note that for any
$X \in {\mathcal {D}} {\smallsetminus } \{ \hat {P} : P \in {\mathcal {C}} \}$
,
$X = \sigma {\widehat {\phantom {\alpha }}} Y$
for some
$\sigma \in 3^{<\omega }$
and
$Y \in [T]$
, and that neither
$\{ \hat {P} : P \in {\mathcal {C}} \}$
nor
$[T]$
has Z-computable members. Therefore
${\mathcal {D}}$
has no Z-computable member. Moreover any
$P \in {\mathcal {C}}$
computes
$\hat {P} \in {\mathcal {D}}$
. ⊣
Corollary 4.5. Avoidance of one closed set in the Cantor space implies avoidance of
$\omega $
closed sets in the Baire space.
Proof. Suppose a problem
${\mathsf {P}}$
admits avoidance of one closed set in the Cantor space. Fix a set Z, countably many closed sets in the Baire space
${\mathcal {C}}_0, {\mathcal {C}}_1, \dots \subseteq \omega ^{\omega }$
with no Z-computable member, and a Z-computable
${\mathsf {P}}$
-instance X. Let
${\mathcal {E}} = \{n^{\frown } P : P \in {\mathcal {C}}_n \}$
. In particular,
${\mathcal {E}}$
is a closed set with no Z-computable member. By Lemma 4.4, there is a closed set
${\mathcal {D}} \subseteq 3^{\omega }$
with no Z-computable member, and such that every member of
${\mathcal {E}}$
computes a member of
${\mathcal {D}}$
. Let
$\tilde {{\mathcal {D}}} \subseteq 2^{\omega }$
be the closed set obtained from
${\mathcal {D}}$
by fixing a binary coding of the ternary strings. In particular, any member of
${\mathcal {C}}_n$
computes a member of
$\tilde {{\mathcal {D}}}$
, and
$\tilde {{\mathcal {D}}}$
has no Z-computable members. Since
${\mathsf {P}}$
admits avoidance of one closed set in the Cantor space, there is a
${\mathsf {P}}$
-solution Y to X such that
$\tilde {{\mathcal {D}}}$
has no
$Z \oplus Y$
-computable member. In particular, for every
$n \in \omega $
,
${\mathcal {C}}_n$
has no
$Z \oplus Y$
-computable member. ⊣
We now prove that preservation of 1 immunity is strictly above the hierarchy of avoidance of constant-bound traces. Let
$ \operatorname {\mathsf{EM}}$
be the problem whose instances are colorings
$f : [\omega ]^2 \to 2$
. An
$ \operatorname {\mathsf{EM}}$
-solution to f is an infinite set
$H \subseteq \omega $
such that for every
$x < y < z \in H$
, and every
$i < 2$
, if
$f(x, y) = i$
and
$f(y, z) = i$
, then
$f(x, z) = i$
.
Theorem 4.6. There is a problem that admits avoidance of constant-bound traces for
$\omega $
closed sets but not preservation of one immunity.
Proof. Patey [Reference Patey22] proved that
$ \operatorname {\mathsf{EM}}$
admits avoidance of constant-bound traces for
$\omega $
closed sets. On the other hand, Rice [Reference Rice27] constructed a computable instance of
$ \operatorname {\mathsf{EM}}$
such that every solution computes a diagonally noncomputable function, while Patey [Reference Patey23] constructed a
$\Delta ^{0}_{2}$
immune set A such that every diagonally noncomputable function computes an infinite subset of A. This shows that
$ \operatorname {\mathsf{EM}}$
does not admit preservation of one immunity. ⊣
The following question is left open:
Question 4.7. Does preservation of one immunity implies avoidance of one closed set?
The combinatorics used to prove that a problem admits preservation of one immunity and avoidance of one closed set are very similar, which could be taken as an argument in favor of a positive answer.
