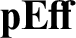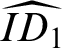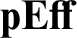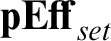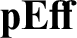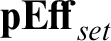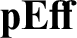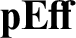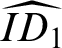1. Introduction
As reported in [Reference van Oosten24] Hyland’s paper “The Effective Topos” [Reference Hyland, Troelstra and van Dalen7] gave input to a whole new strand of research about realizability and its applications to logic, mathematics and computer science. Hyland applied the tripos-to-topos construction in [Reference Hyland, Johnstone and Pitts8] producing one of the first examples of elementary topos, denoted with
![]() ${{\mathbf {Eff} }}$
, that is not a Grothendieck topos. A characteristics of
${{\mathbf {Eff} }}$
, that is not a Grothendieck topos. A characteristics of
![]() ${{\mathbf {Eff} }}$
which attracted a lot of interest in logic is the fact that it provides a realizability interpretation of high-order logic extending Kleene realizability for intuitionistic arithmetic and hence it validates the Formal Church’s thesis (see [Reference van Oosten23]).
${{\mathbf {Eff} }}$
which attracted a lot of interest in logic is the fact that it provides a realizability interpretation of high-order logic extending Kleene realizability for intuitionistic arithmetic and hence it validates the Formal Church’s thesis (see [Reference van Oosten23]).
A predicative study of
![]() ${{\mathbf {Eff} }}$
had been already developed in the context of algebraic set theory by Van den Berg and Moerdijk (see [Reference van den Berg and Moerdijk22]) by taking Aczel’s CZF in [Reference Aczel and Rathjen1] as the set theory to be realized in their categorical structures.
${{\mathbf {Eff} }}$
had been already developed in the context of algebraic set theory by Van den Berg and Moerdijk (see [Reference van den Berg and Moerdijk22]) by taking Aczel’s CZF in [Reference Aczel and Rathjen1] as the set theory to be realized in their categorical structures.
The aim of this paper is to produce a strictly predicative version of
![]() ${{\mathbf {Eff} }}$
, called
${{\mathbf {Eff} }}$
, called
![]() ${\mathbf {pEff}}$
, which can be formalized in Feferman’s predicative theory of non-iterative fixpoints
${\mathbf {pEff}}$
, which can be formalized in Feferman’s predicative theory of non-iterative fixpoints
![]() ${{\widehat {ID_1}}}$
(see [Reference Feferman and Metakides5]) whose proof-theoretic strength is much lower than that of CZF. Our ultimate goal is to use
${{\widehat {ID_1}}}$
(see [Reference Feferman and Metakides5]) whose proof-theoretic strength is much lower than that of CZF. Our ultimate goal is to use
![]() ${\mathbf {pEff}}$
as the effective universe where to validate proofs done in the Minimalist Foundation in order to extract their computational contents.
${\mathbf {pEff}}$
as the effective universe where to validate proofs done in the Minimalist Foundation in order to extract their computational contents.
The Minimalist Foundation (
![]() ${\mathbf {MF}}$
) is a predicative foundation for constructive mathematics ideated in joint work of the first author with Sambin in [Reference Maietti, Sambin, Crosilla and Schuster19] and completed to a two-level system in [Reference Maietti9].
${\mathbf {MF}}$
) is a predicative foundation for constructive mathematics ideated in joint work of the first author with Sambin in [Reference Maietti, Sambin, Crosilla and Schuster19] and completed to a two-level system in [Reference Maietti9].
![]() ${\mathbf {MF}}$
is weaker than CZF (in terms of proof-theoretic strength) because it can be interpreted in Martin-Löf’s type theory with one universe [Reference Nordström, Petersson and Smith20] as shown in [Reference Maietti9], and directly also in
${\mathbf {MF}}$
is weaker than CZF (in terms of proof-theoretic strength) because it can be interpreted in Martin-Löf’s type theory with one universe [Reference Nordström, Petersson and Smith20] as shown in [Reference Maietti9], and directly also in
![]() ${{\widehat {ID_1}}}$
(see [Reference Maietti and Maschio12] and [Reference Maietti and Maschio13]).
${{\widehat {ID_1}}}$
(see [Reference Maietti and Maschio12] and [Reference Maietti and Maschio13]).
![]() ${\mathbf {MF}}$
was called minimalist in [Reference Maietti, Sambin, Crosilla and Schuster19] because it was intended to constitute a common core among the most relevant constructive and classical foundations. It consists of two levels with an interpretation of one into the other: an intensional level suitable as a base for a proof-assistant and for the extraction of computational contents from proofs, an extensional level formulated in a language close to that of ordinary mathematics, and an interpretation of the extensional level in the intensional one by means of a quotient completion (see [Reference Maietti9]). Both the intensional level and the extensional level of
${\mathbf {MF}}$
was called minimalist in [Reference Maietti, Sambin, Crosilla and Schuster19] because it was intended to constitute a common core among the most relevant constructive and classical foundations. It consists of two levels with an interpretation of one into the other: an intensional level suitable as a base for a proof-assistant and for the extraction of computational contents from proofs, an extensional level formulated in a language close to that of ordinary mathematics, and an interpretation of the extensional level in the intensional one by means of a quotient completion (see [Reference Maietti9]). Both the intensional level and the extensional level of
![]() ${\mathbf {MF}}$
consist of dependent type systems based on versions of Martin-Löf’s type theory.
${\mathbf {MF}}$
consist of dependent type systems based on versions of Martin-Löf’s type theory.
A key difference between
![]() ${\mathbf {MF}}$
and Martin-Löf’s type theories is that in
${\mathbf {MF}}$
and Martin-Löf’s type theories is that in
![]() ${\mathbf {MF}}$
propositions are defined in such a way that choice principles, including the axiom of unique choice, are no longer necessarily valid.
${\mathbf {MF}}$
propositions are defined in such a way that choice principles, including the axiom of unique choice, are no longer necessarily valid.
Moreover, there is an analogy between the two-level formal system of
![]() ${\mathbf {MF}}$
and the tripos-to-topos construction of a realizability topos: the role of the tripos is taken by the intensional level of
${\mathbf {MF}}$
and the tripos-to-topos construction of a realizability topos: the role of the tripos is taken by the intensional level of
![]() ${\mathbf {MF}}$
, the role of the realizability topos construction is taken by the quotient model used in [Reference Maietti9] to interpret the extensional level of
${\mathbf {MF}}$
, the role of the realizability topos construction is taken by the quotient model used in [Reference Maietti9] to interpret the extensional level of
![]() ${\mathbf {MF}}$
in its intensional one, and the internal language of a generic elementary topos corresponds to the extensional level of
${\mathbf {MF}}$
in its intensional one, and the internal language of a generic elementary topos corresponds to the extensional level of
![]() ${\mathbf {MF}}$
. The key difference between the tripos-to-topos construction and the construction of
${\mathbf {MF}}$
. The key difference between the tripos-to-topos construction and the construction of
![]() ${\mathbf {MF}}$
is that the quotient completion employed in
${\mathbf {MF}}$
is that the quotient completion employed in
![]() ${\mathbf {MF}}$
does not yield to an exact category. This quotient completion had been studied categorically in joint work of the first author with Rosolini in [Reference Maietti and Rosolini17], [Reference Maietti and Rosolini16] and [Reference Maietti, Rosolini, Probst and Schuster18] under the name of “elementary quotient completion of a Lawvere’s elementary doctrine”. Such a completion turned out to be a generalization of the well-known notion of exact completion on a lex category.
${\mathbf {MF}}$
does not yield to an exact category. This quotient completion had been studied categorically in joint work of the first author with Rosolini in [Reference Maietti and Rosolini17], [Reference Maietti and Rosolini16] and [Reference Maietti, Rosolini, Probst and Schuster18] under the name of “elementary quotient completion of a Lawvere’s elementary doctrine”. Such a completion turned out to be a generalization of the well-known notion of exact completion on a lex category.
Here we build a predicative variant of
![]() ${{\mathbf {Eff} }}$
, called
${{\mathbf {Eff} }}$
, called
![]() ${\mathbf {pEff}}$
, by applying the elementary quotient completion in [Reference Maietti and Rosolini17] to a Lawvere’s hyperdoctrine
${\mathbf {pEff}}$
, by applying the elementary quotient completion in [Reference Maietti and Rosolini17] to a Lawvere’s hyperdoctrine
 ${\overline {\mathbf {Prop}^{r}}}$
. The base category
${\overline {\mathbf {Prop}^{r}}}$
. The base category
![]() $\mathcal {C}_{r}$
of
$\mathcal {C}_{r}$
of
 ${\overline {\mathbf {Prop}^{r}}}$
is a predicative rendering of the subcategory of
${\overline {\mathbf {Prop}^{r}}}$
is a predicative rendering of the subcategory of
![]() ${{\mathbf {Eff} }}$
of recursive functions within
${{\mathbf {Eff} }}$
of recursive functions within
![]() ${{\widehat {ID_1}}}$
and the logical hyperdoctrine structure extends Kleene realizability interpretation of connectives and supports an interpretation (whilst with a pure combinatory non-categorical interpretation of
${{\widehat {ID_1}}}$
and the logical hyperdoctrine structure extends Kleene realizability interpretation of connectives and supports an interpretation (whilst with a pure combinatory non-categorical interpretation of
![]() $\lambda $
-abstraction) of the intensional level of MF extended with the Formal Church’s thesis and the full axiom of choice as in [Reference Ishihara, Maietti, Maschio and Streicher6]. Then, from results in [Reference Maietti9], it follows that
$\lambda $
-abstraction) of the intensional level of MF extended with the Formal Church’s thesis and the full axiom of choice as in [Reference Ishihara, Maietti, Maschio and Streicher6]. Then, from results in [Reference Maietti9], it follows that
![]() ${\mathbf {pEff}}$
validates the extensional level of MF.
${\mathbf {pEff}}$
validates the extensional level of MF.
![]() ${\mathbf {pEff}}$
can be seen as a predicative variant of
${\mathbf {pEff}}$
can be seen as a predicative variant of
![]() ${{\mathbf {Eff} }}$
for the following reasons. First, the construction of
${{\mathbf {Eff} }}$
for the following reasons. First, the construction of
![]() ${\mathbf {pEff}}$
is formalizable in the predicative theory
${\mathbf {pEff}}$
is formalizable in the predicative theory
![]() ${{\widehat {ID_1}}}$
. Second,
${{\widehat {ID_1}}}$
. Second,
![]() ${\mathbf {pEff}}$
is a list-arithmetic locally cartesian closed pretopos with a full subcategory
${\mathbf {pEff}}$
is a list-arithmetic locally cartesian closed pretopos with a full subcategory
![]() ${{\mathbf {pEff}_{set}}}$
of small objects having the same categorical structure which is preserved by the embedding in
${{\mathbf {pEff}_{set}}}$
of small objects having the same categorical structure which is preserved by the embedding in
![]() ${\mathbf {pEff}}$
; furthermore subobjects in
${\mathbf {pEff}}$
; furthermore subobjects in
![]() ${{\mathbf {pEff}_{set}}}$
are classified by a non-small object in
${{\mathbf {pEff}_{set}}}$
are classified by a non-small object in
![]() ${\mathbf {pEff}}$
. Third, the elementary quotient completion construction used to build
${\mathbf {pEff}}$
. Third, the elementary quotient completion construction used to build
![]() ${\mathbf {pEff}}$
coincides with the exact completion on the lex base category
${\mathbf {pEff}}$
coincides with the exact completion on the lex base category
![]() $\mathcal {C}_{r} $
of the doctrine
$\mathcal {C}_{r} $
of the doctrine
 ${\overline {\mathbf {Prop}^{r}}}$
. Finally,
${\overline {\mathbf {Prop}^{r}}}$
. Finally,
![]() ${{\mathbf {pEff} }}$
turns out to be a predicative rendering of a full subcategory of
${{\mathbf {pEff} }}$
turns out to be a predicative rendering of a full subcategory of
![]() ${{\mathbf {Eff} }}$
which validates the Formal Church’s thesis.
${{\mathbf {Eff} }}$
which validates the Formal Church’s thesis.
2. Categorical preliminaries
We just recall some categorical definitions we will use later.
Definition 2.1. A first-order hyperdoctrine is a functor
![]() $\mathbf {P}:\mathcal {C}^{op}\rightarrow \mathbf {preHeyt}$
from a finite product category
$\mathbf {P}:\mathcal {C}^{op}\rightarrow \mathbf {preHeyt}$
from a finite product category
![]() $\mathcal {C}$
to the category of Heyting prealgebras (see, e.g., [Reference van Oosten25]) such that, for every f in
$\mathcal {C}$
to the category of Heyting prealgebras (see, e.g., [Reference van Oosten25]) such that, for every f in
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
![]() $\mathbf {P}_{f}$
has left and right adjoints
$\mathbf {P}_{f}$
has left and right adjoints
![]() $\exists _{f}$
and
$\exists _{f}$
and
![]() $\forall _{f}$
satisfying the Beck–Chevalley condition (see [Reference van Oosten25]). For every object I of
$\forall _{f}$
satisfying the Beck–Chevalley condition (see [Reference van Oosten25]). For every object I of
![]() $\mathbb {C}$
, we use
$\mathbb {C}$
, we use
![]() $\sqsubseteq _{I}$
to denote the preorder relation in
$\sqsubseteq _{I}$
to denote the preorder relation in
![]() $\mathbf {P}(I)$
.
$\mathbf {P}(I)$
.
We say that
![]() $\mathbf {P}$
has weak comprehensions if for every object A of
$\mathbf {P}$
has weak comprehensions if for every object A of
![]() $\mathcal {C}$
and for every
$\mathcal {C}$
and for every
![]() $p\in \mathbf {P}(A)$
, there exists an arrow
$p\in \mathbf {P}(A)$
, there exists an arrow
![]() $\mathsf {cmp}:\mathsf {Cmp}(p)\rightarrow A$
in
$\mathsf {cmp}:\mathsf {Cmp}(p)\rightarrow A$
in
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
 $\top \sqsubseteq _{\mathsf {Cmp}(p)} \mathbf {P}_{\mathsf {cmp}}(p)$
and for every arrow
$\top \sqsubseteq _{\mathsf {Cmp}(p)} \mathbf {P}_{\mathsf {cmp}}(p)$
and for every arrow
![]() $f:B\rightarrow A$
such that
$f:B\rightarrow A$
such that
![]() $\top \sqsubseteq _{B} \mathbf {P}_{f}(p)$
, there exists an arrow
$\top \sqsubseteq _{B} \mathbf {P}_{f}(p)$
, there exists an arrow
![]() $f':B\rightarrow \mathsf {Cmp}(p)$
such that
$f':B\rightarrow \mathsf {Cmp}(p)$
such that
![]() $\mathsf {cmp}\circ f'=f$
.
$\mathsf {cmp}\circ f'=f$
.
Definition 2.2. Let Pord be the category of preorders and Pos be the category of partially ordered sets. If
![]() $\mathbf {C}:\mathcal {C}^{op}\rightarrow \mathbf {Cat}$
is a functor, then its preorder reflection
$\mathbf {C}:\mathcal {C}^{op}\rightarrow \mathbf {Cat}$
is a functor, then its preorder reflection
![]() $\mathbf {P}[\mathbf {C}]:\mathcal {C}^{op}\rightarrow \mathbf {Pord}$
is the functor whose fibres are the preorder reflections of the fibres of
$\mathbf {P}[\mathbf {C}]:\mathcal {C}^{op}\rightarrow \mathbf {Pord}$
is the functor whose fibres are the preorder reflections of the fibres of
![]() $\mathbf {C}$
(and for which P[C](f) is determined by C(f) for every arrow f of
$\mathbf {C}$
(and for which P[C](f) is determined by C(f) for every arrow f of
![]() $\mathcal{C}$
), while its posetal reflection
$\mathcal{C}$
), while its posetal reflection
![]() $\mathbf {PR}[\mathbf {C}]:\mathcal {C}^{op}\rightarrow \mathbf {Pos}$
is the functor whose fibres are the posetal reflections of those of
$\mathbf {PR}[\mathbf {C}]:\mathcal {C}^{op}\rightarrow \mathbf {Pos}$
is the functor whose fibres are the posetal reflections of those of
![]() $\mathbf {C}$
(and for which PR[C](f) is determined by C(f) for every arrow f of
$\mathbf {C}$
(and for which PR[C](f) is determined by C(f) for every arrow f of
![]() $\mathcal{C}$
). The posetal reflection produces a functor also when applied to a pseudofunctor C.
$\mathcal{C}$
). The posetal reflection produces a functor also when applied to a pseudofunctor C.
Definition 2.3. If
![]() $\mathcal {C}$
is a finitely complete category, the doctrine of its weak subobjects
$\mathcal {C}$
is a finitely complete category, the doctrine of its weak subobjects
![]() $\mathbf {wSub}_{\mathcal {C}}$
is the posetal reflection of the slice pseudofunctor.
$\mathbf {wSub}_{\mathcal {C}}$
is the posetal reflection of the slice pseudofunctor.
3. Feferman’s weak theory of inductive definitions
 ${{\widehat {ID_1}}}$
${{\widehat {ID_1}}}$
We give here a brief presentation of Feferman’s theory
![]() ${{\widehat {ID_1}}}$
([Reference Feferman and Metakides5]). Let us consider the language of second-order arithmetic given by countably many individual and set variables, a constant
${{\widehat {ID_1}}}$
([Reference Feferman and Metakides5]). Let us consider the language of second-order arithmetic given by countably many individual and set variables, a constant
![]() $0$
, a unary successor functional symbol
$0$
, a unary successor functional symbol
![]() $succ$
, an n-ary functional symbol for every n-ary (definition of a) primitive recursive function, the equality predicate
$succ$
, an n-ary functional symbol for every n-ary (definition of a) primitive recursive function, the equality predicate
![]() $=$
between individuals, the membership predicate
$=$
between individuals, the membership predicate
![]() $\epsilon $
between individuals and sets, connectives
$\epsilon $
between individuals and sets, connectives
![]() $\wedge , \vee , \rightarrow , \neg $
and individual and set quantifiers. The occurrence of the set variable X in
$\wedge , \vee , \rightarrow , \neg $
and individual and set quantifiers. The occurrence of the set variable X in
![]() $t\,\epsilon \, X$
is positive, while an occurrence of X in a nonatomic formula
$t\,\epsilon \, X$
is positive, while an occurrence of X in a nonatomic formula
![]() $\varphi $
with no set quantifiers is positive (negative resp.) if one of the following holds:
$\varphi $
with no set quantifiers is positive (negative resp.) if one of the following holds:
![]() $\varphi $
is
$\varphi $
is
![]() $\psi \wedge \rho $
or
$\psi \wedge \rho $
or
![]() $\psi \vee \rho $
and the occurrence is positive (neg.) in
$\psi \vee \rho $
and the occurrence is positive (neg.) in
![]() $\psi $
or in
$\psi $
or in
![]() $\rho $
;
$\rho $
;
![]() $\varphi $
is
$\varphi $
is
![]() $\psi \rightarrow \rho $
and the occurrence is positive (neg.) in
$\psi \rightarrow \rho $
and the occurrence is positive (neg.) in
![]() $\rho $
or negative (pos.) in
$\rho $
or negative (pos.) in
![]() $\psi $
;
$\psi $
;
![]() $\varphi $
is
$\varphi $
is
![]() $\neg \psi $
and the occurrence is negative (pos.) in
$\neg \psi $
and the occurrence is negative (pos.) in
![]() $\psi $
;
$\psi $
;
![]() $\varphi $
is
$\varphi $
is
![]() $\exists x\, \psi $
or
$\exists x\, \psi $
or
![]() $\forall x\,\psi $
and the occurrence is positive (neg.) in
$\forall x\,\psi $
and the occurrence is positive (neg.) in
![]() $\psi $
. A second-order formula
$\psi $
. A second-order formula
![]() $\varphi $
is admissible if it does not contain set quantifiers and it has at most one free individual variable x and one free set variable X of which all occurrences are positive.
$\varphi $
is admissible if it does not contain set quantifiers and it has at most one free individual variable x and one free set variable X of which all occurrences are positive.
![]() ${{\widehat {ID_1}}}$
is a first-order classical theory with equality containing
${{\widehat {ID_1}}}$
is a first-order classical theory with equality containing
![]() $0$
,
$0$
,
![]() $succ$
, the functional symbols for the (definitions of) primitive recursive functions and a unary predicate symbol
$succ$
, the functional symbols for the (definitions of) primitive recursive functions and a unary predicate symbol
![]() $P_{\varphi }$
for every admissible second-order formula
$P_{\varphi }$
for every admissible second-order formula
![]() $\varphi (x,X)$
. As usual,
$\varphi (x,X)$
. As usual,
![]() $\bot $
is the formula
$\bot $
is the formula
![]() $0=succ(0)$
.
$0=succ(0)$
.
The axioms of
![]() ${{\widehat {ID_1}}}$
include those of Peano arithmetic (including defining equations for primitive recursive functions) plus the induction principle for every formula of
${{\widehat {ID_1}}}$
include those of Peano arithmetic (including defining equations for primitive recursive functions) plus the induction principle for every formula of
![]() ${{\widehat {ID_1}}}$
and a fixpoint schema:
${{\widehat {ID_1}}}$
and a fixpoint schema:
![]() $P_{\varphi }(x)\leftrightarrow \varphi [P_{\varphi }/X]$
for every admissible second-order formula
$P_{\varphi }(x)\leftrightarrow \varphi [P_{\varphi }/X]$
for every admissible second-order formula
![]() $\varphi $
, where
$\varphi $
, where
![]() $\varphi [P_{\varphi }/X]$
is the result of substituting in
$\varphi [P_{\varphi }/X]$
is the result of substituting in
![]() $\varphi $
all the subformulas of the form
$\varphi $
all the subformulas of the form
![]() $t\,\epsilon \, X$
with
$t\,\epsilon \, X$
with
![]() $P_{\varphi }(t)$
.
$P_{\varphi }(t)$
.
3.1. Notation of recursive functions
In
![]() ${{\widehat {ID_1}}}$
one can encode Kleene’s application
${{\widehat {ID_1}}}$
one can encode Kleene’s application
![]() $\{x\}(y)$
via Kleene’s predicate
$\{x\}(y)$
via Kleene’s predicate
![]() $T(x,y,z)$
and primitive recursive function
$T(x,y,z)$
and primitive recursive function
![]() $U(z)$
: for every formula
$U(z)$
: for every formula
![]() $P(z)$
,
$P(z)$
,
![]() $P(\{x\}(y))$
means
$P(\{x\}(y))$
means
![]() $\exists z\,(T(x,y,z)\wedge P(U(z)))$
. We define
$\exists z\,(T(x,y,z)\wedge P(U(z)))$
. We define
![]() $\{t\}(\,)$
as t and
$\{t\}(\,)$
as t and
![]() $\{t\}(s_{1},...,s_{n+1})$
as
$\{t\}(s_{1},...,s_{n+1})$
as
![]() $\{\{t\}(s_{1},...,s_{n})\}(s_{n+1})$
. In
$\{\{t\}(s_{1},...,s_{n})\}(s_{n+1})$
. In
![]() ${{\widehat {ID_1}}}$
one can also encode pairs of natural numbers with natural numbers via a bijective primitive recursive function
${{\widehat {ID_1}}}$
one can also encode pairs of natural numbers with natural numbers via a bijective primitive recursive function
![]() $pair$
with primitive recursive projections
$pair$
with primitive recursive projections
![]() $p_{1}$
,
$p_{1}$
,
![]() $p_{2}$
represented by numerals
$p_{2}$
represented by numerals
![]() $\mathbf {p}_{1},\mathbf {p}_{2}, \mathbf {pair}$
such that
$\mathbf {p}_{1},\mathbf {p}_{2}, \mathbf {pair}$
such that
![]() $pair(x,y)=\{\mathbf {pair}\}(x,y)$
and
$pair(x,y)=\{\mathbf {pair}\}(x,y)$
and
![]() $p_{i}(x)=\{\mathbf {p}_{i}\}(x)$
(
$p_{i}(x)=\{\mathbf {p}_{i}\}(x)$
(
![]() $i=1,2$
) in
$i=1,2$
) in
![]() ${{\widehat {ID_1}}}$
. Moreover we encode finite lists of natural numbers with natural numbers in a surjective way such that
${{\widehat {ID_1}}}$
. Moreover we encode finite lists of natural numbers with natural numbers in a surjective way such that
![]() $0$
encodes the empty list, the concatenation function is primitive recursive and it is represented by a numeral
$0$
encodes the empty list, the concatenation function is primitive recursive and it is represented by a numeral
![]() $\mathbf{cnc}$
, the length function
$\mathbf{cnc}$
, the length function
![]() $lh$
is primitive recursive, the component function
$lh$
is primitive recursive, the component function
![]() $(x,j)\mapsto (x)_j$
which sends each natural number x, seen as a list of natural numbers, to its
$(x,j)\mapsto (x)_j$
which sends each natural number x, seen as a list of natural numbers, to its
![]() $j$
-component if
$j$
-component if
![]() $j < lh(x)$
or to
$j < lh(x)$
or to
![]() $0$
otherwise, is primitive recursive, and there is a numeral
$0$
otherwise, is primitive recursive, and there is a numeral
![]() $\mathbf{listrec}$
representing the list recursor.
$\mathbf{listrec}$
representing the list recursor.
The successor function can be represented by a numeral
![]() $\mathbf {succ}$
and the natural numbers recursor by a numeral
$\mathbf {succ}$
and the natural numbers recursor by a numeral
![]() $\mathbf {rec}$
. In
$\mathbf {rec}$
. In
![]() ${{\widehat {ID_1}}}$
one can also define
${{\widehat {ID_1}}}$
one can also define
![]() $\lambda $
-astraction
$\lambda $
-astraction
![]() $\Lambda x.t$
of terms built with Kleene brackets, variables and numerals as in any partial combinatory algebra.
$\Lambda x.t$
of terms built with Kleene brackets, variables and numerals as in any partial combinatory algebra.
4. The Kleene effective p-tripos
4.1. The category
 $\mathcal {C}_r$
of realized collections
$\mathcal {C}_r$
of realized collections
Here we define the category
![]() $\mathcal {C}_r$
of realized collections which is a rendering of the subcategory of recursive functions of
$\mathcal {C}_r$
of realized collections which is a rendering of the subcategory of recursive functions of
![]() ${{\mathbf {Eff} }}$
(see [Reference Robinson and Rosolini21]) in
${{\mathbf {Eff} }}$
(see [Reference Robinson and Rosolini21]) in
![]() ${{\widehat {ID_1}}}$
. Then, we will describe its categorical structure. In order to prove that
${{\widehat {ID_1}}}$
. Then, we will describe its categorical structure. In order to prove that
![]() $\mathcal {C}_{r}$
is weakly locally cartesian closed in a straightforward way, we will introduce an indexed category of realized collections over it.
$\mathcal {C}_{r}$
is weakly locally cartesian closed in a straightforward way, we will introduce an indexed category of realized collections over it.
Definition 4.1. A realized collection (or simply a class)
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() ${{\widehat {ID_1}}}$
is a formal expression
${{\widehat {ID_1}}}$
is a formal expression
![]() $\{x|\,\varphi _{\mathsf {A}}(x)\}$
where
$\{x|\,\varphi _{\mathsf {A}}(x)\}$
where
![]() $\varphi _{\mathsf {A}}(x)$
is a formula of
$\varphi _{\mathsf {A}}(x)$
is a formula of
![]() ${{\widehat {ID_1}}}$
with at most x as free variable. We write
${{\widehat {ID_1}}}$
with at most x as free variable. We write
![]() $x\,\varepsilon \, \mathsf {A}$
as an abbreviation for
$x\,\varepsilon \, \mathsf {A}$
as an abbreviation for
![]() $\varphi _{\mathsf {A}}(x)$
. Classes with provably equivalent membership relations in
$\varphi _{\mathsf {A}}(x)$
. Classes with provably equivalent membership relations in
![]() ${{\widehat {ID_1}}}$
are identified. An operation between classes of
${{\widehat {ID_1}}}$
are identified. An operation between classes of
![]() ${{\widehat {ID_1}}}$
from
${{\widehat {ID_1}}}$
from
![]() $\mathsf {A}$
to
$\mathsf {A}$
to
![]() $\mathsf {B}$
is an equivalence class
$\mathsf {B}$
is an equivalence class
![]() $[\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}$
of numerals with
$[\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}$
of numerals with
![]() $x\,\varepsilon \,\mathsf {A}\vdash \{\mathbf {n}\}(x)\,\varepsilon \,\mathsf {B}$
in
$x\,\varepsilon \,\mathsf {A}\vdash \{\mathbf {n}\}(x)\,\varepsilon \,\mathsf {B}$
in
![]() ${{\widehat {ID_1}}}$
. For such
${{\widehat {ID_1}}}$
. For such
![]() $\mathbf {n}$
and
$\mathbf {n}$
and
![]() $\mathbf {m}$
we define
$\mathbf {m}$
we define
![]() $\mathbf {n}\approx _{\mathsf {A},\mathsf {B}} \mathbf {m}$
as
$\mathbf {n}\approx _{\mathsf {A},\mathsf {B}} \mathbf {m}$
as
![]() $x\,\varepsilon \,\mathsf {A}\vdash \{\mathbf {n}\}(x)=\{\mathbf {m}\}(x)$
in
$x\,\varepsilon \,\mathsf {A}\vdash \{\mathbf {n}\}(x)=\{\mathbf {m}\}(x)$
in
![]() ${{\widehat {ID_1}}}$
.
${{\widehat {ID_1}}}$
.
If
![]() $[\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}:\mathsf {A}\rightarrow \mathsf {B}$
and
$[\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}:\mathsf {A}\rightarrow \mathsf {B}$
and
![]() $[\mathbf {m}]_{\approx _{\mathsf {B},\mathsf {C}}}:\mathsf {B}\rightarrow \mathsf {C}$
are operations between classes of
$[\mathbf {m}]_{\approx _{\mathsf {B},\mathsf {C}}}:\mathsf {B}\rightarrow \mathsf {C}$
are operations between classes of
![]() ${{\widehat {ID_1}}}$
, then their composition is defined by
${{\widehat {ID_1}}}$
, then their composition is defined by
 $[\mathbf {m}]_{\approx _{\mathsf {B},\mathsf {C}}}\circ [\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}:=[\Lambda x. \{\mathbf {m}\}(\{\mathbf {n}\}(x))]_{\approx _{\mathsf {A},\mathsf {C}}}$
.
$[\mathbf {m}]_{\approx _{\mathsf {B},\mathsf {C}}}\circ [\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}:=[\Lambda x. \{\mathbf {m}\}(\{\mathbf {n}\}(x))]_{\approx _{\mathsf {A},\mathsf {C}}}$
.
The identity operation for the class
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() ${{\widehat {ID_1}}}$
is defined as
${{\widehat {ID_1}}}$
is defined as
![]() $\mathsf {id}_{\mathsf {A}}:=[\Lambda x.x]_{\approx _{\mathsf {A},\mathsf {A}}}$
.
$\mathsf {id}_{\mathsf {A}}:=[\Lambda x.x]_{\approx _{\mathsf {A},\mathsf {A}}}$
.
Definition 4.2. We denote with
![]() $\mathcal {C}_{r}$
the category whose objects are realized collections of
$\mathcal {C}_{r}$
the category whose objects are realized collections of
![]() ${{\widehat {ID_1}}}$
and arrows are operations in
${{\widehat {ID_1}}}$
and arrows are operations in
![]() ${{\widehat {ID_1}}}$
between them with their composition and identity operations.
${{\widehat {ID_1}}}$
between them with their composition and identity operations.
We will omit subscripts of
![]() $\approx $
when they will be clear from the context.
$\approx $
when they will be clear from the context.
Theorem 4.3.
![]() $\mathcal {C}_{r}$
is a finitely complete category with disjoint stable finite coproducts, parameterized list objects and weak exponentials (see [Reference Maietti10] and [Reference Carboni and Rosolini4]).
$\mathcal {C}_{r}$
is a finitely complete category with disjoint stable finite coproducts, parameterized list objects and weak exponentials (see [Reference Maietti10] and [Reference Carboni and Rosolini4]).
Proof In
![]() $\mathcal {C}_{r}$
the object
$\mathcal {C}_{r}$
the object
![]() $\mathsf {1}:=\{x|\,x=0\}$
is a terminal object;
$\mathsf {1}:=\{x|\,x=0\}$
is a terminal object;
![]() $\mathsf {A}\times \mathsf {B}:=\{x|\,p_{1}(x)\,\varepsilon \, \mathsf {A}\,\wedge \, p_{2}(x)\,\varepsilon \,\mathsf {B}\}$
is a binary product for
$\mathsf {A}\times \mathsf {B}:=\{x|\,p_{1}(x)\,\varepsilon \, \mathsf {A}\,\wedge \, p_{2}(x)\,\varepsilon \,\mathsf {B}\}$
is a binary product for
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $\mathsf {B}$
together with the projections defined by
$\mathsf {B}$
together with the projections defined by
![]() $[\mathbf {p}_{1}]$
and
$[\mathbf {p}_{1}]$
and
![]() $[\mathbf {p}_{2}]$
.
$[\mathbf {p}_{2}]$
.
If
![]() $\mathsf {f}=[\mathbf {n}]_{\approx }$
and
$\mathsf {f}=[\mathbf {n}]_{\approx }$
and
![]() $\mathsf {g}=[\mathbf {m}]_{\approx }$
are arrows in
$\mathsf {g}=[\mathbf {m}]_{\approx }$
are arrows in
![]() $\mathcal {C}_{r}$
from
$\mathcal {C}_{r}$
from
![]() $\mathsf {A}$
to
$\mathsf {A}$
to
![]() $\mathsf {B}$
, then an equalizer for them is
$\mathsf {B}$
, then an equalizer for them is
![]() $\mathsf {Eq}(\mathsf {f},\mathsf {g}):=\{x|\,x\,\varepsilon \,\mathsf {A}\,\wedge \, \{\mathbf {n}\}(x)=\{\mathbf {m}\}(x)\}$
together with the arrow
$\mathsf {Eq}(\mathsf {f},\mathsf {g}):=\{x|\,x\,\varepsilon \,\mathsf {A}\,\wedge \, \{\mathbf {n}\}(x)=\{\mathbf {m}\}(x)\}$
together with the arrow
![]() $[\Lambda x.x]_{\approx }:\mathsf {Eq}(\mathsf {f},\mathsf {g})\rightarrow \mathsf {A}$
;
$[\Lambda x.x]_{\approx }:\mathsf {Eq}(\mathsf {f},\mathsf {g})\rightarrow \mathsf {A}$
;
![]() $\mathsf {0}:=\{x|\,\bot \}$
is an initial object;
$\mathsf {0}:=\{x|\,\bot \}$
is an initial object;
![]() $\mathsf {A}+\mathsf {B}:=\{x|\;( p_{1}(x)=0\,\wedge \, p_{2}(x)\,\varepsilon \,\mathsf {A})\,\vee \, ( p_{1}(x)=1\,\wedge \, p_{2}(x)\,\varepsilon \,\mathsf {B})\}$
gives a binary coproduct for
$\mathsf {A}+\mathsf {B}:=\{x|\;( p_{1}(x)=0\,\wedge \, p_{2}(x)\,\varepsilon \,\mathsf {A})\,\vee \, ( p_{1}(x)=1\,\wedge \, p_{2}(x)\,\varepsilon \,\mathsf {B})\}$
gives a binary coproduct for
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $\mathsf {B}$
together with the injections
$\mathsf {B}$
together with the injections
![]() $\mathsf {j}_{1}:=[\Lambda x.\{\mathbf {pair}\}(0,x)]_{\approx }$
from
$\mathsf {j}_{1}:=[\Lambda x.\{\mathbf {pair}\}(0,x)]_{\approx }$
from
![]() $\mathsf {A}$
to
$\mathsf {A}$
to
![]() $\mathsf {A}+\mathsf {B}$
and
$\mathsf {A}+\mathsf {B}$
and
![]() $\mathsf {j}_{2}:=[\Lambda x.\{\mathbf {pair}\}(1,x)]_{\approx }$
from
$\mathsf {j}_{2}:=[\Lambda x.\{\mathbf {pair}\}(1,x)]_{\approx }$
from
![]() $\mathsf {B}$
to
$\mathsf {B}$
to
![]() $\mathsf {A}+\mathsf {B}$
; the object
$\mathsf {A}+\mathsf {B}$
; the object
![]() $\mathsf {List}(\mathsf {A})$
defined as
$\mathsf {List}(\mathsf {A})$
defined as
![]() $\{x|\,\forall j(\,j < lh(x)\rightarrow (x)_{j}\,\varepsilon \,\mathsf {A})\}$
is a parameterized list object for
$\{x|\,\forall j(\,j < lh(x)\rightarrow (x)_{j}\,\varepsilon \,\mathsf {A})\}$
is a parameterized list object for
![]() $\mathsf {A}$
together with the empty list arrow
$\mathsf {A}$
together with the empty list arrow
![]() $\epsilon :=[\Lambda x.0]_{\approx }:\mathsf {1}\rightarrow \mathsf {List}(\mathsf {A})$
and the append arrow
$\epsilon :=[\Lambda x.0]_{\approx }:\mathsf {1}\rightarrow \mathsf {List}(\mathsf {A})$
and the append arrow
![]() $\mathsf {cons}$
defined as
$\mathsf {cons}$
defined as
![]() $[\Lambda x. \{\mathbf {cnc}\}(\{\mathbf {p}_{1}\}(x),\{\mathbf {p}_{2}\}(x))]_{\approx }$
; the object
$[\Lambda x. \{\mathbf {cnc}\}(\{\mathbf {p}_{1}\}(x),\{\mathbf {p}_{2}\}(x))]_{\approx }$
; the object
![]() $\mathsf {A}\Rightarrow \mathsf {B}:=\{x|\,\forall u\, (u\,\varepsilon \,\mathsf {A}\, \rightarrow \, \{x\}(u)\,\varepsilon \,\mathsf {B})\}$
defines a weak exponential for
$\mathsf {A}\Rightarrow \mathsf {B}:=\{x|\,\forall u\, (u\,\varepsilon \,\mathsf {A}\, \rightarrow \, \{x\}(u)\,\varepsilon \,\mathsf {B})\}$
defines a weak exponential for
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $\mathsf {B}$
together with the evaluation
$\mathsf {B}$
together with the evaluation
![]() $\mathsf {ev}:=[\Lambda x.\{\{\mathbf {p}_{1}\}(x)\}(\{\mathbf {p}_{2}\}(x))]_{\approx }$
from
$\mathsf {ev}:=[\Lambda x.\{\{\mathbf {p}_{1}\}(x)\}(\{\mathbf {p}_{2}\}(x))]_{\approx }$
from
![]() $(\mathsf {A}\Rightarrow \mathsf {B})\times \mathsf {A}$
to
$(\mathsf {A}\Rightarrow \mathsf {B})\times \mathsf {A}$
to
![]() $\mathsf {B}$
. After having noticed that an arrow
$\mathsf {B}$
. After having noticed that an arrow
![]() $\mathsf {j}:=[\mathbf {j}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {j}:=[\mathbf {j}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
is mono if and only if
$\mathcal {C}_{r}$
is mono if and only if
![]() $x\,\varepsilon \, \mathsf {A}\wedge y\,\varepsilon \, \mathsf {A}\wedge \{\mathbf {j}\}(x)= \{\mathbf {j}\}(y)\vdash x=y$
in
$x\,\varepsilon \, \mathsf {A}\wedge y\,\varepsilon \, \mathsf {A}\wedge \{\mathbf {j}\}(x)= \{\mathbf {j}\}(y)\vdash x=y$
in
![]() ${{\widehat {ID_1}}}$
, one can easily verify that finite coproducts are stable and disjoint. ⊣
${{\widehat {ID_1}}}$
, one can easily verify that finite coproducts are stable and disjoint. ⊣
Remark 4.4. A parameterized natural numbers object can be defined using the list object
![]() $\mathsf {List}(\mathsf {1})$
. However one can directly define a parameterized natural numbers object
$\mathsf {List}(\mathsf {1})$
. However one can directly define a parameterized natural numbers object
![]() $\mathsf {N}$
as
$\mathsf {N}$
as
![]() $\{x|\,x=x\}$
together with the arrows
$\{x|\,x=x\}$
together with the arrows
![]() $[\Lambda x.0]_{\approx }:\mathsf {1}\rightarrow \mathsf {N}$
and
$[\Lambda x.0]_{\approx }:\mathsf {1}\rightarrow \mathsf {N}$
and
![]() $[\mathbf {succ}]_{\approx }:\mathsf {N}\rightarrow \mathsf {N}$
. This presentation of natural numbers object will help to avoid encodings when showing the validity of the Formal Church’s thesis in the doctrine.
$[\mathbf {succ}]_{\approx }:\mathsf {N}\rightarrow \mathsf {N}$
. This presentation of natural numbers object will help to avoid encodings when showing the validity of the Formal Church’s thesis in the doctrine.
Definition 4.5. Suppose
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
. A family of realized collections on
$\mathcal {C}_{r}$
. A family of realized collections on
![]() $\mathsf {A}$
is a formal expression
$\mathsf {A}$
is a formal expression
![]() $\{x'|\,\varphi _{\mathsf {C}}(x,x')\}$
where
$\{x'|\,\varphi _{\mathsf {C}}(x,x')\}$
where
![]() $\varphi _{\mathsf {C}}(x,x')$
is a formula of
$\varphi _{\mathsf {C}}(x,x')$
is a formula of
![]() ${{\widehat {ID_1}}}$
with at most x and
${{\widehat {ID_1}}}$
with at most x and
![]() $x'$
as free variables (we write
$x'$
as free variables (we write
![]() $x'\,\varepsilon \, \mathsf {C}(x)$
as an abbreviation for
$x'\,\varepsilon \, \mathsf {C}(x)$
as an abbreviation for
![]() $\varphi _{\mathsf {C}}(x,x')$
) for which
$\varphi _{\mathsf {C}}(x,x')$
) for which
![]() $x'\,\varepsilon \,\mathsf {C}(x)\,\vdash \,x\,\varepsilon \, \mathsf {A}$
in
$x'\,\varepsilon \,\mathsf {C}(x)\,\vdash \,x\,\varepsilon \, \mathsf {A}$
in
![]() ${{\widehat {ID_1}}}$
. Families of realized collections on
${{\widehat {ID_1}}}$
. Families of realized collections on
![]() $\mathsf {A}$
with provably (in
$\mathsf {A}$
with provably (in
![]() ${{\widehat {ID_1}}}$
) equivalent membership relations are identified.
${{\widehat {ID_1}}}$
) equivalent membership relations are identified.
An operation from a family of realized collections
![]() $\mathsf {C}(x)$
on
$\mathsf {C}(x)$
on
![]() $\mathsf {A}$
to another
$\mathsf {A}$
to another
![]() $\mathsf {D}(x)$
is given by an equivalence class
$\mathsf {D}(x)$
is given by an equivalence class
 $[\mathbf {n}]_{\approx _{\mathsf {C}(x),\mathsf {D}(x)}}$
of numerals such that in
$[\mathbf {n}]_{\approx _{\mathsf {C}(x),\mathsf {D}(x)}}$
of numerals such that in
![]() ${{\widehat {ID_1}}}$
we have
${{\widehat {ID_1}}}$
we have
![]() $x'\,\varepsilon \,\mathsf {C}(x)\,\vdash \,\{\mathbf {n}\}(x,x')\,\varepsilon \,\mathsf {D}(x)$
with respect to the equivalence relation defined as follows:
$x'\,\varepsilon \,\mathsf {C}(x)\,\vdash \,\{\mathbf {n}\}(x,x')\,\varepsilon \,\mathsf {D}(x)$
with respect to the equivalence relation defined as follows:
![]() $\mathbf {n}\approx _{\mathsf {C}(x),\mathsf {D}(x)} \mathbf {m}$
if and only if
$\mathbf {n}\approx _{\mathsf {C}(x),\mathsf {D}(x)} \mathbf {m}$
if and only if
 $x'\,\varepsilon \, \mathsf {C}(x)\,\vdash _{{{\widehat {ID_1}}}}\,\{\mathbf {n}\}(x,x')=\{\mathbf {m}\}(x,x')$
.
$x'\,\varepsilon \, \mathsf {C}(x)\,\vdash _{{{\widehat {ID_1}}}}\,\{\mathbf {n}\}(x,x')=\{\mathbf {m}\}(x,x')$
.
If
 $\mathsf {f}=[\mathbf {n}]_{\approx _{\mathsf {C}(x),\mathsf {D}(x)}}:\mathsf {C}(x)\rightarrow \mathsf {D}(x)$
and
$\mathsf {f}=[\mathbf {n}]_{\approx _{\mathsf {C}(x),\mathsf {D}(x)}}:\mathsf {C}(x)\rightarrow \mathsf {D}(x)$
and
 $\mathsf {g}=[\mathbf {m}]_{\approx _{\mathsf {D}(x),\mathsf {E}(x)}}:\mathsf {D}(x)\rightarrow \mathsf {E}(x)$
are operations between families of realized collection on
$\mathsf {g}=[\mathbf {m}]_{\approx _{\mathsf {D}(x),\mathsf {E}(x)}}:\mathsf {D}(x)\rightarrow \mathsf {E}(x)$
are operations between families of realized collection on
![]() $\mathsf {A}$
, then their composition is defined as
$\mathsf {A}$
, then their composition is defined as
 $\mathsf {g}\circ \mathsf {f}:=[\Lambda x.\Lambda x'.\{\mathbf {m}\}(x,\{\mathbf {n}\}(x,x'))]_{\approx _{\mathsf {C}(x),\mathsf {E}(x)}}:\mathsf {C}(x)\rightarrow \mathsf {E}(x)$
.Footnote
1
$\mathsf {g}\circ \mathsf {f}:=[\Lambda x.\Lambda x'.\{\mathbf {m}\}(x,\{\mathbf {n}\}(x,x'))]_{\approx _{\mathsf {C}(x),\mathsf {E}(x)}}:\mathsf {C}(x)\rightarrow \mathsf {E}(x)$
.Footnote
1
If
![]() $\mathsf {C}(x)$
is a family of realized collections on
$\mathsf {C}(x)$
is a family of realized collections on
![]() $\mathsf {A}$
, then its identity operation is defined by
$\mathsf {A}$
, then its identity operation is defined by
 $\mathsf {id}_{\mathsf {C}(x)}:=[\Lambda x.\Lambda x'.x']_{\approx _{\mathsf {C}(x),\mathsf {C}(x)}}:\mathsf {C}(x)\rightarrow \mathsf {C}(x)$
.
$\mathsf {id}_{\mathsf {C}(x)}:=[\Lambda x.\Lambda x'.x']_{\approx _{\mathsf {C}(x),\mathsf {C}(x)}}:\mathsf {C}(x)\rightarrow \mathsf {C}(x)$
.
The proof of the following theorem is an immediate verification.
Theorem 4.6. For every object
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() $\mathcal {C}_{r}$
, families of realized collections on
$\mathcal {C}_{r}$
, families of realized collections on
![]() $\mathsf {A}$
and operations between them together with their composition and identity operations define a category. We denote this category with
$\mathsf {A}$
and operations between them together with their composition and identity operations define a category. We denote this category with
![]() $\mathbf {Col}^{r}(\mathsf {A})$
.
$\mathbf {Col}^{r}(\mathsf {A})$
.
If
![]() $\mathsf {f}:=[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
, then the following assignments give rise to a functor
$\mathsf {f}:=[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
, then the following assignments give rise to a functor
![]() $\mathbf {Col}^{r}_{\mathsf {f}}$
from
$\mathbf {Col}^{r}_{\mathsf {f}}$
from
![]() $\mathbf {Col}^{r}(\mathsf {B})$
to
$\mathbf {Col}^{r}(\mathsf {B})$
to
![]() $\mathbf {Col}^{r}(\mathsf {A})$
:
$\mathbf {Col}^{r}(\mathsf {A})$
:
-
1. for every object
 $\mathsf {C}(x)$
of
$\mathsf {C}(x)$
of
 $\mathbf {Col}^{r}(\mathsf {B})$
,
$\mathbf {Col}^{r}(\mathsf {B})$
,
 $\mathbf {Col}^{r}_{\mathsf {f}}(\mathsf {C}(x)):=\{x'|\,x\,\varepsilon \, \mathsf {A}\wedge x'\,\varepsilon \, \mathsf {C}(\{\mathbf {n}\}(x))\}$
;
$\mathbf {Col}^{r}_{\mathsf {f}}(\mathsf {C}(x)):=\{x'|\,x\,\varepsilon \, \mathsf {A}\wedge x'\,\varepsilon \, \mathsf {C}(\{\mathbf {n}\}(x))\}$
; -
2. for every arrow
 $\mathsf {g}:=[\mathbf {k}]_{\approx }:\mathsf {C}(x)\rightarrow \mathsf {D}(x)$
of
$\mathsf {g}:=[\mathbf {k}]_{\approx }:\mathsf {C}(x)\rightarrow \mathsf {D}(x)$
of
 $\mathbf {Col}^{r}(\mathsf {B})$
,
$\mathbf {Col}^{r}(\mathsf {B})$
,  $$ \begin{align*} \mathbf{Col}^{r}_{\mathsf{f}}(\mathsf{g}):=[\Lambda x.\Lambda x'. \{\mathbf{k}\}(\{\mathbf{n}\}(x),x')]_{\approx}:{\mathbf{Col}^{r}_{\mathsf{f}}(\mathsf{C}(x))\rightarrow \mathbf{Col}^{r}_{\mathsf{f}}(\mathsf{D}(x))}. \end{align*} $$
$$ \begin{align*} \mathbf{Col}^{r}_{\mathsf{f}}(\mathsf{g}):=[\Lambda x.\Lambda x'. \{\mathbf{k}\}(\{\mathbf{n}\}(x),x')]_{\approx}:{\mathbf{Col}^{r}_{\mathsf{f}}(\mathsf{C}(x))\rightarrow \mathbf{Col}^{r}_{\mathsf{f}}(\mathsf{D}(x))}. \end{align*} $$
Moreover, the assignments
![]() $\mathsf {A}\mapsto \mathbf {Col}^{r}(\mathsf {A})$
and
$\mathsf {A}\mapsto \mathbf {Col}^{r}(\mathsf {A})$
and
![]() $\mathsf {f}\mapsto \mathbf {Col}^{r}_{\mathsf {f}}$
define an indexed category
$\mathsf {f}\mapsto \mathbf {Col}^{r}_{\mathsf {f}}$
define an indexed category
![]() $\mathbf {Col}^{r}:\mathcal {C}_{r}^{op}\rightarrow \mathbf {Cat}$
.
$\mathbf {Col}^{r}:\mathcal {C}_{r}^{op}\rightarrow \mathbf {Cat}$
.
The functors
![]() $\mathbf {Col}^{r}_{\mathsf {f}}$
are also called substitution functors. The proof of the following theorem is similar to that of Theorem 4.3.
$\mathbf {Col}^{r}_{\mathsf {f}}$
are also called substitution functors. The proof of the following theorem is similar to that of Theorem 4.3.
Theorem 4.7. For every object
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() $\mathcal {C}_{r}$
,
$\mathcal {C}_{r}$
,
![]() $\mathbf {Col}^{r}(\mathsf {A})$
is a finitely complete category with parameterized list objects, finite coproducts and weak exponentials. Moreover for every arrow
$\mathbf {Col}^{r}(\mathsf {A})$
is a finitely complete category with parameterized list objects, finite coproducts and weak exponentials. Moreover for every arrow
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
, the functor
$\mathcal {C}_{r}$
, the functor
![]() $\mathbf {Col}^{r}_{\mathsf {f}}$
preserves this structure.
$\mathbf {Col}^{r}_{\mathsf {f}}$
preserves this structure.
Moreover substitution functors have left adjoints:
Theorem 4.8. For every
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
, the functor
$\mathcal {C}_{r}$
, the functor
![]() $\mathbf {Col}^{r}_{\mathsf {f}}$
has a left adjoint
$\mathbf {Col}^{r}_{\mathsf {f}}$
has a left adjoint
Proof If
![]() $\mathsf {f}=[\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}:\mathsf {A}\rightarrow \mathsf {B}$
is an arrow in
$\mathsf {f}=[\mathbf {n}]_{\approx _{\mathsf {A},\mathsf {B}}}:\mathsf {A}\rightarrow \mathsf {B}$
is an arrow in
![]() $\mathcal {C}_{r}$
, then a left adjoint
$\mathcal {C}_{r}$
, then a left adjoint
![]() $\Sigma _{\mathsf {f}}$
to
$\Sigma _{\mathsf {f}}$
to
![]() $\mathbf {Col}^{r}_{\mathsf {f}}$
is defined by the following conditions: if
$\mathbf {Col}^{r}_{\mathsf {f}}$
is defined by the following conditions: if
![]() $\mathsf {C}(x)$
is an object of
$\mathsf {C}(x)$
is an object of
![]() $\mathbf {Col}^{r}(\mathsf {A})$
, then
$\mathbf {Col}^{r}(\mathsf {A})$
, then
![]() $\Sigma _{\mathsf {f}}(\mathsf {C}(x)):=\{x'|\,x=\{\mathbf {n}\}(p_{1}(x'))\,\wedge \, p_{2}(x')\,\varepsilon \,\mathsf {C}(p_{1}(x'))\}$
; if
$\Sigma _{\mathsf {f}}(\mathsf {C}(x)):=\{x'|\,x=\{\mathbf {n}\}(p_{1}(x'))\,\wedge \, p_{2}(x')\,\varepsilon \,\mathsf {C}(p_{1}(x'))\}$
; if
![]() $\mathsf {g}:=[\mathbf {m}]_{\approx }$
is an arrow from
$\mathsf {g}:=[\mathbf {m}]_{\approx }$
is an arrow from
![]() $\mathsf {C}(x)$
to
$\mathsf {C}(x)$
to
![]() $\mathsf {D}(x)$
in
$\mathsf {D}(x)$
in
![]() $\mathbf {Col}^{r}(\mathsf {A})$
, then
$\mathbf {Col}^{r}(\mathsf {A})$
, then
![]() $\Sigma _{\mathsf {f}}(\mathsf {g}):\Sigma _{\mathsf {f}}(\mathsf {C}(x))\rightarrow \Sigma _{\mathsf {f}}(\mathsf {D}(x))$
is defined as
$\Sigma _{\mathsf {f}}(\mathsf {g}):\Sigma _{\mathsf {f}}(\mathsf {C}(x))\rightarrow \Sigma _{\mathsf {f}}(\mathsf {D}(x))$
is defined as
![]() $[\Lambda x.\Lambda x'.\{\mathbf {pair}\}\,(\{\mathbf {p}_{1}\}(x'),\,\{\mathbf {m}\}(\{\mathbf {p}_{1}\}(x'),\,\{\mathbf {p}_{2}\}(x')))]_{\approx }$
. ⊣
$[\Lambda x.\Lambda x'.\{\mathbf {pair}\}\,(\{\mathbf {p}_{1}\}(x'),\,\{\mathbf {m}\}(\{\mathbf {p}_{1}\}(x'),\,\{\mathbf {p}_{2}\}(x')))]_{\approx }$
. ⊣
Now we prove that substitution functors have weak versions of right adjoints.
Theorem 4.9. For every arrow
![]() $\mathsf {f}:=[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:=[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
and every object
$\mathcal {C}_{r}$
and every object
![]() $\mathsf {C}(x)$
in
$\mathsf {C}(x)$
in
![]() $\mathbf {Col}^{r}(\mathsf {A})$
, there exists an object
$\mathbf {Col}^{r}(\mathsf {A})$
, there exists an object
![]() $\Pi _{\mathsf {f}}(\mathsf {C}(x))$
in
$\Pi _{\mathsf {f}}(\mathsf {C}(x))$
in
![]() $\mathbf {Col}^{r}(\mathsf {B})$
and an arrow
$\mathbf {Col}^{r}(\mathsf {B})$
and an arrow
 $\mathsf {ev}^{\Pi ,\mathsf {f}}_{\mathsf {C}(x)}:\mathbf {Col}^{r}_{\mathsf {f}}(\Pi _{\mathsf {f}}(\mathsf {C}(x)))\rightarrow \mathsf {C}(x)$
in
$\mathsf {ev}^{\Pi ,\mathsf {f}}_{\mathsf {C}(x)}:\mathbf {Col}^{r}_{\mathsf {f}}(\Pi _{\mathsf {f}}(\mathsf {C}(x)))\rightarrow \mathsf {C}(x)$
in
![]() $\mathbf {Col}^{r}(\mathsf {B})$
such that for every
$\mathbf {Col}^{r}(\mathsf {B})$
such that for every
![]() $\mathsf {D}(x)\in \mathbf {Col}^{r}(\mathsf {B})$
and every arrow
$\mathsf {D}(x)\in \mathbf {Col}^{r}(\mathsf {B})$
and every arrow
 $\mathsf {g}:\mathbf {Col}_{f}^{r}(\mathsf {D}(x))\rightarrow \mathsf {C}(x)$
in
$\mathsf {g}:\mathbf {Col}_{f}^{r}(\mathsf {D}(x))\rightarrow \mathsf {C}(x)$
in
![]() $\mathbf {Col}^{r}(\mathsf {A})$
, there exists an arrow
$\mathbf {Col}^{r}(\mathsf {A})$
, there exists an arrow
![]() $\mathsf {g}':\mathsf {D}(x)\rightarrow \Pi _{\mathsf {f}}(\mathsf {C}(x))$
in
$\mathsf {g}':\mathsf {D}(x)\rightarrow \Pi _{\mathsf {f}}(\mathsf {C}(x))$
in
![]() $\mathbf {Col}^{r}(\mathsf {B})$
such that the following diagram commutes in
$\mathbf {Col}^{r}(\mathsf {B})$
such that the following diagram commutes in
![]() $\mathbf {Col}^{r}(\mathsf {A})$
:
$\mathbf {Col}^{r}(\mathsf {A})$
:

Proof Take
![]() $\Pi _{\mathsf {f}}(\mathsf {C}(x)):=\{x'|\,x\,\varepsilon \,\mathsf {B}\wedge \forall y\,(\, x=\{\mathbf {n}\}(y)\wedge y\,\varepsilon \,\mathsf {A}\rightarrow \{x'\}(y)\,\varepsilon \,\mathsf {C}(y)\,)\}$
and
$\Pi _{\mathsf {f}}(\mathsf {C}(x)):=\{x'|\,x\,\varepsilon \,\mathsf {B}\wedge \forall y\,(\, x=\{\mathbf {n}\}(y)\wedge y\,\varepsilon \,\mathsf {A}\rightarrow \{x'\}(y)\,\varepsilon \,\mathsf {C}(y)\,)\}$
and
 $\mathsf {ev}^{\Pi ,\mathsf {f}}_{\mathsf {C}(x)}:=[\Lambda x.\Lambda x'. \{x'\}(x)]_{\approx }$
. ⊣
$\mathsf {ev}^{\Pi ,\mathsf {f}}_{\mathsf {C}(x)}:=[\Lambda x.\Lambda x'. \{x'\}(x)]_{\approx }$
. ⊣
Definition 4.10. If
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
and
$\mathcal {C}_{r}$
and
![]() $\mathsf {B}(x)$
is an object of
$\mathsf {B}(x)$
is an object of
![]() $\mathbf {Col}^{r}(\mathsf {A})$
, then
$\mathbf {Col}^{r}(\mathsf {A})$
, then
![]() $\Sigma (\mathsf {A},\mathsf {B}(x))$
is the object of
$\Sigma (\mathsf {A},\mathsf {B}(x))$
is the object of
![]() $\mathcal {C}_{r}$
defined as
$\mathcal {C}_{r}$
defined as
![]() $\{x|\,p_{1}(x)\,\varepsilon \, \mathsf {A}\wedge p_{2}(x)\,\varepsilon \, \mathsf {B}(p_{1}(x))\}$
.
$\{x|\,p_{1}(x)\,\varepsilon \, \mathsf {A}\wedge p_{2}(x)\,\varepsilon \, \mathsf {B}(p_{1}(x))\}$
.
The proof of the following lemma consists of an easy verification.
Lemma 4.11. For every
![]() $\mathsf {f}:=[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:=[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
and every
$\mathcal {C}_{r}$
and every
![]() $\mathsf {C}$
in
$\mathsf {C}$
in
![]() $\mathbf {Col}^{r}(\mathsf {B})$
, if
$\mathbf {Col}^{r}(\mathsf {B})$
, if
![]() $\Sigma (\mathsf {f},\mathsf {C})$
is
$\Sigma (\mathsf {f},\mathsf {C})$
is
![]() $[\Lambda x. \{\mathbf {pair}\}(\{\mathbf {n}\}(\{\mathbf {p}_{1}\}(x)),\{\mathbf {p}_{2}\}(x))]_{\approx }$
, the following diagram is a pullback where
$[\Lambda x. \{\mathbf {pair}\}(\{\mathbf {n}\}(\{\mathbf {p}_{1}\}(x)),\{\mathbf {p}_{2}\}(x))]_{\approx }$
, the following diagram is a pullback where
![]() $p_1^{\Sigma}$
means
$p_1^{\Sigma}$
means
![]() $[\mathbf{p}_1]_{\approx}$
$[\mathbf{p}_1]_{\approx}$

Theorem 4.12. For every
![]() $\mathsf {A}$
in
$\mathsf {A}$
in
![]() $\mathcal {C}_{r}$
,
$\mathcal {C}_{r}$
,
![]() $\mathcal {C}_{r}/\mathsf {A}$
and
$\mathcal {C}_{r}/\mathsf {A}$
and
![]() $\mathbf {Col}^{r}(\mathsf {A})$
are equivalent.
$\mathbf {Col}^{r}(\mathsf {A})$
are equivalent.
Proof Suppose
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
. It is sufficient to consider the functor
$\mathcal {C}_{r}$
. It is sufficient to consider the functor
![]() $\mathbf {J}_{\mathsf {A}}:\mathcal {C}_{r}/\mathsf {A}\rightarrow \mathbf {Col}^{r}(\mathsf {A})$
defined by the assignments
$\mathbf {J}_{\mathsf {A}}:\mathcal {C}_{r}/\mathsf {A}\rightarrow \mathbf {Col}^{r}(\mathsf {A})$
defined by the assignments
and the functor
![]() $\mathbf {I}_{\mathsf {A}}:\mathbf {Col}^{r}(\mathsf {A})\rightarrow \mathcal {C}_{r}/\mathsf {A}$
defined by the assignments (see Definition 4.10)
$\mathbf {I}_{\mathsf {A}}:\mathbf {Col}^{r}(\mathsf {A})\rightarrow \mathcal {C}_{r}/\mathsf {A}$
defined by the assignments (see Definition 4.10)
⊣
Corollary 4.13.
![]() $\mathcal {C}_{r}$
is weakly locally cartesian closed.
$\mathcal {C}_{r}$
is weakly locally cartesian closed.
![]() $\mathbf {Col}^{r}$
is a functorial account of the slice pseudofunctor
$\mathbf {Col}^{r}$
is a functorial account of the slice pseudofunctor
![]() $\mathcal {C}_{r}/-$
. In fact, it is immediate to verify that for every
$\mathcal {C}_{r}/-$
. In fact, it is immediate to verify that for every
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}^{r}$
the functor
$\mathcal {C}^{r}$
the functor
![]() $\mathbf {I}_{\mathsf {A}}\circ \mathbf {Col}^{r}_{\mathsf {f}}\circ \mathbf {J}_{\mathsf {B}}$
coincides with the functor
$\mathbf {I}_{\mathsf {A}}\circ \mathbf {Col}^{r}_{\mathsf {f}}\circ \mathbf {J}_{\mathsf {B}}$
coincides with the functor
![]() $\mathcal {C}_{r}/\mathsf {f}$
defined by representing pullbacks using products and equalizers in the standard way.
$\mathcal {C}_{r}/\mathsf {f}$
defined by representing pullbacks using products and equalizers in the standard way.
4.2. The hyperdoctrine
 ${\overline {\mathbf {Prop}^{r}}}$
of realized propositions
${\overline {\mathbf {Prop}^{r}}}$
of realized propositions
Here we define the hyperdoctrine of realized propositions on
![]() $\mathcal {C}_{r}$
.
$\mathcal {C}_{r}$
.
Definition 4.14. The indexed category
![]() $\mathbf {Prop}^{r}:\mathcal {C}_{r}^{op}\rightarrow \mathbf {Pord}$
is defined as the preorder reflection
$\mathbf {Prop}^{r}:\mathcal {C}_{r}^{op}\rightarrow \mathbf {Pord}$
is defined as the preorder reflection
![]() $\mathbf {P}[\mathbf {Col}^{r}]$
of
$\mathbf {P}[\mathbf {Col}^{r}]$
of
![]() $\mathbf {Col}^{r}$
(see Definition 2.2). In this case we write
$\mathbf {Col}^{r}$
(see Definition 2.2). In this case we write
![]() $x'\Vdash \mathsf {P}(x)$
instead of
$x'\Vdash \mathsf {P}(x)$
instead of
![]() $x'\,\varepsilon \, \mathsf {P}(x)$
for an object
$x'\,\varepsilon \, \mathsf {P}(x)$
for an object
![]() $\mathsf {P}(x)$
in
$\mathsf {P}(x)$
in
![]() $\mathbf {Col}^{r}(\mathsf {A})$
seen as an object of
$\mathbf {Col}^{r}(\mathsf {A})$
seen as an object of
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
.
$\mathbf {Prop}^{r}(\mathsf {A})$
.
Remark 4.15. Notice that if
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
and
$\mathcal {C}_{r}$
and
![]() $\mathsf {P}(x)$
and
$\mathsf {P}(x)$
and
![]() $\mathsf {Q}(x)$
are objects of
$\mathsf {Q}(x)$
are objects of
![]() $\mathsf {Prop}^{r}(\mathsf {A})$
, then
$\mathsf {Prop}^{r}(\mathsf {A})$
, then
![]() $\mathsf {P}(x)\sqsubseteq_{A} \mathsf {Q}(x)$
in
$\mathsf {P}(x)\sqsubseteq_{A} \mathsf {Q}(x)$
in
![]() $\mathsf {Prop}^{r}(\mathsf {A})$
if and only if there is a numeral
$\mathsf {Prop}^{r}(\mathsf {A})$
if and only if there is a numeral
![]() $\mathbf {r}$
such that
$\mathbf {r}$
such that
![]() $x'\Vdash \mathsf {P}(x)\vdash \{\mathbf {r}\}(x,x')\Vdash \mathsf {Q}(x)$
in
$x'\Vdash \mathsf {P}(x)\vdash \{\mathbf {r}\}(x,x')\Vdash \mathsf {Q}(x)$
in
![]() ${{\widehat {ID_1}}}$
. So
${{\widehat {ID_1}}}$
. So
![]() $\mathsf {P}(x)$
entails
$\mathsf {P}(x)$
entails
![]() $\mathsf {Q}(x)$
if there is a recursive way (recursively depending on x in
$\mathsf {Q}(x)$
if there is a recursive way (recursively depending on x in
![]() $\mathsf {A}$
) to send realizers of
$\mathsf {A}$
) to send realizers of
![]() $\mathsf {P}(x)$
to realizers of
$\mathsf {P}(x)$
to realizers of
![]() $\mathsf {Q}(x)$
. The fact that
$\mathsf {Q}(x)$
. The fact that
![]() $\mathsf {A}$
is a realized collection of natural numbers allows us to exploit the numerical data from the underlying domain
$\mathsf {A}$
is a realized collection of natural numbers allows us to exploit the numerical data from the underlying domain
![]() $\mathsf {A}$
and include them in the notion of entailment. This does not happen in the effective tripos [Reference Hyland, Troelstra and van Dalen7] where the base category is
$\mathsf {A}$
and include them in the notion of entailment. This does not happen in the effective tripos [Reference Hyland, Troelstra and van Dalen7] where the base category is
![]() $\mathsf {Set}$
and its entailment is uniformly defined with respect to the points in the underlying domain A. Namely, if P and Q are functions from A to
$\mathsf {Set}$
and its entailment is uniformly defined with respect to the points in the underlying domain A. Namely, if P and Q are functions from A to
![]() $\mathcal {P}(\mathbb {N})$
, then in the effective tripos
$\mathcal {P}(\mathbb {N})$
, then in the effective tripos
![]() $P\sqsubseteq _{A}Q$
holds iff
$P\sqsubseteq _{A}Q$
holds iff
 $\bigcap _{a\in A}\{n\in \mathbb {N}|\,\forall x\in P(a) (\{n\}(x){ } \in Q(a))\}\neq \emptyset $
holds. However (see Remark 4.17) these two notions can be compared.
$\bigcap _{a\in A}\{n\in \mathbb {N}|\,\forall x\in P(a) (\{n\}(x){ } \in Q(a))\}\neq \emptyset $
holds. However (see Remark 4.17) these two notions can be compared.
Now we are ready to prove the following theorem:
Theorem 4.16.
![]() $\mathbf {Prop}^{r}$
is a first-order hyperdoctrine with weak comprehensions.
$\mathbf {Prop}^{r}$
is a first-order hyperdoctrine with weak comprehensions.
Proof For every object
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() $\mathcal {C}_{r}$
,
$\mathcal {C}_{r}$
,
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
is a Heyting prealgebra. In fact it is sufficient to consider bottom, top, binary infima, binary suprema and Heyting implications given by
$\mathbf {Prop}^{r}(\mathsf {A})$
is a Heyting prealgebra. In fact it is sufficient to consider bottom, top, binary infima, binary suprema and Heyting implications given by
![]() $\bot _{\mathsf {A}}:=\mathsf {0}_{\mathsf {A}}$
,
$\bot _{\mathsf {A}}:=\mathsf {0}_{\mathsf {A}}$
,
![]() $\top _{\mathsf {A}}:=\mathsf {1}_{\mathsf {A}}$
,
$\top _{\mathsf {A}}:=\mathsf {1}_{\mathsf {A}}$
,
![]() $\mathsf {C}(x)\sqcap _{\mathsf {A}}\mathsf {D}(x):=\mathsf {C}(x)\times _{\mathsf {A}}\mathsf {D}(x)$
,
$\mathsf {C}(x)\sqcap _{\mathsf {A}}\mathsf {D}(x):=\mathsf {C}(x)\times _{\mathsf {A}}\mathsf {D}(x)$
,
![]() $\mathsf {C}(x)\sqcup _{\mathsf {A}}\mathsf {D}(x):=\mathsf {C}(x)+_{\mathsf {A}}\mathsf {D}(x)$
and
$\mathsf {C}(x)\sqcup _{\mathsf {A}}\mathsf {D}(x):=\mathsf {C}(x)+_{\mathsf {A}}\mathsf {D}(x)$
and
![]() $\mathsf {C}(x)\rightarrow _{\mathsf {A}}\mathsf {D}(x):=\mathsf {C}(x)\Rightarrow _{\mathsf {A}}\mathsf {D}(x)$
respectively for all objects
$\mathsf {C}(x)\rightarrow _{\mathsf {A}}\mathsf {D}(x):=\mathsf {C}(x)\Rightarrow _{\mathsf {A}}\mathsf {D}(x)$
respectively for all objects
![]() $\mathsf {C}(x),\mathsf {D}(x)$
in
$\mathsf {C}(x),\mathsf {D}(x)$
in
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
. Moreover from
$\mathbf {Prop}^{r}(\mathsf {A})$
. Moreover from
![]() $4.7$
it immediately follows that
$4.7$
it immediately follows that
![]() $\mathbf {Prop}^{r}_{\mathsf {f}}$
is a morphism of Heyting prealgebras from
$\mathbf {Prop}^{r}_{\mathsf {f}}$
is a morphism of Heyting prealgebras from
![]() $\mathbf {Prop}^{r}(\mathsf {B})$
to
$\mathbf {Prop}^{r}(\mathsf {B})$
to
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
for every arrow
$\mathbf {Prop}^{r}(\mathsf {A})$
for every arrow
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
. From
$\mathcal {C}_{r}$
. From
![]() $4.8$
and
$4.8$
and
![]() $4.9$
one can easily obtain that for every such an arrow,
$4.9$
one can easily obtain that for every such an arrow,
![]() $\exists _{\mathbf {f}}(\mathsf {C}(x)):=\Sigma _{\mathbf {f}}(\mathsf {C}(x))$
and
$\exists _{\mathbf {f}}(\mathsf {C}(x)):=\Sigma _{\mathbf {f}}(\mathsf {C}(x))$
and
![]() $\forall _{\mathsf {f}}(\mathsf {C}(x)):=\Pi _{\mathbf {f}}(\mathsf {C}(x))$
define left and right adjoints to
$\forall _{\mathsf {f}}(\mathsf {C}(x)):=\Pi _{\mathbf {f}}(\mathsf {C}(x))$
define left and right adjoints to
![]() $\mathbf {Prop}^{r}_{\mathsf {f}}$
respectively in the category of preorders. One can easily check that these adjoints satisfy Beck–Chevalley condition.
$\mathbf {Prop}^{r}_{\mathsf {f}}$
respectively in the category of preorders. One can easily check that these adjoints satisfy Beck–Chevalley condition.
If
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
and
$\mathcal {C}_{r}$
and
![]() $\mathsf {P}(x)$
is in
$\mathsf {P}(x)$
is in
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
, then
$\mathbf {Prop}^{r}(\mathsf {A})$
, then
![]() $\mathsf {p}_{1}^{\Sigma }:\Sigma (\mathsf {A},\mathsf {P}(x)) \rightarrow \mathsf {A}$
determines a weak comprehension for
$\mathsf {p}_{1}^{\Sigma }:\Sigma (\mathsf {A},\mathsf {P}(x)) \rightarrow \mathsf {A}$
determines a weak comprehension for
![]() $\mathsf {P}(x)$
. ⊣
$\mathsf {P}(x)$
. ⊣
Remark 4.17. The hyperdoctrine of realized propositions enjoys also another interesting property. To this purpose we give the definition of “separated realized proposition”: if
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
, a realized proposition
$\mathcal {C}_{r}$
, a realized proposition
![]() $\mathsf {P}(x)$
in
$\mathsf {P}(x)$
in
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
is called separated if
$\mathbf {Prop}^{r}(\mathsf {A})$
is called separated if
![]() $x'\Vdash \mathsf {P}(x)\wedge x'\Vdash \mathsf {P}(y)\vdash x=y $
in
$x'\Vdash \mathsf {P}(x)\wedge x'\Vdash \mathsf {P}(y)\vdash x=y $
in
![]() ${{\widehat {ID_1}}}$
. It is very easy to show that if
${{\widehat {ID_1}}}$
. It is very easy to show that if
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {C}_{r}$
, then every object of
$\mathcal {C}_{r}$
, then every object of
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
is equivalent in
$\mathbf {Prop}^{r}(\mathsf {A})$
is equivalent in
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
to a separated one. In fact if
$\mathbf {Prop}^{r}(\mathsf {A})$
to a separated one. In fact if
![]() $\mathsf {P}(x)$
is an object of
$\mathsf {P}(x)$
is an object of
![]() $\mathbf {Prop}^{r}(\mathsf {A})$
, then we can consider the separated object
$\mathbf {Prop}^{r}(\mathsf {A})$
, then we can consider the separated object
![]() $\mathsf {P}_{sep}(x):=\{x'|\,p_{1}(x')=x\wedge p_{2}(x')\Vdash \mathsf {P}(x)\}$
and observe that
$\mathsf {P}_{sep}(x):=\{x'|\,p_{1}(x')=x\wedge p_{2}(x')\Vdash \mathsf {P}(x)\}$
and observe that
![]() $\mathsf {P}(x)\sim _{\mathsf {A}}\mathsf {P}_{sep}(x)$
follows in
$\mathsf {P}(x)\sim _{\mathsf {A}}\mathsf {P}_{sep}(x)$
follows in
![]() ${{\widehat {ID_1}}}$
.
${{\widehat {ID_1}}}$
.
Definition 4.18. We denote with
 $\overline {\mathbf {Prop}^{r}}$
the posetal reflection (see Definition 2.2) of
$\overline {\mathbf {Prop}^{r}}$
the posetal reflection (see Definition 2.2) of
![]() $\mathbf {Prop}^{r}$
(which coincides with the posetal reflection of
$\mathbf {Prop}^{r}$
(which coincides with the posetal reflection of
![]() $\mathbf {Col}^{r}$
).
$\mathbf {Col}^{r}$
).
As an immediate consequence of Theorem 4.12 and the fact that
![]() $\mathbf{Col}^r$
is a functorial account of the slice pseudofunctor on
$\mathbf{Col}^r$
is a functorial account of the slice pseudofunctor on
![]() $\mathcal{C}_r$
we have that:
$\mathcal{C}_r$
we have that:
Theorem 4.19. The first-order hyperdoctrine
 $\overline {\mathbf {Prop}^{r}}$
is naturally isomorphic to the doctrine of weak subobjects
$\overline {\mathbf {Prop}^{r}}$
is naturally isomorphic to the doctrine of weak subobjects
![]() $\mathbf {wSub}_{\mathcal {C}^{r}}$
of
$\mathbf {wSub}_{\mathcal {C}^{r}}$
of
![]() $\mathcal {C}^{r}$
.
$\mathcal {C}^{r}$
.
4.3. Sets and small propositions in
 $\mathcal {C}_{r}$
$\mathcal {C}_{r}$
Here, following [Reference Ishihara, Maietti, Maschio and Streicher6], we define a universe of sets internally in
![]() $\mathcal {C}_{r}$
as a fixpoint of a suitable admissible formula of
$\mathcal {C}_{r}$
as a fixpoint of a suitable admissible formula of
![]() ${{\widehat {ID_1}}}$
. This admissible formula describes the elements of such a universe as codes of realized sets (which are defined in turn with their elements) in an inductive way. However, since we do not need to use induction on our universe of sets, we do not need to work in the proper theory of inductive definitions with least fixpoints and we can work just in
${{\widehat {ID_1}}}$
. This admissible formula describes the elements of such a universe as codes of realized sets (which are defined in turn with their elements) in an inductive way. However, since we do not need to use induction on our universe of sets, we do not need to work in the proper theory of inductive definitions with least fixpoints and we can work just in
![]() ${{\widehat {ID_1}}}$
with fixpoints that are not necessarily the least ones. Following [Reference Ishihara, Maietti, Maschio and Streicher6], we employ an admissible formula
${{\widehat {ID_1}}}$
with fixpoints that are not necessarily the least ones. Following [Reference Ishihara, Maietti, Maschio and Streicher6], we employ an admissible formula
![]() $\varphi $
to obtain its fixpoint
$\varphi $
to obtain its fixpoint
![]() $P_{\varphi }(x)$
in
$P_{\varphi }(x)$
in
![]() ${{\widehat {ID_1}}}$
by which we define formulas
${{\widehat {ID_1}}}$
by which we define formulas
![]() $\mathsf {Set}(x)$
,
$\mathsf {Set}(x)$
,
![]() $ x\,\overline {\varepsilon }\,y$
and
$ x\,\overline {\varepsilon }\,y$
and
![]() $x{\mathrel {\!\not \mathrel {\,\overline {\varepsilon }\!}\,}} y$
, meaning “x is the code of a set”, “x is an element of the set encoded by y” and “x is not an element of the set encoded by y”, respectively.
$x{\mathrel {\!\not \mathrel {\,\overline {\varepsilon }\!}\,}} y$
, meaning “x is the code of a set”, “x is an element of the set encoded by y” and “x is not an element of the set encoded by y”, respectively.
We define the universe of sets in
![]() $\mathcal {C}_{r}$
as
$\mathcal {C}_{r}$
as
![]() $\mathsf {U}_{\mathsf {S}}:=\{x|\;\mathsf {Set}(x)\,\wedge \,\forall t\,(t\,\overline {\varepsilon }\,x\leftrightarrow \neg \, t{\mathrel {\!\not \mathrel {\,\overline {\varepsilon }\!}\,}} x)\}$
and we employ it to define a full subcategory of realized sets
$\mathsf {U}_{\mathsf {S}}:=\{x|\;\mathsf {Set}(x)\,\wedge \,\forall t\,(t\,\overline {\varepsilon }\,x\leftrightarrow \neg \, t{\mathrel {\!\not \mathrel {\,\overline {\varepsilon }\!}\,}} x)\}$
and we employ it to define a full subcategory of realized sets
![]() $\mathcal {S}_{r}$
of
$\mathcal {S}_{r}$
of
![]() $\mathcal {C}_{r}$
and a hyperdoctrine
$\mathcal {C}_{r}$
and a hyperdoctrine
 ${\overline {\mathbf {Prop}^{r}_{s}}}$
of small proposition over it.
${\overline {\mathbf {Prop}^{r}_{s}}}$
of small proposition over it.
Definition 4.20. The category of realized sets is the full subcategory
![]() $\mathcal {S}_{r}$
of
$\mathcal {S}_{r}$
of
![]() $\mathcal {C}_{r}$
of which the objects are those realized collections of the form
$\mathcal {C}_{r}$
of which the objects are those realized collections of the form
![]() $\{x|\,x\,\overline {\varepsilon }\,\mathbf {n}\}$
for some numeral
$\{x|\,x\,\overline {\varepsilon }\,\mathbf {n}\}$
for some numeral
![]() $\mathbf {n}$
for which
$\mathbf {n}$
for which
![]() $\mathbf {n}\,\varepsilon \, \mathsf {U}_{\mathsf {S}}$
holds in
$\mathbf {n}\,\varepsilon \, \mathsf {U}_{\mathsf {S}}$
holds in
![]() ${{\widehat {ID_1}}}$
.
${{\widehat {ID_1}}}$
.
Also here, in order to prove that
![]() $\mathcal {S}_{r}$
is weakly locally cartesian closed in a straightforward way, we introduce an indexed category of realized sets over it.
$\mathcal {S}_{r}$
is weakly locally cartesian closed in a straightforward way, we introduce an indexed category of realized sets over it.
Definition 4.21. Let
![]() $\mathsf {A}$
be an object of
$\mathsf {A}$
be an object of
![]() $\mathcal {S}_{r}$
. The category
$\mathcal {S}_{r}$
. The category
![]() $\mathbf {Set}^{r}(\mathsf {A})$
is the full subcategory of
$\mathbf {Set}^{r}(\mathsf {A})$
is the full subcategory of
![]() $\mathbf {Col}^{r}(\mathsf {A})$
whose objects are families of realized collections on
$\mathbf {Col}^{r}(\mathsf {A})$
whose objects are families of realized collections on
![]() $\mathsf {A}$
of the form
$\mathsf {A}$
of the form
![]() $\tau _{\mathsf {A}}(\mathbf {n}):=\{x'|\,x'\,\overline {\varepsilon }\, \{\mathbf {n}\}(x)\,\wedge \, x\,\varepsilon \,\mathsf {A}\}$
for a numeral
$\tau _{\mathsf {A}}(\mathbf {n}):=\{x'|\,x'\,\overline {\varepsilon }\, \{\mathbf {n}\}(x)\,\wedge \, x\,\varepsilon \,\mathsf {A}\}$
for a numeral
![]() $\mathbf {n}$
defining an operation
$\mathbf {n}$
defining an operation
![]() $[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {U}_{\mathsf {S}}$
in
$[\mathbf {n}]_{\approx }:\mathsf {A}\rightarrow \mathsf {U}_{\mathsf {S}}$
in
![]() $\mathcal {C}_{r}$
. Objects of
$\mathcal {C}_{r}$
. Objects of
![]() $\mathbf {Set}^{r}(\mathsf {A})$
are called families of realized sets on
$\mathbf {Set}^{r}(\mathsf {A})$
are called families of realized sets on
![]() $\mathsf {A}$
.
$\mathsf {A}$
.
The following lemma is an immediate consequence of the previous definition.
Lemma 4.22. Let
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
and
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
and
![]() $\mathsf {g} = [\mathsf {n}]_{\approx}:\mathsf {B}\rightarrow \mathsf {U}_{S}$
be arrows in
$\mathsf {g} = [\mathsf {n}]_{\approx}:\mathsf {B}\rightarrow \mathsf {U}_{S}$
be arrows in
![]() $\mathcal {S}_{r}$
and suppose
$\mathcal {S}_{r}$
and suppose
![]() $\mathbf {m}$
is a numeral such that
$\mathbf {m}$
is a numeral such that
![]() $\mathsf {g}\circ \mathsf {f}=[\mathbf {m}]_{\approx}:\mathsf {A}\rightarrow \mathsf {U}_{S}$
. Then
$\mathsf {g}\circ \mathsf {f}=[\mathbf {m}]_{\approx}:\mathsf {A}\rightarrow \mathsf {U}_{S}$
. Then
![]() $\mathbf {Col}^{r}_{\mathsf {f}}(\tau _{\mathsf {B}}(\mathbf {n}))=\tau _{\mathsf {A}}(\mathbf {m})$
.
$\mathbf {Col}^{r}_{\mathsf {f}}(\tau _{\mathsf {B}}(\mathbf {n}))=\tau _{\mathsf {A}}(\mathbf {m})$
.
As a consequence of the previous lemma we can give the following definition.
Definition 4.23.
![]() $\mathbf {Set}^{r}:\mathcal {S}_{r}^{op}\rightarrow \mathbf {Cat}$
is the indexed category whose fibre over an object
$\mathbf {Set}^{r}:\mathcal {S}_{r}^{op}\rightarrow \mathbf {Cat}$
is the indexed category whose fibre over an object
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() $\mathcal {S}_{r}$
is
$\mathcal {S}_{r}$
is
![]() $\mathbf {Set}^{r}(\mathsf {A})$
and which sends an arrow
$\mathbf {Set}^{r}(\mathsf {A})$
and which sends an arrow
![]() $f:\mathsf {A}\rightarrow \mathsf {B}$
in
$f:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {S}_{r}$
to the restriction of
$\mathcal {S}_{r}$
to the restriction of
![]() $\mathbf {Col}^{r}_{f}$
to
$\mathbf {Col}^{r}_{f}$
to
![]() $\mathbf {Set}^{r}(\mathsf {B})$
, since its image is included in
$\mathbf {Set}^{r}(\mathsf {B})$
, since its image is included in
![]() $\mathbf {Set}^{r}(\mathsf {A})$
.
$\mathbf {Set}^{r}(\mathsf {A})$
.
One can prove the following theorem as a consequence of the clauses determining the fixpoint formula giving rise to
![]() $\mathsf {U}_{\mathsf {S}}$
(see [Reference Ishihara, Maietti, Maschio and Streicher6]).
$\mathsf {U}_{\mathsf {S}}$
(see [Reference Ishihara, Maietti, Maschio and Streicher6]).
Theorem 4.24. For every
![]() $\mathsf {A}$
in
$\mathsf {A}$
in
![]() $\mathcal {S}_{r}$
,
$\mathcal {S}_{r}$
,
![]() $\mathbf {Set}^{r}(\mathsf {A})$
is a finitely complete category with disjoint stable finite coproducts, parameterized list objects and weak exponentials. Moreover, If
$\mathbf {Set}^{r}(\mathsf {A})$
is a finitely complete category with disjoint stable finite coproducts, parameterized list objects and weak exponentials. Moreover, If
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {S}_{r}$
, then
$\mathcal {S}_{r}$
, then
![]() $\mathbf {Set}^{r}_{\mathsf {f}}$
has a left adjoint and for every object
$\mathbf {Set}^{r}_{\mathsf {f}}$
has a left adjoint and for every object
![]() $\mathsf {C}(x)$
in
$\mathsf {C}(x)$
in
![]() $\mathbf {Set}^{r}(\mathsf {A})$
,
$\mathbf {Set}^{r}(\mathsf {A})$
,
![]() $\Pi ^{r}_{\mathsf {f}}(\mathsf {C}(x))$
is isomorphic in
$\Pi ^{r}_{\mathsf {f}}(\mathsf {C}(x))$
is isomorphic in
![]() $\mathbf {Col}^{r}(\mathsf {B})$
to an object of
$\mathbf {Col}^{r}(\mathsf {B})$
to an object of
![]() $\mathbf {Set}^{r}(\mathsf {B})$
.
$\mathbf {Set}^{r}(\mathsf {B})$
.
The functor
![]() $\mathbf {Set}^{r}$
is a functorial account of the slice pseudofunctor
$\mathbf {Set}^{r}$
is a functorial account of the slice pseudofunctor
![]() $\mathcal {S}_{r}/-$
and the embedding of
$\mathcal {S}_{r}/-$
and the embedding of
![]() $\mathbf {Set}^{r}$
in the restriction of
$\mathbf {Set}^{r}$
in the restriction of
![]() $\mathbf {Col}^{r}$
to
$\mathbf {Col}^{r}$
to
![]() $\mathcal {S}_{r}$
preserves finite limits, finite coproducts, parameterized list objects and weak exponentials.
$\mathcal {S}_{r}$
preserves finite limits, finite coproducts, parameterized list objects and weak exponentials.
In particular we have the following
Corollary 4.25.
![]() $\mathcal {S}_{r}$
is a finitely complete category with stable disjoint finite coproducts, parameterized list objects and weak exponentials of which the structure is preserved by the embedding in
$\mathcal {S}_{r}$
is a finitely complete category with stable disjoint finite coproducts, parameterized list objects and weak exponentials of which the structure is preserved by the embedding in
![]() $\mathcal {C}_{r}$
.
$\mathcal {C}_{r}$
.
Now we are ready to define the indexed category of small realized propositions.
Definition 4.26. The functor
![]() $\mathbf {Prop}^{r}_{s}:\mathcal {S}_{r}^{op}\rightarrow \mathbf {Pord}$
is defined as the preorder reflection
$\mathbf {Prop}^{r}_{s}:\mathcal {S}_{r}^{op}\rightarrow \mathbf {Pord}$
is defined as the preorder reflection
![]() $\mathbf {P}[\mathbf {Set}^{r}]$
of the indexed category
$\mathbf {P}[\mathbf {Set}^{r}]$
of the indexed category
![]() $\mathbf {Set}^{r}$
. Then, fibre objects of
$\mathbf {Set}^{r}$
. Then, fibre objects of
![]() $\mathbf {Prop}^{r}_{s}$
are called small realized propositions.
$\mathbf {Prop}^{r}_{s}$
are called small realized propositions.
Similarly to the case of
![]() $\mathbf {Prop}^{r} $
one can obtain from 4.24 the following theorem.
$\mathbf {Prop}^{r} $
one can obtain from 4.24 the following theorem.
Theorem 4.27.
![]() $\mathbf {Prop}_{s}^{r} $
is a first-order hyperdoctrine over
$\mathbf {Prop}_{s}^{r} $
is a first-order hyperdoctrine over
![]() $\mathcal {S}_{r}$
with weak comprehensions.
$\mathcal {S}_{r}$
with weak comprehensions.
Definition 4.28. We define
 $\overline {\mathbf {Prop}^{r}_{s}}$
as the posetal reflection (see Definition 2.2) of the doctrine
$\overline {\mathbf {Prop}^{r}_{s}}$
as the posetal reflection (see Definition 2.2) of the doctrine
![]() $\mathbf {Prop}^{r}_{s}$
(which coincides with the posetal reflection of Set
r) and we use the same notations for order, bottom, top, binary infima and suprema, Heyting implication and left and right adjoints.
$\mathbf {Prop}^{r}_{s}$
(which coincides with the posetal reflection of Set
r) and we use the same notations for order, bottom, top, binary infima and suprema, Heyting implication and left and right adjoints.
Exploiting the definition of the coding and Theorem 4.24 one can easily prove
Theorem 4.29.
![]() $\mathbf {Prop}_{s}^{r}$
is equivalent to the weak subobject doctrine
$\mathbf {Prop}_{s}^{r}$
is equivalent to the weak subobject doctrine
![]() $\mathbf {wSub}_{\mathcal {S}_{r}}$
over
$\mathbf {wSub}_{\mathcal {S}_{r}}$
over
![]() $\mathcal {S}_{r}$
.
$\mathcal {S}_{r}$
.
We can hence give the following definition.
Definition 4.30. The pair
 $({\overline {\mathbf {Prop}^{r}}},{\overline {\mathbf {Prop}^{r}_{s}}})$
is called the Kleene effective p-tripos.
$({\overline {\mathbf {Prop}^{r}}},{\overline {\mathbf {Prop}^{r}_{s}}})$
is called the Kleene effective p-tripos.
4.4. The internal language of the doctrine
 ${\overline {\mathbf {Prop}^{r}}}$
${\overline {\mathbf {Prop}^{r}}}$
As for example in [Reference van Oosten25], we consider the internal language of the doctrine
 ${\overline {\mathbf {Prop}^{r}}}$
in the form of a first-order typed language with equality to show that it extends Kleene realizability interpretation of Heyting arithmetics and hence it validates the Formal Church’s thesis.
${\overline {\mathbf {Prop}^{r}}}$
in the form of a first-order typed language with equality to show that it extends Kleene realizability interpretation of Heyting arithmetics and hence it validates the Formal Church’s thesis.
Following [Reference van Oosten25], contexts
![]() $\Gamma $
are interpreted as objects
$\Gamma $
are interpreted as objects
![]() $\left \| \Gamma \right \|$
of
$\left \| \Gamma \right \|$
of
![]() $\mathcal {C}$
. Terms in context
$\mathcal {C}$
. Terms in context
![]() $t[\Gamma ]$
of type
$t[\Gamma ]$
of type
![]() $\mathsf {A}$
are interpreted as arrows from
$\mathsf {A}$
are interpreted as arrows from
![]() $\left \| \Gamma \right \|$
to A and formulas in context
$\left \| \Gamma \right \|$
to A and formulas in context
![]() $\phi [\Gamma ]$
are interpreted as elements of
$\phi [\Gamma ]$
are interpreted as elements of
 ${\overline {\mathbf {Prop}^{r}}}(\left \| \Gamma \right \|)$
. In particular, terms
${\overline {\mathbf {Prop}^{r}}}(\left \| \Gamma \right \|)$
. In particular, terms
![]() $\mathsf {f}(t_{1},..,t_{n})[\Gamma ]$
are interpreted as
$\mathsf {f}(t_{1},..,t_{n})[\Gamma ]$
are interpreted as
![]() $\mathsf {f}\circ \langle \left \|t_{1}[\Gamma ]\right \|,...,\left \|t_{n}[\Gamma ]\right \| \rangle $
, formulas
$\mathsf {f}\circ \langle \left \|t_{1}[\Gamma ]\right \|,...,\left \|t_{n}[\Gamma ]\right \| \rangle $
, formulas
![]() $\mathsf {R}(t_{1},..,t_{n})[\Gamma ]$
are interpreted as
$\mathsf {R}(t_{1},..,t_{n})[\Gamma ]$
are interpreted as
 ${\overline {\mathbf {Prop}^{r}}}_{\langle \left \|t_{1}[\Gamma ]\right \|,...,\left \|t_{n}[\Gamma ]\right \|\rangle }(\mathsf {R})$
and equality formulas
${\overline {\mathbf {Prop}^{r}}}_{\langle \left \|t_{1}[\Gamma ]\right \|,...,\left \|t_{n}[\Gamma ]\right \|\rangle }(\mathsf {R})$
and equality formulas
![]() $(t=_{\mathsf {A}}s)[\Gamma ]$
as
$(t=_{\mathsf {A}}s)[\Gamma ]$
as
 ${\overline {\mathbf {Prop}^{r}}}_{\langle \left \|t[\Gamma ]\right \|, \left \|s[\Gamma ]\right \|\rangle }(\exists _{\Delta _{\mathsf {A}}}(\top _{\mathsf {A}}))$
. Formulas in context obtained with connectives are interpreted using the relative operators in Heyting algebras and formulas in context obtained with quantifiers are interpreted using the relative adjoints in the first-order hyperdoctrine
${\overline {\mathbf {Prop}^{r}}}_{\langle \left \|t[\Gamma ]\right \|, \left \|s[\Gamma ]\right \|\rangle }(\exists _{\Delta _{\mathsf {A}}}(\top _{\mathsf {A}}))$
. Formulas in context obtained with connectives are interpreted using the relative operators in Heyting algebras and formulas in context obtained with quantifiers are interpreted using the relative adjoints in the first-order hyperdoctrine
 ${\overline {\mathbf {Prop}^{r}}}$
. If
${\overline {\mathbf {Prop}^{r}}}$
. If
![]() $\phi [\Gamma ]$
is a formula in context, we define its validity as follows:
$\phi [\Gamma ]$
is a formula in context, we define its validity as follows:
 ${\overline {\mathbf {Prop}^{r}}}\vdash \phi [\Gamma ]$
if and only if
${\overline {\mathbf {Prop}^{r}}}\vdash \phi [\Gamma ]$
if and only if
![]() $\top _{\left \|\Gamma \right \|}\sqsubseteq _{\left \|\Gamma \right \|} \left \|\phi [\Gamma ]\right \|$
.
$\top _{\left \|\Gamma \right \|}\sqsubseteq _{\left \|\Gamma \right \|} \left \|\phi [\Gamma ]\right \|$
.
The language of
![]() $\mathsf {HA}$
can be translated into the internal language of
$\mathsf {HA}$
can be translated into the internal language of
 $\overline {\mathbf {Prop}^{r}}$
, as every primitive n-ary recursive function f can be represented in
$\overline {\mathbf {Prop}^{r}}$
, as every primitive n-ary recursive function f can be represented in
![]() $\mathcal {C}_{r}$
by an arrow
$\mathcal {C}_{r}$
by an arrow
![]() $\overline {f}:\mathsf {N}^{n}\rightarrow \mathsf {N}$
. The translation which assigns a term
$\overline {f}:\mathsf {N}^{n}\rightarrow \mathsf {N}$
. The translation which assigns a term
![]() $\overline {t}$
of the language of
$\overline {t}$
of the language of
 $\overline {\mathbf {Prop}^{r}}$
to every term t of
$\overline {\mathbf {Prop}^{r}}$
to every term t of
![]() $\mathsf {HA}$
and a formula
$\mathsf {HA}$
and a formula
![]() $\overline {\phi }$
in the internal language of
$\overline {\phi }$
in the internal language of
 $\overline {\mathbf {Prop}^{r}}$
to every formula
$\overline {\mathbf {Prop}^{r}}$
to every formula
![]() $\phi $
of
$\phi $
of
![]() $\mathsf {HA}$
is defined as follows:
$\mathsf {HA}$
is defined as follows:
![]() $\overline {x_{i}}$
is
$\overline {x_{i}}$
is
![]() $x_{i}^{\mathsf {N}}$
for every
$x_{i}^{\mathsf {N}}$
for every
![]() $i=1,...,n,...$
and
$i=1,...,n,...$
and
 $\overline {f(t_{1},...,t_{n})}$
is
$\overline {f(t_{1},...,t_{n})}$
is
![]() $\overline {f}(\overline {t_{1}},...,\overline {t_{n}})$
,
$\overline {f}(\overline {t_{1}},...,\overline {t_{n}})$
,
![]() $\overline {t=s}$
is
$\overline {t=s}$
is
![]() $\overline {t}=_{\mathsf {N}}\overline {s}$
and
$\overline {t}=_{\mathsf {N}}\overline {s}$
and
![]() $\overline {\bot }$
is
$\overline {\bot }$
is
![]() $\bot $
,
$\bot $
,
![]() $\overline {\phi \wedge \psi }$
is
$\overline {\phi \wedge \psi }$
is
![]() $\overline {\phi }\wedge \overline {\psi }$
,
$\overline {\phi }\wedge \overline {\psi }$
,
![]() $\overline {\phi \vee \psi }$
is
$\overline {\phi \vee \psi }$
is
![]() $\overline {\phi }\vee \overline {\psi }$
and
$\overline {\phi }\vee \overline {\psi }$
and
![]() $\overline {\phi \rightarrow \psi }$
is
$\overline {\phi \rightarrow \psi }$
is
![]() $\overline {\phi }\rightarrow \overline {\psi }$
,
$\overline {\phi }\rightarrow \overline {\psi }$
,
![]() $\overline {\forall \xi \, \phi }$
is
$\overline {\forall \xi \, \phi }$
is
![]() $(\forall \overline {\xi }\in \mathsf {N}) \overline {\phi }$
and
$(\forall \overline {\xi }\in \mathsf {N}) \overline {\phi }$
and
![]() $\overline {\exists \xi \, \phi }$
is
$\overline {\exists \xi \, \phi }$
is
![]() $(\exists \overline {\xi }\in \mathsf {N}) \overline {\phi }$
.
$(\exists \overline {\xi }\in \mathsf {N}) \overline {\phi }$
.
Remark 4.31. As a consequence of Theorem 4.19 and results in [Reference Maietti, Pasquali and Rosolini14] and [Reference Maietti, Gopal, Jäger and Steila11], the axiom of choice with respect to weak exponentials holds in
 ${\overline {\mathbf {Prop}^{r}}}$
, that is for every objects
${\overline {\mathbf {Prop}^{r}}}$
, that is for every objects
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $\mathsf {B}$
in
$\mathsf {B}$
in
![]() $\mathcal {C}_{r}$
and
$\mathcal {C}_{r}$
and
 $\mathsf {R}\in \overline {\mathbf {Prop}^{r}}(A\times B)$
$\mathsf {R}\in \overline {\mathbf {Prop}^{r}}(A\times B)$
 $$ \begin{align*} \overline{\mathbf{Prop}^{r}}\vdash (\forall x\in \mathsf{A})(\exists y\in \mathsf{B})\mathsf{R}(x,y)\rightarrow (\exists f\in \mathsf{A}\Rightarrow \mathsf{B})(\forall x\in \mathsf{A})\mathsf{R}(x,\mathsf{ev}(f,x)). \end{align*} $$
$$ \begin{align*} \overline{\mathbf{Prop}^{r}}\vdash (\forall x\in \mathsf{A})(\exists y\in \mathsf{B})\mathsf{R}(x,y)\rightarrow (\exists f\in \mathsf{A}\Rightarrow \mathsf{B})(\forall x\in \mathsf{A})\mathsf{R}(x,\mathsf{ev}(f,x)). \end{align*} $$
The next theorem follows easily from the fact that the interpretation of the internal language of
 $\overline {\mathbf {Prop}^{r}}$
extends Kleene realizability interpretation
$\overline {\mathbf {Prop}^{r}}$
extends Kleene realizability interpretation
![]() $\Vdash$
of
$\Vdash$
of
![]() $\mathsf {HA}$
:
$\mathsf {HA}$
:
Lemma 4.32. Suppose
![]() $\phi $
is a formula of Heyting arithmetic
$\phi $
is a formula of Heyting arithmetic
![]() $\mathsf {HA}$
and
$\mathsf {HA}$
and
![]() $\mathbf {n}$
is a numeral. If
$\mathbf {n}$
is a numeral. If
![]() $\mathsf {HA}\vdash \mathbf {n}\Vdash \phi $
, then
$\mathsf {HA}\vdash \mathbf {n}\Vdash \phi $
, then
 $\overline {\mathbf {Prop}^{r}}\Vdash \overline {\phi }$
.
$\overline {\mathbf {Prop}^{r}}\Vdash \overline {\phi }$
.
Theorem 4.33. (Formal Church’s Thesis)
 $$ \begin{align*} &\overline{\mathbf{Prop}^{r}}\vdash (\forall \overline{x}\in \mathsf{N})(\exists \overline{z}\in \mathsf{N})\mathsf{R}(\overline{x},\overline{z})\\&\quad \rightarrow(\exists \overline{e}\in \mathsf{N})(\forall \overline{x}\in \mathsf{N})(\exists \overline{y}\in \mathsf{N})(\overline{T(e,x,y)}\wedge \mathsf{R}(\overline{x},\overline{U(y)})) \end{align*} $$
$$ \begin{align*} &\overline{\mathbf{Prop}^{r}}\vdash (\forall \overline{x}\in \mathsf{N})(\exists \overline{z}\in \mathsf{N})\mathsf{R}(\overline{x},\overline{z})\\&\quad \rightarrow(\exists \overline{e}\in \mathsf{N})(\forall \overline{x}\in \mathsf{N})(\exists \overline{y}\in \mathsf{N})(\overline{T(e,x,y)}\wedge \mathsf{R}(\overline{x},\overline{U(y)})) \end{align*} $$
where
![]() $T(e,x,y)$
and
$T(e,x,y)$
and
![]() $U(y)$
are Kleene’s predicate and primitive recursive function, respectively.
$U(y)$
are Kleene’s predicate and primitive recursive function, respectively.
5. A predicative version of Hyland’s Effective Topos
Definition 5.1. The Predicative Effective p-Topos
![]() ${\mathbf{pEff}} $
is the category
${\mathbf{pEff}} $
is the category
 $\mathcal {Q}_{\overline {\mathbf {Prop}^{r}}}$
obtained by applying the elementary quotient completion in [Reference Maietti and Rosolini17] to the doctrine
$\mathcal {Q}_{\overline {\mathbf {Prop}^{r}}}$
obtained by applying the elementary quotient completion in [Reference Maietti and Rosolini17] to the doctrine
 ${\overline {\mathbf {Prop}^{r}}}$
, that is, it is the category whose objects are the pairs
${\overline {\mathbf {Prop}^{r}}}$
, that is, it is the category whose objects are the pairs
![]() $(\mathsf {A},\mathsf {R})$
where
$(\mathsf {A},\mathsf {R})$
where
![]() $\mathsf {A}$
is an object of the category
$\mathsf {A}$
is an object of the category
![]() $\mathcal {C}_{r}$
and
$\mathcal {C}_{r}$
and
![]() $\mathsf {R}$
is an object of
$\mathsf {R}$
is an object of
 $\overline {\mathbf {Prop}^{r}}(\mathsf {A}\times \mathsf {A})$
for which the following hold:
$\overline {\mathbf {Prop}^{r}}(\mathsf {A}\times \mathsf {A})$
for which the following hold:
-
1.
 $\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})\mathsf {R}(x,x)$
;
$\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})\mathsf {R}(x,x)$
; -
2.
 $\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\forall y\in \mathsf {A})(\mathsf {R}(x,y)\rightarrow \mathsf {R}(y,x))$
;
$\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\forall y\in \mathsf {A})(\mathsf {R}(x,y)\rightarrow \mathsf {R}(y,x))$
; -
3.
 $\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\forall y\in \mathsf {A})(\forall z\in \mathsf {A})(\mathsf {R}(x,y)\wedge \mathsf {R}(y,z)\rightarrow \mathsf {R}(x,z))$
.
$\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\forall y\in \mathsf {A})(\forall z\in \mathsf {A})(\mathsf {R}(x,y)\wedge \mathsf {R}(y,z)\rightarrow \mathsf {R}(x,z))$
.
An arrow from
![]() $(\mathsf {A},\mathsf {R})$
to
$(\mathsf {A},\mathsf {R})$
to
![]() $(\mathsf {B},\mathsf {S})$
is an equivalence class
$(\mathsf {B},\mathsf {S})$
is an equivalence class
![]() $[\mathsf {f}]_{\simeq }$
of arrows
$[\mathsf {f}]_{\simeq }$
of arrows
![]() $\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
$\mathsf {f}:\mathsf {A}\rightarrow \mathsf {B}$
in
![]() $\mathcal {C}_{r}$
such that
$\mathcal {C}_{r}$
such that
 $\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\forall y\in \mathsf {A})(\mathsf {R}(x,y)\rightarrow \mathsf {S}(\mathsf {f}(x),\mathsf {f}(y)))$
, where
$\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\forall y\in \mathsf {A})(\mathsf {R}(x,y)\rightarrow \mathsf {S}(\mathsf {f}(x),\mathsf {f}(y)))$
, where
![]() $\mathsf {f}\simeq \mathsf {g}$
if and only if
$\mathsf {f}\simeq \mathsf {g}$
if and only if
 $\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\mathsf {R}(x,x)\rightarrow \mathsf {S}(\mathsf {f}(x),\mathsf {g}(x)))$
.
$\overline {\mathbf {Prop}^{r}}\vdash (\forall x\in \mathsf {A})(\mathsf {R}(x,x)\rightarrow \mathsf {S}(\mathsf {f}(x),\mathsf {g}(x)))$
.
As pointed out in [Reference Maietti, Rosolini, Probst and Schuster18] the elementary completion coincides with the ex/lex completion by Carboni and Celia Magno [Reference Carboni and Magno3] when we consider the doctrine of weak subobjects
![]() $\mathbf {wSub}$
of a finitely complete category. As we proved Theorem 4.19, this applies to our case.
$\mathbf {wSub}$
of a finitely complete category. As we proved Theorem 4.19, this applies to our case.
Theorem 5.2.
 ${\mathbf {pEff}}\cong (\mathcal {C}_{r})_{ex/lex}$
. In particular
${\mathbf {pEff}}\cong (\mathcal {C}_{r})_{ex/lex}$
. In particular
![]() ${\mathbf {pEff}}$
is an exact category.
${\mathbf {pEff}}$
is an exact category.
From Theorems 5.2 and 4.13, using the main result in [Reference Carboni and Rosolini4], we get
Theorem 5.3.
![]() ${\mathbf {pEff}}$
is a locally cartesian closed category.
${\mathbf {pEff}}$
is a locally cartesian closed category.
Even more we can show that
![]() ${\mathbf {pEff}}$
is actually a list-arithmetic pretopos.
${\mathbf {pEff}}$
is actually a list-arithmetic pretopos.
Lemma 5.4.
![]() ${\mathbf {pEff}}$
has disjoint stable finite coproducts and list objects.
${\mathbf {pEff}}$
has disjoint stable finite coproducts and list objects.
Proof The existence of disjoint stable finite coproducts follows essentially from results in [Reference Carboni2]. An initial object is
![]() $(\mathsf {0},\top _{\mathsf {0}\times \mathsf {0}})$
. A binary coproduct for
$(\mathsf {0},\top _{\mathsf {0}\times \mathsf {0}})$
. A binary coproduct for
![]() $(\mathsf {A},\mathsf {R})$
and
$(\mathsf {A},\mathsf {R})$
and
![]() $(\mathsf {B},\mathsf {S})$
is determined by the equivalence relation on
$(\mathsf {B},\mathsf {S})$
is determined by the equivalence relation on
![]() $\mathsf {A}+\mathsf {B}$
which is the interpretation of the following formula of the internal language of
$\mathsf {A}+\mathsf {B}$
which is the interpretation of the following formula of the internal language of
 $\overline {\mathbf {Prop}^{r}}$
$\overline {\mathbf {Prop}^{r}}$
in the context
![]() $[x\in (\mathsf {A}+\mathsf {B})\times (\mathsf {A}+\mathsf {B})]$
, together with the injections
$[x\in (\mathsf {A}+\mathsf {B})\times (\mathsf {A}+\mathsf {B})]$
, together with the injections
![]() $[\mathsf {j}_{1}]_{\simeq }$
and
$[\mathsf {j}_{1}]_{\simeq }$
and
![]() $[\mathsf {j}_{2}]_{\simeq }$
. A list object for
$[\mathsf {j}_{2}]_{\simeq }$
. A list object for
![]() $(\mathsf {A},\mathsf {R})$
has as underlying object
$(\mathsf {A},\mathsf {R})$
has as underlying object
![]() $\mathsf {List}(\mathsf {A})$
and as equivalence relation that given by the interpretation of the formula
$\mathsf {List}(\mathsf {A})$
and as equivalence relation that given by the interpretation of the formula
in the context
![]() $[x\in \mathsf {List}(\mathsf {A})\times \mathsf {List}(\mathsf {A})]$
where
$[x\in \mathsf {List}(\mathsf {A})\times \mathsf {List}(\mathsf {A})]$
where
![]() $\mathsf {lh}:\mathsf {List}(\mathsf {A})\rightarrow \mathsf {N}$
is the length arrow and
$\mathsf {lh}:\mathsf {List}(\mathsf {A})\rightarrow \mathsf {N}$
is the length arrow and
![]() $\mathsf {cm}:\mathsf {List}(\mathsf {A})\times \mathsf {N}\rightarrow \mathsf {A}+\mathsf {1}$
is the component arrowFootnote
2
in the category
$\mathsf {cm}:\mathsf {List}(\mathsf {A})\times \mathsf {N}\rightarrow \mathsf {A}+\mathsf {1}$
is the component arrowFootnote
2
in the category
![]() $\mathcal {C}_{r}$
. The empty list and the append arrows are given by
$\mathcal {C}_{r}$
. The empty list and the append arrows are given by
![]() $[\epsilon ]_{\simeq }$
and
$[\epsilon ]_{\simeq }$
and
![]() $[\mathsf {cons}]_{\simeq }$
, respectively. ⊣
$[\mathsf {cons}]_{\simeq }$
, respectively. ⊣
The previous results about
![]() ${\mathbf {pEff}}$
can be summarized in the following theorem.
${\mathbf {pEff}}$
can be summarized in the following theorem.
Theorem 5.5. The category
![]() ${\mathbf {pEff}}$
is a locally cartesian closed list-arithmetic pretopos.
${\mathbf {pEff}}$
is a locally cartesian closed list-arithmetic pretopos.
Now we give the definition of the hyperdoctrine
![]() ${{\mathbf {pEff}_{prop}}}$
of propositions associated by construction to
${{\mathbf {pEff}_{prop}}}$
of propositions associated by construction to
![]() ${\mathbf {pEff}}$
as an elementary quotient completion in [Reference Maietti and Rosolini17] (this doctrine defines the equivalence relations with respect to which the elementary quotient completion is closed under effective quotients):
${\mathbf {pEff}}$
as an elementary quotient completion in [Reference Maietti and Rosolini17] (this doctrine defines the equivalence relations with respect to which the elementary quotient completion is closed under effective quotients):
Definition 5.6. The functor
 ${{\mathbf {pEff}_{prop}}}:{\mathbf {pEff}}^{op}\rightarrow \mathbf {Pos}$
is defined as follows:
${{\mathbf {pEff}_{prop}}}:{\mathbf {pEff}}^{op}\rightarrow \mathbf {Pos}$
is defined as follows:
-
1.
 $\mathsf {P}\in {{\mathbf {pEff}_{prop}}}(\mathsf {A},\mathsf {R})$
if
$\mathsf {P}\in {{\mathbf {pEff}_{prop}}}(\mathsf {A},\mathsf {R})$
if
 $\mathsf {P}\in \overline {\mathbf {Prop}^{r}}(\mathsf {A})$
and
$\mathsf {P}\in \overline {\mathbf {Prop}^{r}}(\mathsf {A})$
and  $$ \begin{align*} \overline{\mathbf{Prop}^{r}}\vdash (\forall x\in \mathsf{A})(\forall y\in \mathsf{A})(\mathsf{P}(x)\wedge \mathsf{R}(x,y)\rightarrow \mathsf{P}(y)); \end{align*} $$
$$ \begin{align*} \overline{\mathbf{Prop}^{r}}\vdash (\forall x\in \mathsf{A})(\forall y\in \mathsf{A})(\mathsf{P}(x)\wedge \mathsf{R}(x,y)\rightarrow \mathsf{P}(y)); \end{align*} $$
-
2.
 $\mathsf {P}\sqsubseteq _{(\mathsf {A},\mathsf {R})}\mathsf {Q}$
in
$\mathsf {P}\sqsubseteq _{(\mathsf {A},\mathsf {R})}\mathsf {Q}$
in
 ${{\mathbf {pEff}_{prop}}}((\mathsf {A},\mathsf {R}))$
iff
${{\mathbf {pEff}_{prop}}}((\mathsf {A},\mathsf {R}))$
iff
 $\mathsf {P}\sqsubseteq _{\mathsf {A}}\mathsf {Q}$
in
$\mathsf {P}\sqsubseteq _{\mathsf {A}}\mathsf {Q}$
in
 $\overline {\mathbf {Prop}^{r}}(\mathsf {A})$
;
$\overline {\mathbf {Prop}^{r}}(\mathsf {A})$
; -
3.
 ${{\mathbf {pEff}_{prop}}}_{[\mathsf {f}]_{\simeq }}(\mathsf {P}):=\overline {\mathbf {Prop}^{r}}_{\mathsf {f}}(\mathsf {P})$
.
${{\mathbf {pEff}_{prop}}}_{[\mathsf {f}]_{\simeq }}(\mathsf {P}):=\overline {\mathbf {Prop}^{r}}_{\mathsf {f}}(\mathsf {P})$
.
From results in [Reference Maietti, Rosolini, Probst and Schuster18] and Theorem 4.19 it follows that:
Theorem 5.7. The functor
![]() ${{\mathbf {pEff}_{prop}}}$
is a first-order hyperdoctrine over
${{\mathbf {pEff}_{prop}}}$
is a first-order hyperdoctrine over
![]() ${\mathbf {pEff}}$
which is equivalent to its subobject doctrine, that is,
${\mathbf {pEff}}$
which is equivalent to its subobject doctrine, that is,
![]() ${{\mathbf {pEff}_{prop}}} \cong \mathbf {Sub}_{{\mathbf {pEff}}}$
.
${{\mathbf {pEff}_{prop}}} \cong \mathbf {Sub}_{{\mathbf {pEff}}}$
.
An important property of the doctrine
![]() ${{\mathbf {pEff}_{prop}}}$
is that it validates the Formal Church’s Thesis as a consequence of the fact that the underlying doctrine
${{\mathbf {pEff}_{prop}}}$
is that it validates the Formal Church’s Thesis as a consequence of the fact that the underlying doctrine
 ${\overline {\mathbf {Prop}^{r}}}$
validates it by Lemma 4.33:
${\overline {\mathbf {Prop}^{r}}}$
validates it by Lemma 4.33:
Theorem 5.8. (Formal Church’s thesis in
 ${{\mathbf {pEff}_{prop}}}$
)
${{\mathbf {pEff}_{prop}}}$
)
![]() ${{\mathbf {pEff}_{prop}}}$
validates
${{\mathbf {pEff}_{prop}}}$
validates
 $$ \begin{align*} (\forall \overline{x}\in \mathsf{N})(\exists \overline{z}\in \mathsf{N})\mathsf{R}(\overline{x},\overline{z})\rightarrow(\exists \overline{e}\in \mathsf{N}_{{\mathbf{pEff}}})(\forall \overline{x}\in \mathsf{N})(\exists \overline{y}\in \mathsf{N})(\overline{T(e,x,y)}\wedge \mathsf{R}(\overline{y},\overline{U(y)})). \end{align*} $$
$$ \begin{align*} (\forall \overline{x}\in \mathsf{N})(\exists \overline{z}\in \mathsf{N})\mathsf{R}(\overline{x},\overline{z})\rightarrow(\exists \overline{e}\in \mathsf{N}_{{\mathbf{pEff}}})(\forall \overline{x}\in \mathsf{N})(\exists \overline{y}\in \mathsf{N})(\overline{T(e,x,y)}\wedge \mathsf{R}(\overline{y},\overline{U(y)})). \end{align*} $$
Let us now define a full subcategory of sets of
![]() ${\mathbf {pEff}}$
.
${\mathbf {pEff}}$
.
Definition 5.9. The category
![]() ${{\mathbf {pEff}_{set}}}$
of sets of
${{\mathbf {pEff}_{set}}}$
of sets of
![]() ${\mathbf {pEff}}$
is the full subcategory of
${\mathbf {pEff}}$
is the full subcategory of
![]() ${\mathbf {pEff}}$
of which the objects are those objects
${\mathbf {pEff}}$
of which the objects are those objects
![]() $(\mathsf {A},\mathsf {R})$
in
$(\mathsf {A},\mathsf {R})$
in
![]() ${\mathbf {pEff}}$
such that
${\mathbf {pEff}}$
such that
![]() $\mathsf {A}$
is an object of
$\mathsf {A}$
is an object of
![]() $\mathcal {S}_{r}$
and
$\mathcal {S}_{r}$
and
 $\mathsf {R}\in \overline {\mathbf {Prop}^{r}_{s}}(\mathsf {A}\times \mathsf {A})$
. Equivalently,
$\mathsf {R}\in \overline {\mathbf {Prop}^{r}_{s}}(\mathsf {A}\times \mathsf {A})$
. Equivalently,
![]() ${{\mathbf {pEff}_{set}}}$
is the base category of the elementary quotient completion in [Reference Maietti and Rosolini17] of
${{\mathbf {pEff}_{set}}}$
is the base category of the elementary quotient completion in [Reference Maietti and Rosolini17] of
![]() ${\mathbf {pEff}_{prop_s}}$
.
${\mathbf {pEff}_{prop_s}}$
.
As we have done above for
![]() ${\mathbf {pEff}}$
, one can easily adapt the proofs and obtain the following.
${\mathbf {pEff}}$
, one can easily adapt the proofs and obtain the following.
Theorem 5.10.
![]() ${{\mathbf {pEff}_{set}}}$
is a locally cartesian closed category with disjoint stable finite coproducts and list objects. Moreover, this structure is preserved by the embedding of
${{\mathbf {pEff}_{set}}}$
is a locally cartesian closed category with disjoint stable finite coproducts and list objects. Moreover, this structure is preserved by the embedding of
![]() ${{\mathbf {pEff}_{set}}}$
into
${{\mathbf {pEff}_{set}}}$
into
![]() ${\mathbf {pEff}}$
.
${\mathbf {pEff}}$
.
Definition 5.11. The functor
 ${\mathbf {pEff}_{prop_s}}:{{\mathbf {pEff}_{set}}}^{op}\rightarrow \mathbf {Pos}$
is the subfunctor of
${\mathbf {pEff}_{prop_s}}:{{\mathbf {pEff}_{set}}}^{op}\rightarrow \mathbf {Pos}$
is the subfunctor of
![]() ${{\mathbf {pEff}_{prop}}}$
restricted to
${{\mathbf {pEff}_{prop}}}$
restricted to
![]() ${{\mathbf {pEff}_{set}}}$
whose value on
${{\mathbf {pEff}_{set}}}$
whose value on
![]() $(\mathsf {A},\mathsf {R})$
in
$(\mathsf {A},\mathsf {R})$
in
![]() ${{\mathbf {pEff}_{set}}}$
is the full subcategory of
${{\mathbf {pEff}_{set}}}$
is the full subcategory of
 ${{\mathbf {pEff}_{prop}}}(\mathsf {A},\mathsf {R})$
whose objects are those
${{\mathbf {pEff}_{prop}}}(\mathsf {A},\mathsf {R})$
whose objects are those
![]() $\mathsf {P}$
which are both in
$\mathsf {P}$
which are both in
 $\overline {\mathbf {Prop}^{r}_{s}}(\mathsf {A})$
and in
$\overline {\mathbf {Prop}^{r}_{s}}(\mathsf {A})$
and in
 ${{\mathbf {pEff}_{prop}}}(\mathsf {A},\mathsf {R})$
.
${{\mathbf {pEff}_{prop}}}(\mathsf {A},\mathsf {R})$
.
Theorem 5.12. There exists an object
![]() $\Omega $
in
$\Omega $
in
![]() ${\mathbf {pEff}}$
which represents
${\mathbf {pEff}}$
which represents
![]() ${\mathbf {pEff}_{prop_s}}$
, that is, there is a natural isomorphism between
${\mathbf {pEff}_{prop_s}}$
, that is, there is a natural isomorphism between
 ${\mathbf {pEff}_{prop_s}}(-)$
and
${\mathbf {pEff}_{prop_s}}(-)$
and
 ${\mathbf {pEff}}(-,\Omega )|_{{{\mathbf {pEff}_{set}}}}$
.
${\mathbf {pEff}}(-,\Omega )|_{{{\mathbf {pEff}_{set}}}}$
.
Proof The object
![]() $\Omega $
is
$\Omega $
is
 $(\mathsf {U}_{\mathsf {S}}, [\mathsf {EQ}(x)]_{\sim _{\mathsf {U}_{\mathsf {S}}\times \mathsf {U}_{\mathsf {S}} }})$
where
$(\mathsf {U}_{\mathsf {S}}, [\mathsf {EQ}(x)]_{\sim _{\mathsf {U}_{\mathsf {S}}\times \mathsf {U}_{\mathsf {S}} }})$
where
![]() $x'\Vdash \mathsf {EQ}(x)$
is defined as
$x'\Vdash \mathsf {EQ}(x)$
is defined as
![]() $\forall t\,(t\,\overline {\varepsilon }\,p_{1}(x)\rightarrow \{p_{1}(x')\}(t)\,\overline {\varepsilon }\,p_{2}(x))\wedge \forall s(s\,\overline {\varepsilon }\,p_{2}(x)\rightarrow \{p_{2}(x')\}(s)\,\overline {\varepsilon }\,p_{1}(x))$
. ⊣
$\forall t\,(t\,\overline {\varepsilon }\,p_{1}(x)\rightarrow \{p_{1}(x')\}(t)\,\overline {\varepsilon }\,p_{2}(x))\wedge \forall s(s\,\overline {\varepsilon }\,p_{2}(x)\rightarrow \{p_{2}(x')\}(s)\,\overline {\varepsilon }\,p_{1}(x))$
. ⊣
As a consequence of Theorem 4.29, we have the following
Theorem 5.13. The functor
![]() ${\mathbf {pEff}_{prop_s}}$
is a first-order hyperdoctrine which is equivalent to the subobject doctrine
${\mathbf {pEff}_{prop_s}}$
is a first-order hyperdoctrine which is equivalent to the subobject doctrine
![]() $\mathbf {Sub}_{{{\mathbf {pEff}_{set}}}}$
over
$\mathbf {Sub}_{{{\mathbf {pEff}_{set}}}}$
over
![]() ${{\mathbf {pEff}_{set}}}$
.
${{\mathbf {pEff}_{set}}}$
.
In particular, from Theorem 5.12 it follows that
Theorem 5.14. There exists a natural isomorphism between
![]() $\mathbf {Sub}_{{{\mathbf {pEff}_{set}}}}$
and
$\mathbf {Sub}_{{{\mathbf {pEff}_{set}}}}$
and
![]() $\mathbf {Hom}_{{\mathbf {pEff}}}(-,\Omega )$
over
$\mathbf {Hom}_{{\mathbf {pEff}}}(-,\Omega )$
over
![]() ${{\mathbf {pEff}_{set}}}$
; that is, there is a subobject classifier for
${{\mathbf {pEff}_{set}}}$
; that is, there is a subobject classifier for
![]() ${{\mathbf {pEff}_{set}}}$
in
${{\mathbf {pEff}_{set}}}$
in
![]() ${\mathbf {pEff}}$
.
${\mathbf {pEff}}$
.
6. Embedding of
 ${\mathbf {pEff}}$
in Hyland’s Effective Topos
${\mathbf {pEff}}$
in Hyland’s Effective Topos
Here we show that the construction of
![]() ${\mathbf {pEff}}$
performed on the subcategory of recursive functions of
${\mathbf {pEff}}$
performed on the subcategory of recursive functions of
![]() ${{\mathbf {Eff} }}$
gives rise to a full subcategory of the Effective Topos
${{\mathbf {Eff} }}$
gives rise to a full subcategory of the Effective Topos
![]() ${{\mathbf {Eff} }}$
whose embedding preserves the list-arithmetic locally cartesian closed pretopos structure.
${{\mathbf {Eff} }}$
whose embedding preserves the list-arithmetic locally cartesian closed pretopos structure.
The Effective Topos (see [Reference Hyland, Troelstra and van Dalen7]) can be presented as the exact on lex completion
 $(\mathbf {pAsm})_{ex/lex}$
of the category
$(\mathbf {pAsm})_{ex/lex}$
of the category
![]() $\mathbf {pAsm}$
of partitioned assemblies (see [Reference Robinson and Rosolini21]). In particular,
$\mathbf {pAsm}$
of partitioned assemblies (see [Reference Robinson and Rosolini21]). In particular,
![]() ${{\mathbf {Eff} }}$
inherits the validity of Formal Church’s thesis from
${{\mathbf {Eff} }}$
inherits the validity of Formal Church’s thesis from
![]() $\mathbf {pAsm}$
as shown in [Reference Maietti, Pasquali and Rosolini15].
$\mathbf {pAsm}$
as shown in [Reference Maietti, Pasquali and Rosolini15].
The category
![]() $\mathbf {pAsm}$
of partitioned assemblies is the category whose objects are pairs
$\mathbf {pAsm}$
of partitioned assemblies is the category whose objects are pairs
![]() $(A,P)$
where A is a set and
$(A,P)$
where A is a set and
![]() $P:A\rightarrow \mathbb {N}$
is a function towards the set
$P:A\rightarrow \mathbb {N}$
is a function towards the set
![]() $\mathbb {N}$
of natural numbers, and whose arrows from such an object
$\mathbb {N}$
of natural numbers, and whose arrows from such an object
![]() $(A,P)$
to another
$(A,P)$
to another
![]() $(B,Q)$
are functions
$(B,Q)$
are functions
![]() $f:A\rightarrow B$
such that there exists a partial recursive function
$f:A\rightarrow B$
such that there exists a partial recursive function
![]() $\varphi :\mathbb {N}\rightharpoonup \mathbb {N}$
such that
$\varphi :\mathbb {N}\rightharpoonup \mathbb {N}$
such that
![]() $Q\circ f=\varphi \circ P$
.
$Q\circ f=\varphi \circ P$
.
The category
![]() $\mathbf {Rec}$
of recursive functions is defined as follows: the objects of
$\mathbf {Rec}$
of recursive functions is defined as follows: the objects of
![]() $\mathbf {Rec}$
are subsets
$\mathbf {Rec}$
are subsets
![]() $A\subseteq \mathbb {N}$
; an arrow from A to B is a function
$A\subseteq \mathbb {N}$
; an arrow from A to B is a function
![]() $f:A\rightarrow B$
such that there exists a (partial) recursive function
$f:A\rightarrow B$
such that there exists a (partial) recursive function
![]() $\overline {f}:\mathbb {N}\rightharpoonup \mathbb {N}$
such that
$\overline {f}:\mathbb {N}\rightharpoonup \mathbb {N}$
such that
![]() $A\subseteq dom(\overline {f})$
and
$A\subseteq dom(\overline {f})$
and
![]() $\overline {f}|_{A}=f$
; composition is given by composition of functions and identities are defined as identity functions.
$\overline {f}|_{A}=f$
; composition is given by composition of functions and identities are defined as identity functions.
The category
![]() $\mathbf {Rec}$
is clearly equivalent to the full subcategory of
$\mathbf {Rec}$
is clearly equivalent to the full subcategory of
![]() $\mathbf {pAsm}$
whose objects are of the form
$\mathbf {pAsm}$
whose objects are of the form
![]() $(A, a\mapsto a)$
with
$(A, a\mapsto a)$
with
![]() $A\subseteq \mathbb {N}$
. Moreover, the functor of weak subobjects over
$A\subseteq \mathbb {N}$
. Moreover, the functor of weak subobjects over
![]() $\mathbf {Rec}$
is equivalent to that of weak subobjects over partitioned assemblies composed with the embedding of
$\mathbf {Rec}$
is equivalent to that of weak subobjects over partitioned assemblies composed with the embedding of
![]() $\mathbf {Rec}$
into it.
$\mathbf {Rec}$
into it.
If
![]() $\mathcal {Q}_{\mathbf {wSub}_{\mathbf {Rec}}}$
is the elementary quotient completion in [Reference Maietti and Rosolini17] applied to the doctrine
$\mathcal {Q}_{\mathbf {wSub}_{\mathbf {Rec}}}$
is the elementary quotient completion in [Reference Maietti and Rosolini17] applied to the doctrine
![]() $\mathbf {wSub}_{\mathbf {Rec}}$
of weak subobjects in
$\mathbf {wSub}_{\mathbf {Rec}}$
of weak subobjects in
![]() $\mathbf {Rec}$
, as a consequence of observations in [Reference Maietti and Rosolini17, Reference Maietti, Rosolini, Probst and Schuster18], we have that:
$\mathbf {Rec}$
, as a consequence of observations in [Reference Maietti and Rosolini17, Reference Maietti, Rosolini, Probst and Schuster18], we have that:
Theorem 6.1. The category
![]() $\mathcal {Q}_{\mathbf {wSub}_{\mathbf {Rec}}}$
is equivalent to the exact on lex completion of the category of recursive functions
$\mathcal {Q}_{\mathbf {wSub}_{\mathbf {Rec}}}$
is equivalent to the exact on lex completion of the category of recursive functions
![]() $\mathbf {Rec}$
. In particular
$\mathbf {Rec}$
. In particular
![]() $\mathcal {Q}_{\mathbf {wSub}_{\mathbf {Rec}}}$
is a full subcategory of the Effective Topos:
$\mathcal {Q}_{\mathbf {wSub}_{\mathbf {Rec}}}$
is a full subcategory of the Effective Topos:
The theory
![]() ${{\widehat {ID_1}}}$
has a standard model in set theory: one can in fact consider the set of natural numbers with the interpretation of Peano arithmetic and interpret the fixpoint formulas in
${{\widehat {ID_1}}}$
has a standard model in set theory: one can in fact consider the set of natural numbers with the interpretation of Peano arithmetic and interpret the fixpoint formulas in
![]() ${{\widehat {ID_1}}}$
using transfinite induction.
${{\widehat {ID_1}}}$
using transfinite induction.
Theorem 6.2. The standard interpretation of
![]() ${{\widehat {ID_1}}}$
in
${{\widehat {ID_1}}}$
in
![]() $\mathsf {ZFC}$
gives rise to a functor
$\mathsf {ZFC}$
gives rise to a functor
![]() $\mathbf {Int}:\mathcal {C}_{r}\rightarrow \mathbf {Rec}$
sending each realized collection
$\mathbf {Int}:\mathcal {C}_{r}\rightarrow \mathbf {Rec}$
sending each realized collection
![]() $\mathsf {A}$
of
$\mathsf {A}$
of
![]() ${{\widehat {ID_1}}}$
to the subset of
${{\widehat {ID_1}}}$
to the subset of
![]() $\mathbb {N}$
given by the interpretation of the formula
$\mathbb {N}$
given by the interpretation of the formula
![]() $x\,\varepsilon \, \mathsf {A}$
and sending each arrow
$x\,\varepsilon \, \mathsf {A}$
and sending each arrow
![]() $[\mathbf {n}]_{\approx }$
to the recursive function encoded by the corresponding natural number n. The interpretation also gives rise to a natural transformation preserving connectives and quantifiers
$[\mathbf {n}]_{\approx }$
to the recursive function encoded by the corresponding natural number n. The interpretation also gives rise to a natural transformation preserving connectives and quantifiers
 $\eta :\overline {\mathbf {Prop}^{r}}\rightarrow \mathbf {wSub}_{\mathbf {Rec}}\circ \mathbf {Int}$
which is defined analogously using Theorem 4.19. In particular this allows one to define a functor
$\eta :\overline {\mathbf {Prop}^{r}}\rightarrow \mathbf {wSub}_{\mathbf {Rec}}\circ \mathbf {Int}$
which is defined analogously using Theorem 4.19. In particular this allows one to define a functor
 $\mathbf {J}:{\mathbf {pEff}}\rightarrow (\mathbf {Rec})_{ex/lex}$
and then also the functor
$\mathbf {J}:{\mathbf {pEff}}\rightarrow (\mathbf {Rec})_{ex/lex}$
and then also the functor
![]() $\mathbf {I}:{\mathbf {pEff}}\rightarrow {{\mathbf {Eff} }}$
obtained by composing
$\mathbf {I}:{\mathbf {pEff}}\rightarrow {{\mathbf {Eff} }}$
obtained by composing
![]() $\mathbf {J}$
with the embedding in Theorem 6.1. The functor
$\mathbf {J}$
with the embedding in Theorem 6.1. The functor
![]() $\mathbf {I}$
preserves finite limits, exponentials, lists, finite coproducts and quotients.
$\mathbf {I}$
preserves finite limits, exponentials, lists, finite coproducts and quotients.
Proof The first part follows from the definition of the interpretation. The functor
![]() $\mathbf {I}$
preserves finite limits, exponentials, lists, finite coproducts and quotients, because
$\mathbf {I}$
preserves finite limits, exponentials, lists, finite coproducts and quotients, because
![]() $\mathbf {J}$
and the embedding from
$\mathbf {J}$
and the embedding from
 $(\mathbf {Rec})_{ex/lex}$
to
$(\mathbf {Rec})_{ex/lex}$
to
![]() ${{\mathbf {Eff} }}$
preserve them. ⊣
${{\mathbf {Eff} }}$
preserve them. ⊣
7. Future work
Our predicative variant
![]() ${\mathbf {pEff}}$
of the Effective Topos has a richer structure than the one shown here. Indeed, first we can lift
${\mathbf {pEff}}$
of the Effective Topos has a richer structure than the one shown here. Indeed, first we can lift
![]() $\mathbf {Set}^r$
on
$\mathbf {Set}^r$
on
![]() $\mathcal {C}_r$
in the Kleene effective p-tripos to define dependent sets which can be used to interpret those of the intensional level of the Minimalist Foundation in [Reference Maietti9]; second, we can use this lifting to define dependent sets over
$\mathcal {C}_r$
in the Kleene effective p-tripos to define dependent sets which can be used to interpret those of the intensional level of the Minimalist Foundation in [Reference Maietti9]; second, we can use this lifting to define dependent sets over
![]() ${\mathbf {pEff}}$
which can be used to interpret those in the extensional level of the Minimalist Foundation in [Reference Maietti9].
${\mathbf {pEff}}$
which can be used to interpret those in the extensional level of the Minimalist Foundation in [Reference Maietti9].
Acknowledgments
The authors acknowledge S. Awodey, M. Hyland, P. Rosolini, and T. Streicher for very helpful discussions and suggestions and their colleagues F. Ciraulo and G. Sambin for supporting this line of research.