Le paradigme de théorie stable est la théorie T d'un corps algébriquement clos; une autre théorie stable T′ est celle de la structure formée d'un corps algébriquement clos, avec en outre un symbole relationnel unaire interprétant un de ses sous-corps propres algébriquement clos. C'est à l'éclaircissement des rapports de T et de T′ qu'est consacré cet article.

J'y considère une théorie complète T stable, et les structures formées d'un modèle N de T, avec en outre un symbole relationnel unaire 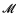(x) interprétant une restriction élémentaire M de N; j'appelle ces structures paires de modèles de T.

Et je dis que la paire (N, M) est belle si d'une part M est ∣T∣+-saturé, et d'autre part pour tout n-uplet ā d'éléments de N, tout type, au sens de T, sur M ⋃ {α} est réalisé dans N.

Le premier résultat (Théorème 4) est que deux belles paires sont élémentairement équivalentes. Plus précisément, si (N1, M1) et (N2, M2) sont deux belles paires, et si ā est dans la première, b¯ dans la seconde, le fait que le type de ā sur M1 et celui de b¯ sur M2 soient équivalents dans l'ordre fondamental au sens de T suffit (et est bien sûr nécessaire) pour que ā at b¯ aient même type (sur ⊘) au sens de la théorie T′ des belles paires.