We continue our study of the class ${\cal C}\left( D \right)$, where D is a uniform ultrafilter on a cardinal κ and 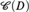${\cal C}\left( D \right)$ is the class of all pairs 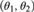$\left( {{\theta _1},{\theta _2}} \right)$, where 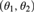$\left( {{\theta _1},{\theta _2}} \right)$ is the cofinality of a cut in 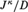${J^\kappa }/D$ and J is some ${\left( {{\theta _1} + {\theta _2}} \right)^ + }$-saturated dense linear order. We give a combinatorial characterization of the class 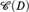${\cal C}\left( D \right)$. We also show that if 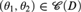$\left( {{\theta _1},{\theta _2}} \right) \in {\cal C}\left( D \right)$ and D is 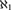${\aleph _1}$-complete or 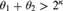${\theta _1} + {\theta _2} > {2^\kappa }$, then 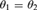${\theta _1} = {\theta _2}$.