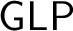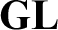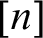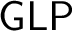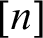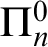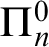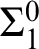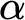1 Introduction
As mentioned in the abstract, by Solovay’s celebrated completeness result [Reference Solovay31] on provability we know that the provability logic
${\textbf {GL}}$
describes exactly all provable structural properties for any sound and strong enough arithmetical theory with a decidable axiomatisation. Japaridze generalised this result in [Reference Japaridze22] by considering a polymodal version
${\mathsf {GLP}}$
of
${\textbf {GL}}$
with modalities
$[n]$
for each natural number n referring to ever increasing notions of provability.
Japaridze considered an arithmetical interpretation of the logic
${\mathsf {GLP}}$
where the
$[n]$
referred to a natural formalisation of “provable over the base theory T using at most n nested applications of the
$\omega $
-rule.” Beklemishev introduced in [Reference Beklemishev, Hájek, Valdés-Villanueva and Westerståhl6] the logics
${\mathsf {GLP}}_\Lambda $
that are like
${\mathsf {GLP}}$
only that they now include a sequence of provability predicates
$[\alpha ]$
of ever increasing strength for each ordinal
$\alpha $
below some fixed ordinal
$\Lambda $
. In [Reference Fernández-Duque and Joosten18] the authors generalised Japaridze’s result into the transfinite by providing an interpretation of
${\mathsf {GLP}}_\Lambda $
for recursive
$\Lambda $
into second order arithmetic by allowing for
$[\alpha ]$
at most
$\alpha $
nestings of the omega rule, thereby providing a first arithmetical interpretation of
${\mathsf {GLP}}_\Lambda $
for
$\Lambda>\omega $
. In a recent paper [Reference Beklemishev and Pakhomov9] Beklemishev and Pakhomov provide an alternative interpretation in first order arithmetic enriched with a collection of ever more expressive truth predicates indexed by the ordinals.
Modern treatments of
${\mathsf {GLP}}_\omega $
tend to interpret the
$[n]$
provability notion as “provable in a base theory T together with all true
$\Pi ^0_n$
formulas.” Let us call this the truth-interpretation here. The main reason for the popularity of the truth-interpretation is that the resulting provability hierarchies run in phase with the arithmetical hierarchy and they imply good preservation properties between different consistency statements giving rise to the so-called reduction property. In particular, due to these good properties Beklemishev was able to set
${\mathsf {GLP}}_\omega $
to work to perform proof-theoretical analyses of Peano Arithmetic and its kin [Reference Beklemishev3–Reference Beklemishev5]. Below we shall give more circumstantial evidence to why the truth interpretation is optimal.
As mentioned, the first arithmetical interpretation of transfinite polymodal provability logic [Reference Fernández-Duque and Joosten18] was, like Japaridze’s original approach, based on iterating applications of the omega rule. Although it was observed in [Reference Joosten23] that soundness of the interpretation is sufficient for the purpose of an ordinal analysis, the paper also contained a completeness proof in such general lines that it can be applied to a wide range of interpretations.
It seemed, however, that the omega-rule interpretation does not have all the desirable properties to make it directly a useful tool for ordinal analyses. Even though various known fragments of second order arithmetic like
$\mathrm {ATR}_0$
,
$\Pi ^1_1-\mathrm {CA}_0$
, and
$\Pi ^1_1-\mathrm {CA}_0 + \mbox {Bar Induction}$
can be characterised [Reference Cordón Franco, Fernández-Duque, Joosten and Lara Martín10, Reference Fernández-Duque12] in terms of reflection principles using versions of the omega rule interpretation of
$GLP_\Lambda $
, the fine-structure between various consistency statements could not be proven.
One possible reason may be that the omega provability predicates do not tie up with the arithmetical hierarchy and Turing jumps as observed in [Reference Joosten, Beckmann, Mitrana and Soskova24, Lemma 9]. A more concrete and serious objection is given in an unpublished simple observation from Fernández Duque: using only one application of the omega-rule one can prove any induction axiom so that the one-consistency of primitive recursive arithmetic in the omega-rule sense suffices to prove the consistency of Peano arithmetic.
In short, the truth interpretation of
${\mathsf {GLP}}_\omega $
has better properties than the omega-rule interpretation. However, one advantage of the omega-rule interpretation is its amenability to transfinite generalisations. The formalisation of the truth interpretation relies on a syntactical characterisation of the arithmetical hierarchy in terms of the
$\Sigma ^0_n$
formulas. It remained unclear how to generalise this in a canonical way to the hyperarithmetical setting or beyond without extending the language in a way that often seems rather ad-hoc.
The idea of this paper to overcome this is very simple yet turns out to be rather powerful. The Friedman–Goldfarb–Harrington theorem (FGH) tells us that for a wide range of theories, in a sense, the canonical consistency predicate is
$\Pi ^0_1$
complete. Thus, instead of using a true
$\Pi ^0_1$
sentence as oracle for the
$[1]_T$
provability predicate in the truth interpretation, one can use a provably equivalent consistency statement.
Via a generalisation of the FGH theorem proven in [Reference Joosten, Beckmann, Mitrana and Soskova24, Reference Joosten26] one can see that the consistency notion corresponding to
$[1]$
provability is in a sense
$\Pi ^0_2$
complete and so on. Thus, it makes sense to consider the following recursion as in [Reference Joosten, Beckmann, Mitrana and Soskova24]: provability at level n means provable from an oracle which is a consistency statement of level m for some
$m<n$
. It feels like lifting oneself up from the swamp by pulling ones hairs as the Baron von Münchhausen did. Moreover, the recursion lends itself to an easy transfinite generalisation and that is exactly what this paper does. Before we close the introduction with an overview of how the current paper does so, we would like to point out how this paper fits in the landscape of related literature thereby trying to provide an ample justification for it.
Ordinal analysis via polymodal provability logics seems to have various benefits over other methods of ordinal analysis. An important benefit is it allows to tell different incomplete theories apart at the lowest possible level of
$\Pi ^0_1$
sentences. It is good to recall that the classical
$\Pi ^1_1$
proof theoretical ordinal will not even discern theories at the level of
$\Sigma ^1_1$
-level. Another benefit may seem the modularity of ordinal analysis: the ordinal analysis of different theories will all share the same template and re-use various tools and theorems.
We see another stronghold in the fact that the approach relates various different fields in a natural way. In particular, the closed formulas of
${\mathsf {GLP}}$
—called worms—are important in this. Worms can be used to denote various notions central to foundational issues. For one, they are simple and well-behaved elements from a well-behaved logic. Even though the logic
${\mathsf {GLP}}$
is known to be PSPACE-complete [Reference Shapirovsky, Areces and Goldblatt29] it is Kripke incomplete. However, natural topological semantics do exist [Reference Aguilera and Fernández-Duque1, Reference Beklemishev and Gabelaia8, Reference Fernández-Duque11, Reference Icard20, Reference Ignatiev21] even though it is known to depend on strong cardinal assumptions for various natural topological spaces [Reference Bagaria, Magidor and Sakai2].
Moreover, the closed fragment of
${\mathsf {GLP}}_\Lambda $
is very well behaved, well studied, and in particular does allow for natural relational semantics [Reference Fernández-Duque, Joosten, Bolander, Braüner, Ghilardi and Moss15, Reference Fernández-Duque and Joosten16, Reference Ignatiev21]. In addition, and this provides a second interpretation of worms, the worms are known to define a well-ordered relation as studied in [Reference Beklemishev, Hájek, Valdés-Villanueva and Westerståhl6, Reference Beklemishev, Fernández-Duque and Joosten7, Reference Fernández-Duque13, Reference Fernández-Duque and Joosten17] and thus can provide for ordinal notation systems [Reference Beklemishev, Hájek, Valdés-Villanueva and Westerståhl6, Reference Fernández-Duque13, Reference Fernández-Duque, Hermo Reyes, Iemhoff, Moortgat and de Queiroz14].
Some simple worms are just consistency statements which are known to be related to reflection principles so that by classical results they are related to fragments of arithmetic [Reference Kreisel and Lévy27]. Thus, worms—apart from being privileged elements of a decidable logic—can denote both ordinals and fragments of arithmetic. A possibly more important use, however, lies in their relation to Turing progressions: each Turing progression below
$\varepsilon _0$
can be approximated by the arithmetical interpretation of a
${\mathsf {GLP}}_\omega $
worm. The relation goes even that far so that points in a universal modal model for the closed fragment of
${\mathsf {GLP}}_\omega $
can be seen as arithmetical theories axiomatised by Turing progressions [Reference Joosten25] so that the model displays all conservation results between the different theories. It is these four different possible denotations for worms that make them so versatile and make new interpretations of
${\mathsf {GLP}}_\Lambda $
as the current paper so promising.
1.1 Plan of the paper
Section 2 provides some useful lemmata and settles on notation which otherwise is quite standard so that it can be skipped by the initiate readers only to come back to it when needed. Then, in Section 3 the central provability notion of this paper is introduced: one-Münchhausen provability. The usage of the word “one” in there refers to the fact that provability at level
$\alpha $
is allowed to use a single oracle sentence of a lower level consistency statement.
Section 4 mainly dwells on the fact that in general we cannot prove that different Münchhausen provability predicates are provably equivalent even if they are so on the low levels. It is observed that we do have uniqueness in case the object theory and the meta theory are provably the same.
Section 5 then proceeds to prove soundness for one-Münchhausen provability for a large class of theories and Section 6 proves arithmetical completeness. In Section 7 it is sketched how one-Münchhausen provability can be formalised in second order arithmetic. The formalisation requires a substantial amount of transfinite induction both in the object and meta theory so that applications to ordinal analysis will become difficult. Finally, in Section 8 some first steps are taken on how to weaken the needed strength of the object and meta theory. By allowing for multiple oracles sentences instead of just one, soundness can be proven without any transfinite induction.
2 Preliminaries
In this section we dwell succinctly on the necessary notions from both formal arithmetic and modal provability logics. Apart from proving a few new observations, we mainly settle on notation and refer to the literature for details.
2.1 Arithmetic
This paper deals with interpretations of transfinite provability logic. Even though the set-up of such interpretations starts schematically so that our analysis applies to a wide range of theories, we will in particular have second order arithmetic in mind. We refer the reader to standard references for details [Reference Beklemishev5, Reference Hájek and Pudlák19, Reference Simpson30] and only include some minimal comments for expository purposes.
For first-order arithmetic, we shall work with theories with identity in the language
$\{ 0,1, \exp , +, \cdot , < \}$
of arithmetic where
$\exp $
denotes the unary function
$x\mapsto 2^x$
. We define
$\Delta ^0_0=\Sigma ^0_0=\Pi ^0_0$
formulas (also referred to as elementary formulas) as those where all quantifiers occur bounded, that is we only allow quantifiers of the form
$\forall \, x{<}t$
or
$\exists \, x{<}t$
where t is some term not containing x. We inductively define
$\Pi ^0_{n+1}$
/
$\Sigma ^0_{n+1}$
formulas as allowing a block of universal/existential quantifiers up-front a
$\Sigma ^0_n$
/
$\Pi ^0_n$
formula. The union of these classes is called the arithmetical formulas and denoted by
$\Pi ^0_\omega $
.
If P is a predicate, the classes relativized to P are defined the same with the sole difference that we consider the predicate P as an atomic formula. We flag relativisation by including the predicate in brackets after the class like, for example, in
$\Pi ^0_1(P)$
.
Peano Arithmetic (
${\mathrm {PA}}$
) contains the basic axioms describing the non-logical symbols together with induction formulas
$I_\varphi $
for any formula
$\varphi $
where as always
$I_\varphi : = \varphi (0) \wedge \forall x(\varphi (x) \to \varphi (x+1)) \to \forall x \varphi (x)$
. When
$\Gamma $
is a complexity class, by
$\mathrm {I}\Gamma $
we denote the theory which is like
${\mathrm {PA}}$
except that induction is restricted to formulas in
$\Gamma $
. The theory
$\mathrm {I}\Delta ^0_0$
is also referred to as elementary arithmetic
Footnote
1
or Kalmar elementary arithmetic (
${\mathrm {EA}}$
).
In this paper we also mention collection axioms
$\mathrm {B}_\varphi $
which basically state that the range of a function with finite domain is finite:
$B_\varphi : = \forall z{<}y\, \exists x \varphi (z,x) \to \exists u\, \forall z{<}y\, \exists \, x{<}u \varphi (z,x)$
. Again, for a formula class
$\Gamma $
, by
$\mathrm {B}\Gamma $
we denote the set of collection axioms for formulas from
$\Gamma $
.
Second order arithmetic is an extension of first order arithmetic where we now add second order set variables together with a binary symbol
$\in $
for membership. Instead of extending identity to second order terms we stipulate that second order identity is governed by extensionality:
$X = Y :\Leftrightarrow \forall x\ (x\in X \leftrightarrow x\in Y)$
. The formula classes
$\Sigma ^1_n$
and
$\Pi ^1_n$
are defined as their first-order counterpart only that we now count second order quantification alternations. Likewise, by
$\Pi ^1_\omega $
we denote the class of all second order formulas.
The strength of various fragments of second order arithmetics is in large determined by their set existence axioms. The comprehension axiom for
$\varphi $
tells us that
$\varphi $
not containing x defines a set:
$\exists X \forall x (x\in X \leftrightarrow \varphi )$
. The second order system
${{\textrm {ACA}}_0}$
contains the defining axioms for the first-order non-logical symbols together with set-induction
$0\in X \wedge \forall x (x{\in } X \to x{+}1 {\in } X) \to \forall x \ x{\in } X$
and comprehension for all arithmetical formulas.
The theory
${\text {ACA}_0}$
is conservative over
${\mathrm {PA}}$
for first-order formulas. In [Reference Fernández-Duque and Joosten18] the system
${\text {ECA}_0}$
is introduced as
${\text {ACA}_0}$
except that comprehension is restricted to
$\Delta ^0_0$
formulas. In [Reference Cordón Franco, Fernández-Duque, Joosten and Lara Martín10, Lemma 3.2] it is proven that
${\text {ECA}_0}$
is conservative over
${\mathrm {EA}}$
for first-order formulas.
We will tacitly assume that when we are given a theory T, we are actually given a decidable formula
$\tau $
that binumerates the axioms of T. That is to say,
$\chi $
is an axiom of T if and only ifFootnote
2
$T\vdash \tau (\chi )$
. For each theory T we denote by
$\Box _T$
the unary
$\Sigma ^0_1$
-predicate that defines provability in T. That is,
$\mathbb N \models \varphi $
if and only if
$\varphi $
is provable in T. When we write
$\Box _T \varphi (\dot x)$
we denote the formula with free variable x that expresses that for each number x, the formula
$\varphi (\overline n)$
is provable in T. Here,
$\overline n$
denotes the numeral of n which is a syntactical expression denoting n, for example defined as
$\overline 0 = 0; \overline {x+1} =\overline x + 1$
.
The Friedman–Goldfarb–Harrington Theorem (FGH for short) states that for any computably enumerable theory U, the corresponding formalised provability predicate is provably
$\Sigma ^0_1$
-complete provided U is consistent. Since the theorem provides an important tool in this paper, let us give a precise formulation.
Theorem 2.1 (Friedman–Goldfarb–Harrington)
Let U be a computably enumerable theory with corresponding provability predicate
$\Box _U$
. We have that for any
$\Sigma ^0_1$
formula
$\sigma (x)$
, there is a
$\Sigma ^0_1$
formula
$\rho (x)$
so that
$$ \begin{align*} {\mathrm{EA}} \vdash \Diamond_U\top \to \forall x\ \big( \sigma (x) \leftrightarrow \Box_U \rho (\dot x)\big). \end{align*} $$
The theorem was given its name in [Reference Visser32] in acknowledgment to the intellectual parents. Generalisations to other arithmetical provability predicates were studied in [Reference Joosten, Beckmann, Mitrana and Soskova24, Reference Joosten26]. In particular, the quantification over
$\Sigma ^0_1$
formulas (in the language without exponentiation however) can be made internal in
${\mathrm {EA}}$
and the
$\rho $
is obtained from
$\sigma $
by means of an elementary function. A very useful corollary of the FGH theorem is so-called weak closure of provability under disjunctions.
Corollary 2.2. Let U be a computably enumerable theory with corresponding provability predicate
$\Box _U$
. We have
$$ \begin{align*} {\mathrm{EA}} \vdash \forall \varphi \forall \psi \exists \chi \ (\Box_U \varphi \vee \Box_U \psi \leftrightarrow \Box_U \chi). \end{align*} $$
2.2 Transfinite provability logic
Even though via the FGH theorem the provability predicate
$\Box _T$
is in a sense
$\Sigma _1$
complete for a wide variety of theories, the provable structural behaviour of the predicate can be described with well-behaved PSPACE decidable propositional modal logics.
The simplest modal logics have one unary modal operator
$\Box $
which syntactically behaves like negation. The dual modality
$\Diamond $
can be seen as an abbreviation of
$\neg \Box \neg $
. The basic logic
${\textbf {K}}$
is axiomatised by all propositional tautologies (in the signature with
$\Box $
) and all so-called distribution axioms
$\Box (A \to B) \to (\Box A \to \Box B)$
. The rules of
${\textbf {K}}$
are modus ponens and Necessitation: from A conclude
$\Box A$
.
The logic
${\textbf {K4}}$
arises by adding the transitivity axioms to
${\textbf {K}}$
:
$\Box A \to \Box \Box A$
. Gödel–Löb’s logic
${\textbf {GL}}$
arises to adding Löb’s axiom scheme to
${\textbf {K}}$
:
$\Box (\Box A \to A) \to \Box A$
. It is known that
${\textbf {GL}}$
is a proper extension of
${\textbf {K4}}$
and that it exactly describes the provable structural properties of the provability predicate for a wide range of theories.
In this paper we are interested in provability logics of a collection of provability predicates
$[\alpha ]$
of increasing strength indexed by ordinals
$\alpha $
. For the finite ordinals, this logic was discovered by Japaridze in [Reference Japaridze22]. We now present this logic, which would be
${\mathsf {GLP}}_\omega $
in our notation as given in the following definition.
Definition 2.3. For
$\Lambda $
an ordinal or the class of all ordinals, the logic
$\mathsf {GLP}_\Lambda $
is given by the following axioms
$:$
-
1. all propositional tautologies,
-
2. Distributivity
$:$
$[\xi ](\varphi \to \psi ) \to ([\xi ]\varphi \to [\xi ]\psi )$
for all
$\xi <\Lambda $
, -
3. Transitivity
$:$
$[\xi ] \varphi \to [\xi ] [\xi ]\varphi $
for all
$\xi <\Lambda $
, -
4. Löb
$:$
$[\xi ]([\xi ]\varphi \to \varphi )\to [\xi ]\varphi $
for all
$\xi <\Lambda $
, -
5. Negative introspection
$:$
$\left <\zeta \right>\varphi \to \left <\xi \right>\varphi $
for
$\xi <\zeta <\Lambda $
, -
6. Monotonicity
$:$
$\left <\xi \right>\varphi \to [\zeta ]\left <\xi \right>\varphi $
for
$\xi <\zeta <\Lambda $
.
The rules are Modes Ponens and Necessitation for each modality
$: \displaystyle \frac {\varphi }{[\xi ]\varphi }$
.
The following lemma is proven in [Reference Beklemishev, Fernández-Duque and Joosten7].
Lemma 2.4. The logic
${\mathsf {GLP}}_\Lambda $
is conservative over
${\mathsf {GLP}}_{\Lambda '}$
for
$\Lambda '<\Lambda $
.
The lemma is particularly useful in proofs where you only have access to reasoning up to
${\mathsf {GLP}}_\Lambda '$
and tells you that any statement formulated in this fragment can actually be proven there. We shall use this result throughout the paper, mostly without explicit mention. Let us now prove some basic properties that shall be needed later in the paper.
Lemma 2.5.
-
1.
${\mathsf {GLP}} \vdash [\alpha ] \langle \beta \rangle \top $
whenever
$\alpha>\beta $
. -
2. For
$\alpha> \beta $
we have
$nn \vdash \langle \alpha \rangle \top \to \Big ( \langle \beta \rangle \varphi \leftrightarrow \langle \alpha \rangle \langle \beta \rangle \varphi \Big )$
. -
3. For
$\alpha \geq \beta>0$
we have
${\mathsf {GLP}} \vdash \langle \alpha \rangle \top \ \to \ \Big ( \langle \beta \rangle \phi \vee \Box \psi \Big ) \ \leftrightarrow \ \Big ( \langle \beta \rangle \big ( \phi \vee \Box \psi \big ) \Big )$
.
Proof We reason in
${\mathsf {GLP}}$
.
For Item 1: If
$\langle \beta \rangle \top $
, then
$[\alpha ] \langle \beta \rangle \top $
by the negative introspection axiom. In case
$[\beta ]\bot $
we get by an ex falso under the
$[\beta ]$
modality that
$[\beta ]\langle \beta \rangle \top $
whence
$[\alpha ]\langle \beta \rangle \top $
by monotonicity.
For Item 2 we work under the assumption that
$\langle \alpha \rangle \top $
. From
$\langle \beta \rangle \varphi $
we get, since
$\beta <\alpha $
, that
$[\alpha ]\langle \beta \rangle \varphi $
so from
$\langle \alpha \rangle \top $
we get
$\langle \alpha \rangle \langle \beta \rangle \varphi $
. For the other direction, from
$\langle \alpha \rangle \langle \beta \rangle \varphi $
we get by monotonicity that
$\langle \beta \rangle \langle \beta \rangle \varphi $
whence by transitivity we obtain the required
$\langle \beta \rangle \varphi $
.
For Item 3: We now work under the assumption that
$\langle \alpha \rangle \top $
. The only case to consider in the
$\rightarrow $
direction is when
$\Box \psi $
holds. Then,
$\Box \Box \psi $
whence
$[\alpha ] \Box \psi $
which together with
$\langle \alpha \rangle \top $
yields
$\langle \alpha \rangle \Box \psi $
whence
$\langle \beta \rangle \big ( \phi \vee \Box \psi \big )$
.
For the
$\leftarrow $
direction we need to prove
$\langle \beta \rangle \big ( \phi \vee \Box \psi \big ) \to \langle \beta \rangle \phi \vee \Box \psi $
. So, suppose
$\langle \beta \rangle \big ( \phi \vee \Box \psi \big )$
and
$\neg \Box \psi $
whence
$[\beta ]\neg \Box \psi $
. But since
$\langle \beta \rangle \big ( \phi \vee \Box \psi \big )$
we must have
$\langle \beta \rangle \phi $
and by weakening
$\langle \beta \rangle \phi \vee \Box \psi $
.⊣
2.3 Transfinite induction and its kin
In various arguments we will have to prove that a statement
$\varphi $
holds for all ordinals
$\alpha $
. Often we will prove this by transfinite recursion on
$\alpha $
. However, in certain cases, transfinite induction is not available. In such cases there is a technique called reflexive induction.
The principle of reflexive induction can syntactically be seen as twice weakening regular transfinite induction. Recall that transfinite induction for a formula
$\varphi $
is
$$ \begin{align*} {\sf TI}_\varphi \ \ := \ \ \forall \alpha \big( \forall \, \beta{<}\alpha \varphi (\beta) \to \varphi (\alpha) \big) \ \to \ \forall \alpha \varphi (\alpha), \end{align*} $$
and for a set of formulas
$\Gamma $
the principle
${\sf TI}(\Gamma )$
denotes the collection of all
${\sf TI}_\varphi $
for
$\varphi \in \Gamma $
. As a first weakening one could consider the rule-based version: from
$T\vdash \forall \alpha \big ( \forall \, \beta {<}\alpha \varphi (\beta ) \to \varphi (\alpha ) \big )$
, conclude
$T\vdash \forall \alpha \varphi (\alpha )$
. Now, one can change the antecedent to
$T\vdash \forall \alpha \big ( \Box _T\forall \, \beta {<}\alpha \varphi (\dot \beta ) \to \varphi (\alpha ) \big )$
to arrive at reflexive induction. However, it turns out that by doing so, it has lost all its strength. That is, the resulting principle is provable in almost any theory:
Theorem 2.6 (Reflexive induction)
Let T be any theory capable of coding syntax. If
$T\vdash \forall \alpha \Big ( \Box _T \big (\forall \beta < \dot \alpha \ \varphi (\beta )\big ) \to \varphi (\alpha ) \Big )$
, then
$T\vdash \forall \alpha \varphi (\alpha )$
.
Although this principle is well known since Schmerl’s work [Reference Schmerl28] we include a proof to emphasize that the principle actually does not rely at all on the fact that
$<$
is a well-order. As a matter of fact, the proof goes through for any kind of relation and basically boils down to an application of Löb’s Theorem.
Proof We shall see that from the assumption
$$ \begin{align*} T\vdash \forall \alpha \Big( \Box_T \big(\forall \, \beta {<} \dot \alpha \ \varphi (\beta)\big) \to \varphi(\alpha) \Big), \end{align*} $$
we get
$T\vdash \Box _T \forall \alpha \varphi (\alpha ) \to \forall \alpha \varphi (\alpha )$
so that the conclusion
$T\vdash \forall \alpha \varphi (\alpha )$
follows by Löb’s Theorem.
Thus, we reason in T, pick
$\alpha $
arbitrary, assume
$\Box _T \forall \alpha \varphi (\alpha )$
, or equivalently
$\Box _T \forall \theta \varphi (\theta )$
, and set out to prove
$\varphi (\alpha )$
. But using
$\Box _T \big (\forall \, \beta {<} \dot \alpha \ \varphi (\beta )\big ) \to \varphi (\alpha )$
in the last step of the following reasoning, we clearly have
$$ \begin{align*} \begin{array}{lll} \Box_T \forall \theta \varphi (\theta) &\to& \Box_T \forall \theta \forall \, \beta{<}\theta \ \varphi (\beta)\\ \ & \to &\forall \theta \, \Box_T \forall \, \beta{<}\dot\theta \ \varphi (\beta)\\ \ & \to &\Box_T \forall \, \beta{<}\dot\alpha \ \varphi (\beta)\\ \ & \to &\varphi (\alpha).\\ \end{array}\\[-2.9pc] \end{align*} $$
⊣
On occasion, in this paper we will have to combine regular transfinite induction and reflexive induction. We call this amalgamate transfinite reflexive induction.
Lemma 2.7 (Transfinite reflexive induction)
Let T be a theory with a sufficient amount of transfinite induction as specified below and let
$\prec $
be a well-order in T.
$$ \begin{align*} \begin{array}{ll} \mbox{If } & \\ & T\vdash \forall \, \alpha \Big(\forall\, \beta{\prec}\alpha \, \varphi(\beta) \ \wedge \ \Box_T \big( \forall\, \beta{\prec}\dot\alpha \, \varphi(\beta)\big) \ \to \ \varphi (\alpha) \Big),\\ \mbox{then} & \\ & T\vdash \forall \alpha \ \varphi (\alpha). \end{array} \end{align*} $$
To prove transfinite reflexive induction for
$\varphi $
it suffices that T is capable of coding syntax and proves transfinite induction for formulas of the form
$\Box _T\chi \to \varphi $
.
Proof To start our proof we assume
$$ \begin{align} T\vdash \forall \, \alpha \Big(\forall\, \beta{\prec}\alpha \, \varphi(\beta) \ \wedge \ \Box_T \big( \forall\, \beta{\prec}\dot\alpha \, \varphi(\beta)\big) \ \to \ \varphi (\alpha) \Big). \end{align} $$
We will prove by transfinite induction on
$\alpha $
that
$$ \begin{align} T \vdash \forall \alpha\ \Big(\Box_T \forall\, \beta{\prec}\dot\alpha \, \varphi (\beta) \to \varphi (\alpha)\Big), \end{align} $$
so that the result
$T\vdash \forall \alpha \, \varphi (\alpha )$
follows by reflexive induction (Lemma 2.6). Proving (2) for
$\alpha =0$
amounts to showing that
$T\vdash \varphi (0)$
which follows directly from (1).
For the inductive step, we reason in T, fix some
$\alpha>0$
, assume that
$$ \begin{align} \forall \, \beta{\prec}\alpha\ \Big(\Box_T \forall\, \gamma{\prec}\dot\beta \, \varphi (\gamma) \to \varphi (\beta)\Big), \end{align} $$
and set out to prove
$$ \begin{align} \Box_T \forall\, \gamma{\prec}\dot\alpha \, \varphi (\gamma) \to \varphi (\alpha). \end{align} $$
To this end, we further assume that
$\Box _T \forall \, \gamma {\prec }\dot \alpha \, \varphi (\gamma )$
, so that certainly we have
$\forall \, \beta {\prec }\alpha \ \Box _T \forall \, \gamma {\prec }\dot \beta \, \varphi (\gamma )$
. Combining the latter with (3) yields
$\forall \, \beta {\prec }\alpha \ \varphi (\beta )$
. This, together with our assumption
$\Box _T \forall \, \gamma {\prec }\dot \alpha \, \varphi (\gamma )$
is the antecedent of (1) so that we may conclude
$\varphi (\alpha )$
which finishes the proof.⊣
3 Theories for Single Oracle Münchhausen provability
Throughout this section, we fix some ordinal
$\Lambda $
and understand that all other ordinals denoted in this section are majorized by
$\Lambda $
.
3.1 Single Oracle Münchhausen provability
We are interested in theories T that can formalize a provability notion so that provably in T the following recursion holds:
$$ \begin{align} {[\zeta]}^\Lambda_T \phi \ \ :\Leftrightarrow \ \ \Box_T \phi \ \vee \ \exists \psi\, \exists \, \xi{<}\zeta\ \big({\langle \xi \rangle}^\Lambda_T \psi \ \wedge \ \Box_T ({\langle \xi \rangle}^\Lambda_T \psi \to \phi)\big). \end{align} $$
Here,
$\Box _T \varphi $
will denote a standard predicate on the natural numbers expressing “the formula (with Gödel number)
$\varphi $
is provable in the theory T.” Further, it is understood that
${\langle \xi \rangle }^\Lambda _T$
stands for
$\neg [\xi ]^\Lambda _T \neg $
.
Rather than exposing a concrete theory where this recursion is formalizable in a particular way and provable, we will define a class of theories that are able to define and prove this recursion and have some additional desirable properties.
Next we shall see which properties of the predicates
$[\zeta ]^\Lambda _T$
can be proven from the mere recursion defined in (5). It will turn out that under some fairly general conditions we can prove the collection of predicates
$[\zeta ]^\Lambda _T$
for
$\zeta <\Lambda $
to provide a sound interpretation for
${\mathsf {GLP}}_\Lambda $
.
In Section 6 we shall see that by requiring slightly more on our predicate and theory, this will give us arithmetical completeness.
In principle it would make sense to study (5) at a higher level of generality. For example, T could be some version of set-theory allowing for uncountable
$\Lambda $
. As long as (5) is provable together with some additional conditions, most of the results of this paper will carry over. It would be natural to require
$\Box _T$
to be such that all
${\textbf {GL}}$
theorems are schematically provable in T in such a setting.
Of course, this generalised setting would require one to overcome various substantial technical problems. For one, if each element in the uncountable ordering should be denotable by a syntactical term, the basic language itself should be uncountable so that coding and ordinal representations should be rethought. However, such a generalisation falls outside the scope of the current paper.
3.2 Theories amenable for Single Oracle Münchhausen provability
For the sake of readability we shall often not distinguish between an ordinal
$\alpha <\Gamma $
, a notation for such an
$\alpha $
, or even an arithmetization of such a notation for
$\alpha $
. We shall, however, be explicit about the difference between the ordering
$<$
on the ordinals and the arithmetization
$\prec $
of this ordering on ordinals.
Definition 3.1. Let T be a theory and let
$\Lambda $
denote an ordinal equipped with a representation in the language of T with corresponding represented ordering
$\prec $
. For this representation, it is required that
We callFootnote
3
T a Single Oracle
$\Lambda $
-Münchhausen Theory—or a
$\Lambda $
-One-Münchhausen Theory for short—whenever there is a binary predicate
$[\xi ]_T^\Lambda \varphi $
with free variables
$\xi $
and
$\varphi $
so that
$$ \begin{align*} T\vdash \forall \phi\ \forall \zeta{\prec}\Lambda \Big(\ {[\zeta]_T^\Lambda} \phi \ \leftrightarrow \ \Box_T \phi \ \vee \ \exists \psi\, \exists \, \xi{\prec}\zeta\ \big({\langle \xi \rangle^\Lambda_T} \psi \ \wedge \ \Box_T (\, {\langle \xi \rangle^\Lambda_T} \psi \to \phi) \, \big) \, \Big). \end{align*} $$
In this case, we call the binary predicate
$[\xi ]_T^\Lambda \varphi $
a corresponding 1-Münchhausen provability predicate.
The “One” in “
$\Lambda $
-One-Münchhausen Theory” refers to the fact that provability
$[\zeta ]_T^\Lambda $
at level
$\zeta $
makes use of one single oracle sentence
$\langle \xi \rangle ^\Lambda _T \psi $
. In Section 8 we shall see variations where we allow various oracle sentences to occur.
Often shall we simply drop the, or some of the indices of
$[\xi ]^\Lambda _T$
like for example in
$[\xi ]_T \varphi $
in case the ordinal
$\Lambda $
is clear from the context. To shorten nomenclature further, we shall mostly simply speak of 1-Münchhausen theories and the corresponding 1-Münchhausen provability. Often, when we speak of 1-Münchhausen theories we implicitly assume that we have fixed some 1-Münchhausen provability predicate
$[\alpha ]\varphi $
.
Observation 3.2. Since any 1-Münchhausen theory T proves that there is a
$\prec $
-minimal element, we shall use the notation
$0$
for this element even if the natural number
$($
or object
$)$
representing this minimal element is not the natural number zero. Likewise, from right-discreteness we know that for any element
$\alpha \prec \Lambda $
, there is a next bigger element that we shall suggestively call
$\alpha +1$
. In analogy, we shall denote
$0+1$
by
$1$
,
$1+1$
by
$2$
,
$2+1$
by
$3$
, et cetera.
The following observation is immediate.
Lemma 3.3. Let T be a Single Oracle
$\Lambda $
-Münchhausen Theory with corresponding 1-Münchhausen provability predicate
$[\alpha ]^\Lambda _T$
. We have that
$$ \begin{align*} T \vdash \ \forall \varphi \ \big( [0]_T^\Lambda \varphi \ \leftrightarrow \Box_T \varphi \big). \end{align*} $$
When working with sound theories in the language of arithmetic, we know that all the corresponding 1-Münchhausen consistency statements are actually true:
Proposition 3.4. Let T be a sound Single Oracle
$\Lambda $
-Münchhausen Theory in the language of arithmetic with corresponding 1-Münchhausen provability predicate
$[\alpha ]^\Lambda _T$
. Then for each
$\xi \prec \Lambda $
we have
$\mathbb N \models \langle {\xi }\rangle _T^\Lambda \top $
.
Proof By a simple case distinction. In case
$\xi =0$
, we get from a hypothetical
$\mathbb N \models [0]_T \bot $
together with the soundness and the above lemma that
$\mathbb N \models \Box _T \bot $
so that
$T\vdash \bot $
which cannot be.
In case
$\xi \succ 0$
, suppose for a contradiction that
$\mathbb N\models [{\xi }]_T \bot $
. Then, using soundness of T, we only need to consider the case that
$$ \begin{align*} \mathbb N \models \exists \psi\, \exists \, \zeta{\prec}\xi\ \big(\langle{\zeta}\rangle_T \psi \wedge \Box_T(\langle{\zeta}\rangle_T \psi\to \bot) \big), \end{align*} $$
so that for some ordinal
$\zeta \prec \xi $
and some formula
$\psi $
we have
$\mathbb N \models \langle {\zeta }\rangle _T \psi $
. Also
$\mathbb N \models \Box _T(\langle {\zeta }\rangle _T \psi \to \bot )$
so that
$T\vdash \langle {\zeta }\rangle _T \psi \to \bot $
whence by soundness of T we see that
$\mathbb N \models \neg \langle {\zeta }\rangle _T \psi $
which is a contradiction.⊣
We note that the above argument does not use transfinite induction.
4 On uniqueness of Münchhausen provability
The definition of 1-Münchhausen provability allows for various different 1-Münchhausen predicates to exist. Of course, it would be highly desirable that the defining equivalence (5) for 1-Münchhausen provability defined a T provably unique predicate. We can prove uniqueness of the predicate via an external induction up to any level below
$\omega $
.
Lemma 4.1. Let T be a sound Single Oracle
$\Lambda $
-Münchhausen Theory for
$\Lambda \geq \omega $
, with corresponding 1-Münchhausen provability predicates
$[\alpha ]^\Lambda _T$
and
$\overline {[\alpha ]}^\Lambda _T$
. We have for any natural number n that
$$ \begin{align*} T\vdash \forall \varphi \ \big( [n]^\Lambda_T \varphi \ \leftrightarrow \ \overline{[n]}^\Lambda_T \varphi \big). \end{align*} $$
Proof We proceed by an external induction where the base case follows directly from Lemma 3.3. We shall omit super and sub indices.
For the inductive step, we reason in T, fix some formula
$\varphi $
, fix the
$(n+1)$
th element in the
$\prec $
ordering, and assume
$[n+1]\varphi $
. In the non-trivial case, there is some formula
$\psi $
and an element
$\tilde m{\prec }n+1$
so that
$\langle \tilde m \rangle \psi $
and
$\Box (\langle \tilde m \rangle \psi \to \varphi )$
. Here we end our reasoning inside T. Since we can prove that any element
$\prec $
-below the externally given
$n+1$
is either the zero-th, or the first, or …or, the n-th element, we know that
$\tilde m$
corresponds to some natural number
$m<n+1$
. Thus, we can appeal to the external induction hypothesis that tells us that
$$ \begin{align} T\vdash \forall \psi \ ([m] \psi \leftrightarrow \overline{[m]}\psi), \end{align} $$
and consequently
$$ \begin{align} T\vdash \Box \forall \psi \ ([m] \psi \leftrightarrow \overline{[m]}\psi). \end{align} $$
These two ingredients are sufficient to conclude
$\overline {[m]} \psi $
. Of course the other direction goes exactly the same.⊣
Let us make some observations about this simple proof. First, we observe that we could only conclude (7) from (6) by necessitation since the meta-theory as in
$T\vdash \ldots $
is the same as the object-theory as in
$\Box _T$
. Second, we observe that we only had access to the inductive hypothesis since we can express in the language of first order logic that being smaller than the
$(n+1)$
th element implies being equal to one of the zero-th, or …, or the nth element. Of course, we cannot generalize this to the first limit ordinal and hence our external induction cannot be extended to the transfinite.
If we wish to generalize our argument to the transfinite, we should replace our external induction by an internal one. Of course, then in our meta-theory, we should have access to transfinite induction. However, we only see how to continue the proof in the case where the object theory equals the meta-theory and consequently also has the same amount of transfinite induction.
Lemma 4.2. Let T be a theory that proves the recursion from (5) for two predicates
$[\zeta ]_U$
and
$\overline {[\zeta ]}_U$
. We further suppose that T proves the basic facts about the ordering
$\langle \Lambda ,\prec \rangle $
. Also, we assume that T proves transfinite
$\Pi _1([\alpha ], \overline {[\alpha ]})$
induction.
If T and U are T-provably equivalent, then we have that
$[\zeta ]_U$
and
$\overline {[\zeta ]}_U$
are T-provably equivalent predicates.
Proof We have chosen a formulation where T and U are different from the outset so that we clearly see at what point we need to assume that T is T-provably equivalent to U.
Thus, we reason in T and will as a first attempt prove by transfinite
$\Pi _1([\alpha ], \overline {[\alpha ]})$
induction that
$$ \begin{align*} \forall \zeta \,\forall \varphi \ ([\zeta]_U\varphi \ \leftrightarrow \ \overline{[\zeta]}_U \varphi). \end{align*} $$
For
$\zeta =0$
the equivalence is obvious. Thus, we fix some
$\zeta \succ 0$
and focus on one implication the other being analogous. Thus, we assume that
$[\zeta ]_U \varphi $
and set out to prove
$\overline {[\zeta ]}_U \varphi $
.
From the assumption
$[\zeta ]_U \varphi $
we find—in the non-trivial case—some formula
$\psi $
and ordinal
$\xi \prec \zeta $
so that
$\langle \xi \rangle _U \psi $
and
$\Box _U (\langle \xi \rangle _U \psi \to \varphi )$
. The inductive hypothesis now will tell us that
$\langle \xi \rangle _U \psi \leftrightarrow \overline {\langle \xi \rangle }_U \psi $
.
However, there is no way that we know that this equivalence is provable, that is, that we have
$\Box _U \Big ( \langle \xi \rangle _U \psi \leftrightarrow \overline {\langle \xi \rangle }_U \psi \Big )$
. The latter would be needed to conclude
$\Box _U (\overline {\langle \xi \rangle }_U \psi \to \varphi )$
so that
$\overline {[\zeta ]}_U \varphi $
.
The problem cannot be solved by strengthening the induction to for example
$$ \begin{align*} \forall \phi\ \big [([\zeta]_U \phi \leftrightarrow \overline{[\zeta]}_U\phi) \ \wedge\ \Box_U ([\dot\zeta]_U \phi \leftrightarrow \overline{[\dot \zeta]}_U\phi) \big ], \end{align*} $$
since then the problem will simply come back but now under a box.
However, when
$T = U$
we have access to transfinite reflexive induction as formulated in Lemma 2.7. That is, in order to show that
$\forall \varphi \ ([\zeta ]_U\varphi \ \leftrightarrow \ \overline {[\zeta ]}_U \varphi )$
for a particular
$\zeta $
we may assume both
$\forall \, \xi {\prec }\zeta \, \forall \varphi \ ([\zeta ]_U\varphi \ \leftrightarrow \ \overline {[\zeta ]}_U \varphi )$
and also
$\Box _U \big (\forall \, \xi {\prec }\dot \zeta \, \forall \varphi \ ([\zeta ]_U\varphi \ \leftrightarrow \ \overline {[\zeta ]}_U \varphi ) \big )$
which makes that the proof now goes through easily.⊣
This lemma tells us that solutions to the recursion equivalence (5) possibly need not be provably unique if the object theory U is different from the meta theory T or in case we do not have the sufficient amount of transfinite induction available. Actually, we conjecture that it is possible to come up with theories T and U and with two predicates
$[\xi ]_U$
and
$\overline {[\xi ]}_U$
both satisfying the recursive equivalence such that T does not prove the equivalence of
$[\xi ]_U$
and
$\overline {[\xi ]}_U$
. We observe that not having provably unique fixpoints need not necessarily be a big problem and similar phenomena occur with for example Rosser fixpoints.
However, as we shall see in Section 5, we also need the object theory to be equal to the meta theory if we wish to prove the soundness of
${\mathsf {GLP}}_\Lambda $
with respect to the
$[\zeta ]^\Lambda _U$
predicates. In particular, the arithmetical soundness of the Necessitation rule requires the object and meta theory to be equal.
In case the object theory is not equal to the meta-theory, we can only prove a weak form of uniqueness as expressed in the following lemma.
Lemma 4.3. Let T be a theory that proves the recursion expressed in Equation (5) for two predicates
$[\zeta ]_U$
and
$\overline {[\zeta ]}_{V}$
with V possibly different from U. We further suppose that T proves the basic facts about the ordering
$\langle \Lambda ,\prec \rangle $
. In case T proves the arithmetical soundness of
${\mathsf {GLP}}_\Lambda $
for both predicates
$[\zeta ]_U$
and
$\overline {[\zeta ]}_{V}$
, then (omitting subscripts)
$$ \begin{align*} T \vdash \forall \, \alpha {\prec}\Lambda \Big ( \ \big( \langle \alpha \rangle \top \leftrightarrow \overline {\langle \alpha\rangle} \top \big) \ \longrightarrow \forall \varphi\, \exists \psi \ ([\alpha]\varphi \leftrightarrow \overline{[\alpha]} \psi)\Big). \end{align*} $$
Proof We reasonFootnote
4
in the theory T, consider some
$\alpha \prec \Lambda $
and sentence
$\varphi $
, assume that
$\langle \alpha \rangle \top \leftrightarrow \overline {\langle \alpha \rangle } \top $
, and claim that there exists
$\psi $
such that
$[\alpha ]\varphi \leftrightarrow \overline {[\alpha ]} \psi $
. If
$[\alpha ] \varphi $
, then we put to be
$\top $
. Further, assume that
$\neg [\alpha ] \varphi $
. In this case we have
$\neg [\alpha ] \bot $
, i.e.,
$\langle \alpha \rangle \top $
. Thus we have
$\neg \overline {[\alpha ]} \bot $
and hence we could put
$\psi $
to be
$\bot $
.⊣
Of course, this proof is not constructive and as such little informative since the
$\psi $
formula is not uniformly obtained from
$\varphi $
. In [Reference Joosten26] this question is taken up and addressed.
So far, in this section we have seen that with the techniques presented here we cannot prove that 1-Münchhausen provability predicates are uniquely defined by the recursion in (5) and we actually conjecture that non-equivalent solutions do exist. Only in the finite ordinals we can prove uniqueness. This allows us to relate the provability notions from this paper to similar ones from the literature. The most prominent example is given by the predicate
$$ \begin{align*} [n]^{\sf True}_T \varphi \ \ \ \mbox{ which stands for } \ \ \ \ \exists \, \pi {\in} \Pi^0_1\ \Big({\sf True}_{\Pi^0_1}(\pi) \wedge \Box_T\big( \pi \to \varphi \big)\Big ). \end{align*} $$
Furthermore, in [Reference Joosten, Beckmann, Mitrana and Soskova24] a reading is given where the modal operators
$[n]\varphi $
are interpreted as follows.
$$ \begin{align} [0]^{\Box}_T\phi \ \ \ &:= \Box_T \phi, \ \ \mbox{ and }\nonumber\\ [n+1]^{\Box}_T \phi \ \ \ &:= \ \Box_T \phi \ \vee \ \exists \, \psi \ \bigvee_{0\leq m \leq n} \Big(\langle m \rangle^{\Box}_T \psi \ \wedge \ \Box (\langle m \rangle^{\Box}_T \psi \to \phi)\Big). \end{align} $$
Soundness for this interpretation in
${\mathrm {PA}}$
was proven and a strong relation was given to the truth provability predicates
$[n]^{\sf True}_T$
. The next lemma is a strengthening on the one hand since we weaken the base theory to
${\mathrm {EA}}$
and a weakening on the other hand since we only consider two modalities.
Lemma 4.4. Let T be a theory that contains
${\mathrm {EA}}$
. We have that
-
1.
${\mathrm {EA}} \vdash \forall \varphi \ ([1]^{\Box }_T \varphi \leftrightarrow [1]^{\sf True}_T \varphi );$
-
2.
${\mathsf {GLP}}_2$
is sound for T when interpreting
$[0]$
as
$\Box _T$
and
$[1]$
as
$[1]^{\Box }_T;$
-
3. In case that moreover T proves the
$\Sigma ^0_1$
-collection principle we have
$T \vdash \forall \, \varphi \, \forall \psi \, \exists \chi \ \big ( [1]^{\Box }_T \varphi \vee [1]^{\Box }_T \psi \leftrightarrow [1]^{\Box }_T \chi \big )$
.
Proof It is easy to prove inside
${\mathrm {EA}}$
that
$[0]^{\Box } \varphi \leftrightarrow \Box \varphi $
(we omit the subscripts). Likewise,
$[0]^{\Box } \varphi \to [1]^{\Box } \varphi $
and
$[1]^{\Box } \bot \to [1]^{\Box } \varphi $
are easy to prove. With these ingredients the first item easily follows: one direction is obvious since any oracle sentence of the form
$\Diamond \psi $
is in
$\Pi ^0_1$
. The other direction is immediate in case
$ [0]^{\Box } \bot $
and in the case
$\langle 1 \rangle ^{\Box } \top $
it follows from the FGH theorem since under the consistency assumption, any
$\Pi ^0_1$
formula is equivalent and provably so to a formula of the form
$\Diamond \psi $
.
The second item follows from the first since the statement holds for the
$[n]^{\sf True}_T$
provability predicates (see, e.g., [Reference Beklemishev5]).
The third item is implicit in [Reference Joosten, Beckmann, Mitrana and Soskova24] and explicitly stated and proven in [Reference Joosten26] for the
$[1]^{\sf True}_T$
predicate which suffices by the first item of this lemma.⊣
Via an easy external induction we can prove that (8) and (5) define provably equivalent predicates for all natural numbers. That is to say, if T is a 1-Münchhausen theory, then for each natural number n we have that
$$ \begin{align} T\vdash \forall \varphi \ \big( [n]^{\Box}_T \varphi \leftrightarrow [n]_T^\Lambda \varphi \big) \end{align} $$
for any 1-Münchhausen provability predicate
$[\alpha ]_T^\Lambda $
. Moreover, in Lemma 4.1 we know that any 1-Münchhausen provability predicate
$[\alpha ]_T^\Lambda $
will be uniquely defined up to
$\omega $
. For later in the paper, we formulate the following corollary:
Corollary 4.5. Let T be a
$\Lambda $
-1-Münchhausen theory with
$\Lambda>2$
and corresponding 1-Münchhausen provability predicate
$[\alpha ]_T^\Lambda $
. Moreover, let T contain
${\sf B}\Sigma _1^0$
.
-
1.
${\mathsf {GLP}}_2$
is sound for T when interpreting
$[0]$
as
$[0]_T^\Lambda $
and
$[1]$
as
$[1]^\Lambda _T;$
-
2.
$T \vdash \forall \, \varphi \, \forall \psi \, \exists \chi \ \big ( [1]^\Lambda _T \varphi \vee [1]^\Lambda _T \psi \leftrightarrow [1]^\Lambda _T \chi \big )$
.
5 Arithmetical soundness for one-Münchhausen provability
In this section we will consider
$\Lambda $
-One-Münchhausen theories T and their corresponding
$\Lambda $
-One-Münchhausen provability predicates for some fixed ordinal
$\Lambda $
represented in T. We shall see that from the mere defining recursion on the provability predicate we can obtain soundness of
${\mathsf {GLP}}_\Lambda $
.
Many arguments in this section require transfinite induction. As we have observed in Section 4 this means that the base theory should also prove a decent amount of transfinite induction. In Section 8 we shall see how the need of transfinite induction can be circumvented by slightly altering the defining recursion.
5.1 Basic properties
Let us start the soundness proof by some basic observations that need very little arithmetical strength to be proven. In particular, the following facts do not require transfinite induction.
Lemma 5.1. Let T be a
$\Lambda $
-One-Münchhausen theory with corresponding provability predicate
$[\xi ]_T^\Lambda $
. We have the following.
-
1.
$T \vdash \forall \xi \, \forall \chi \ \big ( [\xi ]_T \bot \to [\xi ]_T \chi \big )$
and more in general, -
2.
$T \vdash \forall \xi \, \forall \varphi , \chi \ \Big ( [\xi ]_T \varphi \, \wedge \, \Box _T (\varphi \to \chi ) \to [\xi ]_T\chi \Big )$
, -
3.
$T \vdash \forall \varphi \, \forall \psi \ \Big ( [\xi ]_T \varphi \, \wedge \, \Box _T \psi \to [\xi ]_T(\varphi \wedge \psi )\Big )$
, -
4.
$T \vdash \exists x \ [\xi ]_T \varphi (\dot x) \ \to \ [\xi ]_T \exists x\varphi ( x)$
.
Proof Clearly, the first item follows from the second, so we reason in T and assume
$[\xi ]_T \varphi $
. Thus, in the non-trivial case, for some
$\psi $
and for some
$\zeta \prec \xi $
we have
$\langle \zeta \rangle _T \psi $
and
$\Box _T (\langle \zeta \rangle _T \psi \to \varphi )$
. Clearly, since
$\Box _T (\varphi \to \chi )$
, we have also
$\Box _T (\langle \zeta \rangle _T \psi \to \chi )$
so that
$[\xi ]_T\chi $
.
The third item follows from the second since in case of
$\Box _T \psi $
we also have
$\Box _T \big ( \varphi \to (\varphi \wedge \psi )\big )$
.
The fourth item follows by an easy case distinction on
$\xi $
being zero or not and both cases essentially follow from the fact that provably
$\exists x \Box _T \varphi (\dot x) \to \Box _T \exists x \varphi (x)$
.⊣
From our defining recursion (5), we get the axiom of negative introspection and the axiom of monotonicity almost for free.
Lemma 5.2. Let
$\xi < \zeta < \Lambda $
be ordinals in a
$\Lambda $
-One-Münchhausen theory T. We have
-
1.
$T \vdash \forall \varphi \ \big ( \langle \xi \rangle _T \varphi \ \to \ [\zeta ]_T \langle \xi \rangle _T \varphi \big );$
-
2.
$T \vdash \forall \varphi \ \big ( [\xi ]_T \varphi \ \to \ [\zeta ]_T \varphi \big ).$
Proof Item 1 is immediate since
$\Box _T(\langle \xi \rangle ^{\Box }_T \varphi \to \langle \xi \rangle ^{\Box }_T \varphi )$
using the fact that
$\xi < \zeta $
implies
$T\vdash \xi \prec \zeta $
. Likewise, Item 2 follows directly from the definition since provably
$\eta \prec \xi \to \eta \prec \zeta $
(recall that we required that Münchhausen theories prove the transitivity of
$\prec $
and moreover,
$\xi < \zeta $
implies
$T\vdash \xi \prec \zeta $
).⊣
It is easy yet important to observe that we actually have a formalized version of the previous lemma where we internally quantify over the ordinals. As such, the formalized lemma can be used for example in an induction where possibly non-standard ordinals are called upon.
Lemma 5.3. Let T be a
$\Lambda $
-One-Münchhausen theory. We have
-
1.
$T \vdash \forall \xi {\prec } \zeta {\prec } \Lambda \, \forall \varphi \ \big ( \langle \xi \rangle _T \varphi \ \to \ [\zeta ]_T \langle \xi \rangle _T \varphi \big );$
-
2.
$T \vdash \forall \xi {\prec } \zeta {\prec } \Lambda \, \forall \varphi \ \big ( [\xi ]_T \varphi \ \to \ [\zeta ]_T \varphi \big ).$
These cross axioms are for many interpretations of
${\mathsf {GLP}}_\Lambda $
actually the harder axioms to prove sound. But in the Münchhausen interpretations they come almost for free.
The above lemma can also be interpreted that any 1-Münchhausen provability predicate is monotone in the ordinal parameter. We note that it is not trivial to see that the 1-Münchhausen provability predicate is monotone in the underlying base theory: Suppose that, for example, we have a formulation of elementary arithmetic and axiomatic set theory so that provably
${\mathrm {EA}} \subset {\mathrm {ZFC}}$
. This means that for any formula
$\varphi $
we have
$\Box _{\mathrm {EA}} \varphi \to \Box _{\mathrm {ZFC}} \varphi $
. Is it now easy to see that we also have the expected
$[1]_{\mathrm {EA}} \varphi \to [1]_{\mathrm {ZFC}} \varphi $
?
Let us suppose that
$[1]_{\mathrm {EA}} \varphi $
because of some
$\langle 0 \rangle _{\mathrm {EA}}\psi $
with
$\Box _{\mathrm {EA}} (\langle 0 \rangle _{\mathrm {EA}} \psi \to \varphi )$
. A priori it is not at all clear how this information will yield us a
$\psi '$
so that
$\Box _{\mathrm {ZFC}} \Big (\langle 0 \rangle _{\mathrm {ZFC}} \psi ' \to \varphi \Big )$
and furthermore
$\langle 0 \rangle _{\mathrm {ZFC}} \psi '$
: where would we get so much
${\mathrm {ZFC}}$
consistency strength from?Footnote
5
At this point we can prove the soundness of the necessitation rule.
Lemma 5.4. Let T be a
$\Lambda $
-One-Münchhausen theory with corresponding 1-Münchhausen provability predicate
$[\alpha ]_T^\Lambda $
. For any
$\alpha \prec \Lambda $
we have that if
$T\vdash \varphi $
, then
$T\vdash [\alpha ]^\Lambda _T \varphi $
.
Proof We will only show
$\frac {\varphi }{\Box _T \varphi }$
. This is sufficient since necessitation for larger ordinals
$\frac {\varphi }{[\alpha ]_T \varphi }$
follows from the monotonicity of the predicate in
$\alpha $
. But, as always
$T\vdash \varphi $
can be expressed as a
$\Sigma ^0_1$
sentence which is true whence by
$\Sigma ^0_1$
completeness we get
$T\vdash \Box _T \varphi $
.⊣
We shall now prove the remaining
${\mathsf {GLP}}$
axioms to be sound. The following lemma, which was proven in [Reference Fernández-Duque and Joosten18], tells us that we don’t need to care about Löb’s axiom
$[\xi ]^{\Box } ([\xi ]^{\Box } \varphi \to \varphi ) \to [\xi ]^{\Box } \varphi $
.
Lemma 5.5. Let
${\sf GL}^\blacksquare $
denote the extension of
$\sf GL$
with a new operator
$\blacksquare $
and the following axioms for all formulas
$\phi ,\mbox { and }\psi\! :$
-
1.
$\vdash {\Box }\phi \to \blacksquare \phi $
, -
2.
$\vdash \blacksquare (\phi \to \psi )\to (\blacksquare \phi \to \blacksquare \psi )$
and, -
3.
$\vdash \blacksquare \phi \to \blacksquare \blacksquare \phi $
.
Then, for all
$\phi $
,
$$ \begin{align*}{\sf GL}^\blacksquare\vdash \blacksquare(\blacksquare\phi\to\phi)\to \blacksquare\phi.\end{align*} $$
Consequently, we only need to focus on the transitivity axioms
$[\xi ]\varphi \to [\xi ][\xi ]\varphi $
and distribution axioms
$[\xi ] (\varphi \to \psi ) \to ([\xi ] \varphi \to [\xi ] \psi )$
in our soundness proof. It is in this part where we need to assume that the object and meta theory are equal so that we have access to transfinite reflexive induction as formulated in Lemma 2.7.
5.2 On weak closure
A basic modal principle has that provability commutes with conjunctions:
$\Box A \wedge \Box B \leftrightarrow \Box (A\wedge B)$
. To have this reflected in our arithmetical soundness proof of 1-Münchhausen provability we shall need to combine two oracle calls
$\langle \beta \rangle \varphi '$
and
$\langle \beta \rangle \psi '$
into a single one. Clearly, we cannot expect consistency statements to be closed under conjunctions (or dually, provability statements to be closed under disjunctions). However, weak closure under conjunctions in the sense of
$\forall \varphi ' \forall \psi ' \exists \chi \ (\langle \beta \rangle \varphi ' \wedge \langle \beta \rangle \psi ' \leftrightarrow \langle \beta \rangle \chi )$
as expressed in its dual form in Corollary 2.2 is sufficient for our purpose.
This subsection is dedicated to proving the weak closure property for 1-Münchhausen provability. We shall see how the well-known proof for the FGH theorem can be generalised to the current setting.
The standard proof for the FGH theorem goes via witness comparison statements of the form: one witness/proof occurs before another witness/proof. To generalise this, we will introduce the notion of an
$\alpha $
-proof.
Definition 5.6. Let T be a single oracle
$\Lambda $
-Münchhausen Theory with corresponding 1-Münchhausen provability predicate
$[\alpha ]^\Lambda _T$
. An
$\alpha $
-proof x for
$\varphi $
is defined inside T as a triple
$x=\langle \beta , \varphi ', p \rangle $
so that either
${\sf Proof}_T(p, \varphi )$
or otherwise
$(\beta \prec \alpha ) \wedge (\langle \beta \rangle \varphi ' ) \wedge {\sf Proof}_T(\langle \beta \rangle \varphi ' \to \varphi )$
. We will write
${\sf Proof}^\alpha _T(x, \varphi )$
.
Under the assumption that our predicate
$[\beta ]_T^\Lambda $
is sound for
${\mathsf {GLP}}_{\alpha +1}$
we can prove that the
$[\alpha ]^\Lambda _T$
predicate is complete for any Boolean combination of statements of the form
${\sf Proof}^\alpha _T(p, \psi )$
. This is reflected in the following lemma.
Lemma 5.7. Let T be a single oracle
$\Lambda $
-Münchhausen Theory with corresponding 1-Münchhausen provability predicate
$[\alpha ]^\Lambda _T$
so that T proves all the instantiations of axioms of
${\mathsf {GLP}}_{\alpha +1}$
. Then we have that
-
1.
$T\vdash {\sf Proof}^\alpha _T(x, \varphi ) \to [\alpha ]^\Lambda _T {\sf Proof}^\alpha _T(x, \varphi );$
-
2.
$T\vdash \neg {\sf Proof}^\alpha _T(x, \varphi ) \to [\alpha ]^\Lambda _T \neg {\sf Proof}^\alpha _T(x, \varphi )$
.
Proof The proof is easy and basically follows from the soundness for
${\mathsf {GLP}}_{\alpha +1}$
. Let us briefly comment on the second item. So, suppose that
$\neg {\sf Proof}^\alpha _T(x, \varphi )$
. In case x is not a triple or not a triple of the required format, we can express this in a decidable way so that we also know this under
$\Box _T$
whence also under
$[\alpha ]_T$
. We now omit subscripts on the boxes in the remainder of this proof.
For
$x= \langle \beta , \varphi ', p\rangle $
of the right format we know from
$\neg {\sf Proof}^\alpha _T(x, \varphi )$
that (a.)
$\neg {\sf Proof}_T(p, \varphi )$
and (b.)
$\neg (\beta \prec \alpha )$
or
$\neg \langle \beta \rangle \varphi '$
or
$\neg {\sf Proof}^\alpha _T(p, \langle \beta \rangle \varphi '\to \varphi )$
. We recall that
$\neg \langle \beta \rangle \varphi '$
is just
$[\beta ] \neg \varphi '$
and by soundness we know
$[\beta ] \neg \varphi ' \to [\alpha ] [\beta ] \neg \varphi '$
. Thus, for each of the disjuncts in (b.) we can obtain that disjunct and whence the whole disjunction under the
$[\alpha ]$
predicate. Likewise, we get
$(a.)$
under the
$[\alpha ]$
predicate. By soundness, the
$[\alpha ]$
predicate commutes with conjunctions so that we obtain
$[\alpha ]^\Lambda _T \neg {\sf Proof}^\alpha _T(x, \varphi )$
.⊣
The notion of
$\alpha $
-proofs allows us to compare them so that we can prove our main theorem.
Theorem 5.8. Let T be a single oracle
$\Lambda $
-Münchhausen Theory with corresponding 1-Münchhausen provability predicate
$[\alpha ]^\Lambda _T$
so that T proves transfinite
$\Sigma _1^0([\alpha ]^\Lambda _T)$
induction and all the instantiations of axioms of
${\mathsf {GLP}}_{\alpha +1}$
. We then have
$$ \begin{align*} T\vdash \vdash \forall \alpha \, \forall \varphi\, \forall \psi \, \exists \chi \ \Big([\alpha]_T^{\Lambda}\varphi \vee [\alpha]_T^{\Lambda}\psi \ \ \leftrightarrow [\alpha]_T^{\Lambda}\chi \Big). \end{align*} $$
Proof We omit sub and superscripts, reason in T, fix
$\varphi $
and
$\psi $
arbitrary, and consider the following fixpoint:
$$ \begin{align*} \rho \leftrightarrow ([\alpha] \varphi \vee [\alpha] \psi) \leq [\alpha] \rho, \end{align*} $$
where
$([\alpha ] \varphi \vee [\alpha ] \psi ) \leq [\alpha ] \rho $
is short for
$$ \begin{align*} \exists x \Big( \big({\sf Proof}^\alpha(x_0,\varphi) \vee {\sf Proof}^\alpha(x_1,\psi)\big) \wedge \forall \, y{<}x \neg {\sf Proof}^\alpha(y, \rho)\Big). \end{align*} $$
We now claim that
$([\alpha ] \varphi \vee [\alpha ] \psi ) \leftrightarrow [\alpha ] \rho $
. In case that
$[\alpha ]\bot $
this is trivial so we may work under the assumption that
$\langle \alpha \rangle \top $
and set out to prove both directions.
$\to $
: For a contradiction we suppose
$([\alpha ] \varphi \vee [\alpha ] \psi )$
but
$\neg [\alpha ] \rho $
. Then certainly
$([\alpha ] \varphi \vee [\alpha ] \psi ) \leq [\alpha ] \rho $
. In particular for some x, we have
$\big ({\sf Proof}^\alpha (x_0,\varphi ) \vee {\sf Proof}^\alpha (x_1,\psi )\big ) \wedge \forall \, y{<}x \neg {\sf Proof}^\alpha (y, \rho )$
. Using Lemma 5.7 we may now conclude
$[\alpha ] \big ({\sf Proof}^\alpha (x_0,\varphi ) \vee {\sf Proof}^\alpha (x_1,\psi )\big ) \wedge \forall \, y{<}x [\alpha ] \neg {\sf Proof}^\alpha (y, \rho )$
. From the latter conjunct,
$\Sigma _1^0([\alpha ]^\Lambda _T)$
induction and closure of the
$[\alpha ]$
predicate under conjunctions we obtain
$[\alpha ] \Big ( \neg {\sf Proof}^\alpha (0, \rho ) \wedge \cdots \wedge \neg {\sf Proof}^\alpha (x-1, \rho ) \Big )$
whence
$ [\alpha ] \forall \, y{<}\dot x \neg {\sf Proof}^\alpha (y, \rho )$
. Collecting our insights under the
$[\alpha ]$
we see that
$$ \begin{align*} [\alpha] \exists x \Big( \big({\sf Proof}^\alpha(x_0,\varphi) \vee {\sf Proof}^\alpha(x_1,\psi)\big) \wedge \forall \, y{<}x \neg {\sf Proof}^\alpha(y, \rho)\Big), \end{align*} $$
which is by the definition of our fixpoint nothing but
$[\alpha ]\rho $
which is a contradiction.
$\leftarrow $
: For a contradiction we suppose
$[\alpha ] \rho $
but
$\neg ([\alpha ] \varphi \vee [\alpha ] \psi )$
and recall that we may employ the additional assumption that
$\langle \alpha \rangle \top $
. From
$[\alpha ] \rho $
and
$\neg ([\alpha ] \varphi \vee [\alpha ] \psi )$
we obtain
$$ \begin{align*} \exists y \Big( {\sf Proof}^\alpha(y, \rho) \wedge \forall \, x{<}y{+}1 \neg \big({\sf Proof}^\alpha(x_0,\varphi) \vee {\sf Proof}^\alpha(x_1,\psi)\big) \Big). \end{align*} $$
By a reasoning analogous to the proof of the other implication we conclude
$$ \begin{align*} [\alpha] \exists y \Big( {\sf Proof}^\alpha(y, \rho) \wedge \forall \, x{<}y{+}1 \neg \big({\sf Proof}^\alpha(x_0,\varphi) \vee {\sf Proof}^\alpha(x_1,\psi)\big) \Big). \end{align*} $$
From the properties of
$<$
being a total order, we obtain
$$ \begin{align*} [\alpha] \neg \exists x \Big( \big({\sf Proof}^\alpha(x_0,\varphi) \vee {\sf Proof}^\alpha(x_1,\psi)\big) \wedge \forall \, y{<}x \neg {\sf Proof}^\alpha(y, \rho)\Big), \end{align*} $$
which is nothing but
$[\alpha ] \neg \rho $
. Combining this with our assumption
$[\alpha ] \rho $
yields via the soundness of
${\mathsf {GLP}}_{\alpha +1}$
that
$[\alpha ] \bot $
but that contradicts our additional assumption
$\langle \alpha \rangle \top $
.⊣
We emphasise that both Lemma 5.7 and Theorem 5.8 assume that soundness for
${\mathsf {GLP}}_{\alpha +1}$
holds. This assumption justifies that in particular we may use the fact that the
$[\alpha ]$
provability predicate commutes with conjunctions. Indeed, soundness for
${\mathsf {GLP}}_{\alpha +1}$
is a rather strong assumption, however, at the place where Theorem 5.8 is used in Item 5 of Theorem 5.9 below, we shall indeed have established the required soundness.
5.3 Soundness
Now that we have proven weak closure of one-Münchhausen provability under disjunctions we can finally prove arithmetical soundness.
Theorem 5.9. Let T be a
$\Lambda $
-One-Münchhausen theory and let
$[\alpha ]^\Lambda _T$
be a corresponding provability predicate. If T proves transfinite
$\Pi _1^0([\alpha ]^\Lambda _T)$
and
$\Sigma _1^0([\alpha ]^\Lambda _T)$
induction we have that
-
1. T proves that all the rules and axioms of
${\mathsf {GLP}}$
are sound w.r.t. T by interpreting
$[\alpha ]$
as
$[\alpha ]_T^\Lambda ;$
in particular -
2. Distributivity
$:$
$T \vdash \forall \alpha \, \forall \varphi \, \forall \psi \ \Big ( [\alpha ]_T^\Lambda (\varphi \to \psi ) \to ([\alpha ]_T^{\Lambda }\varphi \to [\alpha ]_T^{\Lambda }\psi )\Big );$
-
3. Closure under conjunctions
$:$
$$ \begin{align*} T\vdash \forall \alpha \, \forall \varphi\, \forall \psi \ \Big( [\alpha]_T^{\Lambda}\varphi \wedge [\alpha]_T^{\Lambda}\psi \ \ \leftrightarrow \ \ [\alpha]_T^{\Lambda}(\varphi \wedge \psi) \Big); \end{align*} $$
-
4. Transitivity
$:$
$T \vdash \forall \alpha \, \forall \varphi \ \Big ( [\alpha ]_T^{\Lambda } \varphi \to [\alpha ]_T^{\Lambda } [\alpha ]_T^{\Lambda }\varphi \Big );$
-
5. Weak closure under disjunctions
$:$
$$ \begin{align*} T\vdash \forall \alpha \, \forall \varphi\, \forall \psi \, \exists \chi \ \Big([\alpha]_T^{\Lambda}\varphi \vee [\alpha]_T^{\Lambda}\psi \ \ \leftrightarrow [\alpha]_T^{\Lambda}\chi \Big). \end{align*} $$
Proof If we wish to prove Item 1, we should prove the soundness of the rules and of the axioms.
As to the rules, the only rules of
${\mathsf {GLP}}$
are modus ponens and a necessitation rule for each modality:
$\displaystyle \frac {\varphi }{[\xi ]^{\Box }_T\varphi }$
. As pointed out in Lemma 5.4 the soundness of the necessitation rules follows from necessitation for
$\Box _T$
and by monotonicity, Lemma 5.3. As always, the soundness of modus ponens is immediate.
In the remainder of our proof we shall thus focus on the axioms. Since we proved the correctness of the negative introspection axioms—axioms of the form
$\langle \beta \rangle \varphi \to [\alpha ] \langle \beta \rangle \varphi $
for
$\beta < \alpha $
—and of the monotonicity axioms—axioms of the form
$[\beta ] \varphi \to [\alpha ] \varphi $
for
$\beta < \alpha $
—without any induction in Lemma 5.3 and since by Lemma 5.5 we may disregard Löb’s axiom, we set out to prove the remaining axioms which are just the distribution and the transitivity axioms to complete a proof of Item 1. In other words, to complete the proof of Item 1 we should prove Items 2 and 4.
To prove that both items hold up to a certain level
$\alpha <\Lambda $
we proceed by an internal transfinite reflexive induction on
$\alpha $
as expressed in Lemma 2.7. We need to prove both items simultaneously since they depend on each other. As a matter of fact, to get the proof going we will need to do some induction building and prove Items 2–4 of the proof simultaneously by a transfinite reflexive induction on
$\alpha $
.
Thus, we will reason in T and shall mostly omit the subscript T and the superscript
$\Lambda $
in the remainder of this proof. The base case of the theorem is known to hold via the soundness of
${\textbf {GL}}$
and the FGH theorem.
For the reflexive inductive step, we are to prove our four items (Items 2–4) at level
$\alpha $
assuming that we have access to all four items at any level
$\beta \prec \alpha $
and we also have these four items under a regular provability predicate
$\Box _T$
at any level
$\beta '\prec \alpha $
. As we observed before, Item 1 at level
$\alpha $
(soundness of
${\mathsf {GLP}}_\alpha $
) follows directly from Items 2–4 for levels
$\beta \prec \alpha $
. Thus, we may in our inductive step assume that we have access—and T-provably so—to all
${\mathsf {GLP}}_\alpha $
reasoning. Let us thus focus on the first item to prove:
Item 3:
$ \forall \varphi \, \forall \psi \ \Big ( [\alpha ]_T^{\Lambda }\varphi \wedge [\alpha ]_T^{\Lambda }\psi \ \ \leftrightarrow \ \ [\alpha ]_T^{\Lambda }(\varphi \wedge \psi ) \Big )$
. We fix some
$\varphi $
and
$\psi $
and assume
$[\alpha ]\varphi $
and
$[\alpha ]\psi $
. We consider two cases. In the easy case, we have that at least one of
$\Box \varphi $
or
$\Box \psi $
holds in which case the result directly follows from Lemma 5.1.3.
In the remaining case, by the recursion equation for
$[\alpha ]$
, we find ordinals
$\beta , \beta ' <\alpha $
and some formulas
$\varphi ', \psi '$
so that
$\langle \beta \rangle \varphi '$
,
$\langle \beta ' \rangle \psi '$
,
$\Box \big (\langle \beta \rangle \varphi ' \to \varphi \big )$
, and
$\Box \big (\langle \beta ' \rangle \psi '\to \psi \big )$
.
We first remark that w.l.o.g. we may assume
$\beta '=\beta $
. For, if, e.g.,
$\beta '<\beta $
, then by Lemma 2.5.2. we see that
$\langle \beta \rangle \top \ \to \ \big ( \langle \beta ' \rangle \psi ' \ \leftrightarrow \ \langle \beta \rangle \langle \beta ' \rangle \psi '\big )$
with
$\langle \beta \rangle \varphi ' \to \langle \beta \rangle \top $
. Since we perform a transfinite reflexive induction, we also have our inductive hypotheses under a
$\Box $
and in particular
$\Box \big (\langle \beta \rangle \langle \beta ' \rangle \psi ' \to \langle \beta ' \rangle \psi ' \big )$
. Thus, we see that
$\langle \beta \rangle \langle \beta ' \rangle \psi ' \wedge \Box \big (\langle \beta \rangle \langle \beta ' \rangle \psi ' \to \psi \big )$
whence
$$ \begin{align*} \exists \psi'' \ \Big(\langle \beta \rangle\psi'' \wedge \Box\big(\langle \beta \rangle\psi'' \to \psi \big) \Big). \end{align*} $$
So, we assume
$\beta '=\beta < \alpha $
, and by the inductive hypothesis (on Item 5), we find
$\chi $
with
$\langle \beta \rangle \chi \ \leftrightarrow \ \langle \beta \rangle \varphi ' \wedge \langle \beta \rangle \psi '$
whence by the reflexive induction hypothesis also
$\Box \big ( \langle \beta \rangle \chi \ \leftrightarrow \ \langle \beta \rangle \varphi ' \wedge \langle \beta \rangle \psi '\big )$
. Consequently, we have that
$\Box (\langle \beta \rangle \chi \to \varphi \wedge \psi )$
and we are done with the direction
$[ \alpha ] \varphi \wedge [ \alpha ] \psi \to [\alpha ](\varphi \wedge \psi )$
. The other direction follows directly from Lemma 5.1 since
$\Box \big ( (\varphi \wedge \psi ) \to \varphi \big )$
and
$\Box \big ( (\varphi \wedge \psi ) \to \psi \big )$
.
Item 2:
$\forall \varphi \, \forall \psi \ \Big ( [\alpha ]_T^\Lambda (\varphi \to \psi ) \to ([\alpha ]_T^{\Lambda }\varphi \to [\alpha ]_T^{\Lambda }\psi )\Big )$
. From the previous item we know that
$$ \begin{align*} [{\alpha}] (\varphi\to \psi) \wedge [{\alpha}]\varphi \ \leftrightarrow \ [{\alpha}]\Big ( (\varphi\to \psi) \wedge \varphi \Big), \end{align*} $$
so that the result follows from Lemma 5.1.
Item 4:
$\forall \varphi \ \Big ( [\alpha ]_T^{\Lambda } \varphi \to [\alpha ]_T^{\Lambda } [\alpha ]_T^{\Lambda }\varphi \Big )$
. While reasoning in T we assume
$[\alpha ]\varphi $
and only consider the non-trivial case. Thus, for some
$\varphi '$
and some
$\beta \prec \alpha $
we get
$\langle \beta \rangle \varphi '$
and
$\Box (\langle \beta \rangle \varphi ' \to \varphi )$
. By negative introspection we get
$[\alpha ] \langle \beta \rangle \varphi '$
. Since T is a 1-Münchhausen theory it proves some properties of the order
$\prec $
. In particular, from
$\beta \prec \alpha $
, we also get
$[\alpha ] (\beta \prec \alpha )$
. From
$\Box (\langle \beta \rangle \varphi ' \to \varphi )$
we obtain by applying successively provable
$\Sigma ^0_1$
completeness and monotonicity that
$[\alpha ]\Box (\langle \beta \rangle \varphi ' \to \varphi )$
. Since we already proved closure of the
$[\alpha ]$
predicate under conjunctions, we can collect all the information under the
$[\alpha ]$
and applying Lemma 5.3.4. we see that we have obtained
$[\alpha ][\alpha ]\varphi $
.
Item 5:
$\forall \varphi \, \forall \psi \, \exists \chi \ \Big ([\alpha ]_T^{\Lambda }\varphi \vee [\alpha ]_T^{\Lambda }\psi \ \ \leftrightarrow [\alpha ]_T^{\Lambda }\chi \Big )$
. Here we can now simply invoke Theorem 5.8. We stress a subtle issue here that the order in which we proved the items of this theorem is indeed quite important. In particular, at the point we have proved Items 1–4 for
$[\alpha ]$
, we have established the soundness of
${\mathsf {GLP}}_{\alpha +1}$
which is needed among the assumptions of Theorem 5.8.⊣
6 Completeness of Münchhausen provability
In this section we shall prove that under some modest set of extra assumptions, we can obtain completeness of one-Münchhausen provability. Basically, this section consist of invoking a result from [Reference Fernández-Duque and Joosten18] and recasting it in our context. Let us first recall some definitions and results.
6.1 Uniform proof and provability predicates
The definitions and results from this subsection all come from [Reference Fernández-Duque and Joosten18] where an arithmetical completeness proof is given that is schematic in an abstract kind of provability predicates. A first step in defining these provability predicates consists of defining so-called
$\Lambda $
-uniform proof and provability predicates over T.
Definition 6.1. Let T be representable and
$\Lambda $
a linear order. Given a formula
$\pi (c,\lambda ,\phi )$
, we introduce the notation
$[c:\lambda ]_{\pi} {\phi }=\pi (c,\lambda ,\phi )$
, as well as
$[{\lambda }]_{\pi}\phi = \exists c[c: \lambda]_{\pi}\phi$
. The dual notions
$\langle c:\lambda \rangle _{\pi }{\phi }$
and
$\langle {\xi }\rangle _{\pi }{\phi }$
are defined as
$\neg \pi (c,\lambda ,\neg \phi )$
and
$\neg \exists c [c: {\lambda}]_{\pi} {\neg \phi }$
respectively.
A
$\Lambda $
-uniform proof predicate over T is a formula
$\pi (c,\lambda ,\phi )$
(with all free variables shown) satisfying
-
1.
$T\vdash {\mathrm {I}\Sigma _{1}^0}(\pi );$
-
2.
$T\vdash \forall \lambda \forall \phi \ ({\Box }_T\phi \rightarrow [{\lambda }]_{\pi }\phi );$
-
3.
$T\vdash \forall \lambda \forall \phi \forall \psi \ \Big ([{\lambda }]_{\pi }(\psi \to \phi )\wedge [{\lambda }]_{\pi }\psi \rightarrow [{\lambda }]_{\pi }\phi \Big );$
-
4.
$T\vdash \forall c\, \forall \lambda \, \forall \xi {\leq _\Lambda }\lambda \, \forall \phi \ \Big ([c:\xi ]_{ }\pi {\phi }\rightarrow [c:\lambda ]_{ }\pi \phi \Big );$
-
5.
$T\vdash \forall c\, \forall \lambda \, \forall \phi \ \Big ([c:\lambda ]_{\pi }{\phi }\rightarrow [{\lambda }]_{ }\pi [\dot c:\dot \lambda ]_{\pi }{\dot \phi }\Big );$
-
6.
$T\vdash \forall c \forall \lambda \, \forall \phi \ \Big (\langle c:\lambda \rangle _{\pi }{\phi }\rightarrow [{\lambda }]_{ }\pi \langle \dot c:\dot \lambda \rangle _{\pi }{\dot \phi }\Big );$
-
7.
$T\vdash \forall \lambda \, \forall \, \xi {<_\Lambda }\lambda \, \forall \phi \ \Big ( \langle {\xi }\rangle _{\pi }{\phi }\rightarrow [{\lambda }]_{\pi }{{\langle {\dot \xi }\rangle _{\pi }{\dot \phi }}}\Big )$
.
We say that
$\pi $
is sound
Footnote
6
if, moreover,
$\mathbb N\models \forall \lambda \forall \phi \ ([{\lambda }]_{\pi }\phi \rightarrow \phi )$
.
A formula
$\hat \pi $
is a
$\Lambda $
-uniform provability predicate over T if
$T\vdash \hat \pi \leftrightarrow \exists c\ \pi $
, where
$\pi $
is a
$\Lambda $
-uniform proof predicate.
Moreover, the provability predicates are required to require a modicum of good behaviour as captured in the following definition.
Definition 6.2. Let
$\pi $
be a
$\Lambda $
-uniform proof predicate over a theory T. We say that
$\pi $
is normalized if it is provable in T that for every
$\lambda $
we have that every
$\lambda $
-derivable formula has infinitely many
$\lambda $
-derivations and, whenever
$[c:\lambda ]_{ }\pi \phi $
and
$[c:\lambda ]_{ }\pi \psi $
, it follows that
$\phi =\psi ;$
in other words, every derivation must be a derivation of a single formula.
Modal formulas are linked to arithmetical ones via an arithmetic interpretation.
Definition 6.3. An arithmetic interpretation is a functionFootnote
7
$f:\mathbb P\to {\mathcal S}^1_\omega $
.
If
$\pi $
is a
$\Lambda $
-uniform proof predicate over T, we denote by
$f_\pi $
the unique extension of f such that
$f_\pi (p)=f(p)$
for every propositional variable p,
$f_\pi (\bot )=\bot $
,
$f_\pi $
commutes with Booleans, and
$f_\pi ([\lambda ]\phi )=[\overline \lambda ]_\pi f_\pi (\phi )$
.
The following uniform completeness theorem is proven in [Reference Fernández-Duque and Joosten18, Theorem 10.2] and provides us with an easy way to prove completeness for our current interpretation.
Theorem 6.4. If
$\Lambda $
is a computable linear order, T is any sound, representable theory extending
${\mathrm {RCA}}_0$
,
$\pi $
is a sound, normalized,
$\Lambda $
-uniform proof predicate over T, and
$\phi $
is any
${\mathcal L}_{\Box }$
-formula,
${\sf GLP}_\Lambda \vdash \phi $
if and only if, for every arithmetic interpretation f,
$T\vdash f_\pi (\phi )$
.
6.2 Arithmetical completeness for Münchhausen provability
We can now combine the results from this paper and the previous subsection to see that under some extra conditions we obtain arithmetical completeness for one-Münchhausen provability.
Theorem 6.5 Arithmetical completeness
Let
$\Lambda $
be a computable linear order, and T is any sound, representable one-Münchhausen theory extending
${\mathrm {RCA}}_0$
with corresponding provability predicate
${[\alpha ]_T}^\Lambda \varphi $
so that
$T\vdash {\mathrm {I}\Sigma _{1}^0}({[\alpha ]_T}^\Lambda \varphi )$
. We then have that
${[\alpha ]_T}^\Lambda \varphi $
is a uniform provability predicate and in particular,
$$ \begin{align*} {\mathsf{GLP}}_\Lambda \vdash \varphi \ \ \Longleftrightarrow \ \ \forall * \ T \vdash \varphi^*. \end{align*} $$
Proof As always, the
$*$
in the statement of the theorem is understood to range over arithmetical interpretations that map propositional variables to arbitrary sentences, so that
$*$
commutes with the Boolean connectives and each modal formula
$[\alpha ] \psi $
is mapped to
${{[\overline \alpha ]_T}}^\Lambda \psi ^*$
.
From our provability predicate (omitting sub and superscripts)
$[\alpha ] \varphi $
we will define a proof predicate
$\pi (c,\lambda ,\phi )$
for which we will observe that over T it is a normalized uniform proof predicate so that provably
$\exists c\ \pi (c,\lambda ,\phi ) \ \leftrightarrow \ [\lambda ] \phi $
. To this end we define a slight variation of Definition 5.6
$$ \begin{align*} \pi (c,\lambda,\phi) \ := \ c=\langle c_0, c_1\rangle \wedge \left \{ \begin{array}{lcll} \Big ( c_0 =0 &\wedge& {\sf Proof}_T(c_1, \phi) \Big) & \!\!\vee\\ \Bigg( c_0 =1 &\wedge & c_1 = \langle \xi, \psi, p\rangle \ \wedge \ \xi \prec \lambda \ \ \ \wedge & \\ & & \langle \xi \rangle^{\Box} \psi \wedge {\sf Proof}_T(p, \langle \xi \rangle^{\Box} \psi \to \phi)\Bigg).\\ \end{array} \right. \end{align*} $$
It is straightforward to see that, indeed,
$T \vdash \exists c\ \pi (c,\lambda ,\phi ) \ \leftrightarrow \ [\lambda ] \phi $
. Since
${\sf Proof}_T$
is a normalized proof predicate, so is
$\pi $
. Thus, we should only check Properties 1–7 from Definition 6.1. Property 1 is one of the assumptions of the theorem and Properties 2, 3, and 7 follow directly from the arithmetical soundness of one-Münchhausen provability. Property 4 follows since T is a one-Münchhausen theory whence proves transitivity of
$\prec $
. Properties 5 and 6 are a direct consequence of the definition of
$\pi $
and the soundness of the one-Münchhausen provability predicate in very much the same spirit as the proof of Lemma 5.7.⊣
7 Some notes on the formalisation of one-Münchhausen provability
Throughout this paper we have been talking about Münchhausen provability predicates and proving all sorts of properties of them. The reserved reader may now question whether there exist one-Münchhausen theories with corresponding one-Münchhausen provability predicates at all. In this section we sketch how to formalize a Münchhausen provability predicate in second order arithmetic.
Just as in [Reference Fernández-Duque and Joosten18] we start our formalization by reserving a set parameter X where we will collect all the pairs
$\langle \alpha , \varphi \rangle $
of ordinals
$\alpha $
and formulas
$\varphi $
so that
$[\alpha ] \varphi $
holds. Next, we will write down a predicate that all and only the correct pairs
$\langle \alpha , \varphi \rangle $
are in X. Thus, we write the recursion for one-Münchhausen provability replacing every occurrence of
$[ \alpha ] \varphi $
by
$\langle \alpha , \varphi \rangle \in X$
and consequently replacing
$\langle \alpha \rangle \varphi $
by
$\langle \alpha , \neg \varphi \rangle \notin X$
. We define any set satisfying our predicate to be an
$1{-}\sf IMC$
for Iterated one-Münchhausen Class.
By naively doing so, a problem arises namely that we get occurrences of the set variable X under the regular provability predicate
$\Box _T$
. By using numerals we can speak under a box about numbers that ‘live outside the box’. However, we do not have any syntactical artefact to denote arbitrary sets. A possibly way out here would be to resort to oracle-provability as introduced in [Reference Cordón Franco, Fernández-Duque, Joosten and Lara Martín10]. Thus, for one-Münchhausen provability, the predicate would look something like:
$$ \begin{align*} \begin{array}{lll} 1{-}{\sf IMC}(X,\alpha):= & & \\ \ \ \ \forall \, \xi{\leq}\alpha\, \forall \varphi \Big[ \langle \xi, \varphi \rangle \in X &\leftrightarrow & \Big( \Box_T \varphi \, \vee \, \exists \psi \, \exists \, \zeta{<}\xi \ \big( \, \langle \zeta, \neg \psi \rangle \notin X \ \wedge \\ & & \ \ \ \ \ \ \ \Box_{T | X } (\langle \zeta, \neg \psi \rangle \notin X \to \varphi) \big) \Big)\Big]. \end{array} \end{align*} $$
With such a predicate we can then define:
$$ \begin{align*} [\alpha]_{T,1} \varphi := \forall X \Big( 1{-}{\sf IMC}(X,\alpha) \to \langle \alpha, \varphi \rangle \in X\Big). \end{align*} $$
However, it is not clear if such a predicate will satisfy the required recursive equation since the relation between oracle provability and regular provability is not yet entirely understood in all its details.
For these and other reasons we choose a different approach. We will anticipate that hopefully/probably the
$1{-}\sf IMC$
predicate will define a unique set. Then, under the box we can just use any set that satisfies
${\sf IMC}(X)$
. Of course, the fixpoint theorem allows us to do so. In the formalisation of Münchhausen provability we will closely follow [Reference Fernández-Duque and Joosten18]. As such we allow ourselves to be rather sketchy and refer to [Reference Fernández-Duque and Joosten18] for the details.
Definition 7.1. We define the predicate
$1{-}{\sf IMC}(X,\gamma )$
using the fixpoint theorem so that it satisfies (provably in
${\text {ECA}_0}$
) the following recursion.
$$ \begin{align*} \begin{array}{lll} 1{-}{\sf IMC}&\hspace{-.2cm}(X,\gamma) \ \longleftrightarrow& \\ & \Big( \forall\, \alpha {\preceq}\gamma\ \forall \varphi\ \Big[ & \langle \alpha , \varphi\rangle \in X \ \leftrightarrow \\ & & \Box_U \varphi \vee \exists\, \beta{\prec}\alpha \exists \psi \Big( \langle \beta, \neg \psi \rangle\notin X \wedge \\ & & \ \ \ \Box_U \big[ \exists X ( 1{-}{\sf IMC} (X,\dot \beta) \wedge \langle\dot \beta, \neg \dot \psi \rangle \notin X) \to \varphi\big]\Big)\Big]\Big). \end{array} \end{align*} $$
With this Iterated one-Münchhausen Class predicate we define our one-Münchhausen predicate as
$$ \begin{align*} [\alpha]_U \varphi := \forall X \Big( 1{-}{\sf IMC}(X,\alpha) \to \langle \alpha, \varphi \rangle \in X\Big). \end{align*} $$
It is clear that our definition supposes that we fix an ordinal notation system for some ordinal
$\Lambda $
and that all our ordinal quantifications are restricted to this
$\Lambda $
. We observe that
$$ \begin{align*} \langle\alpha\rangle \varphi := \exists X \Big( 1{-}{\sf IMC}(X,\alpha) \wedge \langle \alpha, \neg \varphi \rangle \notin X\Big). \end{align*} $$
Consequently we can rewrite the defining recursion for Iterated one-Münchhausen Classes as
$$ \begin{align*} \begin{array}{lll} 1{-}{\sf IMC}&\hspace{-.2cm}(X,\gamma) \ \longleftrightarrow& \\ & \Big( \forall\, \alpha {\preceq}\gamma\ \forall \varphi\ \Big[ & \langle \alpha , \varphi\rangle \in X \ \leftrightarrow \\ & & \Box_U \varphi \vee \exists\, \beta{\prec}\alpha \exists \psi \big( \langle \beta, \neg \psi \rangle\notin X \wedge \\ & & \ \ \ \Box_U \big[ \langle \beta \rangle \psi \to \varphi\big]\big)\Big]\Big). \end{array} \end{align*} $$
It is clear that
$1{-}{\sf IMC}$
depends on the base theory U and on the ordinal representation
$\Lambda $
but for the sake of readability we suppress these dependencies in our notation. We remark that
$1{-}{\sf IMC} (X,\gamma )$
is of complexity
$\Pi ^0_2$
with free set variable X. Our predicate
$[\alpha ]\varphi $
has a universal quantifier ranging over all sets that are iterated Münchhausen classes. Of course, we would hope that indeed such classes are uniquely defined if they exists at all.
In order to express this, we will fix the following notation:
$$ \begin{align*} X\equiv_\alpha Y \ \ := \ \ \forall \, \beta{\preceq}\alpha\, \forall \varphi \Big( \langle \beta, \varphi \rangle \in X \ \longleftrightarrow \ \langle \beta, \varphi \rangle \in Y \Big), \end{align*} $$
and
$$ \begin{align*} \exists^{\leq 1 \upharpoonright \alpha} X \ {\sf IMC}(X,\alpha) \ \ := \ \ \forall X\, \forall Y\ \Big( {\sf IMC} (X,\alpha) \wedge {\sf IMC} (Y,\alpha) \ \longrightarrow \ X\equiv_\alpha Y\Big). \end{align*} $$
We can now state and prove a key ingredient in proving that our formalisation satisfies the defining recursion for Münchhausen provability.
Lemma 7.2. Let U be a theory extending
${\text {ECA}_0}$
. We have that
$$ \begin{align*} {\text{ACA}_0} + {\sf wo}(\alpha) \vdash \forall \beta {\prec} \alpha \, \exists^{\leq 1 \upharpoonright \beta} X \ {\sf IMC}(X,\beta). \end{align*} $$
Proof We prove by transfinite induction that
${\sf IMC} (X,\beta ) \wedge {\sf IMC} (Y,\beta ) \to X\equiv _\beta Y$
where X and Y are unbounded set variables. Note that this is an arithmetical formula so that
${\text {ACA}_0}$
can prove transfinite induction up to
$\alpha $
for this formula since we assumed
${\sf wo}(\alpha )$
.⊣
Now that we have uniqueness we proceed as in [Reference Fernández-Duque and Joosten18, Theorem 4.3] to observe in Theorem 7.3 that we actually may perform transfinite induction for second order formulas as long as the second order formulas are restricted to the
${\sf IMC}$
s. As in [Reference Fernández-Duque and Joosten18] by
${\boldsymbol {\Pi }^1_\omega }\upharpoonright \theta $
we denote the fragment
${\boldsymbol {\Pi }^1_\omega }$
of second order arithmetic where all second-order quantifiers are of the form
$\forall X\ (\theta (X)\rightarrow \phi )$
or
$\exists X \ (\theta (X)\wedge \phi )$
.
Theorem 7.3. Given a formula
$\theta (X)\in \boldsymbol {\Pi }^1_\omega $
,
$$ \begin{align*} {\mathrm{ACA}}_0\vdash \forall \Lambda \ \Big( \exists^{\leq 1} X\ \theta(X)\wedge{\tt wo}(\Lambda)\rightarrow {\tt TI}(\Lambda,{\boldsymbol{\Pi}^{1}_{\omega}}\upharpoonright \theta)\Big).\end{align*} $$
We are now ready to prove that our formalisation satisfies the required recursion.
Theorem 7.4. Let T be any presentable theory extending
${\text {ECA}_0}$
. We have
$$ \begin{align*} {\text{ACA}_0} &+ {\sf wo}(\beta) + \exists X 1{-}{\sf IMC}(X, \beta) \vdash \forall \, \alpha{\preceq}\beta \ \Big[ [\alpha]_T \varphi \ \leftrightarrow \ \Box_T \varphi \vee \exists \psi \, \exists \, \gamma\\ & \times \Big( \gamma \prec \alpha \wedge \ \langle\gamma\rangle_T \psi \, \wedge \Box_T\big( \langle\gamma\rangle_T \psi \, \to \, \varphi \big) \Big) \Big]. \end{align*} $$
Proof By transfinite induction on
$\alpha $
as in [Reference Fernández-Duque and Joosten18]. Note that we need the existence of a
$1{-}{\sf IMC}$
for the
$\to $
direction. By Theorem 7.3 we have access to the transfinite induction in
${\text {ACA}_0}$
since we proved uniqueness for
$1{-}\sf IMC$
’s.⊣
We refer the reader to [Reference Fernández-Duque and Joosten18, Lemma 6.6] from where we can conclude that adding the assertion of the existence of a one-Münchhausen class to T yields a theory that is equi-consistent with T. Of course, in stronger theories like
$\mathrm {ATR}_0$
we can simply prove the existence of a one-Münchhausen class up to
$\alpha $
for any well ordering
$\alpha $
.
8 Weakening the base theory: Münchhausen provability
In this paper we have introduced the notion of one-Münchhausen provability for which we have proven arithmetical sound and completeness. Furthermore, we have shown in Theorem 7.4 that the notion can be formalised in second order arithmetic. However, the theory where the formalisation takes place is quite strong. In particular, it requires a fair amount of transfinite induction. As pointed out, this proof theoretic strength is consequently also required in the object theory which is not desirable. Via various tricks, one can lower the required proof theoretic strength of the object and meta-theory. A first step in doing so is via the introduction of Münchhausen provability. Further tricks are presented and worked out in [Reference Joosten26].
To define Münchhausen provability we will start out with a very similar but slightly different recursion equivalence:
$$ \begin{align} &[\alpha]^{\boxtimes}_T \varphi \ \leftrightarrow \ \Box_T \varphi \vee \exists \sigma \, \exists \, \tau \ \Big( \ |\sigma | = |\tau | \ \wedge \ \forall \, i{<}| \tau |\, \tau_i {\prec}\alpha \ \wedge \ \forall \, i{<}| \sigma |\, \langle \tau_i \rangle^{\boxtimes}_T \sigma(i) \, \ \ \ \ \ \ \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\wedge \, \Box_T\big( \forall \, i{<}| \sigma |\, \langle \tau_i \rangle^{\boxtimes}_T \sigma(i) \, \to \, \varphi \big) \Big). \end{align} $$
In this recursive equivalence we understand that
$\sigma $
is a finite sequence of formulas with
$|\sigma |$
denoting the length of the sequence and
$\sigma (i)$
denoting the ith element of the sequence. Likewise,
$\tau $
is understood as being a sequence of ordinals all bounded by
$\alpha $
. We will write either
$\tau (i)$
or
$\tau _i$
for the ith element of
$\tau $
. Moreover,
$\langle \alpha \rangle ^{\boxtimes }$
is as always to be read a shorthand for
$\neg [\alpha ]^{\boxtimes } \neg $
.
One of the main complications in proving the arithmetical soundness of one-Münchhausen provability in the previous section was in the proof of the closure of provability under conjunctions, that is,
$[\alpha ] \varphi \wedge [\alpha ] \psi \leftrightarrow [\alpha ] (\varphi \wedge \psi )$
. The proof of this required a weak closure of consistency under conjunctions—
$\forall \varphi , \psi \, \exists \chi \Big ( \langle \alpha \rangle \varphi \wedge \langle \alpha \rangle \psi \leftrightarrow \langle \alpha \rangle \chi \Big )$
—so that the conjunction of two oracle sentences could be conceived as a single oracle sentence. However, in the new recursive equivalence as we just defined in (10), the closure of oracles under conjunctions is built into the definition.
A further complication in proving the arithmetical soundness of one-Münch-hausen provability in the previous sections was caused by the fact that weak closure under conjunctions of consistency needed to be verified under a box. This was obtained by requiring a fair amount of transfinite induction and by requiring that the object and meta-theory be equal. In this last section we shall see that these requirements can also be circumvented.
The defining equation (10) begs for a notational simplification. From now on, the Greek letter
$\sigma $
shall be reserved to denote sequences of formulas and the Greek letter
$\tau $
shall be reserved to denote sequences of ordinals. As such, we settle upon the notational convention that
$\tau \prec \alpha $
is short for
$\forall \, i{<}| \tau |\, \tau _i {\prec } \alpha $
and
$\langle \tau \rangle ^{\boxtimes }_T \sigma $
is short for
$|\sigma | = |\tau | \ \wedge \ \forall \, i{<}| \sigma |\, \langle \tau _i \rangle ^{\boxtimes }_T \sigma (i)$
. Since we shall require that provably
$|\sigma | = |\tau | \to \Box _T |\sigma | = |\tau |$
, the defining recursion can be recasted as
$$ \begin{align} [\alpha]^{\boxtimes}_T \varphi \ \leftrightarrow \ \Box_T \varphi \vee \exists \sigma \, \exists \, \tau{\prec}\alpha\ \Big(\langle \tau \rangle^{\boxtimes}_T \sigma \, \wedge \, \Box_T\big( \langle \tau \rangle^{\boxtimes}_T \sigma \, \to \, \varphi \big) \Big). \end{align} $$
Although we still cannot prove that different predicates that provably satisfy (11) are provably equivalent, at least proving soundness of
${\mathsf {GLP}}_\Lambda $
for such predicates becomes an easy matter. Let us first define some important notions as before but now for Münchhausen provability instead of one-Münchhausen provability.
Definition 8.1. Let us call a theory T a
$\Lambda $
-Münchhausen theory whenever we can define a predicate
${[\alpha ]^{\boxtimes }_T}^\Lambda $
so that T proves (11) together with
Moreover, it is understood that T has a simple coding machinery for finite sequence of objects so that the obvious facts about length and concatenation provably hold. For example,
$T \vdash |\tau | =n \to \Box _T |\tau | =n$
, etc.
In this case we call
${[\alpha ]^{\boxtimes }_T}^\Lambda $
a
$T(\Lambda )$
-Münchhausen provability predicate.
When the theory T and the ordinal
$\Lambda $
are clear from the context, we shall simply speak of a Münchhausen theory and of a Münchhausen provability predicate. On occasion we might only mention the ordinal
$\Lambda $
or only the theory T and speak of, for example, a
$\Lambda $
-Münchhausen theory and a T-Münchhausen provability predicate respectively. As with one-Münchhausen provability we see that the interaction axioms become trivial to prove for any Münchhausen provability predicate. In what follows we will revisit and simplify the soundness proof.
Lemma 8.2. Let T be a
$\Lambda $
-Münchhausen theory with corresponding predicate
${[\alpha ]^{\boxtimes }_T}^\Lambda $
. Omitting sub and superscripts, we have that
-
1.
$T\vdash \forall \alpha \, \forall \varphi \, \forall \, \beta {\prec } \alpha {\prec }\Lambda \ \big ( [\beta ]^{\boxtimes } \varphi \to [\alpha ]^{\boxtimes } \varphi \big )$
, -
2.
$T\vdash \forall \alpha \, \forall \varphi \, \forall \, \beta {\prec } \alpha {\prec }\Lambda \ \big ( \langle \beta \rangle ^{\boxtimes } \varphi \to [\alpha ]^{\boxtimes } \langle \beta \rangle ^{\boxtimes } \varphi \big )$
, and more in general -
3.
$T\vdash \forall \alpha \, \forall \sigma \, \forall \, \tau {\prec } \alpha {\prec }\Lambda \ \big ( \langle \tau \rangle ^{\boxtimes } \sigma \to [\alpha ]^{\boxtimes } \langle \tau \rangle ^{\boxtimes } \sigma \big )$
.
Proof The proof is straightforward and completely analogous to the proof of Lemma 5.3. Let us just shortly comment on the second item. So, we reason in T and pick a formula
$\varphi $
and ordinals
$\alpha $
and
$\beta $
as indicated, assuming
$\langle \beta \rangle ^{\boxtimes } \varphi $
. We now consider the sequence
$\sigma _\varphi $
of length 1 whose only element is the formula
$\varphi $
. Likewise, we consider the sequence
$\tau _\beta $
of length 1 whose only element is the ordinal
$\beta $
. Clearly,
$T \vdash \langle \tau _\beta \rangle ^{\boxtimes } \sigma _\varphi \to \langle \beta \rangle ^{\boxtimes } \varphi $
so that
$[\alpha ]^{\boxtimes } \langle \beta \rangle ^{\boxtimes } \varphi $
follows.⊣
Contrary to the case of 1-Münchhausen provability it becomes now an easy exercise to see that each (internally quantified) provability predicate satisfies the distribution axioms for the basic modal logic
${\textbf {K}}$
. Moreover, necessitation is also a routine matter. Before we prove this, we first need a technical easy lemma similar to Lemma 5.1 whose proof is immediate.
Lemma 8.3. Let T be a
$\Lambda $
-Münchhausen theory with corresponding predicate
${[\alpha ]^{\boxtimes }_T}^\Lambda $
. Again, omitting sub and superscripts, we have that
$$ \begin{align*} U\vdash \forall \, \alpha{\prec}\Lambda\, \forall\, \varphi, \psi, \chi\ \Big( \, [\alpha]^{\boxtimes} \psi \wedge \Box \varphi \wedge \Box (\varphi \wedge \psi \to \xi) \ \to \ [\alpha]^{\boxtimes} \xi \,\Big). \end{align*} $$
With this technical lemma at hand it becomes very easy to see that each Münchhausen provability predicate
${[\alpha ]^{\boxtimes }_T}^\Lambda $
defines a normalFootnote
8
modal logic.
Lemma 8.4. Let T be a
$\Lambda $
-Münchhausen theory with corresponding predicate
${[\alpha ]^{\boxtimes }_T}^\Lambda $
. Again, omitting sub and superscripts, we have that
-
1.
$T \vdash \forall \, \alpha {\prec }\Lambda \, \forall \varphi , \forall \psi \ \Big ( [\alpha ]^{\boxtimes } (\varphi \to \psi ) \ \to \ \big ( [\alpha ]^{\boxtimes } \varphi \to [\alpha ]^{\boxtimes } \psi \big ) \Big )$
, and -
2. for any ordinal
$\alpha $
below
$\Lambda $
, if
$T\vdash \varphi $
, then
$T\vdash [\alpha ]^{\boxtimes } \varphi $
.
Proof The proof of the second item is easy and identical to the proof Lemma 5.4. It is in the first item where we see that working with sequences of formulas instead of formulas in our oracles is essential. So, let us reason in T and fix
$\alpha $
and
$\varphi $
as stated. We assume
$[\alpha ]^{\boxtimes } (\varphi \to \psi )$
and
$ [\alpha ]^{\boxtimes } \varphi $
and need to prove
$[\alpha ]^{\boxtimes } \psi $
.
The case that both
$\Box (\varphi \to \psi )$
and
$\Box \varphi $
hold is trivial and in case one of them holds, Lemma 8.3 provides a proof.
So, in the remaining and only non-trivial case, we find two pairs of sequences
$\sigma _\varphi $
with
$\tau _\varphi $
and
$\sigma _{\varphi \to \psi }$
with
$\tau _{\varphi \to \psi }$
so that
$\tau _\varphi \prec \alpha \wedge \langle \tau _\varphi \rangle \sigma _\varphi \ \wedge \ \Box (\langle \tau _\varphi \rangle \sigma _\varphi \to \varphi )$
and also
$\tau _{\varphi \to \psi }\prec \alpha \wedge \langle \tau _{\varphi \to \psi } \rangle \sigma _{\varphi \to \psi } \ \wedge \ \Box \Big (\langle \tau _{\varphi \to \psi } \rangle \sigma _{\varphi \to \psi }\to ({\varphi \to \psi })\Big )$
. We now consider the concatenation
$\tau _\varphi \star \tau _{\varphi \to \psi }$
of both
$\tau $
-sequences and likewise
$\sigma _\varphi \star \sigma _{\varphi \to \psi }$
denotes the concatenation of both
$\sigma $
-sequences. Clearly, we have
$|\tau _\varphi \star \tau _{\varphi \to \psi }| = |\sigma _\varphi \star \sigma _{\varphi \to \psi }|$
and
$\tau _\varphi \star \tau _{\varphi \to \psi } \prec \alpha $
. Likewise, from our assumptions it is easy to observe that
$\langle \tau _\varphi \star \tau _{\varphi \to \psi }\rangle \sigma _\varphi \star \sigma _{\varphi \to \psi }$
and
$\Box \Big ( \langle \tau _\varphi \star \tau _{\varphi \to \psi }\rangle \sigma _\varphi \star \sigma _{\varphi \to \psi } \to \psi \Big )$
so that indeed
$[\alpha ]^{\boxtimes }\psi $
.⊣
As a consequence of our previous lemmas, we know that all reasoning of the modal logic
${\textbf {K}}$
can be applied to any Münchhausen provability predicate. We now turn to the transitivity axiom to conclude that each predicate
$[\alpha ]^{\boxtimes }$
actually is sound for
${\textbf {K4}}$
. Before proving this, we need one easy technical observation.
Lemma 8.5. Let T be a
$\Lambda $
-Münchhausen theory with corresponding predicate
$[\alpha ]^{\boxtimes }$
. We have that
$$ \begin{align*} T\vdash \exists x \ [\alpha]^{\boxtimes} \varphi (\dot x) \ \to \ [\alpha]^{\boxtimes} \exists x \, \varphi ( x). \end{align*} $$
Proof We reason in T and assume that for some x we gave
$[\alpha ]^{\boxtimes } \varphi (\dot x)$
. Thus, for some (possibly empty)
$\sigma $
and some ordinal
$\beta $
(less than
$\alpha $
in case
$\sigma $
is non-empty) we have
$\langle \alpha \rangle ^{\boxtimes } \sigma $
and
$\Box \big ( \langle \beta \rangle ^{\boxtimes } \sigma \to \varphi (\dot x)\big )$
whence also
$\Box \big ( \langle \beta \rangle ^{\boxtimes } \sigma \to \exists x \varphi ( x)\big )$
as was to be shown.⊣
We can now prove the soundness of the transitivity axiom.
Lemma 8.6. Let T be a
$\Lambda $
-Münchhausen theory with corresponding predicate
$[\alpha ]^{\boxtimes }$
. We have that
$$ \begin{align*} T\vdash \forall \, \alpha{\prec}\Lambda\, \forall\, \varphi\ \Big( \, [\alpha]^{\boxtimes} \varphi \ \to \ [\alpha]^{\boxtimes} [\alpha]^{\boxtimes} \varphi \,\Big). \end{align*} $$
Proof The proof is very similar to Item 4 of Theorem 5.9 but now, there is no need for induction since we already know our predicate to be sound for
${\textbf {K}}$
reasoning. Thus, we reason in T, fix some ordinal
$\alpha \prec \Lambda $
and formula
$\varphi $
, and assume
$[\alpha ]^{\boxtimes } \varphi $
. Now either
$\Box \varphi $
or there is some sequence of ordinals
$\tau \prec \alpha $
and sequence
$\sigma $
so that
$\langle \beta \rangle ^{\boxtimes } \sigma $
and
$\Box \Big ( \langle \beta \rangle ^{\boxtimes } \sigma \to \varphi \Big )$
. In the first case, we get from
$\Box \varphi $
that
$\Box \Box \varphi $
whence by applying monotonicity twice that
$[\alpha ]^{\boxtimes } [\alpha ]^{\boxtimes } \varphi $
. Thus we focus on the second case and fix a particular sequences
$\tau $
and
$\sigma $
so that
-
1.
$\tau \prec \alpha $
; -
2.
$\langle \tau \rangle ^{\boxtimes } \sigma $
; -
3.
$\Box \Big ( \langle \tau \rangle ^{\boxtimes } \sigma \to \varphi \Big )$
.
From the first item, we get by assumptions on Münchhausen theories that
$[\alpha ]^{\boxtimes } (\tau \prec \alpha )$
. From the second item we get by negative introspection that
$[\alpha ]^{\boxtimes } \langle \tau \rangle ^{\boxtimes } \sigma $
. From the third item we get
$\Box \Box \Big ( \langle \tau \rangle ^{\boxtimes } \sigma \to \varphi \Big )$
whence
$[\alpha ]^{\boxtimes } \Box \Big ( \langle \tau \rangle ^{\boxtimes } \sigma \to \varphi \Big )$
. Collecting these three consequences and applying provable closure of provability under conjunctions we obtain
$$ \begin{align*} \exists \sigma \exists \tau \ [\alpha]^{\boxtimes} \Big( \tau{\prec}\alpha \, \wedge \, \langle \tau \rangle^{\boxtimes} \sigma \, \wedge \, \Box \big( \langle \tau \rangle^{\boxtimes} \sigma \to \varphi \big)\Big), \end{align*} $$
so that by Lemma 8.5 we conclude
$$ \begin{align*} [\alpha]^{\boxtimes} \exists \sigma \, \exists \tau{\prec}\alpha \, \ \Big( \langle \tau \rangle^{\boxtimes} \sigma \, \wedge \, \Box \big( \langle \tau \rangle^{\boxtimes} \sigma \to \varphi \big)\Big), \end{align*} $$
which implies
$[\alpha ]^{\boxtimes } [\alpha ]^{\boxtimes } \varphi $
as was to be shown.⊣
In the light of Lemma 5.5 we may now conclude arithmetical soundness for
${\mathsf {GLP}}_\Lambda $
for Münchhausen provability.
Theorem 8.7. Let T be a
$\Lambda $
-Münchhausen theory and let
$[\alpha ]^{\boxtimes }_T$
be a corresponding Münchhausen provability predicate. Then,
${\mathsf {GLP}}_\Lambda $
is sound for T when the
$[\alpha ]$
-modalities
$(\alpha \prec \Lambda )$
are interpreted as
$[\alpha ]^{\boxtimes }_T$
.
Proof As always we prove by induction on a
${\mathsf {GLP}}_\Lambda $
proof that if
${\mathsf {GLP}}_\Lambda \vdash \varphi $
, then for any arithmetical realization
$*$
we have that
$T \vdash \varphi ^*$
.⊣
It is clear how the completeness proof and formalisation can be adapted to the new provability notion. Actually, it seems that in a sense Münchhausen provability is more fundamental than one-Münchhausen provability. We have chosen to start this paper with one-Münchhausen provability instead for two reasons. Firstly, the defining recursion for one-Münchhausen provability is slightly easier and more perspicuous. But secondly, it is important to be aware of the tension between provable properties and provable provable properties in the notion of one-Münchhausen provability and how this tension can be mitigated via transfinite reflexive induction.
Acknowledgments
We would like to thank the anonymous referee for his report which contained various excellent suggestions to improve the presentation of the paper. More seriously, the referee spotted a genuine error in an earlier draft of this paper. Not only did the referee spot the error but also did he provide a suggestion on how to repair it. Indeed, we were able to repair the proof following the suggestions. Independently, the error was also pointed out to me by David Fernández Duque to whom I am most grateful for his patience to wait for this paper to come out. Further, I would like to thank Lev Beklemishev, Volodya Shavrukov, Albert Visser, and the attendants of my Seminari Cuc. I am grateful to Ana Borges for asking the right questions and suggesting improvements on notation.
